基于微流控芯片技术的微生物加固可视化研究

何想; 马国梁; 汪杨; 赵常; 刘汉龙; 楚剑; 肖杨

doi:10.11779/CJGE202006003

基于微流控芯片技术的微生物加固可视化研究 English Version

何想^{1, 2,},
马国梁^{1, 2},
汪杨^{1, 2},
赵常^{1, 2},
刘汉龙^{1, 2, 3},
楚剑⁴,
肖杨^{1, 2, 3, ,}

1.
重庆大学土木工程学院,重庆　400045
2.
重庆大学山地城镇建设与新技术教育部重点实验室,重庆　400045
3.
库区环境地质灾害防治国家地方联合工程研究中心（重庆）,重庆　400045
4.
南洋理工大学土木与环境工程学院,新加坡　639789

基金项目:

国家自然科学基金项目 51922024

国家自然科学基金项目 41831282

重庆市研究生科研创新项目 CYB18035

中央高校基本科研业务经费 2019CDQYTM031

详细信息

作者简介:
何想(1992—),男,博士研究生,主要从事微生物土加固机理方面的研究。E-mail: medihe@163.com

通讯作者:
肖杨, E-mail: hhuxyanson@163.com

中图分类号: TU43
计量
- 文章访问数: 627
- HTML全文浏览量: 29
- PDF下载量: 257
出版历程
- 收稿日期: 2019-11-03
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-05-31

Visualization investigation of bio-cementation process based on microfluidics

HE Xiang^{1, 2,},
MA Guo-liang^{1, 2},
WANG Yang^{1, 2},
ZHAO Chang^{1, 2},
LIU Han-long^{1, 2, 3},
CHU Jian⁴,
XIAO Yang^{1, 2, 3, ,}

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400045, China
3.
National Joint Engineering Research Center of Geohazards Prevention in the Reservoir Areas (Chongqing), Chongqing 400045, China
4.
School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

摘要

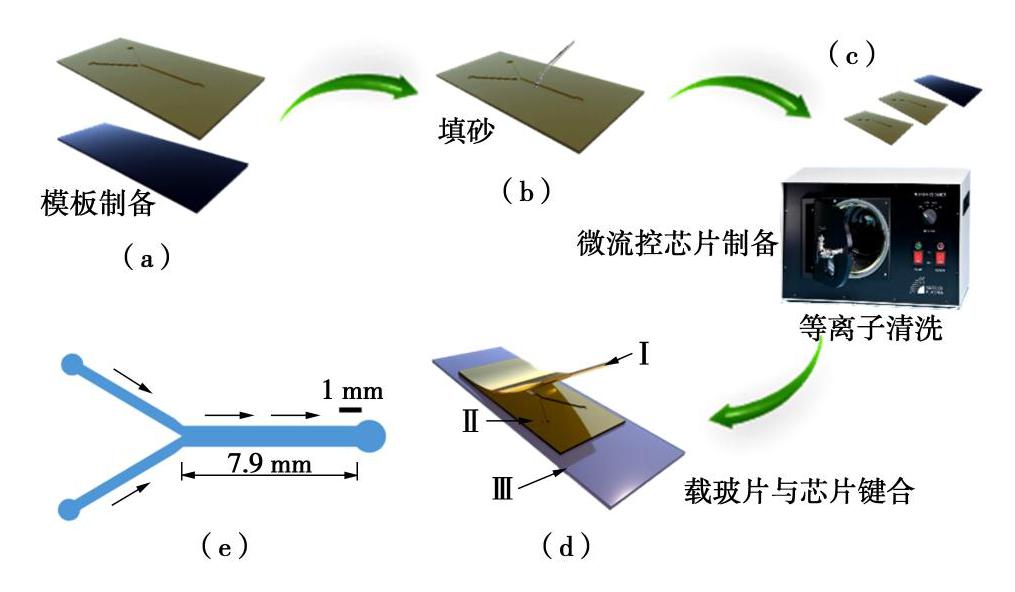
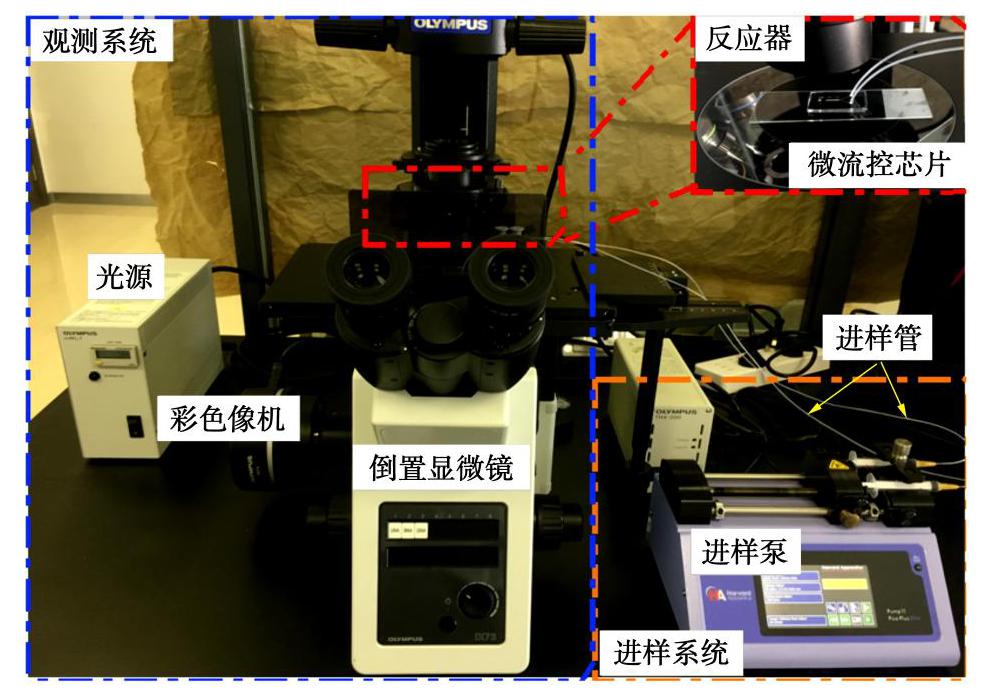
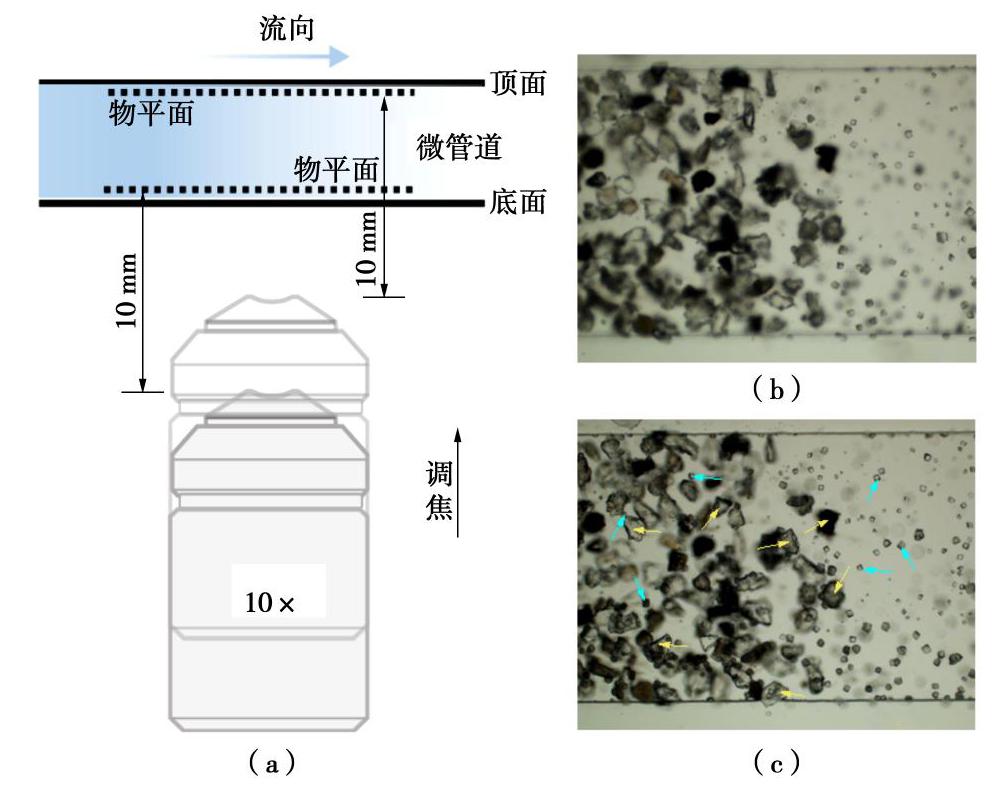
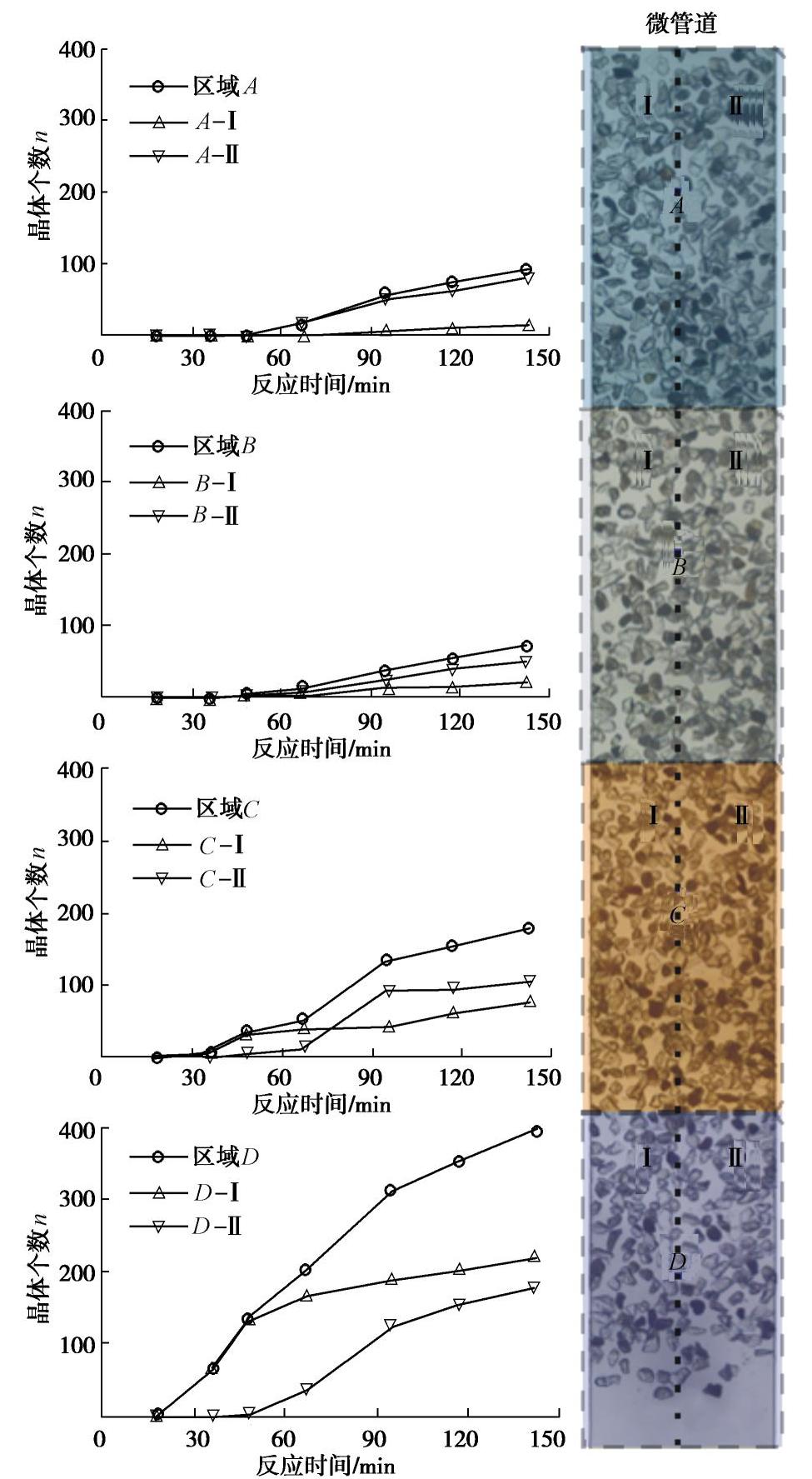
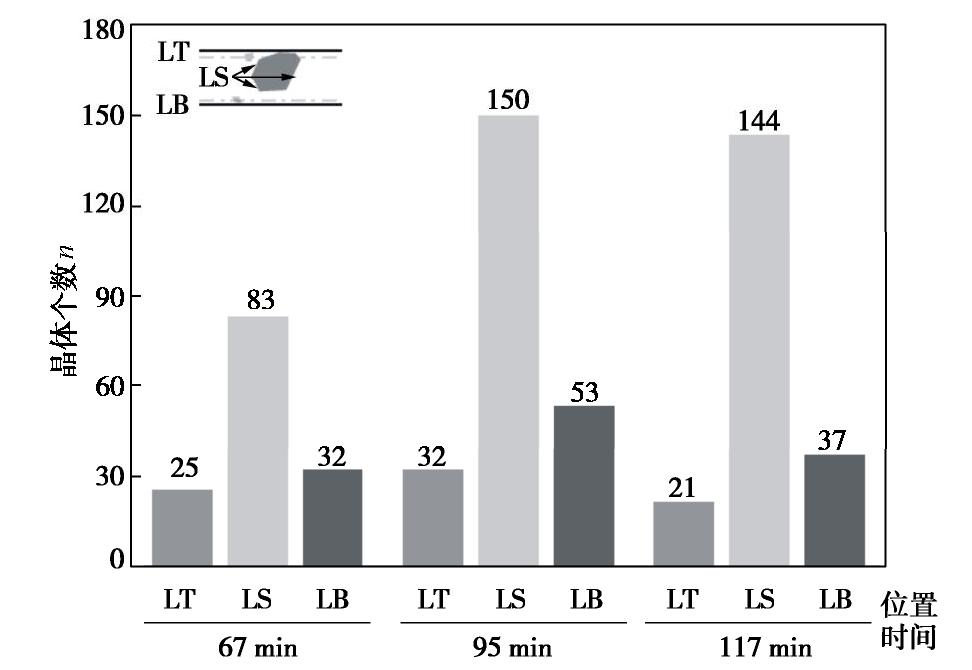
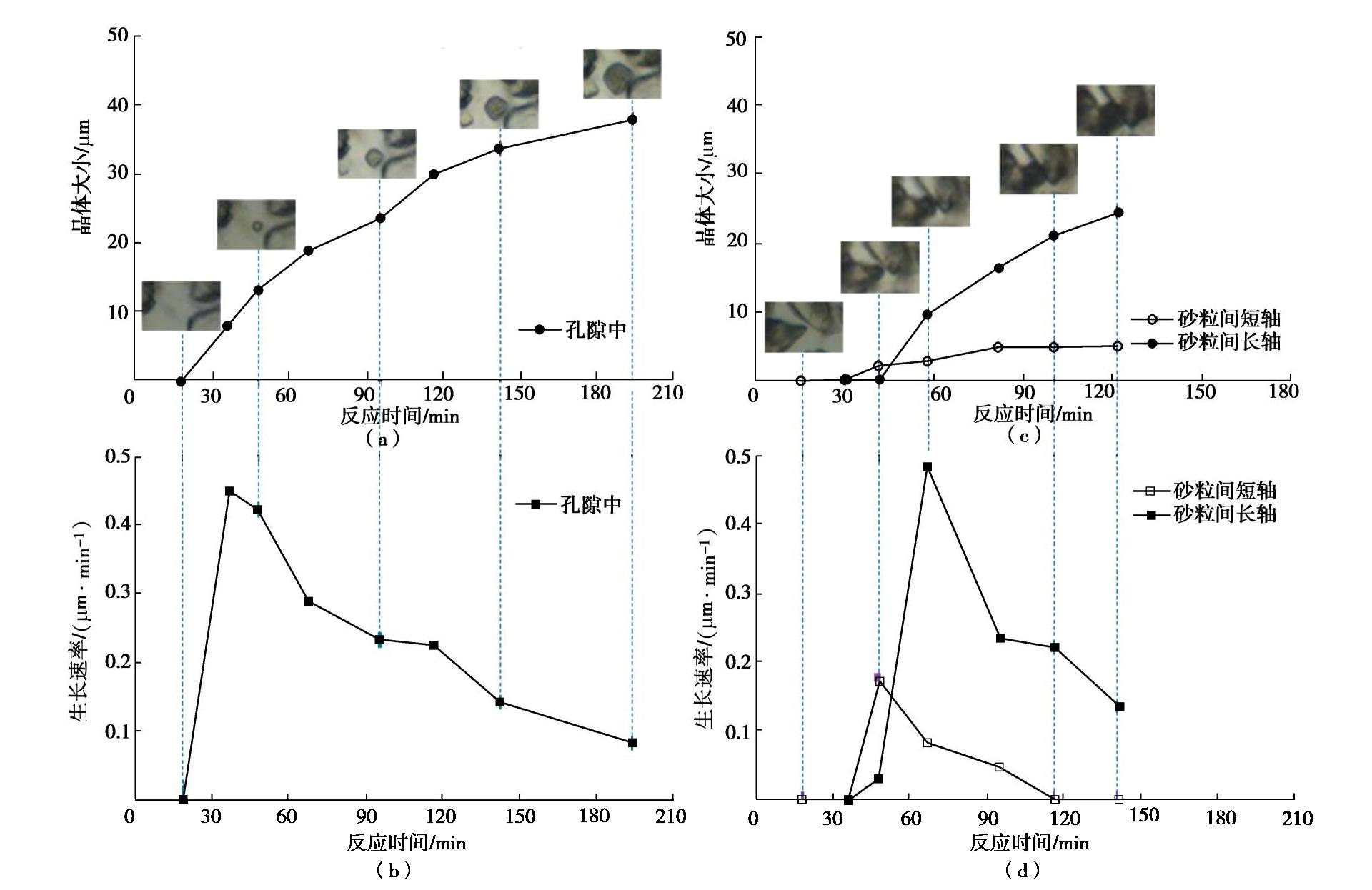
摘要: 微生物诱导碳酸钙沉积（MICP）能够加固散粒土体,是岩土工程中新兴绿色加固技术之一。然而,关于微生物加固机理以及矿化形成过程的研究尚不多见。基于微流控芯片技术开发了微生物加固可视化系统,利用该系统开展了微生物诱导碳酸钙矿化机理的原位微细观研究,通过对微生物加固过程中碳酸钙晶体的沉积进行了观测,并对其时空分布、沉积模式、生长速率进行了量化。结果表明溶质分子的对流和扩散作用对碳酸钙晶体分布影响较大,碳酸钙的分布存在时间不均匀和空间不均匀现象,时间不均匀随反应进行呈现弱化现象而空间不均匀在整个反应过程（0～2200 min）中一直存在。研究发现微尺寸管道中碳酸钙存在孔隙中和颗粒间两种沉积模式,孔隙中的碳酸钙均匀长大,而颗粒间碳酸钙存在不同速率的生长轴。研究结果将加深对微生物加固机理的认识,为微生物加固技术的优化和推广应用提供参考。
- 微生物矿化 /
- 微流控芯片 /
- 可视化 /
- 结晶 /
- MICP
Abstract: Biomineralization possesses the capability to bind granular materials, which can be used in the applications of geotechnical engineering as an emerging green ground improvement technology. However, little information is available on the mechanics of biomineralization, especially on the process of biocementation. An optical platform is proposed to visualize the process of biomineralization based on microfluidics. A series of micro-scale investigations related to this process are performed to capture the spatial distribution of calcium carbonate crystals, precipitation patterns and quantitative crystal growth rate. The results show that the convection and diffusion of solvent have significant impacts on the distribution of calcium carbonate, which demonstrates a nonuniform spatiotemporal distribution. The extent of uneven distribution in time scale is reduced as the reaction goes on. However, the phenomenon of uneven distribution in spatial scale is maintained during the whole reaction period (0~2200 min). Two precipitation patterns in biocementation are found in this study, i.e., precipitation at pore and precipitation at sand contacts. The precipitation at pore shows no growth axis, while the precipitation at sand contacts shows growth axis with different growth rates. These investigations may provide new insights into the mechanisms of microbial induced carbonate precipitation and are beneficial for the optimized design of up-scale application.
- biomineralization /
- microfluidics /
- visualization /
- crystallization /
- MICP

HTML全文

0. 引言

随着深部煤炭资源开采的日益发展,深部高瓦斯矿井的开采与治理作为深部科学难题之一^[1],一直是煤炭领域的研究热点。为了高效安全开采,大部分高瓦斯矿井形成工作面后需要放置一段时间,进行瓦斯治理。由于深部煤岩与瓦斯的赋存环境趋于一种高地应力、高地温、高渗透压^[2]的状态,煤体会随着时间的延长发生缓慢的蠕变,影响煤体自身的渗透能力,进而影响瓦斯的治理效果。因此,研究深部强时效下的多场耦合理论^[3]特别是深部煤体蠕变和渗流间的耦合机理具有重要理论和工程意义。

国内外学者针对煤岩体的渗透率模型、蠕变现象分别进行了深入研究。Palmer等^[4]考虑了孔隙压力和基质膨胀收缩对裂隙的孔隙率演化影响,提出了一个基于单轴应变和恒定垂向应力假设的渗透率模型。Shi等^[5]提出的渗透率模型考虑了吸附解吸引起的煤体变形,并提出了考虑水平有效应力的渗透率模型。Cui等^[6]使用线弹性多孔弹性介质理论,考虑吸附解吸效应推导出了与平均有效应力有关的渗透率模型。荣腾龙等^[7]在弹性理论的基础上分析了煤体基质和裂隙变形对渗透率的影响,以火柴棍模型为几何原型,突破传统单轴应变假设,建立了三向应力条件下煤体渗透率演化模型。周宏伟等^[8]从分数阶导数出发,在常黏性系数Abel黏壶基础上提出了一种新的变黏性系数的Abel黏壶元件。利用两种分数阶Abel黏壶代替经典西原模型中Newton黏壶的方法,建立了基于分数阶导数的盐岩流变本构模型,并给出了该模型的解析解,较好地反映了盐岩流变的三阶段尤其是加速流变阶段。尹光志等^[9]对煤层顶底板岩层试件进行卸围压蠕变及周期加载蠕变试验,并采用Burgers体模型对采动影响下的岩体进行蠕变理论分析,建立了采动下煤岩蠕变损伤模型,较好地反映岩体蠕变曲线特征。齐亚静等^[10]通过在西元模型上串联一个带应变触发的非线性黏壶,改进了西元模型并推广到三维蠕变本构方程,利用红砂岩流变试验获得了模型参数,发现在描述岩石的流变规律方面明显优于传统的西元模型。王路军等^[11]基于一维分数阶导数流变模型,推导出包含体积蠕变的煤体三维应力条件下非线性蠕变本构方程,并利用卸围压蠕变试验数据对蠕变本构方程的参数进行拟合,结果表明蠕变本构方程能很好地描述煤体蠕变三阶段,特别是加速阶段,最后对本构方程中关键参数进行了敏感性分析。

上述理论研究对揭示煤体蠕变和渗流间的耦合机理起到了至关重要的作用,而前人同样从试验角度对蠕变–渗流耦合机理进行深入研究。尹光志等^[12]运用自制的含瓦斯煤三轴蠕变加载渗流试验系统,进行了含瓦斯煤卸围压蠕变与渗流试验研究,改进了Chaboche黏塑性本构模型,进而用来描述含瓦斯煤的卸压短期蠕变破坏。通过试验又得到了考虑Klinkenberg效应的卸围压过程中瓦斯流量的变化规律、视渗透率和滑脱系数。蔡婷婷等^[13]研究了不同温度和应力下煤体蠕变中的渗流规律,得出不同温度下贫煤分级蠕变过程中体积变形基本经历压密硬化、体积压缩的蠕变变形和体积膨胀的蠕变变形3个阶段,渗透率表现为先逐渐降低再增加的趋势。江宗斌等^[14]进行了循环加卸载条件下岩石蠕变–渗流耦合试验,得出渗透率随着加载次数的增加先降低后逐渐增大,体积应变随着加载次数的增加呈非线性减小的趋势。何峰等^[15]基于煤岩瞬态渗透法,对煤岩试件进行蠕变–渗流耦合试验,得出在初始蠕变变形阶段,渗透率逐渐减小；在非线性变形阶段,当应变增加的时候,渗透率曲线变缓,并开始缓慢增加,失稳破坏后出现大的阶跃。曹亚军等^[16]采用分级加载方式,开展不同围压和渗压作用下渗流–应力耦合三轴流变试验得出岩石在较低应力水平作用下渗透率变化基本保持稳定趋势,而在破坏应力蠕变加速阶段,渗透率会发生明显的加速增长现象的规律。

相关学者以前人在渗透率模型、蠕变本构方程、蠕变–渗流试验方面^[17-18]的研究成果为基础,建立了考虑蠕变影响的相应理论模型。Danesh等^[19]以一维西原蠕变本构方程为基础,建立了考虑蠕变和吸附解吸影响的渗透率模型,并分析和对比了在煤层气抽采过程中考虑蠕变影响的渗透率演化情况。考虑到煤层气领域通常以单轴应变假设为基础进行建立渗透率模型,无法描述深部煤矿开采过程中渗透率演化情况。本文以深部煤层三向应力状态为出发点,结合考虑体积蠕变的煤体三维蠕变本构方程^[11],建立了考虑蠕变影响的深部煤体分数阶渗透率模型,同时利用常规三轴蠕变-渗流试验数据对模型进行了验证,并对模型的适用性和参数敏感性进行了分析。

1. 深部煤体分数阶三维蠕变本构方程

在三向应力条件下,煤体作为一种典型的黏弹塑性体,其受力状态可分解为球应力与偏应力共同作用,王路军等^[11]对偏应力引起的蠕变变形与球应力引起的体积蠕变进行了推导,将一维分数阶蠕变本构方程推广到三维分数阶蠕变本构方程。为了能够体现分数阶在蠕变过程中的作用,本文从偏应力和球应力两个角度分别详细介绍了对应的蠕变本构方程。

如图1所示的蠕变模型,假设煤体为各向同性材料,泊松比不随蠕变过程而变化,偏应力作用下三维蠕变方程为

$ε_{i j} (t) = \frac{s_{i j}}{2 G_{0}} + \frac{s_{i j}}{2 G_{1}} - \frac{s_{i j}}{2 G_{1}} E_{γ, 1} [- G_{1} \frac{t^{γ}}{η_{1}^{γ}}] (F < 0)$ ,

(1a)

$\begin{matrix} ε_{i j} (t) = \frac{s_{i j}}{2 G_{0}} + \frac{s_{i j}}{2 G_{1}} - \frac{s_{i j}}{2 G_{1}} E_{γ, 1} [- G_{1} \frac{t^{γ}}{η_{1}^{γ}}] + \\ (\frac{F}{F_{0}}) \frac{\partial F}{\partial σ_{i j}} \frac{t^{γ}}{2 η_{2}^{γ}} E_{1, 1 + γ} (α_{0} t) (F \geq 0) \end{matrix}$ 。

(1b)

图 1 偏应力下煤体分数阶蠕变模型

Figure 1. Fractional creep model for coal under deviatoric stress

下载: 全尺寸图片幻灯片

式中 S_ij为应力偏张量； $G_{0}$ 为剪切模量；G₁为黏弹性剪切模量； $γ$ 为分数阶导数； $η_{1}^{γ}$ 为黏弹性黏滞系数； $η_{2}^{γ}$ 为黏塑性黏滞系数；F为岩石屈服函数；F₀为岩石屈服函数初始参考值；α₀为与煤体性质相关的系数。

屈服函数取如下形式^[10]：

$F = \sqrt{J_{2}} - σ_{s} / \sqrt{3}$ ,

(2)

式中,J₂为应力偏量第二不变量。

如图2所示的蠕变模型,可以得到在球应力作用的煤体三维蠕变方程：

$ε_{v} (t) = \frac{σ_{m}}{K_{0}} + \frac{σ_{m}}{K_{1}} - \frac{σ_{m}}{K_{1}} E_{γ_{v}, 1} [- K_{1} \frac{t^{γ_{v}}}{η_{v 1}^{γ_{v}}}] (F < 0)$ ,

(3a)

$\begin{matrix} ε_{v} (t) = \frac{σ_{m}}{K_{0}} + \frac{σ_{m}}{K_{1}} - \frac{σ_{m}}{K_{1}} E_{γ_{v}, 1} [- K_{1} \frac{t^{γ_{v}}}{η_{v 1}^{γ_{v}}}] + \\ \frac{σ_{1} - σ_{3} - σ_{s}}{2 η_{v 2}^{γ_{v}}} t^{γ_{v}} E_{1, 1 + γ_{v}} (α_{v} t) (F \geq 0) \end{matrix}$ ,

(3b)

图 2 球应力下煤体分数阶体积蠕变模型

Figure 2. Fractional volumetric creep model for coal under spherical stress

下载: 全尺寸图片幻灯片

式中, $K_{0}$ , $K_{1}$ 为体积模量,γ_v为体积蠕变的分数阶导数, $η_{v 1}^{γ_{v}}$ , $η_{v 2}^{γ_{v}}$ 为体积蠕变的黏滞系数, $α_{v}$ 为与煤体性质相关的系数。

通过结合偏应力与球应力对煤体蠕变的共同作用,并将式（2）代入式（1b）得到煤体三维分数阶蠕变本构方程,具体形式如下：

$\begin{array}{l} ε_{i j} (t) = (\frac{σ_{m}}{3 K_{0}} + \frac{σ_{m}}{3 K_{1}} - \frac{σ_{m}}{3 K_{1}} E_{γ_{v}, 1} [- K_{1} \frac{t^{γ_{v}}}{η_{v 1}^{γ_{v}}}]) δ_{i j} + \\ \frac{s_{i j}}{2 G_{0}} + \frac{s_{i j}}{2 G_{1}} - \frac{s_{i j}}{2 G_{1}} E_{γ, 1} [- G_{1} \frac{t^{γ}}{η_{1}^{γ}}] (F < 0) \end{array}$ ,

(4a)

(4b)

式中,δ_ij为Kronecker符号。

2. 考虑蠕变影响的分数阶渗透率模型

在实际高瓦斯矿井瓦斯治理过程中,工作面需要静置时间较长,含瓦斯煤体极易发生蠕变现象,如图3所示,因此本文尝试建立能描述煤体屈服前后蠕变–渗流过程的渗透率演化模型。由于工作面形成过程中巷道掘进扰动的影响,使得煤体处于不同的应力状态。当煤体处于低应力状态时,即 $F < 0$ 时,煤层内部只存在弹性及黏弹性蠕变过程；当煤体满足甚至超过屈服条件即 $F \geq 0$ 时,煤层内部不仅存在弹性及黏弹性蠕变过程,而且还会发生黏塑性蠕变过程。考虑到实际蠕变过程以屈服条件为界限的分段情况,本文提出的渗透率模型同样以屈服条件为界限进行分段考虑,分别建立了弹性及黏弹性蠕变阶段的渗透率模型和黏塑性蠕变阶段的渗透率模型,具体的建模假设和推导过程下文会依次叙述。

图 3 含瓦斯煤体蠕变过程示意图

Figure 3. Schematic diagram of creep process of gas-containing coal

下载: 全尺寸图片幻灯片

2.1 弹性及黏弹性蠕变阶段的渗透率模型

深部煤体较浅部显得更为致密,煤体内部存在孔隙及微裂隙,无明显贯穿裂隙。假设未达到屈服条件之前的煤层中的瓦斯渗流仅发生在煤体基质的孔隙内,不存在裂隙中瓦斯渗流的过程,如图3（b）所示,当 $F < 0$ 时,基质内的孔隙率变化程度直接影响到深部煤体的渗透情况。

为了准确描述未达到屈服条件煤体的渗透率演化过程,本文以Kozeny-Carman方程为出发点,推导弹性及黏弹性蠕变阶段的渗透率模型。

根据Kozeny-Carman方程^[20],渗透率可写为

$k = \frac{φ^{3}}{C {(1 - φ)}^{2} S^{2}}$ ,

(5)

式中,C为系数, $φ$ 为孔隙率,S为单位体积煤体的表面积。

假设煤体的初始孔隙度为

$φ_{0} = \frac{V_{P 0}}{V_{b 0}}$ ,

(6)

式中, $V_{P 0}$ 为煤体内部初始孔隙体积, $V_{b 0}$ 为煤体初始体积。

假设骨架变形和孔隙变形共同体现在孔隙体积的变化上,煤体在受压过程中孔隙度是动态变化的,孔隙度变为

$φ = \frac{(V_{P 0} - Δ V_{P}) / V_{b 0}}{(V_{b 0} - Δ V_{P}) / V_{b 0}} = \frac{φ_{0} - ε_{v}}{1 - ε_{v}}$ ,

(7)

式中, $φ_{0}$ 为初始孔隙率, $ε_{v}$ 为体应变, $Δ V_{P}$ 为孔隙体积变化量。

由式（7）可知,渗透率可表示为

$k = \frac{{(φ_{0} - ε_{v})}^{3}}{C (1 - ε_{v}) {(1 - φ_{0})}^{2} S^{2}}$ 。

(8)

煤体的初始渗透率为^[21]

$k_{0} = \frac{φ_{0}^{3}}{C {(1 - φ_{0})}^{2} S^{2}}$ ,

(9)

式中, $k_{0}$ 为初始渗透率。

结合式（8）,（9）可得到渗透率具体形式：

$k = \frac{k_{0}}{1 - ε_{v}} {(1 - \frac{ε_{v}}{φ_{0}})}^{3}$ 。

(10)

渗流过程中煤体受到外部载荷及孔隙压力共同作用,假设孔隙压力在煤体内均匀分布,则根据有效应力原理,实际作用于煤体有效应力可表示为

${σ^{'}}_{i j} = σ_{i j} - α p δ_{i j}$ ,

(11)

式中, ${σ^{'}}_{i j}$ 为有效应力, $α$ 为Biot系数,通常取 $α = 1$ ,p为孔隙压力。

将式（11）代入式（4）,可推导出考虑孔隙压力作用时的深部煤体三维蠕变本构方程：

$\begin{matrix} {ε^{'}}_{i j} (t) = [\frac{{σ^{'}}_{m}}{3 K_{0}} + \frac{{σ^{'}}_{m}}{3 K_{1}} - \frac{{σ^{'}}_{m}}{3 K_{1}} E_{γ_{v}, 1} (- K_{1} \frac{t^{γ_{v}}}{η_{v 1}^{γ_{v}}})] δ_{i j} + \\ \frac{{s^{'}}_{i j}}{2 G_{0}} + \frac{{s^{'}}_{i j}}{2 G_{1}} - \frac{{s^{'}}_{i j}}{2 G_{1}} E_{γ, 1} (- G_{1} \frac{t^{γ}}{η_{1}^{γ}}) (F < 0) \end{matrix}$ ,

(12a)

(12b)

通过式（10）可知体积应变对煤体的渗透率演化有较大影响^[21],由于考虑蠕变的体积应变与各方向应变存在如下关系：

${ε^{'}}_{v} (t) = {ε^{'}}_{x x} (t) + {ε^{'}}_{_{y y}} (t) + {ε^{'}}_{z z} (t)$ 。

(13)

将式（13）代入式（10）可得到弹性及黏弹性蠕变阶段的渗透率模型,具体形式如下：

$k = \frac{k_{0}}{1 - ε^{'} (t)} {(1 - \frac{{ε^{'}}_{v} (t)}{φ_{0}})}^{3}$ 。

(14)

2.2 黏塑性蠕变阶段的渗透率模型

煤体在达到屈服条件之后将会产生不可恢复的塑性变形和明显的贯穿裂隙,式（2）为屈服判别条件。如图3（b）所示,当 $F$ ≥ $0$ 时,煤层中瓦斯渗流过程不仅发生在基质孔隙内,还发生贯穿裂隙内。现假设黏塑性蠕变阶段含裂隙煤体渗透率的计算方程由基质渗透率和裂隙渗透率两部分组成,计算方程表达式如下：

$k_{total} = k_{m} + k_{f}$ ,

(15)

式中, $k_{total}$ 为屈服之后的总渗透率, $k_{m}$ 为基质渗透率,k_f为裂隙渗透率,假设在黏塑性阶段基质渗透率 $k_{m}$ 为满足屈服条件时的恒定渗透率数值,总渗透率 $k_{total}$ 的变化取决于裂隙渗透率k_f。

为了揭示深部煤体屈服之后的裂隙演化过程对渗透率的影响,本文将煤体简化为薄板进行分析^[7],具体过程如图4（a）所示, $e_{i}$ 为裂隙开度, $h_{i}$ 为裂隙间距, $σ_{x}$ 为x方向载荷, $σ_{y}$ 为y方向载荷, $σ_{z}$ 为z方向载荷。

图 4 含裂隙煤体示意图

Figure 4. Schematic diagram of fractured coal

下载: 全尺寸图片幻灯片

根据雷诺方程,煤体的裂隙渗透率k_f与裂隙开度的立方成正比,与裂隙间距成反比。假设所有裂隙沿z方向分布,则关于煤体裂隙渗透率的方程可写为^[22]

$k_{f} = \sum_{i = 1}^{n} k_{f i} = k_{f0} \exp (3 Δ ε_{x})$ ,

(16)

式中, $ε_{x}$ 为裂隙x方向应变, $k_{f0}$ 为初始渗透率。

若将平面薄板扩展到三维状态,如图4（b）所示,可得到同时考虑x和y两个方向裂隙变形影响的煤体在z方向的渗透率表达式为

$k_{f} = \sum_{i = 1}^{n} k_{f i} = k_{f0} \exp [3 (Δ ε_{x} + Δ ε_{y})]$ 。

(17)

假设煤体在x,y方向横观各向同性,可认为煤体在x,y方向的裂隙变形量相等,且屈服之后的裂隙变形由煤体黏塑性变形控制。假设x方向的煤体总变形量等于裂隙变形量与煤体基质变形量之和,则x方向裂隙应变增量为

$Δ ε_{x} = Δ ε_{t x} - Δ ε_{r x}$ ,

(18)

式中, $Δ ε_{t x}$ , $Δ ε_{r x}$ 分别为沿x方向煤体的应变增量、煤基质的应变增量。文献[23]中假设裂隙间距 $h_{i}$ 为常数,即可认为煤基质的应变增量 $Δ ε_{r x}$ =0。则式（18）可简化为

$\begin{array}{l} Δ ε_{x} = Δ ε_{t x}, \\ Δ ε_{t x} = {ε^{'}}_{i j} (t) - {ε^{'}}_{i j} (t_{1}), \end{array}}$

(19)

式中,煤体x方向应变增量 $Δ ε_{t x}$ 为屈服后与屈服点处的黏塑性应变差值,t₁为达到屈服条件的时间,且t₁时刻黏塑性应变为零,则通过式（12b）可知满足屈服条件煤体沿x方向的黏塑性应变增量：

$\begin{matrix} Δ ε_{x} = \frac{{σ^{'}}_{1} - {σ^{'}}_{3} - {σ^{'}}_{s}}{6 η_{v 2}^{γ_{v}}} t^{γ_{v}} E_{1, 1 + γ_{v}} (α_{v} t) + \\ \frac{{σ^{'}}_{1} - {σ^{'}}_{3} - {σ^{'}}_{s}}{6 η_{2}^{γ}} t^{γ} E_{1, 1 + γ} (α_{0} t) \end{matrix}$ 。

(20)

将式（20）代入式（17）,得到裂隙的渗透率模型,具体形式为

$\begin{matrix} k_{f} = k_{f0} \exp [\frac{{σ^{'}}_{1} - {σ^{'}}_{3} - {σ^{'}}_{s}}{3 η_{v 2}^{γ_{v}}} t^{γ_{v}} E_{1, 1 + γ_{v}} (α_{v} t) + \\ \frac{{σ^{'}}_{1} - {σ^{'}}_{3} - {σ^{'}}_{s}}{3 η_{2}^{γ}} t^{γ} E_{1, 1 + γ} (α_{0} t)] \end{matrix}$ 。

(21)

则将式（14）,（21）代入式（15）得到黏塑性蠕变阶段的渗透率模型：

$\begin{array}{l} k = \frac{k_{0}}{1 - {ε^{'}}_{v} (t_{1})} {(1 - \frac{{ε^{'}}_{v} (t_{1})}{φ_{0}})}^{3} + \\ k_{f 0} \exp (\frac{{σ^{'}}_{1} - {σ^{'}}_{3} - {σ^{'}}_{s}}{3 η_{v2}^{γ v}} t^{γ v} E_{1, 1 + γ v} (α_{v} t) + \\ \frac{{σ^{'}}_{1} - {σ^{'}}_{3} - {σ^{'}}_{s}}{3 η_{2}^{γ}} t^{γ} E_{1, 1 + γ} (α_{0} t)) \end{array}$ 。

(22)

3. 分数阶渗透率模型应用分析

3.1 渗透率模型有效性验证

为了验证本文模型的有效性,选取李祥春等^[23]所做的常规三轴应力状态下含瓦斯煤蠕变–渗流试验结果进行了对比分析。采用分级加载的方法分级加载轴压,进行了瓦斯压力为0.13 MPa下型煤煤样的蠕变–渗流试验。试验过程保持围压恒为2 MPa,轴压为6,9,12 MPa依次加载,煤样发生稳定蠕变时每级轴压加载至少12 h,以避免稳定蠕变时间过短。

根据试验分级加载结果,对式（14）,（22）应用非线性最小二乘法,则可以确定渗透率模型的各参数：K₀=68.28 GPa,K₁=0.62 GPa, $η_{v1}^{γ_{v}}$ =18.58 $GPa \cdot h^{γ}$ , $γ_{v}$ = 0.6, $φ_{0}$ =0.027,k_f0=0.0002 mD, $α_{0} =$ 0.83/h^-1, $α_{v}$ = 0.83/h^-1, $η_{v 2}^{γ_{v}}$ =10.96 $GPa \cdot h^{γ}$ , $γ$ =0.6, $η_{2}^{γ}$ =10.96 $GPa \cdot h^{γ}$ 。

基于参数,利用式（14）,（22）可以给出蠕变煤体的渗透率演化规律,具体的变化趋势和数值结果如图5所示。

图 5 蠕变条件下的渗透率演化曲线

Figure 5. Evolution curves of permeability under creep

下载: 全尺寸图片幻灯片

当煤体所受应力小于煤体屈服强度时,煤样发生稳定蠕变。本文只考虑加载目标值（6,9 MPa）下的蠕变过程,不考虑轴压从0加载至6 MPa（或6 MPa加载至9 MPa）的中间过程。从图5（a）中可以看出煤样发生衰减蠕变,渗透率呈现小幅下降的趋势。由图5（a）可知,在瓦斯压力为0.13 MPa的情况下,第一级加载轴压为6 MPa的加载过程中,渗透率模型数值从0.046 mD将至0.037 mD,降幅为19.6%。第二级轴压加载为9 MPa时,渗透率模型数值从0.033 mD降至0.026 mD,降幅为21.2%。

当煤体所受应力大于煤体屈服强度时,煤样极易发生非稳定蠕变。如图5（b）所示,轴压加载为12 MPa时,煤体由稳态蠕变阶段进入加速蠕变阶段,相应的渗透率模型数值从0.030 mD升至0.042 mD,增幅为40.0%。

由图5中模型计算结果和实际试验数据对比分析可知,针对不同加载应力水平的蠕变–渗流试验,煤体在弹性及黏弹性蠕变阶段、黏塑性蠕变阶段的蠕变–渗流演化规律基本可以用本文提出的渗透率模型表征。渗透率模型不但可以表征在低应力作用下内部的孔隙逐渐被压密及渗透率逐渐减小的过程,同样能体现加速蠕变阶段产生明显裂隙及渗透率突增的过程。

3.2 不同试验条件下的渗透率模型分析

为了分析不同瓦斯压力情况下蠕变–渗流过程中的渗透率演化情况,利用本文提出的渗透率模型对屈服前后渗透率演化情况进行了模拟。参照3.1节的试验方案及参数拟合结果,将具体参数分别代入式（14）,（22）,保持轴压为6 MPa,围压2 MPa不变,仅改变瓦斯压力水平,取瓦斯压力分别为0.2,0.5,0.8,1.0 MPa,即可得到屈服前后不同瓦斯压力水平的渗透率变化曲线,如图6所示。

图 6 不同瓦斯压力下的渗透率演化曲线

Figure 6. Evolution curves of permeability under different gas pressures

下载: 全尺寸图片幻灯片

瓦斯压力对蠕变–渗流过程中渗透率的影响可分为屈服前后两部分考虑。在弹性及黏弹性蠕变阶段,随着蠕变的时间的增长,不同的瓦斯压力水平所对应的渗透率都呈现降低趋势,当瓦斯压力为0.2 MPa时,渗透率由0.046 mD下降至0.035 mD,降幅为24 %；当瓦斯压力为1.0 MPa时,渗透率由0.046 mD下降至0.038 mD,降幅为17.4%,瓦斯压力越大渗透率下降幅度越小。揭示了在恒定外部载荷作用下的煤体,瓦斯压力越大,有效应力越小,则基质内的孔隙度越大,导致渗透率下降幅度越小的物理过程。

在黏塑性蠕变阶段,当瓦斯压力为0.2 MPa时,渗透率由0.030 mD升至0.056 mD,增幅为46.4 %；瓦斯压力为1.0 MPa时,渗透率由0.030 mD升至0.56 mD,增幅已高出0.2 MPa时几个量级。瓦斯压力越大,越容易出现加速蠕变阶段即渗透率突增阶段,且突增幅度更大。该现象表明随着瓦斯压力的增大,裂隙的开度越来越大,发生渗透率突增的几率要比低瓦斯压力水平要高。

不同轴向载荷对蠕变–渗流过程中的渗透率演化同样存在较大影响,为了研究渗透率演化情况,结合渗透率模型及具体参数对屈服前后渗透率演化情况进行了模拟。保持围压2 MPa,瓦斯压力0.2 MPa不变,仅改变轴向载荷水平,即可得到屈服前后不同轴向载荷水平的渗透率变化曲线,如图7所示。

图 7 不同轴压下的渗透率演化曲线

Figure 7. Evolution curves of permeability under different axial pressures

下载: 全尺寸图片幻灯片

轴向载荷水平对蠕变–渗流过程中渗透率的影响可分为屈服前后两部分考虑。在弹性及黏弹性蠕变阶段,取轴向载荷分别为2,6,10,12 MPa,如图7（a）所示,渗透率随着蠕变时间的增长而逐渐降低,当轴压为2 MPa时,渗透率由0.046 mD下降至0.039 mD,降幅为15.2%；当轴压为12 MPa时,渗透率由0.046 mD下降至0.028 mD,降幅为39.1%。随着轴向载荷的逐渐增大,渗透率下降幅度同样逐渐增大。该模拟结果体现了在恒定瓦斯压力作用下的煤体,随着外部载荷水平的增大,有效应力同样增大,则基质内的孔隙度减小,导致渗透率下降幅度增大的物理过程。

在黏塑性蠕变阶段,取轴向载荷分别为12,13,14,15 MPa,如图7（b）所示,渗透率随着蠕变时间的增长而逐渐升高,特别是在加速蠕变阶段渗透率会出现突增趋势。当轴压为12 MPa时,渗透率由初始0.030 mD增至0.032 mD；当轴压为15 MPa时,渗透率由初始0.030 mD增至0.31 mD,并且发生渗透率突增的时间较其他轴向载荷水平更早。表明黏塑性蠕变阶段的渗透率模型不仅能体现渗透率突增的过程,同样揭示了当煤体所受载荷超过屈服强度时,载荷越大越容易提前进入加速蠕变阶段的实际物理现象。

4. 渗透率模型参数敏感性分析

4.1 煤体参数 $α_{0}, α_{v}$ 的影响

通过式（22）可以发现黏塑性阶段的渗透率模型包括考虑损伤积累的变黏性系数的参数 $α_{0}, α_{v}$ ^[8],该参数与煤体力学性质有关,尤其是变形特性,本文假设参数 $α_{0} = α_{v}$ 。考虑到 $α_{0}$ 的影响,保持其他参数不变,仅改变 $α_{0}$ ,可得到黏塑性阶段渗透率演化曲线随 $α_{0}$ 的变化规律,如图8所示。图中 $α_{0}$ 均大于零,且随着 $α_{0}$ 的增加,加速蠕变阶段即渗透率突增阶段越容易出现。

图 8 不同

$α_{0}$ 下渗透率演化曲线

Figure 8. Evolution curves of permeability under different values of

$α_{0}$

下载: 全尺寸图片幻灯片

4.2 分数阶导数 $γ$ 的影响

在渗透率模型的有效性验证过程中发现分数阶导数 $γ$ 与体积蠕变分数阶导数 $γ_{v}$ 相等,故分析导数阶次的影响时均用 $γ$ 代表。保持其他参数不变,仅改变分数阶导数 $γ$ ,可得到不同 $γ$ 对应的一组渗透率变化曲线,如图9所示。

图 9 不同分数阶导数

$γ$ 的渗透率变化曲线

Figure 9. Evolution curves of permeability under different values of

$γ$

下载: 全尺寸图片幻灯片

通过图中渗透率曲线演化可知分数阶渗透率模型中渗透率数值大小十分依赖于分数阶导数。弹性及黏弹性蠕变阶段分数阶次越高,渗透率下降速率越快；黏塑性蠕变阶段分数阶次越高,渗透率突增趋势越缓慢,充分反映了分数阶导数在描述深部煤体在蠕变影响下渗透情况变化的灵活性。

5. 结论

本文通过结合考虑体积蠕变的分数阶三维蠕变本构方程、Kozeny-Carman方程、含裂隙煤体渗透率计算方程,建立了考虑蠕变影响的深部煤体分数阶渗透率模型,通过该模型的验证与分析,得出如下3点结论：

（1）弹性及黏弹性蠕变阶段渗透率模型呈现了煤体低应力蠕变阶段的渗透率演化趋势,揭示了体积蠕变对煤体渗透情况的影响。

（2）黏塑性蠕变阶段的渗透率模型能够充分表征屈服后渗透率的演化情况,特别是在加速蠕变过程中的渗透率突增阶段,与实际物理过程的渗透率演化趋势相符。

（3）对屈服前后的渗透率模型中的煤体性质参数 $α_{0}$ 和分数阶导数 $γ$ 进行了敏感性分析,发现随着 $α_{0}$ 数值的升高,加速蠕变阶段即渗透率突增阶段越容易出现。分数阶导数阶次越高,弹性及黏弹性蠕变阶段渗透率下降速率越快,黏塑性蠕变阶段渗透率突增趋势越缓慢。

图 1 微流控芯片制备示意图

Figure 1. Schematic images of fabrication process of microchip

下载: 全尺寸图片幻灯片

图 2 微流控系统示意图

Figure 2. Schematic images of microfluidics system

下载: 全尺寸图片幻灯片

图 3 显微拍摄示意图及图像

Figure 3. Schematic diagram of microscopy and digital photographs

下载: 全尺寸图片幻灯片

图 4 微生物矿化胶结砂颗粒时序图

Figure 4. Sequence photographs of cementation of sand particles over course of MICP experiment

下载: 全尺寸图片幻灯片

图 5 微管道中碳酸钙晶体随时间分布图

Figure 5. Spatial distribution of bulk crystals during different reaction periods in microchannel

下载: 全尺寸图片幻灯片

图 6 管道横截面不同位置处晶体分布图

Figure 6. Spatial distribution of bulk crystals at microchannel cross-section

下载: 全尺寸图片幻灯片

图 7 不同沉积模式下碳酸钙晶体的生长速率

Figure 7. Crystal growth rate of different precipitation patterns

下载: 全尺寸图片幻灯片

参考文献(25)

[1]	何稼, 楚剑, 刘汉龙, 等. 微生物岩土技术的研究进展[J]. 岩土工程学报, 2016, 38(4): 643-653. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604010.htm HE Jia, CHU Jian, LIU Han-long, et al. Research advances in biogeotechnologies[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 643-653. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604010.htm
[2]	刘汉龙, 肖鹏, 肖杨, 等. 微生物岩土技术及其应用研究新进展[J]. 土木与环境工程学报(中英文), 2019, 41(1): 1-14. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201901001.htm LIU Han-long, XIAO Peng, XIAO Yang, et al. State-of-the-art review of biogeotechnology and its engineering applications[J]. Journal of Civil and Environme- ntal Engineering, 2019, 41(1): 1-14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201901001.htm
[3]	WHIFFIN V S, VAN PAASSEN L A, HARKES M P. Microbial carbonate precipitation as a soil improvement technique[J]. Geomicrobiology Journal, 2007, 24(5): 417-423. doi: 10.1080/01490450701436505
[4]	DEJONG J T, SOGA K, KAVAZANJIAN E, et al. Biogeochemical processes and geotechnical applications: Progress, opportunities and challenges[J]. Geotechnique, 2013, 63(4): 287-301. doi: 10.1680/geot.SIP13.P.017
[5]	VAN PAASSEN L A, GHOSE R, VAN DER LINDEN T J M, et al. Quantifying biomediated ground improvement by ureolysis: large-scale biogrout experiment[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(12): 1721-1728. doi: 10.1061/(ASCE)GT.1943-5606.0000382
[6]	CUI M J, ZHENG J J, ZHANG R J, et al. Influence of cementation level on the strength behaviour of bio-cemented sand[J]. Acta Geotechnica, 2017, 12(5): 971-986. doi: 10.1007/s11440-017-0574-9
[7]	XIAO Y, WANG Y, DESAI C S, et al. Strength and deformation responses of biocemented sands using a temperature-controlled method[J]. International Journal of Geomechanics, 2019, 19(11): 04019120. doi: 10.1061/(ASCE)GM.1943-5622.0001497
[8]	崔明娟, 郑俊杰, 章荣军, 等. 化学处理方式对微生物固化砂土强度影响研究[J]. 岩土力学, 2015, 36(增刊1): 392-396. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S1068.htm CUI Ming-juan, ZHENG Jun-jie, ZHANG Rong-jun, et al. Study of effect of chemical treatment on strength of bio-cemented sand[J]. Rock and Soil Mechanics, 2015, 36(S1): 392-396. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S1068.htm
[9]	XIAO P, LIU H, STUEDLEIN A W, et al. Effect of relative density and biocementation on cyclic response of calcareous sand[J]. Canadian Geotechnical Journal, 2019, 56(12): 971-986.
[10]	XIAO Y, HE X, EVANS T M, et al. Unconfined compressive and splitting tensile strength of basalt fiber-reinforced biocemented sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(9): 04019048. doi: 10.1061/(ASCE)GT.1943-5606.0002108
[11]	彭劼, 温智力, 刘志明, 等. 微生物诱导碳酸钙沉积加固有机质黏土的试验研究[J]. 岩土工程学报, 2019, 41(4): 733-740. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904022.htm PENG Jie, WEN Zhi-li, LIU Zhi-ming, et al. Experimental research on MICP-treated organic clay[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 733-740. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904022.htm
[12]	XIAO Y, STUEDLEIN A W, RAN J Y, et al. Effect of particle shape on strength and stiffness of biocemented glass beads[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(11): 06019016. doi: 10.1061/(ASCE)GT.1943-5606.0002165
[13]	CHENG L, CORD-RUWISCH R, SHAHIN M A. Influence of key environmental conditions on microbially induced cementation for soil stabilization[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(1): 04016083. doi: 10.1061/(ASCE)GT.1943-5606.0001586
[14]	DEJONG J T, FRITZGES M, B, NüSSLEIN K. Microbially induced cementation to control sand response to undrained shear[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1381-1392.
[15]	TAGLIAFERRI F, WALLER J, ANDÒ E, et al. Observing strain localisation processes in bio-cemented sand using X-ray imaging[J]. Granular Matter, 2011, 13(3): 247-250.
[16]	DEJONG J T, MORTENSEN B M, MARTINEZ B C, et al. Bio-mediated soil improvement[J]. Ecological Engineering, 2010, 36(2): 197-210.
[17]	ZHANG W, JU Y, ZONG Y, et al. In situ real-time study on dynamics of microbially induced calcium carbonate precipitation at a single-cell level[J]. Environmental Science & Technology, 2018, 52(16): 9266-9276.
[18]	WHITESIDES G M. The origins and the future of microfluidics[J]. Nature, 2006, 442(7101): 368-373.
[19]	WANG Y, SOGA K, DEJONG J T, et al. A microfluidic chip and its use in characterising the particle-scale behaviour of microbial-induced calcium carbonate precipitation (MICP)[J]. Géotechnique, 2019, 69(12): 1086-1094.
[20]	ROSSY T, NADELL C D, PERSAT A. Cellular advective-diffusion drives the emergence of bacterial surface colonization patterns and heterogeneity[J]. Nature Communications, 2019, 10(1): 2471-2480.
[21]	CHILTON T H, COLBURN A P. Pressure drop in packed tubes[J]. Industrial and Engineering Chemistry, 1931, 23(8): 913-919.
[22]	HAYNES W M. CRC Handbook of Chemistry and Physics[M]. Boca Raton: CRC Press, 2014.
[23]	GOSTING L J, AKELEY D F. A study of the diffusion of urea in water at 25-degrees with the Gouy interference method[J]. Journal of the American Chemical Society, 1952, 74(8): 2058-2060.
[24]	ZENG Y, CAO J, WANG Z, et al. Formation of amorphous calcium carbonate and its transformation mechanism to crystalline CaCO₃ in laminar microfluidics[J]. Crystal Growth & Design, 2018, 18(3): 1710-1721.
[25]	MCDONALD J C, DUFFY D C, ANDERSON J R, et al. Fabrication of microfluidic systems in poly (dimethylsiloxane)[J]. Electrophoresis, 2000, 21(1): 27-40.

施引文献(24)

期刊类型引用(8)

1.	刘雪莹，俞缙，周先齐，姚玮，任崇鸿，蔡燕燕. 一种新的岩石各向异性蠕变-渗透率模型. 岩土工程学报. 2025(02): 275-283 . 本站查看
2.	郭建春，张涛，武玺，赵志红，李宗源，曾杰. 煤层气压裂水平井生产动态分析及其渗透率协同演化机制. 煤炭学报. 2025(01): 516-531 . 百度学术
3.	张磊丽，蔡婷婷，石磊，姜玉龙，夏瑾. 不同温度-围压-气体压力下煤体蠕变-渗流演化规律. 煤矿安全. 2024(03): 36-45 . 百度学术
4.	赵一博. 计算多孔介质流线迂曲度及其分形维数的新几何模型. 材料导报. 2024(S2): 282-286 . 百度学术
5.	李钊，倪冠华，杨威，温永瓒，王刚，刘震，王振洋. 不同冲击倾向性煤体孔隙结构及瓦斯吸附特征研究. 煤炭科学技术. 2024(S2): 56-70 . 百度学术
6.	张学博，王豪，杨明，王攀，韩林秀. 抽采钻孔失稳坍塌对瓦斯抽采的影响机制研究及应用. 煤炭学报. 2023(08): 3102-3115 . 百度学术
7.	王科文. 瓦斯抽采钻孔新型封孔工艺试验研究. 山东煤炭科技. 2023(09): 128-130 . 百度学术
8.	许江，饶豪魁，彭守建，陈奕安，陈灿灿，马天宇. 三轴应力条件下凝灰岩广义应力松弛流变模型的构建. 采矿与安全工程学报. 2023(06): 1264-1272 . 百度学术