Characteristic functions of regional soils: convergence
-
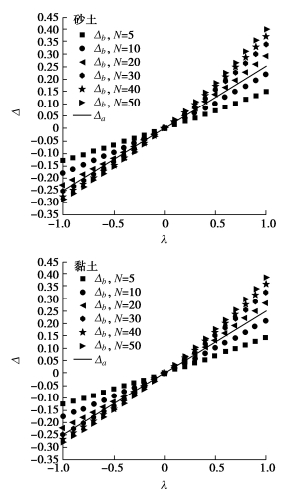
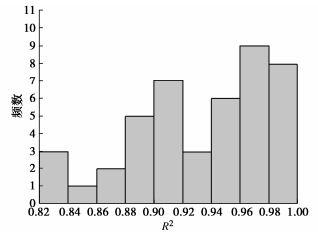
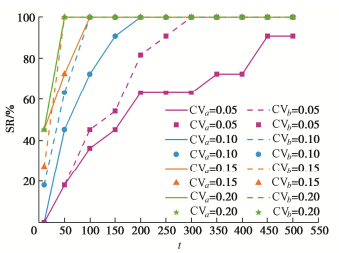
摘要: 无论从一个地区内建立N - vs关系曲线的工程应用角度还是作为区域土特征理论的必要组成部分，构建科学的N - vs函数所需的数组量都是重要问题，但以往研究为空白。采用实测数据的随机分析，研究不同样本数量下N - vs特征函数的稳定性和收敛性，并提出构建不同精度N - vs特征函数的数组阈值。实测数据来源于4个国家9个地区，共11个工况，对此分别进行随机分析的结果表明，随样本数量增加，N - vs特征函数具有稳定性与收敛性。研究表明，一个地区内取N - vs数组超过50，100，200和800，则可分别得到变异系数小于0.2，0.15，0.10和0.05的N-vs特征函数。Abstract: Whether from the perspective of engineering application of establishing N - vs relationship curve in a region or as an essential part of regional soil characteristic theory, the number of arrays required for constructing scientific N - vs function is an important problem, but this issue has not been involved before. The stability and convergence of N - vs characteristic functions under different sample numbers are studied by using the random analysis of measured data, and the array thresholds for constructing N - vs characteristic functions with different precisions are proposed. The measured data come from 9 regions in four countries, and there are 11 working conditions in total. The results of random analysis show that the N - vs characteristic function is stable and convergent with the increase of the number of samples. The research shows that if the N - vs array exceeds 50, 100, 200 and 800 in a region, the N - vs characteristic functions with coefficients of variation less than 0.2, 0.15, 0.10 and 0.05 can be obtained respectively.
-
0. 引言
颗粒材料广泛存在于自然界和工程界，具有复杂的力学特性[1-2]。受限于颗粒材料非连续性、离散性等特点，基于连续域网格离散的有限元（finite element method, FEM）、有限差分（finite difference method, FDM）等数值方法往往难以完全反映其宏观力学特性，更不能从细观层面解释其应力变形的内在机制。离散单元法（discrete element method, DEM）的出现弥补了FEM、FDM等方法的不足，为颗粒材料的数值研究提供了一种重要手段，因而被广泛应用于颗粒材料复杂运动[3]和力学特性[4]等方面的研究中。为了还原更加真实的颗粒特征，研究者们还在DEM方法中引入了复杂颗粒形状[5-6]和颗粒破碎[7-10]。相比于DEM方法，在其基础上发展的连续-离散耦合分析（combined finite-discrete element method, FDEM）方法在颗粒材料模拟方面则有着更天然的优势。FDEM方法不仅能通过接触计算再现颗粒材料的离散特性，还会对每个颗粒进行有限元网格离散，因而可以更自然地引入复杂形状和颗粒破碎[11-17]。
然而，无论是DEM方法还是FDEM方法，在进行大规模颗粒材料的数值模拟时，颗粒间的复杂接触计算都会带来巨大的计算开销，面临高昂计算成本的问题，亟需能够提高计算效率的手段。在最近的研究中，提升DEM或者FDEM数值计算效率的方法可以分为两类：①基于硬件的加速策略，如采用GPU并行的手段来加速FDEM方法的计算效率[18-19]，GPU包含大量的计算单元，通过并行计算能够提升FDEM方法的数值模拟效率；②基于计算方法的加速策略，如采用粗粒化方法来降低颗粒系统的计算规模，以加快DEM模拟速度[20-23]，粗粒化通过使用较少的大颗粒来替代大量的小颗粒，在保持颗粒材料离散属性的同时，能减少计算系统中的颗粒数量，从而降低计算规模，提升计算效率。
本文关注于第②种策略，将粗粒化的方法引入到FDEM方法的数值模拟中。在粗粒化方法中，大颗粒替代小颗粒会引起颗粒集合体接触关系的改变，因此需要对粗粒化模型的计算参数进行调整，使其能还原原始系统的宏观力学特性。一种直接的做法是通过细观参数标定的方式率定粗粒化参数，尽管这种方法能得到不错的模拟结果，但是缺乏理论指导和解释性，同时会增加参数标定的复杂度，提高参数标定的难度和成本。赵婷婷等[21]给出了一种更一般性的粗粒化参数取定方案，即通过引入精确缩尺准则来指导粗粒化参数的取值。精确缩尺理论具有严格的理论推导过程，通过建立原始系统和缩尺系统之间的比例关系，能够使缩尺系统还原原始系统的物理属性[21, 24-25]。
将这一思想引入到FDEM方法中，推导了采用基于罚函数线性接触模型FDEM方法的精确缩尺准则，并结合宏细观2个方面解释了该方法作用的内在机理，为加速FDEM方法用于颗粒材料数值模拟提供了一种解决方案。
1. 基本原理
1.1 FDEM方法基本理论
FDEM方法综合了FEM方法和DEM方法的特点，在颗粒与颗粒之间设置接触模型来计算接触力，在颗粒内部进行有限元网格离散来描述颗粒形态并计算颗粒变形[26]。
在进行接触力计算时，本文采用考虑阻尼力的线性接触模型[13-14]，同时，颗粒间接触服从库伦摩擦定律，即切向接触力Fs的最大值受限于法向接触力Fn和粒间摩擦系数μ，具体计算公式为
Fn=|knδn−fnvd|,Fs=min(|ksδs−fsvd|,μFn)。} (1) 式中：Fn，Fs分别为法向和切向的接触力；kn，ks分别为法向和切向的接触刚度；δn为接触面上法向的嵌入量；δs为接触面上切向的相对位移量；μ为粒间摩擦系数；fnvd，fsvd分别为法向和切向的阻尼力。
接触刚度通过罚函数定义，法向和切向接触刚度为
kc=pcA。 (2) 式中：kc为法向或切向的接触刚度；pc为相应方向的罚刚度；A为顶点接触的控制面积。
阻尼力依据阻尼力定律计算，即
fvd=2βc√mkcvr。 (3) 式中：fvd为法向或切向的阻尼力；βc为相应方向的阻尼系数；m为节点质量；kc为相应方向的接触刚度；vr为接触处相应方向上的相对滑动速度。
在进行颗粒变形计算时，本文采用各向同性线弹性模型，具体计算公式可表达为
dσij=λdεvδij+2Gdεij。 (4) 式中：dσij为应力增量的分量；dεv为体积应变增量；dεij为应变增量的分量；λ，G为拉梅系数，由弹性模量E和泊松比ν计算得到：
λ=Ev(1+v)(1−2v),G=E2(1+v)∘} (5) 1.2 精确缩尺和粗粒化
精确缩尺方法采用等比例放大的方式来处理大规模颗粒系统的计算问题[24-25]。该方法中，原始颗粒系统的计算区域和颗粒一起被放大到h倍，通过选取恰当的物理量建立精确缩尺准则，从而得到精确缩尺系统。在精确缩尺准则的约束下，精确缩尺系统能够较精确地再现原始颗粒系统的力学特性。
粗粒化方法采用等效替代的方式来处理大规模颗粒系统的计算效率问题[21]。该方法中，在不改变原始颗粒系统计算区域大小的前提下，将原始颗粒系统中的颗粒按照一定的特征长度缩放比尺h放大，达到用较少大颗粒替代大量小颗粒的目的。由于粗粒化后颗粒系统的计算规模显著降低，可以大幅度提升计算效率，但粗粒化系统中的颗粒数量等几何特征发生了明显的改变，在力学特性上往往和原始颗粒系统存在一定的偏差，需要进行参数的校正。
尽管精确缩尺和粗粒化是2种不同的方法，但是，分别由其建立的精确缩尺系统和粗粒化系统并非完全割裂。如图 1所示，精确缩尺系统和粗粒化系统均是对原始颗粒系统的放大，区别在于计算区域的大小和精确缩尺准则的引入。将精确缩尺系统中建立的精确缩尺准则引入到粗粒化系统中，则引入精确缩尺准则的粗粒化系统和精确缩尺系统互为局部与整体。
![]()
图 1 精确缩尺系统和粗粒化系统的关联性Figure 1. Relevance between exact scaling system and coarse-grained system图 2进一步阐述了引入精确缩尺准则的粗粒化系统及其与原始颗粒系统的关联性。对于一个近乎均质的原始颗粒系统，将其按照特定缩放比尺进行放大可以分别建立粗粒化系统和精确缩尺系统，粗粒化系统与原始颗粒系统力学特性存在差异，而精确缩尺系统与原始颗粒系统力学特性却基本一致。将精确缩尺系统中应满足的精确缩尺准则施加到粗粒化系统之后，可以建立引入精确缩尺准则的粗粒化系统，该系统可视为精确缩尺系统的一个局部区域。当原始颗粒系统足够均质时，由其建立的精确缩尺系统也是足够均质的，因而整体和局部具有相近的力学特性。以精确缩尺系统为桥梁，可以得出引入了精确缩尺准则的粗粒化系统能较精确地还原原始颗粒系统的宏观宏观力学特性的结论。然而，实际颗粒系统是各向异性的，局部特征和整体特征存在一定差异，因而引入精确缩尺准则的粗粒化系统表现出来的宏观力学特性仍会和精确缩尺系统存在偏差，但能够近似还原原始颗粒系统的宏观力学特性。
1.3 精确缩尺准则推导
依据量纲分析理论，若只考虑颗粒间的机械运动，则力学相关的物理量的量纲均能表示为国际标准单位制下的3个基本物理量量纲——长度[L]、时间[T]和质量[M]的组合，即对系统中任意力学相关的物理量q，其量纲[q]可表示为
[q]=[L]α[T]β[M]γ。 (6) 式中：α，β，γ分别为长度、时间、质量量纲的指数。
在精确缩尺系统中，可基于3个基本物理量的缩放比尺来确定该系统相对于原始颗粒系统完整的缩放法则。现假定精确缩尺系统和原始颗粒系统中3个基本物理量的缩放比尺分别为λL，λT，λM，则对原始颗粒系统中的任一物理量q及其精确缩尺系统中相对应的物理量ˉq，定义该物理量的缩放比尺为λq，即
ˉq=λqq。 (7) 将该物理量的量纲依照式（6）所示的形式进行展开，3个基本物理量量纲的指数表示为α，β，γ，则该物理量的缩放比尺与3个基本物理量的缩放比尺间应满足关系式为[25]
λq=λαL⋅λβT⋅λγM。 (8) 在精确缩尺中，通常采用密度比尺为1来替代质量比尺[21, 24-25]，考虑到密度量纲可由长度量纲[L]和质量量纲[M]进行表示，经过换算，可得到长度、时间、质量3个基本物理量的缩放比尺分别为
λL=h,λT=h,λM=h3。 (9) 式中：h为精确缩尺系统对原始颗粒系统的缩放比例。
为了确保精确缩尺系统和原始颗粒系统的可比性，需要建立各主要物理量之间的精确缩尺准则。采用前文述及的推导方式，可通过物理关系将目标物理量量纲表达为长度、时间、质量3个物理量量纲的幂积形式，例如，对于罚刚度pc，可通过接触刚度[kc]、接触面积量纲[A]逐步得到式（6）所示的格式：
[pc]=[kc][A]−1=[F][δc]−1[A]−1 =[M][a][δc]−1[A]−1=[L]−2[T]−2[M]。 (10) 进而由式（8），（9），计算得到力的缩放比尺为
λpc=λ−2L⋅λ−2T⋅λM=h−2⋅h−2⋅h3=h−1。 (11) 边界荷载、材料本构参数和接触模型参数中主要物理量的缩放比尺如表 1所示。
表 1 主要物理量的精确缩尺准则Table 1. Exact scaling criteria for major physical quantities物理量 符号 量纲 缩放比尺 长度 L [L] h 时间 T [T] h 质量 m [M] h3 力 F [L][T]−2[M] h2 应力 σ [L]−1[T]−2[M] 1 应变 ε [1] 1 弹性模量 E [L]−1[T]−2[M] 1 泊松比 ν [1] 1 罚刚度 pc [L]−2[T]−2[M] h−1 摩擦系数 μ [1] 1 阻尼系数 βc [1] 1 2. 数值试验验证
2.1 试验流程
为进一步论证基于精确缩尺和粗粒化的FDEM方法在颗粒材料数值模拟中的适用性，本文通过颗粒材料三轴剪切数值试验进行效果验证。如图 3所示，三轴剪切数值试验主要包含数值试样制备和固结剪切2个步骤。
首先进行数值试样制备，参照室内三轴剪切试验的试样尺寸，制备尺寸为ϕ300 mm×600 mm的圆柱形试样。如图 3所示，本文采用动力法进行制样[26]，即先在一个较高但与试验试样等径的刚性圆柱容器中生成指定总体积与粒径分布的随机颗粒得到疏松颗粒集合体试样，然后通过施加位移边界控制容器上下底面加载板将松散的颗粒集合体试样压缩为指定高度的密实集合体试样。
完成数值试样制备后，即可进行三轴剪切数值试验。如图 4所示，将圆柱容器侧面设置为允许发生大变形的柔性膜单元，上下底板设置为不能变形的刚体单元，下加载板施加完全约束，上加载板则通过位移边界控制加载。剪切试验分为2个荷载步：①用来模拟围压固结过程，即在上加载和侧膜上施加指定围压使试样固结；②模拟剪切过程，保持侧膜上的围压为不变，并给上加载板施加竖直向下的位移增量使试样发生变形，剪切过程中持续监测加载板的轴向力大小。
2.2 试验设计
为了降低试验的复杂性，不考虑颗粒形状、颗粒破碎等因素，采用较简单的等径颗粒系统和二元颗粒系统进行数值试验，2类颗粒系统的固相体积分数为65%。在等径颗粒系统中，设定原始颗粒系统中颗粒粒径为15 mm，将其分别按照h=2.0，h=3.0，h=4.0等3种缩放比尺建立粗粒化模型，得到颗粒粒径分别为30，45，60 mm的数值试样。在二元颗粒系统中，采用2种不同粒径的颗粒生成数值试样，2种粒径的颗粒质量比为1︰1，原始颗粒系统中颗粒粒径分别为15，30 mm，分别将其按照h=1.5和h=2.0的缩放比尺建立粗粒化模型，得到颗粒粒径为22.5~45，30~60 mm的二元颗粒系统数值试样。统计所制备颗粒试样的信息如表 2所示。
表 2 数值试样信息Table 2. Information of numerical samples类别 粒径/mm 颗粒数量 单元数 节点数 等径颗粒系统 15 15186 1214880 3113130 30 1898 151840 389090 45 562 44960 115210 60 237 18960 48585 二元颗粒系统 15~30 8543 683440 1751315 22.5~45 2532 202560 519060 30~60 1072 85760 219760 本文数值试验的目的在于研究精确缩尺准则和粗粒化方法对原始颗粒系统的力学响应以及计算效率的影响。为了对比是否引入精确缩尺准则引起的力学响应差异性，将粗粒化试样设置为引入精确缩尺准则的试验组和不引入精确缩尺准则的对照组，原始颗粒系统的参数设定如表 3所示。各组数值试验的设置情况如表 4所示。
表 3 原始颗粒系统材料和接触参数Table 3. Contact parameters of original particle system materials参数名称 参数值 单位 弹性模量 40 GPa 泊松比 0.2 — 罚刚度 1.8×1011 N/m3 罚刚度比 1 — 摩擦系数 0.3 — 阻尼系数 0.2 — 阻尼系数比 1 — 表 4 各组数值试验设置Table 4. Settings for each numerical test类别 编号 粒径/mm 缩放比尺h 是否引入精确缩尺准则 等径颗粒系统 E1 15 1.0 — E2 30 2.0 × E3 45 3.0 × E4 60 4.0 × E2s 30 2.0 √ E3s 45 3.0 √ E4s 60 4.0 √ 二元颗粒系统 B1 15~30 1.0 — B2 22.5~45 1.5 × B3 30~60 2.0 × B2s 22.5~45 1.5 √ B3s 30~60 2.0 √ 2.3 宏观应力变形响应
参照传统物理试验的处理方法，通过提取不同时刻试样高度H，试样体积V和上加载板上的轴向力Fl，分别计算各个时刻相应的轴向应变εl、体积应变εV和轴向应力σl。考虑到试样加载过程中发生了大变形，采用对数格式计算应变值，采用平均截面积计算轴向应力值[26]，即分别按照下式计算剪切过程中试样在不同时刻时的轴向应变εl、体积应变εV和轴向应力σl：
εl=∫HH0−dH′H′=−ln(HH0)， (12) εV=∫VV0−dV′V′=−ln(VV0)， (13) σl=FlA∗=FlV/H。 (14) 式中：H0，V0分别为初始时刻的试样高度和体积；H，V分别为计算时刻的试样高度和体积；Fl为计算时刻的轴向力值；A∗为计算时刻试样的平均截面积，由试样体积和高度给出。
根据三轴应力状态特点，按下式计算应力比η：
η=qp=σl−σ0(σl+2σ0)/3=3(σl−σ0)σl+2σ0。 (15) 采用上述方法计算各组数值试验在不同加载时刻的应力与应变，绘制等径颗粒系统的应力比曲线和体积应变曲线分别如图 5，6所示，绘制二元颗粒系统的应力比曲线和体积应变曲线分别如图 7，8所示。
从图 5~8中可以看出，无论是等径颗粒体系还是二元颗粒体系，在不引入精确缩尺准则的情况下，粗粒化系统和原始颗粒系统的宏观力学响应均存在较大的偏差，且这种偏差随着粗粒化缩放比尺的增大逐渐变大。具体表现为：随着粗粒化缩放比尺的增加，峰值应力比及应力比曲线初始切线模量均逐渐提高，峰值状态逐渐前移，但最终状态的残余应力比基本不改变，尤其是当缩放比尺达到4时，峰值应力比到残余应力比发生显著的降低，引起数值模拟结果失真；试样的剪缩能力减弱，剪胀能力显著增强，剪胀点前移。当引入精确缩尺准则后，粗粒化引起的宏观力学响应偏差均得到了效果显著的修正，相比于未引入精确缩尺准则的对照组，试验结果更接近于未进行粗粒化的原始颗粒系统。
因此，对等径颗粒系统和二元颗粒系统，纯粹的粗粒化系统与原始颗粒系统在力学特性上差异性明显，当缩放比尺较大时，甚至会引起数值模拟结果的失真，因此必须进行模型参数的修正以逼近原始颗粒系统的力学特性，而引入精确缩尺准则能够减弱粗粒化带来的力学特性差异，但当缩放比尺较大时，力学特性上仍存在一定差异。
2.4 细观接触力
为了从细观力学特性的角度进一步探讨引入精确缩尺准则的粗粒化方法的效果，揭示前述宏观力学响应的内在细观机理，本节通过提取颗粒间接触力对各试样进行细观分析。与DEM方法不同，由于FDEM方法中进行了颗粒的有限元网格剖分，颗粒的接触力信息被保存在颗粒的有限元节点上，1个颗粒的某一接触可能同时包含1个或多个有限元节点。因此，进行粒间接触力统计分析前需先对颗粒节点接触力进行聚类。本文采用密度聚类算法进行接触聚类[14]，具体算法如下：
（1）对任意颗粒，统计颗粒表面法向接触力不为0的节点，建立各颗粒的样本点集。
（2）遍历样本点集中的节点，使任一节点及其邻域内其他法向接触力不为0节点合并为簇。
（3）邻域内无其他节点的节点为噪声点，由于较小接触处可能存在仅含1个节点的接触，因而噪声点单独成簇。
对各颗粒进行接触力聚类，并检索其邻域内的其他颗粒，在接触力相近的颗粒间建立接触力对。通过设置合适的接触力聚类阈值和接触对匹配阈值，提取各组数值试验在峰值应力比处的接触力。由于法向接触力对颗粒材料的传力影响更为显著[27]，本文主要考察法向接触力的统计规律。经整理，各组数值试验的平均接触力水平如表 5所示。
表 5 峰值处平均法向接触力Table 5. Mean normal contact forces at peak类别 编号 峰值平均法向接触力/N 对原系统比值 等径颗粒系统 E1 80.30 1.00 E2 1172.19 4.18 E3 2703.42 9.64 E4 3831.52 13.67 E2s 1046.27 3.73 E3s 2070.92 7.39 E4s 3109.17 11.09 二元颗粒系统 B1 306.42 1.00 B2 788.65 2.57 B3 1323.10 4.32 B2s 658.55 2.15 B3s 1122.34 3.66 从表 5可以看出，在等径颗粒系统和二元颗粒系统内，无论是否引入精确缩尺准则，粗粒化后颗粒间平均法向接触力的大小均随着粗粒化缩放比例的增大而增大。这是因为在外界的边界条件不变的情况下，随着缩放比尺的增加，边界处的接触数量逐渐减少，使得边界接触力水平有所提升，进而通过粒间接触力链传递提高粒间接触力水平。依据前文对精确缩尺理论的分析，将颗粒系统放大到h倍后，粒间接触力应放大到原系统的h2倍。从表 5的统计结果来看，粗粒化系统中粒间接触力同样近似符合精确缩尺系统下的这一缩放规律，这也佐证了粗粒化系统可以视为精确缩尺系统的局部的观点。
将各组数值试验的法向接触力归一化，绘制等经颗粒系统和二元颗粒系统法向接触力分布图分别如图 9，10所示。从图 9，10可以看出，不同缩放比尺下的粗粒化系统与引入精确缩尺准则的粗粒化系统中法向接触力的分布总体上比较一致，随着粗粒化缩放比尺的增加，超强（Fn/ˉFn>4）和极弱（Fn/ˉFn<0.2）接触力的比例稍有增大，接触力大小分布不均匀性稍微增强。
![]()
图 9 等径颗粒试验法向接触力分布Figure 9. Distribution of normal contact force of equal diameter particle tests![]()
图 10 二元颗粒试验法向接触力分布Figure 10. Distribution of normal contact force of binary particle tests结合前文的理论分析，在理想情况下，对于缩放比尺为h的粗粒化系统，在相同的外荷载作用下，粒间接触力的分布特征无明显改变，粒间接触力水平近似提升到原始颗粒系统的h2倍。若不引入精确缩尺准则，根据式（1）中的接触力计算方法，颗粒间嵌入量与原系统近似相同，但由于接触数量的降低，因颗粒嵌入产生的体积重叠量会减小，因而宏观上表现出比原始颗粒系统更弱的剪缩和更强的剪胀；引入精确缩尺准则后，根据式（1）中的可知粗粒化系统的粒间嵌入量近似增大到原始颗粒系统的h倍，产生与原始颗粒系统相近的体积重叠，宏观上表现出与原始颗粒系统相似的体积响应。
2.5 计算效率
统计各组数值试验的计算时间，结合计算使用的并行计算核数，绘制不同缩放比尺粗粒化的计算核时曲线如图 11所示，由于粗粒化方法大幅降低了数值试样的计算规模，因此大幅降低数值计算所需核时，提升计算效率。同时，随着粗粒化缩放比尺的逐渐增大，颗粒规模的减小程度逐渐降低，计算核时的降幅逐渐减小，缩放比尺增加带来的效率收益有所下降。
综合前述对力学特性和计算效率的分析可知，随着粗粒化缩放比尺的增大，引入精确缩尺的粗粒化系统相对原始颗粒系统的计算偏差会逐渐提升，且计算效率增幅变缓。因此，本方法更适用于较低的缩放比尺，达到牺牲少量精度换取较高计算效率的目的。
3. 适用性和局限性讨论
根据前文的论述，本文提出的精确缩尺和粗粒化FDEM方法中，要使得粗粒化系统能够尽可能还原原始颗粒系统的力学特性，需要满足2个重要的条件：①存在一个能包含粗粒化系统的精确缩尺系统；②原始颗粒系统应尽可能均质。
对于第一个条件，相对较容易满足，只要按照特定的比尺对颗粒系统进行全局粗粒化操作，理论上会存在一个相同比尺的精确缩尺系统，并且该粗粒化系统能够近似视为该精确缩尺系统的一部分。然而，对于局部粗粒化问题，即对原始颗粒系统中的一部分特定颗粒进行粗粒化操作，而另一部分颗粒保持不变，如谢亦朋等[23]研究的土石混合体问题，由于这种粗粒化方式仅对局部细颗粒进行，会改变原始颗粒系统的级配特征，无法找到一个包含该粗粒化系统的精确缩尺系统，因而难以通过引入精确缩尺法则来得到能够还原原始颗粒系统的粗粒化参数。
对于第②个条件，与之相关联的因素包括颗粒形状、颗粒在系统中的分布状况、颗粒自身的物理性质等，情况较复杂。在实际问题中，颗粒系统通常会表现出各向异性，局部性质很难完全等效全局性质。对于存在明显颗粒分层，如表层岩石颗粒发生风化、湿化等引起的非均质情况，即便存在一个包含粗粒化系统的精确缩尺系统，由于其局部和全局性质的差异性，引入精确缩尺法则的粗粒化系统对原始颗粒系统力学特性的还原也会十分有限。
综上所述，本文所提方法主要针对的是颗粒分布比较均匀的颗粒体系的全局粗粒化问题。对于局部粗粒化和非均匀分布的颗粒体系具体的量化分析，还有待更加深入的研究。
4. 结论
以颗粒材料作为研究对象，在FDEM方法中引入了精确缩尺和粗粒化方法，通过理论推导和数值试验论证，得到4点主要结论。
（1）精确缩尺和粗粒化的方法不仅适用于基于DEM方法的颗粒计算，同样能应用于基于FDEM方法的颗粒计算。主要区别在于在FDEM方法中采用的是基于罚函数的接触模型，故需建立接触模型中罚刚度等参数的精确缩尺准则。
（2）宏观应力变形结果表明，粗粒化在提升计算效率的同时会引起颗粒系统的宏观力学响应发生明显的改变，且变化程度随着粗粒化缩尺比例增大而不断增大，尤其是当缩放比尺较大时，会引起数值模拟结果失真，因而在颗粒系统中采用粗粒化方法进行计算时，必须要对模型参数进行必要修正以逼近原始颗粒系统的宏观力学特性。引入精确缩尺准则后，粗粒化系统与原始颗粒系统的偏差得到补正，能够近似还原原始颗粒系统的宏观力学响应。
（3）细观接触力分析结果表明，粗粒化系统与原始颗粒系统具有相似的接触力分布特征，且接触力水平近似服从精确缩尺理论的缩尺关系，与引入精确准则无关。在引入精确缩尺准则的情况下，相近的接触力水平下将引起更大的颗粒嵌入，增强粗粒化系统的剪缩性，减弱粗粒化系统的剪胀性，使粗粒化系统更符合原始颗粒系统的宏观力学特性。
（4）引入精确缩尺和粗粒化方法后，使用FDEM方法进行颗粒材料数值模拟的效率明显提升，本文提出的方法能够为颗粒材料的FDEM数值模拟方法提供一种加速方式。但试验结果也表明，在较大的缩放比尺下，粗粒化系统的宏观力学特性与原始颗粒系统相差较大，且计算效率的提升幅度较小，因而本文所提方法仅宜采用较低缩放比尺。
-
![]()
图 1 N - vs函数关系中两个系数的敏感性分析
Figure 1. Sensitivity analysis of two coefficients in N - vs function relationship
![]()
图 2 随机分析下系数a和b的离散度（σa, σb, CVa和CVb）随N - vs数组t的变化
Figure 2. Variation of dispersion of coefficients a and b (σa, σb, CVa and CVb) with N - vs array t under random analysis
![]()
图 3 随机分析下系数a和b的离散度（σa, σb, CVa和CVb）与N - vs数组t回归方程拟合优度R2的频数分布图
Figure 3. Frequency distribution of goodness of fitting R2 of regression equation dispersion of coefficients a and b
(σa, σb, CVa and CVb and N - vs array t under random analysis
![]()
图 4 11个工况下系数a和 b的离散度随N - vs数组t的变化曲线及其一阶导数
Figure 4. Variation curves and their first derivatives of dispersion of coefficients a and b with N - vs array t under 11 working conditions
![]()
图 5 不同精度和成功率下N - vs特征函数的收敛阈值
Figure 5. Convergence thresholds of N - vs characteristic functions under different accuracies and success rates
表 1 11个工况的基本信息
Table 1 Basic information of 11 working conditions
研究者 国家(地区) 土类 单元数 回归方程 相关系数R Hanumantharao(2008) 印度(新德里) 砂土 133 vs=79N0.434 R=0.99 Dikmen(2009) 土耳其(埃斯基谢希尔) 砂土 82 vs=73N0.33 R=0.72 Maheswari(2010) 印度(钦奈) 砂土 81 vs=100.53N0.265 R=0.92 Thaker(2011) 印度(苏拉特) 砂土 142 vs=51.21N0.45 R=0.88 Tsiambaos(2011) 希腊(*) 砂土 78 vs=79.7N0.365 R=0.79 Anbazhagan(2013) 印度(勒克瑙) 砂土 110 vs=60.17N0.56 R=0.93 王梦龙(2016) 中国(巴楚) 砂土 146 vs=98.787N0.22483 R=0.90 袁晓铭(2020) 中国(哈尔滨) 砂土 1001 vs=116.55N0.3149 R=0.85 Anbazhagan(2013) 印度(勒克瑙) 黏土 121 vs=106.63N0.39 R=0.86 Kumar(2018) 印度(古瓦哈提) 黏土 212 vs=47.84N0.6 R=0.87 Maheswari(2010) 印度(钦奈) 黏土 63 vs=89.31N0.358 R=0.96 
下载: 导出CSV
表 2 不同精度和成功率下的N - vs特征函数的收敛阈值
Table 2 Convergence thresholds of N - vscharacteristic functions under different accuracies and success rates
成功率SR/% CV=0.05 CV=0.10 CV=0.15 CV=0.20 TCVa TCVb T TCVa TCVb T TCVa TCVb T TCVa TCVb T 50 200 150 200 100 50 100 50 50 50 50 50 50 60 200 200 200 100 50 100 50 50 50 50 50 50 70 350 200 350 100 100 100 50 50 50 50 50 50 80 450 200 450 150 100 150 100 50 100 50 50 50 90 450 250 450 150 100 150 100 50 100 50 50 50 100 800 300 800 200 100 200 100 50 100 50 50 50
下载: 导出CSV
-
[1] KANAI K. Conference on cone penetrometer[R]. Ankara: The Ministry of Public Works and Settlement, 1966.
[2] HANUMANTHARAO C, RAMANA G V. Dynamic soil properties for microzonation of Delhi, India[J]. Journal of Earth System Science, 2008, 117(2): 719-730.
[3] DIKMEN Ü. Statistical correlations of shear wave velocity and penetration resistance for soils[J]. Journal of Geophysics and Engineering, 2009, 6(1): 61-72. doi: 10.1088/1742-2132/6/1/007
[4] 王梦龙. 国家标准液化判别方法区域化修正初探[D]. 哈尔滨: 中国地震局工程力学研究所, 2016. WANG Menglong. Preliminary Study on Regional Method of National Standard of Liquefaction Discrimination Formula[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2016. (in Chinese)
[5] UMA MAHESWARI R, BOOMINATHAN A, DODAGOUDAR G R. Use of surface waves in statistical correlations of shear wave velocity and penetration resistance of Chennai soils[J]. Geotechnical and Geological Engineering, 2010, 28(2): 119-137. doi: 10.1007/s10706-009-9285-9
[6] KUMAR A, HARINARAYAN N H, VERMA V, et al. Seismic site classification and empirical correlation between standard penetration test N value and shear wave velocity for guwahati based on thorough subsoil investigation data[J]. Pure and Applied Geophysics, 2018, 175(8): 2721-2738. doi: 10.1007/s00024-018-1858-1
[7] 袁晓铭, 卢坤玉, 林颖, 等. 哈尔滨地区砂土层N-V关系特征曲线及对比研究[J]. 地震工程与工程振动, 2020, 40(6): 1-15. YUAN Xiaoming, LU Kunyu, LIN Ying, et al. The N-V relationship curve of sand layers in Harbin region and its comparison with those in other regions of China[J]. Earthquake Engineering and Engineering Dynamics, 2020, 40(6): 1-15. (in Chinese)
[8] ANBAZHAGAN P, KUMAR A, SITHARAM T G. Seismic site classification and correlation between standard penetration test N value and shear wave velocity for Lucknow city in indo-gangetic basin[J]. Pure and Applied Geophysics, 2013, 170(3): 299-318. doi: 10.1007/s00024-012-0525-1
[9] RAHIMI S, WOOD C M, WOTHERSPOON L M. Influence of soil aging on SPT - vs correlation and seismic site classification[J]. Engineering Geology, 2020, 272: 105653. doi: 10.1016/j.enggeo.2020.105653
[10] XIAO S H, ZHANG J, YE J M, et al. Establishing region-specific N - vs relationships through hierarchical Bayesian modeling[J]. Engineering Geology, 2021, 287: 106105. doi: 10.1016/j.enggeo.2021.106105
[11] 袁晓铭, 卢坤玉, 汪云龙, 等. 区域土特征函数: 概念与原理[J]. 岩土工程学报, 2023, 45(12): 2429-2437. doi: 10.11779/CJGE20220828 YUAN Xiaoming, LU Kunyu, WANG Yunlong, et al. Characteristic functions of regional soils: concepts and principles[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(12): 2429-2437. (in Chinese) doi: 10.11779/CJGE20220828
[12] 周镜. 岩土工程中的几个问题[J]. 岩土工程学报, 1999, 21(1): 2-8. http://cge.nhri.cn/cn/article/id/10244 ZHOU Jing. Some cases in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(1): 2-8. (in Chinese) http://cge.nhri.cn/cn/article/id/10244
[13] 龚晓南. 21世纪岩土工程发展展望[J]. 岩土工程学报, 2000, 22(2): 238-242. http://cge.nhri.cn/cn/article/id/10487 GONG Xiaonan. Prospects for the development of geotechnical engineering in the 21th century[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(2): 238-242. (in Chinese) http://cge.nhri.cn/cn/article/id/10487
[14] FABBROCINO S, LANZANO G, FORTE G, et al. SPT blow count vs. shear wave velocity relationship in the structurally complex formations of the Molise Region (Italy)[J]. Engineering Geology, 2015, 187: 84-97. doi: 10.1016/j.enggeo.2014.12.016
[15] THAKER T, RAO K S. Development of statistical correlations between shear wave velocity and penetration resistance using MASW technique[R]. Toronto: 2011 Pan-Am CGS Geotechnical Conference, 2011.
[16] TSIAMBAOS G, SABATAKAKIS N. Empirical estimation of shear wave velocity from in situ tests on soil formations in Greece[J]. Bulletin of Engineering Geology and the Environment, 2011, 70(2): 291-297. doi: 10.1007/s10064-010-0324-9
-
其他相关附件
计量
- 文章访问数: 422
- HTML全文浏览量: 72
- PDF下载量: 120
