0.   引言

地震是威胁人类生命和财产的最具破坏性的自然灾害之一。在地震过程中,饱和松散砂土发生液化是常见的现象,其特点是砂土强度和刚度完全丧失。为了提高砂土地基抗液化能力,在过去,研究人员提出了诸如振动压实、水泥混合或化学灌浆等方法^[1-3]。由于传统地基处理方法存在能耗高、污染环境、成本高等特点,近年来,微生物诱导钙质胶结技术开始被岩土工程师所重视和采用^[4-5]。水泥混合、化学灌浆和微生物诱导钙质胶结技术均可以在砂土颗粒之间形成胶结物质,可称为人工胶结砂土。除此之外,天然胶结砂土广泛分布于自然界中,其中胶结物质主要来源于方解石、二氧化硅、氧化铁甚至黏土矿物等的沉积^[6-7]。研究人员^[8-13]通过试验研究指出,胶结砂土抗液化能力明显强于净砂,且随胶结程度的增加而提高。然而,当前试验条件很难定量、连续获取胶结砂土内部微观结构信息演变规律,阻碍了进一步探究胶结砂土在循环荷载条件下的微观力学响应。

离散元法^[14]通常将土体作为刚性颗粒集合体,颗粒运动满足质心运动定理和动量矩定理,能够对土样内部微观结构信息进行实时连续观测,已被广泛地应用于胶结颗粒材料的模拟中^[15],其中单元试验应力路径主要包括等向/单向压缩^[16-17]、静三轴^[18-19]、真三轴试验^[20]等。然而,针对不排水循环荷载条件下胶结砂土力学性质的离散元数值模拟还很缺乏^[21]。

基于上述分析,本文拟开展净砂和胶结砂土在不同循环应力比条件下的循环三轴剪切试验三维离散元模拟,首先从宏观尺度分析偏应力、轴应变、孔压等在试验过程中的变化规律,其次研究胶结破坏、力学配位数、组构、能量等微观力学响应,旨在通过宏微观相结合的研究方法探究颗粒间胶结对砂土抗液化性能的影响及其作用机理。

1.   胶结砂土不排水循环剪切试验模拟

1.1   胶结接触模型简介

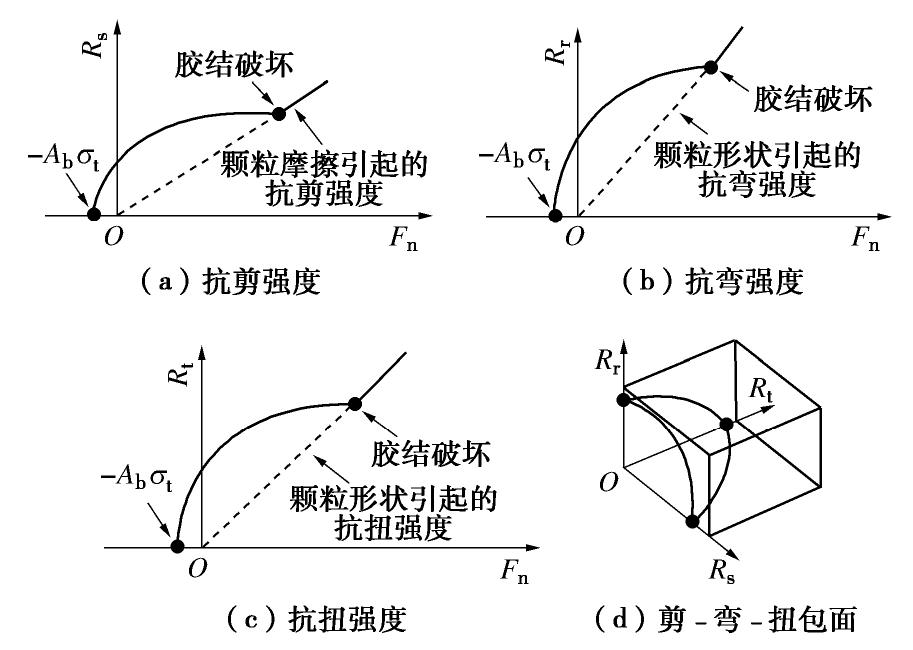
在胶结砂土离散元模拟中,颗粒间的接触力/力矩可由颗粒间胶结接触本构模型求得,而每个颗粒单元的运动则完全根据该单元所受合力/合力矩按牛顿第二运动定律确定。其中,颗粒间的胶结接触模型是胶结砂土离散元模拟的关键和核心。一般地,胶结接触模型包含两方面具体涵义：①接触模型力学响应；②接触模型强度准则。其中,接触模型力学响应又称颗粒间力-位移关系,定义了颗粒间接触力/力矩与接触点相对位移量的关系,也即由接触点相对位移量即可求取颗粒间接触力/力矩；接触模型强度准则对胶结接触状态进行判别,当胶结受力超过其强度时,胶结发生破坏,接触模型力学响应相应地发生改变。

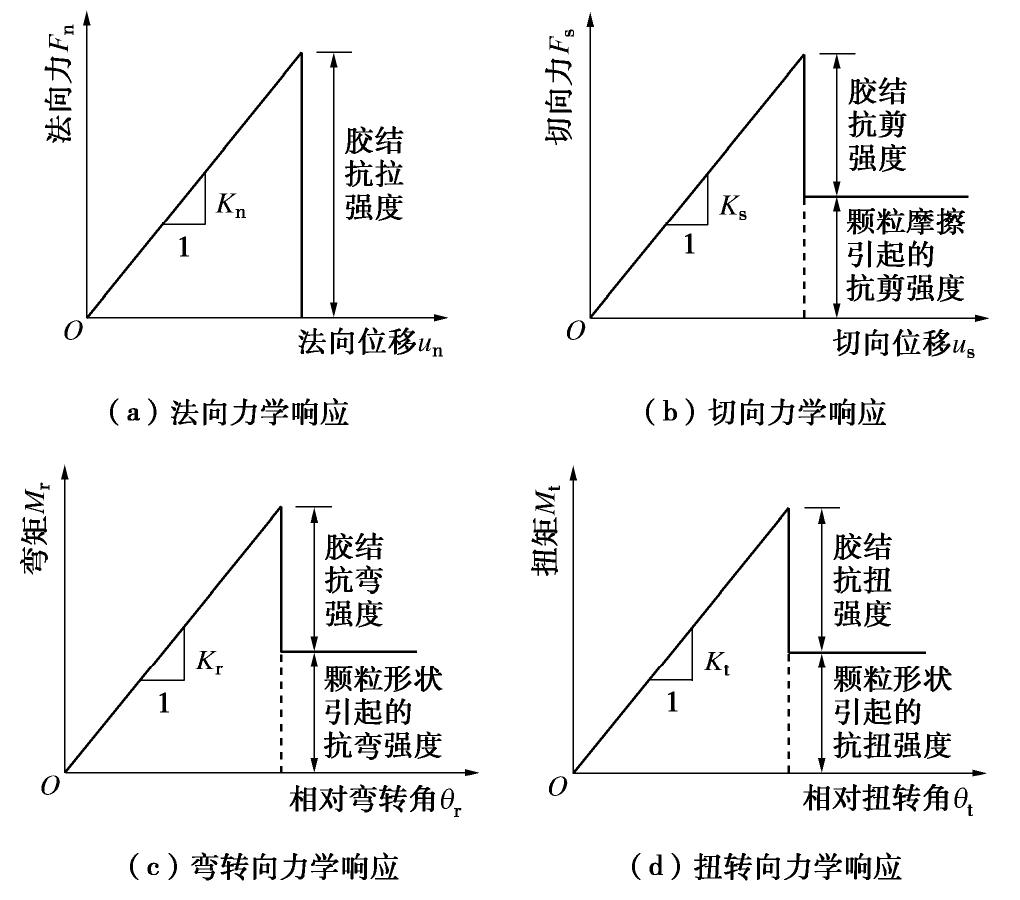
本文采用Shen等^[22]提出的三维完整胶结接触模型对胶结砂土力学性质进行模拟。在该模型中,刚度考虑了胶结宽度、厚度和颗粒半径的影响,总强度准则不仅考虑了胶结宽度、厚度和颗粒半径的影响,同时也考虑了胶结所受到的法向力、切向力、弯矩和扭矩之间的耦合作用,接触模型力学响应和强度准则示意图如图1和图2所示。当颗粒间胶结失效之后,上述三维完整胶结接触模型将退化为三维含抗弯转和抗扭转接触模型,该模型已应用于净砂循环荷载试验离散元模拟研究^[23]。

图  1  三维完整胶结接触模型力学响应^[22]

Figure  1.  Mechanical responses of bond contact model^[22]

下载: 全尺寸图片 幻灯片

图  2  三维完整胶结接触模型强度准则^[22]

Figure  2.  Strenth criterion of bond contact model^[22]

下载: 全尺寸图片 幻灯片

1.2   试样制备及参数确定

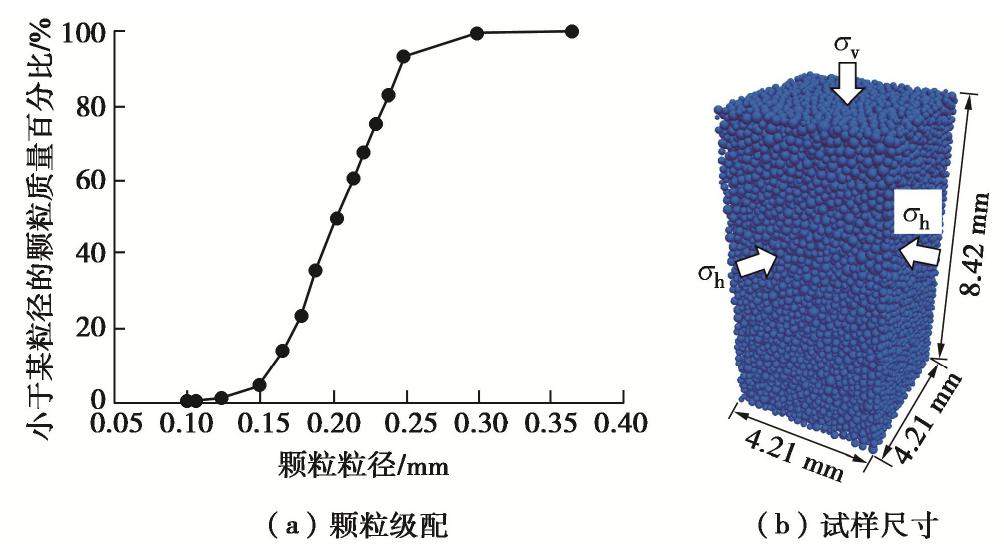
本文采用的离散元试样颗粒级配与丰浦砂相同,粒径范围0.1～0.3 mm,如图3（a）所示,试样尺寸为4.21 mm×4.21 mm×8.42 mm,颗粒数目为20000,如图3（b）所示。

图  3  离散元试样

Figure  3.  Numerical specimen used in DEM simulations

下载: 全尺寸图片 幻灯片

离散元胶结试样制备包括以下步骤：①采用分层欠压法^[24]生成均匀松散的净砂试样,孔隙比e₀=0.84；②等向压缩至50 kPa使试样达到稳定状态；③在符合胶结生成条件的颗粒之间生成胶结,此时离散元试样由净砂转变为胶结砂土。已有研究人员针对不同水泥胶结含量（如0.5%,1%,2%,3%,5%,8%等）的砂样进行了室内动三轴试验研究,本研究中水泥胶结含量设置为1%。

表1为本文离散元模拟采用的材料参数,其中颗粒部分的参数与Jiang等^[23]相同,胶结部分的弹性模量、泊松比、临界长细比与Shen等^[22]基本相同,抗拉强度与抗压强度比值（0.1）与Shen等^[22]相同,但其具体数值通过试算确定。另外,通过设置不同的胶结半径乘子可反映胶结程度,半径乘子是指胶结半径与组成该胶结接触的两颗粒半径之间较小值的比值。

表  1  离散元模型参数

Table  1.  Material parameters used in DEM simulations

	微观参数	数值
颗粒部分	弹性模量/(N·m-2)	7.0×108
	法向切向刚度比	5
	抗转动系数	0.25
	局部压碎系数	2.1
	摩擦系数	0.5
胶结部分	弹性模量/(N·m-2)	3.5×107
	泊松比	0.32
	抗拉强度/(N·m-2)	0.5×106
	抗压强度/(N·m-2)	0.5×107
	临界长细比	0.05
	半径乘子	0.332

下载: 导出CSV 

| 显示表格

Jiang等^[25]调查统计了天然和人工胶结砂土的SEM照片,发现颗粒间胶结作用有两种类型：薄胶结和厚胶结。其中,薄胶结是指两颗粒相互接触,胶结分布在该接触周围；厚胶结是指两颗粒未直接接触,胶结将两颗粒相连接。为了反映胶结分布特征,本文的离散元数值模型中考虑了这两种分布形态。对于特定孔隙比、级配及尺寸的数值试样,水泥胶结与主体砂的质量比（胶结含量）可转化为两相体积比。当胶结含量确定时,胶结体积可以确定下来。本文引入胶结物临界长细比（h_min/D_b,h_min是两颗粒间的最小距离,D_b是胶结物圆形截面直径）判定颗粒间是否生成胶结,只有当胶结物长细比小于临界长细比时,颗粒间才会生成胶结物（颗粒直接接触时,生成的胶结为薄胶结；颗粒未直接接触,生成的胶结为厚胶结）。参考文献[26],取临界长细比0.05。这样,就可以通过调整胶结半径乘子同时结合临界长细比得到某一胶结点的体积,进而获取整个试样中的目标胶结体积。

1.3   试验模拟步骤

首先,对制备完成的胶结砂土试样进行等向固结,固结应力为100 kPa。然后,采用文献[27]等应力幅循环加载的方法：上下墙体匀速加载（加载应变率1×10^-5）,当偏应力达到目标应力幅值q_cyc时,上下墙体反向运动,待达到相反方向的应力幅值q_cyc再次反向。在模拟中,不排水条件通过保证试样体积恒定来实现,采用伺服系统控制侧墙,伺服应力为围压（100 kPa）减去孔压后的有效应力。胶结砂土不排水循环荷载试验离散元模拟方案如表2所示。其中,循环应力比CSR=q_cyc/2p_c,p_c为固结后的平均有效应力（100 kPa）。

表  2  数值模拟方案

Table  2.  Program of DEM simulation

离散元试样	循环应力比CSR
净砂	0.1, 0.125, 0.15, 0.2
胶结砂土	0.2, 0.4, 0.425, 0.45, 0.5

下载: 导出CSV 

| 显示表格

2.   离散元模拟结果

2.1   宏观力学性质

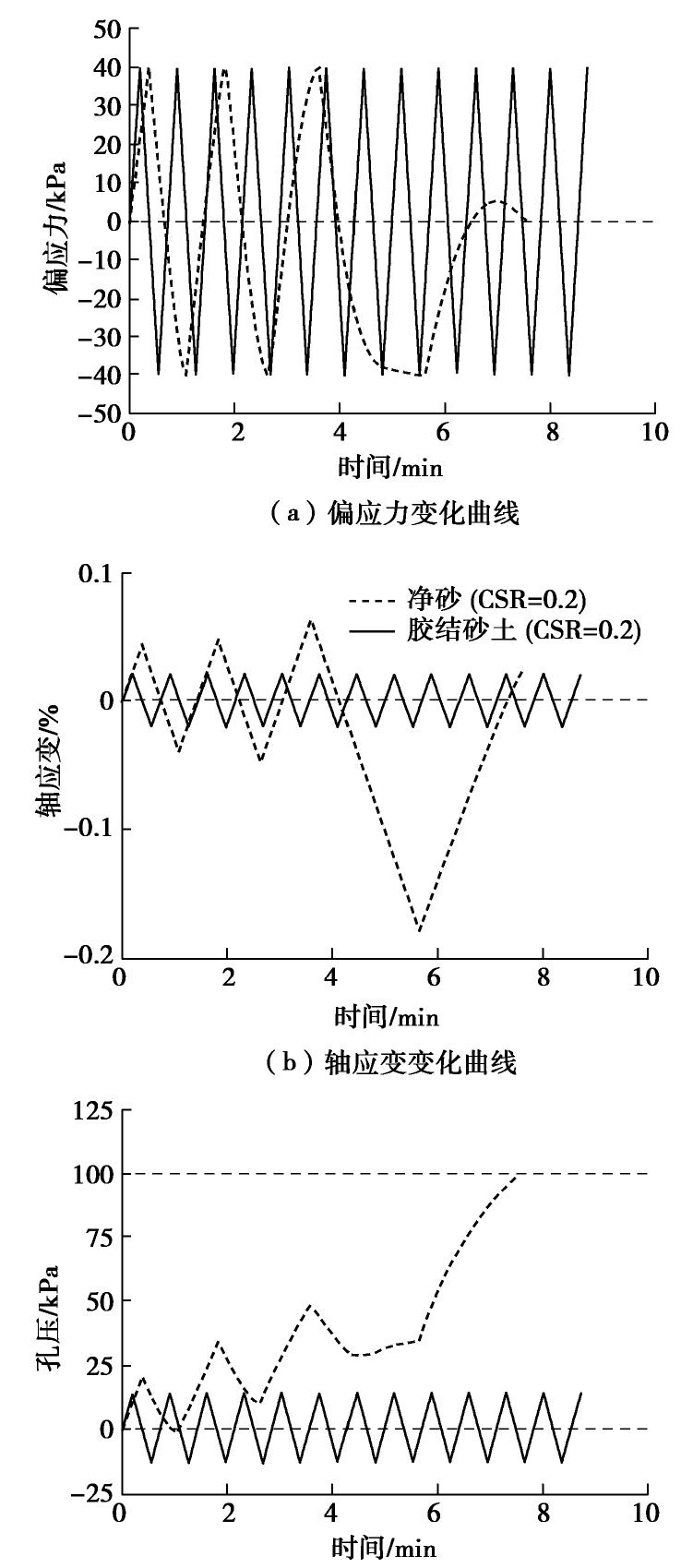
图4给出了循环应力比CSR=0.2条件下净砂和胶结砂土试样的偏应力、轴应变和孔压发展规律。由图可知,净砂试样在循环应力作用下,轴应变在经历初始较稳定的2个周期后开始急剧增长,在此过程中孔压快速增长,当振动3周次后孔压达到围压（100 kPa）,试样发生初始液化。对于胶结砂土试样,在进行的12周次试验中,最大轴应变仅为0.02%,最大孔压约为14 kPa（仅为围压的14%左右）,说明胶结的存在能够抑制轴应变和孔压的发展。

图  4  净砂与胶结砂土动力学响应

Figure  4.  Cyclic responses of pure sand and cemented sand

下载: 全尺寸图片 幻灯片

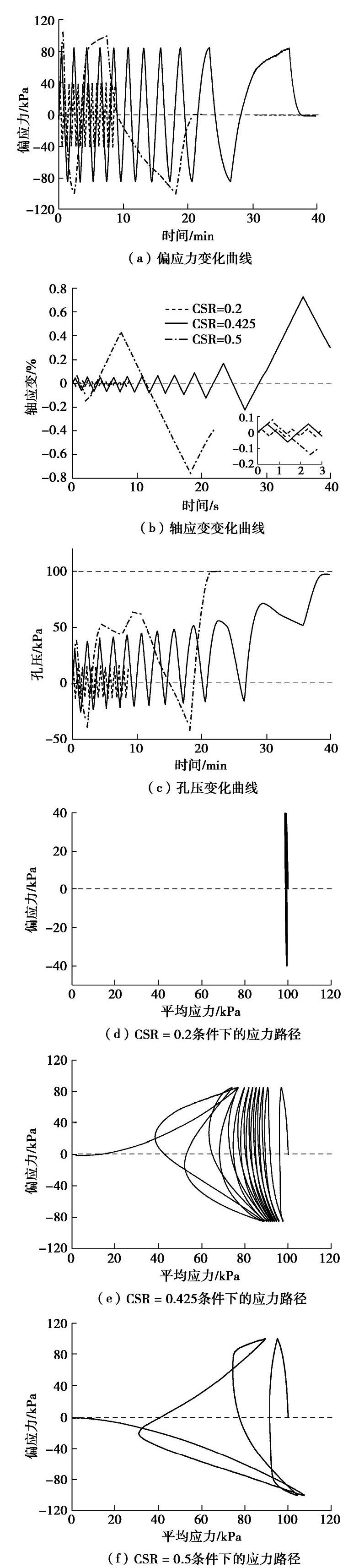
图5给出了不同循环应力比条件下（0.2,0.425,0.5）胶结砂土的偏应力、轴应变、孔压、应力路径变化曲线。由轴应变和孔压变化曲线可以看出,当循环应力比由0.2增至0.425时,胶结砂土轴应变和孔压均缓慢增长,在振动10周次后,轴应变开始急剧增加,孔压增至围压,在振动10.5周次时试样发生初始液化；当CSR=0.5时,胶结试样的轴应变在振动2周次时开始快速增大,孔压达到围压水平,试样发生初始液化。在p-q应力空间内,当循环应力比由0.2增至0.5时,应力路径逐渐向左偏移,偏应力最终减至0 kPa。由上可知,增大循环应力比可以使胶结砂土更快地达到初始液化状态。对比已有试验结果^[13]可知,模拟结果可以反映水泥胶结砂土的动力学特性。

图  5  不同循环应力比条件下胶结砂土动力学响应

Figure  5.  Cyclic responses of cemented sand under different cyclic stress ratios

下载: 全尺寸图片 幻灯片

综上,相同循环应力比条件下的净砂和胶结砂土,以及不同循环应力比条件下的同一胶结程度的砂土试样,均表现出了不同的动力学响应,这主要是因为在外荷载作用下试样内部微观结构发生了不同变化,后文将从微观角度对此进行详细阐述。

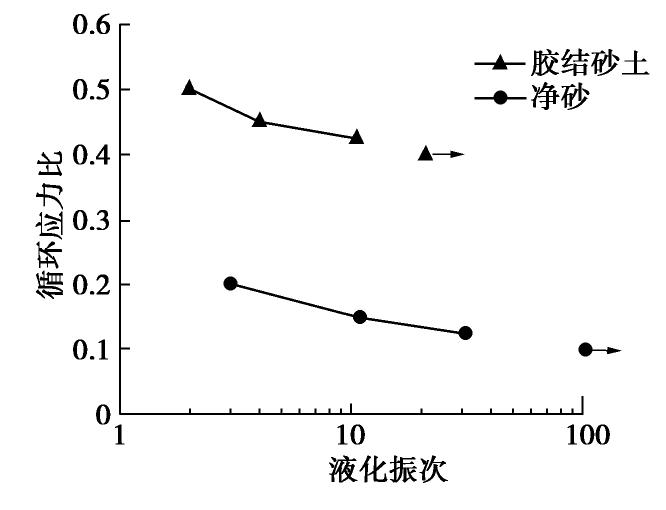
为了分析颗粒间胶结作用对砂土抗液化强度的影响,将净砂和胶结砂土在不同循环应力比条件下对应的初始液化振次绘制于半对数坐标系中,如图6（图中的右指向箭头表示在该循环振次时试样尚未达到初始液化状态）。由图可知,相比于净砂,胶结砂土的抗液化强度有大幅度提升,且循环应力比与液化振次之间呈指数函数关系,这与已有室内试验结果^[11-13]相符。

图  6  胶结对抗液化强度的影响

Figure  6.  Effects of cementation on liquefaction resistance

下载: 全尺寸图片 幻灯片

综上所述,本文离散元模型能够反映不排水循环荷载条件下颗粒材料的宏观动力学响应。

2.2   微观力学性质

由于胶结效应的存在,胶结砂土的动力学性质与净砂明显不同。在荷载作用下,胶结砂土的屈服和破坏均与粒间胶结破坏具有密切关系^[13],本文采用胶结破坏率（加载过程中发生破坏的胶结数目与加载开始时总的胶结数目之比）来量化胶结破坏情况。对于颗粒材料而言,其力学特性主要受密度影响,反映到微观层面,则受到颗粒间接触点密度的影响,可以采用颗粒的力学配位数^[28]（试样中平均每个颗粒所含有的接触数目,不包含接触数小于或等于1的悬浮颗粒）来描述。需要注意的是,对于胶结砂土,接触点包括胶结接触点和无胶结接触点。

此外,散粒体在加载过程中的能量存储及耗散是其宏观力学响应的深层次原因^[29],其破坏实际上经历了能量耗散直至失稳的演化过程,下文将重点关注颗粒和胶结弹性能（分别是指储存于无胶结接触处和胶结接触处的变形能量）、颗粒摩擦、弯转和扭转耗能（分别是指颗粒间通过滑动摩擦、抗转动和塑性扭转耗散的能量）的演化规律。其中,颗粒弹性能$E_{\text{e}}^{\text{p}}$可用下式计算：

式中,$F^{\text{p}}$为颗粒接触传递的相互作用力,$K^{\text{p}}$为相应刚度,$N^{\text{p}}$为接触数量。$F^{\text{p}}$包括法向力、切向力、弯矩和扭矩,4种作用的弹性能单独计算后相加。

塑性耗能$E_{\text{p}}^{\text{p}}$可用下式计算：

式中,$\text{Δ}{d}_{\text{p}}$为相应的塑性位移或转动量。

胶结弹性能$E_{\text{e}}^{\text{b}}$可用下式计算：

式中,$F^{\text{b}}$为胶结接触传递的相互作用力,$K^{\text{b}}$为相应刚度,$N^{\text{b}}$为接触数量。$F^{\text{b}}$包括法向力、切向力、弯矩和扭矩,4种作用的弹性能单独计算后相加。

同时,颗粒材料的宏观力学响应是材料内部所有颗粒在接触点处相互作用的外在表现,鉴于此,下文将偏组构概念^[30]扩展应用于胶结砂土接触点组构特征的定量描述（包括无胶结接触点、胶结接触点和破坏胶结接触点）。砂土中颗粒接触方向的主值分别为${\varphi }_1$,${\varphi }_2$,${\varphi }_3$,偏组构主值可表达为

偏组构主值φ_d可以表征砂土各向异性的强弱。在本文的离散元模拟中,荷载形式为轴对称应力状态,且大主应力和小主应力方向周期转化,偏组构主值可简化为φ_d = φ_z-φ_x。

综上,为揭示胶结砂土在不排水循环荷载条件下宏观力学性质的微观机理,下文将探究胶结破坏、配位数、能量及接触点组构等演变规律。

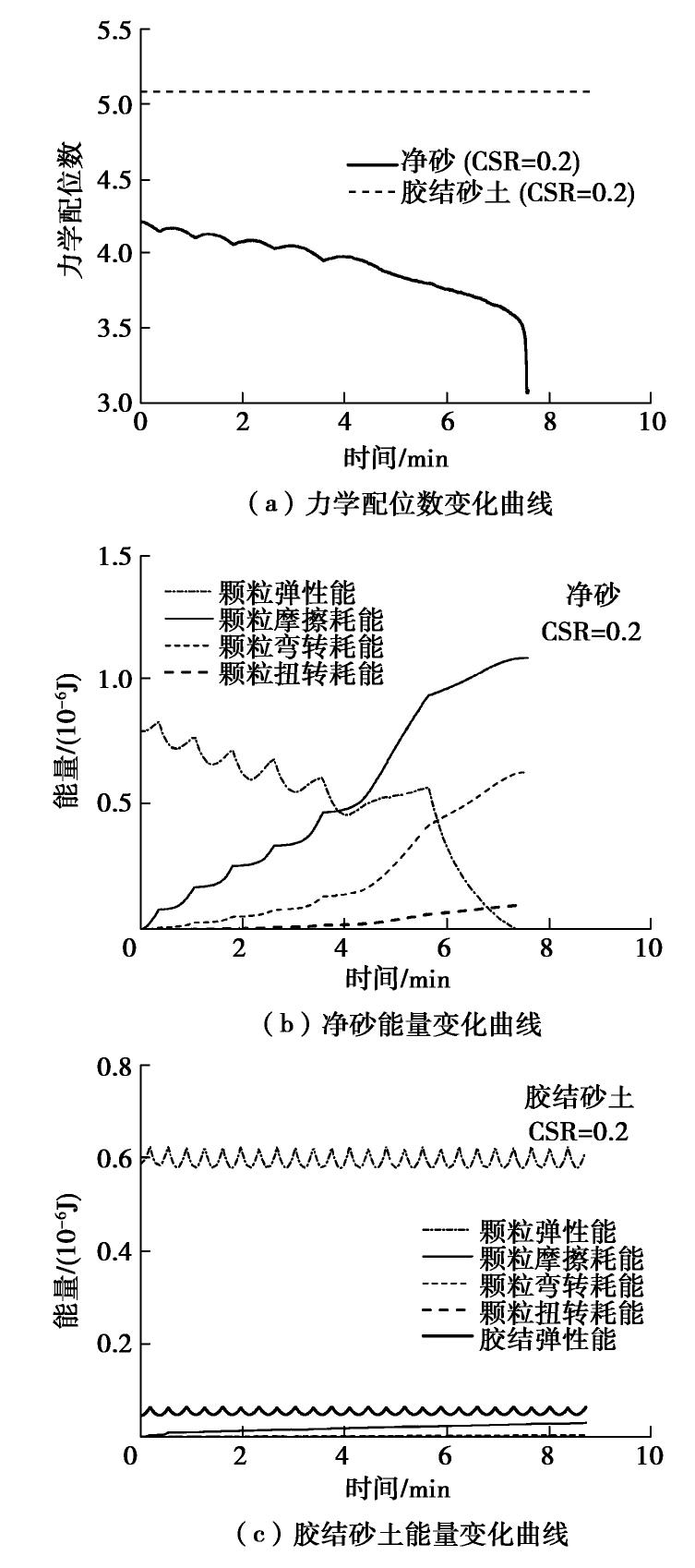
图7给出了循环应力比0.2条件下净砂和胶结砂土微观力学响应。

图  7  净砂与胶结砂土微观力学性质

Figure  7.  Micro-mechancial behaviors of pure sand and cemented sand

下载: 全尺寸图片 幻灯片

由图7（a）可以看出,净砂力学配位数在加载时减小、卸载时增加,但总体呈缓慢下降规律,在接近初始液化状态时突降至3.0附近,试样开始失稳,这与Martin等^[31]净砂三维离散元模拟结果相同。与本文相似,Martin等^[31]同样采用了含抗转动和抗扭转接触模型。与净砂不同,胶结砂土力学配位数大于净砂,且在循环应力作用下几乎没有发生变化。这是因为,胶结砂土试样内部存在两种胶结类型,分别为薄胶结和厚胶结,其中厚胶结可以在相互分离的颗粒间生成,使得在固结阶段开始时胶结砂土试样力学配位数高于净砂,在固结（固结应力100 kPa）完成后（仅有少量胶结发生破坏）,胶结砂土力学配位数仍高于净砂,由于在循环荷载作用下粒间胶结基本未发生破坏（仅5个,占比0.0106%）,因此力学配位数基本不变,也即胶结试样始终处于结构稳定状态。

图7（b）为净砂试样的能量演化曲线。由图可知,在循环荷载开始时,颗粒接触处储存着一定的弹性能,随着加载和卸载的循环进行,弹性能相继增加和降低,但降低的幅度要大于增加的幅度,也即颗粒弹性能逐渐释放,其在试样振动3周次后急剧下降至0,此时试样开始发生初始液化。另外,自循环荷载作用开始,颗粒间首先发生相对滑移（产生摩擦耗能）,随后,颗粒间开始发生不同程度的弯转和扭转（产生弯转和扭转耗能）,在振动3周次时摩擦、弯转、扭转耗能增速均有明显提高,并在初始液化时达到最大值。

由图7（c）可以看出,对于胶结砂土来说,颗粒和胶结弹性储能占据主导,其幅值在整个加载过程中基本未发生变化,而累积产生的颗粒摩擦耗能较小,弯转耗能和扭转耗能数值更小,可以认为胶结砂土试样在循环荷载作用下（12周次）基本表现为弹性性质,结构稳定,不会出现初始液化现象。

为对比分析不同循环应力比条件下胶结砂土微观力学性质,图8和图9分别给出了循环应力比0.425和0.5时胶结试样的胶结破坏、力学配位数、能量及接触点组构的演变曲线。这里,将胶结破坏划分为受拉破坏和受压破坏：在胶结接触点受力超过其能承受的峰值荷载时,如果其受力状态为纯拉或受拉情况下的复杂受力状态,则判定其为受拉破坏,相反,如果其受力条件为纯压或受压情况下的复杂受力状态,则判定为受压破坏。

图  8  循环应力比0.425条件下胶结砂土微观力学性质

Figure  8.  Micro-mechancial behaviors of cemented sand under cyclic stress ratio of 0.425

下载: 全尺寸图片 幻灯片

图  9  循环应力比0.5条件下胶结砂土微观力学性质

Figure  9.  Micro-mechancial behaviors of cemented sand under cyclic stress ratio of 0.5

下载: 全尺寸图片 幻灯片

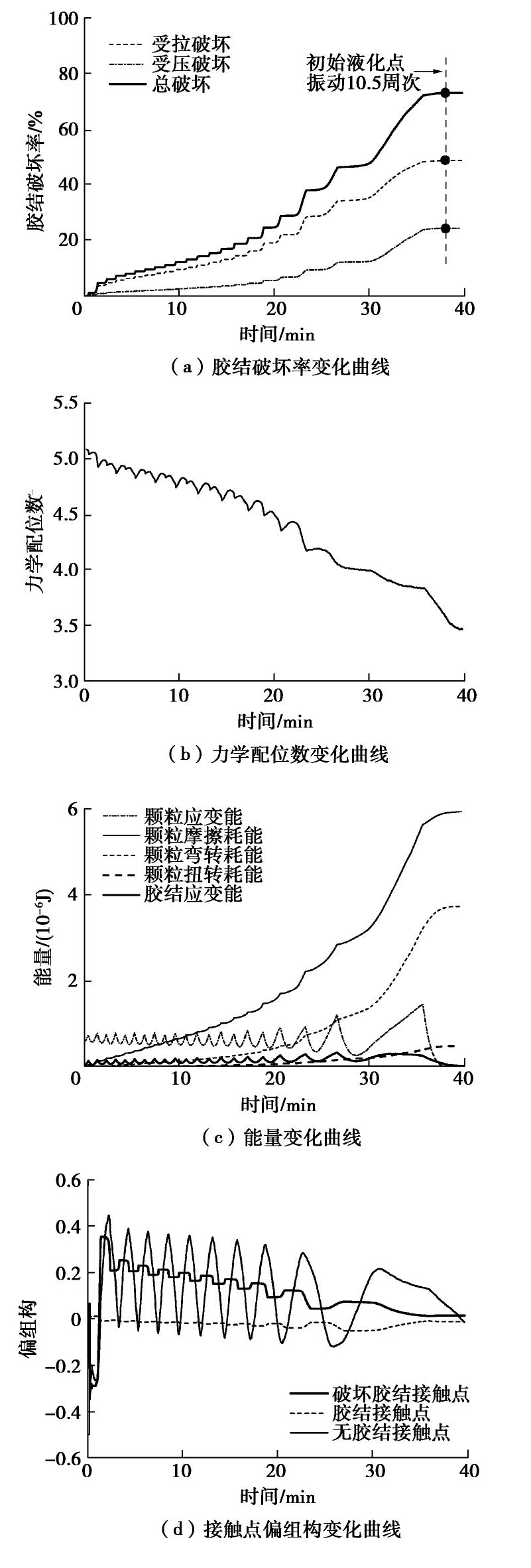
将循环应力比由0.2增至0.425,胶结砂土试样开始发生胶结破坏。由图8（a）和图5（a）可以看出,胶结破坏主要发生在加载阶段,且越接近应力幅值胶结破坏越剧烈,在卸载阶段仅有少量胶结破坏发生,在振动第10周次时胶结破坏速率有明显提高,在振动10周次后,胶结破坏急剧发生,在接近初始液化时,胶结破坏率基本稳定在73.30%,且胶结受拉破坏数量大于受压破坏数量。

由图8（b）可知,在初始液化之前,力学配位数总体呈缓慢下降规律,在接近初始液化时力学配位数下降幅度增大,与胶结砂土循环应力比0.2时的结果截然不同。与图7（a）中净砂结果相比,尽管胶结砂土循环应力比比较大,但接近初始液化时配位数下降速率仍小于净砂,且胶结砂土液化时的力学配位数（3.46）大于净砂（3.08）。

对比图8（c）与图7（b）,（c）可以看出,当循环应力比由0.2增加至0.425,胶结砂土试样的颗粒摩擦耗能、弯转耗能和扭转耗能均有了较大程度的发展,其演变规律与净砂相似,在循环荷载后期开始占据主导。由于胶结效应的存在,胶结砂土的颗粒弹性能演变规律与净砂存在差异,主要表现在颗粒弹性能变化曲线的极大值点总体上随循环应力作用逐渐增大（反向加载时的极大值点大于正向加载时的极大值点）。此外,胶结弹性能随加载和卸载循环进行而相继增加和降低,但增加幅度大于降低幅度,使得胶结弹性能变化曲线的极大值和极小值总体上呈缓慢增加的规律（其中,反向加载时的极大值点大于正向加载时的极大值点）,但在振动10周次后开始减小,并在试样发生初始液化时降至0附近。

图8（d）给出了循环应力比0.425条件下胶结砂土试样的破坏胶结接触点、胶结接触点、无胶结接触点的偏组构变化曲线。偏组构能够反映接触点的各向异性程度,例如,当无胶结接触点为正值时,表明无胶结接触点法方向在竖直方向占优势,反之,当无胶结接触点为负值时,表明无胶结接触点法方向在水平方向占优势。破坏胶结接触点是指发生胶结破坏的接触点,这里特指胶结发生破坏时的接触点。在胶结接触点受力超过其能承受的峰值荷载时,离散元程序会计算该胶结接触点的法方向。由破坏胶结接触点变化规律可知,在第1个循环周次的加载阶段,胶结破坏主要发生在水平方向,在反向加载阶段,胶结破坏主要发生在竖直方向,在第1个循环周次结束后,破坏胶结接触点偏组构约为0.36；在接下来的循环周次中,偏组构随正向加载和反向加载而减小和增大,在初始液化时接近0,也即破坏胶结接触点在初始液化时基本呈各向同性的分布规律。对于无胶结接触点,初始循环周次内在水平方向上占优势,但不太稳定,主要是因为此时的无胶结接触点数目较少所致；在接下来的循环周次内,无胶结接触点偏组构表现出正弦曲线的演变形式,极大值点和极小值点分别对应偏应力-轴应变曲线的极大值和极小值点,并且,在偏应力-轴应变曲线的极小值点附近,无胶结接触点在水平方向占优势,在其他时刻均在竖直方向上占优势,偏组构的极值均随循环荷载逐渐减小,在初始液化时接近0。对于胶结接触点,其仅在第1个循环周次内反向加载且胶结破坏发生之前在竖直方向占优势,在接下来的循环周次内在水平方向占优势,同样在初始液化时接近0。由上可知,在胶结砂土试样达到初始液化状态时,破坏胶结接触点、无胶结接触点和胶结接触点均表现出各向同性的分布性质。

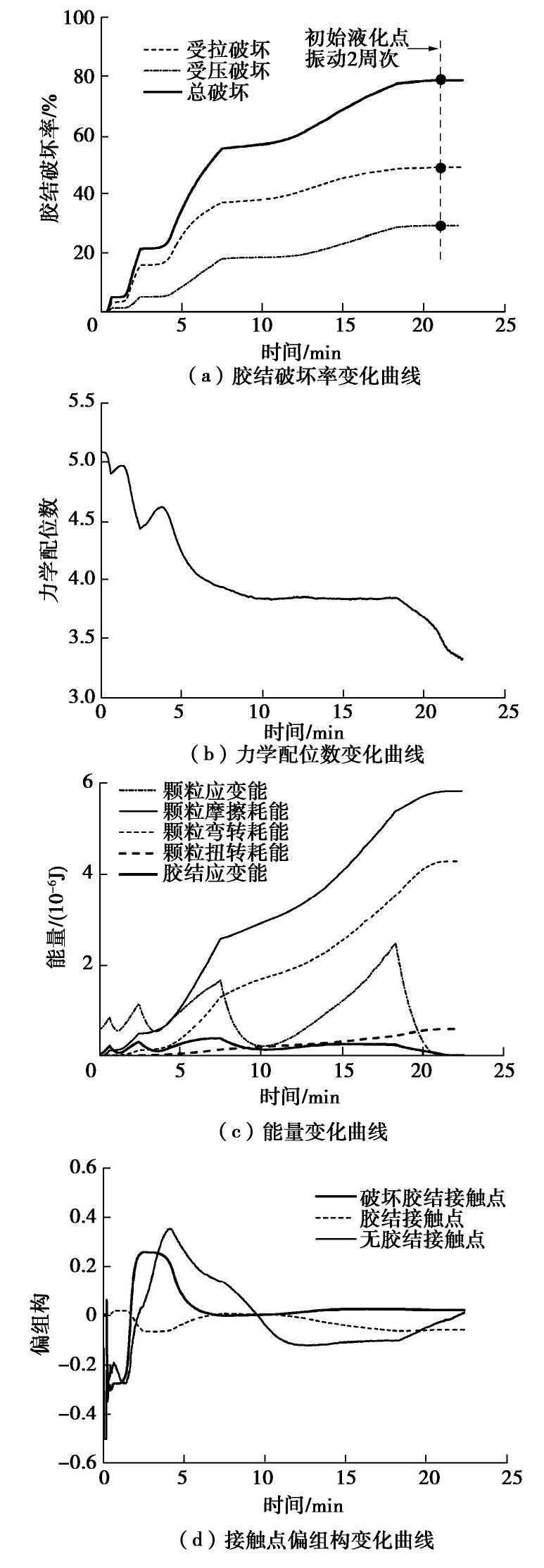
对比图9和图8可知,当循环应力比由0.425增加至0.5时,胶结破坏更为剧烈,且初始液化时的胶结破坏数目也相应地增大。同时,当循环应力比为0.5时,力学配位数减小更快,且初始液化时的数值更小。另外,胶结试样在循环应力比0.5时的能量和偏组构演化规律与循环应力比0.425时大致相同,但同时可以看出,随着循环应力比的增加,颗粒和胶结弹性能、偏组构更快地趋向于0,颗粒摩擦耗能、弯转耗能、扭转耗能更快地达到最大值。

3.   结论

本文将已有的三维完整胶结接触模型引入到三维离散元程序中,对不排水循环荷载条件下的胶结砂土宏微观力学性质开展研究。主要得出以下结论：

（1）当循环应力比较小时（0.2）,特定胶结程度的砂土试样在指定循环周次内产生了很小的轴应变和孔压,并未达到初始液化,主要是因为仅有极少量胶结发生破坏,力学配位数增加并在循环荷载作用下基本保持不变,外界输入功主要用于增加颗粒和胶结弹性能,而颗粒摩擦耗能、弯转耗能、扭转耗能则很小,这与净砂的微观力学性质截然不同。

（2）对于特定胶结程度的离散元试样,在初始液化发生之前,随着循环应力比的增加,胶结破坏更为剧烈,主要的胶结破坏形式为受拉破坏,其次为受压破坏,力学配位数下降速率更快且初始液化时对应的力学配位数更低,颗粒和胶结弹性能、接触点偏组构（包括破坏胶结接触点、胶结接触点、无胶结接触点）更快地趋向于0,颗粒摩擦耗能、弯转耗能、扭转耗能更快地达到最大值。

限于篇幅,论文仅研究了多种循环应力比条件下净砂和一种胶结程度的胶结砂土宏微观力学性质,而有关多种胶结程度砂土试样的离散元模拟结果将在后续文章详细介绍。