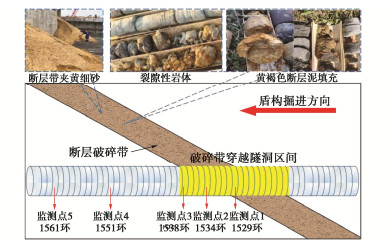
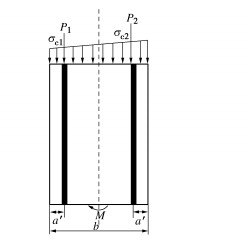
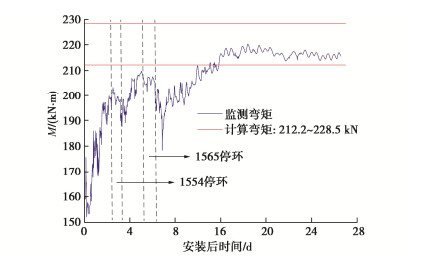
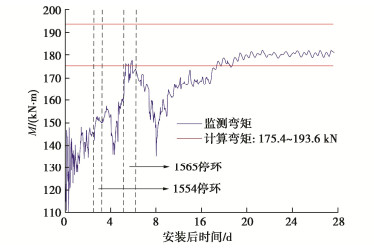
本文全文图片
本文全文表格
-
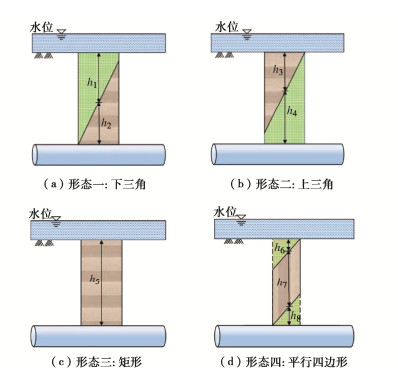
4种特征形态下海底盾构隧道纵向上覆荷载
形态 纵向上覆荷载 ${B_t}$取值 形态一 $ {q_{\text{1}}}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left| {{h_{{\text{a1}}}}{\text{ = }}{h_{\text{1}}}{\text{, }}} \right.{h_{{\text{a1}}}}{\text{ = }}{h_{\text{1}}}{\text{, }}{h_{{\text{a3}}}}{\text{ = 0}} $ ${B_t} = {B_{\text{1}}}$ 形态二 ${q_{\text{2}}}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left| {{h_{{\text{a1}}}}{\text{ = 0, }}} \right.{h_{{\text{a2}}}}{\text{ = }}{h_3}{\text{, }}{h_{{\text{a3}}}}{\text{ = }}{h_4}$ ${B_t} = {B_{\text{2}}}$ 形态三 ${q_3}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left| {{h_{{\text{a1}}}} = {h_{{\text{a3}}}} = 0, } \right.{h_{{\text{a2}}}} = {h_5}$ ${B_t} = {B_{\text{1}}}$ 形态四 ${q_4}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left| {{h_{{\text{a1}}}} = {h_{\text{6}}}, {h_{{\text{a2}}}} = {h_7}, } \right.{h_{{\text{a3}}}} = {h_8}$ ${B_t} = {B_{\text{2}}}$ -
不同倾角断层破碎带海底隧道纵向上覆荷载
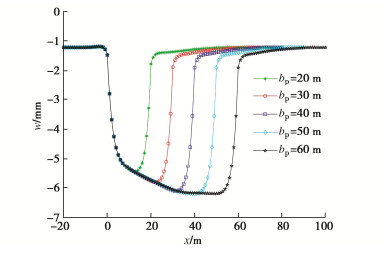
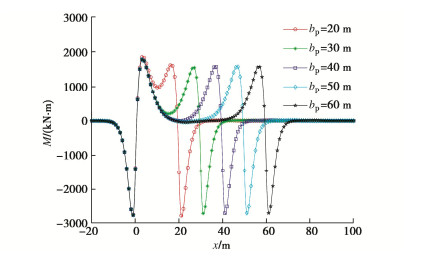
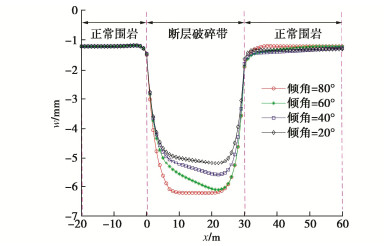
倾角 上覆荷载 $\alpha = {90^ \circ }$ ${q_0}(x{\text{)}}$$ - \infty {\text{ < }}x{\text{ < 0}}$ ${q_3}(x{\text{)}}$${\text{0}} \leqslant x{\text{ < }}{b_{\text{p}}}$ ${q_0}(x{\text{)}}$${b_{\text{p}}} \leqslant x{\text{ < + }}\infty $ $\tan \alpha > \frac{H}{{{b_{\text{p}}}}}$ ${q_0}(x{\text{)}}$$ - \infty {\text{ < }}x{\text{ < 0}}$ ${q_1}(x{\text{)}}$${\text{0}} \leqslant x{\text{ < }}\frac{H}{{{\text{tan}}\alpha }}$ ${q_3}(x{\text{)}}$$\frac{H}{{{\text{tan}}\alpha }} \leqslant x \leqslant {b_{\text{p}}}$ ${q_2}(x{\text{)}}$${b_{\text{p}}}{\text{ < }}x{\text{ < }}{b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }}$ ${q_0}(x{\text{)}}$${b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }} \leqslant x < + \infty $ $\tan \alpha = \frac{H}{{{b_{\text{p}}}}}$ ${q_0}(x{\text{)}}$$ - \infty {\text{ < }}x{\text{ < 0}}$ ${q_1}(x{\text{)}}$${\text{0}} \leqslant x{\text{ < }}{b_{\text{p}}}$ ${q_3}(x{\text{)}}$$x = {b_{\text{p}}}$ ${q_2}(x{\text{)}}$$ {b_{\text{p}}}{\text{ < }}x \leqslant {\text{2}}{b_{\text{p}}} $ ${q_0}(x{\text{)}}$${\text{2}}{b_{\text{p}}}{\text{ < }}x{\text{ < + }}\infty $ $\tan \alpha < \frac{H}{{{b_{\text{p}}}}}$ ${q_0}(x{\text{)}}$$ - \infty {\text{ < }}x{\text{ < 0}}$ ${q_1}(x{\text{)}}$${\text{0}} \leqslant x{\text{ < }}{b_{\text{p}}}$ ${q_4}(x{\text{)}}$${b_{\text{p}}} \leqslant x < \frac{H}{{{\text{tan}}\alpha }}$ ${q_2}(x{\text{)}}$$\frac{H}{{{\text{tan}}\alpha }} \leqslant x \leqslant {b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }}$ ${q_0}(x{\text{)}}$${b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }}{\text{ < }}x{\text{ < }} + \infty $ -
4种破碎带形态及其对应上覆荷载
破碎带形态 $\alpha = {90^ \circ }$ $\tan \alpha > \frac{H}{{{b_{\text{p}}}}}$ $\tan \alpha = \frac{H}{{{b_{\text{p}}}}}$ $\tan \alpha < \frac{H}{{{b_{\text{p}}}}}$ 上覆荷载 f1(x) f2(x) f3(x) f4(x) -
断层破碎带及围岩力学参数
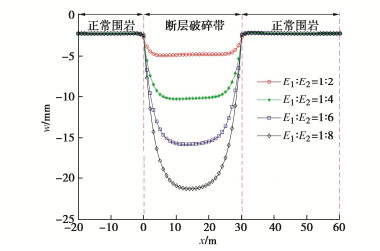
类型 $\gamma {\text{/}}$${\text{(kN}} \cdot {{\text{m}}^{ - {\text{3}}}}{\text{)}}$ $\varphi $/(°) $c{\text{/}}$kPa $E{\text{/}}$GPa $\nu $ k 正常围岩 26 30 100 1.6 0.33 0.49 断层破碎带 20 25 30 0.5 0.40 0.67 -
螺栓及钢筋相关参数
a'/mm Ee/GPa n1 n2 Ec/GPa 50 210 20 10 3.15×104 nb Eb/GPa lb/mm Ab/m2 ${\alpha _{\text{b}}}{\text{/}}$(°) 28 210 730 7.069×10-4 35 注:$a'$为钢筋保护层厚度;Ee为钢筋弹性模量;n1为管片内侧环向主筋数量;n2为管片外侧环向主筋数量;Ec为管片弹性模量;nb为纵向螺栓个数;Eb为螺栓弹性模量;lb为螺栓长度,Ab为螺栓横截面面积;${\alpha _{\text{b}}}$为螺栓倾角。


 下载:
下载: