断层破碎带海底盾构隧道管片纵向沉降解析解及应用

付艳斌; 王福道; 陆岸典; 张小龙; 洪成雨; 肖惠

doi:10.11779/CJGE20220507

断层破碎带海底盾构隧道管片纵向沉降解析解及应用 English Version

付艳斌^{1, 2, 3,},
王福道^{1, 2},
陆岸典⁴,
张小龙⁵,
洪成雨^{1, 3},
肖惠^{1, 2}

1.
深圳大学土木与交通工程学院, 广东深圳 518060
2.
深圳大学滨海城市韧性基础设施教育部重点实验室, 广东深圳 518060
3.
深圳市地铁站绿色高效智能建造重点实验室, 广东深圳 5180603
4.
广东粤海珠三角供水有限公司, 广东广州 511458
5.
上海隧道工程与轨道交通设计研究院, 上海 200235

基金项目:

国家自然科学基金项目 52078304

国家自然科学基金项目 51938008

国家自然科学基金项目 52090084

广东省重点领域研发计划项目 2019B111108001

广东省重点领域研发计划项目 2022B0101070001

深圳市科技计划项目 20220525163716003

深圳市科技计划项目 KQTD20200909113951005

详细信息

作者简介:
付艳斌(1977—)，男，博士，主要从事隧道及地下工程方面的教学与研究工作。E-mail: fuyanbin999@163.com

中图分类号: TU43;U45
计量
- 文章访问数: 287
- HTML全文浏览量: 64
- PDF下载量: 104
出版历程
- 收稿日期: 2022-04-25
- 网络出版日期: 2023-02-23
- 刊出日期: 2023-06-30

Analytical solution to longitudinal settlement of segments of subsea shield tunnels in fault fracture zones and its application

FU Yanbin^{1, 2, 3,},
WANG Fudao^{1, 2},
LU Andian⁴,
ZHANG Xiaolong⁵,
HONG Chengyu^{1, 3},
XIAO Hui^{1, 2}

1.
College of Civil and Transportation Engineering, Shenzhen University, Shenzhen 518060, China
2.
Key Laboratory of Coastal Urban Resilient Infrastructures (MOE), Shenzhen University, Shenzhen 518060, China
3.
Shenzhen Key Laboratory of Green, Efficient and Intelligent Construction of Underground Metro Station, Shenzhen 518060, China
4.
Guangdong GDH Pearl River Delta Water Supply Co., Ltd., Guangzhou 518060, China
5.
Shanghai Tunnel Engineering & Rail Transit Design and Research Institute, Shanghai 200235, China

摘要

摘要: 断层破碎带地层隧道沉降控制是海底盾构隧道建设的关键问题之一，隧道的不均匀沉降诱发管片环缝张开、错台、螺栓应力增大乃至接缝渗漏水等现象，严重影响隧道结构稳定和运营安全。针对断层破碎带地层海底盾构隧道纵向沉降问题，分析隧道穿越断层破碎带地层全过程，提出了归一化上覆荷载理论公式。通过泰勒级数公式将复杂上覆荷载在5%误差内简化为多段三次多项式函数，结合Timoshenko梁理论推导建立了海底盾构隧道管片纵向沉降及内力系列解析解。最后结合工程实例对理论模型进行了验证。研究表明：断层破碎带内隧道的沉降曲线表现为激增段、缓增段和骤减段。断层破碎带倾角越大，断层破碎带与正常围岩界面附近不均匀沉降越大，断层破碎带对延伸侧1倍破碎带宽度范围内隧道的沉降影响较大；随着断层破碎带宽度的增加，断层破碎带范围内隧道的沉降峰值逐渐增大并趋于稳定，当断层破碎带宽度超过6倍洞径时，隧道的沉降峰值基本保持不变。研究结果可为断层破碎带海底盾构隧道纵向沉降计算和性能评估提供依据。
- 断层破碎带 /
- 纵向沉降 /
- 解析解 /
- 海底盾构隧道 /
- Timoshenko梁
Abstract: The settlement control of tunnels in fault fracture zones is one of the key problems in the construction of subsea shield tunnels. The differential settlement of the tunnels induces the opening and dislocation of circumferential segment joint, increase of bolt stress and even leakage, which seriously affect the stability of tunnel structure and operation safety. Aiming at the longitudinal settlement of the subsea shield tunnels in the fault fracture zone stratum, through the analysis of the whole process of the tunnels crossing the fault fracture zone stratum, the theoretical formula for the normalized overlying loads is proposed, and the Taylor series expansion method is used to simplify the complex overburden loads into a multi-segment cubic polynomial function within 5% error. Combined with the Timoshenko beam theory, the analytical solution of the longitudinal settlement and internal force of the subsea shield tunnel segments is derived. Finally, the theoretical model is verified by an engineering example. The research shows that the settlement curve of the tunnel in the fault fracture zone shows surge section, slow increase section and sudden decrease section. The greater the dip angle of the fault fracture zone, the greater the differential settlement near the interface between the fault fracture zone and the normal surrounding rock. The fault fracture zone has a great influence on the settlement of the tunnels within the width of one time the fracture zone at the extension side. With the increase of the width of the fault fracture zone, the peak settlement of the tunnel in the fault fracture zone gradually increases and tends to be stable. When the width of the fault fracture zone exceeds 6 times the tunnel diameter, the peak settlement of the tunnel basically remains unchanged. The research results may provide a basis for the longitudinal settlement calculation and performance evaluation of subsea shield tunnels in fault fracture zones.
- fault fracture zone /
- longitudinal settlement /
- analytical solution /
- subsea shield tunnel /
- Timoshenko beam

HTML全文

0. 引言

黏性土体由于具有渗透性低、廉价、易于获取的优点，工程上常被选作为污染场地如垃圾填埋场、固废处置场的防渗阻隔屏障材料^[1-3]。黏性土体的防渗性能除与黏土颗粒性质有关外，还与其压实程度密切相关。为提高黏性土体的防渗性能，其在使用前通常需进行压密处理。尽管如此，危害性较大的污染物仍会通过对流、扩散等方式在压实黏土垫层中发生运移，从而对地下水和周围土体造成污染^[3-7]。因此，有必要对污染物的运移规律进行研究，以合理的评估压实黏土垫层的服役性能。

近几十年来，考虑到堆填的固体废弃物会使压实黏土发生变形，许多学者在探究压实黏土垫层中污染物的运移特性时融入了固结变形的影响^[5-12]。例如，Smith^[6]建立了准稳态状态下黏土垫层中一维固结与污染物运移耦合模型，并分析了固结对污染物运移规律的影响；Lewis等^[9-10]基于大变形理论发展了黏土垫层中一维固结与污染物运移的理论模型，该模型可考虑固结参数随孔隙比变化；李江山等^[12]考虑到污染场地内部的生化反应会使压实黏土垫层中的温度发生变化，研究了非等温分布条件对固结与污染物运移耦合过程的影响。然而，上述研究大多针对有机污染物，且忽略了污染物运移过程中化学渗透导致的黏土体积及结构变化^{[3, 13-16]}。实际上，在复杂工程环境下，压实黏土垫层的固结变形不仅会受力学荷载影响，还会受污染物浓度变化引起的化学荷载影响^{[3, 14-20]}。因此，有必要研究考虑力学-化学荷载影响下压实黏土垫层中污染物的一维运移过程。

Kaczmarek等^[14-15]建立了黏土中一维化学-力学固结与污染物运移的耦合模型，该模型可考虑污染物浓度变化对沉降量影响。在Kaczmarek等^[14-15]研究基础上，Peters等^[16]探究了对流运移对黏土中一维化学-力学固结过程的影响。基于Peters等^[16]的研究，张志红等^[3]考虑了固结变形对污染物运移参数如扩散系数的影响，并发展了黏土垫层中一维化学-力学固结与污染物运移耦合模型。进一步，Zhang等^[19]推导得到了考虑温度影响下黏土垫层中一维化学-力学固结与污染物运移的耦合模型。田改垒等^[20]分析了考虑一维化学-力学固结情况下，热效应对压实黏土垫层中污染物运移规律的影响。这些研究促进了考虑力学-化学荷载影响下压实黏土垫层中一维固结与污染物运移耦合理论的发展。然而，上述研究大多忽略了固结过程黏土压缩性和渗透性随孔隙比的非线性变化。

在垃圾填埋场等污染场地运行过程中，压实黏土垫层上部通常会产生较大堆填荷载^[21-23]。在该种情况下，考虑压缩性和渗透性随应力增大而降低可更为准确的描述黏土固结过程^{[9-10, 24]}。Peters等^[7]通过对比分析发现，相比于非线性的压缩性关系，假定体积压缩系数为常数会高估污染物运移的击穿时间。Li等^[25]研究指出，上部荷载的增大会使黏土压缩性显著下降。此外，试验研究表明，固结过程中黏土体积压缩系数和渗透系数会随孔隙比发生非线性变化^[26-28]。因此，为更为合理的分析和评价考虑力学-化学荷载影响下压实黏土垫层中一维固结与污染物运移的耦合过程，有必要融入黏土的非线性压缩和渗透特性。

本文通过引入非线性压缩和渗透关系，推导得到了非线性固结和污染物运移的控制方程，并结合相应的初始条件和边界条件建立了考虑力学-化学荷载下压实黏土垫层中一维非线性固结与污染物运移耦合模型。基于有限差分法，对该耦合模型进行了求解。通过将所建耦合模型的计算结果与其他数值方法和已有解析解的计算结果进行比较，验证了模型的正确性。最后，利用所建模型，对比分析了两种假定情况下一维固结与污染物运移的耦合行为。

1. 耦合模型的建立

1.1 计算简图和基本假定

为建立考虑力学-化学荷载下压实黏土垫层中一维非线性固结与污染物运移的耦合模型，这里参考Peters等^[16]研究，给出了相应的计算简图，如。在中，从上至下依次为堆填体、一级渗滤液收集系统(primary leachate collection system，简称PLCS)、渗滤液、压实黏土垫层以及二级渗滤液收集系统(secondary leachate collection system，简称SLCS)。对于渗滤液，其水头大小记为 ${h_{\text{b}}}$ ，污染物浓度记为 ${C_b}$ 。对于压实黏土垫层，其厚度记为 $L$ 。此外，中建立了垂直向下的坐标系 $z$ 。

图 1 耦合模型的计算简图

Figure 1. Schematic diagram of coupled model

下载: 全尺寸图片幻灯片

为发展得到相应的耦合模型，在已有相关理论和试验研究的基础上^{[3, 13-18]}，作如下假定：①土体是均质、各向同性，且完全饱和的；②污染物是可溶解的无机化学物；③污染物浓度变化对孔隙水(液相)密度和土颗粒(固相)密度的影响可忽略；④固结变形和污染物运移只发生在竖直方向；⑤土体的固结变形满足小应变假定；⑥液相的渗流过程满足广义的Darcy定律；⑦考虑固结过程中黏土的压缩性和渗透性随孔隙比的减小发生非线性变化。

1.2 非线性固结控制方程

在压实黏土垫层一维固结过程中，液相和固相的质量守恒方程有^[6-7]：

$\frac{{\partial {\text{(}}n{v_{\text{t}}}{\rho _{\text{f}}}{\text{)}}}}{{\partial z}} + \frac{{\partial {\text{(}}n{\rho _{\text{f}}}{\text{)}}}}{{\partial t}} = 0 \text{，}$

(1a)

$\frac{{\partial {\text{[(1}} - n{\text{)}}{v_{\text{s}}}{\rho _{\text{s}}}{\text{]}}}}{{\partial z}} + \frac{{\partial {\text{[(1}} - n{\text{)}}{\rho _{\text{s}}}{\text{]}}}}{{\partial t}} = 0 。$

(1b)

式中： $n$ 为压实黏土垫层的孔隙率； ${v_{\text{t}}}$ 为液相的流动速度； ${\rho _{\text{f}}}$ 为液相的密度； ${v_{\text{s}}}$ ， ${\rho _{\text{s}}}$ 分别为固相的移动速度和密度； $t$ 为时间。

考虑到污染物浓度的变化对孔隙水和土颗粒密度的影响通常可忽略^[16-18]，式(1)可进一步改写为

$\frac{{\partial {\text{(}}n{v_{\text{t}}}{\text{)}}}}{{\partial z}} + \frac{{\partial n}}{{\partial t}} = 0 \text{，}$

(2a)

$\frac{{\partial {\text{[(1}} - n{\text{)}}{v_{\text{s}}}{\text{]}}}}{{\partial z}} - \frac{{\partial n}}{{\partial t}} = 0 。$

(2b)

对式(2)进行整理可得：

$\frac{{\partial {v_{\text{s}}}}}{{\partial z}} + \frac{{\partial {v_{\text{d}}}}}{{\partial z}} = 0。$

(3)

式中： ${v_{\text{d}}}$ 为达西流速， ${v_{\text{d}}} = n({v_{\text{t}}} - {v_{\text{s}}})$ 。

根据广义的达西定律，在力学-化学荷载作用下，达西流速 ${v_{\text{d}}}$ 的表达式为^{[3, 16]}

${v_{\text{d}}} = {v_{\text{u}}} + {v_\pi }。$

(4)

式中：

${v_{\text{u}}} = - \frac{{{k_{\text{v}}}}}{{{\rho _{\text{f}}}g}}\frac{{\partial u}}{{\partial z}}\text{；}$

(5a)

${v_{\text{π }}} = \frac{{{k_{\text{π }}}}}{{{\rho _{\text{f}}}g}}\frac{{\partial {\text{π }}}}{{\partial z}} = \omega \frac{{{k_{\text{v}}}}}{{{\rho _{\text{f}}}g}}\frac{{\partial {\text{π }}}}{{\partial z}}。$

(5b)

式中： ${v_{\text{u}}}$ ， ${v_{\text{π }}}$ 分别为因力学荷载和化学荷载产生的达西流速； ${k_{\text{v}}}$ 为压实黏土垫层的渗透系数； $g$ 为重力加速度； $u$ 为超孔隙水压力； ${k_{\text{π }}}$ 为化学渗透系数， ${k_{\text{π }}} = \omega {k_{\text{v}}}$ ， $\omega$ 为化学渗透效率系数， $\omega$ 为处于0~1的常数； ${\text{π }}$ 为化学渗透压力， ${\text{π }} = RTC$ ， $R$ 为通用气体常数， $R = 8.314{{{\text{ J}}} \mathord{\left/ {\vphantom {{{\text{ J}}} {{\text{(mol}} \cdot {\text{K)}}}}} \right. } {{\text{(mol}} \cdot {\text{K)}}}}$ ， $T$ 为绝对温度， $C$ 为压实黏土垫层中无机污染物的摩尔质量浓度。

在压实黏土垫层固结变形过程中，渗透系数会随孔隙比的减小发生非线性变化^[24-25]：

$e = {e_0} + {C_{\text{k}}}\lg ({k_{\text{v}}}/{k_{{\text{v0}}}})。$

(6)

式中： ${e_0}$ ， $e$ 分别为初始孔隙比和孔隙比； ${k_{{\text{v0}}}}$ 为初始渗透系数； ${C_{\text{k}}}$ 为土体的渗透指数。在小应变假定下， $e = n/(1 - {n_0})$ ，其中 ${n_0}$ 为初始孔隙率。

因此，渗透系数与孔隙比的变化关系可改写为

${k_{\text{v}}} = {k_{{\text{v0}}}} \cdot {10^{\frac{{e - {e_0}}}{{{C_{\text{k}}}}}}}。$

(7)

根据渗流连续性条件，液相的达西渗流会使得压实黏土垫层发生固结变形，则有

$\frac{{\partial {v_{\text{d}}}}}{{\partial z}} = \frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} = \frac{{\partial {\varepsilon _{\text{m}}}}}{{\partial t}} + \frac{{\partial {\varepsilon _{\text{π }}}}}{{\partial t}}。$

(8)

式中： ${\varepsilon _{\text{v}}}$ ， ${\varepsilon _{\text{m}}}$ ， ${\varepsilon _{\text{π }}}$ 分别为总应变、力学荷载引起的应变和化学荷载引起的应变。

对于力学荷载引起的应变 ${\varepsilon _{\text{m}}}$ ，有^{[3, 16-18]}

$\frac{{\partial {\varepsilon _{\text{m}}}}}{{\partial t}} = {m_{\text{v}}}\frac{{\partial \sigma {'}}}{{\partial t}}。$

(9)

式中： ${m_{\text{v}}}$ 为土体中力学荷载引起的体积压缩系数； $\sigma {'}$ 为有效应力。

对于化学荷载引起的应变 ${\varepsilon _{\text{π }}}$ ，有^{[3, 16-18]}

$\frac{{\partial {\varepsilon _{\text{π }}}}}{{\partial t}} = {m_{\text{π }}}\frac{{\partial {\text{π }}}}{{\partial t}}。$

(10)

式中： ${m_{\text{π }}}$ 为土体中化学荷载引起的体积改变系数。

考虑到压实黏土衬垫固结变形过程通常呈现非线性，则在力学荷载下压缩性的变化关系为^[24-25]

$e = {e_0} - {C_{\text{c}}}\lg (\sigma {'}/{\sigma {'}_0})。$

(11)

式中： ${\sigma {'}_0}$ 为初始有效应力； ${C_{\text{c}}}$ 为压缩指数。

结合式(11)，根据小应变假定下体积压缩系数 ${m_{\text{v}}}$ 的定义， ${m_{\text{v}}}$ 可写为^[25-27]

${m_{\text{v}}} = \frac{{{C_{\text{c}}}}}{{(1 + {e_0})\ln 10 \cdot \sigma {'}}}。$

(12)

结合式(4)，(8)~(10)可得

$\frac{\partial }{{\partial z}}\left[ { - \frac{{{k_{\text{v}}}}}{{{\rho _{\text{f}}}g}}\left( {\frac{{\partial u}}{{\partial z}} - \omega \frac{{\partial {\text{π }}}}{{\partial z}}} \right)} \right] = {m_{\text{v}}}\left( {\zeta \frac{{\partial {\text{π }}}}{{\partial t}} + \frac{{\partial \sigma {'}}}{{\partial t}}} \right)。$

(13)

式中： $\zeta = {m_{\text{π }}}/{m_{\text{v}}}$ 。一般情况下，可认为 $\zeta$ 为常数^[16]。

根据有效应力原理，并参考张志红等^[3]研究，有

$\sigma {'} = {\sigma {'}_0} + {p_{\text{u}}} + {h_{\text{b}}}{\rho _{\text{f}}}g - u。$

(14)

式中： ${p_{\text{u}}}$ 为施加的力学荷载^[3]。

进一步，式(13)可改写为

$\frac{\partial }{{\partial z}}\left[ {\frac{{{k_{\text{v}}}}}{{{\rho _{\text{f}}}g}}\left( {\frac{{\partial u}}{{\partial z}} - \omega RT\frac{{\partial C}}{{\partial z}}} \right)} \right] = {m_{\text{v}}}\left[ {\frac{{\partial u}}{{\partial t}} - \zeta RT\frac{{\partial C}}{{\partial t}}} \right]。$

(15)

式(15)即为考虑力学-化学荷载下压实黏土垫层中一维非线性固结的控制方程。

参考Peters等^[16]研究，固结变形会使得土体的孔隙率减小，进而使得压实黏土垫层发生沉降。考虑到土体的压缩性会随时间和空间位置发生变化，在任意时刻，沉降量的表达式可写为

${S_{\text{s}}} = \int_0^t {\left[ {\int_0^L {\left( { - \frac{{\partial n}}{{\partial t}}} \right){\text{d}}z} } \right]} {\text{d}}t 。$

(16)

$- \frac{{\partial n}}{{\partial t}} = {m_{\text{v}}}\frac{{\partial \sigma {'}}}{{\partial t}} + {m_{\text{v}}}\zeta RT\frac{{\partial C}}{{\partial t}} 。$

(17)

式中： ${S_{\text{s}}}$ 为任意时刻的沉降量。

1.3 污染物运移控制方程

对于污染物在压实黏土垫层中的运移过程，根据Peters等^[7]研究，液相中污染物运移的连续方程为

$- \frac{{\partial {J_{\text{f}}}}}{{\partial z}} = \frac{{\partial (nC)}}{{\partial t}} + s。$

(18)

式中： ${J_{\text{f}}}$ 为液相中污染物的运移通量； $s$ 为单位体积污染物的汇项^[6-7]。

对于液相中污染物的运移过程，考虑到黏性土具有半透膜特性^[3]，因而液相中污染物运移通量 ${J_{\text{f}}}$ 的表达式可写为^{[16, 18-19]}

${J_{\text{f}}} = - (1 - \omega )n{D_{\text{e}}}\frac{{\partial C}}{{\partial z}} + (1 - \omega ){v_{\text{u}}}C + {v_{\text{π }}}C。$

(19)

式中： ${D_{\text{e}}}$ 为污染物在压实黏土垫层中的有效扩散系数， ${D_{\text{e}}} = \tau {D_0}$ ； ${D_0}$ 为污染物在液相中的自由扩散系数； $\tau$ 为弯曲因子； $\tau = {n^\beta }$ ， $\beta$ 为经验系数^[29-30]。

相似地，根据Peters等^[7]研究，固相中污染物运移的连续方程可写为

$- \frac{{\partial {J_{\text{s}}}}}{{\partial z}} = \frac{{\partial [(1 - n){\rho _{\text{s}}}S]}}{{\partial t}} - s。$

(20)

式中： ${J_{\text{s}}}$ 为固相中污染物的运移通量； ${\rho _{\text{s}}}$ 为土颗粒的密度； $S$ 为单位质量土颗粒所吸附的污染物质量； $s$ 为单位体积污染物的源项^[6-7]。

对于固相中污染物运移通量 ${J_{\text{s}}}$ ，其表达式为^[18]

${J_{\text{s}}} = (1 - n){v_{\text{s}}}{\rho _{\text{s}}}S。$

(21)

对于土颗粒对污染物的吸附作用，参考现有研究^{[3, 18-19]}，采用等温线性吸附模型来描述：

$S = {K_{\text{d}}} \cdot C。$

(22)

式中： ${K_{\text{d}}}$ 为线性吸附系数。

结合上述关系式，整理式(18)，(20)可得：

$\begin{array}{l}\frac{\partial (n{R}_{\text{d}}C)}{\partial t}=\\ \frac{\partial }{\partial z}\left[(1-\omega )n{D}_{\text{e}}\frac{\partial C}{\partial z}-(1-\omega ){v}_{\text{u}}C-{v}_{\text{π}}C-(1-n){v}_{s}{\rho }_{s}{K}_{\text{d}}C\right]。\end{array}$

(23)

式中： ${R_{\text{d}}} = 1 + {{(1 - n){\rho _{\text{s}}}{K_{\text{d}}}} \mathord{\left/ {\vphantom {{(1 - n){\rho _{\text{s}}}{K_{\text{d}}}} n}} \right. } n}$ ， ${R_{\text{d}}}$ 为阻滞因子，其值反映了固相土颗粒对污染物的吸附作用^{[1, 4]}。

式(23)即为压实黏土垫层中污染物一维运移的控制方程。

1.4 初始条件和边界条件

一般认为，在初始时刻，压实黏土垫层未受污染。因此，结合压实黏土垫层上部的加荷条件，初始条件可写为^{[3, 16]}

$u(z, 0) = {p_{\text{u}}}\text{，}$

(24a)

$C(z, 0) = 0。$

(24b)

考虑到渗滤液的水头高度为 ${h_{\text{b}}}$ ，其污染物浓度为 ${C_{\text{b}}}$ ，则相应的上部边界条件可写为^[3]

$u(0, t) = {h_{\text{b}}}{\rho _{\text{f}}}g\text{，}$

(25a)

$C(0, t) = {C_{\text{b}}}。$

(25b)

压实黏土垫层底部为二级渗滤液收集系统，则相应的底部边界条件可写为

$u(L, t) = 0\text{，}$

(26a)

$C(L, t) = 0。$

(26b)

2. 耦合模型的解

对于本文所建一维非线性固结与污染物运移的耦合模型，考虑到模型中相关参数如渗透系数和有效扩散系数会随时间和空间发生变化。因此，以下将采用有限差分法对耦合模型进行求解^{[12, 16]}。

2.1 固结控制方程的有限差分格式

设 $\Delta z$ 和 $\Delta t$ 分别为计算空间步长和时间步长，并将其在空间坐标和时间坐标分别进行 $I$ 等分和 $K$ 等分，则有 ${z_i} = i\Delta z$ ， $i = 0, 1, 2, \cdots I$ ， $\Delta z = {L \mathord{\left/ {\vphantom {L I}} \right. } I}$ ， ${t_k} = k\Delta t$ ， $k = 0, 1, 2, \cdots K$ ， $\Delta t = {{{t_0}} \mathord{\left/ {\vphantom {{{t_0}} K}} \right. } K}$ ， ${t_0}$ 为给定时间。因此，控制方程式(15)修正的隐式差分格式可写为

$\begin{array}{l}{X}_{i+1/2}^{k}\frac{{u}_{i+1}^{k+1}-{u}_{i}^{k+1}}{\Delta {z}^{2}}+{X}_{i-1/2}^{k}\frac{{u}_{i-1}^{k+1}-{u}_{i}^{k+1}}{\Delta {z}^{2}}-\omega RT{X}_{i+1/2}^{k}\frac{{C}_{i+1}^{k}-{C}_{i}^{k}}{\Delta {z}^{2}}-\\ \omega RT{X}_{i-1/2}^{k}\frac{{C}_{i-1}^{k}-{C}_{i}^{k}}{\Delta {z}^{2}}={m}_{v, i}^{k}\left(\frac{{u}_{i}^{k+1}-{u}_{i}^{k}}{\Delta t}-\zeta RT\frac{{C}_{i}^{k}-{C}_{i}^{k-1}}{\Delta t}\right)。\end{array}$

(27)

在式(27)中，相关系数的表达式为

$X_i^k = \frac{{{k_{{\text{v0}}}}}}{{{\rho _{\text{f}}}g}} \cdot {10^{\frac{{e_i^k - {e_0}}}{{{C_{\text{k}}}}}}} \text{，}$

(28a)

$X_{i \pm 1/2}^k = {{(X_i^k + X_{i \pm 1}^k)} \mathord{\left/ {\vphantom {{(X_i^k + X_{i \pm 1}^k)} 2}} \right. } 2} \text{，}$

(28b)

$m_{{\text{v}}, i}^k = \frac{{{C_{\text{c}}}}}{{(1 + {e_0})\ln 10 \cdot \sigma {'}_i^k}}\text{，}$

(28c)

$\sigma {'}_i^k = {\sigma {'}_0} + {p_{\text{u}}} + {h_{\text{b}}}{\rho _{\text{f}}}g - u_i^k。$

(28d)

初始条件和边界条件的差分格式为

$u_i^0 = {p_{\text{u}}}\text{，}$

(29)

$\left. \begin{array}{l}{u}_{0}^{k}={h}_{\text{b}}{\rho }_{\text{f}}g\text{ }\text{，}\\ {u}_{I}^{k}=0\text{ }。\end{array} \right\}$

(30)

此外，在 ${t_{\text{k}}} = k\Delta t$ 时刻，沉降量 ${S_{\text{s}}}$ 的差分格式为

$S_s^k = S_s^{k - 1} + \\ \sum\limits_{r = 1}^I {\frac{{\Delta z}}{2}(m_{v, r - 1/2}^{k - 1} + m_{v, r - 1/2}^k)[(\sigma {'}_{r - 1/2}^k - \sigma {'}_{r - 1/2}^{k - 1}) + } \\ \zeta RT(C_{r - 1/2}^k - C_{r - 1/2}^{k - 1})] 。$

(31)

2.2 运移控制方程的有限差分格式

相似地，参考式(27)中所采用的差分格式，控制方程式(23)修正的隐式差分格式可写为

$\frac{{(A_i^{k + 1}C_i^{k + 1} - A_i^kC_i^k)}}{{\Delta t}} = B_{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}^k\frac{{C_{i + 1}^{k + 1} - C_i^{k + 1}}}{{\Delta {z^2}}} +\\ B_{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}^k\frac{{C_{i - 1}^{k + 1} - C_i^{k + 1}}}{{\Delta {z^2}}} - E_i^k\frac{{(C_{i + 1}^{k + 1} - C_{i - 1}^{k + 1})}}{{2\Delta z}}。$

(32)

在式(32)中，相应系数的差分表达式为

$A_i^k = n_i^kR_{{\text{d}}, i}^k = n_i^k + (1 - n_i^k){\rho _{\text{s}}}{K_{\text{d}}}\text{，}$

(33a)

$n_i^k = n_i^{k - 1} - \\ \frac{{(m_{v, i}^{k - 1} + m_{v, i}^k)[(\sigma {'}_i^k - \sigma {'}_i^{k - 1}) + \zeta RT(C_i^k - C_i^{k - 1})]}}{2}\text{，}$

(33b)

$B_i^k = (1 - \omega ){(n_i^k)^{\beta + 1}}{D_0}\text{，}$

(33c)

$B_{i \pm 1/2}^k = {{(B_i^k + B_{i \pm 1}^k)} \mathord{\left/ {\vphantom {{(B_i^k + B_{i \pm 1}^k)} 2}} \right. } 2}\text{，}$

(33d)

$E_i^k = (1 - \omega )v_{{\text{u}}, i}^k + v_{{\text{π }}, i}^k + (1 - n_i^k)v_{{\text{s}}, i}^k{\rho _{\text{s}}}{K_{\text{d}}}。$

(33e)

相应地，初始条件和边界条件的差分格式为

$C_i^0 = 0\text{，}$

(34)

$\left. \begin{array}{l}{C}_{0}^{k+1}={C}_{\text{b}}\text{ }\text{，}\\ {C}_{I}^{k+1}=0\text{ }。\end{array} \right\}$

(35)

需说明的是，出于简化考虑，一些参数的差分格式并未给出，如因力学荷载产生的达西流速 ${v_{\text{u}}}$ 和因化学荷载产生的达西流速 ${v_{\text{π }}}$ 等，但这些参数的表达式均可根据理论模型的推导过程获得。值得注意的是，在压实黏土垫层的边界处，参数的差分格式需结合相应边界条件确定。利用上述差分格式和求解条件即对所建耦合模型展开运算。此外，对于考虑力学-化学荷载下压实黏土垫层中的非线性固结过程与污染物运移过程，考虑到污染物的运移过程通常较慢，这里采用了先对非线性固结过程进行差分求解，后对污染物运移过程进行差分求解的计算方法。因此，在式(27)中，当 $k = 0$ 时，可取 $c_i^0 = c_i^{ - 1}$ 。对于其他参数，同该方法进行取值。

3. 耦合模型的验证

对于土体中一维固结与污染物运移的耦合过程，除采用有限差分法进行研究外，也可利用有限元软件COMSOL Multiphysics展开分析^[18-19]。因此，这里可将所建耦合模型有限差分解的计算结果与COMSOL Multiphysics的计算结果进行比较，以验证所建模型的正确性。此外，当不考虑污染物运移时，所建耦合模型将退化为传统的一维非线性固结模型。Li等^[31]求解获得了土体一维非线性固结近似解析解，并指出C_c/C_k越接近于1，近似解析解与精确解越为接近。因此可对所建耦合模型进行简化，并将其有限差分解与Li等^[31]近似解析解展开对比，以进一步说明所建模型的合理性。在后续分析中，参考Peters等^[16]研究，取NaCl溶液为例，其摩尔质量为0.0585 kg/mol。

3.1 与COMSOL Multiphysics的计算结果对比

如图 2为本文所建耦合模型有限差分解计算结果与COMSOL Multiphysics计算结果的对比情况，其中采用了表 1中所示的计算参数。从图 2可知，在不同时刻，基于两种方法计算所得的超孔隙水压力分布曲线和污染物浓度分布曲线均具有很好的一致性，这既验证了本文所建模型的正确性，也表明所建耦合模型可用于研究考虑力学-化学荷载下压实黏土垫层中一维非线性固结与污染物运移的耦合过程。

图 2 本文所建耦合模型与COMSOL Multiphysics的对比情况

Figure 2. Comparison between proposed coupled model and COMSOL Multiphysics

下载: 全尺寸图片幻灯片

3.2 与Li等^[31]近似解析解的计算结果对比

为将本文所建模型有限差分解与Li等^[31]近似解析解进行对比，这里取表 1中所示参数，设定渗滤液中污染物浓度C_b=0 mol/m³，渗滤液水头h_b=0 m，并假定C_c保持不变。如图 3为不同C_c/C_k下本文所建耦合模型有限差分解计算结果与Li等^[31]近似解析解计算结果的对比情况。从图 3可以看出，在不同的C_c/C_k下，两种方法计算所得的超孔隙水压力分布曲线与沉降量随时间变化曲线均较为吻合，且当C_c/C_k为0.99时，两种方法所得结果具有很高吻合度，这进一步说明了本文所建耦合模型的合理性。

表 1 耦合模型的计算参数

Table 1. Parameters for proposed coupled model

参数	取值
厚度L/m	1.0
初始孔隙率n₀	0.5
液相密度 ${\rho _{\text{f}}}$ /(kg·m^-3)	1000
固相密度 ${\rho _{\text{s}}}$ /(kg·m^-3)	2600
渗透指数C_k	0.198
压缩指数C_c	0.13
初始有效应力 ${\sigma {'}_0}$ /kPa	60
渗透系数k_v0/(m·s^-1)	1.0×10^-10
力学荷载p_u/kPa	100
渗滤液水头h_b/m	0.3
比值ζ	0.005
化学渗透效率系数ω	0.005
温度T/K	293.15
污染物浓度C_b/(kmol·m^-3)	4
线性吸附系数K_d/(m³·kg^-1)	0.8142×10^-3
经验系数β	1.82
自由扩散系数D₀/(m²·s^-1)	5.0×10^-10
注：表中参数的取值源于参考文献[3, 16~19, 24, 30]。

下载: 导出CSV

| 显示表格

图 3 本文所建耦合模型与Li等^[31]近似解析解的对比情况

Figure 3. Comparison between proposed coupled model and Li et al' s approximate analytical solutions

下载: 全尺寸图片幻灯片

4. 模拟分析

对于压实黏土垫层中一维非线性固结与污染物运移耦合过程，以往研究大多未考虑压缩性和渗透性的非线性变化^{[3, 14-16]}。因此，为认识非线性压缩和渗透特性对该物理过程的影响，可基于表 1中所示的物理力学参数展开模拟分析，并与忽略非线性压缩和渗透特性的情况(假定体积压缩系数和渗透系数始终为初始值)进行比较。

4.1 力学荷载的影响

图 4展示了不同力学荷载p_u下压实黏土垫层中沉降量随时间的变化情况(图 4中忽略或考虑非线性是指忽略或考虑土体的非线性压缩和渗透特性，下同)。从图 4可知，无论是否考虑非线性压缩和渗透特性，p_u越大，同一时间下沉降量越大。与此同时，p_u的增大也使得忽略和考虑非线性两种情况下沉降量的差值增大。例如，表 2给出了t=10 a时不同力学荷载p_u下的沉降量。从表 2可知，当p_u=50 kPa时，两种假定情况下的沉降差为1.29 cm；当p_u=150 kPa时，两种假定情况下的沉降差达4.39 cm。这说明，忽略非线性压缩和渗透特性不利于准确预测压实黏土垫层的固结变形特性，尤其在力学荷载较大的情况下。

图 4 不同力学荷载p_u下沉降量的变化

Figure 4. Variation of settlement with time under different p_u

下载: 全尺寸图片幻灯片

表 2 t=10 a时不同力学荷载p_u下的沉降量

Table 2. Settlements under different p_u when t=10 a

力学荷载 p_u/kPa	忽略非线性/ cm	考虑非线性/ cm	沉降差/ cm
50	3.57	2.28	1.29
100	5.92	3.19	2.73
150	8.27	3.88	4.39

下载: 导出CSV

| 显示表格

图 5描述了力学荷载p_u对污染物浓度分布情况的影响。从图 5可知，当忽略非线性时，p_u越大，同一时间下污染物浓度越低，这主要是由于固结变形会使土体孔隙率降低，从而使有效扩散系数减小。然而，当考虑非线性时，p_u的增大反而使得同一时间下污染物浓度升高。出现这一现象的主要原因在于，在考虑非线性情况下，固结变形不仅会使有效扩散系数减小，也会使化学渗透系数等参数降低。由于化学渗透系数降低会减弱化学荷载产生的达西流速，且该达西流速的方向是向上的，因而该达西流速的减小会使阻碍污染物向下运移的作用减弱。对于污染物的运移过程，其会受对流和扩散作用的综合影响^{[3, 16-19]}。在考虑非线性固结特性下，有效扩散系数减小对运移过程的影响较小，化学渗透系数降低对运移过程的影响更为显著。此外，对比考虑非线性和忽略非线性两种情况可知，考虑非线性情况下污染物浓度较高，其原因主要在于，考虑非线性情况下孔隙率的减小量较小。基于上述分析可知，忽略压实黏土垫层非线性压缩和渗透特性会低估污染物的运移速率^[7]。

总的来说，力学荷载p_u越大，同一时间下压实黏土垫层沉降量越大。当忽略非线性时，p_u增大会使污染物浓度降低，但考虑非线性时，p_u增大会使污染物浓度增大。相比于忽略非线性情况，考虑非线性情况下沉降量会减小，污染物运移速率会加快。

图 5 不同力学荷载p_u下污染物浓度的分布

Figure 5. Distribution of contaminant concentration under different p_u

下载: 全尺寸图片幻灯片

4.2 渗滤液中污染物浓度的影响

图 6所示为不同渗滤液中污染物浓度C_b下压实黏土垫层中沉降量随时间变化情况。从图 6可知，C_b越高，同一时间下沉降量越大，这主要是污染物浓度升高会增强土体的化学固结效应^{[3, 16]}。对比忽略和考虑非线性两种情况可以看出，在忽略非线性情况下，C_b对沉降量影响更大。出现这一现象的主要原因在于，在忽略非线性情况下，土体的压缩性更大。

图 6 不同渗滤液中污染物浓度C_b下沉降量的变化

Figure 6. Variation of settlement with time under different C_b

下载: 全尺寸图片幻灯片

图 7展示了不同渗滤液中污染物浓度C_b下超孔隙水压力的分布情况。从图 7可以看出，对于忽略和考虑非线性两种情况，同一时间下超孔隙水压力均随C_b的增大而减小，且当时间较大时，如t=10 a时，土体中的超孔隙水压力基本变为负值，这主要是由于化学荷载会使土体中的孔压降低，从而增大应力^{[3, 16]}。与此同时，对比不同时间下超孔隙水压力的分布规律可知，负的超孔隙水压力绝对值呈现先增大，后减小的趋势，这主要在于前期污染物浓度增大速率较快，后期的浓度分布逐渐趋于稳定(结合控制方程式(15)开展分析)。与此同时，相比于忽略非线性情况，考虑非线性情况下土体中的超孔隙水压力较大，这可能与压缩性降低会减弱化学荷载产生的固结效应有关。

图 7 不同渗滤液中污染物浓度C_b下超孔隙水压力的分布

Figure 7. Distribution of excess pore water pressure under different C_b

下载: 全尺寸图片幻灯片

图 8描述了渗滤液中污染物浓度C_b对污染物浓度分布情况的影响。从图 8可知，C_b越大，同一时间下污染物的相对浓度越低，这说明污染物浓度的升高减慢了污染物运移速率，这一现象主要与污染物浓度升高会增大固结变形量有关。此外，对比可知，在C_b相同的情况下，考虑非线性情况时污染物浓度较高，且不同C_b下污染物浓度的差异较小。

图 8 不同渗滤液中污染物浓度C_b下污染物浓度的分布

Figure 8. Distribution of contaminant concentration under different C_b

下载: 全尺寸图片幻灯片

从上述分析可以看出，渗滤液中污染物浓度C_b越大，同一时间下沉降量越大，超孔隙水压力值越小，污染物相对浓度越低(即污染物运移速率越慢)。与忽略非线性情况相比，在考虑非线性压缩和渗透特性情况下，C_b对沉降量、超孔隙水压力和污染物运移速率的影响会减小。

5. 结论

为认识力学-化学荷载下压实黏土垫层中一维非线性固结与污染物运移的耦合特性，首先推导得到了非线性固结与污染物运移控制方程，并建立了耦合模型，该模型可考虑土体压缩性及渗透性的非线性变化。利用数值方法，获得了该耦合模型有限差分解。随后，通过开展对比分析，验证了所建耦合模型的正确性。最后，基于所建模型，对比探究了忽略与考虑土体非线性压缩和渗透特性两种假定情况下一维固结和污染物运移的耦合行为，得到4点结论。

(1) 随着力学荷载p_u增大，同一时间下压实黏土垫层中沉降量越大，且p_u增大会使忽略和考虑非线性压缩和渗透特性两种情况下沉降量的差值增大。

(2) 当忽略非线性时，p_u的增大会使得污染物运移速率降低；但当考虑非线性时，p_u的增大会使污染物运移速率增大，这主要是由于污染物运移过程会受对流和扩散作用的综合影响。在考虑非线性固结特性情况下，相比于有效扩散系数减小对运移过程的影响，化学渗透系数降低的影响更显著。

(3) 渗滤液中污染物浓度C_b越大，同一时间下沉降量越大，超孔隙水压力值越小，且污染物的相对浓度越低(即污染物运移速率越慢)，其原因主要在于污染物浓度的升高会增大固结变形量。

(4) 相比于忽略非线性压缩和渗透特性情况，在考虑非线性情况下，C_b对沉降量、超孔隙水压力和污染物运移速率的影响会减弱。

图 1 盾构隧道分段示意图

Figure 1. Sectional diagram of shield tunnel

下载: 全尺寸图片幻灯片

图 2 断层破碎带地层典型特征形态

Figure 2. Typical characteristics and morphologies of strata in fault fracture zone

下载: 全尺寸图片幻灯片

图 3 隧道松动土压力计算模型

Figure 3. Computational model for loosening earth pressure in tunnel

下载: 全尺寸图片幻灯片

图 4 盾构隧道管片结构纵向理论模型

Figure 4. Longitudinal theoretical model for segment structure of shield tunnel

下载: 全尺寸图片幻灯片

图 6 断层破碎带与隧道剖面图

Figure 6. Section of fault fracture zone and tunneling position

下载: 全尺寸图片幻灯片

图 7 光纤传感器分布示意图

Figure 7. Distribution of optical fiber sensors

下载: 全尺寸图片幻灯片

图 8 管片内力计算示意图

Figure 8. Calculation of internal force of segment

下载: 全尺寸图片幻灯片

图 9 1529环管片实测弯矩与计算弯矩

Figure 9. Measured and calculated bending moments of segments of No. 1529 ring

下载: 全尺寸图片幻灯片

图 10 1538环管片实测弯矩与计算弯矩

Figure 10. Measured and calculated bending moments of segments of No. 1538 ring

下载: 全尺寸图片幻灯片

图 11 不同断层破碎带倾角隧道纵向沉降图

Figure 11. Longitudinal settlements of tunnel with different inclination angles of fault fracture zone

下载: 全尺寸图片幻灯片

图 12 不同断层破碎带宽度隧道纵向沉降图

Figure 12. Longitudinal settlements of tunnel with different widths of fault fracture zone

下载: 全尺寸图片幻灯片

图 13 不同断层破碎带宽度隧道弯矩图

Figure 13. Bending moments of tunnel with different widths of fault fracture zone

下载: 全尺寸图片幻灯片

图 14 不同断层破碎带弹性模量隧道纵向沉降图

Figure 14. Longitudinal settlements of tunnel with different elastic moduli of fault fracture zone

下载: 全尺寸图片幻灯片

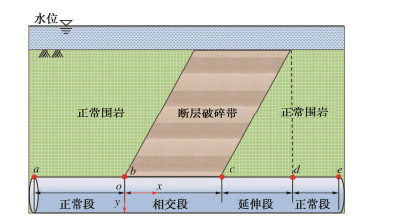
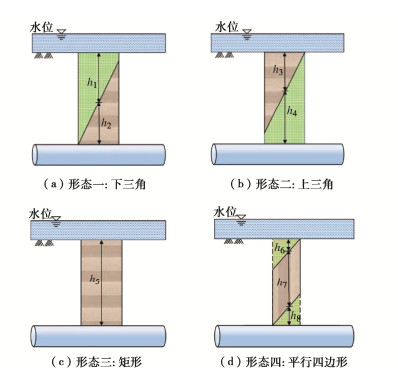
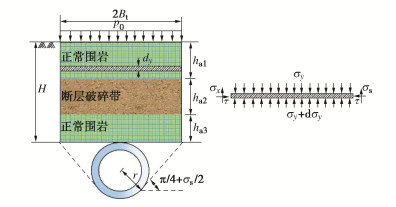
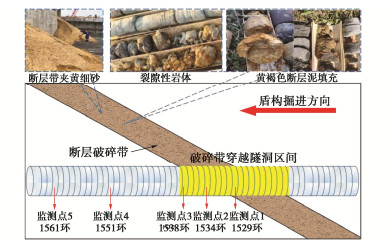
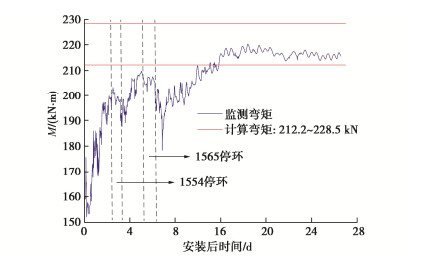
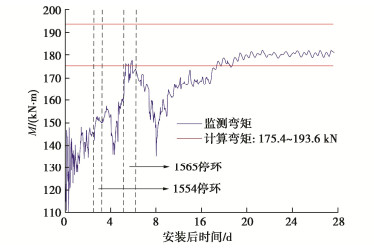
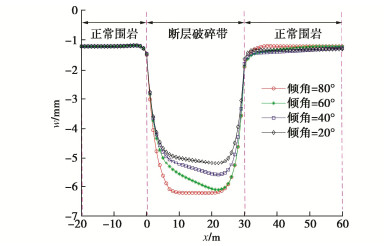
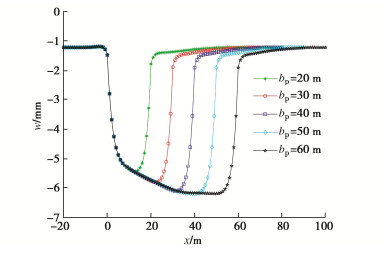
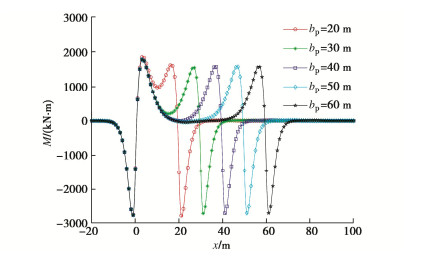
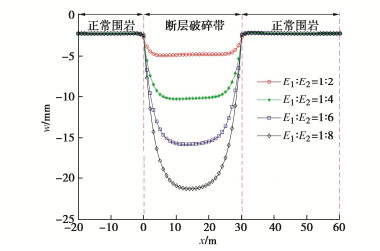
表 1 4种特征形态下海底盾构隧道纵向上覆荷载

Table 1 Longitudinal overlying loads of subsea shield tunnel for four characteristic forms

形态	纵向上覆荷载	${B_t}$ 取值
形态一	${q_{\text{1}}}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left\| {{h_{{\text{a1}}}}{\text{ = }}{h_{\text{1}}}{\text{, }}} \right.{h_{{\text{a1}}}}{\text{ = }}{h_{\text{1}}}{\text{, }}{h_{{\text{a3}}}}{\text{ = 0}}$	${B_t} = {B_{\text{1}}}$
形态二	${q_{\text{2}}}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left\| {{h_{{\text{a1}}}}{\text{ = 0, }}} \right.{h_{{\text{a2}}}}{\text{ = }}{h_3}{\text{, }}{h_{{\text{a3}}}}{\text{ = }}{h_4}$	${B_t} = {B_{\text{2}}}$
形态三	${q_3}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left\| {{h_{{\text{a1}}}} = {h_{{\text{a3}}}} = 0, } \right.{h_{{\text{a2}}}} = {h_5}$	${B_t} = {B_{\text{1}}}$
形态四	${q_4}{\text{(}}x{\text{)}} = q{\text{(}}x{\text{)}}\left\| {{h_{{\text{a1}}}} = {h_{\text{6}}}, {h_{{\text{a2}}}} = {h_7}, } \right.{h_{{\text{a3}}}} = {h_8}$	${B_t} = {B_{\text{2}}}$

下载: 导出CSV

表 2 不同倾角断层破碎带海底隧道纵向上覆荷载

Table 2 Longitudinal overlying loads of subsea tunnel in fault fracture zone with different inclination angles

倾角	上覆荷载
$\alpha = {90^ \circ }$	${q_0}(x{\text{)}}$ $- \infty {\text{ < }}x{\text{ < 0}}$	${q_3}(x{\text{)}}$ ${\text{0}} \leqslant x{\text{ < }}{b_{\text{p}}}$	${q_0}(x{\text{)}}$ ${b_{\text{p}}} \leqslant x{\text{ < + }}\infty$
$\tan \alpha > \frac{H}{{{b_{\text{p}}}}}$	${q_0}(x{\text{)}}$ $- \infty {\text{ < }}x{\text{ < 0}}$	${q_1}(x{\text{)}}$ ${\text{0}} \leqslant x{\text{ < }}\frac{H}{{{\text{tan}}\alpha }}$	${q_3}(x{\text{)}}$ $\frac{H}{{{\text{tan}}\alpha }} \leqslant x \leqslant {b_{\text{p}}}$	${q_2}(x{\text{)}}$ ${b_{\text{p}}}{\text{ < }}x{\text{ < }}{b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }}$	${q_0}(x{\text{)}}$ ${b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }} \leqslant x < + \infty$
$\tan \alpha = \frac{H}{{{b_{\text{p}}}}}$	${q_0}(x{\text{)}}$ $- \infty {\text{ < }}x{\text{ < 0}}$	${q_1}(x{\text{)}}$ ${\text{0}} \leqslant x{\text{ < }}{b_{\text{p}}}$	${q_3}(x{\text{)}}$ $x = {b_{\text{p}}}$	${q_2}(x{\text{)}}$ ${b_{\text{p}}}{\text{ < }}x \leqslant {\text{2}}{b_{\text{p}}}$	${q_0}(x{\text{)}}$ ${\text{2}}{b_{\text{p}}}{\text{ < }}x{\text{ < + }}\infty$
$\tan \alpha < \frac{H}{{{b_{\text{p}}}}}$	${q_0}(x{\text{)}}$ $- \infty {\text{ < }}x{\text{ < 0}}$	${q_1}(x{\text{)}}$ ${\text{0}} \leqslant x{\text{ < }}{b_{\text{p}}}$	${q_4}(x{\text{)}}$ ${b_{\text{p}}} \leqslant x < \frac{H}{{{\text{tan}}\alpha }}$	${q_2}(x{\text{)}}$ $\frac{H}{{{\text{tan}}\alpha }} \leqslant x \leqslant {b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }}$	${q_0}(x{\text{)}}$ ${b_{\text{p}}}{\text{ + }}\frac{H}{{{\text{tan}}\alpha }}{\text{ < }}x{\text{ < }} + \infty$

下载: 导出CSV

表 3 4种破碎带形态及其对应上覆荷载

Table 3 Four types of fracture zones and their corresponding overlying loads

破碎带形态	$\alpha = {90^ \circ }$	$\tan \alpha > \frac{H}{{{b_{\text{p}}}}}$	$\tan \alpha = \frac{H}{{{b_{\text{p}}}}}$	$\tan \alpha < \frac{H}{{{b_{\text{p}}}}}$
上覆荷载	f₁(x)	f₂(x)	f₃(x)	f₄(x)

下载: 导出CSV

表 4 断层破碎带及围岩力学参数

Table 4 Mechanical parameters of fault fracture zone and surrounding rock

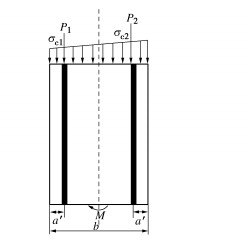
类型	$\gamma {\text{/}}$ ${\text{(kN}} \cdot {{\text{m}}^{ - {\text{3}}}}{\text{)}}$	$\varphi$ /(°)	$c{\text{/}}$ kPa	$E{\text{/}}$ GPa	$\nu$	k
正常围岩	26	30	100	1.6	0.33	0.49
断层破碎带	20	25	30	0.5	0.40	0.67

下载: 导出CSV

表 5 螺栓及钢筋相关参数

Table 5 Relevant parameters of bolt and reinforcement

a'/mm	E_e/GPa	n₁	n₂	E_c/GPa
50	210	20	10	3.15×10⁴

n_b	E_b/GPa	l_b/mm	A_b/m²	${\alpha _{\text{b}}}{\text{/}}$ (°)
28	210	730	7.069×10^-4	35
注： $a'$ 为钢筋保护层厚度；E_e为钢筋弹性模量；n₁为管片内侧环向主筋数量；n₂为管片外侧环向主筋数量；E_c为管片弹性模量；n_b为纵向螺栓个数；E_b为螺栓弹性模量；l_b为螺栓长度，A_b为螺栓横截面面积； ${\alpha _{\text{b}}}$ 为螺栓倾角。

下载: 导出CSV

参考文献(20)

[1]	张顶立. 海底隧道不良地质体及结构界面的变形控制技术[J]. 岩石力学与工程学报, 2007, 26(11): 2161-2169. doi: 10.3321/j.issn:1000-6915.2007.11.001 ZHANG Dingli. Deformation control techniques of unfavorable geologic bodies and discontinuous surfaces in subsea tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2161-2169. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.11.001
[2]	BURFORD D. Heave of tunnels beneath the shell centre, London, 1959–1986[J]. Géotechnique, 1988, 38(1): 135-137. doi: 10.1680/geot.1988.38.1.135
[3]	王春浩. 超大断面黄土公路隧道围岩压力计算方法分析[J]. 现代隧道技术, 2015, 52(3): 175-181. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201503026.htm WANG Chunhao. Calculation method for surrounding rock pressure of a loess highway tunnel with an extra-large section[J]. Modern Tunnelling Technology, 2015, 52(3): 175-181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201503026.htm
[4]	李鸿博, 郭小红. 公路连拱隧道土压力荷载的计算方法研究[J]. 岩土力学, 2009, 30(11): 3429-3434. doi: 10.3969/j.issn.1000-7598.2009.11.035 LI Hongbo, GUO Xiaohong. Research on calculation metheods of earth pressure on Muti-arch tunnel for highway[J]. Rock and Soil Mechanics, 2009, 30(11): 3429-3434. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.11.035
[5]	铁路隧道设计规范: TB 10003—2016[S]. 北京: 中国铁道出版社, 2017. Code for Design of Railway Tunnel: TB 10003—2016[S]. Beijing: China Railway Publishing House, 2017. (in Chinese)
[6]	黎春林. 盾构隧道施工松动土压力计算方法研究[J]. 岩土工程学报, 2014, 36(9): 1714-1720. doi: 10.11779/CJGE201409019 LI Chunlin. Method for calculating loosening earth pressure during construction of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1714-1720. (in Chinese) doi: 10.11779/CJGE201409019
[7]	TERZAGHI K. Theoretical Soil Mechanics[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 1943.
[8]	王浩, 杨新安, 王斌, 等. 3洞小净距隧道围岩压力计算方法[J]. 中国铁道科学, 2020, 41(3): 68-75. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK202003008.htm WANG Hao, YANG Xin'an, WANG Bin, et al. Calculation method for surrounding rock pressure of closely spaced triple tunnels[J]. China Railway Science, 2020, 41(3): 68-75. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK202003008.htm
[9]	颉永斌, 董建华. 断层破碎带内隧道纵向受荷特征和变形分析[J]. 中国公路学报, 2021, 34(11): 211-224. doi: 10.3969/j.issn.1001-7372.2021.11.017 XIE Yongbin, DONG Jianhua. Analysis of longitudinal deformation and stress characteristics of tunnel crossing fault fracture zone[J]. China Journal of Highway and Transport, 2021, 34(11): 211-224. (in Chinese) doi: 10.3969/j.issn.1001-7372.2021.11.017
[10]	ZHANG Z G, HUANG M S, WANG W D. Evaluation of deformation response for adjacent tunnels due to soil unloading in excavation engineering[J]. Tunnelling and Underground Space Technology, 2013, 38: 244-253. doi: 10.1016/j.tust.2013.07.002
[11]	LIANG R Z, XIA T D, HONG Y, et al. Effects of above-crossing tunnelling on the existing shield tunnels[J]. Tunnelling and Underground Space Technology, 2016, 58: 159-176. doi: 10.1016/j.tust.2016.05.002
[12]	LIU X, FANG Q, ZHANG D L, et al. Behaviour of existing tunnel due to new tunnel construction below[J]. Computers and Geotechnics, 2019, 110: 71-81. doi: 10.1016/j.compgeo.2019.02.013
[13]	WU H N, SHEN S L, LIAO S M, et al. Longitudinal structural modelling of shield tunnels considering shearing dislocation between segmental rings[J]. Tunnelling and Underground Space Technology, 2015, 50: 317-323. doi: 10.1016/j.tust.2015.08.001
[14]	LIAO S M, PENG F L, SHEN S L. Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction[J]. Tunnelling and Underground Space Technology, 2008, 23(4): 421-430. doi: 10.1016/j.tust.2007.07.001
[15]	ZHANG D M, HUANG Z K, LI Z L, et al. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath[J]. Computers and Geotechnics, 2019, 108: 197-211.
[16]	陈祖煜. 土质边坡稳定分析: 原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003. CHEN Zuyu. Soil Slope Stability Analysis: Theory, Methods and Programs[M]. Beijing: China Water & Power Press, 2003. (in Chinese)
[17]	志波由纪夫, 川岛一彦, 大日方尚己, 等. 应答变位法にょるツ—ルドトンネルの地震时断面力の算定法[J]. 土木学会论文集, 1989, 404(11): 385–394. SHIBA Y, KAWASHIMA K, OBINATA N, KANO K. Evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analysis[J]. Proceedings of the Japan Society of Civil Engineers, 1989, 404(11): 385-394. (in Japanese)
[18]	ATTEWELL P B, YEATES J, SELBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. Glawsgow: Blackie, 1986.
[19]	张厚美. 地铁盾构工程设计与施工过程的若干问题研究[D]. 上海: 上海交通大学, 2004. ZHANG Houmei. Research on Some Problems in the Design and Construction Process of Subway Shield Engineering[D]. Shanghai: Shanghai Jiao Tong University, 2004. (in Chinese)
[20]	城市轨道交通结构安全保护技术规范: GJJ/T 202—2013[S]. 北京: 北京建筑工业出版社, 2013. Technical Code for Protection Structures of Urban Rail Transit: GJJ/T 202—2013[S]. Beijing: China Architecture and Builiding Press, 2013. (in Chinese)

施引文献(10)

期刊类型引用(6)

1.	华龙飞，万勇，陈之祥，李顺群. 考虑水油分离的柴油污染土持液特性试验研究. 岩土工程学报. 2025(05): 995-1003 . 本站查看
2.	郭浩天，江珊，李向群. 长春地区非饱和粉质黏土的土-水特征试验研究. 吉林建筑大学学报. 2024(02): 58-64 . 百度学术
3.	黄楠，朱斌，王路君. 考虑水合物孔隙赋存模式演化的含水合物沉积物渗透率模型. 岩土力学. 2024(08): 2387-2396+2410 . 百度学术
4.	肖泽镛. 赣南地区红黏土毛细渗透系数变化规律及影响因素. 四川建材. 2024(08): 81-83 . 百度学术
5.	付佳妮，于晓曦，傅晓敏，赵航，刘昌岭，马云，刘乐乐. 孔隙水盐度与黏土类型对海洋沉积物水分特征曲线的影响研究. 地质学报. 2024(09): 2795-2805 . 百度学术
6.	徐卫平，丁拼搏，张峰，狄帮让，蔡志光，梅璐璐. 天然气水合物岩石物理实验研究进展. 石油物探. 2023(06): 1016-1029 . 百度学术

其他类型引用(4)

资源附件(1)

其他相关附件

图(13) / 表(5)

计量

文章访问数: 287
HTML全文浏览量: 64
PDF下载量: 104
被引次数: 10

0. 引言
1. 耦合模型的建立
1.1 计算简图和基本假定
1.2 非线性固结控制方程
1.3 污染物运移控制方程
1.4 初始条件和边界条件
2. 耦合模型的解
2.1 固结控制方程的有限差分格式
2.2 运移控制方程的有限差分格式
3. 耦合模型的验证
3.1 与COMSOL Multiphysics的计算结果对比
3.2 与Li等[31]近似解析解的计算结果对比
4. 模拟分析
4.1 力学荷载的影响
4.2 渗滤液中污染物浓度的影响
5. 结论

0. 引言
1. 耦合模型的建立
1.1 计算简图和基本假定
1.2 非线性固结控制方程
1.3 污染物运移控制方程
1.4 初始条件和边界条件
2. 耦合模型的解
2.1 固结控制方程的有限差分格式
2.2 运移控制方程的有限差分格式
3. 耦合模型的验证
3.1 与COMSOL Multiphysics的计算结果对比
3.2 与Li等^[31]近似解析解的计算结果对比
4. 模拟分析
4.1 力学荷载的影响
4.2 渗滤液中污染物浓度的影响
5. 结论

参考文献(20)

施引文献

资源附件(1)

断层破碎带海底盾构隧道管片纵向沉降解析解及应用 English Version

作者简介: 付艳斌(1977—)，男，博士，主要从事隧道及地下工程方面的教学与研究工作。E-mail: fuyanbin999@163.com

计量

出版历程

Analytical solution to longitudinal settlement of segments of subsea shield tunnels in fault fracture zones and its application

0. 引言

1. 耦合模型的建立

1.1 计算简图和基本假定

1.2 非线性固结控制方程

1.3 污染物运移控制方程

1.4 初始条件和边界条件

2. 耦合模型的解

2.1 固结控制方程的有限差分格式

2.2 运移控制方程的有限差分格式

3. 耦合模型的验证

3.1 与COMSOL Multiphysics的计算结果对比

3.2 与Li等[31]近似解析解的计算结果对比

4. 模拟分析

4.1 力学荷载的影响

4.2 渗滤液中污染物浓度的影响

5. 结论

期刊类型引用(6)

其他类型引用(4)

其他相关附件

计量

出版历程

目录

0. 引言

1. 耦合模型的建立

1.1 计算简图和基本假定

1.2 非线性固结控制方程

1.3 污染物运移控制方程

1.4 初始条件和边界条件

2. 耦合模型的解

2.1 固结控制方程的有限差分格式

2.2 运移控制方程的有限差分格式

3. 耦合模型的验证

3.1 与COMSOL Multiphysics的计算结果对比

3.2 与Li等[31]近似解析解的计算结果对比

4. 模拟分析

4.1 力学荷载的影响

4.2 渗滤液中污染物浓度的影响

5. 结论

作者简介:
付艳斌(1977—)，男，博士，主要从事隧道及地下工程方面的教学与研究工作。E-mail: fuyanbin999@163.com

3.2 与Li等^[31]近似解析解的计算结果对比

3.2 与Li等^[31]近似解析解的计算结果对比