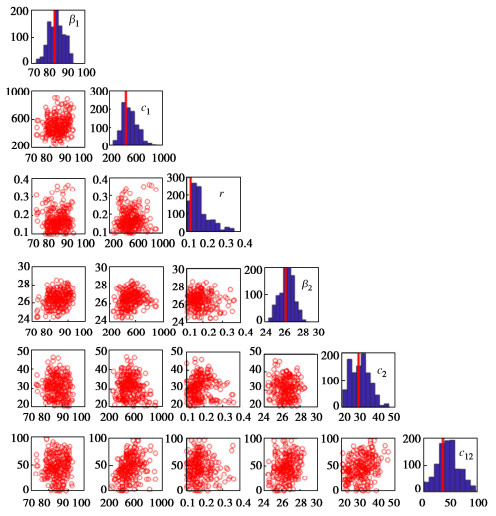
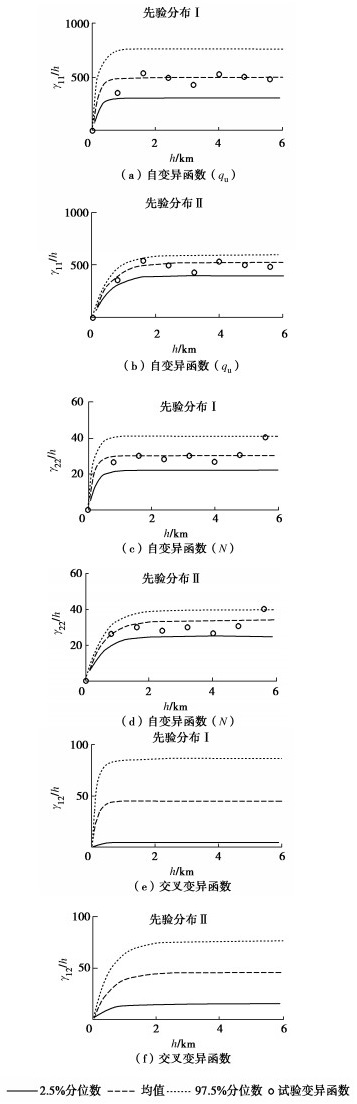
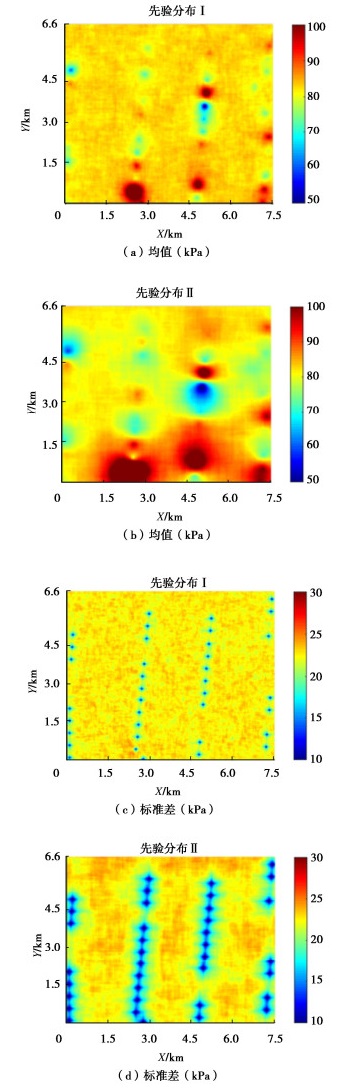
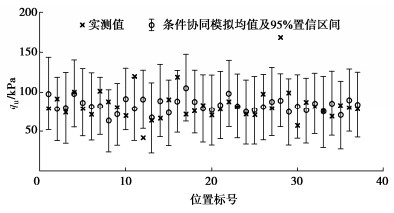
| 参数 | β1/kPa | c1/kPa | r/km | β2/击 | c2/击 | c12 |
| 下限 | 0 | 0 | 0.1 | 0 | 0 | 0 |
| 上限 | 200 | 1000 | 2 | 50 | 100 | 200 |
先验分布Ⅰ
本文全文图片
本文全文表格
-
常用的变异函数与协方差函数模型
类型 变异函数 协方差函数 指数模型 $ \left\{ \begin{array}{l} {c_1}\left[ {1 - \exp \left( { - \frac{h}{r}} \right)} \right]{\text{ (}}h > 0) \hfill \\ 0{\text{ (}}h = 0) \hfill \\ \end{array} \right. $ $ \left\{ {\begin{array}{*{20}{l}} {{c_1}\exp \left( { - \frac{h}{r}} \right){\text{ (}}h > 0)} \\ {{c_1}{\text{ (}}h = 0)} \end{array}} \right. $ 高斯模型 $\left\{ {\begin{array}{*{20}{l}} {{c_1}\left[ {1 - \exp \left( { - \frac{{{h^2}}}{{{r^2}}}} \right)} \right]{\text{ (}}h > 0)} \\ {0{\text{ (}}h = 0)} \end{array}} \right.$ $ \left\{ {\begin{array}{*{20}{l}} {{c_1}\exp \left( { - \frac{{{h^2}}}{{{r^2}}}} \right){\text{ (}}h > 0)} \\ {{c_1}{\text{ (}}h = 0)} \end{array}} \right. $ 球状模型 $ \left\{ \begin{array}{l} 0{\text{ (}}h = 0) \hfill \\ {c_1}\left( {\frac{{3h}}{{2r}} - \frac{{{h^3}}}{{2{r^3}}}} \right){\text{ (}}0 < h \leqslant r) \hfill \\ {c_1}{\text{ (}}h > r) \hfill \\ \end{array} \right. $ $ \left\{ \begin{array}{l} {c_1}{\text{ (}}h = 0) \hfill \\ {c_1}\left( {1 - \frac{{3h}}{{2r}} + \frac{{{h^3}}}{{2{r^3}}}} \right){\text{ (}}0 < h \leqslant r) \hfill \\ 0{\text{ }}(h > r) \hfill \\ \end{array} \right. $ -
先验分布Ⅰ
参数 β1/kPa c1/kPa r/km β2/击 c2/击 c12 下限 0 0 0.1 0 0 0 上限 200 1000 2 50 100 200 -
先验分布Ⅱ
参数 β1/kPa c1/kPa r/km β2/击 c2/击 c12 下限 0 100 0.5 0 0 10 上限 200 600 2 50 40 100


 下载:
下载: