低渗地层盾构隧道壁后注浆压密-劈裂扩散模型研究

叶飞; 李思翰; 夏天晗; 苏恩杰; 韩兴博; 张才飞

doi:10.11779/CJGE20220812

低渗地层盾构隧道壁后注浆压密-劈裂扩散模型研究 English Version

长安大学公路学院, 陕西西安 710064

基金项目:

国家自然科学基金项目 51878060

国家自然科学基金青年基金项目 52108360

中国博士后科学基金项目 2020M683398

详细信息

作者简介:
叶飞(1977—)，男，博士，教授，主要从事隧道及地下工程方面的研究与教学工作。E-mail: xianyefei@126.com

通讯作者:
韩兴博, E-mail: xingbo.han@chd.edu.cn

中图分类号: U455
计量
- 文章访问数: 363
- HTML全文浏览量: 64
- PDF下载量: 139
出版历程
- 收稿日期: 2022-06-27
- 网络出版日期: 2023-10-16
- 刊出日期: 2023-09-30

Compaction-fracture diffusion model for backfill grouting of shield tunnels in low permeability strata

School of Highway, Chang'an University, Xi'an 710064, China

摘要

摘要: 通过对盾构隧道环向浆液压力分布、起劈压力分布的计算，建立了低渗地层盾构隧道壁后注浆压密-劈裂扩散模型，提出了环向劈裂区间角及其计算方法，给出了浆液扩散距离与劈裂通道宽度计算式，并分析土体侧压力系数、盾构埋深对劈裂区间角的影响及土体弹性模量、浆液黏度对浆液最大扩散距离与劈裂通道宽度的影响，结合理论对盾构掘进过程中地表冒浆问题进行了讨论。研究结果表明：在低渗地层进行盾构隧道壁后注浆时，浆液在劈裂区间角内以劈裂形式扩散，在其余区域以压密形式扩散；劈裂区间角与土体侧压力系数、隧道埋深均呈负相关关系；最大扩散距离与注浆压力差，最大通道宽度与最大扩散距离均呈指数关系，其指数分别为4，0.25；正常注浆参数下，浆液向下扩散距离远大于向上扩散距离，结合某城际铁路盾构隧道实际注浆参数及地层参数，分析了地表冒浆的原因，进一步验证了该扩散模型的合理性。
- 盾构隧道 /
- 壁后注浆 /
- 劈裂扩散 /
- 扩散距离
Abstract: Based on the calculation of annular grout pressure distribution and fracturing pressure distribution of shield tunnels, the grouting compaction-fracture diffusion model for shield tunnel segments in low permeability strata is established, the annular fracturing interval angle and its calculation method are proposed, and the formula for calculating the diffusion distance and channel width is given. The influences of lateral pressure coefficient of soils and buried depth of shield on the fracturing interval angle as well as those of elastic modulus of soils and grout viscosity on the maximum diffusion distance and channel width are analyzed. The results show that the grout diffuses in fracture mode in the fracture interval angle, and the grout diffuses in compaction mode in the other regions. The fracturing interval angle is negatively correlated with lateral pressure coefficient of soils and tunnel depth. The relationship between the maximum diffusion distance and the grouting pressure difference and that between the maximum channel width and the maximum diffusion distance are both exponential, and the indices are 4 and 0.25, respectively. Under the normal grouting parameters, the downward diffusion distance of the diffusion grout is much larger than the upward one. Based on the actual grouting parameters and stratum parameters of an inter-city railway shield tunnel, the causes for surface grout-oozing are analyzed, and the rationality of diffusion model is further verified.
- shield tunnel /
- backfill grouting /
- fracture diffusion /
- diffusion distance

HTML全文

0. 引言

盾构法因其较小的施工扰动、高机械化等优势逐渐成为城市隧道建设的主要施工方法^[1]。截至2023年8月，中国共计54座城市开通轨道交通，累计线路297条，运营里程9771.8 km^[2]。

盾构法隧道施工中需着重考量其开挖面稳定、掘进参数控制、管片质量及壁后注浆等方面^[3]。盾构掘进时，因刀盘直径较管片外径大，管片外径与地层之间会形成一圈空隙，该空隙被称为盾尾间隙，壁后注浆的主要作用之一便是填充盾尾间隙^[4-5]。同时，盾构隧道壁后注浆还具有加固周边地层以提高隧道抗渗能力、降低地层变形、减小施工扰动等作用^[6]。浆液的扩散模式主要分为充填扩散、渗透扩散、压密扩散及劈裂扩散4种模式，且各扩散模式可协同发生^[7]。充填扩散理论通过建立环向和纵向充填模型，得出了浆液充填过程及压力分布^[8]；渗透扩散理论基于毛细管理论、达西定律等，并结合浆液流形、黏度时变性、渗滤效应等特点建立了渗透扩散模型^[9-11]；压密扩散理论主要通过采用弹塑性理论，得出了土体有效应力与径向位移^[12-14]。

现行对浆液劈裂扩散模型的研究多体现在地基加固、隧道超前注浆加固等方面，在盾构隧道壁后注浆方面考虑浆液劈裂扩散模式一般较少，其原因是普遍研究认为只有浆液压力较大时才会发生劈裂扩散^[15]，但在研究^[16-18]中当注浆压力为0.1~0.5 MPa时浆液已经发生了劈裂扩散模式，与盾构隧道壁后注浆时常用的注浆压力0.2~0.4 MPa较为一致。同时考虑到浆液劈裂扩散对隧道结构本体影响的不确定性，低渗地层盾构隧道壁后注浆劈裂扩散模式是需要被重视的。劈裂注浆时土体会经历一个先压密再劈裂的过程，可分为鼓泡压密、劈裂流动、被动土压力3个阶段^[19]。劈裂通道可以简化成管道和平板两种模式，给出了针对幂律流体^[20]、宾汉姆流体、牛顿流体^[21]的注浆压力、扩散半径、劈裂通道宽度等参数间关系。

目前综合考量盾构隧道壁后注浆压密-劈裂扩散模型的研究较少，本文基于弹性力学、流体力学理论，通过对盾尾环向起劈压力与浆液压力分布的计算，建立低渗地层盾构隧道壁后注浆压密-劈裂扩散模型，提出劈裂区间角及其计算方法，并给出劈裂扩散时浆液的运动方程、劈裂通道宽度控制方程、通道内浆液压力分布方程，最后结合工程实际注浆参数，分析各参数间的相关规律并针对实际工程问题进行讨论。

1. 压密-劈裂扩散模式界定

1.1 压密劈裂区域界定

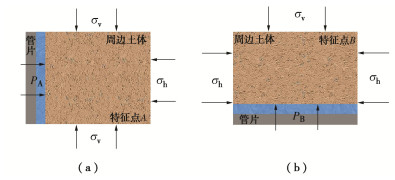
考虑当浆液充填满盾尾间隙后，随着浆液的继续注入，盾尾环向周边土体首先发生压密现象，浆液的继续注入进而引起浆液压力增大，浆液会在环向部分区域内进行劈裂扩散，考虑地层的水平主应力和竖直主应力方向，选取过圆心水平、垂直轴线上两点为特征点，对特征点A，B进行微元体受力分析（如图 1）。此时，假定浆液、水均不可压缩，注浆过程中其流型不变，且不考虑浆液的流失和地层应力分布的不均匀性。

图 1 浆液充填及特征点位置示意图

Figure 1. Schematic diagram of grout filling and location of feature points

下载: 全尺寸图片幻灯片

取A点处进行微元体受力分析，因微元体远小于管片直径，忽略管片曲率，如图 2（a）所示。

图 2 特征点A, B微元体受力情况

Figure 2. Stress conditions of element body at feature points A and B

下载: 全尺寸图片幻灯片

P_A为A点处浆液压力， ${\sigma _{\text{h}}}$ ， ${\sigma _{\text{v}}}$ 为土体水平和竖直主应力，一般情况下，土体水平主应力为小主应力，竖直主应力为大主应力，即 ${\sigma _{\text{h}}}$ ＜ ${\sigma _{\text{v}}}$ ，其比值为土体侧压力系数K₀，一般小于1。

随着壁后注浆的进行，微元体受力依次存在4个阶段：①无压充填阶段，P_A=0，此时浆液首先填充盾尾间隙，浆液阻力较小，浆液压力基本为0；②压密阶段，P_A= ${\sigma _{\text{h}}}$ 时，周边土体开始压缩，土体水平应力随着浆液压力的增大协同增大；③P_A＞ ${\sigma _{\text{v}}}$ = ${\sigma _{\text{h}}}$ 时，微元体由受压状态转为受拉状态；④当土体拉应力大于其抗拉强度时开始劈裂，此时的浆液压力称为起劈压力。

取B点处微元体进行受力分析，基本参数选取和假定同上，如图 2（b）所示。协同考虑A点状态，B点处微元体受力存在2个阶段：①无压充填阶段，P_B=0，此时浆液首先填充盾尾间隙，此阶段浆液阻力较小，浆液压力基本为0；②因 ${\sigma _{\text{h}}}$ ＜ ${\sigma _{\text{v}}}$ ，当P_B达到起劈压力，土体发生劈裂。

由对特征点A，B的分析可知，盾尾环向劈裂发生区域应沿其最大主应力方向，存在于一定角度内，在考量低渗地层的情况下，其余区域为压密注浆。

1.2 盾尾环向起劈压力分布

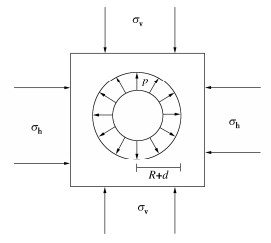
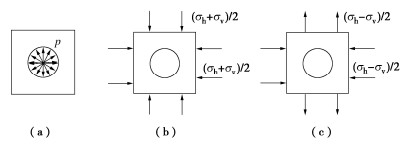
盾构壁后注浆平面受力图可简化为图 3，R为管片外径，土体受到浆液压力为p，盾尾间隙厚度为d，θ为周边土体任意一点与圆心连线和 ${\sigma _{\text{h}}}$ 的夹角， ${r_\theta }$ 为任意一点到圆心的距离，规定拉应力为正，根据扩孔理论，盾尾间隙附近应力状态可分解为图 4（a），（b），（c）叠加。

图 3 盾构壁后注浆平面受力图

Figure 3. Forces on backfill grouting of shield tunnel

下载: 全尺寸图片幻灯片

图 4 盾尾间隙附近应力状态分解图

Figure 4. Decomposition of stress state near shield tail

下载: 全尺寸图片幻灯片

叠加后盾尾间隙周围土体的拉应力可以表达为

$\begin{array}{r} \sigma_\theta=\left(\frac{R+d}{r_\theta}\right)^2 p-\frac{\sigma_{\mathrm{h}}+\sigma_{\mathrm{v}}}{2}\left[1+\left(\frac{R+d}{r_\theta}\right)^2\right]+ \\ \frac{\sigma_{\mathrm{h}}-\sigma_{\mathrm{v}}}{2} \cos 2 \theta\left[1+3\left(\frac{R+d}{r_\theta}\right)^2\right] 。 \end{array}$

(1)

当 ${r_\theta }$ =R+d时， ${\sigma _\theta }$ 为径向拉力最大值，即近邻盾尾间隙处的土体产生最大拉应力。由式（1）和 ${\sigma _{\text{h}}}$ ＜ ${\sigma _{\text{v}}}$ 可知，当θ=π/2， ${r_\theta }$ =R+d时，拉应力最大，此方向即为最大主应力方向。

记R_m为土体抗拉强度，当 ${\sigma _\theta }$ ＞R_m时，土体发生劈裂，此时的浆液压力为起劈压力 ${P_{\text{q}}}$ ，表达式为

${P_{\text{q}}} = {R_{\text{m}}} + ({\sigma _{\text{h}}} + {\sigma _{\text{v}}}) - 2({\sigma _{\text{h}}} - {\sigma _{\text{v}}})\cos 2\theta 。$

(2)

水平主应力与垂直主应力之比为土体侧压力系数K₀，土体的侧压力系数K₀一般小于1，表达式为

${K}_{0}=\frac{{\sigma }_{\text{h}}}{{\sigma }_{\text{v}}}\text{ }({K}_{0}＜1) 。$

(3)

考虑垂直主应力为隧道上部覆土重量，则盾尾环向各处垂直主应力 ${\sigma _{\text{v}}}$ 可表达为

${\sigma _{\text{v}}} = \gamma [H - (R + d)\sin \theta ] 。$

(4)

式中： $\gamma$ 为上覆土体重度；H为盾构中心埋深。

联立式（2）~（4），得盾构隧道环向起劈压力分布：

$\begin{aligned} P_{\mathrm{q}}= & R_{\mathrm{m}}+\gamma[H-(R+d) \sin \theta]\left[\left(K_0+1\right)-\right. \\ & \left.2\left(K_0-1\right) \cos 2 \theta\right] 。 \end{aligned}$

(5)

1.3 盾尾环向浆液压力分布

引入文献[22]中盾尾同步注浆浆液充填压力分布模型，并保持其基本假定。

因盾构推进速率较慢，模型将盾尾间隙考量为环形薄饼空间，其厚度为单位时间内盾构推进距离。因厚度和盾尾间隙宽度存在数量级差距，在盾尾注浆过程中，忽略浆液沿隧道轴向的流动，认为浆液仅沿盾尾间隙环向流动。

根据推导，浆液由i号注浆孔填充盾尾间隙的充填压力分布式 ${P_{\text{h}}}$ 表示为

${P_{\text{h}}} = {P_i} + A(\sin {\theta _i} - \sin \theta ) \pm B({\theta _i} - \theta ) 。$

(6)

式中：P_i为i号注浆孔注浆压力；θ为浆液的充填位置偏离水平方向角度（同周边土体任意一点与圆心连线和 ${\sigma _{\text{h}}}$ 的夹角）；θ_i为注浆孔i偏离水平方向的角度；A=ρgR(ρ为浆液密度，g为重力加速度；R为管片外半径)。

上式中的“±”，浆液向下填充取“+”；浆液向上填充取“-”。

当浆液作牛顿流体考虑时，参数B的表达式为

$B = \frac{{12R\mu q}}{{{\text{d}}{\delta ^3}}} 。$

(7)

式中：μ为浆液塑性黏度；q为注浆孔截面流量；δ为浆液流动饼环厚度。

注浆孔截面流量q，饼环厚度δ的表达式为

$q = \frac{{{\text{π }}\left[ {{{(R + d)}^2} - {R^2}} \right]{v_{\text{s}}}\mathit{\lambda} }}{{2n}} \approx \frac{{{\text{π }}Rd{v_{\text{s}}}\mathit{\lambda} }}{n} \text{，}$

(8)

$\delta = {v_{\text{s}}}{t_0} \quad。$

(9)

式中： $\mathit{\lambda}$ 为注入率；n为盾尾注浆孔数量； ${v_{\text{s}}}$ 为盾构推进速度；t₀为盾尾同步注浆时浆液填充盾尾间隙所需的平均时间。

联立式（6）~（9），可计算得出盾尾环向浆液压力分布。

1.4 压密-劈裂扩散模型的确定

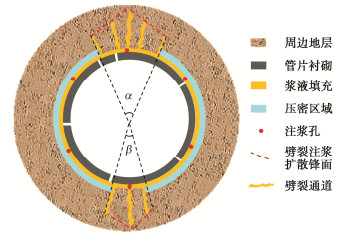
当P_h-P_q＞0时，认定土体存在劈裂可能，对特征点、盾尾环向起劈压力分布、盾尾环向浆液压力分布进行分析，得出沿土体最大主应力方向一定角度内浆液存在发生劈裂的空间，其余P_h-P_q＜0的环向角度内，浆液以压密形式扩散，记劈裂区域角度为劈裂区间角α和β，则低渗地层盾构隧道壁后注浆压密-劈裂扩散模型示意如图 5。

图 5 低渗地层盾构隧道壁后注浆压密-劈裂扩散模型示意

Figure 5. Compaction fracture diffusion model for backfill grouting of shield tunnel in low permeability strata

下载: 全尺寸图片幻灯片

2. 劈裂扩散模型推导

2.1 模型假设

在进行劈裂扩散模型推导前，做出如下假设：①浆液、水均不可压缩，注浆过程中其流型不变；②注浆口附近，浆液为层流运动，劈裂通道边界处浆液流速为0；③不考虑地层应力分布的不均匀性和浆液的流失；④劈裂通道侧壁与劈裂通道对称轴的夹角很小，认为侧壁受力垂直于劈裂通道对称轴；⑤劈裂区域定义为盾尾注浆范围的c，其余区域则为压密注浆，其中c=(α+β)/360°，盾尾注浆范围为2π。

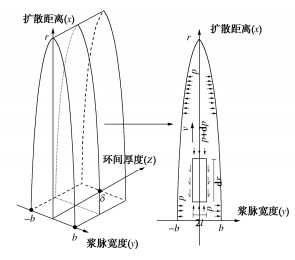
环向劈裂过程应是压力差最大处先产生劈裂通道，随后再产生其余劈裂通道，环厚δ为浆脉厚度，r为浆脉扩散距离，2b为浆脉宽度。取扩散模型中劈裂通道中一纵剖面进行推导，模型推导示意图如图 6所示。

图 6 盾构壁后注浆劈裂扩散推导示意图

Figure 6. Schematic diagram of fracture diffusion model for backfill grouting in shield tunnel

下载: 全尺寸图片幻灯片

2.2 浆液本构模型

根据流体的本构方程，可以将浆液分为宾汉姆流体、牛顿流体、幂律流体，以牛顿流体为例进行推导，其中牛顿流体的本构方程为

$\tau = \mu \dot \gamma \quad。$

(10)

式中：τ为浆液剪切应力；μ为浆液黏度； $\dot \gamma$ 为浆液剪切速率， $\dot \gamma = - \frac{{{\text{d}}v}}{{{\text{d}}l}}$ 。

2.3 模型推导

盾尾间隙填充完成后，因假设浆液不流失，在劈裂阶段注入的浆液体积与劈裂通道内浆液体积相等。因此在此阶段，根据质量守恒，浆液在劈裂通道内部任意扩散断面上的单位时间流量与注浆孔处的单位时间流量q（注浆速率）相等，其关系可表示为

$nq{\text{ = }}2b\delta \bar v 。$

(11)

式中：b为劈裂通道宽度； $\bar v$ 为劈裂通道内浆液宽度方向的平均流速。

根据文献[]，可推出本模型劈裂通道内浆脉宽度方向的平均流速 $\bar v$ 为

$\bar v = \frac{{{b^2}}}{{3\mu }}\left( { - \frac{{{\text{d}}{P_{\text{t}}}}}{{{\text{d}}r}}} \right) 。$

(12)

式中：r为扩散距离；P_t为劈裂通道内浆液压力，当r = 0时，P_t=P_h。

劈裂通道内部浆液压力梯度为

$\frac{{{\text{d}}{P_{\text{t}}}}}{{{\text{d}}r}} = - \frac{{3\mu \overline v }}{{{b^2}}} = - \frac{{3n\mu q}}{{2\delta {b^3}}} 。$

(13)

劈裂通道宽度控制式为

$2b = 2{w_{\max }} = G({P_{\text{t}}} - \left| {{\sigma _{\text{v}}}\cos \theta } \right| - \left| {{\sigma _{\text{h}}}\sin \theta } \right|) \text{，}$

(14)

其中

$G = D\frac{{(1 + \nu )(1 - 2\nu )}}{{E(1 - \nu )}} 。$

(15)

式中：D为劈裂注浆影响半径；ν为泊松比；E为土体弹性模量。

联立式（13）~（15），可得劈裂通道宽度与扩散距离关系式为

$2b = 2\sqrt[\begin{subarray}{l} 4 \\ \end{subarray} ]{{\frac{{6nq\mu G}}{\delta }({r_{\max }} - r)}} 。$

(16)

联立式（14）~（16），可得浆液压力与扩散距离关系式为

${P_{\text{t}}} = 2\sqrt[4]{{\frac{{6nq\mu }}{{\delta {G^3}}}({r_{\max }} - r)}} + {\text{(}}\left| {{\sigma _{\text{v}}}\cos \theta } \right| + \left| {{\sigma _{\text{h}}}\sin \theta } \right|{\text{)}} 。$

(17)

3. 扩散模型规律分析

盾构隧道参数见表 1，同步注浆注浆孔布置参数见表 2，其他计算参数见表 3。

表 1 盾构隧道参数

Table 1. Parameters of shield tunnel

管片外半径/m	盾尾间隙厚度/m	隧道埋深/m
4.725	0.16	12

下载: 导出CSV

| 显示表格

表 2 同步注浆注浆孔布置参数

Table 2. Parameters for layout of synchronous grouting holes

参数	注浆孔序号
参数	1	2	3	4	5	6
位置/(°)	35	90	145	215	270	325
注浆压力/kPa	230	200	230	340	370	340

下载: 导出CSV

| 显示表格

表 3 其他计算参数

Table 3. Other parameters

浆液密度/(kg·m^-3)	浆液黏度/(Pa·s)	环厚δ/m
2190	2	0.0216

截面流量/(m³·s^-1)	土体抗拉强度/ kPa	侧压力系数
4.3453×10^-4	40	0.5

下载: 导出CSV

| 显示表格

3.1 劈裂区间与土体侧压力系数、盾构隧道埋深的关系

（1）劈裂区间与土体侧压力系数的关系

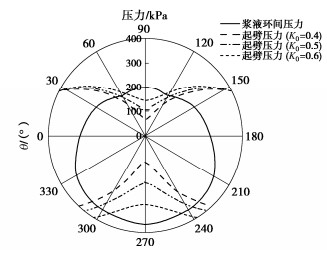
根据式（5），（6），计算环向浆液压力与起劈压力，取土体侧压力系数分别为0.4，0.5，0.6，其余参数保持不变，分析劈裂区间与土体侧压力系数的关系，见图 7。

图 7 不同侧压力系数下劈裂区间

Figure 7. Fracturing intervals under different lateral pressure coefficients

下载: 全尺寸图片幻灯片

在3种侧压力系数下，管片环上部起劈压力均小于下部起劈压力，且随着侧压力系数的增大，土体的起劈压力协同增大，与90°区间附近相比，270°区间附近的起劈压力增大趋势更为明显。

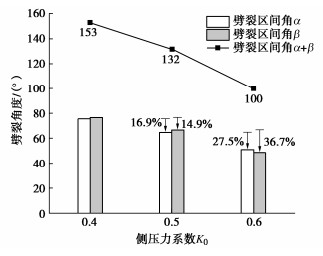
劈裂区间角 $\alpha$ 在侧压力系数0.4，0.5情况下均小于劈裂区间角 $\beta$ ，侧压力系数为0.6时 $\alpha$ 略大于 $\beta$ ，见。表明在盾构隧道环向下部产生劈裂的范围较大，这是由于正常注浆参数下盾构隧道下部的注浆压力普遍大于上部注浆压力。随着侧压力系数的增大， $\alpha$ 和 $\beta$ 的减小趋势均增大，分别由16.9%，14.9%增加至27.5%，36.7%；同时，由于土体劈裂所抵抗的水平主应力增大，劈裂区间角总和α+β则随着侧压力系数的增大而减小。

图 8 不同侧压力系数下劈裂角度

Figure 8. Fracturing angles under different lateral pressure coefficients

下载: 全尺寸图片幻灯片

（2）劈裂区间与盾构隧道埋深的关系

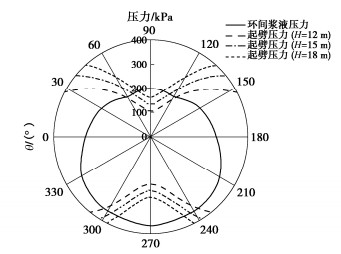
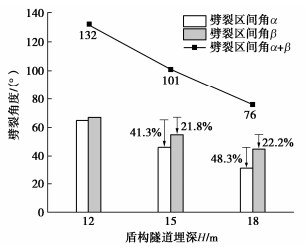
根据式（5），（6），计算环向浆液压力与起劈压力，调整盾构隧道埋深分别为12，15，18 m，并保持其余参数不变，分析劈裂区间与盾构隧道埋深的关系，见图 9。

图 9 不同盾构隧道埋深下劈裂区间

Figure 9. Fracturing intervals under different depths of shield tunnel

下载: 全尺寸图片幻灯片

随着盾构隧道埋深的增加，土体的起劈压力协同增大，整体劈裂区域变化不大，仍在90°及270°附近。相较于不同土体侧压力系数下的增长趋势，不同盾构隧道埋深下土体的起劈压力在90°与270°附近增长趋势较为一致。

如所示，劈裂区间角 $\alpha$ 在3种盾构隧道埋深下均小于劈裂区间角 $\beta$ 。随着埋深的增加， $\alpha$ 和 $\beta$ 的减小趋势均增大，分别由41.3%，21.8%增加至48.3%，22.2%，且 $\alpha$ 的减小趋势明显大于 $\beta$ 的减小趋势；同时，由于埋深引起的垂直主应力的增大，劈裂区间角总和 $\alpha$ + $\beta$ 同样随着埋深的增大而减小。

图 10 不同盾构隧道埋深下劈裂角度

Figure 10. Fracturing angles under different buried depths

下载: 全尺寸图片幻灯片

3.2 最大扩散距离、最大通道宽度与注浆压力差的关系

记注浆压力差为P_c=P_t-|σ_vcosθ|-|σ_hsinθ|，其大小控制着浆液扩散距离，将相关参数代入式（17），可得扩散距离、通道宽度与注浆压力差的关系。

（1）最大扩散距离与注浆压力差的关系

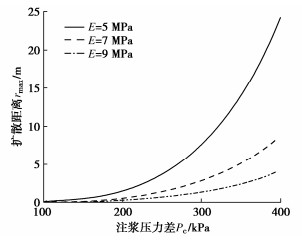
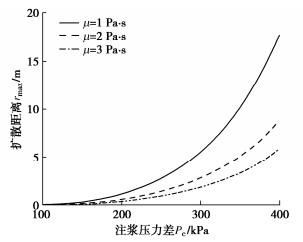
根据式（17），泊松比ν=0.4，浆液黏度μ=2 Pa·s，注浆影响半径D=3 m。当r=0时，计算不同土体弹性模量5，7，9 MPa下最远扩散距离r_max与注浆压力差P_c的关系（如图 11）；其他参数不变，土体弹性模量E=7 MPa，计算不同浆液黏度1，2，3 Pa·s下最大扩散距离r_max与注浆压力差P_c的关系（如图 12）。

图 11 扩散距离与注浆压力差的关系（弹性模量）

Figure 11. Relationship between diffusion distance and grouting pressure difference (elasticity modulus)

下载: 全尺寸图片幻灯片

图 12 扩散距离与注浆压力差的关系（浆液黏度）

Figure 12. Relationship between diffusion distance and grouting pressure difference (grout viscosity)

下载: 全尺寸图片幻灯片

随着注浆压力差的增大，浆液的最大扩散距离呈指数增长，其指数为4，在注浆压力较小时，扩散距离增长不明显。该模型具有较大的扩散距离，但由于地层不均、地应力场等因素，在实际工程中浆液扩散范围可能小于理论值。

由图 11可知：在相同注浆压力差下，随着土体弹性模量的增大，浆液最大扩散距离减小，主要原因是由于土体弹性模量增大后，浆液在浆脉中的扩展压力增大导致的。

由图 12可知：在相同注浆压力差下，随着浆液黏度的增大，浆液最大扩散距离减小，这是由于浆液黏度增大时，浆液的切向力增大，导致浆液受到的阻力增大导致的。

（2）最大通道宽度与最大扩散距离的关系

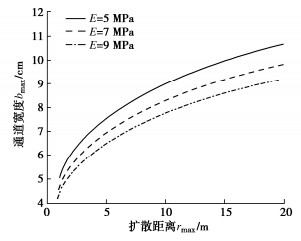
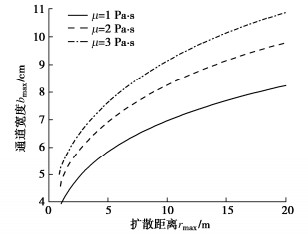
根据式（16），取泊松比 $\nu$ =0.4，浆液黏度μ=2 Pa·s，注浆影响半径D=3 m。当r=0时，计算不同土体弹性模量5，7，9 MPa下最大通道宽度b_max与扩散距离r_max的关系（如图 13），计算不同浆液黏度1，2，3 Pa·s下最大通道宽度b_max与扩散距离r_max的关系（如图 14）。

图 13 扩散距离与通道宽度的关系（弹性模量）

Figure 13. Relationship between diffusion distance and channel width (elasticity modulus)

下载: 全尺寸图片幻灯片

图 14 扩散距离与通道宽度的关系（浆液黏度）

Figure 14. Relationship between diffusion distance and channel width (viscosity)

下载: 全尺寸图片幻灯片

随着扩散距离的增大，浆液的最大通道宽度呈指数增长，其指数为0.25。这表明浆液的扩散形式与假设一致，为子弹形。同时，劈裂通道宽度远小于扩散距离，且两者差距为数量级，这表明在较少的注浆量下浆液亦可扩散至较大距离。

由图 13可知：在相同扩散距离时，随着土体弹性模量的增大，最大通道宽度减小。由图 14可知：在相同扩散距离时，随着浆液黏度的增大，最大通道宽度减小。

3.3 盾构隧道环向劈裂扩散锋面分析

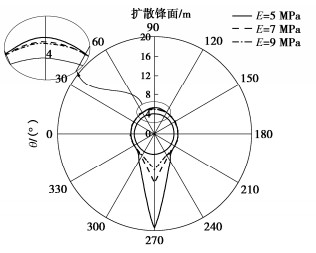
取表 1~3中相关参数进行计算，取弹性模量分别为5，7，9 MPa，求解盾构隧道环向劈裂扩散锋面，如图 15。

图 15 盾构隧道环向劈裂扩散锋面

Figure 15. Circumferential fracturing diffusion front of shield tunnel

下载: 全尺寸图片幻灯片

经计算，劈裂区间角 $\alpha$ =62°，β=66°。随着土体模量的增大，浆液扩散锋面逐渐减小。在图 15中为浆液锋面的分布情况，其数值为浆液扩散距离与管片外径（R=4.25 m）之和。土体模量为5 MPa时，环向劈裂距离最大，上部最大值在90°处，其值r₅₍₉₀₎=0.591 m，下部最大值在270°处，其值r₅₍₂₇₀₎=14.629 m；土体模量为9 MPa时，环向劈裂距离最小，上部最大值在90°处，其值r₉₍₉₀₎=0.101 m，下部最大值在270°处，其值r₉₍₂₇₀₎=2.509 m。

正常注浆参数情况下，浆液向下扩散距离远大于向上扩散距离，这主要是因为壁后注浆环向压力的分布不均匀，下部浆液压力约为上部浆液压力的1.5~2倍。

4. 讨论

某城际铁路某盾构区间采用盾构机类型为土压平衡盾构，其上半部主要穿越地层为粉质黏土层，上覆地层主要为人工填土层、第四系全新统冲积层（2-1粉质黏土、2-2粉质黏土），隧道中心埋深15 m，顶部覆土厚度为10.75 m，采用外径8.5 m、内径7.7 m的管片。根据砂浆配合比验证报告得知浆液的水灰比为3.3，根据文献[23]研究，浆液可当作牛顿流体考量，其黏度考量为1.5 Pa·s。由于该区间盾构隧道存在上浮问题，故采取顶部注浆孔先行注浆且压力较大的方法。根据施工具体注浆参数，顶部注浆压力控制在400 kPa，注浆孔6孔中4孔注浆（n=4）。根据实际推进速度，注浆速率取q=6×10^-4 m³·s^-1，环厚δ=0.02 m。

施工过程中，盾构上方地表出现冒浆现象，冒浆过程如图 16所示。其过程先为小范围泥浆涌出，随着涌出量的增加，逐渐呈灰色状水泥浆液。

图 16 某盾构隧道冒浆过程

Figure 16. Grout-oozing process of shield tunnel

下载: 全尺寸图片幻灯片

根据已有数据进行计算，因该盾构上部注浆孔注浆压力较大，同时粉质黏土的渗透系数较小，根据压密劈裂模型推导，该盾构上部浆液极易发生劈裂扩散，且劈裂扩散距离的理论值为11.56 m。11.56 m已经大于隧道顶部覆土深度，同时在后期勘探中发现该区域表层的人工填土存在部分盲孔，给予了浆液继续上涌的通道。

此案例基于实际工程问题，其相应的计算参数与进行扩散模型规律分析时的盾构隧道参数不同。依据此案例，一是验证了本文低渗地层盾构隧道压密-劈裂模型的合理性；二是对盾构隧道掘进过程中发生地表冒浆原因提供了一种分析思路。根据分析结果，建议盾构穿越低渗地层时，应严格控制上部注浆孔注浆压力，避免出现地表冒浆现象。

5. 结论

（1）基于对浆液环向压力分布与环向起劈压力的计算，建立了低渗地层盾构隧道壁后注浆压密-劈裂扩散模型，提出了环向劈裂区间角及其计算方法，并给出了劈裂区域浆液扩散半径及通道宽度计算式。

（2）劈裂区间角与土体侧压力系数、隧道埋深均呈负相关关系；最大扩散距离与注浆压力差、最大通道宽度与最大扩散距离均呈指数关系，其指数分别为4，0.25。

（3）注浆压力差一定时，浆液最大扩散距离随土体弹性模量、浆液黏度的增大而减小；最大扩散距离一定时，最大通道宽度随土体弹性模量的增大而减小，随浆液黏度的增大而增大。

（4）正常注浆参数下，浆液向下扩散距离远大于向上扩散距离；结合某城际铁路盾构隧道冒浆情况，在低渗地层中，上部注浆孔注浆压力过大可能会导致上部浆液劈裂扩散距离较大，进而引发地表冒浆。

图 1 浆液充填及特征点位置示意图

Figure 1. Schematic diagram of grout filling and location of feature points

下载: 全尺寸图片幻灯片

图 2 特征点A, B微元体受力情况

Figure 2. Stress conditions of element body at feature points A and B

下载: 全尺寸图片幻灯片

图 3 盾构壁后注浆平面受力图

Figure 3. Forces on backfill grouting of shield tunnel

下载: 全尺寸图片幻灯片

图 4 盾尾间隙附近应力状态分解图

Figure 4. Decomposition of stress state near shield tail

下载: 全尺寸图片幻灯片

图 5 低渗地层盾构隧道壁后注浆压密-劈裂扩散模型示意

Figure 5. Compaction fracture diffusion model for backfill grouting of shield tunnel in low permeability strata

下载: 全尺寸图片幻灯片

图 6 盾构壁后注浆劈裂扩散推导示意图

Figure 6. Schematic diagram of fracture diffusion model for backfill grouting in shield tunnel

下载: 全尺寸图片幻灯片

图 7 不同侧压力系数下劈裂区间

Figure 7. Fracturing intervals under different lateral pressure coefficients

下载: 全尺寸图片幻灯片

图 8 不同侧压力系数下劈裂角度

Figure 8. Fracturing angles under different lateral pressure coefficients

下载: 全尺寸图片幻灯片

图 9 不同盾构隧道埋深下劈裂区间

Figure 9. Fracturing intervals under different depths of shield tunnel

下载: 全尺寸图片幻灯片

图 10 不同盾构隧道埋深下劈裂角度

Figure 10. Fracturing angles under different buried depths

下载: 全尺寸图片幻灯片

图 11 扩散距离与注浆压力差的关系（弹性模量）

Figure 11. Relationship between diffusion distance and grouting pressure difference (elasticity modulus)

下载: 全尺寸图片幻灯片

图 12 扩散距离与注浆压力差的关系（浆液黏度）

Figure 12. Relationship between diffusion distance and grouting pressure difference (grout viscosity)

下载: 全尺寸图片幻灯片

图 13 扩散距离与通道宽度的关系（弹性模量）

Figure 13. Relationship between diffusion distance and channel width (elasticity modulus)

下载: 全尺寸图片幻灯片

图 14 扩散距离与通道宽度的关系（浆液黏度）

Figure 14. Relationship between diffusion distance and channel width (viscosity)

下载: 全尺寸图片幻灯片

图 15 盾构隧道环向劈裂扩散锋面

Figure 15. Circumferential fracturing diffusion front of shield tunnel

下载: 全尺寸图片幻灯片

图 16 某盾构隧道冒浆过程

Figure 16. Grout-oozing process of shield tunnel

下载: 全尺寸图片幻灯片

表 1 盾构隧道参数

Table 1 Parameters of shield tunnel

管片外半径/m 盾尾间隙厚度/m 隧道埋深/m

4.725 0.16 12

下载: 导出CSV

表 2 同步注浆注浆孔布置参数

Table 2 Parameters for layout of synchronous grouting holes

参数注浆孔序号

1 2 3 4 5 6

位置/(°) 35 90 145 215 270 325

注浆压力/kPa 230 200 230 340 370 340

下载: 导出CSV

表 3 其他计算参数

Table 3 Other parameters

浆液密度/(kg·m^-3) 浆液黏度/(Pa·s) 环厚δ/m

2190 2 0.0216

截面流量/(m³·s^-1) 土体抗拉强度/
kPa 侧压力系数

4.3453×10^-4 40 0.5

下载: 导出CSV

参考文献(23)

[1]	何川, 封坤, 方勇. 盾构法修建地铁隧道的技术现状与展望[J]. 西南交通大学学报, 2015, 50(1): 97-109. doi: 10.3969/j.issn.0258-2724.2015.01.015 HE Chuan, FENG Kun, FANG Yong. Review and prospects on constructing technologies of metro tunnels using shield tunnelling method[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 97-109. (in Chinese) doi: 10.3969/j.issn.0258-2724.2015.01.015
[2]	交通运输部. 2023年8月城市轨道交通运营数据速报[EB/OL]. [2023-09-09]. https://www.mot.gov.cn/fenxigongbao/yunlifenxi/202309/t20230905_3908942.html. Ministry of Transport of the People's Republic of China. Urban rail transit operation data report in August[EB/OL]. [2023-09-09]. https://www.mot.gov.cn/fenxigongbao/yunlifenxi/202309/t20230905_3908942.html. (in Chinese
[3]	张凤祥. 盾构隧道[M]. 北京: 人民交通出版社, 2004. ZHANG Fengxiang. Shield Tunnelling Method[M]. Beijing: China Communications Press, 2004. (in Chinese)
[4]	LOGANATHAN N. Analytical prediction for tunneling- induced ground movements in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 846-856. doi: 10.1061/(ASCE)1090-0241(1998)124:9(846)
[5]	LEE K M, ROWE R K, LO K Y. Subsidence owing to tunnelling Ⅰ: estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29(6): 929-940. doi: 10.1139/t92-104
[6]	SHIRLAW J N, RICHARDS D P, Ramond P, et al. Recent experience in automatic tail void grouting with soft ground tunnel boring machines[C]// Proceedings of the ITA-AITES World Tunnel Congress. Singapore, 2004: 22-27.
[7]	叶飞. 软土盾构隧道施工期上浮机理分析及控制研究[D]. 上海: 同济大学, 2007. YE Fei. Analysis and Control for Upward Movement of Shield Tunnel During Construction[D]. Shanghai: Tongji University, 2007. (in Chinese)
[8]	李培楠, 石来, 李晓军, 等. 盾构隧道同步注浆纵环向整体扩散理论模型[J]. 同济大学学报(自然科学版), 2020, 48(5): 629-637. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ202005001.htm LI Peinan, SHI Lai, LI Xiaojun, et al. Theoretical model of synchronous grouting longitudinal- circumferential integrated diffusion of shield tunnels[J]. Journal of Tongji University (Natural Science), 2020, 48(5): 629-637. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ202005001.htm
[9]	梁禹, 阳军生, 王树英, 等. 考虑时变性影响的盾构壁后注浆浆液固结及消散机制研究[J]. 岩土力学, 2015, 36(12): 3373-3380. doi: 10.16285/j.rsm.2015.12.005 LIANG Yu, YANG Junsheng, WANG Shuying, et al. A study on grout consolidation and dissipation mechanism during shield backfilled grouting with considering time effect[J]. Rock and Soil Mechanics, 2015, 36(12): 3373-3380. (in Chinese) doi: 10.16285/j.rsm.2015.12.005
[10]	杨琪, 耿萍, 唐睿, 等. 非饱和地层中盾构隧道壁后注浆浆液渗透扩散机理[J]. 中国铁道科学, 2020, 41(6): 100-108. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK202006011.htm YANG Qi, GENG Ping, TANG Rui, et al. Slurry seepage and diffusion mechanism of shield tunnel backfilling grouting in unsaturated stratum[J]. China Railway Science, 2020, 41(6): 100-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK202006011.htm
[11]	叶飞, 苟长飞, 陈治, 等. 盾构隧道黏度时变性浆液壁后注浆渗透扩散模型[J]. 中国公路学报, 2013, 26(1): 127-134. doi: 10.3969/j.issn.1001-7372.2013.01.018 YE Fei, GOU Changfei, CHEN Zhi, et al. Back-filled grouts diffusion model of shield tunnel considering its viscosity degeneration[J]. China Journal of Highway and Transport, 2013, 26(1): 127-134. (in Chinese) doi: 10.3969/j.issn.1001-7372.2013.01.018
[12]	叶飞, 陈治, 苟长飞, 等. 基于球孔扩张的盾构隧道壁后注浆压密模型[J]. 交通运输工程学报, 2014, 14(1): 35-42. https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201401008.htm YE Fei, CHEN Zhi, GOU Changfei, et al. Grouting compaction model behind shield tunnel wall based on spherical hole expansion[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 35-42. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201401008.htm
[13]	白云, 戴志仁, 张莎莎, 等. 盾构隧道同步注浆浆液压力扩散模式研究[J]. 中国铁道科学, 2011, 32(4): 38-45. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201104009.htm BAI Yun, DAI Zhiren, ZHANG Shasha, et al. Study on the grout pressure dissipation mode in simultaneous backfill grouting during shield tunneling[J]. China Railway Science, 2011, 32(4): 38-45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201104009.htm
[14]	毛家骅. 基于渗滤效应的盾构隧道壁后注浆浆液扩散机理研究[D]. 西安: 长安大学, 2016. MAO Jiahua. Study on the Grouts Diffusion Mechanism of Shield Tunnel Back-Filled Grouts Based on Filtration[D]. Xi'an: Changan University, 2016. (in Chinese)
[15]	叶飞, 王斌, 韩鑫, 等. 盾构隧道壁后注浆试验与浆液扩散机理研究进展[J]. 中国公路学报, 2020, 33(12): 92-104. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202012008.htm YE Fei, WANG Bin, HAN Xin, et al. Review of shield tunnel backfill grouting tests and its diffusion mechanism[J]. China Journal of Highway and Transport, 2020, 33(12): 92-104. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202012008.htm
[16]	王腾. 湿陷性黄土劈裂注浆理论分析及试验研究[D]. 兰州: 兰州理工大学, 2017. WANG Teng. The Theoretical Analysis and Experimental Study of Fracturing Grouting of Collapsible Loess[D]. Lanzhou: Lanzhou University of Technology, 2017. (in Chinese)
[17]	金鑫, 张松林, 邱子涵, 等. 水泥浆液在黄土中注浆扩散的现场试验研究[J]. 西安工业大学学报, 2021, 41(3): 292-299. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGY202103007.htm JIN Xin, ZHANG Songlin, QIU Zihan, et al. Field tests of grouting diffusion of cement slurry in loess[J]. Journal of Xi'an Technological University, 2021, 41(3): 292-299. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGY202103007.htm
[18]	马连生, 王腾, 周茗如, 等. 黄土劈裂注浆土体裂纹扩展模型研究[J]. 地下空间与工程学报, 2018, 14(4): 962-967. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201804012.htm MA Liansheng, WANG Teng, ZHOU Mingru, et al. Study on the crack extended model for loess with fracturing grouting[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(4): 962-967. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201804012.htm
[19]	周书明, 陈建军. 软流塑淤泥质地层地铁区间隧道劈裂注浆加固[J]. 岩土工程学报, 2002, 24(2): 222-224. http://www.cgejournal.com/cn/article/id/10925 ZHOU Shuming, CHEN Jianjun. Hydrofracture grouting in soft flowing mucky ground for a metro tunnel[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 222-224. (in Chinese) http://www.cgejournal.com/cn/article/id/10925
[20]	张忠苗, 邹健. 桩底劈裂注浆扩散半径和注浆压力研究[J]. 岩土工程学报, 2008, 30(2): 181-184. http://www.cgejournal.com/cn/article/id/12751 ZHANG Zhongmiao, ZOU Jian. Penetration radius and grouting pressure in fracture grouting[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 181-184. (in Chinese) http://www.cgejournal.com/cn/article/id/12751
[21]	张庆松, 张连震, 刘人太, 等. 基于"浆-土"界面应力耦合效应的劈裂注浆理论研究[J]. 岩土工程学报, 2016, 38(2): 323-330. doi: 10.11779/CJGE201602016 ZHANG Qingsong, ZHANG Lianzhen, LIU Rentai, et al. Split grouting theory based on slurry-soil coupling effects[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(2): 323-330. (in Chinese) doi: 10.11779/CJGE201602016
[22]	苟长飞. 盾构隧道壁后注浆浆液扩散机理研究[D]. 西安: 长安大学, 2013. GOU Changfei. Study on the Grouts Diffusion Mechanism of Shield Tunnel Back-Filled Grouts[D]. Xi'an: Chang'an University, 2013. (in Chinese)
[23]	阮文军. 基于浆液黏度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报, 2005, 24(15): 2709-2714. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200515020.htm RUAN Wenjun. Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2709-2714. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200515020.htm