Measurement of distribution of rock joint stiffness based on active ultrasonic excitation
-
摘要: Goodman提出采用节理刚度表征复杂岩石节理面的拓扑行为并为其提供定量值，而无需对节理面的粗糙度、接触面积等参数进行详细测量分析。然而目前对岩石节理刚度的测量仍存在局限，因此，在试验室环境下采用压电陶瓷换能器对完整平板试件和含节理平板试件进行弹性波激励，同时采用三维扫描激光多普测振仪监测平板内弹性波的传播数据。将采集的波场信号数据进行滤波、插值、积分等一系列处理，并基于Schoenberg线性滑移模型计算节理刚度分布，实现岩石节理接触行为的全局参数表征，同时进一步验证了岩石节理全场超声表征的可行性。全场波形数据清晰地揭示了岩石节理界面接触行为，为后续深入探索岩石节理几何形状、孔径、界面性质及其地震特征之间的相互关系奠定了基础。Abstract: Goodman proposed to use the joint stiffness to characterize the topological behaviors of complex rock joint interfaces and provide quantitative values for them, without measuring and analyzing the geometric parameters such as roughness and contact area of joint interfaces in detail. However, it is difficult to measure the stiffness of rock joints at present. Therefore, the piezoelectric ceramic transducer is used to excite the elastic waves of the intact granite plate specimen and the cracked granite plate specimen in the laboratory environment. At the same time, the scanning laser Doppder Vibrometer is used to monitor propagation data of the elastic waves in the plate. On this basis, the collected signal data of wave fields are processed by filtering, interpolation, integration, etc., and the distribution of joint stiffness is calculated based on the Schoenberg linear sliding model. Then, the joint stiffness is used to parameterize the contact behaviors of rock joints, which further proves the feasibility of ultrasonic characterization of whole rock joints. By using the full-field waveform data, the interface contact behaviors of rock joints are clearly revealed, which lays a foundation for further exploring the relationship among rock joint geometry, pore sizes, interface properties and seismic characteristics.
-
Keywords:
- rock joint /
- contact behavior /
- elastic wave /
- shear stiffness /
- normal stiffness
-
0. 引言
岩石节理、断层的界面特性对天然气和地热资源的能源开采、地震学、水文地质学、环境保护等科学技术领域都至关重要[1-3]，其中岩石节理、断层界面的特征主要包括粗糙度、接触面积、孔径分布等。Goodman等[4]引入节理刚度作为一个有效参数来捕获复杂节理界面的拓扑行为并为其提供定量值，而无需对节理界面几何特征参数进行详细测量分析。研究发现节理刚度与应力分布直接相关，可用于岩质边坡、地下结构的稳定性分析[5-6]；同时节理水力特性与节理刚度的时空变化之间存在很强的相关性，可用于地热、石油等地质资源的开采[7-9]；其次节理剪切刚度的变化可以作为岩石节理发生剪切破坏的前兆[10-11]。因此，确定岩石节理刚度分布具有重要的工程应用价值。
目前，国内外专家学者对岩石节理刚度的测量计算开展了大量研究。Kulatilake等[12]使用从不同地理位置和地层中获取的岩石制备相对光滑节理和锯切节理试件，通过单轴压缩和直剪试验估算岩石节理法向刚度和剪切刚度，建立了现场节理刚度估算的经验关系数据库。Jiang等[13]开发了自动伺服控制直剪装置和计算机控制系统，以自适应恒定法向刚度边界条件下法向应力的变化，通过假设恒定的法向刚度条件来确定节理剪切刚度。Nassir等[14]基于常规节理面参数和约束荷载，提出了节理峰前剪切刚度模型。同时，建立了用于评估节理岩石变形行为的本构矩阵。Li等[15]研究了剪切破坏时测量岩石节理剪切刚度的可行性，并分析了剪切破坏和剪切刚度之间的关系。
上述测量计算方法的刚度值表示整个岩石节理界面的平均刚度，但是岩石节理是非均质的，不同位置的刚度往往不同，平均值无法表征节理不同位置的接触行为。对此，Hedayat等[16]对石灰岩试样进行直剪试验，同时测量穿过节理传输和反射的纵波和横波。根据透射波振幅与反射波振幅计算激励位置的节理剪切刚度。Lubbe等[17]在不同围压下，使用脉冲反射技术测量节理法向刚度和剪切刚度，发现两者之比取决于节理填充流体。Acosta等[18]分析了不同测量尺度对节理刚度测量结果的影响。上述测量计算方法只适用于垂直于节理的入射波，同时要求节理界面是平面。
针对目前节理刚度测量计算的局限性，本文在试验室环境下通过压电陶瓷换能器对花岗岩平板试件进行激励，同时采用扫描激光多普勒测振仪非接触式监测试件平面内的波形传播数据，将数据信号处理后，根据线性滑移模型描述弹性波作用下的岩石节理本构响应[19]，计算节理刚度沿节理几何形状的分布，从而实现岩石节理接触行为的全局参数表征，验证岩石节理全场超声表征的可行性。
1. 波形运动数据监测
1.1 试验装置
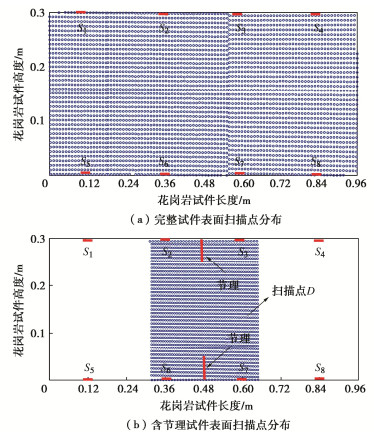
节理全场超声表征试验采用尺寸为0.96 m×0.30 m×0.03 m的花岗岩平板试件，试件密度为2750 kg/m3，泊松比为0.23，杨氏模量为62.6 GPa。在S1至S8共8个位置处（如图 1）采用压电换能器分别进行S波和P波激励，频率为10，30 kHz；激励的同时使用扫描激光多普勒测振仪（SLDV）进行非接触式采集试件表面的波形运动数据，平面应力假设条件下整个试件厚度方向波形运动恒定[20]。完整试件的扫描范围是0.96 m×0.30 m，扫描点分布如图 1（a）所示。为了更好地关注节理周围的波形运动，将含节理试件扫描范围缩小为0.34 m×0.32 m区域，扫描点分布如图 1（b）所示。
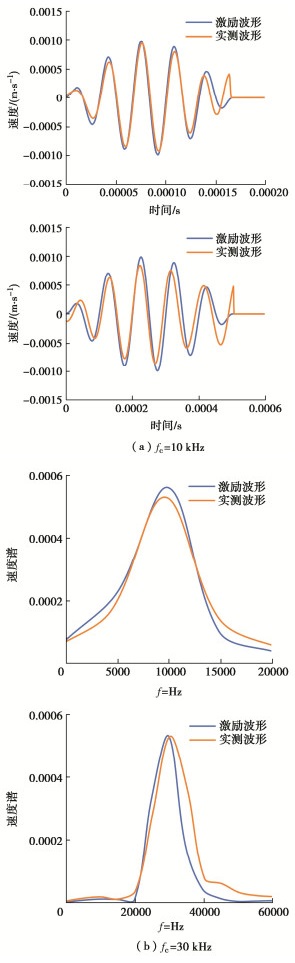
为了保证波形数据测量的精度，要求每段波形占据10~20个扫描点，采用的波长约为10 cm，扫描点在x方向和y方向的空间分辨率均约为1 cm，所以每段波形占据10个扫描点，符合测量精度要求。对压电换能器产生的激励波形和试件中实际传播的波形进行比较，理论速度vy的波形和SLDV测得的激励位置S3附近的实际粒子速度vy，在时域和频域上的结果如图 2所示。对比发现换能器的信号波形和试件中实际传播的信号波形一致，表明压电换能器与试件耦合良好。
1.2 试验步骤
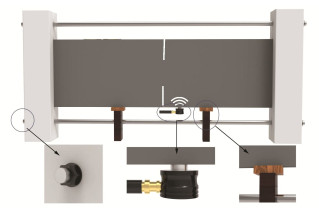
首先对轴向应力为0 MPa的完整试件进行全场超声表征试验，测量数据可计算由于节理产生的散射波场（散射波场=总场-自由场），其中含节理试件的数据为总场，完整试件的数据为自由场。接着在试件顶部和底部边缘中间位置制造3 cm长的缺口，然后以三点弯曲方式压裂形成两条非贯通节理。最后将试件安装到图 3所示的固定装置，载荷框架由两个铝制块组成，铝制块的两端均带有螺纹钢，通过拧紧螺纹钢上的螺母对节理施加轴向应力。试件在0 MPa和3 MPa轴向应力作用下分别产生宏观节理和微观节理，微观节理肉眼不可见。采用相同方式对3 MPa轴向应力状态下的含节理试件进行全场超声表征试验。
2. 数据可视化处理
试验共在8个不同位置进行激励，因为篇幅有限，仅以激励作用于S2和S3位置时试件中的波形运动为例。从激励开始到扫描结束整个过程共持续0.001 s，激励频率为10 kHz时完整试件的所有扫描点在4个不同时刻的速度场vx和vy如图 4所示。
![]()
图 4 10 kHz激励作用于S2时完整试件不同时刻的速度场vx和vyFigure 4. Velocity fields vx and vy at different moments of intact granite specimen with excitation acting of 10 kHz on S2激励频率为30 kHz时完整试件的所有扫描点在4个不同时刻的速度场vx和vy如图 5所示。
![]()
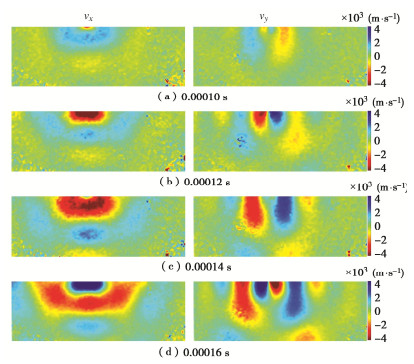
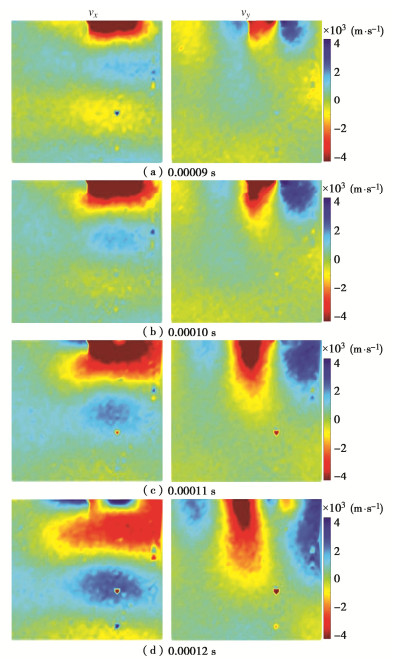
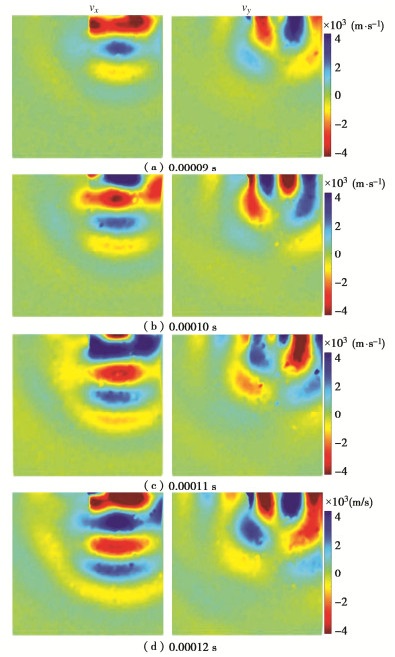
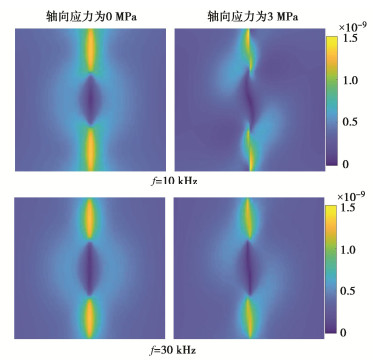
图 5 30 kHz激励作用于S2时完整试件不同时刻的速度场vx和vyFigure 5. Velocity fields vx and vy at different moments of intact granite specimen with excitation acting of 30 kHz on S2激励频率为10 kHz时含节理试件的所有扫描点在4个不同时刻的速度场vx和vy如图 6所示。
![]()
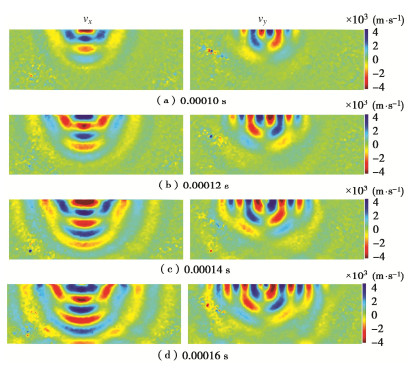
图 6 10 kHz激励作用于S3时含节理试件不同时刻的速度场vx和vyFigure 6. Velocity fields vx and vy at different moments of fractured granite specimen with excitation acting of 10 kHz on S3激励频率为30 kHz时含节理试件的所有扫描点在4个不同时刻的速度场vx和vy如图 7所示。
![]()
图 7 30 kHz激励作用于S3时含节理试件不同时刻的速度场vx和vyFigure 7. Velocity fields vx and vy at different moments of fractured granite specimen with excitation acting of 30 kHz on S33. 波形信号处理
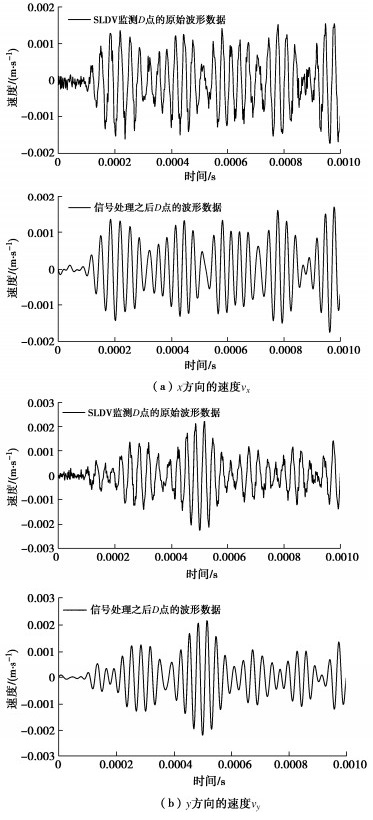
首先设计带通滤波器对原始速度场进行滤波处理，带通滤波器只允许特定频段的信号通过，抑制低于或高于该频段的信号和噪声，从而适应频率为10 kHz和30 kHz的激励波形。含节理试件表面扫描点D的原始速度曲线以及经过带通滤波器处理之后的速度变化曲线如图 8所示。
![]()
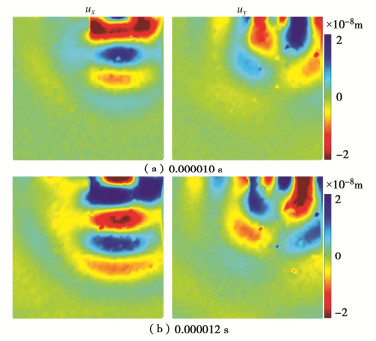
图 8 扫描点D记录的原始速度以及经过带通滤波器处理之后的速度Figure 8. Original recorded velocities and velocity fields after bandpass filtering at scanming point D将滤波后的速度场积分转换成可微分的位移波场数据，计算节理界面的牵引力时位移场需要满足二次可微[21]，接着采用具有λs/10×λs/10窗口的中值滤波器消除位移波场中突然出现尖峰的信噪比极低的扫描点，并采用具有相同大小窗口的均值滤波器进行滤波处理，最后进行一维傅里叶级数近似，获得时间和空间可微分的平滑位移波场。信号处理之后试件表面散射场的位移ux和uy如图 9所示。
4. 节理面接触行为
4.1 节理几何形状重建
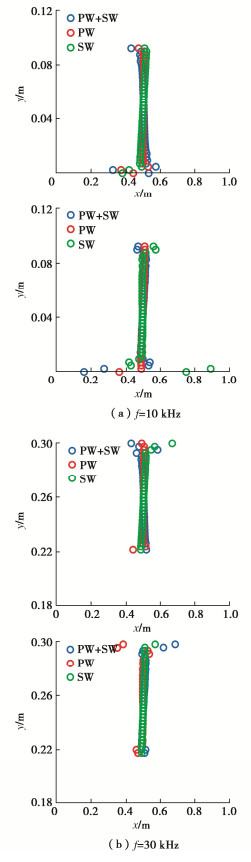
从激励开始到扫描结束整个过程共持续了0.001 s，SLDV每间隔0.000002 s采集一次试件表面的波形运动数据，共采集了500组数据。弹性波与岩石节理发生相互作用时产生不连续现象，弹性波在不含节理区域传播时波形连续。因此，为了获得节理的几何形状，在每个时间间隔之间计算x方向和y方向位移场分布的跳跃。然后，在整个时间范围内对x方向和y方向位移跳跃的绝对值进行积分，其中累积位移跳跃最大的点暴露了节理的真实几何形状，通过编译代码运算之后的检测结果如图 10所示。
为了提高检测精度，在时间间隔段进行傅里叶变换得到频域波形数据，对频域上的波形数据进行分析。首先选择检测窗口window_size = 5，循环次数等于列数减去window_size加1，在每个检测窗口检测频域上所有大于jump_lim的点，跳跃极限jump_lim取0.5×10-9；如果窗口不存在跳跃点，则采用pchip插值进行处理。如果存在跳跃，则将跳跃两侧的位移取平均值。计算梯度，接着按行依次计算duxx的值，按列依次求duxy的值，按行依次求duxy的值，按列依次求duyy的值，取所有计算结果的绝对值，并在每个检测窗口检测所有大于extreme_val的点，设置extr_val = 1×10-8；如果不存在异常点，则采用pchip插值进行处理。如果存在异常点，则将两侧的值取平均值。最后对整理好的每行每列数据在x方向和y方向进行积分，绝对值最小值即裂缝点的位置。通过编译代码运算之后轴向应力为0 MPa时节理几何形状的检测结果如图 11所示。节理几何形状的重建为计算节理刚度沿节理几何形状分布奠定基础。
4.2 节理刚度分布计算
岩石节理、断层界面凹凸不平且存在局部相互接触，为弹性波揭示节理的几何形状和残余接触行为提供了可能[22-23]。因此，通过线性滑移模型描述弹性波作用下岩石节理本构响应：
n⋅C:∇u=K(ξ)⋅[[u]],ξ∈Γ。 (1) 式中：u为位移场；n=n−为节理的单位法线；C:=λI2⊗I2+2μI4，其中μ和λ为拉梅常数，Im(m=2,4)为m阶对称恒等张量，等式左侧整体表示节理界面牵引力，[[u]]:=u|Γ+−u|Γ−为节理界面跳跃位移，K(ξ)∈C2×2是描述节理ξ∈Γ刚度的对称张量[24]。因此，线性滑移模型通过节理刚度描述了节理界面牵引力和跳跃位移之间的局部线性关系。
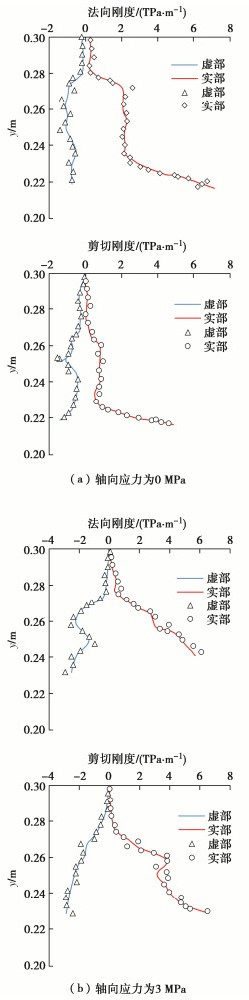
基于重建的节理几何形状，将二次可微分的位移波场数据转换成节理界面牵引力和跳跃位移，然后通过傅里叶变换到频域，最后根据线性滑移模型计算每个节理点频域上切向（法向）牵引力和切向（法向）跳跃位移之比从而获得节理剪切（法向）刚度沿节理几何形状分布。依次计算8个不同位置激励作用下的节理刚度并取平均值，试件顶部位置节理刚度分布结果如图 12所示。图中虚线和实线分别表示频率f为10 kHz和30 kHz的节理刚度分布。
由图 12可以看出激励频率为10 kHz和30 kHz时节理刚度计算结果变化趋势一致。朝节理尖端方向节理界面之间的孔径减小，接触面积增大，节理剪切刚度和法向刚度均逐渐增大。观察发现轴向应力作用下节理界面闭合，增大了节理界面接触面积，导致节理的法向刚度和剪切刚度整体增大。同时，该方法可以重构试件中多条节理的几何形状和刚度分布。试验成功获得岩石节理刚度分布，实现了节理接触行为的全局参数表征。文中计算节理刚度的方法与激励频率无关，对于不同尺度级别的节理、断层可采用不同频率的弹性波。当岩石节理、断层距离激励声源较近时可采用频率较大的弹性波；当岩石节理、断层距离激励声源较远时，可采用频率较小的弹性波，从而使探测距离达到几百米。因此提出的岩石节理几何形状的重建以及节理刚度分布的计算方法对岩石节理、断层均适用。
5. 结论
在试验室环境下实现了岩石试件中节理的全场超声表征，得到以下3点结论。
（1）通过三维扫描激光多普勒测振仪监测压电换能器激励作用下平板试件的波形传播数据，基于线性滑移理论重构试件中多条节理几何形状以及刚度分布，实现岩石节理接触行为的表征。
（2）朝节理尖端方向节理界面之间的孔径减小，接触面积增大，节理剪切刚度和法向刚度均逐渐增大，通过节理刚度分布可判断节理的开裂区域以及扩展方向；不同轴向荷载作用下节理刚度变化明显著，可通过节理刚度实现节理界面受力分析；不同激励频率条件下节理刚度计算结果变化趋势一致。
（3）后续将开展复杂加载路径下岩石节理刚度分布的演化规律及机制研究，通过节理刚度分布的时空变化实现不同条件下岩石节理、断层界面不同位置接触状态的实时动态监测分析。
-
![]()
图 4 10 kHz激励作用于S2时完整试件不同时刻的速度场vx和vy
Figure 4. Velocity fields vx and vy at different moments of intact granite specimen with excitation acting of 10 kHz on S2
![]()
图 5 30 kHz激励作用于S2时完整试件不同时刻的速度场vx和vy
Figure 5. Velocity fields vx and vy at different moments of intact granite specimen with excitation acting of 30 kHz on S2
![]()
图 6 10 kHz激励作用于S3时含节理试件不同时刻的速度场vx和vy
Figure 6. Velocity fields vx and vy at different moments of fractured granite specimen with excitation acting of 10 kHz on S3
![]()
图 7 30 kHz激励作用于S3时含节理试件不同时刻的速度场vx和vy
Figure 7. Velocity fields vx and vy at different moments of fractured granite specimen with excitation acting of 30 kHz on S3
![]()
图 8 扫描点D记录的原始速度以及经过带通滤波器处理之后的速度
Figure 8. Original recorded velocities and velocity fields after bandpass filtering at scanming point D
-
[1] CRAWFORD B R, TSENN M C, HOMBURG J M, et al. Incorporating scale-dependent fracture stiffness for improved reservoir performance prediction[J]. Rock Mechanics & Rock Engineering, 2017, 50: 3349-3359.
[2] MCLASKEY G C, THOMAS A M, GLASER S D, et al. Fault healing promotes high-frequency earthquakes in laboratory experiments and on natural faults[J]. Nature, 2012, 491(7422): 101-104. doi: 10.1038/nature11512
[3] PYRAK-NOLTE L J, NOLTE D D. Frequency dependence of fracture stiffness[J]. Geophysical Research Letters, 2013, 19(3): 325-328.
[4] GOODMAN R E, TAYLOR R L, BREKKE T L A. A model for the mechanics of jointed rock[J]. ASCE Soil Mechanics and Foundation Division Journal, 1968, 99(5): 637-659.
[5] 唐志成, 王晓川. 不同接触状态岩石节理的剪切力学性质试验研究[J]. 岩土工程学报, 2017, 39(12): 2312-2319. doi: 10.11779/CJGE201712021 TANG Zhicheng, WANG Xiaochuan. Experimental studies on mechanical behaviour of rock joints with varying matching degrees[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2312-2319. (in Chinese) doi: 10.11779/CJGE201712021
[6] LANG P S, PALUSZNY A, ZIMMERMAN R W. Evolution of fracture normal stiffness due to pressure dissolution and precipitation[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 88: 12-22. doi: 10.1016/j.ijrmms.2016.06.004
[7] PYRAK-NOLTE L J, NOLTE D D. Approaching a universal scaling relationship between fracture stiffness and fluid flow[J]. Nature Communications, 2016, 7: 10663. doi: 10.1038/ncomms10663
[8] PETROVITCH C L, PYRAK-NOLTE L J, NOLTE D D. Combined scaling of fluid flow and seismic stiffness in single fractures[J]. Rock Mechanics & Rock Engineering, 2014, 47(5): 1613-1623.
[9] QIAO Y D, ZHANG C, ZHANG L. Numerical simulation of fluid-solid coupling of fractured rock mass considering changes in fracture stiffness[J]. Energy Science & Engineering, 2019, 10: 519-536.
[10] HEDAYAT A, PYRAK-NOLTE L J, BOBET A. Precursors to the shear failure of rock discontinuities[J]. Geophysical Research Letters, 2015, 41(15): 5467-5475.
[11] 刘日成, 尹乾, 杨瀚清, 等. 恒定法向刚度边界条件下三维粗糙节理面循环剪切力学特性[J]. 岩石力学与工程学报, 2021, 40(6): 1092-1109. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106002.htm LIU Richeng, YIN Qian, YANG Hanqing, et al. Cyclic shear mechanical properties of 3D rough joint surface under constant normal stiffness(CNS) boundary conditions[J]. Chinese Journal of Rock mechanics and Engineering, 2021, 40(6): 1092-1109. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106002.htm
[12] KULATILAKE P, SHREEDHARAN S, SHERIZADEH T, et al. Laboratory estimation of rock joint stiffness and frictional parameters[J]. Geotechnical & Geological Engineering, 2016, 34(6): 1-13.
[13] JIANG Y, XIAO J, TANABASHI Y, Et al. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(2): 275-286.
[14] NASSIR M A, WAN SETTARI R, et al. Joint stiffness and deformation behaviour of discontinuous rock[J]. The Journal of Canadian Petroleum Technology, 2010, 49(9): 78-86. doi: 10.2118/140119-PA
[15] LI J, QIU Z, ZHONG H, et al. Parametric study on near-wellbore fracture geometry for wellbore strengthening in anisotropic formation[J]. Journal of Petroleum Science and Engineering, 2019, 184: 106549.
[16] HEDAYAT A, PYRAK-NOLTE L J, BOBET A. Detection and quantification of slip along non-uniform frictional discontinuities using digital image correlation[J]. Geotechnical Testing Journal, 2014, 37(5): 1-14.
[17] LUBBE R, WORTHINGTON M H. A field investigation of fracture compliance[J]. Geophysical Prospecting, 2006, 54(3): 319-331. doi: 10.1111/j.1365-2478.2006.00530.x
[18] ACOSTA-COLON A, PYRAK-NOLTE L J, NOLTE D D. Laboratory-scale study of field of view and the seismic interpretation of fracture specific stiffness[J]. Geophysical Prospecting, 2010, 57(2): 209-224.
[19] Schoenberg, Michael. Elastic wave behavior across linear slip interfaces[J]. Journal of the Acoustical Society of America, 1998, 68(5): 1516-1521.
[20] 邓华锋, 熊雨, 肖瑶, 等. 基于单试件法的节理岩体抗剪强度参数分析[J]. 岩土工程学报, 2020, 42(8): 1509-1515. doi: 10.11779/CJGE202008016 DENG Huafeng, XIONG Yu, XIAO Yao, et al. Shear strength parameters of jointed rock mass based on single test sample method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1509-1515. (in Chinese) doi: 10.11779/CJGE202008016
[21] POURAHMADIAN F, GUZINA B B. On the elastic-wave imaging and characterization of fractures with specific stiffness[J]. International Journal of Solids & Structures, 2015, 71: 126-140.
[22] WANG P, WANG S, ZHANG Z, et al. Reconstruction of fracture geometry in material medium by elastic wave[J]. Construction and Building Materials, 2021, 287(2): 123001.
[23] WANG P, WANG S, YANG T. Spatial distribution of mechanical parameters along a fracture interface[J]. Soil Dynamics and Earthquake Engineering, 2022, 157(5): 107222.
[24] NGUYEN T P, GUZINA B B. Generalized linear sampling method for the inverse elastic scattering of fractures in finite bodies[J]. Inverse Problems, 2019, 35(10): 516-532.
-
期刊类型引用(0)
其他类型引用(1)
-
其他相关附件
下载:
计量
- 文章访问数: 252
- HTML全文浏览量: 42
- PDF下载量: 54
- 被引次数: 1
