Particle breakage and shape evolution of calcareous and quartz sands under compression
-
摘要: 颗粒破碎现象对土体力学性能具有显著影响。以往关于颗粒破碎的研究多关注于粒径的变化,忽视了颗粒形状的变化。为研究破碎过程中颗粒形状的演化规律,开展了钙质砂和石英砂的侧限压缩试验,对试验过程中颗粒形状参数的进行了量化研究。结果表明两种砂土的相对破碎率均随着单位体积塑性功的增加而增加,表现出明显的双曲线关系。钙质砂的长径比、球形度和圆度会随着破碎程度的增加而增加,凸度变化不明显;随破碎量的增加,石英砂颗粒的长径比和球形度先减少后增加,凸度持续减少至稳定,球形度持续增加。通过定义试样整体的形状值能很好的量化颗粒形状的变化规律。并且钙质砂整体形状值与相对破碎率满足双曲线关系,石英砂则为抛物线关系。Abstract: The influences of particle breakage on the mechanical properties of soil are significant. The previous studies mainly focus on the variation of particle size during particle breakage but neglect the change of particle shape. In order to study the evolution of particle breakage, a series of one-dimensional compression experiments are carried out with calcareous sand and quartz sand, and the changes of particle shape are quantified. The results show that the relative breakage index of the two sands increases with the increase of plastic work per unit volume with an obvious hyperbolic relationship. The aspect ratio, sphericity and roundness of the calcareous sand increase with the expanded breakage, but the variation of convexity is unobvious. For the quartz sand, the aspect ratio and sphericity decrease first and then increase, while the convexity decreases to be stable and the sphericity continues to increase. This trend can be well quantified by defining the overall shape value of the samples. In addition, the overall shape value of the calcareous sand shows a hyperbola relationship with the relative breakage, and that of the quartz sand shows a parabola relationship.
-
Keywords:
- particle breakage /
- shape evolution /
- calcareous sand /
- quartz sand /
- one-dimensional compression
-
0. 引言
颗粒破碎是指颗粒处于足够大应力下发生断裂产生更小颗粒的现象。颗粒破碎会改变砂土的微观结构,从而显著影响砂土的力学和物理特性。颗粒破碎现象广泛存在于钙质砂等易破碎岩土体和高土石坝、桩基工程等高应力条件的相关工程领域,研究岩土材料的颗粒破碎问题具有十分重要的意义[1-4]。
目前岩土领域对颗粒破碎的研究已取得一定进展。Coop等[5]通过试验,证明了颗粒破碎的有限性,即破碎不可能无限发展下去,最终会到达一种基本稳定的状态即分形状态。试验和理论研究表明固体材料破碎的最终态满足分形规律。受加载条件等因素的影响,分形维数α虽略有差异,基本在理论值2.5左右[6-8]。颗粒破碎受到诸多因素影响,如荷载类型、矿物组成、孔隙比、颗粒形状等。就单颗粒而言,如钙质砂和堆石料,破碎是由于内部裂隙的扩展与贯通,颗粒尺寸越大所含有裂隙越多,强度越低,并且单颗粒强度大致服从Weibull分布[9-10]。从群颗粒角度而言,级配较好的土体,颗粒之间接触面多,颗粒相互咬合,在荷载作用下的破碎越少[11]。颗粒破碎会导致土体内摩擦角的降低、临界状态线下移,土体抗剪强度降低。为了研究此现象,出现了许多基于临界状态理论的颗粒破碎本构模型研究[12-14]。颗粒的破碎同样影响土体其它性质。如颗粒破碎产生的细小颗粒能显著降低土体的渗透系数[15]。基于离散元等方法的颗粒破碎数值模拟与试验结果得到的颗粒破碎规律类似[16-17]。此外模拟结果表明发生破碎后颗粒形状的演化存在一定规律性[18]。
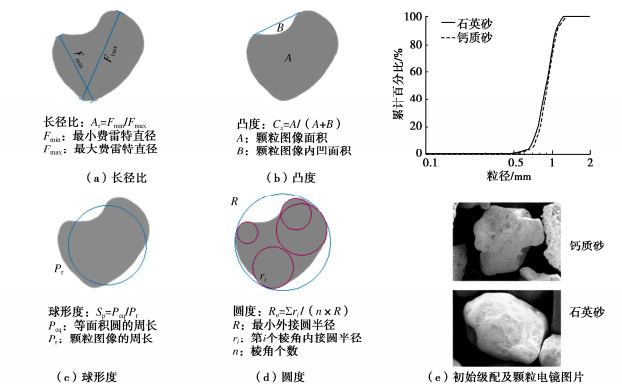
另一方面,颗粒的形状也能影响土体的力学性质,如Xiao等[19]通过试验验证,土体颗粒整体越接近球形,土体的内摩擦角越低,反映为土体抗剪强度的降低。颗粒形状的几何分析可分成3个尺度:颗粒整体尺度,如长径比和球形度;局部尺度,如圆度;表面结构,如粗糙度[20]。本文采用长径比、凸度、球形度和圆度描述颗粒的几何形状。图 1(a)~(d)展示了这4类形状参数的定义。长径比是用来描述颗粒形状的常用参数,球形颗粒长径比为1,颗粒越细长越接近0;凸度是描述颗粒密实程度参数,颗粒越紧实,内凹面积越小,凸度值越接近1;球形度量化了颗粒与理想球体的接近程度,理想球体球形度为1;圆度是量化颗粒棱角的参数,棱角越少则越接近1[21-22]。有学者指出颗粒破碎会显著改变颗粒的形状[23-24]。目前针对形状演化的研究多集中在数值模拟方面,缺少对天然土体颗粒形状演化规律系统的试验研究。本文研究了两种典型的砂土材料在侧限压缩条件下的变形特性、粒径和形状演化的规律,探究颗粒破碎与形状的联系,为考虑颗粒形状和粒径两方面研究破碎创造条件。
1. 试验设计
1.1 试验材料
试验所用钙质砂取自南海,主要成分为碳酸钙,由海洋软体动物的遗体和残骸经过海洋作用形成,为典型的海源性砂土,具有粗糙多孔、棱角较多、疏松易碎等特点。石英砂为福建标准砂,其颗粒由岩石碎裂、搬运、磨蚀等风化作用形成,主要成分为二氧化硅,为陆源性岩土材料。试验前将两种材料清洗烘干,并用筛分法取出0.8~1.0 mm粒径的颗粒。
两种材料的物理性质和初始平均形状如表 1所示。由于两种材料的颗粒形状不同,即使二者具有相似的不均匀系数和曲率系数,但孔隙比差异较大。两种砂颗粒的扫描电子显微镜图(SEM)和初始粒径分布如图 1(e)所示,两者形状和孔隙的差异较明显。
表 1 试验用砂土物理性质和初始形状Table 1. Physical properties and initial shapes of test sand类别 emin emax Gs d50 /μm Cu Cc Ar Cx Sp Rn 钙质砂 0.98 1.37 2.74 903 1.32 1.02 0.675 0.949 0.794 0.214 石英砂 0.61 0.88 2.67 909 1.27 1.00 0.734 0.968 0.823 0.251 注:emin,emax为最小、最大孔隙比;Gs为相对密度;d50为累计质量为50%时对应颗粒直径;Cu为不均匀系数;Cc为曲率系数;Ar,Cx,Sp,Rn为初始形状分布累计达50%质量时对应形状参数值。 1.2 试验设备
侧限压缩加载仪器为MTS万能试验机,如图 2(a)所示,最大量程为100kN,应力位移数据自动采集,可预设程序自动循环加载。试验中采用位移控制,加载速率为0.15 mm/min,确保试样受到准静态加载[30]。轴向力加载至目标值后位移不发生变化则认为试样达到稳定。
颗粒粒径和形状的检测装置采用SYMPATEC公司生产的激光粒度仪(QICPIC),如图 2(b)所示。工作原理如图 2(c)所示:在测试过程中,仪器通过控制高压气流将颗粒吹散,形成稳定的颗粒流,通过高分辨、高帧率相机,获得颗粒运动中的二维图像进行分析。所采用的M7镜头,形状有效识别范围为38~2888 μm,最小像素点5.5 μm2。该仪器可在不产生二次破碎的情况下对颗粒粒径和形状进行精准分析[22, 26]。所得数据为颗粒的二维图像,相比筛分法更为精确,采用最小弦长对颗粒粒径进行评估与筛分法最为接近。由于图像识别精度问题,该设备对微小颗粒形状识别效果较差。并且土体中粉粒的形状对于土体的影响较为次要,对颗粒形状进行分析时已将小于75 μm颗粒排除在外。
1.3 试验方案
现有研究表明,粗粒土在侧限压缩条件下存在明显的屈服点[27],本试验实测0.8~1.0 mm单粒径钙质砂屈服点σCy为2 MPa,石英砂屈服点σQy为12 MPa。因为矿物成分和内部结构的差异,两种颗粒材料的单颗粒强度差别较大,采用相同的应力水平产生的破碎量差异较大,不能分析比较。所以此处定义终止应力比值β=σu/σy,其中σu为加载的终止应力。两种砂土颗粒形状的差异很大,导致无法采用相同的初始孔隙比进行压缩,所以试验控制初始相对密实度Dr=80%。本试验采用试样的高度与直径比值为0.75以减小拱效应的影响[15],圆柱体试样尺寸如图 2(a)。压缩后破碎颗粒进行重新排布再次压缩会使得破碎进一步发展,本试验也将破碎后颗粒是否重排考虑在内,颗粒重排组在每次加载完成后完全取出,重新填装进行下次加载;循环加载的试样则保持一次加载后状态,卸载之后再加载,重复至相应次数。试样加载信息如表 2所示。
表 2 试验组信息及编号Table 2. Information and number of samples钙质砂 β 加载情况 石英砂 β 加载情况 C0 0 不加载 Q0 0 不加载 C1 2 1次加载 Q1 1 1次加载 C2 4 1次加载 Q2 2 1次加载 C3 8 1次加载 Q3 3 1次加载 C4 12 1次加载 Q4 4 1次加载 C5 12 4次循环加载 Q5 4 4次循环加载 C6 12 2次重排加载 Q6 4 2次重排加载 C7 12 4次重排加载 Q7 4 4次重排加载 2. 压缩特性
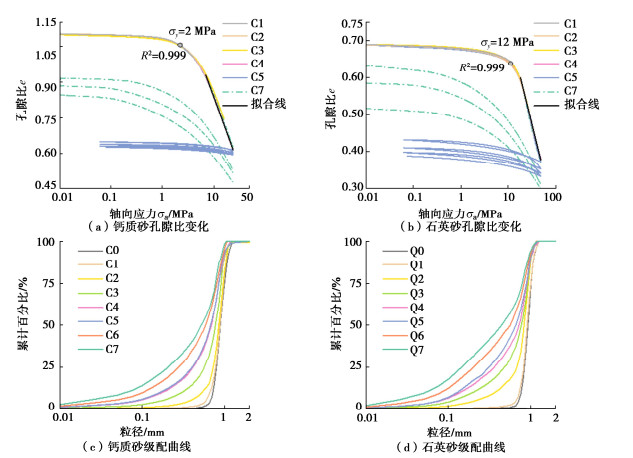
如图 3(a),(b)所示,两种砂土压缩过程中,孔隙比e随轴向应力σa的增加而降低。两种砂分别加载至不同的终止轴向应力,压缩曲线重合度较高。在轴向应力为对数-孔隙比为线性的坐标系下,压缩曲线曲率值最大点所对应的轴向应力即为此种砂土的屈服点,即有上述钙质砂和石英砂的屈服点。两种材料的压缩曲线均满足由直到曲,最后线性稳定的特征。根据经典土力学,土体的一维压缩曲线符合下式[8]:
e=e′−Cclgσa, (1) 式中,e′为直线在纵坐标轴的截距,Cc为压缩指数,为土体的经验常数。根据此公式对两种砂土的压缩曲线末端进行拟合,得出所用钙质砂压缩指数为0.587,石英砂则为0.520。随着轴向应力的增加初始孔隙比对土体压缩特性的影响会逐渐降低[28],由此可见钙质砂相比石英砂具有更高的可压缩程度。C5和C7展示了钙质砂颗粒不重排与颗粒重排条件下的压缩曲线。C7曲线每次初始值的不同,表明试样颗粒破碎后进行的重排会使得密实状态下孔隙比低于初始状态,同时最终孔隙比低于不进行重排颗粒的孔隙比。不重排循环压缩同样会使得孔隙比降低,但程度较小。加载—卸载的循环过程中土体表现出明显的弹性特征,钙质砂和石英砂压缩后卸载回弹的弹性模量E,分别稳定在2.0 GPa和2.4 GPa,接近完全卸载时弹性模量会降低。
3. 粒径演化
如图 3(c), (d)所示钙质砂和石英砂的粒径累计分布曲线。随着终止轴向应力的增加,粒径分布曲线左移,小粒径颗粒增多。同时重新排布土体的再次加载会使得破碎进一步发展,这一现象在两种砂土中都十分明显。C4和C5曲线接近说明不进行颗粒重排的钙质砂试样在加载卸载循环中破碎几乎不再发展,而Q4和Q5存在差距表明对于石英砂不进行重新排布的循环加载卸载同样会使得破碎进一步发展。
为更好地描述颗粒破碎程度,许多学者通过粒径分布曲线定义了量化破碎量的方法[29-32]。在此引入Einav定义的相对破碎率[31]。以分形维数α=2.5的曲线为颗粒破碎的最终级配,确定方式为[33]
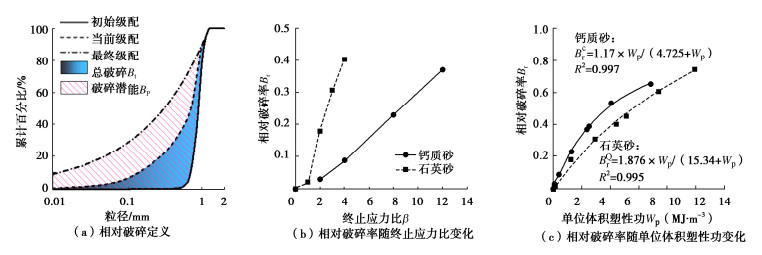
F(d)=(d/dM)3−α, (2) 式中,d为某一直径,F(d)为小于直径d颗粒百分比,dM为最大粒径。相对破碎率Br定义为
Br=Bt/Bp, (3) 其中,Bp为破碎潜能,Bt为总破碎。两者取值如图 4(a)所示,破碎潜能为最终级配和初始级配围成的面积值、总破碎为当前级配与初始级配围成的面积值。石英砂相对破碎率随终止应力比线性增加,但增幅逐步降低,钙质砂在β≥2时具有同样的规律。石英砂和钙质砂增加相同倍数的屈服应力时,石英砂发生的破碎要多于钙质砂。已有研究发现颗粒相对破碎率与单位体积塑性功Wp近似存在双曲线关系[34],
Br=a×Wp/(b+Wp), (4) 式中,a,b均为拟合系数。单位体积塑性功采用下式简化计算:
Wp=∫σadεa−EΔεa2, (5) 其中,dεa为轴向应变增量,E为砂土卸载回弹弹性模量,Δεa为卸载回弹轴向应变。图 4(c)展示了单位体积塑性功与相对破碎率的关系,可以看出二者具有明显的双曲线函数关系。钙质砂相对石英砂在相同单位体积塑性功时具有更多的破碎量。
4. 形状演化
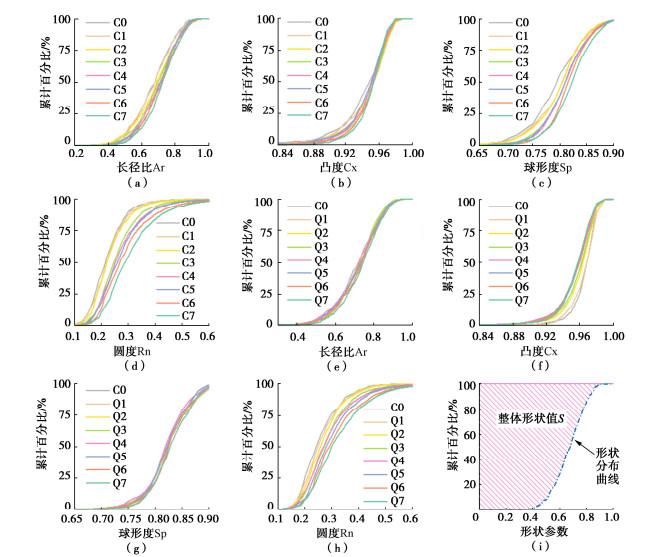
通过QICPIC对加载后两种砂土进行检测,得出如图 5所示的形状参数累计分布演化图。从图 5(a)~(d)中可以看出,钙质砂的长径比、球形度和圆度累计曲线均发生了明显的右移,表明颗粒的最大、最小费雷特直径差值减小;颗粒图像趋向于圆形,颗粒本身趋向于球形;颗粒局部棱角减少。相反,凸度曲线变化有限,即颗粒内凹面积并没有太大变化。凸度对钙质砂是一个对颗粒破碎变化不敏感的形状参数。从图 5(e)~(h)中可以看出,石英砂的圆度变化规律与钙质砂相同。长径比和球形度的分布曲线同样有右移趋势,但与钙质砂不同的是石英砂的变化并不是单调右移,表现为先减少后增加。而石英砂的凸度表现为减少的趋势。为了更好的量化形状参数的变化趋势,定义砂土试样的整体形状值S,如图 5(i)所示,形状分布曲线左侧围成的面积值即为整体形状值。
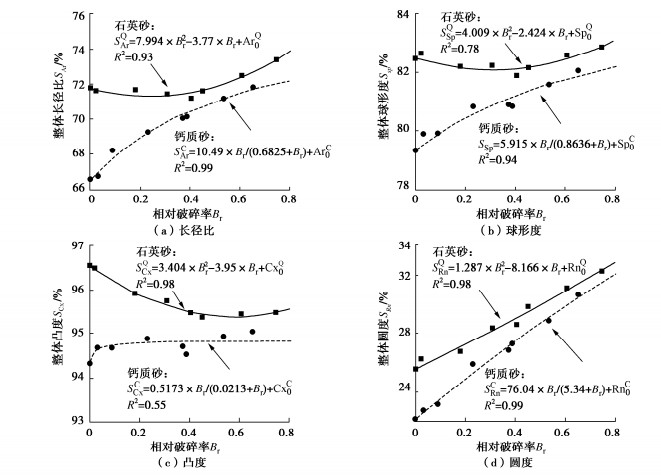
根据对整体形状值S的定义,绘制整体形状值与相对破碎的关系如图 6所示。钙质砂除凸度的整体形状值基本不变外,其余整体形状值均随着破碎率的增加而增长。钙质砂整体形状值与相对破碎率有较强的双曲线关系,如长径比整体形状值满足
SCAr=a×Br/(b+Br)+ArC0, (6) 式中,SCAr为长径比整体形状值,下标为长径比,上标C代表钙质砂,a,b为拟合参数,ArC0为钙质砂初始长径比整体形状值,其他形状参数同理。因Br与S具有较好的对应关系,由此可根据破碎情况估计形状变化程度。
石英砂的整体形状值除圆度持续增加外,长径比和球形度的整体形状值先下降后上升,凸度下降至稳定。四者均近似满足二次函数关系,如长径比整体形状值满足
SQAr=a×Br2+b×Br+ArQ0, (7) 式中,上标Q对应石英砂。石英砂在较大破碎后整体形状值上升,原因是颗粒的重新排布造成的破碎进一步发展,为更好地说明这一问题,对破碎进行颗粒尺度的分析。
颗粒的破碎可以按照破碎后形成的颗粒质量比例分为破裂、磨碎和磨损[35],如图 7(a)所示。破裂会产生许多大小相近的子颗粒;磨碎会产生一个与原来颗粒大小相近的颗粒和许多较小颗粒;磨损是从原颗粒上脱离一些细小颗粒。石英砂颗粒初始形状较为规则,在磨碎破坏掉部分棱角之后,轴向压力逐渐增加至颗粒破裂,产生一些具有棱角的子颗粒,造成长径比和球形度的整体形状值的降低。随后试样被压实,破碎产生更多的接触面使得Br增长减缓。后续颗粒重新排布降低了颗粒间的接触面积,使不规则颗粒的棱角容易形成应力集中,发生磨碎破坏使得子颗粒更为规则。这一过程表现为长径比和球形度呈现下凸的抛物线形式。相反,由于钙质砂初始形状的不规则,破碎后产生的子颗粒的形状相比于原颗粒并没有变得不规则,所以在荷载作用下多种破坏模式并存,使得颗粒总体的形状总是趋向于规则,表现为增长逐步放缓的双曲线函数。不同加载程度下钙质砂(C0,C3,C7)和石英砂(Q0,Q3,Q7)的电镜图片如图 7(b)所示,由此可见随着位体积塑性功的增加,颗粒粒径减小,破碎量增加。钙质砂颗粒的形状从图中可以看出向着更为规则发展。石英砂初步的破碎会产生一些具有棱角的子颗粒,随着破碎的进一步发展,子颗粒进一步破碎,会使得颗粒形状趋于规则。
由上述分析和试验结果可以提出一个关于颗粒形状变化的猜想:砂土颗粒在经历破碎之后, 颗粒形状会趋于一个稳定的区间,即形状演化的最终值。目前已有数值模拟研究得出这一结论[18],本试验研究已存在变化趋势,关于距离形状稳定区间还需要进一步试验研究。
5. 结论
本文通过对单粒径钙质砂和石英砂进行不同程度的侧限压缩试验,并且利用图像测量对颗粒的破碎与形状变化进行了分析。提出了土体的整体形状值S来量化颗粒的形状及形状演化,得到了3点结论。
(1)钙质砂和石英砂的侧限压缩会使孔隙比与应力的对数趋向线性关系。砂土的颗粒破碎率与单位体积塑性功具有显著的双曲线关系。在相同单位体积塑性功下钙质砂破碎多于石英砂。
(2)颗粒破碎过程中,颗粒粒径变化的同时颗粒形状也在发生明显的变化。不同的形状参数对形状变化的敏感程度不同。对于钙质砂,在凸度基本不变的同时,长径比、球形度和圆度都随破碎量的扩大而增加。石英砂的长径比和球形度随破碎先下降后上升,凸度先下降后稳定,圆度持续增加。
(3)采用砂土的整体形状值S能较好地量化颗粒形状、反映颗粒形状的变化趋势。钙质砂的整体形状值与相对破碎率呈现显著的双曲线关系,随破碎的增加形状参数增长放缓;石英砂则具有下凸的抛物线关系。
-
表 1 试验用砂土物理性质和初始形状
Table 1 Physical properties and initial shapes of test sand
类别 emin emax Gs d50 /μm Cu Cc Ar Cx Sp Rn 钙质砂 0.98 1.37 2.74 903 1.32 1.02 0.675 0.949 0.794 0.214 石英砂 0.61 0.88 2.67 909 1.27 1.00 0.734 0.968 0.823 0.251 注:emin,emax为最小、最大孔隙比;Gs为相对密度;d50为累计质量为50%时对应颗粒直径;Cu为不均匀系数;Cc为曲率系数;Ar,Cx,Sp,Rn为初始形状分布累计达50%质量时对应形状参数值。 表 2 试验组信息及编号
Table 2 Information and number of samples
钙质砂 β 加载情况 石英砂 β 加载情况 C0 0 不加载 Q0 0 不加载 C1 2 1次加载 Q1 1 1次加载 C2 4 1次加载 Q2 2 1次加载 C3 8 1次加载 Q3 3 1次加载 C4 12 1次加载 Q4 4 1次加载 C5 12 4次循环加载 Q5 4 4次循环加载 C6 12 2次重排加载 Q6 4 2次重排加载 C7 12 4次重排加载 Q7 4 4次重排加载 -
[1] XIAO Y, WANG L, JIANG X, et al. Acoustic emission and force drop in grain crushing of carbonate sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(9): 04019057.
[2] 张家铭, 汪稔, 张阳明, 等. 土体颗粒破碎研究进展[J]. 岩土力学, 2003, 24(增刊2): 661–665. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2003S2157.htm ZHANG Jia-ming, WANG Ren, ZHANG Yang-ming, et al. Advance in studies of soil grain crush[J]. Rock and Soil Mechanics, 2003, 24(S2): 661–665. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2003S2157.htm
[3] 赵飞翔, 迟世春, 米晓飞. 基于颗粒破碎特性的堆石材料级配演化模型[J]. 岩土工程学报, 2019, 41(9): 1707–1714. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909017.htm ZHAO Fei-xiang, CHI Shi-chun, MI Xiao-fei. Gradation evolution model based on particle breakage characteristics for rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1707–1714. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909017.htm
[4] 贾宇峰, 王丙申, 迟世春. 堆石料剪切过程中的颗粒破碎研究[J]. 岩土工程学报, 2015, 37(9): 1692–1697. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509024.htm JIA Yu-feng, WANG Bing-shen, CHI Shi-chun. Particle breakage of rockfill during triaxial tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1692–1697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509024.htm
[5] COOP M R, SORENSEN K K, BODAS FREITAS T, et al. Particle breakage during shearing of a carbonate sand[J]. Géotechnique, 2004, 54(3): 157–163.
[6] 张季如, 胡泳, 张弼文, 等. 石英砂砾破碎过程中粒径分布的分形行为研究[J]. 岩土工程学报, 2015, 37(5): 784–791. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505004.htm ZHANG Ji-ru, HU Yong, ZHANG Bi-wen, et al. Fractal behavior of particle-size distribution during particle crushing of quartz sand and gravel[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 784–791. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505004.htm
[7] XIAO Y, LIU H, XIAO P, et al. Fractal crushing of carbonate sands under impact loading[J]. Géotechnique Letters, 2016, 6(3): 199–204.
[8] MCDOWELL G R, BOLTON M D. On the micromechanics of crushable aggregates[J]. Géotechnique, 1998, 48(5): 667–679. doi: 10.1680/geot.1998.48.5.667
[9] 孟敏强, 王磊, 蒋翔, 等. 基于尺寸效应的粗粒土单颗粒破碎试验及数值模拟[J]. 岩土力学, 2020, 41(9): 2953–2962. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202009012.htm MENG Min-qiang, WANG Lei, JIANG Xiang, et al. Single-particle crushing test and numerical simulation of coarse grained soil based on size effect[J]. Rock and Soil Mechanics, 2020, 41(9): 2953–2962. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202009012.htm
[10] 童晨曦, 张升, 李希, 等. 基于Markov链的岩土材料颗粒破碎演化规律研究[J]. 岩土工程学报, 2015, 37(5): 870–877. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505017.htm TONG Chen-xi, ZHANG Sheng, LI Xi, et al. Evolution of geotechnical materials based on Markov chain considering particle crushing[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 870–877. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505017.htm
[11] 蔡正银, 李小梅, 关云飞, 等. 堆石料的颗粒破碎规律研究[J]. 岩土工程学报, 2016, 38(5): 923–929. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm CAI Zheng-yin, LI Xiao-mei, GUAN Yun-fei, et al. Particle breakage rules of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 923–929. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm
[12] XIAO Y, WANG C G, ZHANG Z C, et al. Constitutive modeling for two sands under high pressure[J]. International Journal of Geomechanics, 2021, 21(5): 04021042. doi: 10.1061/(ASCE)GM.1943-5622.0001987
[13] 曾凯锋, 刘华北. 考虑颗粒破碎的钙质砂修正邓肯-张E-B模型[J]. 工程地质学报, 2020, 28(1): 94–102. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202001011.htm ZENG Kai-feng, LIU Hua-bei. A modified Duncan-Chang E-B model with particle breakage for calcareous sand[J]. Journal of Engineering Geology, 2020, 28(1): 94–102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202001011.htm
[14] 蔡正银, 李小梅, 韩林, 等. 考虑级配和颗粒破碎影响的堆石料临界状态研究[J]. 岩土工程学报, 2016, 38(8): 1357–1364. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201608001.htm CAI Zheng-yin, LI Xiao-mei, HAN Lin, et al. Critical state of rockfill materials considering particle gradation and breakage[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1357–1364. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201608001.htm
[15] DAVID SUITS L, SHEAHAN T C, VALDES J R, et al. Monitoring the hydraulic conductivity of crushing sands[J]. Geotechnical Testing Journal, 2006, 29(4): 13302.
[16] 刘萌成, 高玉峰, 刘汉龙. 模拟堆石料颗粒破碎对强度变形的影响[J]. 岩土工程学报, 2011, 33(11): 1691–1699. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201111010.htm LIU Meng-cheng, GAO Yu-feng, LIU Han-long. Effect of particle breakage on strength and deformation of modeled rockfills[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1691–1699. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201111010.htm
[17] 徐琨, 周伟, 马刚, 等. 基于离散元法的颗粒破碎模拟研究进展[J]. 岩土工程学报, 2018, 40(5): 880–889. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805016.htm XU Kun, ZHOU Wei, MA Gang, et al. Review of particle breakage simulation based on DEM[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 880–889. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805016.htm
[18] ZHU F, ZHAO J D. Interplays between particle shape and particle breakage in confined continuous crushing of granular media[J]. Powder Technology, 2021, 378: 455–467.
[19] XIAO Y, LONG L H, MATTHEW EVANS T, et al. Effect of particle shape on stress-dilatancy responses of medium-dense sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(2): 04018105.
[20] BARRETT P J. The shape of rock particles, a critical review[J]. Sedimentology, 1980, 27(3): 291–303.
[21] CHO G C, DODDS J, SANTAMARINA J C. Particle shape effects on packing density, stiffness, and strength: natural and crushed sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(5): 591–602.
[22] LI L Z, BEEMER R D, ISKANDER M. Granulometry of two marine calcareous sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(3): 04020171.
[23] MIAO G, AIREY D. Breakage and ultimate states for a carbonate sand[J]. Géotechnique, 2013, 63(14): 1221–1229.
[24] YU J D, SHEN C M, LIU S H, et al. Exploration of the survival probability and shape evolution of crushable particles during one-dimensional compression using dyed gypsum particles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(11): 04020121.
[25] XIAO Y, YUAN Z X, CHU J, et al. Particle breakage and energy dissipation of carbonate sands under quasi-static and dynamic compression[J]. Acta Geotechnica, 2019, 14(6): 1741–1755.
[26] 张小燕, 蔡燕燕, 王振波, 等. 珊瑚砂高压力下一维蠕变分形破碎及颗粒形状分析[J]. 岩土力学, 2018, 39(5): 1573–1580. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201805004.htm ZHANG Xiao-yan, CAI Yan-yan, WANG Zhen-bo, et al. Fractal breakage and particle shape analysis for coral sand under high-pressure and one-dimensional creep conditions[J]. Rock and Soil Mechanics, 2018, 39(5): 1573–1580. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201805004.htm
[27] MCDOWELL G R. On the yielding and plastic compression of sand[J]. Soils and Foundations, 2002, 42(1): 139–145.
[28] 张家铭, 汪稔, 石祥锋, 等. 侧限条件下钙质砂压缩和破碎特性试验研究[J]. 岩石力学与工程学报, 2005, 24(18): 3327–3331. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200518021.htm ZHANG Jia-ming, WANG Ren, SHI Xiang-feng, et al. Compression and crushing behavior of calcareous sand under confined compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3327–3331. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200518021.htm
[29] 田海, 孔令伟, 赵翀. 基于粒度熵概念的贝壳砂颗粒破碎特性描述[J]. 岩土工程学报, 2014, 36(6): 1152–1159. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201406027.htm TIAN Hai, KONG Ling-wei, ZHAO Chong. Characterization of particle breakage with grading entropy on shell sand[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1152–1159. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201406027.htm
[30] XIAO Y, CHEN H, STUEDLEIN A W, et al. Restraint of particle breakage by biotreatment method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(11): 04020123.
[31] EINAV I. Breakage mechanics—part Ⅰ: theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(6): 1274–1297.
[32] XIAO Y, WANG C G, WU H R, et al. New simple breakage index for crushable granular soils[J]. International Journal of Geomechanics, 2021, 21(8): 04021136.
[33] TYLER S W, WHEATCRAFT S W. Application of fractal mathematics to soil water retention estimation[J]. Soil Science Society of America Journal, 1989, 53(4): 987–996.
[34] YU F W. Characteristics of particle breakage of sand in triaxial shear[J]. Powder Technology, 2017, 320: 656–667.
[35] DAOUADJI A, HICHER P. An enhanced constitutive model for crushable granular materials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(6): 555–580.



 下载:
下载: