Statistical damage model for fiber-reinforced vegetation concrete substrate
-
摘要:
为研究纤维加筋植被混凝土基材的本构模型和损伤演化规律,考虑围压和纤维掺量两个因素,基于Weibull分布建立了能反映基材力学特性的统计损伤模型,给出了模型参数的确定方法,探讨了Weibull分布参数与围压、纤维掺量的关系。利用该模型对基材三轴试验结果进行对比验证;根据基材的破坏准则,推导了损伤阈值的确定方法;通过分析损伤演化特征与微元体的失效过程,对基材应力–应变关系和损伤软化规律进行了阐释。分析结果表明该模型曲线与试验结果吻合度较高,能较好反映纤维加筋基材加载过程中的损伤软化特性;加筋基材损伤阈值与峰值应变之比保持在0.4~0.6之间。本文研究为准确分析和评价基材的力学性质提供了理论参考。
Abstract:This study attempts to investigate the constitutive model and damage evolution law of the fiber-reinforced vegetation concrete substrate. Taking the two factors of confining pressure and fiber content into account, a statistical damage model that can reflect the mechanical properties of the substrate is established based on the Weibull distribution. The method for determining model parameters is given, and the relationship among the Weibull distribution parameters, the confining pressure and the fiber contents is discussed. The model is then used to verify the results of the triaxial tests on the substrate. According to the destruction criterion of the substrate, the method for determining the damage threshold is deduced. By analyzing the damage evolution characteristics and the failure process of the micro-element, the stress-strain relationship and the law of damage softening of the substrate are elaborated. The results show that the model curves agree well with the tests, which can reflect the damage softening characteristics during the loading process of the fiber-reinforced substrate. Besides, the ratio of the damage threshold to the peak strain is found to range from 0.4 to 0.6. This study provides a theoretical reference for the accurate analysis and evaluation of the mechanical properties of substrate.
-
0. 引言
植被混凝土基材由种植土、水泥、有机质、活化添加剂等材料配置而成,为裸露岩质边坡的生态修复提供了一种有效的解决方案[1]。目前该技术在水利、交通、市政等众多工程领域取得广泛应用,并成为国家能源行业推荐标准[2]。为更好地服务于工程实践应用,植被混凝土基材的理化性质、活化特性、力学性能的改良和探索研究持续开展。在基材力学性能改良方面,尽管试验结果表明[3],掺入纤维可以显著提高基材强度,改善基材软化性能,但对加筋基材变形演化机理尚缺乏深入认识,有待进一步探索。
由于岩土材料内部存在微缺陷,将岩土介质的变形破坏视为损伤演化过程已获得普遍共识。基于Kachanov于1958年提出的连续损伤力学理论,国内外学者对岩土损伤进行了广泛深入的有益探索[4-11]。岩土介质缺陷具有随机性,可将连续损伤理论和统计强度理论结合,建立统计损伤模型描述其应力–应变关系和演化特征[5]。基于单轴或三轴压缩试验条件,众多研究者开展了岩土体的统计损伤分析,建立了相应的统计损伤本构模型。研究表明,统计损伤分析中的微元体强度分布可采用Weibull分布[7]、正态分布[8]、对数正态分布[9]、熵分布[10]等描述,而微元体破坏准则多采用Mohr-Coulomb(M-C)准则或Drucker-Prager(D-P)准则。
本文拟以Weibull分布描述微元体强度分布,在三轴压缩条件下,采用M-C准则表征的基材微元体强度准则,建立基材统计损伤本构方程;结合三轴试验结果,考虑围压、纤维掺量等影响分析并确定模型参量,进行纤维加筋基材应力–应变、损伤演化分析。本文研究有助于深入认识纤维加筋植被混凝土基材损伤性能与演变规律,为准确分析和评价基材力学性能提供理论参考。
1. 统计损伤模型的建立
1.1 基本假定
在统计损伤理论中,一般把岩土体材料的损伤看作是微元体不断破坏引起的。本文基于以下基本假定建立基材的统计损伤模型:
(1)基材的微元强度f服从Weibull分布。
(2)在外荷载作用下,基材包括损伤部分和未损伤部分,基材任意微元体上的荷载由未损伤部分承担。
(3)在加载过程中微元体的损伤演化是一个连续的变化过程。
(4)基材的微元强度破坏规律符合M-C准则。
(5)基材为各向同性损伤材料,未损伤微元的应力–应变符合胡克定律。
1.2 基材统计损伤本构模型
根据已有研究[7],基于假定(1),基材微元强度f的概率密度函数以Weibull分布的形式表示为
p(f)=mf0(ff0)m−1⋅exp[−(ff0)m], (1) 式中,m和f0为Weibull分布中的形状参数与尺度参数,在一定程度上能反映基材的力学特性。
在基材加载过程中,当应力水平处在某一区间[f,f +df]时,微元体失效的概率为p(f)df,失效的微元体数目增量为Np(f)df。由假定(2),(3),则已失效的微元体数目可以表示为
Nd=∫f0Np(x)dx=N{1−exp[−(ff0)m]}, (2) 式中,Nd为外荷载作用下已失效的微元数目,N为微元体总数目。进一步地,可将损伤变量定义为
D=NdN。 (3) 结合式(2),(3),可得到基材的损伤演化方程
D=P(f)=1−exp[−(ff0)m]。 (4) 研究表明,材料在加载过程中并非只要产生变形或承受荷载就发生损伤[11]。故本文认为基材的损伤存在某一阈值,应将式(4)进行分段表示更为合理,即
D={01−exp[−(ff0)m]f<0f⩾ (5) 根据Lemaitre应变等价假说[12],可用材料未损伤部分承担的应力来表示损伤材料的本构关系:
\sigma = (1 - D)\sigma _{}^* = (1 - D)E\varepsilon \text{,} (6) 式中, \sigma 为名义应力, \sigma _{}^* 为材料未损伤部分承担的应力,D为损伤变量,E为弹性模量, \varepsilon 为应变。
基材的微元强度f是确定损伤演化、建立损伤模型的关键。材料的微元强度由应力函数 h(\sigma _{}^*) 和材料的内在强度参数 k 共同决定[13],即
f = h(\sigma _{}^*) - k \text{,} (7) 由假定(4),在M-C准则下,分别得到
h(\sigma _{}^*) = {\text{(}}\sigma _1^* - \sigma _3^*{\text{)}} - {\text{(}}\sigma _1^* + \sigma _3^*{\text{)sin}}\varphi \text{,} (8) k = 2c\cos \varphi \text{,} (9) 材料未损伤部分承担的应力 \sigma * 产生的轴向应变可由假定(5)的广义胡克定律表示:
\varepsilon _1^{} = \frac{1}{E}[\sigma _1^* - \nu {\text{(}}\sigma _1^* + \sigma _3^*{\text{)}}] \text{,} (10) 式中, \nu 为基材的泊松比。
但 \sigma _i^* 不能在试验中直接得到,名义应力 \sigma _i^{} 却能从中简单获取。故由式(6),可转换为
\sigma _i^* = \frac{{{\sigma _i}}}{{1 - D}}(i = 1,2,3) \text{,} (11) 常规三轴试验中 {\sigma _2} = {\sigma _3} ,则式(10)可记为
\varepsilon _1^{} = \frac{{\sigma _1^{} - 2\nu \sigma _2^{}}}{{E(1 - D)}} \;。 (12) 结合式(5),(12),可得到基材统计损伤模型
\sigma_{1}=\left\{\begin{array}{ll} E \varepsilon_{1}+2 v \sigma_{3} & f <0, \\ E \varepsilon_{1} \exp \left[\left(\frac{f}{f_{0}}\right)^{m}\right]+2 v \sigma_{3} & f \geqslant 0, \end{array}\;,\right. (13) 由于损伤变量D演化是连续且非线性变化的过程,故式(13)可以揭示基材应力–应变非线性规律:f < 0时,基材未发生损伤,表现为线弹性;f≥0,损伤启动并逐渐发展,表现为非线性。
2. 模型参数及确定方法
2.1 模型参数
在基材统计损伤模型式(13)中,涉及4个模型参量,即泊松比 \nu 、弹性模量E、Weibull分布的形状参数m和尺度参数f0。
分析中,忽略纤维掺入的影响,认为加载前后泊松比保持不变,取为0.3。对于弹性模量,有研究表明,素土的弹性模量是围压的函数[14];对于纤维加筋土,弹性模量还随纤维掺量的增加而增大[15]。因此本文将纤维加筋基材的整体弹性模量 {E_{{\text{fc}}}} 表示为以纤维掺量 \lambda 和围压 {\sigma _3} 为变量的二元函数,即
{E_{{\text{fc}}}} = g(\lambda ,{\sigma _3}) \text{,} (14) 式中,函数 g(\lambda ,{\sigma _3}) 根据三轴试验结果确定。
Weibull分布参数m和f0不仅受加载条件的影响,还与纤维掺量密切相关。故将式(14)代入式(13),由三轴试验的应力–应变值,可以确定出参数m和f0。
2.2 加筋基材三轴试验
植被混凝土基材由种植土、水泥、有机质、活化添加剂分别按质量比100∶8∶6∶4配制而成。制样时,控制所有试样的干密度为1.35 g/cm3。用于三轴试验的基材空白对照样不含纤维,而加筋试样使用的纤维为棕榈纤维、玄武岩纤维,纤维长度均为20 mm;按纤维在试样中的质量分数掺入纤维,设置0.2%,0.4%,0.6%,0.8%共4个纤维掺入梯度。将纤维加筋混合料拌和均匀后,称重并将其均匀分成3份,然后依次加入模具内,分层击实,制成试验所需的尺寸39.1 mm×80 mm的圆柱体(图 1(a))。
采用TSZ30-2.0型应变控制式三轴仪进行三轴剪切试验(图 1(b))。由基材在坡体中的实际受力情况,试验围压设置为10,30,50 kPa,试验后的部分试样见图 1(c)。由试验结果,得到各加筋基材在不同围压下的抗剪强度参数(表 1)、弹性模量(表 2,3)和应力–应变值。
表 1 纤维加筋基材抗剪强度测试值Table 1. Values of shear strength tests on fiber-reinforced substrateλ/% 棕榈纤维加筋基材 玄武岩纤维加筋基材 c/kPa φ/(°) c/kPa φ/(°) 0 75.4 33.7 75.4 33.7 0.2 95.5 33.4 86.6 33.5 0.4 99.0 33.9 91.1 33.7 0.6 104.0 34.0 94.1 33.3 0.8 108.3 34.1 97.4 33.7 表 2 棕榈纤维加筋基材弹性模量实际值与拟合值Table 2. Actual and fitted values of elastic modulus of palm fiber-reinforced substrateλ/% σ3=10 kPa σ3=30 kPa σ3=50 kPa 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 0 7.98 7.78 -0.0251 10.16 10.55 0.0384 11.95 11.84 -0.0092 0.2 8.63 8.55 -0.0093 10.80 11.19 0.0361 12.62 12.41 -0.0166 0.4 9.66 9.32 -0.0352 11.66 11.83 0.0146 12.77 12.99 0.0172 0.6 11.30 10.10 -0.1062 12.36 12.46 0.0081 13.61 13.56 -0.0037 0.8 11.46 10.87 -0.0515 12.52 13.10 0.0463 13.61 14.14 0.0389 表 3 玄武岩纤维加筋基材弹性模量实际值与拟合值Table 3. Actual and fitted values of elastic modulus of basalt fiber-reinforced substrateλ/% σ3=10 kPa σ3=30 kPa σ3=50 kPa 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 0 7.98 7.87 -0.0132 10.16 10.86 0.0691 11.95 12.25 0.0249 0.2 8.60 8.83 0.0270 12.58 11.88 -0.0552 13.83 13.23 -0.0432 0.4 10.34 9.79 -0.0531 12.88 12.90 0.0020 14.76 14.21 -0.0371 0.6 10.71 10.75 0.0037 13.62 13.93 0.0225 15.21 15.19 -0.0007 0.8 11.74 11.71 -0.0023 14.67 14.95 0.0186 16.21 16.18 -0.0023 2.3 参数确定
根据相关研究[14-15],考虑围压和纤维掺量,确定空白基材(纤维掺量按0计)和纤维加筋基材的弹性模量。通过二元非线性拟合,得到棕榈纤维加筋基材弹性模量表达式为
{E_{{\text{fcp}}}} = ( - 0.61\ln {\sigma _3} + 5.26)\lambda + 2.52\ln {\sigma _3} + 1.98 \text{,} (15) 玄武岩纤维加筋基材的弹性模量表达式为
{E_{{\text{fcb}}}} = ( - 0.42{\ln ^2}{\sigma _3} + 2.68\ln {\sigma _3} + 0.85)\lambda + \\\;\;\;\;\;\;\;\;\;\;\;2.72\ln {\sigma _3} + 1.61 \text{,} (16) 上述两式中, {\sigma _3} 为围压, \lambda 为纤维掺量。
表 2,3分别给出了试验和式(15),(16)计算得到的弹性模量值,其最大偏差均在±0.5%以内,相关系数R2超过0.9600,表明上述两式均能够很好反映纤维加筋基材弹性模量与围压、纤维掺量的关系。
为求解Weibull参数,结合式(7)~(9),(11),(12),(14)可得
f=\frac{E_{\mathrm{fc}} \varepsilon_{1}}{\sigma_{1}-2 v \sigma_{3}}\left[\sigma_{1}-\sigma_{3}-\left(\sigma_{1}+\sigma_{3}\right) \sin \varphi\right]-2 c \cos \varphi (17) 将式(17)代入(13),经变形得
m\text{ln}\frac{{\frac{{{E_{{\text{fc}}}}{\varepsilon _1}}}{{{\sigma _1} - 2\nu {\sigma _3}}}[{\sigma _1} - {\sigma _3} - ({\sigma _1} + {\sigma _3})\sin \varphi )] - 2c\cos \varphi }}{{{f_0}}} \\\;\;\;\;\;\;\;\;\; = \text{ln}\left( { - \text{ln}\frac{{{\sigma _1} - 2\nu {\sigma _3}}}{{{E_{{\text{fc}}}}{\varepsilon _1}}}} \right) \text{,} (18) 再分别令
y = \text{ln}\left\{ {\frac{{{E_{{\text{fc}}}}{\varepsilon _1}[{\sigma _1} - {\sigma _3} - ({\sigma _1} + {\sigma _3})\sin \varphi )]}}{{{\sigma _1} - 2\nu {\sigma _3}}} - 2c\cos \varphi } \right\} \text{,} (19) x = \text{ln}\left( { - \text{ln}\frac{{{\sigma _1} - 2\nu {\sigma _3}}}{{{E_{{\text{fc}}}}{\varepsilon _1}}}} \right) \text{,} (20) 整理后,可得
y = \frac{1}{m}x + \ln {f_0} \text{,} (21) 记 a=\frac{1}{m},b=\mathrm{ln}{f}_{0} ,把三轴试验测试得到的各组应力–应变值代入式(19),(20),通过线性回归,最终确定Weibull分布参数表达式:
\left.\begin{array}{l} m=\frac{1}{a}, \\ f_{0}=e^{b} \end{array}\right\} (22) 式中,a,b分别为回归方程的斜率与截距。
3. 结果与讨论
3.1 Weibull参数
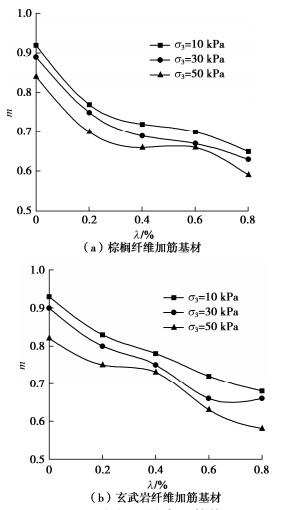
图 2给出了形状参数m随纤维掺量和围压变化的结果:纤维掺量越大,围压越大,m越小。除空白试样外,在相同纤维掺量、同一围压下,棕榈纤维加筋基材统计损伤参数m小于玄武岩纤维加筋基材。以纤维掺量 \lambda (%)和围压 {\sigma _3} (kPa)为自变量,对m进行二元回归分析,得到了两种纤维加筋基材Weibull参数m的表达式,相关系数分别为0.9355,0.9809。
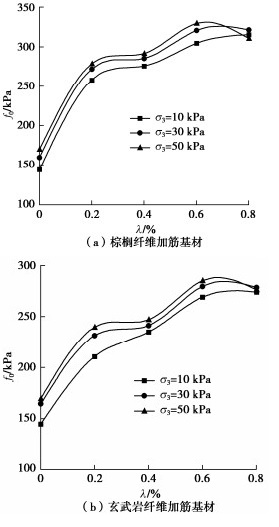
{m_{\text{p}}} = (0.0009{\sigma _3} - 0.3159)\lambda - 0.0019{\sigma _3} + 0.8963 \text{,} (23) {m_{\text{b}}} = (0.0001{\sigma _3} - 0.3068)\lambda - 0.0022{\sigma _3} + 0.9360 。 (24) 如图 3所示,尺度参数f0的总体变化趋势与m相反,即纤维掺量越大,围压越大,f0也越大。但纤维掺量达到0.6%后,f0呈现下降趋势,玄武岩纤维加筋基材比棕榈纤维加筋基材的下降更为显著。
早期研究一般地将m和f0视为影响和决定模型曲线形态变化的两个参数,但较少阐释其物理力学意义。近年来,有部分研究指出,参数m反映了微元体强度分布的集中程度[16]。结合本文分析认为,参数m实际上是对基材脆性的表征。m值越大,在剪切变形过程中,微元强度越集中,基材的脆性越明显;加载过程中峰后曲线越陡,损伤软化越明显。参数f0在一定程度上是基材宏观统计平均强度大小的反映。
分析表明,加入纤维能够有效分摊基材微元强度分布的集中程度,减小脆性破坏,增强基材整体的平均强度,提升基材的峰值应力,同时能使其在外荷载作用下具有较大的塑性变形能力,降低基材在加载过程中峰后的软化程度。这种变化由基材的物理力学性质决定,并受纤维类型、掺量、围压因素影响,在模型中可由Weibull分布参数定量地表征出来。下文应力–应变曲线很好地反映了模型参数的影响。
3.2 基于统计损伤的应力–应变关系
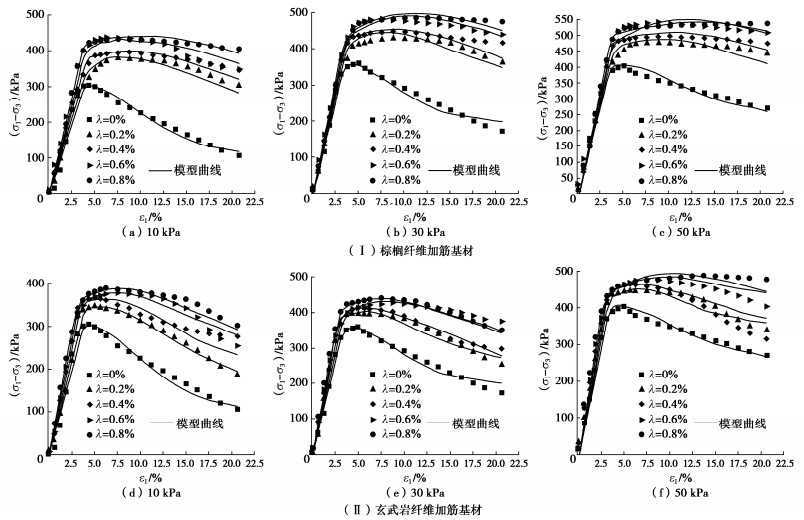
根据上述参数,由式(13)计算得到基于统计损伤模型的应力–应变曲线(图 4)。从图 4中可以看出,试验结果与模型曲线基本吻合,可以分为3个阶段:
(1)弹性阶段:加载初期,各基材的应力应变过程近似于一条直线,其斜率基本反映了各纤维掺量下加筋基材的弹性模量大小。
(2)塑性硬化阶段:当应力增长至超越基材的屈服极限时,基材发生非线性变形,应力–应变曲线斜率逐渐减小至0,最终达到峰值点。
(3)应变软化阶段:应力超过强度极限后,基材随变形出现不同程度的软化,逐步达到残余强度。
基材应力–应变特征与围压大小、纤维类型及掺量密切相关,随着围压和纤维掺量增加,峰值应力出现明显增长,基材软化受到更大程度的抑制,且显然棕榈纤维对基材损伤的抑制作用要好于玄武岩纤维。此阶段的各模型曲线与之对应的试验结果基本吻合,结果比较理想。
由此可见,统计损伤模型能较好地描述纤维加筋基材剪切应力–应变行为,该模型可用于分析和预测不同围压、不同纤维掺量对基材剪切性能的影响。
3.3 损伤阈值的确定
当加载达到某一应力水平,产生一定的变形时,材料才会发生损伤。因此,损伤阈值通常可用相应的临界应变来表示。对于损伤阈值,有的学者按峰值应变折减来取值[7],但未给出合理的确定依据。鉴于此,本文结合损伤定义式(5),推导并给出损伤阈值的计算公式。
由式(5),基材发生损伤的条件为微元强度f为零,可认为此时对应于微元屈服状态[17],由此确定的轴向应变 {\varepsilon _{\text{1}}} 即为损伤阈值 {\varepsilon _{\text{d}}} ,则
f = h({\sigma ^*}) - {k_0} = 0 \text{,} (25) 式中, {k_{\text{0}}} 可由基材微元屈服时的黏聚力 {c_{\text{y}}} 和内摩擦角 {\varphi _{\text{y}}} 来表示,即
{k_{\text{0}}} = 2{c_{\text{y}}}\cos {\varphi _{\text{y}}} \text{,} (26) 根据Kawamoto等[18]的研究, {c_{\text{y}}} , {\varphi _{\text{y}}} 可由峰值强度指标折减得到。本文中,具体取值如下:
\left.\begin{array}{l} c_{\mathrm{y}}=0.85 c \\ \varphi_{\mathrm{y}}=0.90 \varphi \end{array}\right\} (27) 结合式(17),可得
\frac{{{E_{{\text{fc}}}}{\varepsilon _{\text{d}}}[({\sigma _1} - {\sigma _3}) - ({\sigma _1} + {\sigma _3})\sin {\varphi _{\text{y}}}]}}{{{\sigma _1} - 2\nu {\sigma _3}}} - 2{c_{\text{y}}}\cos {\varphi _{\text{y}}} = 0 \text{,} (28) 由于阈值点处损伤为0,故式(12)变为
{\sigma _1} = {E_{{\text{fc}}}}{\varepsilon _{\text{d}}} + 2\nu {\sigma _3} \text{,} (29) 结合式(29),(30),经整理,可得损伤阈值表达式
{\varepsilon _{\text{d}}} = \frac{{2{c_{\text{y}}}\cos {\varphi _{\text{y}}} + [(1 + 2\nu )\sin {\varphi _{\text{y}}} + (1 - 2\nu )]{\sigma _3}}}{{{E_{{\text{fc}}}}(1 - \sin {\varphi _{\text{y}}})}} = 0 。 (30) 以围压30 kPa时为例,确定了不同纤维掺量下基材的损伤阈值,如表 4所示。可以看出,相同纤维掺量下,棕榈纤维加筋基材损伤阈值大于玄武岩纤维加筋基材的损伤阈值,这表明掺入棕榈纤维对基材塑性演化的抑制效应要略好于玄武岩纤维。对于同种纤维加筋基材,计算得到的损伤阈值总体上呈随纤维掺量增加而减小趋势。表 4也给出了损伤阈值与峰值应变的比值在0.4~0.6之间,经计算,在10 kPa和50 kPa围压下,该比值也处于这个范围之内。
表 4 纤维加筋基材损伤阈值( {\sigma _3} =30 kPa)Table 4. Damage thresholds of fiber-reinforced substrate ( {\sigma _3} =30 kPa)\lambda /% 棕榈纤维加筋基材 玄武岩纤维加筋基材 {\varepsilon _{\text{d}}}/\% {\varepsilon _{\text{d}}}/{\varepsilon _{\text{p}}} {\varepsilon _{\text{d}}}/\% {\varepsilon _{\text{d}}}/{\varepsilon _{\text{p}}} 0 2.81 0.58 2.73 0.55 0.2 3.16 0.51 2.76 0.57 0.4 3.12 0.45 2.88 0.56 0.6 3.08 0.49 2.51 0.43 0.8 3.04 0.49 2.43 0.47 注: \lambda =0(空白试样)Efc分别采用式(15),(16)计算。 本文研究表明,损伤阈值与峰值应变的比值不是固定值。对比文献[7],尽管存在材料差异,损伤阈值直接以峰值应变 {\varepsilon _{\text{p}}} 的0.7倍取值,并不合理。本文从损伤定义出发,考虑微元屈服确定基材损伤阈值,较为合理,可为后续研究提供有益参考。
3.4 损伤演化特征
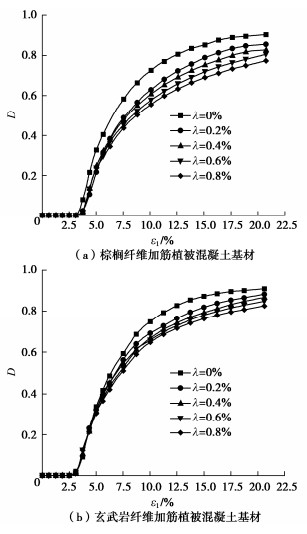
为进一步揭示基材在三轴剪切条件下的应力–应变特征,以围压30 kPa时的结果为例,从纤维加筋基材的损伤演化规律的角度出发,通过式(5)以及上述确定的损伤阈值,得到了损伤变量的演化过程。
由图 5可知,损伤演化曲线呈单调递增的弧形。以损伤阈值和峰值应变为界,其演化特征可以分为以下几个过程:
(1)损伤为零阶段:当轴向应变 {\varepsilon _1} < {\varepsilon _d} 时,荷载较小,基材逐步被压密,几乎无微元体发生失效,累积损伤为零。该阶段基材变形处于弹性阶段。
(2)损伤加速阶段:当 {\varepsilon _d} < {\varepsilon _1} < {\varepsilon _p} 时,超过损伤阈值后,基材内部空隙、微缺陷快速发展,微元体达到破坏强度而发生失效,损伤速率迅速增加。在外荷载作用下,塑性应变快速增长,这恰对应着应力–应变曲线的塑性硬化阶段。由式(5)损伤变量在临界点 {\varepsilon _d} 左右极限均为零,是连续的,因此,损伤模型能模拟应力–应变的连续变化。
(3)损伤稳定阶段:当 {\varepsilon _1} > {\varepsilon _p} 时,荷载进一步增加,此时微裂纹逐步向宏观裂纹扩展,即宏观剪切带贯通[19];此后,纤维加筋作用占据主导地位,纤维与基材土体的摩擦强度得到充分调动后,逐渐趋于稳定[13]。该阶段随着变形增加,损伤速率不断降低;纤维含量越高,最终损伤越小。
从损伤演化曲线可以看出,两种基材的损伤演化在前期加载时都较为接近。随着应变的不断增加,纤维类型与掺量对损伤发展的限制得到了充分体现。总体上,纤维掺量越高,基材损伤软化的抑制作用越为显著。在0.8%的纤维掺量下两种加筋基材的损伤变量
表现出最低水平,与未加筋基材的损伤相比,分别相差21.4%和14.2%,可见棕榈纤维对基材损伤的改善作用更有成效。
4. 结论
本文基于Weibull概率分布建立了纤维加筋植被混凝土基材的统计损伤模型,通过计算与分析主要得出以下结论:
(1)Weibull参数具有较为明确的物理意义,m和f0分别反映基材脆性大小和统计平均强度高低,二者共同影响了模型曲线的形态。
(2)在不同的围压和纤维掺量下,统计损伤模型能够较好反映纤维加筋基材的剪切力学行为。
(3)按本文得到的损伤阈值公式计算,发现各围压下,损伤阈值与峰值应变之比在0.4~0.6之间变化。
(4)损伤演化规律反映了基材内部微元强度失效和累积损伤的进程,有助于从细观角度对基材加载过程中应力–应变规律进行解释。
-
表 1 纤维加筋基材抗剪强度测试值
Table 1 Values of shear strength tests on fiber-reinforced substrate
λ/% 棕榈纤维加筋基材 玄武岩纤维加筋基材 c/kPa φ/(°) c/kPa φ/(°) 0 75.4 33.7 75.4 33.7 0.2 95.5 33.4 86.6 33.5 0.4 99.0 33.9 91.1 33.7 0.6 104.0 34.0 94.1 33.3 0.8 108.3 34.1 97.4 33.7 表 2 棕榈纤维加筋基材弹性模量实际值与拟合值
Table 2 Actual and fitted values of elastic modulus of palm fiber-reinforced substrate
λ/% σ3=10 kPa σ3=30 kPa σ3=50 kPa 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 0 7.98 7.78 -0.0251 10.16 10.55 0.0384 11.95 11.84 -0.0092 0.2 8.63 8.55 -0.0093 10.80 11.19 0.0361 12.62 12.41 -0.0166 0.4 9.66 9.32 -0.0352 11.66 11.83 0.0146 12.77 12.99 0.0172 0.6 11.30 10.10 -0.1062 12.36 12.46 0.0081 13.61 13.56 -0.0037 0.8 11.46 10.87 -0.0515 12.52 13.10 0.0463 13.61 14.14 0.0389 表 3 玄武岩纤维加筋基材弹性模量实际值与拟合值
Table 3 Actual and fitted values of elastic modulus of basalt fiber-reinforced substrate
λ/% σ3=10 kPa σ3=30 kPa σ3=50 kPa 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 试验值/MPa 拟合值/MPa 相对误差 0 7.98 7.87 -0.0132 10.16 10.86 0.0691 11.95 12.25 0.0249 0.2 8.60 8.83 0.0270 12.58 11.88 -0.0552 13.83 13.23 -0.0432 0.4 10.34 9.79 -0.0531 12.88 12.90 0.0020 14.76 14.21 -0.0371 0.6 10.71 10.75 0.0037 13.62 13.93 0.0225 15.21 15.19 -0.0007 0.8 11.74 11.71 -0.0023 14.67 14.95 0.0186 16.21 16.18 -0.0023 表 4 纤维加筋基材损伤阈值( {\sigma _3} =30 kPa)
Table 4 Damage thresholds of fiber-reinforced substrate ( {\sigma _3} =30 kPa)
\lambda /% 棕榈纤维加筋基材 玄武岩纤维加筋基材 {\varepsilon _{\text{d}}}/\% {\varepsilon _{\text{d}}}/{\varepsilon _{\text{p}}} {\varepsilon _{\text{d}}}/\% {\varepsilon _{\text{d}}}/{\varepsilon _{\text{p}}} 0 2.81 0.58 2.73 0.55 0.2 3.16 0.51 2.76 0.57 0.4 3.12 0.45 2.88 0.56 0.6 3.08 0.49 2.51 0.43 0.8 3.04 0.49 2.43 0.47 注: \lambda =0(空白试样)Efc分别采用式(15),(16)计算。 -
[1] 夏振尧, 许文年, 王乐华. 植被混凝土生态护坡基材初期强度特性研究[J]. 岩土力学, 2011, 32(6): 1719–1724. doi: 10.3969/j.issn.1000-7598.2011.06.021 XIA Zhen-yao, XU Wen-nian, WANG Le-hua. Research on characteristics of early strength of ecological slope-protected base material of vegetation-growing concrete[J]. Rock and Soil Mechanics, 2011, 32(6): 1719–1724. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.06.021
[2] 水电工程陡边坡植被混凝土生态修复技术规范: NB/T 35082—2016[S]. 2016. Technical Code for Eco-Restoration of Vegetation Concrete on Steep Slope of Hydropower Projects: NB/T 35082—2016[S]. 2016. (in Chinese)
[3] 潘波, 丁瑜, 黄晓乐, 等. 棕榈纤维加筋植被混凝土三轴试验研究[J]. 硅酸盐通报, 2020, 39(4): 1153–1159. https://www.cnki.com.cn/Article/CJFDTOTAL-GSYT202004020.htm PAN Bo, DING Yu, HUANG Xiao-le, et al. Triaxial experimental study on palm fiber-reinforced vegetation concrete[J]. Bulletin of the Chinese Ceramic Society, 2020, 39(4): 1153–1159. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GSYT202004020.htm
[4] 沈珠江, 胡再强. 黄土的二元介质模型[J]. 水利学报, 2003(7): 1–6. doi: 10.3321/j.issn:0559-9350.2003.07.001 SHEN Zhu-jiang, HU Zai-qiang. Binary medium model for loess[J]. Journal of Hydraulic Engineering, 2003(7): 1–6. (in Chinese) doi: 10.3321/j.issn:0559-9350.2003.07.001
[5] KRAJCINOVIC D, SILVA M A G. Statistical aspects of the continuous damage theory[J]. International Journal of Solids and Structures, 1982, 18(7): 551–562. doi: 10.1016/0020-7683(82)90039-7
[6] KUMAR PANDEY P, SINGH K K, GAURAV A. Mechanical properties of woven GFRP angle ply laminates: a statistical analysis based on two parameters weibull distribution[J]. Materials Today: Proceedings, 2020, 22: 1318–1325. doi: 10.1016/j.matpr.2020.01.424
[7] CUI T, HE H X, YAN W M, et al. Compression damage constitutive model of hybrid fiber reinforced concrete and its experimental verification[J]. Construction and Building Materials, 2020, 264: 1–11.
[8] 朱振南, 蒋国盛, 田红, 等. 基于Normal分布的岩石统计热损伤本构模型研究[J]. 中南大学学报(自然科学版), 2019, 50(6): 1411–1418. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201906020.htm ZHU Zhen-nan, JIANG Guo-sheng, TIAN Hong, et al. Study on statistical thermal damage constitutive model of rock based on normal distribution[J]. Journal of Central South University (Science and Technology), 2019, 50(6): 1411–1418. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201906020.htm
[9] 张明, 王菲, 杨强. 基于三轴压缩试验的岩石统计损伤本构模型[J]. 岩土工程学报, 2013, 35(11): 1965–1971. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201311003.htm ZHANG Ming, WANG Fei, YANG Qiang. Statistical damage constitutive model for rocks based on triaxial compression tests[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1965–1971. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201311003.htm
[10] DENG J, GU D S. On a statistical damage constitutive model for rock materials[J]. Computers & Geosciences, 2011, 37(2): 122–128.
[11] 周永强, 盛谦, 冷先伦, 等. 考虑残余强度和阈值影响的岩石弹性损伤统计模型[J]. 长江科学院院报, 2016, 33(3): 48–53. https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB201603013.htm ZHOU Yong-qiang, SHENG Qian, LENG Xian-lun, et al. Statistical constitutive model of elastic damage for rock considering residual strength and threshold[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(3): 48–53. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB201603013.htm
[12] JEAN L. How to use damage mechanics[J]. Nuclear Engineering and Design, 1984, 80(2): 233–245. doi: 10.1016/0029-5493(84)90169-9
[13] ZHAO H, SHI C J, ZHAO M H, et al. Statistical damage constitutive model for rocks considering residual strength[J]. International Journal of Geomechanics, 2017, 17(1): 04016033. doi: 10.1061/(ASCE)GM.1943-5622.0000680
[14] DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(5): 1629–1653.
[15] 胡亚元, 余启致, 张超杰, 等. 纤维加筋淤泥固化土的邓肯-张模型[J]. 浙江大学学报(工学版), 2017, 51(8): 1500–1508. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201708004.htm HU Ya-yuan, YU Qi-zhi, ZHANG Chao-jie, et al. Duncan-Chang model for fiber reinforced solidified sludge[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(8): 1500–1508. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201708004.htm
[16] XIE S J, LIN H, WANG Y X, et al. A statistical damage constitutive model considering whole joint shear deformation[J]. International Journal of Damage Mechanics, 2020, 29(6): 988–1008.
[17] 李树春, 许江, 李克钢, 等. 基于Weibull分布的岩石损伤本构模型研究[J]. 湖南科技大学学报(自然科学版), 2007, 22(4): 65–68. https://www.cnki.com.cn/Article/CJFDTOTAL-XTKY200704016.htm LI Shu-chun, XU Jiang, LI Ke-gang, et al. Study on damages constitutive model of rocks based on weibull distributing[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2007, 22(4): 65–68. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTKY200704016.htm
[18] KAWAMOTO T, ICHIKAWA Y, KYOYA T. Deformation and fracturing behaviour of discontinuous rock mass and damage mechanics theory[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1988, 12(1): 1–30.
[19] XU Y, YANG R Z. Dynamic mechanics and damage evolution characteristics of rubber cement mortar under different curing humidity levels[J]. Journal of Materials in Civil Engineering, 2020, 32(10): 04020309.
-
期刊类型引用(2)
1. 刘振贤,丁瑜,夏振尧,彭博识. 根系影响下粗糙土-岩接触面剪切损伤模型研究. 人民长江. 2024(01): 216-222 .  百度学术
百度学术
2. 成词峰,赵海燕,曾家鹏,安家金,戴仕鹏. 水泥-BPSF改良尾矿型植生基材强度与微观机理. 矿业研究与开发. 2024(06): 248-257 .  百度学术
百度学术
其他类型引用(3)




 下载:
下载: