Hysteretic model for fitting soil-water characteristic curves considering contact angle and grain-size distribution
-
摘要: 土水特征曲线描述了非饱和土中含水率(或饱和度)与基质吸力(或土水势)之间的关系。土水特征曲线存在滞回效应,即在相同的吸力下,土体在蒸发或重力排水的脱湿过程中赋存的水量比土体在入渗、毛细上升的增湿过程中所赋存的水量多。针对影响土水特征曲线滞回特性的两个关键因素——接触角及由颗粒粒径级配(孔隙分布)引起的墨水瓶效应,首先,基于势能最小原理采用数值模拟方法研究了斜面液滴行为,提出了增湿、脱湿过程微细观界面关键参数接触角与含水率的演化关系;其次,通过修正颗粒间液桥体积表达式,使Young-Laplace方程可用于计算w-lns平面上边界影响区、过渡区及部分残余区的基质吸力;最后,通过引入Rosin-Rammler颗粒粒径分布函数,建立了考虑接触角及粒径级配影响的土水特征曲线滞回模型,该模型参数物理意义明确,能够较好地描述接触角及颗粒粒径对土水特征曲线滞回特性的影响。以西安曲江某基坑压实黄土土水特征曲线为例进行模型验证,结果表明该模型能够很好地反映基质吸力与含水率的非线性关系,该模型可进一步用于非饱和土抗剪强度、本构模型等的研究。
-
关键词:
- 土水特征曲线 /
- 滞回模型 /
- 接触角 /
- 粒径级配 /
- Young-Laplace方程 /
- Rosin-Rammler分布
Abstract: The soil-water characteristic curve (SWCC) describes the relationship between water content (or saturation) and matric suction (or soil-water potential) in unsaturated soils. It is worth noting that the amount of water stored in soils during the drying process caused by evaporation or gravity drainage is more than that during the wetting process caused by infiltration and capillary rise under the same matric suction level. This phenomenon is described by the hysteretic behavior of the SWCCs. Based on existing knowledge, the contact angle and the ink-bottle effect caused by the grain-size distribution (or pore-size distribution) are the two main factors that affect the hysteretic behaviors of the SWCCs. First, the behaviors of a liquid drop sitting on an inclined surface are investigated by the numerical method, and a relationship between the contact angle and the water content during the wetting and drying processes is proposed based on the principle of the minimum potential energy. Second, the expression for the volume of the liquid bridge is modified to make the Young-Laplace equation keep valid in calculating the matric suction in the boundary affected zone, transition zone and the part of the residual zone on the w-lns plane. Finally, an analytical model for analyzing the hysteretic behaviors of SWCCs is proposed after introducing the Roshin-Rammler grain-size distribution function. The model has a clear physical meaning, and the parameters can be obtained easily. Moreover, the model can describe the hysteretic behaviors of the SWCCs. Taking the SWCC of recompacted loess in a foundation pit in Qujiang, Xi'an as an example, the model is verified. The results show that the proposed model can well reflect the nonlinear relationship between the matric suction and the water content. The model can also be used for studying the shear strength and the constitutive model for unsaturated soils. -
0. 引言
土水特征曲线与非饱和土的强度、变形、渗透等性质息息相关,可以用吸力s与质量含水率w/体积含水率Θ/饱和度Sr的关系来描述(本文如无特殊说明,含水率均指质量含水率),它反映了非饱和土的持水能力[1]。土水特征曲线的影响因素很多,如土的矿物成分、粒径级配、应力状态、应力历史、孔隙比和温度等。学者们[2-3]通过研究发现,土水特征曲线存在滞回现象并将滞回原因主要归结于两个原因:①脱湿和增湿过程接触角不同;②由不规则孔隙分布引起的墨水瓶效应。很多学者认为孔隙分布控制着土水特征曲线的形状,在此基础上提出了很多模型[4-5],而这些模型中大部分都采用颗粒粒径级配曲线确定孔隙分布。Assouline等[6]也提出了一个描述孔隙半径与颗粒粒径关系的经验公式。孔隙不规则分布引起的墨水瓶效应,一方面可由颗粒粒径级配反映,颗粒粒径分布越不均匀,颗粒间大小颗粒可以相互填充,这将进一步加剧孔隙的不规则分布[7];另一方面颗粒粒径对土水特征曲线的影响也是通过改变土体孔隙状况表现的[8]。尽管发现了这种滞回现象,但在大多数研究和实践中常常被忽略[9-10]。研究表明研究滞回现象有助于解决诸如干湿循环过程非饱和土产生的不可恢复的变形、水分迁移及溶质运移等问题。
完整的滞回曲线的室内测试耗时长,成本高,同时,如果试验数据没有模型拟合,应用范围有限,这是因为大部分情况需要SWCC连续且可微,如确定土的渗透系数、预测非饱和土抗剪强度等。拟合方法常用于确定边界滞回曲线,常见的模型有Van Genuchten[11]模型,Frendlund等[12]模型,Brooks等[13]模型以及Brutsaert[14]模型。受测试设备精度及测试水平高低的影响,直接拟合试验数据点误差较大[15],部分学者给出了置信区间[16-17]。近年来,为解决直接拟合误差大的缺陷,学者们采用土壤转函数(PTFs)从土的基本物理力学参数入手建立土SWCC预测模型。土壤转换函数的核心是在假设试验数据满足特定模型的基础上,寻求模型参数与土的基本物性参数之间的关系。如Li等[18]基于Brutsaert模型建立了土水特征曲线的预测模型,并给出了模型参数与干密度、液塑限及粒径级配等参数间关系;Bayat等[19]给出了21种土壤转换函数(PTFs),并基于Van Genuchten模型对模型预测能力进行了对比研究;Fredlund等[5]建立了粒径级配与Frendlund等模型参数间的关系;Tomasella等[20]建立了有机碳含量,粉粒含量及黏粒含量与Brooks等模型参数间的关系。
随着计算机人工智能的发展,神经网络也被用于构建SWCC模型[21],其优点在于通过深度学习获得含水率与基质吸力之间的关系不用假设特定模型,缺点是前期需要大量数据进行模型训练。
在边界滞回模型的基础上,基于不同的方法和原理,建立了扫描滞回模型,主要有热力学原理[22-23]、经验/半经验方法[24]、离散元方法[25]及域方法[26-27]。其中域方法通过改变积分路径也可实现对边界滞回的模拟,常见的预测边界滞回的域模型有Mualem模型[26-27]。
以上模型一定程度上均可以预测土水特征曲线的滞回特性,然而不能很好地反映土水特征曲线滞回机理,主要原因是非饱和土在微细观尺度存在固-液、固-气及气-液交界面,这些界面的存在对孔隙内液体流动、输运、相变和质量交换等行为有重要影响[28],而限于现有实验条件,目前无法真正获得增湿、脱湿过程界面参数的变化规律。
近年来,越来越多的学者尝试[29-31]基于描述气-液界面的Young-Laplace方程建立土水特征曲线的理论模型。然而模型中未充分考虑界面关键参数(接触角)及由颗粒粒径级配(孔隙分布)引起的墨水瓶效应的影响,如张鹏程等[29]忽略了接触角影响,使得模型不具备预测SWCC滞回特性的能力;Zhou等[30]人将边界脱湿及增湿过程的接触角视为常数。同时Young-Laplace方程用于计算全过程基质吸力也遇到了挑战,这主要是因为:Young-Laplace方程基于液桥模型,而随着含水率的增加,液桥会发生融合[32],一旦液桥发生融合,将不能直接使用Young-Laplace方程进行吸力计算。
为解决上述问题,本文基于界面系统势能最小原理,首先,采用数值模拟方法分析增湿、脱湿过程接触角的演化规律;其次,考虑液桥融合过程,修正含水率与液桥体积表达式,使Young-Laplace方程可用于计算w-lns平面上边界影响区、过渡区及部分残余区的基质吸力;最后通过引入Rosin-Rammler粒径分布函数,建立了考虑粒径级配及接触角影响的土水特征曲线的边界滞回模型。
1. 接触角演化规律
接触角是用来描述固-液、固-气及气-液交界面特性的关键物理参数,获取接触角的关键在于确定气-液交界面的形状。Young-Laplace方程建立了气液交界面形状与气液界面两边压降(基质吸力)的联系,大部分情况下Young-Laplace方程没有解析解,因此,常采用数值方法进行求解。根据现有研究[33],获得界面热力学势能最小状态下的气液交界面形状等价于求解Young-Laplace方程。
Surface Evolver(SE)[34]是美国数学家Brakke创立的一个通过最小化各种能量来研究曲面形状的程序包,其主要用于模拟液体和气体的静态界面。由于其可以处理各种边界条件和能量,模拟各种现实问题,因而被广泛用于表面物理、材料物理、流体力学等领域。
为了采用SE研究增湿、脱湿过程接触角的演化规律,本文做出如下假设:①液桥位于两个等粒径球体间;②土体含水率(w)与液桥体积V满足一一对应关系,即w=w(V),V=$ {V^{ - 1}} $(w);③液桥体积与水滴体积同样满足一一对应关系,即V=V(v),v=$ {v^{ - 1}} $(V),脱湿(v减小)及增湿(v增加)过程小水滴沿颗粒表面准静态迁移;④结合①和③可将颗粒间水分的迁移看作水滴位于倾角连续变化的斜面上。
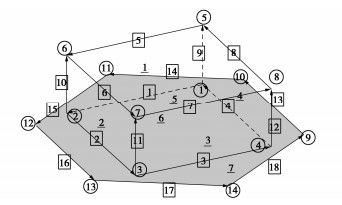
根据以上4点假设,采用SE建立如图 1所示的液滴位于光滑平面(α=0°)的数值模型,模型由点(1—14),线(1—18),面(1—7)组成,其边界条件为定义接触角。为了在数值模型中引入接触角,需要在接触面6上引入一向量值函数,由格林公式及斯托克斯定理可知,该向量值函数在接触面6上需满足:
$$ \iint\limits_C {\sigma {{\rm{cos}}}\theta {\text{d}}S} = \sigma {{\rm{cos}}}\theta \iint\limits_C {\frac{\mathit{\boldsymbol{v}}}{{\mathit{\boldsymbol{v}}{{\bf{.}}}\mathit{\boldsymbol{v}}}}{\text{d}}\mathit{\boldsymbol{S}}} \text{, } $$ (1a) $$ \iint\limits_C {\sigma {{\rm{cos}}}\theta {\text{d}}S} = \sigma {{\rm{cos}}}\theta \int\limits_{\partial C} \mathit{\boldsymbol{w}} {\text{d}}\mathit{\boldsymbol{l}}{ = }\sigma {{\rm{cos}}}\theta \iint\limits_C {\nabla \times }\mathit{\boldsymbol{w}} \cdot {\text{d}}\mathit{\boldsymbol{S}} \text{, } $$ (1b) $$ \nabla \cdot {\text{(}}\nabla \times \mathit{\boldsymbol{w}}{\text{)}} = 0 \text{, } $$ (1c) 式中,C为由液滴所位于的斜面,$ \mathit{\boldsymbol{v}} $为斜面C的法向量,w为向量值函数。
当液滴位于水平面时:
$$ \mathit{\boldsymbol{w}} = - {y}\mathit{\boldsymbol{i}} 。 $$ (2) 文献中通常通过调节斜面倾角$ \alpha $,使模型坐标变化,从而实现液滴位于斜面上的模拟。本文假设斜面C方程为{(x, y, z)|-tanαy+z = 0}(斜面模型与平面模型类似),可得该向量值函数为
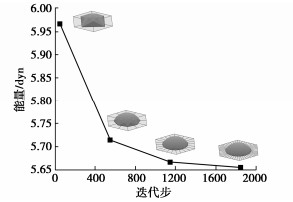
$$ \mathit{\boldsymbol{w}} = - \frac{{{\text{(}}{\rm{tan}}\alpha z + y{\text{)}}\mathit{\boldsymbol{i}}}}{{\left\| { - {\rm{tan}}\alpha \mathit{\boldsymbol{j}} + \mathit{\boldsymbol{k}}} \right\|}} 。 $$ (3) 为了阐述SE的原理,以液滴位于水平面($ \alpha $= 0°)为例,其迭代过程的液滴形状如图 2所示,由图 2可知,在液滴形状演化过程中,其能量趋于最小,同时当液滴位于水平面时接触角可以唯一确定。
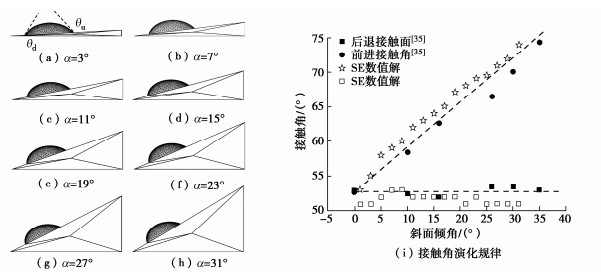
当液滴位于斜面时,为了与Chou等[35]做的液滴位于斜面的试验结果对比,初始时刻斜面倾角$ \alpha $=0°,θ=θr=52°,其中θr为后退接触角,液滴体积v=30 uL,斜面倾角α=0°,1°,3°,5°,7°,9°,11°,13°,15°,17°,19°,21°,23°,25°,27°,29°,31°,33°,不同倾角时液滴形状如图 3所示。
由图 3可知,受重力的影响,液滴在垂直于纸面方向不对称,因而采用一个接触角无法准确描述液滴位于斜面时的界面形状,Chou等[35]采用两个接触角,坡顶接触角θu(uphill contact angle)及坡脚接触角θd(downhill contact angle)描述液滴位于斜面时的界面特征(下标u和d分别代表uphill和down)。统计图 3中θu及θd随倾角的变化情况,如图 3(i)所示。由图 3(i)可知,增湿过程中,随着$ \alpha $的增加,θu基本保持不变,而θd逐渐增加,即θu=θu($ \alpha $, v)= constant,θd=θd($ \alpha $, v)。当斜面倾角增加到某一临界值αw时(下标w代表增湿),θd等于θa,液滴处于极限平衡状态,即满足θd=θa=θa($ {\alpha _{\text{w}}} $, v),该结论与Berejnov等[36],Chou等[35],Thampi等[37]研究结果一致。更进一步考虑,增湿过程随着液滴体积增加,$ {\alpha _{\text{w}}} $将会减小,即$ {\alpha _{\text{w}}} $=$ {\alpha _{\text{w}}} $(v)。
研究表明[35, 38]脱湿过程与增湿过程类似,给定液滴体积v,随着$ \alpha $的增加,θu减小,而θd几乎保持不变,当$ \alpha $到某一临界值αd时,θu等于后退接触角θr,液滴此时处于脱湿过程的极限平衡状态。脱湿过程随着液滴体积减小,$ {\alpha _{\text{d}}} $将会增加,同样$ {\alpha _{\text{d}}} $=$ {\alpha _{\text{d}}} $ (v)。
对于固液气三相系统,本文采用临界饱和角$ {\beta _{\text{w}}} $和$ {\beta _{\text{d}}} $描述接触角演化关系,其与$ {\alpha _{\text{w}}} $和$ {\alpha _{\text{d}}} $满足$ {\beta _{\text{w}}} $= π/2-$ {\alpha _{\text{w}}} $,$ {\beta _{\text{d}}} $=π/2-$ {\alpha _{\text{d}}} $。
根据假设V=$ {V^{ - 1}} $(w),v=$ {v^{ - 1}} $(V),因此增湿过程中θa= θa($ {\beta _{\text{w}}} $, v)=θa($ {\alpha _{\text{w}}} $, v)=θa(v)=θa(V)=θa(w),脱湿过程θr= θr($ {\beta _{\text{d}}} $, v)=θr($ {\alpha _{\text{d}}} $, v)=θr(v)=θr(V)=θr(w),从而建立了增湿及脱湿过程接触角与液滴体积、液桥体积及含水率之间的联系。
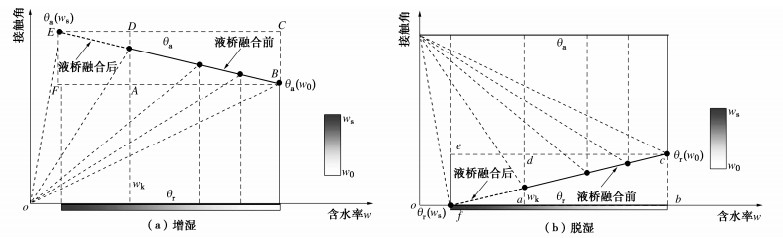
综上所述,液桥融合前增湿过程中,前进接触角位于如图 4(a)所示的矩形区域ABCD,而脱湿过程,后退接触角位于图 4(b)所示的矩形区域abcd。
现有研究结果表明[31],液桥体积V与颗粒半径R,颗粒间距D,接触角θ及饱和角β相关,即V=V(R, D, θ, β)。根据Young-Laplace方程增湿过程基质吸力可表示为s=s(R, θa, β),而脱湿过程s=s(R, θr, β)。
综上所述V=V(R, D, θ, β),V=V(w),β=β(w),s=s(R, θa, β),s=s(R, θr, β),θa=θa(w)和θr=θr(w)是建立SWCC滞回模型所需要的表达式,下文将给出具体的表达式。
2. 液桥细观尺度的变化
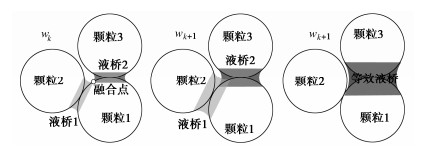
以上的讨论针对液桥未发生融合的情况,如图 4和5所示,当含水率增加到wk时,液桥1与液桥2相遇,随着含水率继续增加,液桥1和液桥2将会发生融合,一旦液桥发生融合,液桥模型将不能直接用于计算基质吸力,此时需要新的理论和方法[32]。然而发展新的理论和方法非常困难,因为细观尺度液桥的分布及细观水的形态非常复杂。因此,通过一种简单的方法使得液桥模型仍然适用于吸力的计算是必要的,其中最有效的方法是修正含水率与液桥体积的表达式。
张鹏程等[29]采用平均液桥体积,得到了液桥体积与含水率以及液桥数量关系,并采用配位数表示液桥数量与含水率关系:
$$ V(w) = \frac{{8G{\rm{ \mathsf{ π} }}{R^3}w}}{{3{N_{\text{c}}}}} \text{, } $$ (4) 式中,G为土粒相对密度,w为含水率,Nc为配位数。在液桥发生融合之前,假设液桥数目等于接触数,而当液桥发生融合后,液桥数目减少,为了保持总体积不变,单个液桥体积增加,因此可以通过等效接触数来表示液桥细观尺度的变化,具体见3.1节。考虑细观尺度变化能够使Young-Laplace方程用于计算w–lns平面上边界影响区、过渡区及部分残余区的基质吸力。
通过该修正,当含水率w > wk时,液桥模型依然成立,因此在增湿过程中,前进接触角位于如图 4(a)所示的矩形区域ADEF,而脱湿过程,后退接触角位于图 4(b)所示的矩形区域adef。
3. 土水特征曲线滞回模型的建立
3.1 确定V=V(R,D,θ,β)和V=V(w)
确定液桥体积V=V(R,D,θ,β)和含水率与液桥关系w=w(V)是建立土水特征曲线理论模型的基础,同时也是建立微细观和宏观物理量联系的桥梁。简单起见,假设D=0,Fisher[39]修正了W B Haines提出的计算等粒径土颗粒间液桥体积的表达式,表述为
$$ V{\text{(}}R{\text{, }}\theta {\text{, }}\beta {\text{)}} = 2{\rm{ \mathsf{ π} }}{R^3}{{\text{(}}{{\rm{sec}}}\beta - 1{\text{)}}^2}\left[ {1 - \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - \beta } \right){\rm{tan}}\beta } \right] \text{, } $$ (5) 式中,R为平均颗粒半径,β为饱和角,增湿过程β=βw,脱湿过程β=βd(下标w和d代表增湿和脱湿)。
在含水率很低时,颗粒间一般无法形成液桥,颗粒间主要以结合水的形式存在,当颗粒平均半径为R,结合水膜厚度为$ \mathit{\Delta} $时,结合水膜的体积可以写为
$$ V{\text{(}}\mathit{\Delta} {\text{)}} = \frac{4}{3}{\rm{ \mathsf{ π} }}\left[ {{{{\text{(}}R + \mathit{\Delta} {\text{)}}}^3} - {{{\text{(}}R{\text{)}}}^3}} \right] 。 $$ (6) 现有的研究普遍认为结合水膜的厚度与孔隙结构、离子强度、pH值和矿物类型等有关。近期日本学者Nishiyam等[40]采用试验和理论相结合的方式研究了不同离子强度和pH值下二氧化硅、蒙脱石、方解石和针铁矿的水膜厚度,其计算结果表明当离子强度和pH值与雨水、河水和地下水的离子强度和pH值相似时,预计粉粒、砂粒和砾石中二氧化硅的典型水膜厚度分别为 < 14 nm、14~45 nm和 > 23 nm。
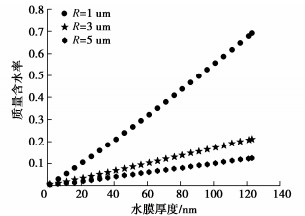
联立式(4)和式(6),可得含水率与颗粒平均半径及结合水膜的关系如图 6所示。当含水率较低时,颗粒间无法形成液桥,液桥是以水膜形式存在,而当含水率增加到某一临界含水率时候,颗粒间将会形成液桥,该临界含水率与颗粒半径、水膜厚度有关。由图 6可知,当颗粒半径R=1 um,水膜厚度为10 nm时,该临界含水率约为5.0%。
张鹏程等[29]推导得出的液桥体积与含水率之间的关系是在将含水率平均分配到每个液桥这个假设的基础上提出的,一方面这个假设高估了融合发生前的液桥体积,另一方面含水率与液桥体积是线性关系。当含水率大于形成液桥所需要的临界含水率时,即颗粒间能够形成液桥时,本文引入修正系数m0(0<m0≤1),使得液桥位于初始状态,初始状态的含水率称为为增湿的起点,而脱湿时为终点。
$$ {V^0}{\text{(}}{w}{\text{)}} = \frac{{8G{\rm{ \mathsf{ π} }}{m_0}{R^3}w}}{{3{N_{\text{c}}}}} 。 $$ (7) 由于m0的有界性,假设m0=sinϕ。同时根据根据液桥细观尺度的变化规律,进一步可将式(4)改写为
$$ V{\text{(}}{w}{\text{)}} = \frac{{8G{\rm{ \mathsf{ π} }}{m_0}{R^3}w}}{{3{N_{\text{c}}}}}\frac{{{{\rm{sin}}}\mathit{\Phi } }}{{{{\rm{sin}}}{\mathit{\Phi } _1}}} \text{, } $$ (8) 式中,m1=sinΦ/sinΦ1描述了液桥非线性变化过程,液桥发生融合前Φ=Φ1,m1=1。
式(8)中Nc/sinΦ可理解为等效配位数,在增湿过程(Φ增加),等效配位数减小,而在脱湿过程(Φ减小),等效配位数增加,其与第2节液桥细观尺度的变化规律相一致。在增湿过程中,Φ的最大值为90°,而在脱湿过程该值将会减小,本文取其值为60°。
通过式(8)的修正,Young-Laplace方程可用于计算w-lns平面上边界影响区、过渡区及部分残余区基质吸力吸力的计算,当残余区颗粒间水以结合水膜形式存在时,本文暂时无法考虑。
联立式(5),(8)可得β=β(w)。式(8)中的Nc描述了微细观颗粒接触状态,不方便直接使用,应建立其与孔隙比的关系。Smith等[41]通过试验,获得了5种不同孔隙率等粒径堆积球体与配位数的方程,该方程与观测到的实验数据吻合较好,适用于所有粉末材料。根据土壤分类标准,砂粒(> 75 um)、粉砂(2~75 um)、黏土(< 2 um)颗粒均在粉体粒度范围内。因此,Smith公式适用于非饱和土,其表达式为
$$ n = \frac{e}{{1 + e}} = \frac{{0.414{N_{\text{c}}} - 6.527}}{{0.414{N_{\text{c}}} - 10.968}} \text{, } $$ (9) 式中,n为孔隙率,e为孔隙比。
3.2 确定θa =θa (w)和θr =θr (w)
由前面的分析可知,增湿过程中,当液滴处于极限平衡状态时,θa=θa($ {\alpha _{\rm{w}}} $),脱湿过程中,θr=θr($ {\alpha _{\rm{d}}} $),从而有
$$ {\text{d}}{\theta _{a}} = \frac{{\partial {\theta _{a}}}}{{\partial {\alpha _{\rm{w}}}}}{\text{d}}{\alpha _{\rm{w}}} \text{, } $$ (10a) $$ {\text{d}}{\theta _{\rm{r}}} = \frac{{\partial {\theta _{\rm{r}}}}}{{\partial {\alpha _{\rm{d}}}}}{\text{d}}{\alpha _{\rm{d}}} 。 $$ (10b) 将极限平衡状态时接触角平衡关系方程式代入式(10),可得θa∝1/$ {\alpha _{\rm{w}}} $∝w,θr∝$ {\alpha _{\rm{d}}} $∝1/w,据此可假设接触角与含水率符合线性关系,分别为图 4(a)中BE及图 4(b)中cf,可写为
$$ {\theta _{\rm{w}}} = - \frac{{{\theta _{\rm{a}}}{\kern 1pt} {\text{(}}{{w}_{\rm{s}}}{\text{)}} - {\theta _{\rm{a}}}{\kern 1pt} {\text{(}}{{w}_{0}}{\text{)}}}}{{{{w}_{\rm{s}}} - {{w}_{0}}}}{\text{(}}{{w}_{\rm{s}}} - {w}{\text{)}} + {\theta _{\rm{a}}}{\text{(}}{{w}_{\rm{s}}}{\text{)}} \text{, } $$ (11a) $$ {\theta _{\rm{d}}} = \frac{{{\theta _{\rm{r}}}{\text{(}}{{w}_{0}}{\text{)}} - {\theta _{\rm{r}}}{\text{(}}{{w}_{\rm{s}}}{\text{)}}}}{{{{w}_{0}} - {{w}_{\rm{s}}}}}{\text{(}}{w} - {{w}_{\rm{s}}}{\text{)}} + {\theta _{\rm{r}}}{\text{(}}{{w}_{\rm{s}}}{\text{)}} \text{, } $$ (11b) 式中,θa(ws)是饱和含水率情况下的前进接触角,θa(w0)是残余含水率情况下的前进接触角,θr(ws)是饱和含水率情况下的后退接触角,θr(w0)是残余含水率情况下的后退接触角,ws是饱和含水率,w0是增湿的起点,脱湿的终点。
3.3 确定s=s(R, θa, β)和s=s(R, θr, β)
基质吸力由Young-Laplace方程描述,其表述为
$$ s = \sigma \left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right) 。 $$ (12) Butt等[42]结合几何关系推导得到了r1和r2分别为
$$ {r_1} = \frac{{{R_1}{\text{(}}1 - {{\rm{cos}}}{\beta _1}{\text{)}} + {R_2}{\text{(}}1 - {{\rm{cos}}}{\beta _2}{\text{)}} + D}}{{{{\rm{cos}}(}{\theta _1} + {\beta _1}{)} + {{\rm{cos}}}{\text{(}}{\theta _2} + {\beta _2}{\text{)}}}} \text{, } $$ (13a) $$ {r_2} = {R_1}{{\rm{sin}}}{\beta _1} - {r_1}\left[ {1 - {{\rm{sin}}(}{\theta _1} + {\beta _1}{)}} \right] 。 $$ (13b) 由式(13a),(13b)可知,r1和r2与接触角,饱和角相关,当R1=R2且D=0时,由对称性可得$ {\beta _1} $= $ {\beta _2} $=$ \beta $。给定含水率联立式(5),(8),(9)可求得$ \beta $,将$ \beta $及接触角演化模型代入式(13a),(13b),可计算得r1和r2,进一步将r1和r2代入式(12)可以计算基质吸力的大小。
值得注意的是对于饱和角$ \beta $,其理论取值为[0,π/2],然而饱和度、孔隙比与含水率满足式(14),且当饱和度趋近于1时,其吸力应接近于0。饱和角的取值必须使得式(12)计算得到的基质吸力大于0[29]。
$$ {S_{\text{r}}} = \frac{{Gw}}{e} \leqslant {1} 。 $$ (14) 4. 颗粒粒径级配与平均颗粒半径关系
以上在建立土水特征曲线的滞回模型的过程中,只考虑了接触角并假设了液桥位于两个等粒径球体间。事实上由不规则的孔隙分布引起的墨水瓶效应也是影响土水特征曲线滞回特性的重要因素。如黎澄生等[43]建立了考虑孔隙不规则分布引起的墨水瓶效应的土水特征曲线滞回模型。由于本文基于颗粒间的液桥模型,因此很难直接考虑孔隙分布。如前所述,一方面孔隙的不规则分布可由粒径级配间接影响且孔隙分布也与粒径级配存在某种关联。另一方面郑方等[7]、Kasangaki等[44]通过试验也发现颗粒粒径级配显著影响土水特征曲线的滞回特性。因此,本文将不规则孔隙分布引起的墨水瓶效应对土水特征曲线滞回特性的影响映射为粒径级配对土水特征曲线滞回特性的影响。
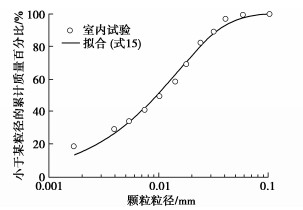
Esmaeelnejad等[45]研究表明,Weibull、Fredlund、Roshin-Rammle和Van Genuchten是模拟颗粒粒径分布最准确的4个模型,它们的差异并不显著。由于Rosin-Rammler模型参数少使用简单,本文采用Rosin-Rammler模型来描述颗粒粒径级配,其表述为[46]
$$ F({D_{\text{p}}}) = 1 - {{\rm{exp}}}\left[ { - {{\left( {\frac{{{D_{\text{p}}}}}{b}} \right)}^a}} \right] \text{, } $$ (15) 式中,Dp为粒径,F(Dp)为粒径Dp的累计质量分数,a,b为与分布特征有关的常数。其中,均匀指数a表示粒径分布范围的宽窄程度,a值越大,说明粒度分布范围越窄。
将粒径级配曲线引入土水特征曲线模型的关键在于如何建立颗粒粒径级配表述式(15)中参数a,b与颗粒平均半径之间的关系,本文基于Rosin-Rammler模型推导得出脱湿以及增湿过程中颗粒半径与基质吸力之间的关系表达式:
脱湿
$$ R = {R_{0}}\left\{ {1 - {{\rm{exp}}}\left[ { - {{\left( {\frac{{2\sigma }}{{\lambda sb}}} \right)}^a}} \right]} \right\} \text{, } $$ (16a) 增湿
$$ {R_n} = {R_{n - 1}}\left\{ {1 + {{\rm{exp}}}\left[ { - {{\left( {\frac{{2\sigma }}{{\lambda sb}}} \right)}^a}} \right]} \right\} \text{, } $$ (16b) 式中,$ \sigma $为表面张力,s为基质吸力,a和b为模型参数,可由粒径级配曲线确定,$ \lambda $为平均孔隙半径与平均粒径的比值,通过分析文献[47,48]中压汞试验结果及颗粒粒径级配曲线,$ \lambda $的取值范围约为0.5~0.00001。在脱湿过程中,R0为起点的等效颗粒半径,其可根据黏粒、粉粒以及砂粒含量确定,具体计算方法可以参考文献[49,50];在增湿过程中,其起点等效颗粒半径为脱湿时的终点值。式(16)给出的颗粒半径与基质吸力的关系,其可以理解为当基质吸力较大时,土体中能够发挥作用的颗粒是小颗粒。
5. 模型影响因素分析
刘建维[51]研究了非饱和黄土平均意义上的接触角与孔隙比的关系,结果表明接触角变化范围在10°~25°,且含水率不同接触角不同,烘干状态下的接触角大于天然含水状态,这也说明本文考虑接触角演化的合理性与必要性。
该土水特征曲线滞回模型包括11个参数,分别为孔隙比e、相对质量密度G,气-液交界面表面张力$ \sigma $,与含水率相关的4个接触角(θa(w0),θa(ws),θr(ws),θr(w0))以及4个与粒径级配相关的R0,a,b,和$ \lambda $。其中孔隙比、相对质量密度及表面张力可以通过室内快速获得。与粒径级配相关的参数R0,a和b可以通过黏粒、粉粒以及砂粒含量及粒径级配曲线获取,$ \lambda $可以通过压汞试验进行估计。
与含水率相关的4个接触角,一方面当室内测得含水率–吸力离散点时,可以通过其中4个点反算得到,其中两个点位于脱湿曲线上,两个点位于增湿曲线上;另一方面可采用光学接触角测试仪器获得前进、后退接触角的变化范围。与Van Genuchten[11],Frendlund等[12]传统模型相比,本文提出的模型虽然参数较多,但参数物理意义明确,理论完善,同时能够反映接触角以及颗粒粒径的影响。另外由于模型参数中包括了孔隙比e,因此借助孔隙比与应力之间的关系式,该模型也可扩展为考虑变形及应力状态的SWCC模型。在本节后面的分析中,为了更直观地反映不同参数对土水特征曲线的影响,将脱湿、增湿曲线分开描述。
5.1 接触角对土水特征曲线的影响
栾茂田等[52]认为理论土水特征曲线强烈依赖于接触角的变化,在用微观球颗粒来分析基质吸力与含水率的关系时,考虑接触角的变化是非常必要的。
大部分土水特征曲线的研究将接触角视为一定值,有时甚至忽略。从前面的讨论中可知:增湿、脱湿过程接触角与含水率存在一定的关系。因此有必要讨论当接触角为定值及采用本文所提接触角的演化模型时,其对土水特征曲线的影响。
在增湿过程中,首先假设式(11)中θa(w0)=19.5°,依据本文所提接触角演化模型,增湿过程θa(ws)>θa(w0),因此取θa(ws)=19.5°,20.2°,21.0°,21.7°,22.4°,23.2°;其次假设θa(ws)=23.2°,θa(w0)= 23.2°,22.4°,21.7°,21.0°,20.2°,19.5°。其目的为研究θa(w0)以及θa(ws)对增湿土水特征曲线起点及终点的影响。
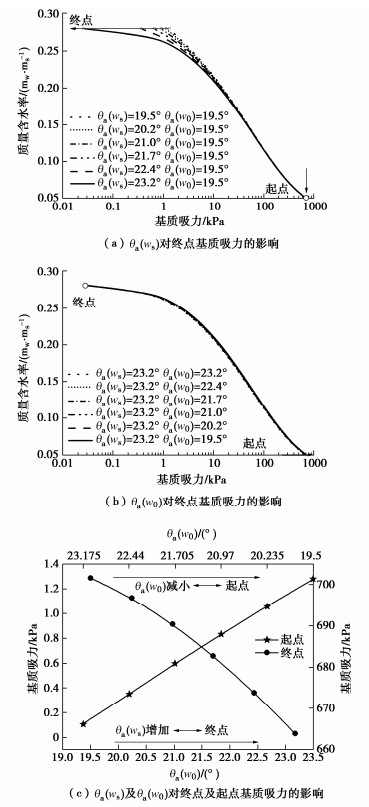
接触角演化对边界影响区及残余区基质吸力的影响,计算结果如图 7(a),(b),(c)所示。由图 7(a)可知,在w–lns平面当θa(ws)=θa(w0)时,土水特征曲线无明显边界影响区,当θa(ws)按照接触角演化模型逐渐增加时,曲线表现出明显的边界影响区及进气值;由图 7(b)可知,当θa(ws)保持不变,θa(w0)逐渐减小时,残余区吸力逐渐增加,残余区更加明显;如图 7(c)可知,随θa(ws)增加,增湿终点含水率对应的基质吸力趋近于0,而随θa(w0)减小,增湿起点含水率对应的基质吸力逐渐增加,因此考虑接触角演化能够更好地描述土水特征曲线的滞回特性,尤其是边界影响区及残余区吸力与含水率的非线性关系。
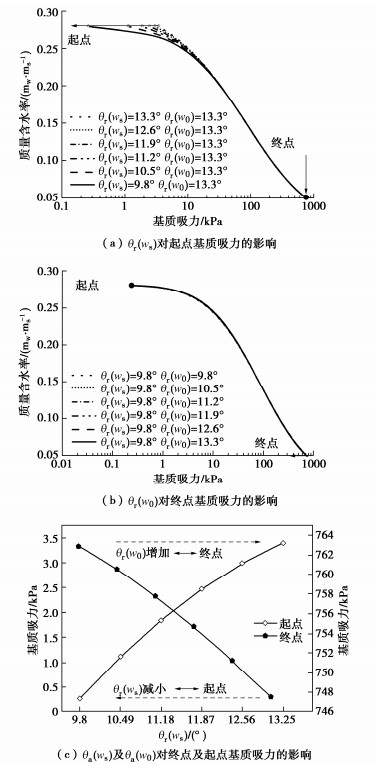
在脱湿过程中,首先假设式(11)中,θr(w0)= 13.3°,依据本文所提接触角演化模型,脱湿过程θr(ws)<θr(w0),因此θr(ws)=13.3°,12.6°,11.9°,11.2°,10.5°,9.8°;其次假设θr(ws)=9.8°,θr(w0)=9.8°,10.5°,11.2°,11.9°,12.6°,13.3°,其目的分别为研究接触角对边界影响区及残余区基质吸力的影响,计算结果如图 8(a),(b),(c)所示。由图 8(a)可知当θr(ws)= θr(w0)时,土水特征曲线无明显边界影响区,当θr(ws)按照接触角演化模型逐渐减小时,曲线表现出明显的进气值及边界影响区。由图 8(b)可知,当θr(ws)保持不变,θr(w0)逐渐增加时,残余区吸力逐渐减小;由图 8(c)可知,随θr(ws)减小,脱湿起点含水率对应的基质吸力趋近于0,而随θr(w0)增加,脱湿终点含水率对应的基质吸力减小,也就是说在残余区,通过考虑接触角的演化,将会降低残余区的滞回,这也能反映部分学者的研究结论,即在残余区,滞回度较小。综上所述,考虑接触角演化关系能够更好地描述土水特征曲线的滞回特性,尤其是边界影响区及残余区吸力与含水率的非线性关系。
5.2 粒径级配及其对土水特征曲线的影响
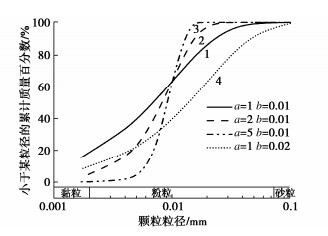
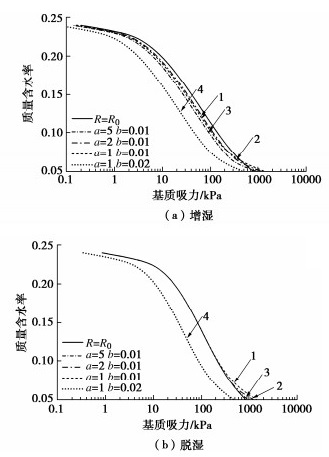
为了分析颗粒粒径级配对土水特征曲线的影响,首先利用式(15)中的参数a和b得到4种不同的颗粒粒径级配曲线,如图 9所示。其中粒径级配曲线1,2和3为参数a的影响,1和4为参数b的影响。进一步根据黏粒、粉粒和砂粒的含量可确定曲线1,2和3的R0为1 um,曲线4的R0为2.5 um。本模型通过粒径级配参数a和b反映其对土水特征曲线的影响,计算得到的土水特征曲线如图 10所示。刘星志等[53],陈宇龙等[8]通过试验发现对于不同颗粒级配的土水特征曲线,同一含水率下细土颗粒含量越多的土样其基质吸力越大。对于粒径级配曲线1和4,曲线1细土颗粒占比多,因此土水特征曲线1在4上方,表明在相同的含水率下,曲线1所对应的基质吸力大,其规律与试验结果一致,说明本文所建立的模型能够反映颗粒粒径级配的影响。此外,以图 10中不考虑粒径级配的土水特征曲线为基准(R=R0),可知粒径级配也影响了土水特征曲线的滞回特性。
6. 模型验证
本研究中所用黄土取自西安某基坑[54-55],土样运回实验室后,按照土工试验规范获得了基本物理力学参数,结果如表 1所示。此外,采用密度计法对其粒径分布进行了测试,结果如图 11所示。本文采用压力板仪测试了压实试样的土水特征曲线,其孔隙比等于原状孔隙比。
根据粒径级配,采用EXCEL中的规划求解功能求解式(15)中的参数a和b,当残差平方和最小时求得a=0.9236,b=0.0142。参考文献[49,50],根据黏粒、粉粒以及砂粒含量确定平均颗粒半径R=1 um,本文选择$ \lambda $=0.00002。气-液交界面表面张力$ \sigma $在20°时为0.072 N/m。理论上4个与含水率有关的接触角可以通过实验获得,然而现阶段对于颗粒间的接触角测试还停留在理论方面,通过现有设备获得的接触角大部分是定性结果,无法定量分析,因此,本文提出借助土水特征曲线上的4个点进行拟合,其中两个点位于增湿曲线上,两个点位于脱湿曲线上,拟合方程为
$$ {s_{{{\rm{model}}}}}\left[ {{\theta _{{{\rm{a}}|{\rm{r}}}}}({w_m})} \right] - {s_{{{\rm{experiment}}}}}({w_m}) = {\text{0 }} \text{, } $$ (17) 式中,smodel为模型计算所得基质吸力,m的取值为1,2,3,4,其中1和2位于脱湿曲线上,用以确定θr;3和4位于增湿曲线上,用以确定θa。
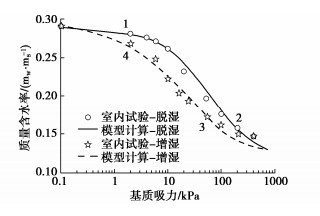
选择图 12中的1,2,3,4,最终确定θa(w0)=19.3°,θa(ws)=23.0°,θr(ws)=9.4°,θr(w0)=13.2°,在此基础上计算脱湿和增湿过程不同含水率下的基质吸力,结果如图 12中实线和虚线所示,由此可知,该模型能够较好地拟合土水特征曲线的滞回特性,模型准确性高。
7. 结论
首先,本文基于势能最小原理采用数值模拟方法研究了斜面液滴行为,提出了增湿、脱湿过程微细观界面关键参数接触角与含水率的演化关系;其次通过修正颗粒间液桥体积表达式,使Young-Laplace方程可用于计算w–lns平面上边界影响区、过渡区及部分残余区的基质吸力;最后通过引入Rosin-Rammler颗粒粒径分布函数,建立了考虑接触角及粒径级配影响的土水特征曲线滞回模型,该模型也可考虑孔隙比、相对质量密度等因素影响。主要研究结论如下:
(1)给定液滴体积,增湿过程中θd随斜面倾角的增加而增加,而θu保持不变,最大θd为前进接触角;而在脱湿过程中,θd保持不变,而θu随斜面倾角的增加逐渐减小,最小θu为后退接触角。
(2)Rosin-Rammler颗粒粒径分布函数可以描述颗粒粒径级配的分布。
(3)本文建立的考虑接触角及粒径级配影响的土水特征曲线滞回模型能够更好地描述土水特征曲线的滞回特性,尤其是边界影响区及残余区吸力与含水率的非线性关系,同时其变化规律与试验结果一致。
-
-
[1] 高游, 孙德安, 张俊然, 等. 考虑孔隙比和水力路径影响的非饱和土土水特性研究[J]. 岩土工程学报, 2019, 41(12): 2191–2196. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18065.shtml GAO You, SUN De-an, ZHANG Jun-ran, et al. Soil-water characteristics of unsaturated soils considering initial void ratio and hydraulic path[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2191–2196. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18065.shtml
[2] ANANDARAJAH A, AMARASINGHE P M. Microstructural investigation of soil suction and hysteresis of fine-grained soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(1): 38–46. doi: 10.1061/(ASCE)GT.1943-5606.0000555
[3] 刘艳, 于建涛. 动态土水特征曲线滞后模型研究[J]. 岩土工程学报, 2021, 43(1): 62–68. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18420.shtml LIU Yan, YU Jian-tao. Hysteresis model for soil-water characteristic curve under dynamic conditions[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 62–68. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18420.shtml
[4] ARYA L M, PARIS J F. A physicoempirical model to predict the soil moisture characteristic from particle‐size distribution and bulk density data[J]. Soil Science Society of America Journal, 1981, 45(6): 1023–1030. doi: 10.2136/sssaj1981.03615995004500060004x
[5] FREDLUND M D, WILSON G W, FREDLUND D G. Use of the grain-size distribution for estimation of the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 2002, 39(5): 1103–1117. doi: 10.1139/t02-049
[6] ASSOULINE S, TESSIER D, BRUAND A. A conceptual model of the soil water retention curve[J]. Water Resources Research, 1998, 34(2): 223–231. doi: 10.1029/97WR03039
[7] 郑方, 刘奉银, 王磊. 粒度对非饱和土土水特征曲线滞回特性的影响[J]. 水利与建筑工程学报, 2019, 17(5): 19–24. https://www.cnki.com.cn/Article/CJFDTOTAL-FSJS201905003.htm ZHENG Fang, LIU Feng-yin, WANG Lei. Influence of unsaturated soil granularity on hysteretic behavior of soil-water characteristic curve[J]. Journal of Water Resources and Architectural Engineering, 2019, 17(5): 19–24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FSJS201905003.htm
[8] 陈宇龙, 内村太郎. 粒径对土持水性能的影响[J]. 岩石力学与工程学报, 2016, 35(7): 1474–1482. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201607018.htm CHEN Yu-long Uchimura Taro. Influence of particle size on water retention of soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1474–1482. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201607018.htm
[9] 朱青青, 苗强强, 陈正汉, 等. 考虑基质势影响的非饱和土水分运移规律测试系统研制[J]. 岩土工程学报, 2016, 38(增刊2): 240–244. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16687.shtml ZHU Qing-qing, MIAO Qiang-qiang, CHEN Zheng-han, et al. Development of test system for unsaturated soil water movement law considering influence of matrix potential[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(S2): 240–244. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16687.shtml
[10] 姚仰平, 王琳. 影响锅盖效应因素的研究[J]. 岩土工程学报, 2018, 40(8): 1373–1382. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17471.shtml YAO Yang-ping, WANG Lin. Influence factors for "pot-cover effect"[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1373–1382. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17471.shtml
[11] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892–898. doi: 10.2136/sssaj1980.03615995004400050002x
[12] FREDLUND D G, XING A. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521–532. doi: 10.1139/t94-061
[13] BROOKS R H, COREY A T. Hydraulic properties of porous media and their relation to drainage design[J]. Transactions of the ASAE, 1964, 7(1): 26–0028. doi: 10.13031/2013.40684
[14] BRUTSAERT W. Some methods of calculating unsaturated permeability[J]. Transactions of the ASAE, 1967, 10(3): 400–404. doi: 10.13031/2013.39683
[15] ZAPATA C E, HOUSTON W N, HOUSTON S L, et al. Soil–water characteristic curve variability[J]. Advances in Unsaturated Geotechnics, 2000: 84–124.
[16] ZHAI Q, RAHARDJO H. Quantification of uncertainties in soil–water characteristic curve associated with fitting parameters[J]. Engineering Geology, 2013, 163: 144–152. doi: 10.1016/j.enggeo.2013.05.014
[17] LIKOS W J, LU N, GODT J W. Hysteresis and uncertainty in soil water-retention curve parameters[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 140(4): 04013050.
[18] LI P, LI T L, VANAPALLI S K. Prediction of soil-water characteristic curve for Malan loess in Loess Plateau of China[J]. Journal of Central South University, 2018, 25(2): 432–447. doi: 10.1007/s11771-018-3748-1
[19] BAYAT H, MAZAHERI B, MOHANTY B P. Estimating soil water characteristic curve using landscape features and soil thermal properties[J]. Soil and Tillage Research, 2019, 189: 1–14. doi: 10.1016/j.still.2018.12.018
[20] TOMASELLA J, HODNETT M G. Estimating soil water retention characteristics from limited data in Brazilian Amazonia[J]. Soil Science, 1998, 163(3): 190–202. doi: 10.1097/00010694-199803000-00003
[21] PHAM K, KIM D, YOON Y, et al. Analysis of neural network based pedotransfer function for predicting soil water characteristic curve[J]. Geoderma, 2019, 351: 92–102. doi: 10.1016/j.geoderma.2019.05.013
[22] WEI C, DEWOOLKAR M M. Formulation of capillary hysteresis with internal state variables[J]. Water Resources Research, 2006, 42(7): 260–273.
[23] LI X S. Modelling of hysteresis response for arbitrary wetting/drying paths[J]. Computers and Geotechnics, 2005, 32(2): 133–137. doi: 10.1016/j.compgeo.2004.12.002
[24] NIMMO J R. Semiempirical model of soil water hysteresis[J]. Soil Science Society of America Journal, 1992, 56(6): 1723–1730. doi: 10.2136/sssaj1992.03615995005600060011x
[25] GAN Y, MAGGI F, BUSCARNERA G, et al. A particle–water based model for water retention hysteresis[J]. Géotechnique Letters, 2013, 3(4): 152–161. doi: 10.1680/geolett.13.00046
[26] MUALEM Y. Extension of the similarity hypothesis used for modeling the soil water characteristics[J]. Water Resources Research, 1977, 13(4): 773–780. doi: 10.1029/WR013i004p00773
[27] MUALEM Y. Prediction of the soil boundary wetting curve[J]. Soil Science, 1984, 137(6): 379–390. doi: 10.1097/00010694-198406000-00001
[28] 刘艳, 赵成刚, 李舰, 等. 相间交界面对非饱和土应力状态的影响[J]. 力学学报, 2017, 49(2): 335–343. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201702010.htm LIU Yan, ZHAO Cheng-gang, LI Jian, et al. The influence of interfaces on the stress state in unsaturated soils[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 335–343. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201702010.htm
[29] 张鹏程, 汤连生, 姜力群, 等. 基质吸力与含水量及干密度定量关系研究[J]. 岩石力学与工程学报, 2013, 31(增刊1): 2792–2797. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S1027.htm ZHANG Peng-cheng, TANG Lian-sheng, JIANG Li-qun, et al. Research of quantitative relations of matric suction with water content and dry density[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 31(S1): 2792–2797. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S1027.htm
[30] ZHOU A N. A contact angle-dependent hysteresis model for soil–water retention behaviour[J]. Computers and Geotechnics, 2013, 49: 36–42. doi: 10.1016/j.compgeo.2012.10.004
[31] LIKOS W J, LU N. Hysteresis of capillary stress in unsaturated granular soil[J]. Journal of Engineering Mechanics, 2004, 130(6): 646–655. doi: 10.1061/(ASCE)0733-9399(2004)130:6(646)
[32] WANG X, LI J. A novel liquid bridge model for estimating SWCC and permeability of granular material[J]. Powder Technology, 2015, 275: 121–130. doi: 10.1016/j.powtec.2015.01.044
[33] SOLIGNO G, DIJKSTRA M, VAN ROIJ R. The equilibrium shape of fluid-fluid interfaces: derivation and a new numerical method for Young's and Young-Laplace equations[J]. The Journal of Chemical Physics, 2014, 141(24): 244702. doi: 10.1063/1.4904391
[34] BRAKKE K A. The surface evolver[J]. Experimental Mathematics, 1992, 1(2): 141–165. doi: 10.1080/10586458.1992.10504253
[35] CHOU T H, HONG S J, SHENG Y J, et al. Drops sitting on a tilted plate: receding and advancing pinning[J]. Langmuir, 2012, 28(11): 5158–5166. doi: 10.1021/la300257t
[36] BEREJNOV V, THORNE R E. Enhancing drop stability in protein crystallization by chemical patterning[J]. Acta Crystallographica Section D, Biological Crystallography, 2005, 61(12): 1563–1567. doi: 10.1107/S0907444905028866
[37] THAMPI S P, GOVINDARAJAN R. Minimum energy shapes of one-side-pinned static drops on inclined surfaces[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 84(4): 046304. doi: 10.1103/PhysRevE.84.046304
[38] SANTOS M J, VELASCO S, WHITE J A. Simulation analysis of contact angles and retention forces of liquid drops on inclined surfaces[J]. Langmuir, 2012, 28(32): 11819–11826. doi: 10.1021/la3019293
[39] FISHER R A. On the capillary forces in an ideal soil; correction of formulae given by WB Haines[J]. The Journal of Agricultural Science, 1926, 16(3): 492–505. doi: 10.1017/S0021859600007838
[40] NISHIYAMA N, YOKOYAMA T. Water film thickness in unsaturated porous media: effect of pore size, pore solution chemistry, and mineral type[J]. Water Resources Research, 2021, 57, e2020WR029257.
[41] SMITH W O, FOOTE P D, BUSANG P F. Packing of homogeneous spheres[J]. Physical Review, 1929, 34(9): 1271–1274. doi: 10.1103/PhysRev.34.1271
[42] BUTT H J, KAPPL M. Normal capillary forces[J]. Advances in Colloid and Interface Science, 2009, 146(1/2): 48–60.
[43] 黎澄生, 孔令伟, 柏巍, 等. 土–水特征曲线滞后阻塞模型[J]. 岩土力学, 2018, 39(2): 59–604. LI Cheng-sheng, KONG Ling-Wei, Bai Wei, et al. Hysteresis model of soil-water characteristic curve[J]. Rock and Soil Mechanics, 39(2): 598–604. (in Chinese)
[44] KASANGAKI G J, MEDERO G M, OOI J Y. Factors Influencing Water Retention Characteristics of Granular Materials[M]// Multiphysical Testing of Soils and Shales, Berlin: Springer, 2013.
[45] ESMAEELNEJAD L, SIAVASHI F, SEYEDMOHAMMADI J, et al. The best mathematical models describing particle size distribution of soils[J]. Modeling Earth Systems and Environment, 2016, 2(4): 1–11.
[46] ROSIN P, RAMMLER E. The laws governing the fineness of powdered coal[J]. Journal of the Institute of Fuel, 1933, 7: 29–36.
[47] 井彦林, 王昊, 陶春亮, 等. 非饱和黄土的接触角与孔隙特征试验[J]. 煤田地质与勘探, 2019, 47(5): 157–162. doi: 10.3969/j.issn.1001-1986.2019.05.022 JING Yan-lin, WANG Hao, TAO Chun-liang, et al. Experimental study on contact angle and pore characteristics of unsaturated loess[J]. Coal Geology & Exploration, 2019, 47(5): 157–162. (in Chinese) doi: 10.3969/j.issn.1001-1986.2019.05.022
[48] 陶高梁, 朱学良, 胡其志, 等. 黏性土压缩过程临界孔径现象及固有分形特征[J]. 岩土力学, 2019, 40(1): 81–90. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201901005.htm TAO Gao-liang, ZHU Xue-liang, HU Qi-zhi, et al. Critical pore-size phenomenon and intrinsic fractal characteristic of clay in process of compression[J]. Rock and Soil Mechanics, 2019, 40(1): 81–90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201901005.htm
[49] SHIRAZI M A, BOERSMA L, HART J W. A unifying quantitative analysis of soil texture: improvement of precision and extension of scale[J]. Soil Science Society of America Journal, 1988, 52(1): 181–190. doi: 10.2136/sssaj1988.03615995005200010032x
[50] SHIRAZI M A, BOERSMA L. A unifying quantitative analysis of soil texture[J]. Soil Science Society of America Journal, 1984, 48(1): 142–147. doi: 10.2136/sssaj1984.03615995004800010026x
[51] 刘建维. 面向润湿作用的黄土结构性及吸附特性试验研究[D]. 西安: 长安大学, 2017. LIU Jian-wei. Experimental Study on the Structure and Adsorption Characteristics of Loess oriented to Wetting Function[D]. Xi'an: Changan University, 2017. (in Chinese)
[52] 栾茂田, 李顺群, 杨庆. 非饱和土的理论土-水特征曲线[J]. 岩土工程学报, 2005, 27(6): 611–615. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract11688.shtml LUAN Mao-tian, LI Shun-qun, YANG Qing. Theoretical soil-water characteristic curve for unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 611–615. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract11688.shtml
[53] 刘星志, 吴悦, 潘诗婷, 等. 颗粒级配对非饱和红土土-水特征曲线的影响[J]. 水利水运工程学报, 2018(5): 103–110. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY201805015.htm LIU Xing-zhi, WU Yue, PAN Shi-ting, et al. Influences of different grain size contents on soil-water characteristic curve of unsaturated laterite based on fractal theory[J]. Hydro-Science and Engineering, 2018(5): 103–110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY201805015.htm
[54] 穆青翼, 党影杰, 董琪, 等. 原状和压实黄土持水特性及湿陷性对比试验研究[J]. 岩土工程学报, 2019, 41(8): 1496–1504. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17975.shtml MU Qing-yi, DANG Ying-jie, DONG Qi, et al. Water-retention characteristics and collapsibity behaviors: comparison between intact and compacted loesses[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(8): 1496–1504. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17975.shtml
[55] 伏映鹏, 廖红建, 刘雪刚, 等. 非线性连续卸荷路径下黄土的强度与变形特性研究[J]. 重庆大学学报, 2021, 44(5): 26–37. https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE202105004.htm FU Ying-peng, LIAO Hong-jian, LIU Xue-gang, et al. Study on strength and deformation characteristics of loess under nonlinear continuous unloading path[J]. Journal of Chongqing University, 2021, 44(5): 26–37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE202105004.htm



 下载:
下载: