基于辛体系的筋箍碎石桩受力变形分析

张玲; 张旭波; 徐泽宇; 欧强

doi:10.11779/CJGE202011009

基于辛体系的筋箍碎石桩受力变形分析 English Version

湖南大学岩土工程研究所,湖南　长沙　410082

基金项目:

国家自然科学基金项目 51678231

国家自然科学基金项目 52078205

国家自然科学基金青年项目 51978255

湖南省自然科学基金项目 2020JJ3013

详细信息

作者简介:
张玲(1982—),女,浙江临海人,副教授,博士生导师,主要从事桩基础和特殊土地基处理等研究。E-mail：zhanglhd@163.com

中图分类号: TU43
计量
- 文章访问数: 290
- HTML全文浏览量: 39
- PDF下载量: 138
出版历程
- 收稿日期: 2020-03-23
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-10-31

Stress and deformation analysis of geosynthetic-encased stone columns based on symplectic system

Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China

摘要

摘要: 因土工格栅套筒的环箍效应,筋箍碎石桩的受力变形机理较普通碎石桩更为复杂。将筋箍碎石桩单桩的受力变形视为空间轴对称问题,基于辛体系理论构建了可考虑桩体横截面剪应力的辛对偶方程,并对方程进行变量分离,再结合边界条件得到了筋箍碎石桩沉降及径向变形的辛体系解答。通过算例分析验证了方法的合理性与可行性。进一步的参数分析表明：筋箍碎石桩的沉降及鼓胀变形随筋材抗拉刚度的增大而减小；随桩土应力比的增大而增大,但增长率逐渐减小；随加筋深度的增大而减小,但超过最优加筋深度时不再变化；而最优加筋深度则随荷载的增大、桩间距的增大及侧压力系数的减小而相应增大。
- 筋箍碎石桩 /
- 辛体系 /
- 空间轴对称 /
- 辛对偶方程 /
- 变量分离 /
- 最优加筋深度
Abstract: Due to the hoop effect of geogrids, the stress and deformation mechanism of geosynthetic-encased stone columns (GESCs) is more complex than that of the ordinary stone columns. In this study, the stress and deformation of a single GESC is regarded as a space axisymmetric problem. Based on the symplectic system theory, a symplectic dual equation considering the shear stress of the cross section of the column is formulated, the variables of the equation are separated, and the distribution functions for the settlement and radial deformation of GESCs are finally obtained according to the boundary conditions. The rationality and feasibility of this method are verified by the practical example, and the parameter analysis shows that the settlement and bulging of GESCs decrease with the increase of encasement stiffness. They increase with the increase of pile-soil stress ratio, but the growth rate decreases gradually. They decrease with the increase of encasement depth, but no longer change when they exceed the optimal encasement depth. The optimal encasement depth increases with the increase of load and pile spacing, and with the decrease of lateral pressure coefficient.
- geosynthetic-encased stone column /
- symplectic system /
- space axisymmetry /
- symplectic dual equation /
- variable separation /
- optimal encasement depth

HTML全文

0. 引言

近年来,中国高速公（铁）路建设的迅猛发展,带来软基处治技术的蓬勃发展。筋箍碎石桩法（或土工材料包裹碎石桩法）作为碎石桩的新发展^[1],出现于软基处治实践并逐渐推广应用。它是在普通碎石桩靠近桩顶部位或全桩长设置土工格栅套筒,利用抗拉性能良好的土工格栅提供额外的侧向约束力,进而增加桩体强度,减少地基沉降,提高地基承载力。

国内外学者对筋箍碎石桩受力变形特性展开了相应研究。理论计算方面,赵明华等^[2]将筋箍碎石桩的受力变形视为平面应变问题,考虑桩、筋材以及土体之间的协调变形,基于圆孔扩张理论得到了筋箍碎石桩承载力的计算方法。Raithel等^[3]基于荷载传递模型,假定桩体体积不变,桩身径向变形沿深度亦不变,得到了土工布包裹砂桩的沉降解析解。上述方法将筋箍碎石桩径向变形视为均值,不考虑其沿深度的变化。然而Duan等^[4]、Zhang等^[5]、Kong等^[6]研究表明：筋箍碎石桩径向变形沿深度是变化的,且主要发生在靠近桩顶部位。因此,有学者在筋箍碎石桩的受力变形分析中考虑这一影响,如Pulko等^[7]基于单元体的概念,将土体视为弹性体、筋箍碎石桩为弹塑性体并服从Mohr-Coulomb屈服准则,得到了筋箍碎石桩径向变形沿深度的变化曲线,但忽略了桩侧摩阻力对筋箍碎石桩受力变形的影响。Zhou等^[8]假定桩侧摩阻力为极限摩阻力,基于圆孔扩张理论分析桩体扩孔压力与径向变形的关系,通过构建应力平衡方程,得到桩体沉降及径向变形曲线。然而,筋箍碎石桩桩身自上而下的非均匀鼓胀变形,与桩身横截面上的剪应力存在必然联系,因此该剪应力在筋箍碎石桩应力应变平衡方程的构建中至关重要,而以上方法并没有考虑该剪应力的影响。赵明华等^[9]基于剪应力互等定理得到桩身横截面剪应力与桩侧摩阻力的代数关系,再由桩身鼓胀段荷载传递模式得到桩身沉降及径向变形计算公式。该方法需先假定横截面径向变形的分布模式,而该分布模式往往难以确定。鉴于此,有必要对筋箍碎石桩的受力变形做进一步深入研究。

取筋箍碎石桩单桩进行受力变形分析时,可将其视为空间轴对称问题,按弹性力学方法进行求解。而以往弹性力学中按应力或按位移求解空间轴对称问题时,往往是将未知函数予以消元,得到只含一类变量的高阶偏微分方程,这样使得变量分离、本征函数展开等有效方法难以实施,加大了问题求解的难度。而且这两种方法都属于拉格朗日体系下的解法,其解往往通过“凑合”得到,只适用于某类特殊问题。

随着最优控制模拟理论的建立,辛体系被引入应用力学和椭圆型偏微分方程中。钟万勰^[10]首次将辛体系引入弹性力学,形成弹性力学求解新体系——辛弹性力学。辛体系中原变量及其对偶变量组成全状态空间,虽未知变量增加,但微分方程阶次有效降低,变量分离、本征函数展开法得以实施。在给定边界条件下,各阶本征解线性组合后可得到问题的完整解答。

本文基于辛体系理论,首先通过构建考虑筋箍碎石桩横截面剪应力的辛对偶方程,将空间轴对称问题基本方程导入辛体系,然后通过变量分离法导出本征方程,再由侧边及端部边界条件获得筋箍碎石桩桩顶沉降及径向变形的辛体系解答,以期能为筋箍碎石桩复合地基受力变形分析提供新思路。

1. 计算模型与分析方法

1.1 计算模型的建立

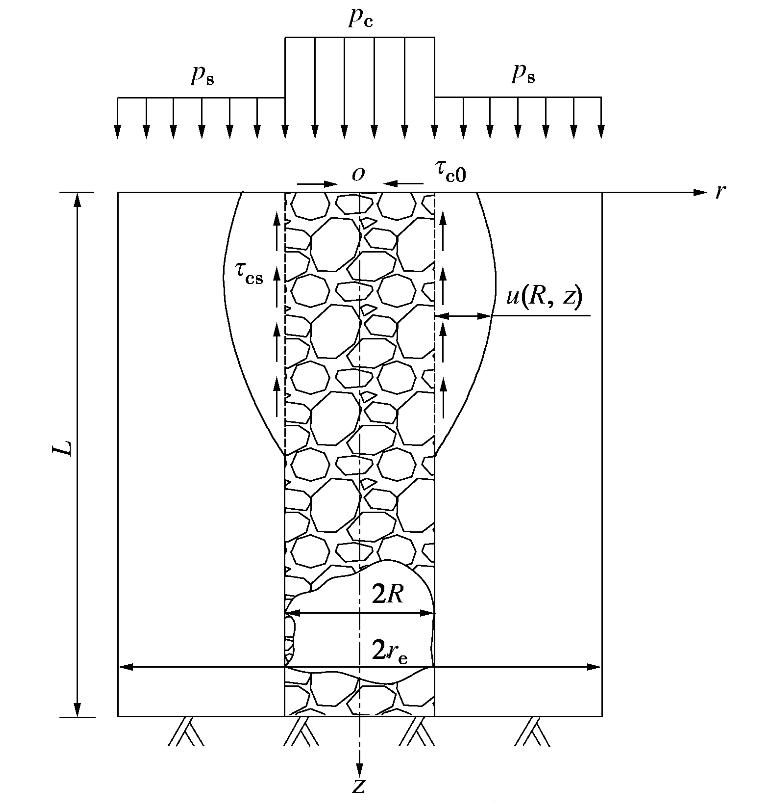
取筋箍碎石桩单桩及加固范围内土体为研究对象,计算模型如图1所示。在柱坐标系(r,θ,z)下,o为坐标原点,R,L为桩体半径及桩长；p_c,p_s为桩顶平面作用于桩上及桩周土上的荷载；τ_c0,τ_cs为桩顶水平向摩阻力及桩侧摩阻力；u(R,z)为桩周径向变形。r_e为单桩加固范围等效圆半径,为0.565s_d（正方形布桩）或0.525s_d（梅花形布桩）,s_d为桩间距。

图 1 单桩加固区计算模型

Figure 1. Computational model for a single GESC in reinforcement area

下载: 全尺寸图片幻灯片

为便于后续分析,并做如下假定：①筋箍碎石桩鼓胀变形视为空间轴对称问题；②桩及桩周土体均为均匀、各向同性弹性体；③各分析单元之间互不影响,即不考虑复合地基群桩效应的影响。

1.2 桩身受力变形分析

（1）辛体系对偶方程

对于存在竖向体力的筋箍碎石桩,其空间轴对称问题的几何方程、物理方程及平衡微分方程可参考文献[11],本文仅给出平衡微分方程：

$\begin{array}{l} \frac{\partial σ_{r}}{\partial r} + \frac{σ_{r} - σ_{θ}}{r} + {\dot{τ}}_{r z} = 0, \\ \frac{\partial τ_{r z}}{\partial r} + \frac{τ_{r z}}{r} + {\dot{σ}}_{z} - γ_{c} = 0, \end{array}}$

(1)

式中, $σ_{r}$ , $σ_{θ}$ , $σ_{z}$ , $τ_{r z}$ 为相应方向上的应力分量,γ_c为桩体重度,上标点表示变量对z的微商。

竖向体力作用下,筋箍碎石桩的拉格朗日函数为

$\begin{matrix} L (u, w) = \frac{E_{c} r}{2 (1 + μ_{c})} [{(\frac{\partial u}{\partial r})}^{2} + \frac{u^{2}}{r^{2}} + {\dot{w}}^{2} + \frac{1}{2} {(\frac{\partial w}{\partial r} + \dot{u})}^{2}] + \\ \frac{E_{c} μ_{c} r}{2 (1 + μ_{c}) (1 - 2 μ_{c})} {(\frac{\partial u}{\partial r} + \frac{u}{r} + \dot{w})}^{2} + r γ_{c} w \end{matrix}$ ,

(2)

式中,E_c,μ_c分别为桩体的弹性模量及泊松比,u,w为r,z方向的位移,记位移向量为 $q = {[\begin{matrix} u & w \end{matrix}]}^{T}$ 。

为建立辛体系,引入对偶变量 $p = {[\begin{matrix} p_{1} & p_{2} \end{matrix}]}^{T}$ ：

$p = \frac{\partial L}{\partial \dot{q}} = [\begin{array}{l} \frac{E_{c} r}{2 (1 + μ_{c})} (\dot{u} + \frac{\partial w}{\partial r}) \\ \frac{E_{c} μ_{c} r}{(1 + μ_{c}) (1 - 2 μ_{c})} (\frac{\partial u}{\partial r} + \frac{u}{r} + \dot{w}) + \frac{E_{c} r \dot{w}}{1 + μ_{c}} \end{array}] = [\begin{matrix} r τ_{r z} \\ r σ_{z} \end{matrix}]$ 。

(3)

由式（3）可见,与u,w对应的对偶变量为rτ_rz,rσ_z。则哈密顿函数 $ℏ$ 可表示为

$ℏ (q, p) = p^{T} \dot{q} - L (q, p)$ 。

(4)

对式（4）变分后再分步积分,可得到辛对偶方程：

$[\begin{matrix} \dot{q} \\ \dot{p} \end{matrix}] = [\begin{matrix} δ ℏ / δ p \\ - δ ℏ / δ q \end{matrix}] = H [\begin{matrix} q \\ p \end{matrix}] + [\begin{matrix} 0 \\ f \end{matrix}]$ ,

(5)

式中, $f = {[\begin{matrix} 0 & r γ_{c} \end{matrix}]}^{T}$ ,哈密顿矩阵H为

$H = [\begin{matrix} 0 & - \frac{\partial}{\partial r} & \frac{2 (1 + μ_{c})}{E_{c} r} & 0 \\ \frac{- μ_{c}}{1 - μ_{c}} (\frac{\partial}{\partial r} + \frac{1}{r}) & 0 & 0 & \frac{(1 + μ_{c}) (1 - 2 μ_{c})}{E_{c} r (1 - μ_{c})} \\ \frac{- E_{c}}{1 - μ_{c}^{2}} (\frac{r \partial^{2}}{\partial r^{2}} + \frac{\partial}{\partial r} - \frac{1}{r}) & 0 & 0 & \frac{- μ_{c}}{1 - μ_{c}} (\frac{\partial}{\partial r} - \frac{1}{r}) \\ 0 & 0 & - \frac{\partial}{\partial r} & 0 \end{matrix}]$ 。

(6)

同时可得到径向应力 $σ_{r}$ 及环向应力 $σ_{θ}$ ：

$\begin{array}{l} σ_{r} = \frac{E_{c}}{1 - μ_{c}^{2}} \frac{\partial u}{\partial r} + \frac{E_{c} μ_{c}}{1 - μ_{c}^{2}} \frac{u}{r} + \frac{μ_{c}}{1 - μ_{c}} \frac{p_{2}}{r}, \\ σ_{θ} = \frac{E_{c} μ_{c}}{1 - μ_{c}^{2}} \frac{\partial u}{\partial r} + \frac{E_{c}}{1 - μ_{c}^{2}} \frac{u}{r} + \frac{μ_{c}}{1 - μ_{c}} \frac{p_{2}}{r} 。 \end{array}}$

(7)

令全状态向量 $ψ = {[\begin{matrix} q & p \end{matrix}]}^{T}$ ,则式（5）可简写为

$\dot{ψ} = H ψ + h$ ,

(8)

式中,非齐次项 $h = [\begin{matrix} 0 & 0 & 0 & r γ_{c} \end{matrix}]$ 为体力项,可由后续特解叠加的方法进行考虑,不妨先假设h=0。即

$\dot{ψ} = H ψ$ 。

(9)

（2）零本征解

首先考虑桩体的齐次侧边条件（非齐次侧边条件可通过后续变量代换的方法齐次化）,即

$σ_{r} = τ_{r z} = 0 \begin{matrix} (r = R) \end{matrix}$ 。

(10)

对式(9)采用广义变量分离法得

$ψ (r, z) = e^{k z} Y (r)$ ,

(11)

式中,k为本征值, $Y (r)$ 为横方向（r坐标方向）上的本征解。记U,W,P₁,P₂分别为u,w,p₁,p₂在横方向上的表达式,则有 $Y (r) = {[\begin{matrix} U & W & P_{1} & P_{2} \end{matrix}]}^{T}$ 。 $Y (r)$ 满足本征方程：

$H Y (r) = k Y (r)$ 。

(12)

当k=0时,由本征方程 $H Y (r) = 0$ 可求得基本本征解向量： $Y_{0} = {[\begin{matrix} 0 & 1 & 0 & 0 \end{matrix}]}^{T}$ ,对应式（9）的解为

$ψ_{1}^{(0)} = {[\begin{matrix} 0 & 1 & 0 & 0 \end{matrix}]}^{T}$ ,

(13)

此解的物理意义为沿z轴方向的刚体平移。

本征解向量Y₀存在约当型,由其一阶约当型控制方程 $H Y_{1} = Y_{0}$ 得到 $Y_{1} = {[\begin{matrix} - μ_{c} r & 0 & 0 & E_{c} r \end{matrix}]}^{T}$ ,对应式（9）的解为

$ψ_{1}^{(1)} = Y_{1} + z Y_{0} = {[\begin{matrix} - μ_{c} r & z & 0 & E_{c} r \end{matrix}]}^{T}$ ,

(14)

此解的物理意义为筋箍碎石桩在z轴方向的压缩。

存在归一化因子η,使得本征解向量Y₀,Y₁满足：

$η \int_{0}^{R} Y_{0}^{T} j Y_{1} d r = 1$ ,

(15)

式中,η=2/(E_cR²), $j = [\begin{matrix} 0 & I \\ - I & 0 \end{matrix}]$ ,I为单位矩阵。

式（15）表明Y₀,Y₁互相辛共轭,故不存在更高阶约当型解^[10],因此空间轴对称问题只存在 $ψ_{1}^{(0)}$ , $ψ_{1}^{(1)}$ 两个零本征解。因竖向荷载作用下筋箍碎石桩会发生轴向压缩变形,故本文只选取零本征解 $ψ_{1}^{(1)}$ 。

（3）非零本征解

式（12）中当k≠0时,本征方程的解可以用完备的Papkovitch-Neuber型解表示^[12]：

$[\begin{matrix} U \\ W \\ P_{1} \\ P_{2} \end{matrix}] = [\begin{matrix} λ_{1} k J_{1} & J_{1} - λ_{1} k r J_{0} \\ λ_{1} k J_{0} & λ_{1} k r J_{1} \\ 0 & λ_{2} k r J_{1} \\ λ_{3} k^{2} r J_{0} & λ_{3} k r (k r J_{1} + 2 μ_{c} J_{0} - 4 μ_{c}^{2} J_{0}) \end{matrix}] [\begin{matrix} c_{1} \\ c_{2} \end{matrix}]$ ,

(16)

式中, $J_{0}$ , $J_{1}$ 分别为零阶及一阶Bessel函数, $λ_{1}$ = 1/(4-4μ_c), $λ_{2}$ =E_c/(2+2μ_c), $λ_{3}$ =E_c/[(4-4μ_c²)(1-2μ_c)],c₁,c₂为待定常数。

式（16）为横方向上的非零本征解表达式,由该式及齐次侧边条件式（10）得到

$[\begin{matrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{matrix}] [\begin{matrix} c_{1} \\ c_{2} \end{matrix}] = 0$ ,

(17)

式中,

$\begin{array}{l} c_{11} = (2 μ_{c} - 1) J_{1} (k R) / R + k J_{0} (k R), \\ c_{12} = (k^{2} R^{2} - 8 μ_{c}^{2} + 12 μ_{c} - 4) J_{1} (k R) / (k R) + \\ \begin{matrix} \end{matrix} (4 μ_{c}^{2} - 8 μ_{c} + 3) J_{0} (k R), \\ c_{21} = 0, \\ c_{22} = J_{1} (k R) 。 \end{array}}$

(18)

若式（17）存在非零解,则其系数行列式为零,由此可建立非零本征值方程：

$| \begin{matrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{matrix} | = 0$ 。

(19)

则c₁,c₂的值可由以下式子进行确定：

$\begin{array}{l} \begin{matrix} c_{1} = c_{12}, c_{2} = - c_{11} & (c_{22} = 0) \end{matrix} \\ \begin{matrix} c_{1} = 1, c_{2} = 0 \begin{matrix} \end{matrix} & (c_{11} = 0) \end{matrix} \end{array}}$ 。

(20)

由式（19）可求得n阶本征值k_n,将本征值按其绝对值由小到大排列,绝对值最小的本征值定义为一阶本征值k₁,依此类推。辛体系下,存在与本征值k互为辛共轭的本征值-k,并由本征值可将非零本征解划分为两类：①向z轴正向衰减的α类本征解ψ_n^(α)（对应本征值k_α满足：Re(k_α)<0或Re(k_α)=0且Im(k_α)<0）；②向z轴负向衰减的β类本征解ψ_n^(β)（对应本征值k_β满足：k_β=-k_α）。对于筋箍碎石桩而言,只需考虑应力及位移向z轴正向衰减的α类本征解。

齐次侧边条件下式（9）的通解ψ_g可由零本征解及非零本征解的线性组合表示（ $ψ_{1}^{(1)}$ 可用 $ψ_{0}^{(α)}$ 表示）：

$\begin{matrix} ψ_{g} = \sum_{n} a_{n} e^{k_{n} z} ψ_{n}^{(α)} (r) & (n = 0, 1, 2, \dots) \end{matrix}$ ,

(21)

式中,a_n为待定系数,可根据端部边界条件确定。由于本文侧边非齐次,故在此不对a_n进行展开叙述。

（4）非齐次侧边条件

对于筋箍碎石桩,当桩体产生鼓胀变形时,由于筋材的约束作用,会对桩体产生径向应力σ_r,geo：

$σ_{r, geo} = \frac{T^{0}}{R} + J \frac{u (R, z)}{R^{2}}$ ,

(22)

式中,T⁰为筋材初始拉力,J为筋材抗拉刚度。

设土体提供的侧向约束力为σ_s,桩土界面处存在径向应力平衡：

$\begin{matrix} σ_{r} - σ_{r, geo} = σ_{s} & (r = R) \end{matrix}$ 。

(23)

又因桩侧摩阻力为τ_cs,则用对偶变量表示的筋箍碎石桩侧边条件为 $(r = R)$

$\begin{array}{l} \frac{E_{c}}{1 - μ_{c}^{2}} \frac{\partial u}{\partial r} + \frac{E_{c} μ_{c}}{1 - μ_{c}^{2}} \frac{u}{r} + \frac{μ_{c}}{1 - μ_{c}} \frac{p_{2}}{r} - (\frac{T^{0}}{R} + \frac{J u}{R^{2}}) = σ_{s}, \\ p_{1} = r τ_{cs} 。 \end{array}}$

(24)

非齐次侧边条件可通过变量代换的方法化为齐次形式,为此引入新的对偶变量 $\bar{ψ}$ ：

$\bar{ψ} = {[\begin{matrix} \bar{u} & \bar{w} & {\bar{p}}_{1} & {\bar{p}}_{2} \end{matrix}]}^{T} = ψ - \bar{φ}$ ,

(25)

式中, $\bar{φ} = {[\begin{matrix} \frac{r R^{2} (σ_{s} + T^{0} / R) (1 - μ_{c})}{R^{2} E_{c} - J r (1 - μ_{c})} & 0 & r τ_{cs} & 0 \end{matrix}]}^{T}$ 。

$\bar{ψ}$ 通过上述齐次化已满足齐次侧边条件,此时考虑体力的新的对偶方程为

$\dot{ψ} = H ψ + \bar{g}$ 。

(26)

在齐次化的过程中,新的对偶方程中出现了非齐次项 $\bar{g}$ ,其满足

$\bar{g} = \dot{\bar{φ}} - H \bar{φ} + h = [\begin{matrix} {\dot{σ}}_{s} r R^{2} (1 - μ_{c}) / t - 2 (1 + μ_{c}) τ_{cs} / E_{c} \\ μ_{c} R (T^{0} + σ_{s} R) [E_{c} R^{2} + t] / t^{2} \\ \frac{r R J E_{c} (T^{0} + σ_{s} R) [2 E_{c} R^{2} + t]}{t^{3} (1 + μ_{c}) / (1 - μ_{c})} + r {\dot{τ}}_{cs} \\ τ_{cs} + r γ_{c} \end{matrix}]$ ,

(27)

式中,t=E_cR²-rJ(1-μ_c)。

在上述齐次化过程中,只改变了式（8）的非齐次项,因此通解ψ_g仍适用于式（26）。式（26）的解可由齐次方程通解ψ_g及非齐次方程特解ψ_s进行叠加求解,即 $ψ = ψ_{g} + ψ_{s}$ 。将特解及非齐次项进行本征展开：

$\begin{array}{l} ψ_{s} = \sum_{n} G_{n}^{(α)} (z) ψ_{n}^{(α)} (r), \\ g = \sum_{n} g_{n}^{(α)} (z) ψ_{n}^{(α)} (r), \end{array}}$

(28)

式中,g_n^(α)可根据共轭辛正交归一关系确定（本文只选用α类本征解,而因两类本征解之间必然存在共轭辛正交归一关系,故可由β类本征解确定g_n^(α)）：

$g_{n}^{(α)} (z) = \int_{0}^{R} g^{T} j ψ_{n}^{(β)} d r$ 。

(29)

将式（28）代入式（26）有：

${\dot{G}}_{n}^{(α)} (z) = k_{n} G_{n}^{(α)} (z) + g_{n}^{(α)} (z)$ 。

(30)

式（30）的解为

$G_{n}^{(α)} (z) = \int_{0}^{z} g_{n}^{(α)} (ξ) e^{k_{n} (z - ξ)} d ξ$ 。

(31)

由通解和特解表示的解的最终形式为

$\begin{matrix} ψ (r, z) = \sum_{n} [a_{n} e^{k_{n} z} + G_{n}^{(α)}] ψ_{n}^{(α)} (r) & (n = 0, 1, 2, \dots) \end{matrix} 。$

(32)

式中,a_n由z=0处的n+1个端部边界条件确定。

（5）端部边界条件

对于筋箍碎石桩,设z=0处的端部边界条件满足： $p = p_{z 0}$ ,将其用本征解展开有

$p_{z 0} = \sum_{n} [a_{n} e^{k_{n} z} + G_{n}^{(α)}] p_{n}^{(α)}$ ,

(33)

式中,p_n^(α)为p在横方向的α类本征解。由共轭辛正交归一关系,可建立关于系数a_n的n+1阶代数方程组：

$\int_{0}^{R} p_{z 0} q_{n}^{(β)} d r = \int_{0}^{R} [\sum_{n} (a_{n} e^{k_{n} z} + G_{n}^{(α)}) p_{n}^{(α)}] q_{n}^{(β)} d r$ ,

(34)

式中,q_n^(β)为q在横方向的β类本征解。由于非零本征解有无穷多个,实际计算中n可取有限项进行计算。

将求得的a_n代入式（32）,则可得到辛体系下筋箍碎石桩的应力及位移分布函数。令r=R,可得到桩周径向变形u(R,z)；令z=0,可得到桩顶直径D范围内的沉降w(r,0),取桩顶平均沉降s作为桩顶沉降：

$s = [\int_{0}^{R} w (r, 0) d r] / R$ 。

(35)

在式（27）中,令T⁰=0、J=0,可得到碎石桩的非齐次项,并由此可最终得到碎石桩的沉降及径向变形曲线。对于部分加筋碎石桩,加筋段采用筋箍碎石桩的辛体系解答,而非加筋段则采用碎石桩的辛体系解答。在求解过程中,先对加筋段进行分析,得到加筋段底部横截面上的竖向应力 ${σ^{'}}_{z} (r)$ 及剪应力 ${τ^{'}}_{r z} (r)$ ,将 ${σ^{'}}_{z} (r)$ , ${τ^{'}}_{r z} (r)$ 作为非加筋段的端部边界条件,从而可对非加筋段做进一步分析。

1.3 计算参数确定

（1）桩周土侧向约束力σ_s

桩周土侧向约束力由两部分组成^[13]：

$σ_{s} (z) = σ_{0} (z) + f_{m} (z)$ ,

(36)

式中,σ₀(z)为桩周土竖向应力引起的静止土压力,f_m(z) 为桩顶平面设置的垫层与垫层下土体之间的摩阻力f₀沿深度的衰减函数。其中, $σ_{0} (z)$ 可由下式确定：

$σ_{0} (z) = K_{0} (γ_{s} z + p_{s})$ ,

(37)

式中, $γ_{s}$ 为土体重度,K₀为桩周土体的侧压力系数,令土体内摩擦角为φ_s,则K₀=1-sinφ_s。

根据文献[13],f_m(z)可按下式确定：

$\begin{array}{l} f_{m} (z) = \frac{f_{0}}{π} {\ln [\frac{{(r_{e} - R)}^{2}}{z^{2}} + 1] - \frac{{(r_{e} - R)}^{2}}{{(r_{e} - R)}^{2} + z^{2}}}, \\ f_{0} = p_{s} tan φ_{s 0} + c_{s 0}, \end{array}}$

(38)

式中,φ_s0,c_s0分别为垫层与桩周土体界面处的外摩擦角及黏聚力。

（2）桩侧摩阻力τ_cs

桩侧摩阻力可由桩土界面处的外摩擦角φ_cs及黏聚力c_cs进行确定：

$τ_{cs} = σ_{s} tan φ_{cs} + c_{cs}$ 。

(39)

（3）桩顶荷载p_c

若作用在复合地基上的荷载为p₀,则p_c、p_s可通过桩土应力比n₀及复合地基置换率m进行确定：

$\begin{array}{l} p_{c} = n_{0} p_{0} / [1 + (n_{0} - 1) m], \\ p_{s} = p_{c} / n_{0} 。 \end{array}}$

(40)

（4）桩顶水平向摩阻力τ_c0

桩顶水平向摩阻力可由垫层与桩顶界面处的外摩擦角φ_c0及黏聚力c_c0进行确定：

$τ_{c 0} = p_{c} tan φ_{c 0} + c_{c 0}$ 。

(41)

2. 计算实例分析

为验证本文方法的合理性及可行性,以文献[14]的碎石桩模型试验及文献[15]的筋箍碎石桩现场试验为例,通过Mathematica软件编制相应程序,计算得到辛体系下桩体的沉降及径向变形,并与已有文献结果进行对比分析。

2.1 碎石桩实例分析

文献[14]通过模型试验及PLAXIS数值分析软件对某一软黏土中碎石桩的受力变形进行了相应研究。该模型试验的比例尺为1∶20,模型箱直径及高度均为300 mm。直径为2.3D的圆形载荷板置于桩顶,桩周土采用高压缩性黏土,桩身采用花岗岩石屑,正方形布桩。数值分析中采用Mohr-Coulomb屈服准则及非关联流动性准则描述桩体的弹塑性行为,土体的非线性行为则用临界状态模型及软土模型表示。采用本文方法试算分析发现：桩顶沉降及径向变形随本征解阶数n值的增加而快速收敛,当取前30阶本征解进行分析,计算结果已有较好的收敛性,故取n=30。计算参数除桩土应力比无实测数据外,其余参数同文献[14],具体如下（ $φ_{c}$ 为桩体内摩擦角,c_c,c_s分别为桩体和土体黏聚力）：E_c=2.5 MPa,μ_c=0.3, $γ_{c}$ =16 kN/m³, $φ_{c}$ =48°,c_c=0.1 kPa, $γ_{s}$ =11 kN/m³, $φ_{s}$ =24°,c_s=6 kPa,D=0.03 m,L=0.3 m,s_d=0.06 m。根据文献[16]的建议,本文取碎石桩的桩土应力比n₀=4；各界面处的外摩擦角及黏聚力参考文献[17～19]：φ_s0=φ_cs=2φ_s/3,c_s0=c_cs=2c_s/3；φ_c0=2φ_c/3,c_c0=2c_c/3。

将上述参数带入本文方法,计算得到碎石桩的桩顶沉降及径向变形结果,及其与文献[14]实测值及数值分析结果的对比如图2,3所示。

图 2 碎石桩p₀-s曲线

Figure 2. p₀-s curves of stone columns

下载: 全尺寸图片幻灯片

图 3 碎石桩径向变形与深度关系曲线

Figure 3. Curves of relationship between radial deformation and depth of stone columns

下载: 全尺寸图片幻灯片

由图2可见,本文方法计算所得复合地基荷载-沉降（p₀-s）曲线近似为直线,且当p₀≤40 kPa时,与文献[14]的实测和数值结果较为接近,但当p₀>40 kPa时,结果出现偏差,其原因是当p₀逐渐增大时,碎石桩的塑性变形逐渐出现,p₀-s曲线呈现非线性,而本文方法分析时,将碎石桩视为弹性体,忽略其塑性变形,因此本算例中当p₀>40 kPa时,本文方法计算所得桩顶沉降偏小。

由图3可见,当p₀为20,30 kPa时,本文方法计算所得径向变形曲线与文献[14]的数值结果较为接近。当p₀为40 kPa时,由于塑性变形的出现,本文方法结果在最大鼓胀点附近与文献[14]的结果差距稍大。而曲线在4.5D深度附近较文献[14]偏大,这是因为从距离桩顶一定深度开始,桩体应力及位移主要受不随z坐标衰减的零本征解所控制,此时桩体径向变形的衰减主要与桩周土侧向约束力的增大有关,故曲线在下半段接近线性,从而与文献[14]的非线性结果差距稍大。但总体而言,两者趋势较为一致。

由图3亦可见,随着荷载增加,碎石桩最大鼓胀点的深度及桩体鼓胀深度逐渐下移,最大鼓胀点的深度在（0.9～1.4）D处变化,而桩体鼓胀深度在（3.3～6.7）D处变化,与文献[14]的数值结果较为接近。

2.2 筋箍碎石桩实例分析

采用本文方法,对文献[15]中韩国浦项某筋箍碎石桩单桩现场载荷试验结果进行分析。该试验中筋箍碎石桩桩径0.76 m,桩长8 m,加筋深度为2D,桩侧三层土：上层为2.3 m填土,重度为20 kN/m³,黏聚力为4 kPa,内摩擦角为28°；中层为6.4 m粉质黏土,重度为17 kN/m³,黏聚力为2 kPa；下层为风化花岗岩土层。试验中与桩同直径的圆形载荷板置于桩顶,桩顶荷载及沉降由相应的应力及位移传感器测得,桩身径向变形由埋设于桩周0.2 m处的测斜仪器测得。

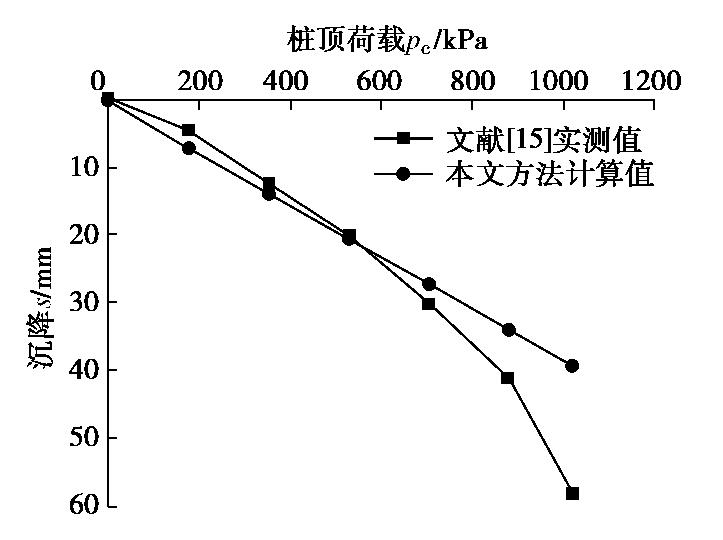
以桩顶荷载p_c=528 kPa为例,并取前30阶本征解进行分析（n=30）。参数取值中,文献[15]无桩体泊松比及粉质黏土内摩擦角的实测资料,故桩体泊松比参考文献[8]取为0.3,粉质黏土内摩擦角根据经验^[20]取为18°,各界面处的外摩擦角及黏聚力取值方法同2.1节。其余参数同文献[15],E_c=45 MPa, $γ_{c}$ =23 kN/m³, $φ_{c}$ =45°,c_c=5 kPa, $γ_{s}$ =17 kN/m³, $φ_{s}$ =28°,c_s=2 kPa,D=0.76 m,L=8 m,J=2500 kN/m。

将上述参数带入本文方法,计算得到筋箍碎石桩的桩顶沉降与径向变形的结果,及其与文献[15]实测值的对比见图4,5。

图 4 筋箍碎石桩p_c-s曲线

Figure 4. p_c-s curves of GESC

下载: 全尺寸图片幻灯片

图 5 筋箍碎石桩径向变形与深度关系曲线

Figure 5. Curves of relationship between radial deformation and depth of GESC

下载: 全尺寸图片幻灯片

由图4可见,本文计算得到的p_c-s曲线近似为直线,且曲线在前半段与实测值较为接近,而当p_c>600 kPa时,与实测值差距逐渐增大,这是因为从600 kPa开始,筋箍碎石桩桩顶沉降增速变快^[15],由此判断桩体从600 kPa开始已产生一定程度的塑性变形,因此曲线在后半段较实测值偏小。

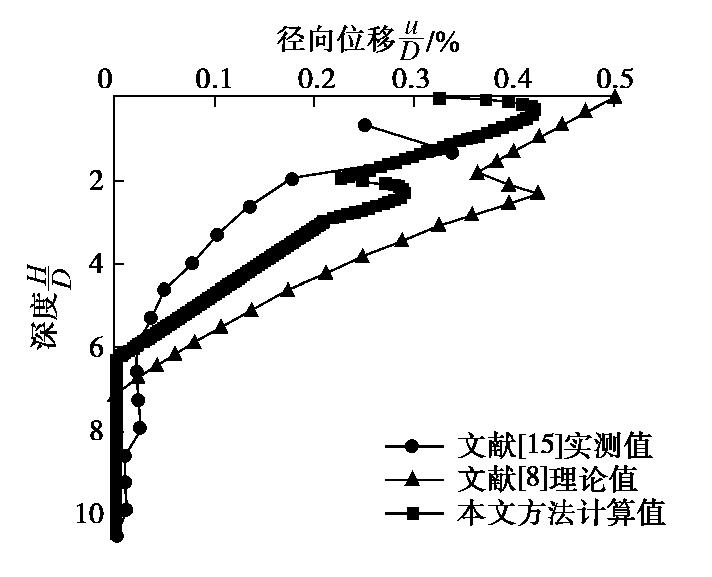
由图5可见,本文方法计算得到的桩周（r=R）径向变形沿桩身的变化曲线总体较实测值偏大,这是因为实测值测得的是距桩周0.2 m处的径向变形,实际桩周的径向变形会稍大于此值。

文献[8]亦对该载荷试验结果进行了理论分析,分析中将筋箍碎石桩等分为N段,由竖向应力平衡方程计算各段顶部竖向应力,再根据满足Mohr-Coulomb屈服准则及非关联流动性准则的应力应变关系计算各段沉降量,并将各段沉降量累加作为桩顶沉降；桩身径向变形则根据圆孔扩张理论计算得到。图5中也给出了文献[8]计算所得桩周（r=R）径向变形曲线。

对比本文方法计算结果与文献[8]计算结果可见,在趋势上两种方法结果较为一致：在加筋段,当深度大于0.5D时,随着深度增加,桩体径向鼓胀变形逐渐减小；在非加筋段,由于桩体未受到筋材的径向约束,使得非加筋段上部桩体产生的鼓胀变形较加筋段底部更大,且该段最大鼓胀点的深度出现在2.5D附近。但在加筋段靠近桩顶位置,文献[8]的结果较本文方法偏大,这是因为文献[8]忽略了桩顶水平向摩阻力的有利影响。在3D深度土层分界处,文献[8]未考虑土性参数的变化,使得该处径向变形曲线斜率变化较小。

3. 参数分析

为进一步研究不同筋材抗拉刚度J、不同加筋深度H_g（以无量纲量 $λ$ 表示, $λ$ =H_g/D）及不同桩土应力比n₀对筋箍碎石桩受力变形的影响,在2.1节的基础上做进一步参数分析。

3.1 筋材抗拉刚度的影响

图6为不同复合地基荷载p₀情况下,筋箍碎石桩桩顶沉降随筋材抗拉刚度的变化曲线。分析中采用全长加筋模式,桩土应力比取n₀=10,其他计算参数同2.1节。由图可见,随着筋材抗拉刚度的增大,筋箍碎石桩沉降逐渐变小,同时荷载的变化对筋箍碎石桩沉降的影响逐渐减小。

图 6 筋材抗拉刚度与筋箍碎石桩沉降关系曲线

Figure 6. Curves of relationship between encasement stiffness and settlement of GESC

下载: 全尺寸图片幻灯片

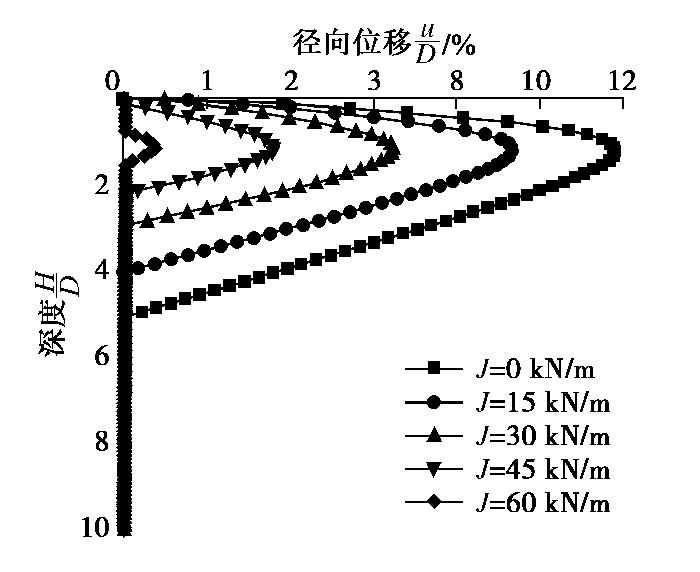
图7为p₀=30 kPa情况下,筋箍碎石桩径向变形随筋材抗拉刚度的变化曲线。由图7可见,筋材的环箍效应可有效约束碎石桩的径向鼓胀变形；筋材抗拉刚度愈大,则可提供的侧向约束力愈大,因而筋箍碎石桩径向鼓胀量愈小,且鼓胀变形深度也愈小。

图 7 不同筋材抗拉刚度下筋箍碎石桩径向变形曲线

Figure 7. Curves of radial deformation of GESC under different encasement stiffnesses

下载: 全尺寸图片幻灯片

3.2 加筋深度的影响

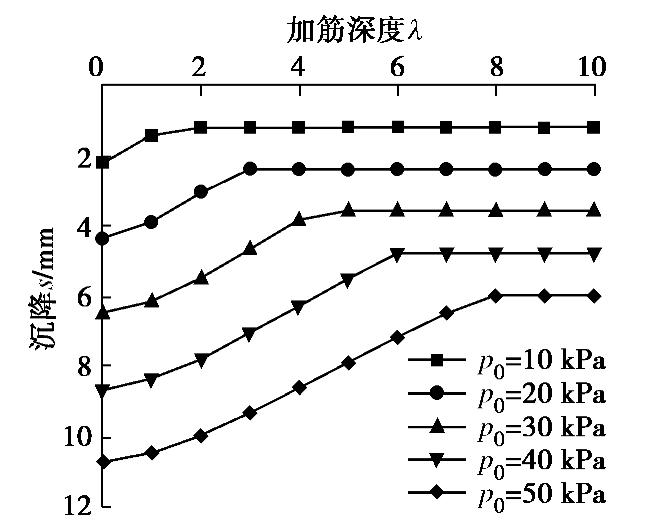
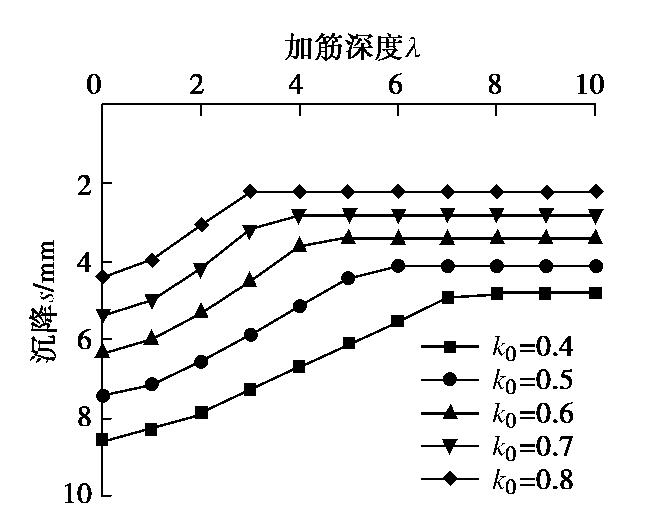
图8为不同p₀情况下,筋箍碎石桩桩顶沉降随加筋深度的变化曲线。计算中取J=30 kN/m,n₀=10,其他计算参数同2.1节。从图中可以看出,在曲线的前半段,随着加筋深度的增大,筋箍碎石桩沉降逐渐变小；当加筋深度达到某个值m₁时（此算例中,p₀=30 kPa时,4<m₁≤5）,桩体在该加筋深度下产生的沉降与全长加筋时产生的沉降相等,继续增大加筋深度并不会影响筋箍碎石桩的沉降。

图 8 不同p₀下筋箍碎石桩加筋深度与沉降关系曲线

Figure 8. Curves of relationship between encasement depth and settlement of GESC under differentp₀

下载: 全尺寸图片幻灯片

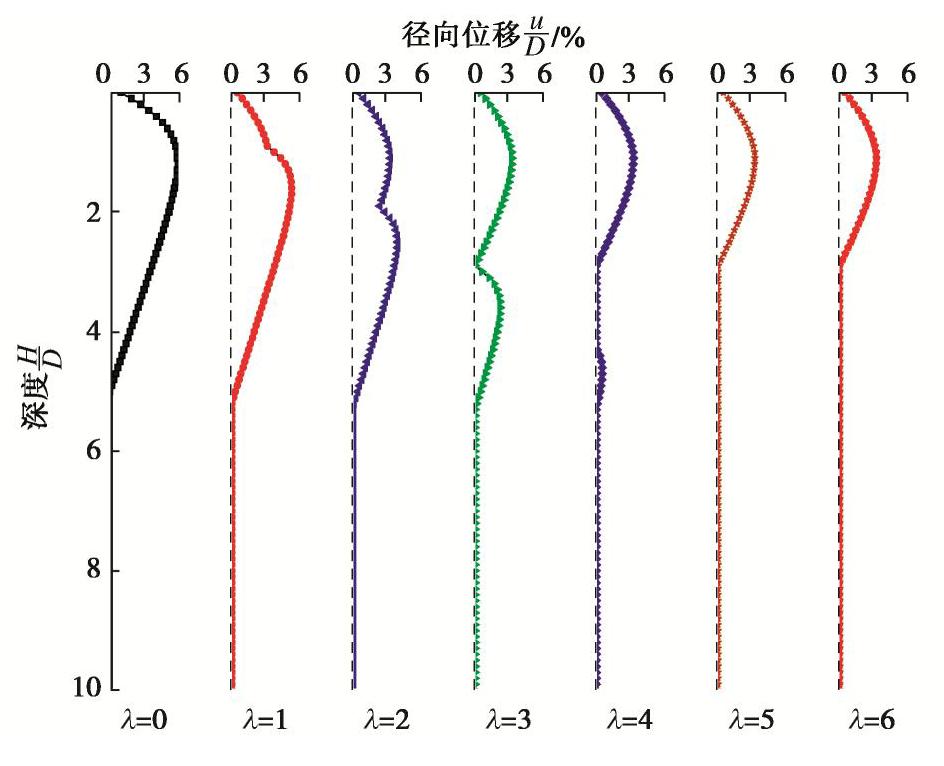
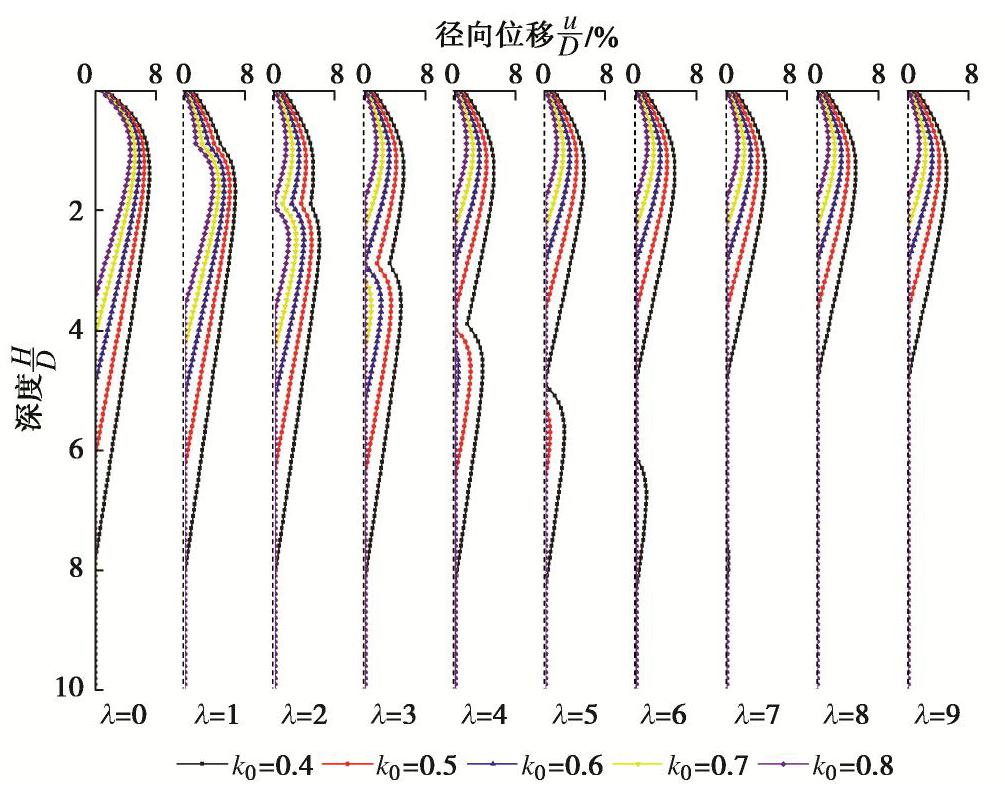
图9为p₀=30 kPa情况下,筋箍碎石桩径向变形随加筋深度的变化曲线。由图可见,随着加筋深度的增大,鼓胀曲线逐渐由“单峰”型曲线变为“双峰”型曲线,最后又变为“单峰”型曲线。同时,加筋段逐渐显现出半长加筋时的鼓胀曲线,非加筋段的径向变形则逐渐变小。当加筋深度较小时（即 $λ$ 为1,2）,桩体最大鼓胀点位于非加筋段；当加筋深度较大时（即 $λ$ 为3,4,5,6）,最大鼓胀点位于加筋段,其所在深度约为1.2D。当加筋深度达到某个值m₂时（此算例中,m₂>4；m₂=m,m₁≤5）,桩体在该加筋深度下产生的径向鼓胀变形与全长加筋时所产生的径向鼓胀变形相等,继续增大加筋深度并不会引起径向变形曲线的改变。

图 9 不同加筋深度下筋箍碎石桩径向变形曲线

Figure 9. Curves of radial deformation of GESC under different encasement depths

下载: 全尺寸图片幻灯片

结合图8,9分析可见,筋箍碎石桩存在一最优加筋深度m₀（m₀=m₁=m₂）,在该加筋深度下,筋箍碎石桩受力变形（包括桩顶沉降与径向变形）与全长加筋时相同,即当加筋深度达到m₀时,继续增大加筋深度并不会引起桩体沉降及径向变形曲线的改变。

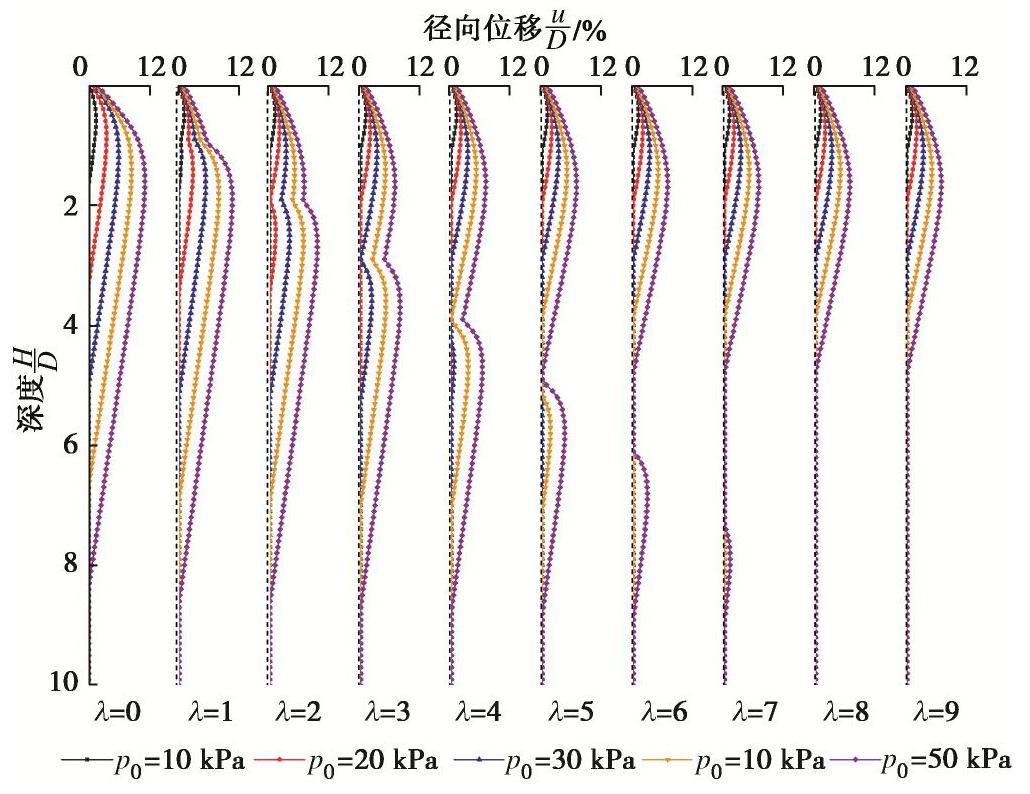
图10为不同p₀情况下,筋箍碎石桩径向变形随加筋深度的变化曲线。结合图8,10可见,荷载对筋箍碎石桩的最优加筋深度存在较大影响,当p₀=10 kPa时,最优加筋深度在（1～2）D；当p₀=50 kPa时,最优加筋深度介于（7～8）D。随着荷载的增大,所需的最优加筋深度也就越大。当荷载足够大时,需采取全长加筋模式,以有效限制桩身的径向变形。

图 10 不同p₀下筋箍碎石桩径向变形与加筋深度关系曲线

Figure 10. Curves of relationship between radial deformation and encasement depth of GESC under differentp₀

下载: 全尺寸图片幻灯片

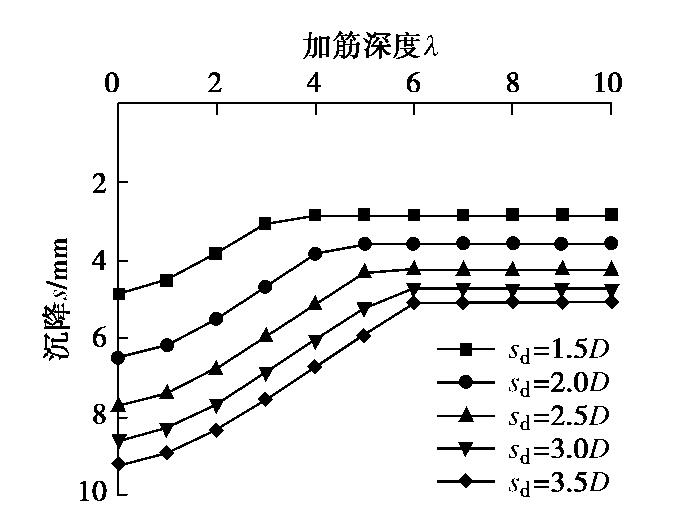
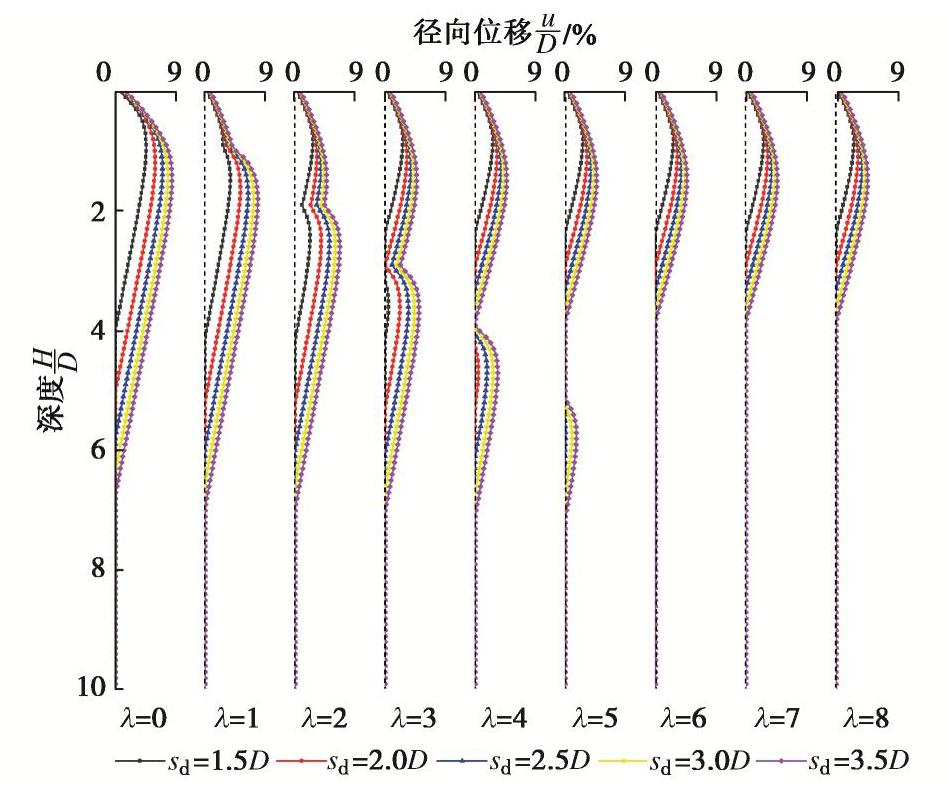
图11,12为不同桩间距s_d情况下,筋箍碎石桩桩顶沉降及桩身径向变形随加筋深度的变化曲线。由图可见,随s_d的增大,桩顶沉降及桩身径向变形随之增大,所需的最优加筋深度亦逐渐变大。当桩间距s_d=1.5D时,所需最优加筋深度约为（3～4）D；当桩间距s_d=3.5D时,所需最优加筋深度约为（6～7）D。此外,由图亦可见,桩间距的增加对最优加筋深度的影响逐渐减弱,最优加筋深度增大的同时逐渐趋于稳定。

图 11 不同s_d下筋箍碎石桩加筋深度与沉降关系曲线

Figure 11. Curves of relationship between encasement depth and settlement of GESC under differents_d

下载: 全尺寸图片幻灯片

图 12 不同s_d下筋箍碎石桩径向变形与加筋深度关系曲线

Figure 12. Curves of relationship between radial deformation and encasement depth of GESC under differents_d

下载: 全尺寸图片幻灯片

图13,14为不同侧压力系数K₀情况下,筋箍碎石桩桩顶沉降及桩身径向变形随加筋深度的变化曲线。由图显见,当侧压力系数K₀逐渐增大时,桩体沉降和径向变形逐渐减小,所需最优加筋深度随之减小。当K₀=0.8时,最优加筋深度为（2～3）D；当K₀=0.4时,最优加筋深度为（7～8）D。因此为减小碎石桩的变形,当地基土体越软弱时,所需加筋深度也越大。

图 13 不同K₀下筋箍碎石桩加筋深度与沉降关系曲线

Figure 13. Curves of relationship between encasement depth and settlement of GESC under differentK₀

下载: 全尺寸图片幻灯片

图 14 不同K₀下筋箍碎石桩径向变形与加筋深度关系曲线

Figure 14. Curves of relationship between radial deformation and encasement depth of GESC under differentK₀

下载: 全尺寸图片幻灯片

由上述分析可知,筋箍碎石桩最优加筋深度与荷载、桩间距及侧压力系数等一系列因素有关,不同参数取值情况下的最优加筋深度可能存在较大差异,因此不能武断地得出统一的结论,实际工程中需要根据具体情况计算得到该值。

3.3 桩土应力比的影响

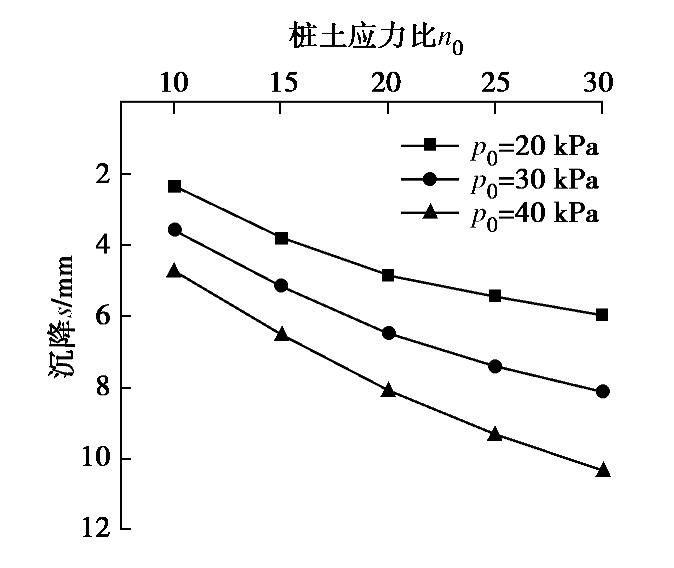
图15为不同复合地基荷载p₀情况下,筋箍碎石桩桩顶沉降随桩土应力比的变化曲线。分析中采用全长加筋模式,筋材抗拉强度取J=30 kN/m,其他计算参数同2.1节。由图15可见,随着桩土应力比的增大,筋箍碎石桩沉降逐渐变大,同时荷载的变化对沉降的影响逐渐加大；而曲线斜率趋于减小,这是因为本文的桩顶分担荷载p_c与桩间土分担荷载p_s由式（40）计算得到,当p₀不变时,p_c,p_s关于n₀的一阶导数p_c′,p_s′分别为：p_c′=(1-m)p₀/(1-m+n₀m)²,p_s′=-mp₀/(1-m+n₀m)²,其中复合地基置换率m满足：0<m<1,当n₀增大时,p_c′,p_s′的绝对值减小,因此p_c,p_s的变化逐渐减缓,从而导致沉降的增长速率减小。

图 15 筋箍碎石桩桩土应力比与沉降关系曲线

Figure 15. Curves of relationship between pile-soil stress ratio and settlement of GESC

下载: 全尺寸图片幻灯片

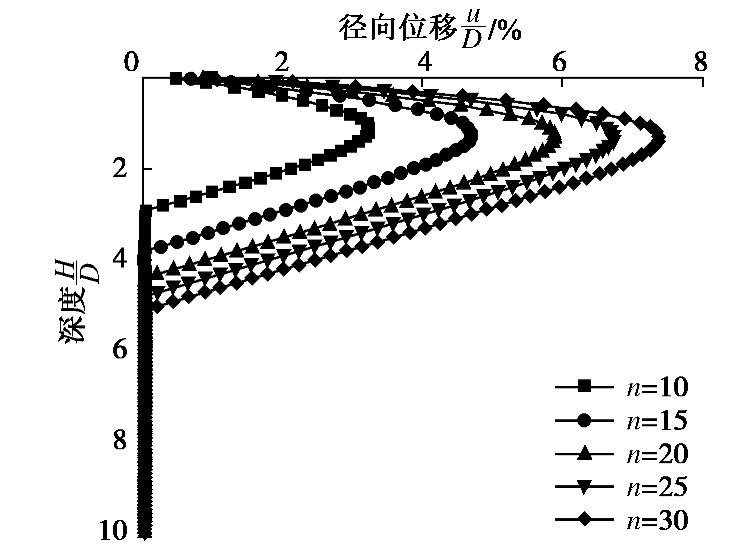
图16为p₀=30 kPa情况下,筋箍碎石桩径向变形随桩土应力比的变化曲线。由图可见,随着桩土应力比的增大,筋箍碎石桩鼓胀量及鼓胀深度逐渐变大,其原因是桩土应力比越大,越多的荷载向桩顶集中,桩上分担的荷载增大,故而导致桩体鼓胀变形加大。但由于桩土应力比逐渐增大时,p_c,p_s的变化逐渐减缓,因此径向变形的增长率不断减小。

图 16 不同桩土应力比下筋箍碎石桩径向变形曲线

Figure 16. Curves of radial deformation of GESC under different pile-soil stress ratios

下载: 全尺寸图片幻灯片

4. 结论

（1）本文首次将辛体系引入到筋箍碎石桩复合地基受力变形分析中。通过将弹性力学空间轴对称问题的偏微分方程导入辛体系,并运用变量分离、本征展开等方法,得到了筋箍碎石桩沉降及径向变形的辛体系解答。通过辛体系的运用,有效求解了偏微分方程,克服了以往拉格朗日体系解法的不足。

（2）将筋箍碎石桩单桩的受力变形视为空间轴对称问题,弥补了圆孔扩张理论平面应变假设的不足,同时微分方程中考虑了桩体横截面上的剪应力,且未对该剪应力分布模式做任何假定,更符合桩体的实际受力变形情况。

（3）参数分析表明提高筋材抗拉刚度、增大加筋深度（不超过最优加筋深度）、降低桩土应力比均有利于减小桩体沉降及径向变形。同时最优加筋深度并非定值,该值与荷载、桩间距正相关,而与侧压力系数负相关,实际工程中需要根据具体情况计算得到该值。

（4）本文在推导及计算的过程中,将桩土应力比视为已知参数,而实际工程中桩土应力比的确定往往比较困难,因此如何合理确定桩土应力比获得筋箍碎石桩沉降及径向变形的辛体系解答有待进一步研究。同时本文将桩体视为弹性体,因此对桩体非线性变形的分析也有待进一步深入。

图 1 单桩加固区计算模型

Figure 1. Computational model for a single GESC in reinforcement area

下载: 全尺寸图片幻灯片

图 2 碎石桩p₀-s曲线

Figure 2. p₀-s curves of stone columns

下载: 全尺寸图片幻灯片

图 3 碎石桩径向变形与深度关系曲线

Figure 3. Curves of relationship between radial deformation and depth of stone columns

下载: 全尺寸图片幻灯片

图 4 筋箍碎石桩p_c-s曲线

Figure 4. p_c-s curves of GESC

下载: 全尺寸图片幻灯片

图 5 筋箍碎石桩径向变形与深度关系曲线

Figure 5. Curves of relationship between radial deformation and depth of GESC

下载: 全尺寸图片幻灯片

图 6 筋材抗拉刚度与筋箍碎石桩沉降关系曲线

Figure 6. Curves of relationship between encasement stiffness and settlement of GESC

下载: 全尺寸图片幻灯片

图 7 不同筋材抗拉刚度下筋箍碎石桩径向变形曲线

Figure 7. Curves of radial deformation of GESC under different encasement stiffnesses

下载: 全尺寸图片幻灯片

图 8 不同p₀下筋箍碎石桩加筋深度与沉降关系曲线

Figure 8. Curves of relationship between encasement depth and settlement of GESC under differentp₀

下载: 全尺寸图片幻灯片

图 9 不同加筋深度下筋箍碎石桩径向变形曲线

Figure 9. Curves of radial deformation of GESC under different encasement depths

下载: 全尺寸图片幻灯片

图 10 不同p₀下筋箍碎石桩径向变形与加筋深度关系曲线

Figure 10. Curves of relationship between radial deformation and encasement depth of GESC under differentp₀

下载: 全尺寸图片幻灯片

图 11 不同s_d下筋箍碎石桩加筋深度与沉降关系曲线

Figure 11. Curves of relationship between encasement depth and settlement of GESC under differents_d

下载: 全尺寸图片幻灯片

图 12 不同s_d下筋箍碎石桩径向变形与加筋深度关系曲线

Figure 12. Curves of relationship between radial deformation and encasement depth of GESC under differents_d

下载: 全尺寸图片幻灯片

图 13 不同K₀下筋箍碎石桩加筋深度与沉降关系曲线

Figure 13. Curves of relationship between encasement depth and settlement of GESC under differentK₀

下载: 全尺寸图片幻灯片

图 14 不同K₀下筋箍碎石桩径向变形与加筋深度关系曲线

Figure 14. Curves of relationship between radial deformation and encasement depth of GESC under differentK₀

下载: 全尺寸图片幻灯片

图 15 筋箍碎石桩桩土应力比与沉降关系曲线

Figure 15. Curves of relationship between pile-soil stress ratio and settlement of GESC

下载: 全尺寸图片幻灯片

图 16 不同桩土应力比下筋箍碎石桩径向变形曲线

Figure 16. Curves of radial deformation of GESC under different pile-soil stress ratios

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	VAN IMPE W F. Soil improvement techniques and their evolution[J]. Animal Science Papers. Sd Reports, DOI: http://dx.doi.org/1989.
[2]	赵明华, 何玮茜, 衡帅, 等. 基于圆孔扩张理论的筋箍碎石桩承载力计算方法研究[J]. 岩土工程学报, 2017, 39(10): 1785-1792. doi: 10.11779/CJGE201710005 ZHAO Ming-hua, HE Wei-xi, HENG Shuai, et al. Calculation method of geogrid-encased stone columns' bearing capacity based on cavity expansion theory[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1785-1792. (in Chinese) doi: 10.11779/CJGE201710005
[3]	RAITHEL M, KEMPFERT H G. Calculation models for dam foundations with geosynthetic coated sand columns[C]//Geotechnical and Geological Engineering, 2000, Lisbon.
[4]	DUAN Y Y, ZHANG Y P, CHAN D, et al. Theoretical elastoplastic analysis for foundations with geosynthetic-encased columns[J]. Journal of Zhejiang University SCIENCE A, 2012, 13(7): 506-518. doi: 10.1631/jzus.A1100334
[5]	ZHANG L, ZHAO M. Deformation analysis of geotextile-encased stone columns[J]. International Journal of Geomechanics, 2015, 15(3): 1-10.
[6]	KONG G Q, ZHOU Y, LIU H L. Nonlinear model analysis of radial bulging deformation of geosynthetic-encased stone columns[J]. International Journal of Geomechanics, 2018, 18(10): 1-12.
[7]	PULKO B, MAJES B, LOGAR J. Geosynthetic-encased stone columns: analytical calculation model[J]. Geotextiles and Geomembranes, 2011, 29(1): 29-39. doi: 10.1016/j.geotexmem.2010.06.005
[8]	ZHOU Y, KONG G Q. Deformation analysis of a geosynthetic-encased stone column and surrounding soil using cavity-expansion model[J]. International Journal of Geomechanics, 2019, 19(5): 1-12.
[9]	赵明华, 牛浩懿, 刘猛, 等. 柔性基础下碎石桩复合地基桩土应力比及沉降计算[J]. 岩土工程学报, 2017, 39(9): 1549-1556. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201709002.htm ZHAO Ming-hua, NIU Hao-yi, LIU Meng, et al. Pile-soil stress ratio and settlement of composite ground with gravel piles in flexible foundation[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(9): 1549-1556. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201709002.htm
[10]	钟万勰. 弹性力学求解新体系[M]. 大连: 大连理工大学出版社, 1995. ZHONG Wan-xie. A New Systematic Methodology for Theory of Elasticity[M]. Dalian: Dalian University of Technology Press, 1995. (in Chinese)
[11]	徐芝纶. 弹性力学(上册)[M]. 北京: 高等教育出版社, 2006. XU Zhi-lun. Elastic Mechanics (I)[M]. Beijing: Higher Education Press, 2006. (in Chinese)
[12]	ZHANG W X, CUI W H, XAIO Z R, et al. The quasi-static analysis for the viscoelastic hollow circular cylinder using the symplectic system method[J]. International Journal of Engineering Science, 2010, 48: 727-741. doi: 10.1016/j.ijengsci.2010.03.003
[13]	弗洛林 В А. 土力学原理(第一卷)[M]. 徐志英,译.北京: 中国建筑工业出版社, 1973: 87-88. ФЛОРИНB A. Fundamentals of Soil Mechanics (First volume)[M]. XU Zhi-ying, trans. Beijing: China Architecture and Building Press, 1973: 87-88. (in Chinese)
[14]	MALARVIZHI , ILAMPARUTHI . Comparative study on the behavior of encased stone column and conventional stone column[J]. Soils and Foundations, 2007, 47(5): 873-885.
[15]	YOO C, LEE D. Performance of geogrid-encased stone columns in soft ground: Full-scale load tests[J]. Geosynthetics International, 2012, 19(6): 480-490. doi: 10.1680/gein.12.00033
[16]	龚晓南. 复合地基设计和施工指南[M]. 北京: 人民交通出版社, 2003: 109-110. GONG Xiao-nan. Composite Foundation Design and Construction Guideline[M]. Beijing: People's Transportation Press, 2003: 109-110. (in Chinese)
[17]	WU C S, HONG Y S. The behavior of a laminated reinforced granular column[J]. Geotextiles and Geomembranes, 2008, 26(4): 302-316. doi: 10.1016/j.geotexmem.2007.12.003
[18]	赵明华. 土力学与基础工程[M]. 第4版. 武汉: 武汉理工大学出版社, 2014. ZHAO Ming-hua. Soil Mechanics and Foundation Engineering[M]. 4th ed. Wuhan: Wuhan University of Technology Press, 2014. (in Chinese)
[19]	ZHANG L, ZHAO M, SHI C, et al. Settlement calculation of composite foundation reinforced with stone columns[J]. International Journal of Geomechanics, 2012, 13(3): 248-256.
[20]	《工程地质手册》编委会. 工程地质手册[M]. 第5版. 北京: 中国建筑工业出版社, 2018: 176-177. Editorial board of Geological Engineering Handbook. Geological Engineering Handbook[M]. 5th ed. Beijing: China Architecture and Building Press, 2018: 176-177. (in Chinese)

施引文献(13)

期刊类型引用(6)

1.	龙军，彭搏程. 基于桩周土围限失效的筋箍料粒桩复合地基承载力计算. 公路工程. 2025(01): 138-143 . 百度学术
2.	李传勋，刘聪. 基于割线模量的散体材料桩复合地基沉降计算. 江苏大学学报(自然科学版). 2024(04): 482-489 . 百度学术
3.	张石平，陈曦菲，姚绍伟，邓晨. 竖向地震作用下饱和土-桩体系的耦合动力响应研究. 工程力学. 2023(09): 81-97 . 百度学术
4.	张玲，刘长捷，赵明华，欧强. 筋箍碎石桩复合体抗剪性能研究. 土木工程学报. 2022(05): 86-96 . 百度学术
5.	陈华裕. 大型储罐振冲碎石桩地基设计及有限元分析. 中国新技术新产品. 2022(14): 122-124 . 百度学术
6.	袁涌筌，赵明华，杨超炜，肖尧. 循环荷载下筋箍碎石桩复合地基动力特性数值分析. 湖南大学学报(自然科学版). 2022(11): 198-205 . 百度学术