三维非饱和土边坡拟动力稳定性分析初探

王龙; 陈国兴; 胡伟; 孙德安; 李洁; 刘文化

doi:10.11779/CJGE20220765

三维非饱和土边坡拟动力稳定性分析初探 English Version

王龙^{1, 2, 3,},
陈国兴²,
胡伟^3, ,,
孙德安⁴,
李洁⁵,
刘文化¹

1.
江南大学环境与土木工程学院, 江苏无锡 214122
2.
南京工业大学岩土工程研究所, 江苏南京 210009
3.
成都理工大学地质灾害防治与地质环境保护国家重点实验室, 四川成都 610059
4.
上海大学力学与工程科学学院, 上海 200444
5.
澳大利亚皇家墨尔本理工大学工学院, 墨尔本 3001

基金项目:

国家自然科学基金项目 52208345

国家自然科学基金项目 52008124

国家自然科学基金项目 52268054

地质灾害防治与地质环境保护国家重点实验室开放基金项目 SKLGP2022K002

江苏省自然科学基金项目 BK20210479

详细信息

作者简介:
王龙(1989—)，男，博士（后），讲师，主要从事岩土力学教学与科研工作。E-mail: longwang@jiangnan.edu.cn

通讯作者:
胡伟, Email: huwei1999@126.com

中图分类号: TU431
计量
- 文章访问数: 585
- HTML全文浏览量: 65
- PDF下载量: 208
出版历程
- 收稿日期: 2022-06-15
- 网络出版日期: 2023-03-09
- 刊出日期: 2023-08-31

Three-dimensional seismic stability of unsaturated soil slopes using pseudo-dynamic approach

WANG Long^{1, 2, 3,},
CHEN Guoxing²,
HU Wei^3, ,,
SUN Dean⁴,
LI Jie⁵,
LIU Wenhua¹

1.
School of Environment and Civil Engineering, Jiangnan University, Wuxi 214122, China
2.
Institute of Geotechnical Engineering, Nanjing Tech University, Nanjing 211816, China
3.
State Key Laboratory of Geohazard Prevention and Geoenvironmental Protection, Chengdu University of Technology, Chengdu 610059, China
4.
School of Mechanics and Engineering Science, Shanghai University, Shanghai 200444, China
5.
School of Engineering, RMIT University, Melbourne 3001, Australia

摘要

摘要: 边坡在地震作用下极易失稳破坏且通常伴随明显的三维破坏特征，增加边坡阶数并结合抗滑桩等加固措施可有效提高边坡的动稳定性，广泛用于滑坡灾害防治中。基于极限分析上限原理并结合拟动力法，将塑性变形理论扩展至非饱和土中，改进已提出的半解析水平片分法，计算具有非线性分布特征的非饱和土重力、地震惯性力和抗滑桩侧阻力所做外功率和表观黏聚力的功率耗散率，与解析解对比，验证了该方法的合理性。通过算例分析，探究了非饱和土边坡的地震响应规律，揭示了吸力对边坡地震稳定性及抗滑桩加固效果的强化作用。结果表明：吸力对边坡稳定性的贡献可达15%~30%，且与地震动特性密切相关，地震波达到峰值时，吸力效应得到显著加强；水平加速度系数和土体剪切模量对边坡地震稳定性影响较大；地震作用下边坡将出现明显的“浅层”滑动现象。
- 非饱和土边坡 /
- 极限分析 /
- 拟动力法 /
- 基质吸力 /
- 三维效应
Abstract: The seismic excitation remains the main factor in triggering the slope failures that present three-dimensional (3D) features universally. The slopes combined with anti-slide piles are the effective reinforcement techniques in improving the slope stability and are widely employed in slope failure preventions. Based on the upper bound limit analysis theorem and the pseudo-dynamic approach, the plasticity deformation theory is extended to unsaturated soils, and a modified horizontal slice method is proposed to calculate the work rates of unsaturated soil gravity, seismic inertial forces and pile lateral resistance forces as well as the energy dissipation rate of apparent cohesion that are all characterized with nonlinear distribution features. The semi-analytical method is validated through comparisons with the analytical solutions. A series of parametric analyses are conducted regarding the seismic responses of unsaturated soil slopes. The improvements in seismic slope stability due to soil suction are studied systematically. The results show that the slope safety is underestimated by 15% ~ 30% when the soil suction is not considered in the analyses. The suction effects depend on the seismic excitations and are enhanced significantly when the seismic wave approaches the peak. The horizontal acceleration coefficient and soil shear modulus both have a great influence on the slope stability. The critical slip surface becomes much shallower under excitation conditions.
- unsaturated soil slope /
- limit analysis /
- pseudo-dynamic approach /
- matric suction /
- 3D effect

HTML全文

0. 引言

中国是一个地震频发国家，地震带发育充分且分布较为广泛，因地震死亡的人数约占全球1/2。滑坡灾害是地震引发的主要次生灾害之一，地震作用下边坡的稳定性问题是岩土工程界和地震工程界关注的重要课题^[1-2]。地震荷载描述方法的合理性是进行边坡地震响应研究的基础，目前常用的地震波描述方法主要有时程曲线法^[3]、拟静力法^[4]和拟动力法^[5-6]3种。地震加速度时程曲线能够真实的描述地震动整个过程中各个方向的地震加速度，通常与计算机仿真技术结合用于实际边坡的地震响应研究。拟动力法克服了拟静力法不能反映地震动时程特性的缺点，常与理论方法结合，用于典型边坡的地震稳定性评价^[7-8]。目前的边坡稳定性分析通常基于边坡土体处于饱和状态的假定而展开，而实际上的边坡土体往往具有显著的非饱和特性。

饱和土与非饱和土的物理和力学性质存在显著的差异^[9-13]。借助土-水特征曲线（SWCC）^[9]，目前国内外学者已提出多种直接或间接预测非饱和土强度的方法。这些方法均将基质吸力引起的强度增加与土中含水率联系以反映非饱和土的强度特性，可归纳为单一变量有效应力（Bishop有效应力）^[12]和Fredlund双参数理论^[13]两大类。非饱和土力学理论的不断完善和发展为边坡稳定性评价提供了现实的理论指导和依据，基于上述非饱和土强度理论，国内外学者针对非饱和土边坡的稳定性问题开展了大量的研究工作，取得了丰硕的研究成果^[14-16]。

统计资料表明^[17]，边坡的失稳破坏通常伴随明显的三维空间特征，边坡横向宽度限制对其稳定性有显著的影响，因此采用三维方法更加符合实际情况，越来越多的工程问题也需要进行三维稳定性评价。极限分析法由于具有力学机制清晰和计算简便的特点，常用于典型边坡的稳定性评价，将极限分析法用于边坡三维稳定性分析的首要困难在于构建满足三维条件下连续体几何相容条件和运动许可条件的速度场。Giger等^[18]、Drescher^[19]、Michalowski等^[20]和Park等^[21]学者相继做出了开拓性的研究工作，提出多种满足运动许可条件的三维滑动机构。后续学者在此基础上开展了大量的研究工作，取得了许多有价值的研究成果。最近，Yang等^[22]基于拟静力法对抗滑桩加固边坡的三维稳定性问题开展了相关研究工作，探讨了抗滑桩桩位、水平地震系数和边坡宽度等因素的影响机制。但上述研究均忽略了基质吸力和地震动特性的影响，由于土中吸力的复杂性，目前三维边坡地震稳定性评价中，关于吸力效应和抗滑桩加固效应的综合研究还相对较少。

本文基于极限分析上限原理和拟动力法研究了抗滑桩加固非饱和土边坡的地震稳定性。将塑性变形理论扩展至非饱和土中来考虑基质吸力对桩侧阻力的提升作用，提出一种改进水平片分法，可有效考虑土中水分含量变化对边坡稳定性的影响，揭示边坡的地震响应规律。通过分析典型边坡的地震稳定性，揭示了吸力效应、三维效应和地震作用对边坡稳定性和临界滑动面的影响规律。

1. 基本原理和计算模型

1.1 极限分析上限法

塑性极限分析根据上限和下限定理求解岩土结构真实极限荷载的上下限^[23]，通过建立合理的运动许可速度场和静力容许应力场，便可将真实极限荷载限定在较小的范围内。根据极限分析上限定理和虚功率方程，可求解真实荷载的上限，假定土体为理想刚塑性材料并遵循莫尔-库仑屈服准则以及相关联流动法则，虚功率方程可表述为

$\int_A {{T_i}} {v_i}\text{d}A + \int_V {{F_i}} {v_i}\text{d}V = \int_V {{\sigma _{ij}}} {\dot \varepsilon _{ij}}\text{d}V \ \ \ \ 。$

(1)

式中：A和V为滑坡体表面积和体积；T_i与F_i为滑坡体所受面力和体力； ${\sigma _{ij}}$ 为与面力T_i和体力F_i相对应的应力场； ${\dot \varepsilon _{ij}}$ 为与速度场v_i相协调的应变率场。

1.2 三维破坏机构

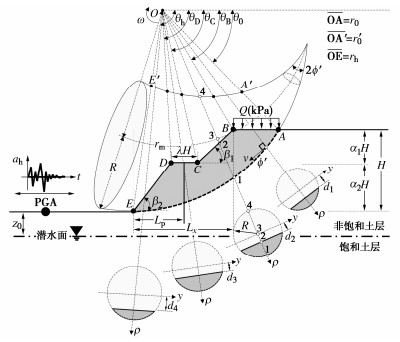
摩擦性土的塑性体积变形必然伴随着其体积膨胀，因此构建三维条件下的运动许可滑动机构变得较为困难。而对于刚性体，构建运动许可的三维滑动机构则相对简单，满足相关联流动法则的三维连续变形场表面必然局部相切于一个角为2ϕ'（ϕ'为土的内摩擦角）的夹角。在各种三维滑动机构中，Michalowski等^[20]构建了一种截面为圆形的牛角状滑动机构，如图 1所示。该机构对称面的上下界分别为逆时针和顺时针旋转的对数螺旋线，以对称面上下界中线r_m为旋转路径，差值为直径，绕旋转轴O旋转便可得到该机构。

图 1 非饱和土边坡地震稳定性计算简图

Figure 1. Diagram of an unsaturated soil slope subjected to seismic excitations

下载: 全尺寸图片幻灯片

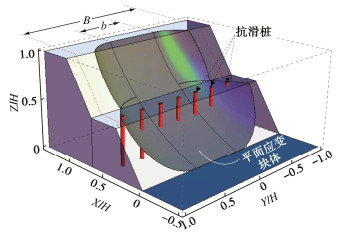
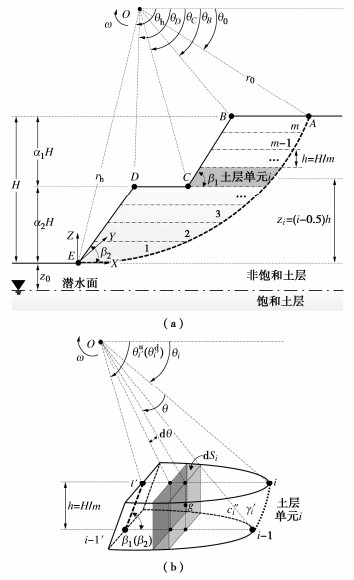
实际工程中的边坡失稳破坏现象以坡趾失稳模式为主，滑动面穿过坡趾并交于坡顶。抗滑桩加固均质非饱和土边坡模型如图 1所示，滑坡体处于理想弹塑性状态，边坡高为H，上下阶坡面倾角分别为β₁和β₂，相对高度分别为α₁H和α₂H（α₁ + α₂ = 1），工作平台宽度为λH，潜水面位于坡趾下方且呈水平分布，滑动面初始和结束极角分别为θ₀和θ_h。抗滑桩垂直插入滑坡体并深入滑动面以下土体中，距坡趾水平距离为L_p。

为了便于比较二维和三维分析方法对边坡稳定性评估结果的影响，评估边坡三维效应的影响规律，对该三维滑动机构作进一步改进^[20]，将其沿对称面剖开并插入与对称面一致宽度为b的平面应变块体，形成复合三维滑动机构，如图 2所示。

图 2 插入平面应变块构成复合三维滑动机构示意图

Figure 2. Diagram of combined 3D mechanism with a plane-strain insert

下载: 全尺寸图片幻灯片

1.3 非饱和土性质

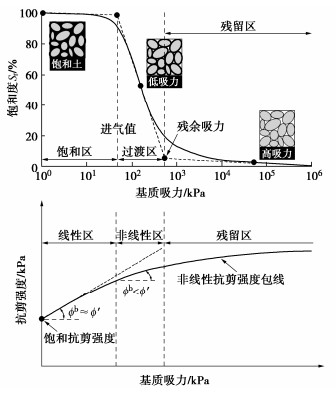
三轴和直剪试验结果表明非饱和土的抗剪强度不仅随净法向应力的增加而增加，也随基质吸力的增加而增加^[12-13]。因此将滑坡体假定为饱和状态对边坡稳定性进行分析稍显保守，边坡安全储备虽得到提高，但经济性也随之降低。典型非饱和土边坡的稳定性评价中，基质吸力对土抗剪强度的贡献通常基于修正Mohr-Coulomb破坏准则将其视为黏聚力来实现^[10-16]，非饱和土毛细黏聚力可表示为^[9]

${c_{{\text{cap}}}} = \psi \left[ {\left( {\frac{{{\theta _{\text{w}}} - {\theta _{\text{r}}}}}{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}}} \right)\tan \phi '} \right] \ \ \ \ 。$

(2)

式中：ψ为基质吸力；θ_w为体积含水量；θ_r和θ_s分别为残余和饱和土体积含水量。饱和土体积含水量可根据饱和单位重度和干重度得到，即θ_s = ( ${\gamma _{{\text{sat}}}}$ - ${\gamma _{\text{d}}}$ )/ ${\gamma _{{\text{sat}}}}$ 。

SWCC表征了非饱和土基质吸力与含水率间的关系，如图 3所示，是研究非饱和土抗剪强度和渗透系数等性质的重要工具。目前对SWCC进行预测和拟合的数学模型较多，其中Fredlund-Xing模型^[10]具有适用吸力范围广和拟合参数物理意义明确等优点，能较好的拟合大部分土的SWCC。基于该模型，非饱和土体积含水量可表示为

图 3 土-水特征曲线和非饱和土抗剪强度包线关系图

Figure 3. Relationship between SWCC and strength of unsaturated soils

下载: 全尺寸图片幻灯片

$\theta_{\mathrm{w}}=\left\{1-\frac{\ln \left(1+\psi / \psi_{\mathrm{r}}\right)}{\ln \left(1+10^6 / \psi_{\mathrm{r}}\right)}\right\} \frac{\theta_{\mathrm{s}}}{\left\{\ln \left[\mathrm{e}+\left(\psi / a_{\mathrm{f}}\right)^{n_{\mathrm{f}}}\right]\right\}^{m_{\mathrm{f}}}} 。$

(3)

式中：ψ_r为残余含水量状态对应的基质吸力；a_f为SWCC拐点对应的基质吸力，可采用图解法测得；m_f和n_f为模型拟合参数。

近地表土层中的基质吸力分布易受环境影响，而较深土层中的基质吸力分布相对稳定，一般不随时间变化。对于多阶多级高大边坡，采用稳态渗流假定可得到较为合理的结果。稳态渗流条件下基质吸力的解析表达式为^[11]

$\psi = - \frac{1}{\alpha }\ln \left[ {(1 + {q \mathord{\left/ {\vphantom {q {{k_{\text{s}}})}}} \right. } {{k_{\text{s}}})}}{{\text{e}}^{ - \alpha {\gamma _{\text{w}}}(z + {z_0})}} - {q \mathord{\left/ {\vphantom {q {{k_{\text{s}}}}}} \right. } {{k_{\text{s}}}}}} \right] \ \ \ \ 。$

(4)

式中：q/k_s为竖向比流量； ${\gamma _{\text{w}}}$ 为水单位重度；α可近似视为进气值的倒数；z为土中某点至坡脚的垂直距离；z₀为潜水面深度。

非饱和土的单位重度可根据土的干重度得到

$\gamma ' = {\gamma _d} + {\theta _w}{\gamma _w} \ \ \ \ 。$

(5)

1.4 拟动力法

拟动力法因具有可以考虑地震动持时、周期和放大效应等优点，被广泛用于支挡结构边坡的地震稳定性评价中。研究表明，正弦波可较好地反映地震动上述特性，揭示岩土支挡结构的地震动响应规律^[5-6]。基于拟动力法，水平和竖向地震加速度可表示为^[5-6]

${a}_{\text{h}}({z}_{\text{s}},t)={k}_{\text{h}}g\left[1+({f}_{\text{a}}-1)\frac{(H-{z}_{\text{s}})}{H}\right]\mathrm{sin}\left[{\omega }_{\text{s}}\left(t-\frac{H-{z}_{\text{s}}}{{V}_{\text{s}}}\right)\right] \ \ \ \ \ \text{，}$

(6)

${a}_{\text{v}}({z}_{\text{s}},t)={k}_{\text{v}}g\left[1+({f}_{\text{a}}-1)\frac{(H-{z}_{\text{s}})}{H}\right]\mathrm{sin}\left[{\omega }_{\mathrm{s}}\left(t-\frac{H-{z}_{\text{s}}}{{V}_{\text{p}}}\right)\right]\ \ \ \ 。$

(7)

式中：V_s和V_p分别为剪切和压缩波速；k_h和k_v分别为水平和竖向地震加速度系数；f_a为放大系数；z_s为至坡顶的垂直距离；t为时间；g为重力加速度；ω_s为地震波角速度（ω_s = 2π/T，T为地震波周期）。

土中剪切和压缩波速可根据土的剪切模量、密度和泊松比采用经验公式估算，对于非饱和土，土单位重度沿土层深度呈非线性分布，因此土中剪切和压缩波速沿土层深度呈非线性增大：

${V_{\text{s}}} = \sqrt {\frac{G}{{{\gamma _\text{d}} + {\theta _\text{w} }{\gamma _\text{w}}}}} \ \ \ \ \ \text{，}$

(8)

${V_{\text{p}}} = \sqrt {\frac{{G(2 - 2\nu )}}{{({\gamma _\text{d}} + {\theta _\text{w}}{\gamma _\text{w}})(1 - 2\nu )}}} \ \ \ \ 。$

(9)

阻尼是描述岩土结构动态响应的重要因素，对于小阻尼水平，瑞利阻尼提供一个较为合理的近似，通常假定为质量和刚度矩阵的线性函数：

$\left[ C \right] = {\alpha _0}\left[ M \right] + {\alpha _1}\left[ K \right] \ \ \ \ 。$

(10)

式中： ${\alpha _0}$ 和 ${\alpha _1}$ 阻尼系数，可根据阻尼比和固有振动频率间的关系来确定。本文假定质量矩阵和刚度矩阵对阻尼的贡献相同，且仅考虑质量矩阵的影响，阻尼比为5%，固有振动频率为1 Hz。

地震波水平和横向传播速度可通过对相应加速度积分得到

${v_{\text{h}}}({z_{\text{s}}},t) = \frac{{({f_{\text{a}}}H - {f_{\text{a}}}{z_{\text{s}}} + {z_{\text{s}}}){k_{\text{h}}}g}}{{H{\omega _\text{s} }}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \left\{ {\cos \frac{{{\omega _\text{s} }({z_{\text{s}}} - H)}}{{{V_{\text{s}}}}} - \cos \frac{{{\omega _\text{s} }\left[ {t{V_{\text{s}}} + ({z_{\text{s}}} - H)} \right]}}{{{V_{\text{s}}}}}} \right\} \ \ \ \ \ \text{，}$

(11)

${v_{\text{v}}}({z_{\text{s}}},t) = \frac{{({f_{\text{a}}}H - {f_{\text{a}}}{z_{\text{s}}} + {z_{\text{s}}}){k_{\text{v}}}g}}{{H{\omega _\text{s} }}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \left\{ {\cos \frac{{{\omega _\text{s} }({z_{\text{s}}} - H)}}{{{V_{\text{p}}}}} - \cos \frac{{{\omega _\text{s} }\left[ {t{V_{\text{s}}} + ({z_{\text{s}}} - H)} \right]}}{{{V_{\text{p}}}}}} \right\} \ \ \ \ 。$

(12)

2. 改进水平片分法

2.1 非饱和土重力所做外功率

由于基质吸力的时空变异性，非饱和土表观黏聚力、土单位重度、地震惯性力和抗滑桩侧阻力均表现出较强的非线性特点，因此求得边坡稳定性上限解析解变得尤为困难。为了构建滑坡体能量平衡方程，改进适用于单阶简单均质边坡的水平片分法^[16]，并将其应用于非饱和土边坡的稳定性评价中。将非饱和滑坡体水平离散为m个土层单元，如图 4所示，上下阶坡面对应的土层单元数分别为m₁（m₁ = m ${\alpha _1}$ ）和m₂（m₂ = m ${\alpha _2}$ ）。累加所有土层单元土体重力所做外功率，可得到滑坡体重力所做总功率：

图 4 改进水平片分法示意图

Figure 4. Diagram of modified horizontal slice method

下载: 全尺寸图片幻灯片

$\begin{array} \left W_\gamma^{\prime}=0.5 \omega h\left\{\sum_\limits { i = 1 } ^ { m _ { 2 } } \gamma _ { i } ^ { \prime } \left[\int_{\theta_i}^{\theta_i^*} \mathrm{~d} S_i l_{\mathrm{g}} \cos \theta_{\mathrm{g}} \mathrm{d} \theta+\right.\right. \\ \ \ \ \ \ \left.\int_{\theta_{i-1}}^{\theta_{i-1^{\prime}}^*} \mathrm{~d} S_{i-1} l_{\mathrm{g}} \cos \theta_{\mathrm{g}} \mathrm{d} \theta\right]+\sum\limits_{i=m_2+1}^m \gamma_i^{\prime}\left[\int_{\theta_i}^{\theta_{i^{\prime}}^{**}} \mathrm{~d} S_i l_{\mathrm{g}^{\prime \prime}} \cos \theta_{\mathrm{g}^{\prime \prime}} \mathrm{d} \theta+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.\left.\int_{\theta_{i-1}}^{\theta_{i-1^{\prime}}^{**}} \mathrm{~d} S_{i-1} l_{\mathrm{g}} \cos \theta_{\mathrm{g}} \mathrm{d} \theta\right]\right\} \end{array}$

(13)

式中：ω为角速度； ${\gamma '_i}$ 为土层单元形心处对应的土单位重度，可根据式（3）~（5）和土层单元形心至坡趾的垂距z_i求得；h为土层单元厚度；dS_i和dS_i-1分别为土层单元上下表面微元面积；l_g和θ_g分别为微元体（阴影部分）形心至旋转轴的极径和极角；角θ_i， $\theta _{i'}^*$ 和 $\theta _{i'}^{**}$ 分别为描述土层单元位置的极角。变量dS_i，dS_i-1，l_g，θ_g，θ_i， $\theta _{i'}^*$ 和 $\theta _{i'}^{**}$ 可根据几何和三角函数关系得到

${r_0}\exp \left[ {({\theta _i} - {\theta _{\text{0}}})\tan \phi '} \right]\sin {\theta _i} = {r_0}\sin {\theta _{\text{0}}} + H - ih \ \ \ \ \ \text{，}$

(14)

$l_{\mathrm{g}}=\sqrt{\begin{array}{l} \left\{r_0 \exp \left[\left(\theta_{i^{\prime}}-\theta_0\right) \tan \phi^{\prime}\right] \sin \theta_{i^{\prime}} \cot \theta\right\}^2+ \\ \left\{0.5 h+r_0 \exp \left[\left(\theta_{i^{\prime}}-\theta_0\right) \tan \phi^{\prime}\right] \sin \theta_{i^{\prime}}\right\}^2 \end{array}},$

(15)

${\theta }_{\mathrm{g}}=\text{arc}\mathrm{cos}\frac{{r}_{0}\mathrm{exp}\left[({\theta }_{{i}^{\prime }}-{\theta }_{0})\mathrm{tan}{\varphi }^{\prime }\right]\mathrm{sin}{\theta }_{{i}^{\prime }}\mathrm{cot}\theta }{\sqrt{\begin{array}{l}{\left\{{r}_{0}\mathrm{exp}\left[({\theta }_{{i}^{\prime }}-{\theta }_{0})\mathrm{tan}{\varphi }^{\prime }\right]\mathrm{sin}{\theta }_{{i}^{\prime }}\mathrm{cot}\theta \right\}}^{2}+\\ {\left\{{r}_{0}\mathrm{exp}\left[({\theta }_{{i}^{\prime }}-{\theta }_{0})\mathrm{tan}{\varphi }^{\prime }\right]\mathrm{sin}{\theta }_{{i}^{\prime }}+0.5h\right\}}^{2}\end{array}}} \ \ \ \ \ \text{，}$

(16)

$\theta _{i'}^* = \arctan \frac{{{r_0}\exp \left[ {({\theta _i} - {\theta _0})\tan \phi '} \right]\sin {\theta _i}}}{{{r_0}\exp \left[ {({\theta _i} - {\theta _0})\tan \phi '} \right]\cos {\theta _i} - L_{ii'}^*}} \ \ \ \ \ \text{，}$

(17)

$\theta _{i'}^{**} = \arctan \frac{{{r_0}\exp \left[ {({\theta _i} - {\theta _0})\tan \phi '} \right]\sin {\theta _i}}}{{{r_0}\exp \left[ {({\theta _i} - {\theta _0})\tan \phi '} \right]\cos {\theta _i} - L_{ii'}^{**}}} \ \ \ \ \ \text{，}$

(18)

$\text{d}{S_i} = \frac{{{r_0}\exp \left[ {({\theta _{i'}} - {\theta _0})\tan \phi '} \right]\sin {\theta _{i'}}}}{{{{\sin }^2}\theta }}\left( {b + 2\sqrt {{R^2} - a_i^{\text{2}}} } \right)\text{d}\theta \ \ \ \ 。$

(19)

式中：L_ii'^*和L_ii'^**分别为上下阶边坡中土层单元表面点i至i'的距离；a_i为对称面上圆形截面与土层单元交点至旋转路径的距离。L_ii'^*，L_ii'^**和a_i可分别表示为

$\begin{array}{r} L_{i i^{\prime}}^*=r_0 \exp \left[\left(\theta_i-\theta_0\right) \tan \phi^{\prime}\right] \cos \theta_i-r_{\mathrm{h}} \cos \theta_{\mathrm{h}}- \\ \quad\left[\left(i-m_2\right) h \cot \beta_1+\alpha_2 H \cot \beta_2+\lambda H\right], \end{array}$

(20)

$\begin{aligned} L_{i i^{\prime}}^*= & r_0 \exp \left[\left(\theta_i-\theta_0\right) \tan \phi^{\prime}\right] \cos \theta_i- \\ & r_{\mathrm{h}} \cos \theta_{\mathrm{h}}-i h \cot \beta_2, \end{aligned}$

(21)

${a_i} = \frac{{{r_0}\sin {\theta _0} + H - ih}}{{\sin \theta }} - {r_{\text{m}}} \ \ \ \ 。$

(22)

同样采用该方法，可累积得到地震惯性力所做总外功率。

2.2 表观黏聚力功率耗散率

表观黏聚力的功率耗散率包含机构端部三维部分和中部插入块体内的功率耗散。端部三维部分表观黏聚力的功率耗散率包含体积内的能量耗散和速度不连

续面上的能量耗散。对每个土层单元采用高斯散度定理，并累加所有土层单元，可得到滑坡体表观黏聚力的功率耗散率：

$D_{c''}^{{\text{3D}}} = \sum\limits_{i = 1}^m {c''({z_i})\cot \phi '} \left\{ {\int_{{S_{ii'}}} {{v_i}{n_i}} \text{d}S + \int_{{S_{i'}}_{i - 1'}} {{v_i}{n_i}} \text{d}S - \int_{{S_{i - 1i - 1'}}} {{v_i}{n_i}} \text{d}S} \right\} \ \ \ \ 。$

(23)

式中：c''(z_i)为土层单元形心处对应的表观黏聚力，为毛细黏聚力与有效黏聚力之和，可根据式（2）~（4）和土层单元形心至坡趾的垂距z_i求得。具体的，表观黏聚力的功率耗散率可表示为

$\begin{array} \left D_{{\text{c''}}}^{{\text{3D}}} = - 2\omega \cot \phi 'r_0^2\left\{ {{{\sin }^2}{\theta _0}} \right.\int_{{\theta _0}}^{{\theta _\text{B} }} {c''(H)\frac{{\cos \theta }}{{{{\sin }^3}\theta }}} \\ \ \ \ \ \ \sqrt {{R^2} - d_1^2} {\text{d}}\theta + {\sin ^2}({\theta _\text{B} } + {\beta _1})\frac{{{{\sin }^2}{\theta _0}}}{{{{\sin }^2}{\theta _\text{B} }}} \\ \ \ \ \ \ \int_{{\theta _\text{B} }}^{{\theta _\text{C}}} {c''({z_1})\frac{{\cos (\theta + {\beta _1})}}{{{{\sin }^3}(\theta + {\beta _1})}}\sqrt {{R^2} - d_2^2} } {\text{d}}\theta + \\ \ \ \ \ \ {\left[ {\sin {\theta _0} + {{{\alpha _1}H} \mathord{\left/ {\vphantom {{{\alpha _1}H} {{r_0}}}} \right. } {{r_0}}}} \right]^2}\int_{{\theta _\text{C} }}^{{\theta _\text{D} }} {c''({\alpha _2}H)\frac{{\cos \theta }}{{{{\sin }^3}\theta }}\sqrt {{R^2} - d_3^2} } {\text{d}}\theta {\text{ + }} \\ \ \ \ \ \ \exp \left[ {2({\theta _\text{h} } - {\theta _0})\tan \phi '} \right]{\sin ^2}({\theta _\text{h} } + {\beta _2}) \cdot \\ \ \ \ \ \ \left. {\int_{{\theta _\text{D}}}^{{\theta _\text{h}}} {c''({z_2})\frac{{\cos (\theta + {\beta _2})}}{{{{\sin }^3}(\theta + {\beta _2})}}\sqrt {{R^2} - d_4^2} } {\text{d}}\theta } \right\} - \\ \ \ \ \ \ 2\omega \cot \phi '\left\{ {\sum\limits_{i = 1}^{{m_2}{\text{ - 1}}} {\exp \left[ {2({\theta _i} - {\theta _{\text{0}}})\tan \phi '} \right] \cdot } } \right. \\ \ \ \ \ \ \left\{ {c''({z_i}) - c''({z_{i + 1}})} \right\}{\sin ^2}{\theta _i}\int_{{\theta _i}}^{\theta _{i'}^*} {\frac{{\cos \theta }}{{{{\sin }^3}\theta }}\sqrt {{R^2} - a_i^2} {\text{d}}\theta } + \\ \ \ \ \ \ \sum\limits_{i = {m_2}}^{m{\text{ - 1}}} {\exp \left[ {2({\theta _i} - {\theta _{\text{0}}})\tan \phi '} \right] \cdot } \\ \left\{{c}^{″}({z}_{i})-{c}^{″}({z}_{i+1})\right\}{\mathrm{sin}}^{2}{\theta }_{i}{\displaystyle {\int }_{{\theta }_{i}}^{{\theta }_{{i}^{\prime }}^{**}}\frac{\mathrm{cos}\theta }{{\mathrm{sin}}^{3}\theta }\sqrt{{R}^{2}-{a}_{i}^{2}}\text{d}\theta }\}\text{ }。\end{array}$

(24)

式中：z₁，z₂，d₁，d₂，d₃，d₄，θ_B，θ_C和θ_D分别为关于三维滑动机构和边坡几何形状的变量，可根据几何和三角函数关系得到，其详细计算过程可参考文献[16，20]。滑动面与坡顶的交点至坡肩的最大垂距L_AB可表示为

${L}_{AB}={r}_{0}\mathrm{cos}{\theta }_{0}-{r}_\text{h}\mathrm{cos}{\theta }_\text{h}-({\alpha }_{1}\mathrm{cot}{\beta }_{1}+{\alpha }_{2}\mathrm{cot}{\beta }_{2}+\lambda )H\ \ \ \ 。$

(25)

对于中部插入块体，表观黏聚力的功率耗散率可用微元速度不连续面的面积与其对应的表观黏聚力和切向速度分量的乘积，沿整个速度不连续面积分得到

$D_{c''}^{{\text{2D}}} = \omega br_0^2\int_{{\theta _{\text{0}}}}^{{\theta _{\text{h}}}} {c''({z_{\text{3}}})} \exp \left[ {2(\theta - {\theta _{\text{0}}})\tan \phi '} \right]{\text{d}}\theta \ \ \ \ 。$

(26)

式中：c''(z₃)为与微元速度不连续面对应的表观黏聚力；z₃为微元速度不连续面至坡趾的垂距，可表示为

${z_3} = {r_\text{h}}\sin {\theta _{\text{h}}} - {r_0}\exp \left[ {(\theta - {\theta _0})\tan \phi '} \right]\sin \theta \ \ \ \ 。$

(27)

根据瑞利阻尼模型，地震振动过程中滑坡体阻尼力的功率耗散率可表示为

$D_\text{s}^\text{h} = \sum\limits_{i = 1}^m {{\alpha _0}{v_\text{h}}\left[ {t,(H - {z_i})} \right]{S_i}\rho '({z_i} + {z_0})} \ \ \ \ \ \text{，}$

(28)

$D_\text{s}^\text{v} = \sum\limits_{i = 1}^m {{\alpha _0}{v_\text{v}}\left[ {t,(H - {z_i})} \right]{S_i}\rho '({z_i} + {z_0})} \ \ \ \ 。$

(29)

2.3 抗滑桩侧阻力功率耗散率

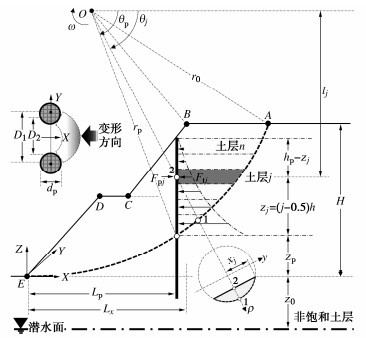
对于非饱和土边坡，假定桩侧土体处于塑性极限状态并遵循修正Mohr-Coulomb破坏准则。为了考虑基质吸力对桩侧阻力的提升作用，将Ito等^[24]塑性变形理论延拓至非饱和土中^[16]。同样采用该水平片分法计算桩侧阻力的功率耗散率，如图 5所示，将桩侧土体划分为n个土层单元，各土层单元内作用在桩上的主动土压力可表示为

图 5 桩侧阻力能量耗散率计算简图

Figure 5. Calculation of energy dissipation rate due to pile resistance forces

下载: 全尺寸图片幻灯片

$p(z') = c''(H - z'){D_1}{\left( {\frac{{{D_1}}}{{{D_2}}}} \right)^A}\left[ {\frac{{(C - 2N_{\phi '}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}\tan \phi ' - 1)}}{{{N_{\phi '}}\tan \phi '}} + \frac{B}{A}} \right] - \\ {c}^{″}(H-{z}^{\prime })\left({D}_{1}\frac{B}{A}-2{D}_{2}{N}_{{\varphi }^{\prime }}^{-1/2}\right)+\frac{{\gamma }^{\prime }(H-{z}^{\prime }){z}^{\prime }}{{N}_{{\varphi }^{\prime }}}\left[{D}_{\text{1}}{\left(\frac{{D}_{1}}{{D}_{2}}\right)}^{A}C-{D}_{2}\right]\ \ \ \ 。$

(30)

式中：D₁为相邻抗滑桩的中心间距；D₂为相邻桩间的净距离；h_p滑动面上抗滑桩埋入土层长度；z'为土层形心至坡趾的垂距；N_ϕ'，A，B和C可表示如下：

${N_{\phi '}} = {\tan ^2}({\text{π }}/4 + \phi '/2) \ \ \ \ \ \text{，}$

(31)

$A = N_{\phi '}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}\tan \phi ' + {N_{\phi '}} - 1 \ \ \ \ \ \text{，}$

(32)

$B = 2\tan \phi ' + 2N_{\phi '}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} + N_{\phi '}^{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \ \ \ \ \ \text{，}$

(33)

$C = \exp \left[ {{{({d_\text{p} }} \mathord{\left/ {\vphantom {{({d_{p} }} {{D_2})}}} \right. } {{D_2})}}{N_{\phi '}}\tan \phi '\sqrt {{N_{\phi '}}} } \right] \ \ \ \ 。$

(34)

式中：d_p为抗滑桩直径（即d_p = D₁ – D₂）。

累加各土层单元内桩侧阻力的功率耗散率，抗滑桩侧阻力总的功率耗散率可表示为

$D_\text{p}^{} = \omega \sum\limits_{j = 1}^n {{F_{\text{p} j}}{l_j}} \ \ \ \ 。$

(35)

式中：F_pj为土层单元内单桩提供单位宽度的最大侧阻力（可通过桩侧阻力除以相邻桩中心距得到）；l_j为桩侧阻力作用点的极径，关于上式的详细计算过程可参考文献[16]。

2.4 安全系数

重度增加法可给出安全系数（FOS）的显式表达式，定义简单明确，便于工程应用。基于该方法，非饱和土边坡安全系数上限目标函数可表示为耗散功率与外力功率之比：

$\operatorname{FOS}(t)=\frac{D_{\mathrm{c}^{\prime \prime}}^{2 \mathrm{D}}+D_{\mathrm{c}^{\prime \prime}}^{3 \mathrm{D}}+D_{\mathrm{s}}^{\mathrm{h}}+D_{\mathrm{s}}^{\mathrm{v}}+D_{\mathrm{p}}}{W_{\gamma^{\prime}}+W_{\gamma^{\prime}}^{\mathrm{ah}}+W_{\gamma^{\prime}}^{\mathrm{av}}}\ \ \ \ 。$

(36)

对边坡安全系数的最小上限解的求解可转化为非线约束条件下的最小值优化问题。借助于商用数值分析软件，开发了一种基于枚举法的计算代码搜索边坡安全系数的最小值。搜索过程中几何变量θ₀，θ_h，r₀/r'₀和b应满足：0° < θ₀ < θ_B < θ_C ≤ θ_D < θ_h < 180°，0 < r₀/r'₀ < 1且b ≥ 0。

对于本文提出的半解析方法，边坡几何参数和土体强度指标等参数均对其计算效率和精度有一定的影响^[16]，但当滑坡体和桩侧土体划分为60层及以上时，该半解析法可得到令人满意的计算结果，因此本文分析计算仍采用该值。

2.5 对比分析

为验证本文半解析方法和优化程序的正确性，将本文计算结果与典型边坡算例计算结果进行对比。边坡几何参数和土体物理力学指标等参数为：H = 10 m，β₁ = β₂ = 45°，α₁ = α₂ = 0.5，λ = 0，ϕ' = 10°，c' = 23.94 kPa，γ_sat = 19.63 kN/m³，D₁/d_p = 2.5，d_p = 0.3 m，k_h = k_v = 0，Q = 0。

表 1给出了该边坡安全系数的解析解和本文得到的半解析解。对比发现本文得到的边坡安全系数与Yang等^[22]得到的结果非常相近，误差均小于2%，表明本文提出的方法是合理的。计算结果间的差异主要是由于采用方法的不同所致，本文半解析法的精度依赖于滑坡体划分层数，当滑坡体和桩侧土体划分60层及以上时，半解析解与解析解存在小于1%的误差^[16]，这在实际应用中是满足使用要求的。

表 1 不同方法得到的边坡安全系数

Table 1. FOSs obtained by different methods

B/H	方法	桩位（L_p/L_x）
B/H	方法	0	0.2	0.4	0.6	0.8	1.0
2	文献[22]	1.27	1.42	1.61	1.79	1.87	1.59
2	本文	1.262	1.391	1.581	1.780	1.835	1.571
5	文献[22]	1.16	1.31	1.48	1.67	1.76	1.49
5	本文	1.148	1.284	1.468	1.658	1.730	1.453
10	文献[22]	1.12	1.28	1.46	1.63	1.72	1.44
10	本文	1.119	1.255	1.409	1.624	1.702	1.407

下载: 导出CSV

| 显示表格

3. 结果与分析

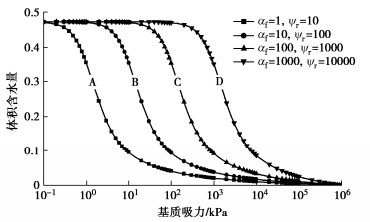
研究了吸力、三维效应和地震动特性对边坡地震稳定性的影响，边坡尺寸等参数如下：H = 13.7 m，B/H = 2， $\lambda$ = 0.2，β₁ = 60°，β₂ = 45°，α₁ = α₂ = 0.5，z₀ = 2 m，c' = 23.94 kPa，ϕ' = 10°，γ_d = 15 kN/m³，γ_sat = 19.63 kN/m³，G = 25 MPa，μ = 0.3，k_h = 0.2，k_v = 0.1，f_a = 1.1，T = 0.25 s，D₁ = 2.0 m，D₂ = 1.6 m，L_p/L_x = 0.5， q/k_s = 0，Q = 10 kPa，m = n = 60。选用4种典型的SWCC，如图 6所示，相关参数见表 2^[14]。4种SWCC基本涵盖了工程中能遇到的大部分土类，通常粗粒土的保水性较差，细粒土的保水性较好。

图 6 4种典型非饱和土的SWCC

Figure 6. SWCC curves for four selected unsaturated soils

下载: 全尺寸图片幻灯片

表 2 4种典型非饱和土SWCC曲线参数

Table 2. Parameters for four selected SWCC curves

SWCC No.	a_f/ kPa	n_f	m_f	ψ_r/ kPa	α/ kPa^-1	θ_r
A	1	2	1	10	2	0.081
B	10	2	1	100	0.2	0.080
C	100	2	1	1000	0.02	0.078
D	1000	2	1	10000	0.002	0.073

下载: 导出CSV

| 显示表格

3.1 吸力的影响

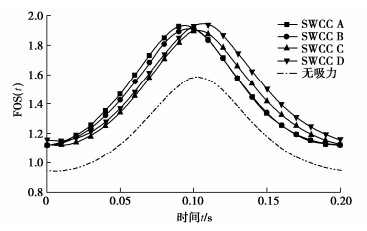
图 7为不同非饱和土中边坡的动安全系数。可以发现边坡稳定性随地震波的传播呈正弦变化，安全系数均在t = 0.1 s左右达到峰值。吸力对边坡稳定性有显著的提升作用，吸力的这种强化作用可达15%~30%，因此不考虑土中吸力会显著低估边坡的稳定性。土体类型对边坡动态稳定性的影响相对较弱，4种SWCC差异较大，但吸力效应却相差较小，这主要是因为土中水分含量变化不仅影响毛细黏聚力，还影响土单位重度。对于保水性强的边坡，高毛细黏聚力有利于边坡稳定性的发挥，而对于保水性差的边坡，其低重度的不利影响相对较弱，也有利于边坡稳定性的发挥。粗粒土和细粒土边坡的安全系数峰值均相对较高，但粗粒土边坡安全系数峰值出现的时间会相对提前，而细粒土边坡的安全系数峰值出现的时间会相对滞后。

图 7 SWCC对边坡动安全系数的影响

Figure 7. Influences of SWCCs on seismic stability of soil slopes

下载: 全尺寸图片幻灯片

3.2 三维效应的影响

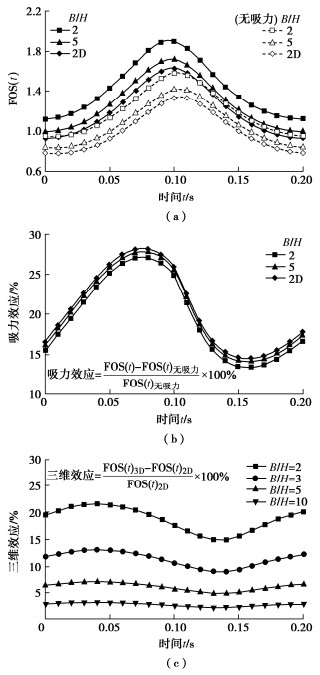
图 8为不同横向宽度限制条件下非饱和土边坡的动安全系数。选取SWCC B，可以发现边坡三维效应对其稳定性评估结果有显著影响，边坡安全系数随宽高比的增加而逐渐减小，并最终趋近于二维结果，表明边坡三维效应愈显著，其稳定性愈高，忽略边坡三维效应会严重低估其稳定性，分析结果较为保守，这与已有的研究结果是一致的^[16]。

图 8 三维效应对边坡动安全系数的影响

Figure 8. Influences of 3D effects on seismic stability of soil slopes

下载: 全尺寸图片幻灯片

值得注意的是，吸力对边坡稳定性的提升效果除了取决于土体类型外，还与地震动特性密切相关。随着地震波传播，吸力效应同样呈正弦曲线变化，在地震波达到峰值时得到加强，在地震波处于峰谷时相对较弱，这主要是因为地震加速度的方向性导致的。此外吸力效应与边坡三维效应间存在一定的相关性，三维效应明显的边坡中吸力效应的影响相对较弱，二维边坡中的吸力效应最为显著，三维效应与吸力效应间的相关性几乎不受地震作用的影响。

边坡三维效应与地震动间同样存在一定的相关性，随着地震波传播，边坡三维效应的影响呈正弦规律变化。随着边坡三维效应的减弱，地震动的这种影响逐渐减弱，并最终消失。对于宽高比B/H = 2的边坡，三维效应对边坡稳定性的影响可达20%，而对于B/H = 5的边坡，三维效应对边坡稳定性的影响稳定在7%左右。

3.3 地震动参数的影响

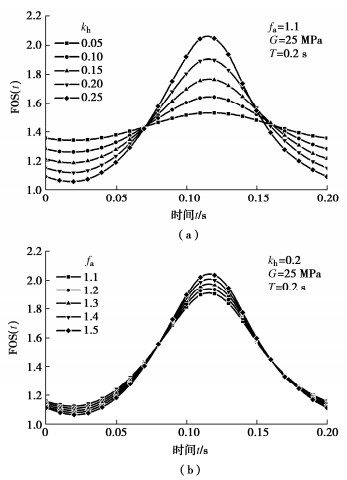
图 9为水平加速度系数和放大系数对边坡地震稳定性的影响。可以发现，边坡安全系数的幅值随水平加速度系数的增加迅速增加，峰值显著增加而谷值略有减小，整个曲线变得更加“瘦高”，这与饶平平等^[8]的研究结果是一致的。放大系数对边坡地震稳定性的影响稍弱，安全系数的幅值随放大系数的增加略有增加，因为放大系数直接决定地震加速度的幅值，导致地震力的增加，进而影响边坡的地震稳定性。

图 9 地震动参数对边坡动安全系数的影响

Figure 9. Influences of seismic features on slope stability

下载: 全尺寸图片幻灯片

3.4 临界滑动面

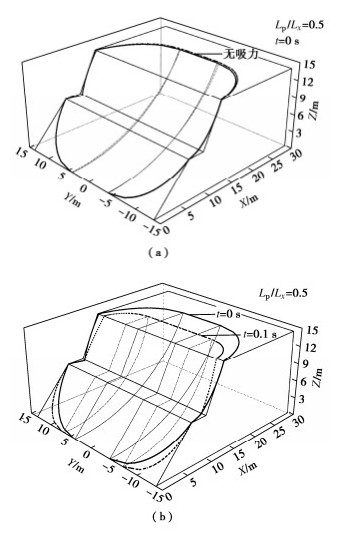
吸力和地震动对边坡临界滑动面的影响，如图 10所示。吸力对边坡稳定性有显著的提升作用，但对临界滑动面的影响较弱，考虑吸力时边坡滑动面相对较深，滑坡体后缘向坡肩靠近。地震动对边坡临界滑动面的影响最为显著，初始时刻的边坡滑动面较深，滑坡体的体量也相对较大；而随着地震波逐渐接近峰值，临界滑动面逐渐变浅，出现“浅层”滑动现象，滑坡体后缘也向坡肩迅速靠近，滑坡体后缘线至坡肩的距离由10.2 m减小至4.9 m，滑坡体的体量也急剧减小，这是因为地震波接近峰值时，水平惯性力逐渐指向坡外侧并做正功，滑动面变浅以使边坡整体能耗达到最小状态，安全系数最小。

图 10 吸力和地震动对滑动面的影响

Figure 10. Influences of suction and seismic action on slip surface

下载: 全尺寸图片幻灯片

4. 结论

基于极限分析上限原理和拟动力法研究了抗滑桩加固非饱和土边坡的地震稳定性。提出一种改进水平片分法，可有效考虑土中水分含量变化对边坡稳定性的影响。对典型非饱和土边坡稳定性进行分析，研究了吸力效应、三维效应和地震作用对边坡稳定性的影响规律及其相互作用关系，主要得到以下4点结论。

（1）不考虑吸力会显著低估边坡的稳定性，吸力对边坡稳定性的提升效果可达15%~30%，且与地震动特性密切相关，当地震波达到峰值时吸力效应得到加强，而当地震波处于峰谷时吸力效应相对较弱。

（2）忽略边坡三维效应同样会低估边坡的稳定性，三维效应对边坡稳定性的提升效果可达20%，且同样与地震动特性密切相关。边坡三维效应的影响在地震波传播过程中，同样呈正弦规律变化，对于三维效应明显的边坡，地震动的这种影响尤为明显。

（3）水平地震加速度系数对边坡地震稳定性影响较大。边坡安全系数幅值随放大系数的增加而略有增加，随着土剪切模量的增加略有增加并向负方向移动，随地震动周期的增加略有增加并向正方向移动。

（4）吸力效应对桩加固边坡临界滑动面的影响较小，地震动对滑动面的影响较为显著，地震波接近峰值时，边坡临界滑动面逐渐变浅，滑坡体体积逐渐减小，出现“浅层”滑动现象。

图 1 非饱和土边坡地震稳定性计算简图

Figure 1. Diagram of an unsaturated soil slope subjected to seismic excitations

下载: 全尺寸图片幻灯片

图 2 插入平面应变块构成复合三维滑动机构示意图

Figure 2. Diagram of combined 3D mechanism with a plane-strain insert

下载: 全尺寸图片幻灯片

图 3 土-水特征曲线和非饱和土抗剪强度包线关系图

Figure 3. Relationship between SWCC and strength of unsaturated soils

下载: 全尺寸图片幻灯片

图 4 改进水平片分法示意图

Figure 4. Diagram of modified horizontal slice method

下载: 全尺寸图片幻灯片

图 5 桩侧阻力能量耗散率计算简图

Figure 5. Calculation of energy dissipation rate due to pile resistance forces

下载: 全尺寸图片幻灯片

图 6 4种典型非饱和土的SWCC

Figure 6. SWCC curves for four selected unsaturated soils

下载: 全尺寸图片幻灯片

图 7 SWCC对边坡动安全系数的影响

Figure 7. Influences of SWCCs on seismic stability of soil slopes

下载: 全尺寸图片幻灯片

图 8 三维效应对边坡动安全系数的影响

Figure 8. Influences of 3D effects on seismic stability of soil slopes

下载: 全尺寸图片幻灯片

图 9 地震动参数对边坡动安全系数的影响

Figure 9. Influences of seismic features on slope stability

下载: 全尺寸图片幻灯片

图 10 吸力和地震动对滑动面的影响

Figure 10. Influences of suction and seismic action on slip surface

下载: 全尺寸图片幻灯片

表 1 不同方法得到的边坡安全系数

Table 1 FOSs obtained by different methods

B/H	方法	桩位（L_p/L_x）
B/H	方法	0	0.2	0.4	0.6	0.8	1.0
2	文献[22]	1.27	1.42	1.61	1.79	1.87	1.59
2	本文	1.262	1.391	1.581	1.780	1.835	1.571
5	文献[22]	1.16	1.31	1.48	1.67	1.76	1.49
5	本文	1.148	1.284	1.468	1.658	1.730	1.453
10	文献[22]	1.12	1.28	1.46	1.63	1.72	1.44
10	本文	1.119	1.255	1.409	1.624	1.702	1.407

下载: 导出CSV

表 2 4种典型非饱和土SWCC曲线参数

Table 2 Parameters for four selected SWCC curves

SWCC No.	a_f/ kPa	n_f	m_f	ψ_r/ kPa	α/ kPa^-1	θ_r
A	1	2	1	10	2	0.081
B	10	2	1	100	0.2	0.080
C	100	2	1	1000	0.02	0.078
D	1000	2	1	10000	0.002	0.073

下载: 导出CSV

参考文献(24)

[1]	郑颖人, 叶海林, 黄润秋, 等. 边坡地震稳定性分析探讨[J]. 地震工程与工程振动, 2010, 30(2): 173-180. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201002028.htm ZHENG Yingren, YE Hailin, HUANG Runqiu, et al. Study on the seismic stability analysis of a slope[J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(2): 173-180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201002028.htm
[2]	黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-454. doi: 10.3321/j.issn:1000-6915.2007.03.001 HUANG Runqiu. Large-scale landslides and their sliding mechanisms in China since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-454. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.03.001
[3]	张江伟, 李小军, 王晓明, 等. 土质边坡地震稳定性状态判定方法研究[J]. 岩土工程学报, 2018, 40(11): 2096-2102. doi: 10.11779/CJGE201811016 ZHANG Jiangwei, LI Xiaojun, WANG Xiaoming, et al. Method for judging seismic stability state of soil slopes[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2096-2102. (in Chinese) doi: 10.11779/CJGE201811016
[4]	NEWMARK N M. Effects of earthquakes on dams and embankments[J]. Géotechnique, 1965, 15(2): 139-160. doi: 10.1680/geot.1965.15.2.139
[5]	STEEDMAN R S, ZENG X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall[J]. Géotechnique, 1990, 40(1): 103-112. doi: 10.1680/geot.1990.40.1.103
[6]	ZENG X, STEEDMAN R S. On the behavior of quay walls in earthquakes[J]. Geotechnique, 1993, 43: 417-431. doi: 10.1680/geot.1993.43.3.417
[7]	宋桂锋, 杜江梅, 柯鉴, 等. 基于拟动力法的顺层岩质边坡稳定性极限分析[J]. 地震工程学报, 2019, 41(4): 931-938. doi: 10.3969/j.issn.1000-0844.2019.04.931 SONG Guifeng, DU Jiangmei, KE Jian, et al. Stability limit analysis of bedding rock slopes based on pseudo-dynamic method[J]. China Earthquake Engineering Journal, 2019, 41(4): 931-938. (in Chinese) doi: 10.3969/j.issn.1000-0844.2019.04.931
[8]	饶平平, 童磊磊, 师昀巍. 基于拟动力法的抗滑桩加固边坡地震稳定性分析[J]. 世界地震工程, 2020, 36(1): 189-196. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC202001024.htm RAO Pingping, TONG Leilei, SHI Yunwei. Seismic stability analysis of slopes reinforced with anti-slide piles based on pseudo-dynamic method[J]. World Earthquake Engineering, 2020, 36(1): 189-196. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC202001024.htm
[9]	VANAPALLI S K, FREDLUND D G, PUFAHL D E, et al. Model for the prediction of shear strength with respect to soil suction[J]. Canadian Geotechnical Journal, 1996, 33(3): 379-392. doi: 10.1139/t96-060
[10]	FREDLUND D, XING A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532. doi: 10.1139/t94-061
[11]	LU N, LIKOS W J. Unsaturated Soil Mechanics[M]. New York: John Wiley, 2004.
[12]	BISHOP A W. The principle of effective stress[J]. Teknisk Ukeblad, 1959, 39: 859-863.
[13]	FREDLUND D G, MORGENSTERN N R, WIDGER R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321. doi: 10.1139/t78-029
[14]	ZHANG L L, FREDLUND D G, FREDLUND M D, et al. Modeling the unsaturated soil zone in slope stability analysis[J]. Canadian Geotechnical Journal, 2014, 51(12): 1384-1398. doi: 10.1139/cgj-2013-0394
[15]	SUN D A, WANG L, LI L. Stability of unsaturated soil slopes with cracks under steady infiltration conditions[J]. International Journal of Geomechanics, 2019, 19(6): 04019044. doi: 10.1061/(ASCE)GM.1943-5622.0001398
[16]	WANG L, SUN D A, YAO Y P, et al. Kinematic limit analysis of three-dimensional unsaturated soil slopes reinforced with a row of piles[J]. Computers and Geotechnics, 2020, 120: 103428. doi: 10.1016/j.compgeo.2019.103428
[17]	卢坤林. 基于极限平衡理论的土质边坡空间效应研究及应用[D]. 合肥: 合肥工业大学, 2013. LU Kunlin. Research on the 3D Effect of Homogeneous Slope Stability Analysis Based on the Limit Equilibrium Method and Its Application to Engineering[D]. Hefei: Hefei University of Technology, 2013. (in Chinese)
[18]	GIGER M W, KRIZEK R J. Stability analysis of vertical cut with variable corner angle[J]. Soils and Foundations, 1975, 15(2): 63-71. doi: 10.3208/sandf1972.15.2_63
[19]	DRESCHER A. Limit plasticity approach to piping in bins[J]. Journal of Applied Mechanics, 1983, 50(3): 549-553. doi: 10.1115/1.3167089
[20]	MICHALOWSKI R, DRESCHER A. Three-dimensional stability of slopes and excavations[J]. Géotechnique, 2009, 59(10): 839-850. doi: 10.1680/geot.8.P.136
[21]	PARK D, MICHALOWSKI R L. Three-dimensional roof collapse analysis in circular tunnels in rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 128(C): 104275.
[22]	YANG S Y, WANG Z, WANG J M, et al. 3D seismic stability analysis of bench slope with pile reinforcement[J]. Geotechnical and Geological Engineering, 2022, 40: 1149-1163. doi: 10.1007/s10706-021-01949-y
[23]	CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam, New York: Elsevier Scientific Pub Co, 1975.
[24]	ITO T, MATSUI T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43-59. doi: 10.3208/sandf1972.15.4_43

施引文献(9)

期刊类型引用(3)

1.	姬羽菲，邵帅，邵生俊，朱学亮，严广艺. 非饱和土边坡三维地震稳定性分析. 岩土工程学报. 2025(03): 627-635 . 本站查看
2.	徐亮，李亮，文嘉辉，李春立，于广明. 快速拟动力法及其在西藏某尾矿坝地震稳定性评价中的应用. 矿业研究与开发. 2025(03): 74-82 . 百度学术
3.	张旭义. 考虑渠基地震动响应水平的改良土设计研究. 水利科学与寒区工程. 2024(10): 136-140 . 百度学术

其他类型引用(6)

资源附件(2)

本文视频
- Video Player is loading.
  Current Time 0:00
  Duration -:-
  Loaded: 0%
  Stream Type LIVE
  Remaining Time -:-
  
  1x
  Chapters
  descriptions off, selected
  subtitles settings, opens subtitles settings dialog
  subtitles off, selected
  This is a modal window.
  The media could not be loaded, either because the server or network failed or because the format is not supported.
  Beginning of dialog window. Escape will cancel and close the window.
  TextColorTransparency
  BackgroundColorTransparency
  WindowColorTransparency
  Font Size
  Text Edge Style
  Font Family
  End of dialog window.
  11-202309-G22-0765BG
其他相关附件
- PDF格式
  11-202309-G22-0765一文审稿意见与作者答复点击下载(525KB)

图(10) / 表(2)

计量

文章访问数: 585
HTML全文浏览量: 65
PDF下载量: 208
被引次数: 9

0. 引言
1. 基本原理和计算模型
1.1 极限分析上限法
1.2 三维破坏机构
1.3 非饱和土性质
1.4 拟动力法
2. 改进水平片分法
2.1 非饱和土重力所做外功率
2.2 表观黏聚力功率耗散率
2.3 抗滑桩侧阻力功率耗散率
2.4 安全系数
2.5 对比分析
3. 结果与分析
3.1 吸力的影响
3.2 三维效应的影响
3.3 地震动参数的影响
3.4 临界滑动面
4. 结论

0. 引言
1. 基本原理和计算模型
1.1 极限分析上限法
1.2 三维破坏机构
1.3 非饱和土性质
1.4 拟动力法
2. 改进水平片分法
2.1 非饱和土重力所做外功率
2.2 表观黏聚力功率耗散率
2.3 抗滑桩侧阻力功率耗散率
2.4 安全系数
2.5 对比分析
3. 结果与分析
3.1 吸力的影响
3.2 三维效应的影响
3.3 地震动参数的影响
3.4 临界滑动面
4. 结论

参考文献(24)

施引文献

资源附件(2)

三维非饱和土边坡拟动力稳定性分析初探 English Version

作者简介: 王龙(1989—)，男，博士（后），讲师，主要从事岩土力学教学与科研工作。E-mail: longwang@jiangnan.edu.cn

通讯作者: 胡伟, Email: huwei1999@126.com

计量

出版历程

Three-dimensional seismic stability of unsaturated soil slopes using pseudo-dynamic approach

0. 引言

1. 基本原理和计算模型

1.1 极限分析上限法

1.2 三维破坏机构

1.3 非饱和土性质

1.4 拟动力法

2. 改进水平片分法

2.1 非饱和土重力所做外功率

2.2 表观黏聚力功率耗散率

2.3 抗滑桩侧阻力功率耗散率

2.4 安全系数

2.5 对比分析

3. 结果与分析

3.1 吸力的影响

3.2 三维效应的影响

3.3 地震动参数的影响

3.4 临界滑动面

4. 结论

期刊类型引用(3)

其他类型引用(6)

本文视频

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 基本原理和计算模型

1.1 极限分析上限法

1.2 三维破坏机构

1.3 非饱和土性质

1.4 拟动力法

2. 改进水平片分法

2.1 非饱和土重力所做外功率

2.2 表观黏聚力功率耗散率

2.3 抗滑桩侧阻力功率耗散率

2.4 安全系数

2.5 对比分析

3. 结果与分析

3.1 吸力的影响

3.2 三维效应的影响

3.3 地震动参数的影响

3.4 临界滑动面

4. 结论

作者简介:
王龙(1989—)，男，博士（后），讲师，主要从事岩土力学教学与科研工作。E-mail: longwang@jiangnan.edu.cn

通讯作者:
胡伟, Email: huwei1999@126.com