Experimental study on liquefaction characteristics of marine fine-grained sand based on critical state theory
-
摘要: 采用饱和海相含细粒土砂开展固结不排水三轴剪切试验和轴向-扭转耦合循环剪切试验,基于临界状态理论,研究砂土状态参数与其液化特性的关系。研究结果表明:对于海相含细粒土砂,其临界孔隙比和归一化有效平均正应力具有很高的线性相关性;轴向-扭转耦合不排水循环剪切试验结果显示,循环应力比CRR相同时,状态参数ψ越大,液化振次NL越小,根据研究结果提出砂土液化振次NL的计算公式,NL与ψ很好的满足指数函数关系。
-
关键词:
- 含细粒土砂 /
- 轴向-扭转耦合循环剪切试验 /
- 临界状态 /
- 液化 /
- 循环应力比
Abstract: The consolidated undrained triaxial shear tests and coupled axial-torsional cyclic shear tests are conducted using the marine fine-grained sand to study the correlation between the critical state parameter and the liquefaction characteristics based on the critical state theory. The tests results show a linear correlation between the critical void ratio and the normalized effective normal stress. The results of the coupled axial-torsional cyclic shear tests show that the cycle number for liquefaction, NL, decreases with the increasing state parameter, ψ, for a certain cyclic resistance ratio. Finally, an exponential function for expressing the relationship between NL and ψ is proposed. -
0. 引言
全球气候变化导致海平面上升与海洋动力条件改变,极大提高了强潮大浪与地震等灾害的发生频率,严重威胁沿海水工建筑物的安全。在地震等动力荷载的作用下,沿海砂土地基易发生液化破坏,即饱和砂土在地震荷载或者波浪循环荷载剪切应力作用下,产生超静孔隙水压力导致有效应力迅速减小,表现为类似液体的性质[1-4]。砂土地基液化会对沿海水工建筑物的稳定带来巨大威胁,如海上平台、防波堤等在地震过程中发生破坏。因此,亟需对海相砂土动力学特性开展研究。
国内外学者已针对砂土在动力荷载作用下的液化特性开展了大量研究。Seed等[4]采用提出的动孔压应力模型预测孔隙水压力发展及描述砂土液化特性;Green等[5]提出动孔压的能量模型描述动孔隙水压力与耗散能量之间的关系;Ni等[2]指出了第一个加载循环累计的孔隙水压力与砂土抗液化能力的关系。由此可见,学者们均在探索砂土液化的有效预测方法。孔隙比e和相对密实度Dr常用于描述洁净砂土的抗液化性能,但由于细颗粒会显著影响砂土单调和循环荷载下的不排水特性,使得在使用e和Dr描述含细粒土砂液化特性时出现差异较大的结论[3]。临界状态土力学(CSSM)提供了一个描述砂土物理力学特性的模型框架。Qadimi等[6]证实了可将临界状态参数应用于砂土循环荷载下的力学特性研究中。Jefferies等[7]将临界状态参数和砂土抗液化性能联系起来。对于含细粒土砂,关于液化特性与其临界状态之间关系的研究也取得一些进展[8-9]。Porcino等[9]对细颗粒含量范围在0~40%的砂土试样进行不排水三轴剪切和循环三轴剪切试验,结果表明仅需通过确定含细粒土砂的临界状态线,即可使修正后状态参数与抗液化强度建立联系。但是已有研究多是针对实验室配置的含细粒砂土试样开展动三轴试验,试验用土的物理力学特性与天然沉积含细粒土砂存在差异,且模拟的应力状态与实际作用于地基土层的地震等动力荷载不完全相符,影响研究成果在实际工程应用中的参考价值。
本文针对海相沉积含细粒土砂,模拟试样在地震荷载下的真实应力状态,开展固结不排水三轴剪切试验和轴向-扭转耦合循环剪切试验,并基于临界状态土力学理论,系统分析临界状态参数与含细粒土砂的液化特性之间的关系。
1. 试验材料与方法
1.1 试验仪器
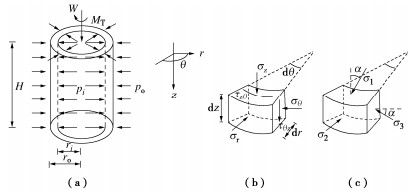
固结不排水三轴试验在全自动三轴仪上完成,用于确定海相含细粒土砂的临界状态线。为更加真实模拟地震荷载作用下地基土层的应力状态,本文采用GDS空心圆柱扭剪仪开展循环剪切试验,图 1为空心圆柱试样的应力状态,试样高度H=200 mm,内、外半径分别为ri=30 mm、ro=50 mm,壁厚20 mm。该仪器可同时独立控制轴力W、扭矩MT、内围压pi和外围压po的动态加载,并在土样薄壁单元上产生4个应力分量轴向应力(轴向应力σz,剪应力τzθ,径向应力σr和环向应力σθ)[10]。试验过程中轴向动应力(σd)和扭转动应力(τd)保持σd=2τd,相位差为0°,对应土体单元中的正应力分量差(σz-σθ)/2和水平剪应力τzθ同步增长,且其对应的应力路径在τzθ- (σz-σθ)/2应力坐标系中为45°倾斜的直线,更加符合实际地震荷载作用下水工建筑物地基土层的应力状态。
1.2 试验土样与试样制备
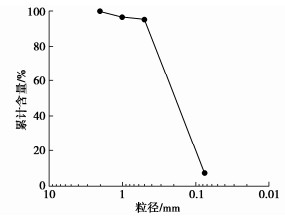
试验所用土样取自洋山港近海,取土深度为10~45 m,烘干土样中明显可见白色NaCl结晶,试验土样的颗粒级配曲线如图 2所示,依据《土工试验方法标准:GB/T50123—2019》相关规定,该土料被定名为含细粒土砂(SF)。土样相对质量密度Gs=2.71,平均粒径D50=0.28 mm,不均匀系数Cu=3.75,曲率系数Cc=0.03,最大孔隙比 emax=1.398,最小孔隙比 emin=0.633,细粒含量Fc=7.33%。
三轴剪切试验与空心圆柱扭剪试验均采用落砂法制备土样,称取所需土样,并均分成5等份,分层装入承膜筒中并压实至相应厚度,层与层之间进行刨毛处理,以保证试样均匀性。干燥试样制备完成后,首先从试样底部通入2 hCO2以置换土体中的空气;然后从试样底部通入无气水,直至试样顶部出口无气泡排出;最后进行反压饱和,当试样孔压系数B值达到0.96以上时,认为试样已经达到饱和状态。
1.3 试验方案
为研究海相含细粒土砂状态参数与其液化特性之间的关系,需要先确定临界状态线,本文采用固结不排水三轴试验,三轴试验的具体参数如表 1所示。
表 1 三轴试验参数Table 1. Triaxial test parameters试验编号 初始有效平均应力p′0 固结后ecs 临界状态有效平均应力P′cs CU1 100 1.051 124 CU2 100 0.980 325 CU3 200 0.964 438 CU4 400 0.942 580 针对所选用含细粒土砂进行轴向-扭转双向耦合动荷载下的不排水空心圆柱循环剪切试验。空心圆柱扭剪试验方案如表 2所示,试验方案中控制初始有效平均应力p′0和循环应力比CRR两个变量,得到相应的轴向动应力和扭转动应力,土样固结后孔隙比即为不排水剪的临界孔隙比,液化振次NL为土样发生液化破坏所需的振动次数。试验过程中均采用应力控制加载,循环轴向和扭剪应力采用周期简谐波,振动频率为0.1 Hz。循环应力比CRR和动强度τf由下式定义:
表 2 空心圆柱循环扭剪试验参数Table 2. Parameters of hollow cylinder torsional tests试验编号 p′0 固结后ecs τd CRR NL ψ HCA1 100 0.984 7.5 0.106 40 -0.166 HCA2 100 0.988 10.0 0.141 14 -0.163 HCA3 100 0.994 12.5 0.177 3 -0.162 HCA4 200 0.969 15.0 0.106 98 -0.215 HCA5 200 0.978 20.0 0.141 25 -0.206 HCA6 200 0.975 25.0 0.177 5 -0.209 HCA7 300 0.958 22.5 0.106 220 -0.258 HCA8 300 0.963 30.0 0.141 39 -0.254 HCA9 300 0.959 37.5 0.177 11 -0.258 CRR=τf/p′0, (1) τf=σ1−σ32=√(σd2)2+τ2d。 (2) 式中:σ1,σ3分别为最大和最小主应力;p′0为初始有效平均应力;σd,τd分别为轴向动应力和扭转动应力。
2. 试验结果与分析
2.1 海相含细粒土砂临界状态线确定
临界状态是指砂土在剪切过程中达到的极限状态,应力不变的情况下,塑性变形无限发展,土样体积和孔隙水压力基本保持不变。临界状态线(CSL)是e-lnp′平面临界状态点的轨迹,砂土CSL的位置与制样方法、初始状态、应力历史、剪切速率、应力路径及排水条件无关,但受细粒含量显著影响[8]。Li等[11]和Cai[12]将有效应力进行归一化,给出了在e-(p′/pa)ξ平面CSL的表达式:
ec=eΓ−λc(p′cpa)ξ。 (3) 式中:pa为大气压力;eΓ为p′=0时对应的孔隙比;λc为临界状态线的斜率;ξ为率定系数,取0.7[12]。
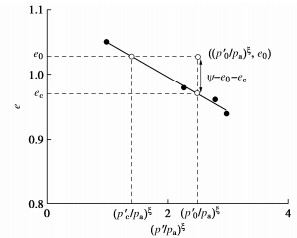
基于临界状态理论,状态参数ψ是指当前状态下的孔隙比e0和当前应力状态的临界孔隙比ec的差值:
ψ=e0−ec=e−[eΓ−λc(p′cpa)ξ]。 (4) 根据三轴剪切试验结果得出海相含细粒土砂的临界状态线如图 3所示,其中eΓ=1.103,λc=0.053。从图 3中可以看出含细粒土砂在e-(p′/pa)ξ平面呈现出很好的线性关系。
2.2 典型不排水循环扭剪试验
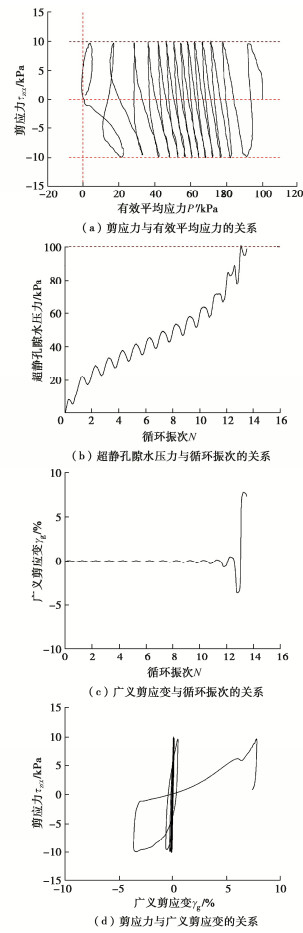
图 4为海相含细粒土砂不排水循环扭剪试验(HCA2)的结果。由图 4(b)可以看出孔隙水压力的变化呈现典型的三段式[2],在开始的几个循环,孔隙水压力快速增加,并在随后的循环中以较低速率稳定增长,最后孔隙水压力快速上升直至液化。平均有效应力与剪应力的关系曲线变化规律与孔压变化相对应,在50~80 kPa曲线较密集,两侧较疏松,见图 4(a)。从图 4(c),4(d)中可以看出剪应变在刚开始的加载中几乎为零,直至孔隙水压力增大到80 kPa左右,剪应变和孔隙水压力开始迅速增大,平均有效应力迅速减小为零,土样几乎丧失所有的强度,发生液化破坏。初始液化后土样变形迅速持续发展,最终发生流动液化。
2.3 状态参数与液化特性
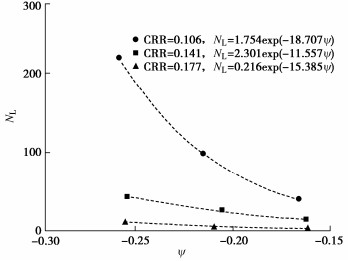
土样的循环应力比CRR及其液化时的动应力循环次数NL通常是描述砂土液化特性的重要参数,同时其液化特性与土样固结后所处的状态密切相关[8]。因此,可基于临界状态土力学理论,通过临界状态参数对砂土的液化特性进行描述,建立海相砂土的液化振次NL和其对应的状态参数之间的关系。图 5展示了不同CRR下土样发生液化时对应的动应力循环次数NL与状态参数ψ的关系,可以看出两者较好的满足如下的指数函数关系:
NL=aexp(bψ)。 (5) 式中:a,b与为拟合参数。
本文所有空心圆柱扭剪试验土样状态参数ψ均小于0,位于临界状态线的下方,土样较为密实,循环应力比CRR相同时,状态参数ψ越大,发生液化破坏所需要的振动次数越小。
3. 结论
通过对海相含细粒土砂开展一系列固结不排水三轴剪切和循环扭剪试验,基于临界状态理论,研究了含细粒土砂临界状态参数与之间的关系。得到2点结论。
(1)海相含细粒土砂的临界状态在e-(p′/pa)ξ平面内呈线性关系。
(2)轴向-扭转耦合不排水循环剪切试验结果显示,液化振次NL与临界状态参数ψ很好的满足指数函数关系。循环应力比CRR相同时,状态参数ψ越大,土样发生液化破坏所需振动次数NL越小。
-
表 1 三轴试验参数
Table 1 Triaxial test parameters
试验编号 初始有效平均应力p′0 固结后ecs 临界状态有效平均应力P′cs CU1 100 1.051 124 CU2 100 0.980 325 CU3 200 0.964 438 CU4 400 0.942 580 表 2 空心圆柱循环扭剪试验参数
Table 2 Parameters of hollow cylinder torsional tests
试验编号 p′0 固结后ecs τd CRR NL ψ HCA1 100 0.984 7.5 0.106 40 -0.166 HCA2 100 0.988 10.0 0.141 14 -0.163 HCA3 100 0.994 12.5 0.177 3 -0.162 HCA4 200 0.969 15.0 0.106 98 -0.215 HCA5 200 0.978 20.0 0.141 25 -0.206 HCA6 200 0.975 25.0 0.177 5 -0.209 HCA7 300 0.958 22.5 0.106 220 -0.258 HCA8 300 0.963 30.0 0.141 39 -0.254 HCA9 300 0.959 37.5 0.177 11 -0.258 -
[1] XU C S, FENG C Q, DU X L, et al. Study on liquefaction mechanism of saturated sand considering stress redistribution[J]. Engineering Geology, 2020, 264: 105302. doi: 10.1016/j.enggeo.2019.105302
[2] NI X Q, ZHANG Z, YE B, et al. Unique relation between pore water pressure generated at the first loading cycle and liquefaction resistance[J]. Engineering Geology, 2022, 296: 106476. doi: 10.1016/j.enggeo.2021.106476
[3] 左康乐, 顾晓强. 不同粒径比下含细颗粒砂土液化特性的试验研究[J]. 岩土工程学报, 2023, 45(7): 1461-1470. doi: 10.11779/CJGE20220401 ZUO Kangle, GU Xiaoqiang. Experimental study on liquefaction characteristics of sand with fines under different particle size ratios[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(7): 1461-1470. (in Chinese) doi: 10.11779/CJGE20220401
[4] SEED H B, MARTIN P P, LYSMER J. The Generation and Dissipation of Pore Water Pressures During Soil Liquefaction[M]. Berkeley: College of Engineering, University of California, Berkeley. 1975.
[5] GREEN R A, MITCHELL J K, POLITO C P. An energy-based excess pore pressure generation model for cohesionless soils[C]// Proceedings of the John Booker Memorial Symposium, Sidney Australia. Rotterdam: A A Balkema Publishers. 2000.
[6] QADIMI A, COOP M R. The undrained cyclic behaviour of a carbonate sand[J]. Géotechnique, 2007, 57(9): 739-750. doi: 10.1680/geot.2007.57.9.739
[7] JEFFERIES M, BEEN K. Soil liquefaction: a critical state approach[M]. Boca Raton: CRC press, 2015.
[8] QADIMI A, MOHAMMADI A. Evaluation of state indices in predicting the cyclic and monotonic strength of sands with different fines contents[J]. Soil Dynamics and Earthquake Engineering, 2014, 66: 443-458. doi: 10.1016/j.soildyn.2014.08.002
[9] PORCINO D D, TRIANTAFYLLIDIS T, WICHTMANN T, et al. Using different state parameters for characterizing undrained static and cyclic behavior of sand with non-plastic fines[J]. Soil Dynamics and Earthquake Engineering, 2022, 159: 107318. doi: 10.1016/j.soildyn.2022.107318
[10] HIGHT D W, GENS A, SYMES M J. The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils[J]. Géotechnique, 1983, 33(4): 355-383. doi: 10.1680/geot.1983.33.4.355
[11] LI X S, CAI Z Y. Effects of low-number previbration cycles on dynamic properties of dry sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(11): 979-987. doi: 10.1061/(ASCE)1090-0241(1999)125:11(979)
[12] CAI Z. A Comprehensive Study of State-Dependent Dilatancy And its Application in Shear Band Formation Analysis[D]. Hong Kong: Hong Kong University of Science and Technology, 2001.



 下载:
下载: