Coupling analysis on mechanical properties of near-well interface of methane hydrate-bearing sediments under depressurization exploitation
-
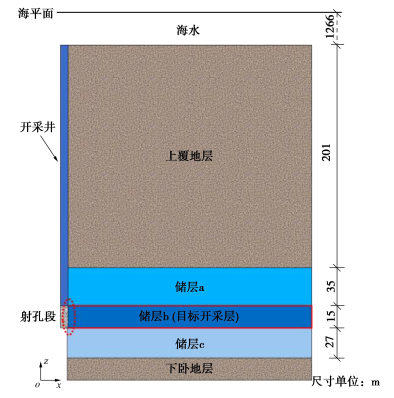
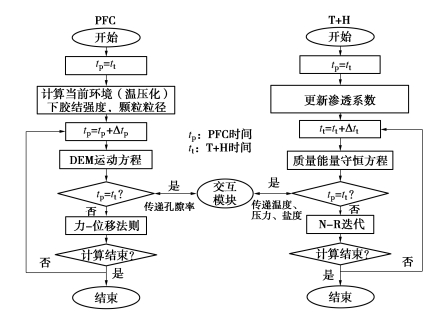
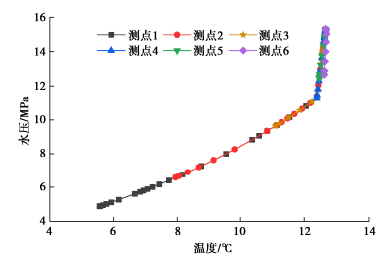
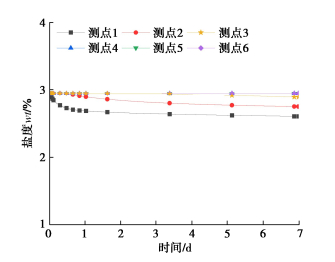
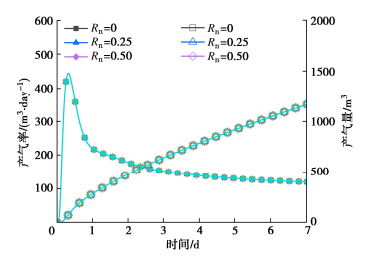
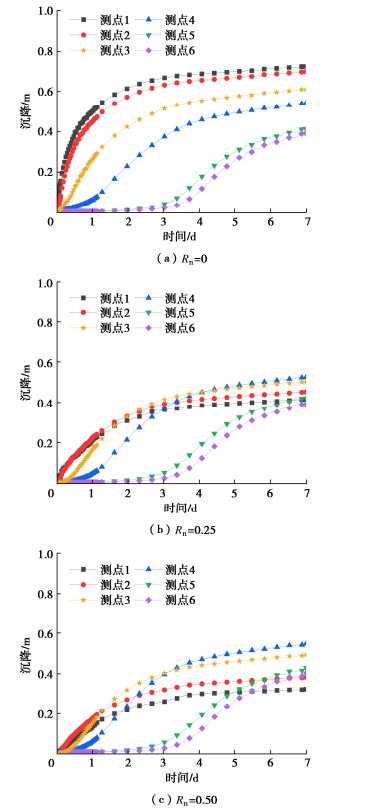
摘要: 天然气水合物作为最有潜力的清洁能源之一备受关注。开采过程中水合物分解将使近井水合物沉积物(即深海能源土)力学特性劣化,引起系列开采风险及工程地质灾害。针对目前大多数研究未从微观角度着眼于开采中的能源土-井筒结构接触界面特性变化,采用实用型水合物开采多场耦合分析框架TOUGH+HYDRATE+PFC,考虑相对更为真实的能源土-井筒接触界面的不同情况,开展了降压开采多场耦合数值模拟,对近井土体以及井筒本身的力学响应进行了对比分析,探讨了井筒表面粗糙度对于开采中土体、井筒间的相互作用的影响规律。结果表明:①不同的井筒表面粗糙程度未对温压化及开采效率方面产生明显影响。②适当提高井筒表面的粗糙程度可有效地减小接触土体沉降幅度,增强井壁接触区域的土体稳定性,降低开采风险以保证开采能够相对稳定地长期进行。③井筒粗糙度的增大会导致井筒受到更大的摩擦力,需控制井筒表面不能过于粗糙以防止井筒本身受力过大影响而失稳破坏。Abstract: The methane hydrate (MH) has been attracting extensive attention as one of the most potential clean energy sources. During its exploitation, hydrate dissociation induces the weakening of mechanical properties of near-well MH bearing sediments (MHBS), which can result in series of engineering problems. Given that most current researches do not focus on the interface properties of MHBS-well structure during exploitation, the practical multi-field TOUGH+HYDRATE+PFC coupling framework is adopted, and considering different conditions of a more real MHBS-well interface, the multi-field coupling numerical simulation of depressurization is performed. Comparison and analysis are made on the mechanical properties of near-well soil and the well, and the influences of surface roughness on wellbore stability are discussed. The results show that: (1) Different well roughnesses doesn't have obvious influences on the thermal-mechanical-chemical evolution and production efficiency. (2) Appropriately increasing the surface roughness of the well can effectively reduce the settlement amplitude of the contact soil, enhance the stability of soil in the contact area with the wellbore, and reduce the risk to ensure a relatively stable long-term production. (3) The increase of well roughness will lead to greater frictional force on the well. It is necessary to control the well surface not to be too rough, in order to prevent the wellbore itself from suffering the impact of the excessive forces, destabilizing and becoming failure.
-
0. 引言
疲劳作用是影响岩石工程安全和长期服役性能的关键问题,一直以来都是研究热点[1-4]。不少学者试图采用各种方法进行岩石疲劳变形和损伤的量化表征:Tao等[5]结合热力学和内时理论,通过强调材料本身内蕴时间的塑性变形特征,建立了应力应变的疲劳本构方程;Xiao等[6]用循环次数的对数函数对比损伤曲线对试验数据进行拟合,构建了考虑初始损伤的疲劳本构;Sun等[7]在Chaboche疲劳损伤模型基础上建立多轴疲劳模型,准确描述了多轴应力下的岩石疲劳损伤;蔡燕燕等[8]对循环加载的初始轴向应变速率归一化后得到其与损伤因子的线性关系;Liu等[9]和Li[10]等研究单个循环滞回圈内裂隙扩展和能量耗散规律,运用损伤力学描述第i次循环内的损伤变化,但未考虑疲劳过程中循环次数累加对岩石性能的影响。上述研究虽然定量描述了岩石的疲劳损伤过程,但大多存在参数物理意义不明确,对疲劳变形与循环加卸载次数等关键因素的考量不充分等问题。
根据Momeni等[11]、Liu等[12]、葛修润等[13]和冯春林等[14]的试验研究可知,岩石疲劳破坏时的不可逆变形可分为初始变形、等速变形和加速变形三阶段,这与岩石蠕变试验结果极为相似。葛修润[15]还曾提出疲劳破坏与流变破坏似乎是“同源”的基本观点(部分学者将蠕变称作为“静疲劳”)。事实上,当加卸载频率确定时,循环加卸载次数可以视作为一个规律性的时间函数。鉴于流变模型能较好反映变形对时间的敏感性,学者开始尝试利用蠕变模型描述岩石疲劳变形。Fuenkajorn等[16]假定疲劳变形是黏塑性变形的积累,建立了岩石疲劳模型。Khaledi等[17]采用弹黏塑性蠕变模型预测岩盐在施工和循环运行阶段洞室周围的应力—应变关系。王军保等[18]、郭建强等[19]分别利用流变元件构建了围压条件下低频循环作用疲劳变形的Burgers模型,及单轴循环荷载下的黏弹塑性岩石疲劳模型。上述研究主要利用正弦函数计算疲劳等效应力,此方法难以合理解释修正系数的原因,同时也不能合理反映加卸载频率和幅值对岩石疲劳变形的影响。当蠕变与疲劳“同源”观点缺乏足够论据支持,直接运用流体元件对疲劳变形进行描述,有失科学严谨性。
本文在大理岩蠕变与疲劳试验数据基础上,首先对时间、变形、疲劳荷载的循环次数进行归一化处理,验证蠕变与疲劳的“同源性”假说。在等寿命Gerber曲线方程与Goodman直线方程基础上提出疲劳应力等效化方法,确定疲劳等效应力。最终,改进西原模型中元件,提出7参数岩石非线性疲劳变形本构模型。
1. 岩石疲劳与蠕变试验
1.1 试样准备
岩样为白色粗晶粒大理岩,质地均匀,无杂质,少裂隙,完整性和均匀性较好。岩样的加工制作符合国际岩石力学学会(ISRM)试验规程,长度为100 mm,直径为50 mm),两端平整度在0.02 mm以内。在试验前,各试验用岩样均经过横纵波波速测试(其中横波:2198~2582 m/s,纵波:3817~4256 m/s),并去除波速异常试样,保证试样的一致性。
1.2 试验方案
试验仪器为TFD—2000/D型电液伺服三轴压缩试验机。试验步骤如下:①单调加载压缩变形试验,获取应力-应变全过程关系曲线(详见文献[8]),确定蠕变和疲劳试验中荷载幅值;②疲劳试验:开展0~90%,0~80%,0~70%峰值强度下低周疲劳荷载试验(加载方式为正弦波,频率为0.01 Hz),记录应力、应变数据,研究疲劳破坏特征和疲劳塑性应变变化规律;③蠕变试验:开展95%,90%,80%峰值强度下蠕变试验,记录应变数据,以研究变形规律。
1.3 试验结果
不同应力幅值疲劳试验应力-应变关系结果如图1所示,在应力幅值为70%峰值应力时,岩石经400次大幅值循环后,变形未发生明显退化,故认为其不会发生疲劳破坏。由图1可知:①疲劳应力幅值越大,破坏所需的循环荷载次数越少;②随着循环次数增加残余应变不断发展,滞回圈随之向右移动,且幅值越大,移动越显著;③首次加卸载滞回圈的面积较大,且在上限应力较大时从第二次循环之后,随着循环次数增加,滞回圈右移速度先减小后稳定再增加,且滞回圈面积明显增大。
图2为蠕变变形-时间关系曲线与残余变形-荷载循环次数关系曲线,从图中可以看出二者在形态上具有很强的相似性,均可大致分为a,b,c三类:a类一般出现在上限应力较大的条件下,变形随时间或循环次数增加,快速增长直至破坏;b类,应变率呈现快—慢—快趋势,可以明显观察到破坏阶段;c类常出现在上限应力较小的条件下,应变最终趋于稳定。显然,可将岩石蠕变与疲劳破坏过程根据应变率划分为减速、等速和加速3个阶段。
2. 蠕变与疲劳“同源”性
从第1节可知蠕变变形曲线与疲劳变形曲线存在宏观相似性,但蠕变时间和循环加卸载次数仍是具有两种不同量纲形式的物理量,蠕变变形和疲劳残余变形的物理意义也有所区别。鉴于此,分别对蠕变试验中的时间和变形,以及疲劳试验中的循环加卸载次数和残余变形,进行归一化处理:
D1=ti−t0tn−t0 , D2=εti−εt0εtn−εt0 ,D3=Ni−N1Nn−N1 ,D4=εNi−εN0εNn−εN0 。} (1) 式中 D1,D2,D3,D4分别为蠕变时间与蠕变变形、疲劳荷载循环次数与残余变形的归一化变量;t0,
εt0 ,N1,εN0 分别为与前述变量依次对应的初始变量;tn,εtn ,Nn,εNn 分别为末变量;ti,εti ,Ni,εNi 分别为中间任意时刻变量。将归一化后的蠕变与疲劳试验数据绘制于对数坐标中,如图3所示,曲线近似为直线。由图可见:①结合图2可知,两者在上限应力比相近或处于同种变形类型时,其对数关系曲线接近甚至重合;②虽然疲劳与蠕变在同类型变形状态的应力峰值相近,但时间尺度上快慢不一。D1与D3相差100倍左右,D2与D4相差1000倍左右,表明蠕变时间和疲劳加卸载循环次数对变形的敏感度不相等。上述现象表明:蠕变与疲劳不仅在三阶段的变形形态上具有相似性,其归一化后变形和时间(循环次数)的无量纲变量上也存在相近关系,也印证了“同源”性假说。因此,参考蠕变模型构建疲劳变形模型是切实可行的,首先需要分析疲劳变形构成,进行疲劳作用的应力等效化处理。
3. 疲劳应变构成与应力等效化
3.1 岩石疲劳变形构成
岩石疲劳塑性应变是由每个循环内微小的塑性变形累积而成。借鉴岩石流变学理论,认为岩石疲劳变形总量
εp(N) 也由弹性应变εe(N) 、黏弹塑性应变εve(N) 及黏塑性应变εvp(N) 三类变形组成,即Δεpi(Ni)=εve(Ni)+εvp(Ni) ,εp(N)=Δεp1(N1)+Δεp2(N2)+ Δεpi(Ni)+⋯+ΔεpN(NN)+εe(N) 。} (2) 式中
εp(N) 为总疲劳变形;Δεpi(Ni) ,Δεve(Ni) ,Δεvp(Ni) ,ΔεpN(NN) 分别为第i个循环周期的塑性变形、黏弹塑性应变和黏塑性应变、末次循环周期的塑性变形。但式(2)不能描述第三阶段加速变形段的非线性变形趋势,故进一步将黏塑性应变分为线性黏塑性应变
Δεvp(Ni) 和非线性黏塑性应变ε′vp(Ni) 。当岩石所受应力超过疲劳应力门槛值σav 时:若循环次数Ni<Ns (Ns 为进入非线性变形时临界循环次数),则只发生线性黏塑性变形,此时岩石为理想黏塑性体:Δεpi(Ni)=εve(Ni)+εvp(Ni)。 (3) 若循环次数
Ni>Ns ,存在非线性黏塑性变形,为非线性黏塑性体:Δεpi(Ni)=εve(Ni)+εvp(Ni)+ε′vp(Ni)。 (4) 3.2 疲劳应力等效方法
关于疲劳应力等效问题,Wohler首次提出采用应力-寿命曲线描述疲劳行为,并提出了“疲劳极限”
σR (R=σmax/σmin ,R为应力上、下限的比值),见图4。图4中,σmax1,σmax2 为循环最大应力值,N1,N2为对应的寿命值,这一概念与岩石的长期强度类似。随后,Gerber提出了考虑平均应力影响的疲劳寿命计算方法,见下式[20]:σaσ-1+(σnσc)2=1 , (5) 式中
σa 为应力振幅,σa= σmax−σmin2 ;σmax ,σmin 为加卸载最大、最小偏应力;σ-1 为材料的疲劳极限值;σn 为加卸载平均偏听偏应力,σn=σmax+σmin2= Δσ2 ;σc 为单调加载下的材料抗压强度。Goodman进一步提出考虑平均应力的简化理论,见下式:
σaσ-1+σnσc=1 。 (6) Gerber与Goodman方程强调在对称循环荷载下(
σmax=−σmin ,R=-1),一定寿命N时的平均应力与幅值关系(如图5所示)。当R为变量时,等寿命曲线与R=-1时的曲线形态相同(如图4,6所示)。可以推断,将两个公式推广至一般的等幅循环荷载条件下也同样适用。图6中每个R都对应一个疲劳极限应力,而σR 与材料寿命存在对应的系数关系,则利用广义Gerber方程与广义Goodman方程求出的σR 可视为一种循环应力下的初步等效应力σe 。运用广义Goodman方程求解初步等效应力时其数值偏大,而利用广义Gerber公式确定初步等效应力时数值又偏小。为使所求初步等效应力更接近真实状态,本文所采取的确定方法为从广义Gerber曲线的外切线与广义Goodman直线之间进行折中取值,以保证大多数应力环境下疲劳荷载的初步等效应力更加合理。令σc =1.0,见图5与下式:σe=σa1.125−σn/σc 。 (7) 式中,
σe 为材料的循环初步等效应力,依次计算岩石疲劳荷载下的初步等效应力水平。图7为运用式(7)求得的初步等效应力,该曲线处在广义Gerber曲线与广义Goodman曲线之间。
初步等效应力只考虑了循环应力上下限的影响,对于岩石类材料,加载频率对岩石的受力性能也有重要的影响,进一步降低应力峰值强度,因此需修正初步等效应力。加卸载频率可反映加载速率引起摩擦内能累积,故引入黏弹性模型公式[21-22]:
σT=σe+η˙εz, (8) 式中,
σT 为循环等效应力,˙εz=4σaf/E 为轴向应变率。将式(7)代入式(8),建立考虑疲劳荷载频率的等效应力公式为
σT=σa1.125−σn/σc+4ησaEf, (9) 式中,
f 为加卸载周期频率,η ,E分别为材料黏性系数和模量系数。4. 疲劳变形本构模型
4.1 疲劳元件
根据前述疲劳变形与等效应力分析,定义疲劳模型中的元件,如图8所示。
图8(a)为弹性疲劳元件,由胡克体构成,当瞬时施加应力
σT 后,弹性疲劳元件产生瞬时弹性应变:σT=E ε(N), (10) 式中,E为弹性疲劳系数。
图8(b)为黏性疲劳元件,由牛顿流体构成,疲劳应力作用下变形随循环次数的增加而增加,其方程为
σT=η˙ε, (11) 式中,η为牛顿体的黏滞系数,
˙ε=dεve(N)dNf ,εve(N) 为黏性应变,dεve(N)dN 为每个循环周期黏性应变增量。对式(11)进行积分,则
ε=σTη⋅Nf+C, (12) 式中,C为常数。
不难看出,由牛顿体构成的黏性疲劳元件无弹性后效,具有永久变形。
图8(c)为摩擦疲劳元件,由摩擦片表示。当疲劳等效应力或应力上限超过临界应力值时,即使应力或循环次数不再增加(即超过临界值时f无限小),变形仍持续增加,其方程为
σT<σcr (ε=σTE) ,σT≥σcr (ε→∞) 。} (13) 式中,
σcr 为临界应力。4.2 疲劳模型建立
西原模型作为传统流变模型,能够描述蠕变三阶段,形式简洁,应用广泛。故可将西原模型中各元件替换成疲劳元件,从而得到西原疲劳模型,如图9(a)所示。
Kelvin体在荷载作用下同时产生可逆与不可逆变形,与荷载超过门槛值
σve 时岩石才有不可逆变形矛盾。为此,将Kelvin体替换为带有疲劳摩擦片的村山体(由疲劳弹性元件、疲劳黏性元件和塑性疲劳元件并联而成),以描述疲劳的减速与等速变形阶段。另外西原疲劳模型中Bingham体模型为线性函数,而一般疲劳变形第三阶段为加速的非线性变形,所以将Bingham体改进为非线性元件,变换后的非线性黏弹塑性疲劳模型见图9(b)。根据流变力学元件理论,在串联组件中,总应力与各元件应力相等,总应变等于各元件的应变总和。并联组件中,总应力等于各元件应力之和,各组件应变相等,这些基本原则同样适用于疲劳元件。假设岩石抵抗变形的能力为抵抗不可回弹变形的门槛值
σve ,又根据本文试验和大量试验[11-15]均表明岩石疲劳破坏存在门槛值σav ,即:只有当σmax>σs 且σT>σav 同时满足时,岩石才会发生疲劳破坏;而当σmax<σav 时,岩石不会发生疲劳破坏,因此可得不同应力状态下的疲劳变形本构方程:(1) 当
σT<σve 时,不会产生残余变形,只有Hooke体发挥作用,本构方程为σT=σΗ=EMεe(N)=EMεp(N), (14) 循环N次后应变为
εp(N)=εe(N)=σTEM, (15) 式中,
EM 为Hooke体弹性疲劳系数,σH 为Hooke体所受应力。(2)当
σmax>σs ,σT≤σav ,σve≤σT 时,应力达到变形门槛值,但未达到疲劳破坏门槛值,只有Hooke体和村山体工作,村山体上状态方程为σT=σH=σC=EKεve+ηKdεve(N)dNf+σve。 (16) 式中
σC 为村山体上所受应力;ηΚ 为村山体的黏滞系数;EK 为村山体的弹性疲劳系数;εve(N) 为黏弹塑性应变;dεve(N)dN 为每个循环周期黏弹性应变增量;f 为周期频率。对式(16)积分可得
εve(N)=σT−σveEK{1−exp[−EKηK(Nf)]}。 (17) 循环N次后总应变为
εp(N)=εe(N)+εve(N)=σTEM+σT−σveEK{1−exp[−EKηK(Nf)]}。 (18) (3)当
σmax≥σs ,σT>σav 且N≤NS 时,岩石进入加速破坏阶段,此时变形主要为线性Bingham黏塑性变形,应力关系有σT=σH=σC=σB=σav+σN=σav+ηMdεvp(N)dNf, (19) 式中,
ηΜ 为Bingham黏塑性体的黏滞系数,dεvp(N)dN 为每个循环周期黏塑性应变增量。σB 为Bingham体上所受应力,σN 为Bingham体中黏性疲劳元件上所受应力。循环N次后总应变为
εp(Ν)=εe(Ν)+εve(Ν)+εvp(Ν)=σTΕΜ+σTΕΚ+ηΚfΔ+σT−σavηΜfΔ, (20) 式中,
Δ=∂∂c ,∂c∂N 为对变量N求偏导。整理式(20),可得串联模型的本构模型为
(η M fE K+η K fE K+η M fEM)˙σT+η Kη M f2E KEM¨σT+(σT−σav−η Kσav fΔE K)=η M f˙εΡ(N)+η Kη Mf2E K¨εΡ(N)。 (21) 同时结合式(18),(21)可得疲劳模型的本构模型如下:
εp(N)=σT(1EM+1EK)−σT−σveEKexp(−EKΝηΚf)+σT−σavηΜ(Νf)=σT(1EM+1EK)+Ρ(N)+Q(N), (22) 式中,
Ρ(N)=−σT−σveEKexp(−EKNηΚf) ,Q(N)=σT−σavηΜ(Nf) 。从式(22)可分析得出:当
N 趋于零或f无限大时,可以认为岩石在σT 作用下有瞬时弹性变形;当f无限接近零时,视为岩石在平均荷载σm 作用下蠕变变形,如图10所示。当N无限大时,函数Ρ(N) 主要描述了岩石等速变形阶段的变形特征,而函数Q(N) 主要描述了加速阶段的变形特点。可以看出,模型中的理想黏塑性体可以很好地描述b类疲劳荷载下岩石变形,岩石存在进入长期疲劳的应力门槛阀值,只有达到阀值时,才会出现等速蠕变,这与实际情况相符。此外,Q(N) 函数只是关于N的线性函数,还无法准确描述岩石后期加速疲劳的非线性变形特征。(4)
σmax≥σs 且σav≤σT ,N>NS 时,岩样进入非线性加速疲劳阶段,岩石的黏滞系数随循环次数的增大而逐渐降低。孙均[23]提出了一种非线性的流变的黏性元件经验本构关系式:˙ε=Ασmtn−1。 (23) 但此模型对进入加速流变的时间敏感性并不强。将其改进为疲劳荷载下加速变形段的本构方程:
˙εvp=dεvpdN=σ′B−σavηΜ(1+Ασmn〈N−Nsf〉n−1)1f。 (24) 式中
A,m,n 均为与岩石性质相关的系数;Ns 为进入加速变形段时的循环次数;σ′B 为改进后的加速度段非线性Bingham黏塑性体上所受应力;< >内部为开关函数:〈N−Nsf〉={0 (N≤Ns)N−Nsf (N>Ns) 。 (25) 不同岩石进入加速变形阶段所需循环圈次数不同,内部损伤也不一样,故定义此时完整度参数
η0 ,以表示岩石进入加速变形时的变形快慢程度。在某个特定应力下,式(24)可简化为˙εvp=dεvpdN=σ′B−σavηΜ(1+nη0〈N−Nsf〉n−1)1f 。 (26) 当
σmax≥σs ,σT≥σav,N≤Ns 时,结合式(25),(26)得σT=σ′B=σav+ηΜdεvpdNf。 (27) 当
σmax≥σs ,σT≥σav,N>Ns 时,得σT=σ′B=σav+ηΜdεvpdNf=σav+ηΜdεvpdNf1+nη0(N−Nsf)n−1。 (28) 至此,建立的非线性黏弹塑性疲劳模型为

(29) 4.3 疲劳模型分析
当N无穷大且满足
σmax≥σs ,σT≥σav,N<Ns 时,整理式(29)可得εΡ(N)=(σTEM+σT−σv eEK)−σT−σv eEKexp(−EKNηΚf)+σT−σa vηΜ(Nf)=(σTEM+σT−σv eEK)+Ρ′1(N)+Q′1(N), (30) 式中,
Ρ′1(N)=−σT−σveEKexp(−EKNηΚf) ,Q′1(N)= σT−σavηΜ(Nf) 。 当N无穷大且满足
σT≥σav,N>Ns 时,整理式(29)可得εΡ(N)=(σTEM+σT−σveEK)−σT−σveEKexp(−EKNηΚf)+σT−σavηΜ[Nf+1η0(N−Nsf)n]=(σTEM+σT−σveEK)+Ρ′2(N)+Q′2(N,n), (31) 式中,
Ρ′2(N)=−σT−σveEKexp(−EKNηΚf) ,Q′2(N,n)= σT−σavηΜ(Nf+1η0(N−Nsf)n) 。对式(30),(31)分析可知:
σT ≥σav ,N无穷大时,σTEM+σT−σveEK 为元件的瞬时弹性应变,由弹性元件产生,函数Ρ′1(N) 和Ρ′2(N) 都收敛于0,为控制等速疲劳变形阶段的函数;当N<Ns 时,Q′1(N) 为线性函数控制等速疲劳变形段的变形;当N>Ns ,且σ≥σav 时,Q′2(N,n) 为发散的非线性函数,可描述加速变形阶段的非线性变化规律。5. 模型适用性验证
运用新构建的非线性疲劳模型对试验和文献数据进行拟合,对各参数利用线性内插法确定各参数值,验证模型的适用性。
拟合参数见表1,2,计算结果见图11。从图11中可以得到如下结论:①图11(a)显示,70%峰值的疲劳试验中最大幅值低于破坏门槛值,岩样未发生破坏,模型中只有Hooke体与村山体工作,效果良好。90%峰值和80%峰值的疲劳试验中最大幅值试验均超过破坏门槛值和疲劳门槛值,曲线拟合结果较好。另外,表2中大理岩的模型疲劳参数
EM ,EK ,ηΚ ,ηΜ 值较其他种类岩石较大,表明大理岩具有黏性较高和延展性较好的特点,与实际相符。②从图11(b),(c)中得出,在单轴疲劳试验中加载幅值的影响程度高于比频率的影响;图11(d),(e)为文献[12]中不同围压下的疲劳试验结果,结合表2中可知,随着围压的增大,η 和EM 呈现不同程度增加趋势,而其他参数ηK ,ηM 减小,随着围压增加,晶体所需运动能增加,因此η 增大,且岩样EM 也随之增大,其疲劳延展性下降,故ηK ,ηM 减小。而当材料参数n一定时,10 MPa的岩样破坏完整度参数η0 明显低于2 MPa的破坏岩样,这一现象也与实际试验现象相符。此外,图12为不同条件下岩石进入加速段时完整度η0 分布图。由图12可知,对于同种岩石,随着破坏时所需循环次数的增加,η0 越来越小。这一趋势说明由于循环次数增加内部积累损伤更大,岩样完整度降低,加速疲劳阶段应变急剧变化。综上可见,新模型各参数能较全面地反映岩石的疲劳变形和损伤特性。表 1 各类岩样的荷载条件Table 1. Load conditions of various types of rock samples文献 岩石种类 单调加载强度 σc /MPa破坏门槛值 σs /MPa变形门槛值 σve /MPa循环荷载值/MPa 频率 f /Hzσmin σmax 文献[11] 花岗岩A56 112.35 89.88 3.00 28.09 106.73 0.2 文献[11] 花岗岩A47 112.35 89.88 3.00 28.09 106.73 1.0 文献[11] 花岗岩A22 112.35 89.88 3.00 22.47 101.11 1.0 文献[12] 砂岩S2 87.55 70.04 2.00 10.00 80.00 0.1 文献[12] 砂岩S2 87.55 70.04 2.00 10.00 80.00 1.0 文献[12] 砂岩S10 134.08 107.26 2.00 10.00 117.30 0.1 文献[12] 砂岩S10 134.08 107.26 2.00 10.00 117.30 1.0 文献[14] 白砂岩#5 119.60 95.68 3.00 23.92 101.66 0.2 文献[14] 白砂岩#3 119.60 95.68 3.00 35.88 107.64 0.2 文献[14] 白砂岩#1 119.60 95.68 3.00 35.88 95.68 0.2 6. 结论
(1)通过对疲劳试验和蠕变试验结果进行归一化处理,发现二者在变形和时间(循环次数)的无量纲变量上存在相近的曲线关系,某种意义上证明了蠕变和疲劳变形具有“同源”性的假说具有一定合理性,其内在力学机理有待进一步研究。
(2)提出一个新的疲劳应力等效计算方法,将传统西原模型中Kelvin体替换成带有开关功能的村山体,并将黏塑性体中的线性黏性元件替换为非线性黏性元件,从而建立了一种可描述岩石疲劳变形的7参数非线性疲劳变形本构模型。该模型可较好得描述岩石衰减、等速、加速疲劳变形的三阶段疲劳特征。
(3)对同一种岩石,模型参数n不变,岩石完整度
η0 随着疲劳破坏次数增加而减小,随着围压增大而减小,与疲劳试验中岩石破碎结果相一致,这表明完整度参数与岩石损伤存在一定关系。 -
表 1 水合物分解模型参数
Table 1 Parameters for methane hydrate dissociation
类型 参数名称 数值 颗粒接触参数 颗粒模量/MPa 700 颗粒法切向刚度比 5.0 颗粒抗转动系数 0.25 颗粒局部压碎系数 4.0 颗粒摩擦系数 0.5 胶结参数 水合物泊松比 0.32 水合物临界长细比 0.05 水合物半径乘子 0.800 T+H输入参数 地层渗透率/m2 2×10-14 土体密度/(kg·m-3) 2650 孔隙率/% 50 土体比热容/(J·kg-1·K-1) 1000 饱和导热系数/(W·m-1·K-1) 2.9 非饱和导热系数/(W·m-1·K-1) 1.0 表面活化能/K 78151 固有分解参数/(mol·m-2·Pa-1·s-1) 8.3×104 -
[1] YAN C L, REN X, CHENG Y F, et al. Geomechanical issues in the exploitation of natural gas hydrate[J]. Gondwana Research, 2020, 81: 403-422. doi: 10.1016/j.gr.2019.11.014
[2] LI X S, XU C G, ZHANG Y, et al. Investigation into gas production from natural gas hydrate: a review[J]. Applied Energy, 2016, 172: 286-322. doi: 10.1016/j.apenergy.2016.03.101
[3] XU W Y, GERMANOVICH L N. Excess pore pressure resulting from methane hydrate dissociation in marine sediments: a theoretical approach[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B1): B01104.
[4] KWON T H, SONG K I, CHO G C. Destabilization of marine gas hydrate-bearing sediments induced by a hot wellbore: a numerical approach[J]. Energy & Fuels, 2010, 24(10): 5493-5507.
[5] RUTQVIST J, MORIDIS G J, GROVER T, et al. Coupled multiphase fluid flow and wellbore stability analysis associated with gas production from oceanic hydrate-bearing sediments[J]. Journal of Petroleum Science and Engineering, 2012, 92/93: 65-81. doi: 10.1016/j.petrol.2012.06.004
[6] HU T, WANG H N, JIANG M J. Analytical approach for the fast estimation of time-dependent wellbore stability during drilling in methane hydrate-bearing sediment[J]. Journal of Natural Gas Science and Engineering, 2022, 99: 104422. doi: 10.1016/j.jngse.2022.104422
[7] BIRCHWOOD R, NOETH S, HOOYMAN P, et al. Wellbore stability model for marine sediments containing gas hydrates[C]// Proceedings of the Proceedings, American Association of Drilling Engineers National Conference and Exhibition, Houston, 2005.
[8] 王华宁, 郭振宇, 高翔, 等. 含水合物地层井壁力学状态的弹塑性解析分析[J]. 同济大学学报(自然科学版), 2020, 48(12): 1696-1706. WANG Huaning, GUO Zhenyu, GAO Xiang, et al. Elastoplastic analytical investigation of mechanical response of wellbore in methane hydrate-bearing sediments[J]. Journal of Tongji University (Natural Science), 2020, 48(12): 1696-1706. (in Chinese)
[9] LI Q C, CHENG Y F, ZHANG H W, et al. Simulating the effect of hydrate dissociation on wellhead stability during oil and gas development in deepwater[J]. Journal of Ocean University of China, 2018, 17(1): 35-45. doi: 10.1007/s11802-018-3544-4
[10] KIM A R, KIM J T, CHO G C, et al. Methane production from marine gas hydrate deposits in Korea: thermal-hydraulic-mechanical simulation on production wellbore stability[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(11): 9555-9569. doi: 10.1029/2018JB015875
[11] SUN J X, NING F L, LEI H W, et al. Wellbore stability analysis during drilling through marine gas hydrate-bearing sediments in Shenhu Area: a case study[J]. Journal of Petroleum Science and Engineering, 2018, 170: 345-367. doi: 10.1016/j.petrol.2018.06.032
[12] 李阳, 程远方, 闫传梁, 等. 南海神狐海域水合物地层多物理场耦合模型及井壁坍塌规律分析[J]. 中南大学学报(自然科学版), 2022, 53(3): 976-990. LI Yang, CHENG Yuanfang, YAN Chuanliang, et al. Multi-physical field coupling model of hydrate formation and analysis of wellbore collapse law in Shenhu Area of South China Sea[J]. Journal of Central South University (Science and Technology), 2022, 53(3): 976-990. (in Chinese)
[13] 张玉, 李建威, 畅元江, 等. 考虑气水两相流固耦合下可燃冰降压分解对井壁稳定性影响[J]. 中国石油大学学报(自然科学版), 2023, 47(1): 148-155. doi: 10.3969/j.issn.1673-5005.2023.01.016 ZHANG Yu, LI Jianwei, CHANG Yuanjiang, et al. Effect of depressurization decomposition of combustible ice on wellbore stability considering gas-water two-phase hydro-mechanical coupling[J]. Journal of China University of Petroleum (Edition of Natural Science), 2023, 47(1): 148-155. (in Chinese) doi: 10.3969/j.issn.1673-5005.2023.01.016
[14] 李莅临, 杨进, 路保平, 等. 深水水合物试采过程中地层沉降及井口稳定性研究[J]. 石油钻探技术, 2020, 48(5): 61-68. LI Lilin, YANG Jin, LU Baoping, et al. Research on stratum settlement and wellhead stability in deep water during hydrate production testing[J]. Petroleum Drilling Techniques, 2020, 48(5): 61-68. (in Chinese)
[15] LI J F, YE J L, QIN X W, et al. The first offshore natural gas hydrate production test in South China Sea[J]. China Geology, 2018, 1(1): 5-16. doi: 10.31035/cg2018003
[16] YE J L, QIN X W, XIE W W, et al. The second natural gas hydrate production test in the South China Sea[J]. China Geology, 2020, 3(2): 197-209. doi: 10.31035/cg2020043
[17] 张超鹏, 陈立超, 张典坤, 等. 非常规油气固井材料发展现状及趋势浅析[J]. 世界石油工业, 2023, 30(6): 1-10. ZHANG Chaopeng, CHEN Lichao, ZHANG Diankun, et al. Analysis on development status and trend of new cementing materials for deep unconventional oil and gas[J]. World Petroleum Industry, 2023, 30(6): 1-10. (in Chinese)
[18] LINGS M L, DIETZ M S. The peak strength of sand-steel interfaces and the role of dilation[J]. Soils and Foundations, 2005, 45(6): 1-14. doi: 10.3208/sandf.45.1
[19] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[20] 蒋明镜, 付昌, 贺洁, 等. 不同开采方法下深海能源土离散元模拟[J]. 岩土力学, 2015, 36(增刊2): 639-647. JIANG Mingjing, FU Chang, HE Jie, et al. Distinct element simulations of exploitation of methane hydrate bearing sediments with different methods[J]. Rock and Soil Mechanics, 2015, 36(S2): 639-647. (in Chinese)
[21] JIANG M J, SUN R H, ARROYO M, et al. Salinity effects on the mechanical behaviour of methane hydrate bearing sediments: a DEM investigation[J]. Computers and Geotechnics, 2021, 133: 104067. doi: 10.1016/j.compgeo.2021.104067
[22] MORIDIS G J. User's Manual for the Hydrate v1.5 Option of TOUGH+ v1. 5: A Code for the Simulation of System Behavior in Hydrate-Bearing Geologic Media[R]: Lawrence Berkeley National Lab (LBNL), Berkeley, CA (United States), 2014.
[23] 蒋明镜, 陈意茹, 卢国文. 一种实用型深海能源土多场耦合离散元数值方法[J]. 岩土工程学报, 2021, 43(8): 1391-1398. JIANG Mingjing, CHEN Yiru, LU Guowen. A practical multi-field coupling distinct element method for methane hydrate bearing sediments[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(8): 1391-1398. (in Chinese)
[24] JIANG M J, LU Y X, WANG H N, et al. Multi-field coupling analysis of mechanical responses in methane hydrate exploitation with a practical numerical approach combining T+H with DEM[J]. Computers and Geotechnics, 2024, 166: 105978. doi: 10.1016/j.compgeo.2023.105978
[25] UESUGI M, KISHIDA H. Frictional resistance at yield between dry sand and mild steel[J]. Soils and Foundations, 1986, 26(4): 139-149. doi: 10.3208/sandf1972.26.4_139
[26] YANG T, JIANG S Y, GE L, et al. Geochemical characteristics of pore water in shallow sediments from Shenhu Area of South China Sea and their significance for gas hydrate occurrence[J]. Chinese Science Bulletin, 2010, 55(8): 752-760. doi: 10.1007/s11434-009-0312-2
[27] SUN J X, NING F L, LI S, et al. Numerical simulation of gas production from hydrate-bearing sediments in the Shenhu Area by depressurising: the effect of burden permeability[J]. Journal of Unconventional Oil and Gas Resources, 2015, 12: 23-33. doi: 10.1016/j.juogr.2015.08.003
[28] JIANG M J, YU H S, LEROUEIL S. A simple and efficient approach to capturing bonding effect in naturally microstructured sands by discrete element method[J]. International Journal for Numerical Methods in Engineering, 2007, 69(6): 1158-1193. doi: 10.1002/nme.1804
[29] YANG S X, ZHANG M, LIANG J Q, et al. Preliminary results of China's third gas hydrate drilling expedition: a critical step from discovery to development in the South China Sea[J]. Center for Natural Gas and Oil, 2015, 412: 386-7614.
[30] 孙嘉鑫. 钻采条件下南海水合物储层响应特性模拟研究[D]. 武汉: 中国地质大学, 2018. SUN Jiaxin. Simulation Study on Response Characteristics of Hydrate Reservoir in South China Sea under Drilling and Production Conditions[D]. Wuhan: China University of Geosciences, 2018. (in Chinese)
[31] 陈意茹. 胶结型深海能源土开采离散元耦合模拟及地层稳定分析[D]. 天津: 天津大学, 2021. CHEN Yiru. Coupling DEM Simulation and Stability Study on Grain-Cementing Type MHBS under Hydrate Dissociation[D]. Tianjin: Tianjin University, 2021. (in Chinese)
[32] CHEN L, FENG Y C, KOGAWA T, et al. Construction and simulation of reservoir scale layered model for production and utilization of methane hydrate: the case of Nankai Trough Japan[J]. Energy, 2018, 143: 128-140. doi: 10.1016/j.energy.2017.10.108
[33] KIM J T, KIM A R, CHO G C, et al. The effects of coupling stiffness and slippage of interface between the wellbore and unconsolidated sediment on the stability analysis of the wellbore under gas hydrate production[J]. Energies, 2019, 12(21): 4177. doi: 10.3390/en12214177
-
期刊类型引用(4)
1. 黄锐,郭成超,曹鼎峰,刘志遐. 珊瑚钙质砂-聚氨酯高聚物复合体蠕变村山流变模型改进. 工程地质学报. 2024(01): 295-302 .  百度学术
百度学术
2. 郭延辉,霍圆,毛肖涓,吴奇,刘星辰. 基于改进西原模型的滑坡临滑切线角预警判据研究. 自然灾害学报. 2024(05): 96-108 .  百度学术
百度学术
3. 丁海滨. 利用SHPB联合测定岩石非线性系数及衰减系数的教学试验. 现代职业教育. 2023(16): 81-84 .  百度学术
百度学术
4. 张强,王军保,宋战平,冯世进,张玉伟,曾涛. 循环荷载作用下盐岩微观结构变化及经验疲劳模型. 岩土力学. 2022(04): 995-1008 .  百度学术
百度学术
其他类型引用(14)
-
其他相关附件




 下载:
下载: