Simplified solutions for longitudinal deformation of shield tunnels considering influences of circumferential joints
-
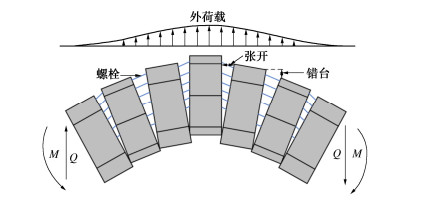
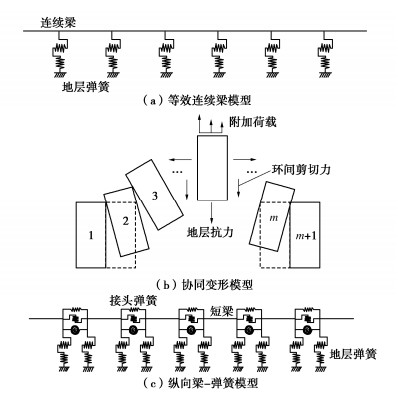
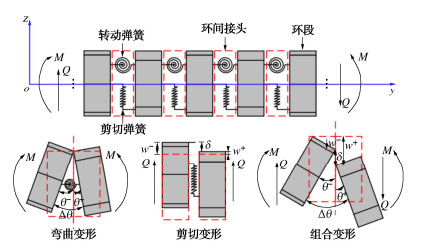
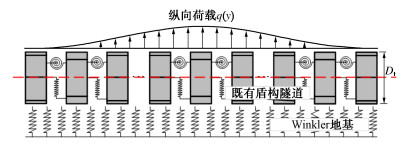
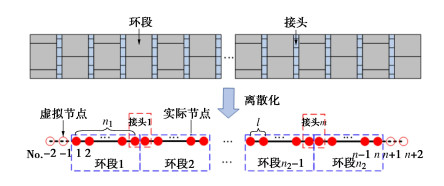
摘要: 为反映外荷载下盾构隧道相邻环间张开和错台，提出考虑环间接头影响的盾构隧道纵向变形简化解答。首先，引入纵向梁-弹簧模型模拟盾构隧道纵向受力变形，其中采用Timoshenko短梁考虑隧道环段变形，引入转动和剪切弹簧分别模拟环间接头转动与错台。其次，构建弹性地基上纵向梁-弹簧模型的有限差分方程，以解决环间接头-管环非连续变形求解问题，并推导外荷载下既有盾构隧道的纵向变形公式。最后，建立新建隧道上穿和下穿引起既有盾构隧道的纵向变形解答，并与新建隧道上、下穿越工程案例及现有理论方法对比验证。研究结果表明：所提方法预测的隧道位移与Timoshenko连续梁模型，协同变形模型和实测数据均具有较好的一致性，但所提方法得到的环间错台略低于Timoshenko梁模型和协同变形模型；所提方法可考虑环间接头的影响，得到的隧道位移曲线呈现既不光滑也不连续的特征，其中环段变形以刚体位移为主，而环间接头主要发生转动和错台；而基于现有理论所得盾构隧道纵向位移均为连续曲线，无法反映环间接头的真实转动与错台位移。Abstract: In order to reflect the opening and dislocation between adjacent rings of a shield tunnel subjected to external loads, an analytical solution for the longitudinal deformation of the shield tunnel is proposed which considering the effects of circumferential joints. Firstly, a simplified longitudinal beam-spring shield tunnel model is introduced to simulate the longitudinal deformation of the shield tunnel. The Timoshenko short beam is used to consider the deformation of the segmental ring. The rotation and shearing springs are used to simulate the rotation and dislocation of the circumferential joints, respectively. Secondly, the finite difference equation of the longitudinal beam-spring model resting on the elastic foundation is established to solve the discontinuous deformation of the circumferential joint-segmental ring. The formula for the longitudinal deformation of the existing shield tunnel under external loads is further derived. Finally, the solutions for the longitudinal deformation of the existing shield tunnel associated with overcrossing tunneling and undercrossing tunneling are established, respectively. The proposed method is verified with new tunnel over-crossing and under-crossing case histories and previous theoretical methods. The results show that the predicted results by the present solution are consistent with those by the Timoshenko continuous beam model and cooperative deformation model and the field measurements, but the dislocations obtained by the present solution are slightly lower than those by the Timoshenko continuous beam model and the cooperative deformation model. The proposed method takes the effects of the circumferential joints into consideration, and it leads to the predicted displacement curve of the tunnel, which is neither smooth nor continuous. It is found that the rigid displacement mainly occurs in the segmental rings, while the rotation and dislocation occur in the circumferential joints. The previous methods always give continuous displacement curves of tunnels, which cannot truly reflect the real rotation and dislocation of joints.
-
0. 引言
中国现阶段正处于水下盾构隧道建设的高峰期，水下隧道的建设总体呈现出大断面、大埋深、高水压和地质条件日益复杂的趋势。不良地质段的沉降控制是海底隧道施工的核心技术之一，它不仅对施工安全至关重要，而且对隧道运营阶段的结构受力及长期安全性也是极其重要的[1]。断层破碎带是海底盾构隧道建设过程中常见的不良地质段，在断层破碎带地层界面附近，地层特性和隧道上覆荷载均发生显著变化，极易造成隧道的不均匀沉降，从而导致环缝张开、错台、螺栓应力增大乃至接缝渗漏水等现象，严重影响盾构隧道的结构稳定和运营安全[2]。
目前常用的隧道上覆荷载计算方法有全土柱法、太沙基理论[3]、普氏理论[4]和规范公式[5]等。黎春林[6]在Terzaghi[7]基础上推导了一种可以考虑地层损失和管片刚度的松动土压力计算公式。王浩等[8]基于普氏平衡拱理论，提出适用于3洞小净距隧道的围岩压力计算方法。颉永斌等[9]用筒仓理论结合地层应力分布特征来求解断层破碎带内隧道的上覆荷载。由于断层破碎带形态各异，填充物复杂，目前断层破碎带地层隧道上覆荷载仍难以全面准确描述。
不同学者[10-12]将既有盾构隧道简化为无限长弹性直梁或Euler-Bernoulli梁放置于Winkler地基模型或Pasternak地基模型上，研究既有隧道的力学响应。然而Euler-Bernoulli梁忽略了实际工程常发生的剪切变形。为更合理地描述隧道的实际变形模式，Wu等[13]针对隧道的剪切变形，基于Liao等[14]接头有一定影响范围思路同样引入剪切刚度影响系数推导隧道管片等效抗剪刚度，将隧道视为Timoshenko梁，从而考虑隧道纵向剪切效应。Zhang等[15]在Wu等[13]基础上将既有隧道简化为能够考虑地层的压缩及剪切效应的kerr三参数地基上Timoshenko梁，并依据高斯曲线推导出新隧道对既有隧道的纵向响应的解析解。目前Timoshenko梁在多段非均布复杂上覆荷载作用下难以直接求解，通常以有限差分法进行数值计算。
为此，本文将隧道上覆荷载概括为4种特征形态断层破碎带松动土压力的线性组合，提出了归一化上覆荷载理论公式，并将复杂上覆荷载在5%的误差内简化为三次泰勒多项式，结合Timoshenko梁理论推导建立了断层破碎带海底盾构隧道管片纵向沉降及内力系列解析解，并通过现场实测结果验证了本文理论模型和解析解的正确性。
1. 断层破碎带隧道纵向上覆荷载分析
1.1 断层破碎带形态分析
断层破碎带是海底隧道建设中经常遇到的不良地质条件，由于断层破碎带内岩体构造发育，渗透性较大，使得海底盾构隧道的上覆荷载比较复杂。如图 1所示，将隧道沿纵向分为4段：ab段为正常段，bc段为相交段，cd段为延伸段，de段为正常段。不同的相交段和延伸段组合可模拟不同形态的断层破碎带。
断层破碎带的规模根据地质构造的不同，从几米到几千米不等。对于任意断层破碎带形态都可以看成以下4种特征形态的线性组合，如图 2所示。其中相交段为形态一、三的线性组合，延伸段为形态二、四的线性组合。
![]()
图 2 断层破碎带地层典型特征形态Figure 2. Typical characteristics and morphologies of strata in fault fracture zone1.2 隧道纵向上覆荷载计算
对断层破碎带范围内海底隧道任意横剖面分析，隧道的横向上覆荷载均可视为多层土体作用下隧道的松动土压力，力学模型如图 3所示。土体上作用水压力p0，忽略水的渗流作用。从上至下3种土层厚度分别为ha1，ha2，ha3。
取第一层正常围岩松动区内深度y处宽为2Bt，厚度为dy的土条单元，根据土条竖向力的平衡，可得
2Btσy+2Btγsdy=2Bt(σy+dσy)+2τsdy。 (1) 式中：γs为正常围岩的重度；σy为深度y处的垂直方向应力；τs为作用于正常围岩地层土条上向上的摩擦应力；Bt为隧道开挖影响宽度的一半，t=1，2，B1为相交段范围内隧道开挖影响宽度的一半，B2为其余段隧道开挖影响宽度的一半，τs和Bt由下式计算：
τs=cs+σxtanφs=cs+ksσytanφs， (2) Bt={rcot(π /4 + φp/22) (t=1)rcot(π /4 + φs/22) (t=2)。 (3) 式中：σx为深度y+dy/2处的水平方向应力；cs为正常围岩黏聚力；φs为正常围岩内摩擦角；φp为断层破碎带内摩擦角；r为隧道的外半径；ks为正常围岩静止侧压力系数，按经验公式k0=1−sinφs进行计算[16]。
将式(2)，(3)代入式(1)，结合边界条件y=0，σy=p0，并代入y=ha1可以得到第一层土体底部荷载：
q(ha1)=Btγs−cskstanφs(1−e−kstanφs⋅ha1/Bt)+p0e−kstanφs⋅ha1/Bt。 (4) 同理，将上层土体底部荷载当作边界条件代入下层土体中进行计算，即可求得3层土体作用下隧道松动土压力：
q(x)=Btγs−cskstanφs(1−e−kstanφs⋅ha3/Bt)+(Btγp−cpkptanφp(1−e−kptanφp⋅ha2/Bt)+(Btγp−cpkptanφp(1−e−kptanφp⋅ha2/Bt))+p0e−kstanφs⋅ha1/Bt)⋅e−kptanφp⋅ha2/Bt)e−kstanφs⋅ha3/Bt。 (5) 式中：cp为断层破碎带的黏聚力；γp为断层破碎带的重度；kp为断层破碎带静止侧压力系数，按经验公式k0=1−sinφp进行计算[16]。
式(5)即为断层破碎带地层海底盾构隧道归一化上覆荷载理论公式。4种特征形态下海底盾构隧道纵向上覆荷载，如表 1所示。
表 1 4种特征形态下海底盾构隧道纵向上覆荷载Table 1. Longitudinal overlying loads of subsea shield tunnel for four characteristic forms形态 纵向上覆荷载 Bt取值 形态一 q1(x)=q(x)|ha1 = h1, ha1 = h1, ha3 = 0 Bt=B1 形态二 q2(x)=q(x)|ha1 = 0, ha2 = h3, ha3 = h4 Bt=B2 形态三 q3(x)=q(x)|ha1=ha3=0,ha2=h5 Bt=B1 形态四 q4(x)=q(x)|ha1=h6,ha2=h7,ha3=h8 Bt=B2 对于正常段ab、de，海底盾构隧道的纵向上覆荷载q0(x)：
q0(x) = B2γs−cskstanφs(1−e−kstanφs⋅ha1/B2) + p0e−kstanφs⋅H/B2。 (6) 结合正常段、相交段、延伸段的纵向上覆荷载，对于不同形态断层破碎带，纵向上覆荷载如表 2所示，其中H为隧道埋深，bp为断层破碎带宽度，α为断层破碎带与隧道轴线的夹角。
表 2 不同倾角断层破碎带海底隧道纵向上覆荷载Table 2. Longitudinal overlying loads of subsea tunnel in fault fracture zone with different inclination angles倾角 上覆荷载 α=90∘ q0(x)−∞ < x < 0 q3(x)0⩽x < bp q0(x)bp⩽x < + ∞ tanα>Hbp q0(x)−∞ < x < 0 q1(x)0⩽x < Htanα q3(x)Htanα⩽x⩽bp q2(x)bp < x < bp + Htanα q0(x)bp + Htanα⩽x<+∞ tanα=Hbp q0(x)−∞ < x < 0 q1(x)0⩽x < bp q3(x)x=bp q2(x)bp < x⩽2bp q0(x)2bp < x < + ∞ tanα<Hbp q0(x)−∞ < x < 0 q1(x)0⩽x < bp q4(x)bp⩽x<Htanα q2(x)Htanα⩽x⩽bp + Htanα q0(x)bp + Htanα < x < +∞ 2. 盾构隧道纵向沉降解析解
2.1 隧道纵向沉降理论模型
为了更加准确计算盾构隧道的纵向沉降与内力, 考虑管片接头对隧道整体剪切刚度的影响，将隧道管片结构视为置于Winkler地基上的Timoshenko梁，其纵向力学理论模型如图 4所示。其中fj(x)为盾构隧道纵向上覆荷载，由表 3可知，隧道纵向上覆荷载fj(x)共分为四类，即j=1~4。k2为断层破碎带地层地基基床系数；k1为正常地层地基基床系数。根据隧道纵向上覆荷载的分段及地层的变化，盾构隧道沿纵向可以分为多段Timoshenko梁。
![]()
图 4 盾构隧道管片结构纵向理论模型Figure 4. Longitudinal theoretical model for segment structure of shield tunnel表 3 4种破碎带形态及其对应上覆荷载Table 3. Four types of fracture zones and their corresponding overlying loads破碎带形态 α=90∘ tanα>Hbp tanα=Hbp tanα<Hbp 上覆荷载 f1(x) f2(x) f3(x) f4(x) 根据Timoshenko梁理论, 各段梁弯矩Mij、剪力Qij、转角θij满足下面的关系：
Mij=−(EI)eqdθij(x)dx， (7) Qij=(kGA)eq(dwij(x)dx−θij(x))， (8) θij=dwij(x)dx + 1(kGA)eq∫[2fj(x)r−2kirwij(x)]dx。 (9) 式中：(EI)eq为隧道纵向等效抗弯刚度；(kGA)eq为隧道纵向等效抗剪刚度；i为梁段号，ki为第i段梁的地基基床系数；Mij为第j类上覆荷载作用在隧道上i段梁产生的弯矩。4类上覆荷载对应破碎带形态如表 3所示。
在纵向上覆荷载fj(x)作用下，可以得到在Winkler地基上Timoshenko梁关于纵向沉降wij(x)的微分方程：
d4wij(x)dx4−2kir(kGA)eqd2wij(x)dx2 + 2kir(EI)eqwij(x)=2rfj(x)(EI)eq−2r(kGA)eqd2fj(x)dx2。 (10) 式(10)对应的齐次方程为
d4wij(x)dx4−Aiad2wij(x)dx2 + Aibwij(x)=0， (11) 式中，Aia=−2kir(kGA)eq，Aib=2kir(EI)eq。
其齐次方程通解为
wij(x)=eαix[ci1cos(βix) + ci2sin(βix)] + e−αix[ci3cos(βix) + ci4sin(βix)]， (12) 式中，αi = √2√Aib−Aia2，βi=4Aib−A2ib√2√Aib−Aia，ci1，ci2，ci3，ci4为待定系数。
2.2 隧道纵向上覆荷载简化
由表 3可知，fj(x)在其作用范围内任意开区间(x0，xn)具有直到n+1阶的导数。xt为开区间(x0，xn)内的一点，对于任意x∈(x0，xn)，由泰勒公式得：
fj(x)=fj(xt)0！+f′j(xt)1！(x−xt)+f″j(xt)2！(x−xt)2+⋯+fnj(xt)n！(x−xt)n+Rn(x)， (13) Rn(x)=f(n+1)j(ξ)(n+1)!(x−xt)n+1。 (14) 式中，ξ为xt与x之间的某个值。当x→xt时，误差|Rn(x)|是比(x−xt)n+1高阶的无穷小，x越趋近于xt，误差就越小。利用泰勒公式这个性质，可以提出高精度泰勒公式分段展开法，即对不同的x进行不同xt处高精度n次多项式展开。
本文将纵向上覆荷载fj(x)展开为三次泰勒多项式，其与fj(x)的误差为
R3(x)=f(4)j(ξ)4!(x−xt)4。 (15) 对于有界函数fj(x)，当x∈(x0，xn)时，∣f(4)j(x)∣ ⩽B，则有下列不等式：
|R3(x)|⩽B4!(x−xt)4。 (16) 若本文最大误差取为5%，可以得到
|R3(x)|⩽0.05fj(x)。 (17) 联立求解式(16)，(17)，可以求出fj(x)在xt处最大误差为5%的展开区间(x0，xn)。即fj(x)可以在5%误差内简化为三次多项式函数：
fj(x)≈fj(xt)0！+f′j(xt)1！(x−xt)+f″j(xt)2！(x−xt)2+f‴j(xt)3！(x−xt)3，x∈(x0,xn)。 (18) 此时纵向沉降微分方程的特解为
w∗ij(x) = fj(x)ki。 (19) 即Timoshenko梁纵向沉降微分方程通解wij(x)为
wij(x)=eαix[ci1cos(βix) + ci2sin(βix)] + e−αix[ci3cos(βix) + ci4sin(βix)] + fj(x)ki。 (20) 假设隧道两端自由，可得边界条件：
limx→ + ∞Qij(x)=limx→ - ∞Qij(x)=0， (21) limx→ + ∞Mij(x)=limx→ - ∞Mij(x)=0。 (22) 假定隧道沉降曲线连续可微可导，在各段梁节点处隧道的弯矩、剪力、转角、纵向变形必然相等，可以列出以下方程：
limx→xpwij(x)=limx→xpwij(x)， (23) limx→xpθij(x) = limx→xpθij(x)， (24) limx→xpMij(x) = limx→xpMij(x)， (25) limx→xpQij(x) = limx→xpQij(x)， (26) 式中，xp为各连接点横坐标。
由式(21)~(26)及式(7)~(9)，(12)可以求出通解中待定系数ci1，ci2，ci3，ci4。
2.3 相关参数的确定
隧道纵向等效抗弯刚度(EI)eq及纵向等效剪切刚度(kGA)eq是决定隧道变形及内力分布的重要参数，其等效纵向抗弯刚度[17]表达式为
{{\text{(}}EI{\text{)}}_{{\text{eq}}}} = \frac{{{\text{co}}{{\text{s}}^{\text{3}}}\varphi }}{{{\text{cos}}\phi {\text{ + }}\left( {\phi {\text{ + }}\frac{{\text{π }}}{{\text{2}}}} \right){\text{sin}{\rm{ \mathsf{ φ} }} }}}{E_{\text{c}}}{I_{\text{c}}}。 (27) 式中：Ec为管片结构弹性模量；Ic为管片环纵向惯性矩；\phi 为中性轴位置的角度，由下式确定：
\phi {\text{ + cot}}\phi = {\text{π }}\left( {{\text{0}}{\text{.5 + }}\frac{{n{k_{\text{b}}}{l_{\text{s}}}}}{{{E_{\text{c}}}{A_{\text{c}}}}}} \right)。 (28) 式中：kb接头螺栓的平均线刚度，{k_{\text{b}}}{\text{ = }}{E_{\text{b}}}{A_{\text{b}}}{\text{/}}{l_{\text{b}}}，Eb为螺栓的弹性模量，Ab为螺栓的横截面积, lb为螺栓长度；n为螺栓个数；ls为管片环宽；Ac为隧道管片横截面积。
盾构隧道等效剪切刚度(kGA)eq公式[13]为
{(kGA)_{{\text{eq}}}} = \zeta \frac{{{l_{\text{s}}}}}{{\frac{{{l_{\text{b}}}}}{{n{\kappa _{\text{b}}}{G_{\text{b}}}{A_{\text{b}}}}} + \frac{{{l_{\text{s}}} - {l_{\text{b}}}}}{{{\kappa _{\text{c}}}{G_{\text{c}}}{A_{\text{c}}}}}}}。 (29) 式中：\zeta 为修正系数，在本文其值取1；{\kappa _{\text{b}}}及{\kappa _{\text{c}}}分别为螺栓及管片环Timoshenko剪切系数，对于圆形截面螺栓，{\kappa _{\text{b}}}取0.9，对于环形隧道管片环结构，{\kappa _{\text{c}}}取0.5；Gb及Gc为分别螺栓剪切刚度及隧道管片剪切刚度，两者与各自弹性模量的关系为{G_{\text{b}}} = \frac{{{E_{\text{b}}}}}{{2(1 + {\nu _{\text{b}}})}}及{G_{\text{c}}} = \frac{{{E_{\text{c}}}}}{{{\text{2(1 + }}{\nu _{\text{c}}}{\text{)}}}}，其中，{\nu _{\text{b}}}及{\nu _{\text{c}}}分别为螺栓及管片的泊松比。
Winkler地基基床系数k表达式[18]为
{k_{\text{s}}} = \frac{{{\text{1}}{\text{.3}}{E_{\text{s}}}}}{{{\text{2}}r{\text{(1}} - \nu _{\text{s}}^{\text{2}}{\text{)}}}}\sqrt[{{\text{12}}}]{{\frac{{{E_{\text{s}}}{{{\text{(2}}r{\text{)}}}^{\text{4}}}}}{{{{{\text{(}}EI{\text{)}}}_{{\text{eq}}}}}}}}\text{，} (30) {k_{\text{p}}} = \frac{{1.3{E_{\text{p}}}}}{{2r(1 - \nu _{\text{p}}^{\text{2}})}}\sqrt[{12}]{{\frac{{{E_{\text{p}}}{{(2r)}^4}}}{{{{(EI)}_{{\text{eq}}}}}}}}。 (31) 式中：Es为正常围岩地层弹性模量；\nu _{\text{s}}^{}为正常围岩地层泊松比；Ep为断层破碎带地层弹性模量；\nu _{\text{p}}^{}为断层破碎带地层泊松比。
3. 工程实例
3.1 工程概况
珠三角水资源配置工程狮子洋段海底输水隧洞长2252 m，埋深40 m，采用泥水平衡盾构法施工，最大水深为27 m。管片采用C50钢筋混凝土管片错缝拼装，外径8.3 m，内径7.5 m，管片环宽度1.6 m。隧洞穿越f114断层破碎带，该断面水深10 m。断层宽度28.5 m，倾角约为40°。表 4给出断层破碎带与周边岩层的力学参数，其中 \gamma 为重度， \varphi 为内摩擦角，c为黏聚力，E为弹性模量， \nu 为泊松比，k为静止侧压力系数。断层破碎带的形态及其与盾构掘进面相对位置关系如图 6所示。
表 4 断层破碎带及围岩力学参数Table 4. Mechanical parameters of fault fracture zone and surrounding rock类型 \gamma {\text{/}}{\text{(kN}} \cdot {{\text{m}}^{ - {\text{3}}}}{\text{)}} \varphi /(°) c{\text{/}}kPa E{\text{/}}GPa \nu k 正常围岩 26 30 100 1.6 0.33 0.49 断层破碎带 20 25 30 0.5 0.40 0.67 由表 3可知，隧道上覆荷载为第四类f4(x)。根据破碎带的上覆荷载及地层的变化将隧道分为5段Timoshenko梁，其范围分别为：(-∞, 0]，(0, bp]，(bp，H/tan \alpha ]，(H/tan \alpha ，bp+H/tan \alpha ]，(bp+H/tan \alpha ，+∞)。纵向沉降微分方程式(20)相关的系数保留两位小数后分别为：c11=-3.49×10-9；c12=7.04×10-9；c13=0；c14=0；c21=4.01×10-10；c22=-2.54×10-10；c23=-14.76；c24= 17.53；c31=-1.26×10-23；c32=-3.22×10-23；c33=2.0×109；c34=8.75×108；c41=-1.14×10-30；c42=-8.73×10-32；c43=1.76×1011；c44=3.60×1011；c51=0；c52=0；c53=7.22×1018；c54=-5.95×1017。
3.2 监测点布设
根据工程地质条件，选取5个代表管片，分别为处于断层破碎带范围内的第1529、1534和1538环，断层破碎带之外的第1551、1561环。采用全分布式光纤传感器对管片进行监测，如图 7所示。
3.3 现场监测试验结果对比分析
采用偏压短柱法[19]通过实测钢筋应变反算盾构管片内力。如图 8所示，将隧洞衬砌考虑成偏心受压短柱，建立力矩平衡方程，计算相关参数见表 5。
M = {n_{\text{c}}}{\text{(}}{P_{\text{2}}} - {P_{\text{1}}}{\text{)}}\left( {\frac{b}{{\text{2}}} - a'} \right){\text{ + }}\frac{{\text{1}}}{{{\text{12}}}}b{\text{(}}{\sigma _{{\text{c1}}}}{\text{ + }}{\sigma _{{\text{c2}}}}{\text{)}}{A_{\text{c}}}。 (32) 表 5 螺栓及钢筋相关参数Table 5. Relevant parameters of bolt and reinforcementa'/mm Ee/GPa n1 n2 Ec/GPa 50 210 20 10 3.15×104 nb Eb/GPa lb/mm Ab/m2 {\alpha _{\text{b}}}{\text{/}}(°) 28 210 730 7.069×10-4 35 注：a'为钢筋保护层厚度；Ee为钢筋弹性模量；n1为管片内侧环向主筋数量；n2为管片外侧环向主筋数量；Ec为管片弹性模量；nb为纵向螺栓个数；Eb为螺栓弹性模量；lb为螺栓长度，Ab为螺栓横截面面积；{\alpha _{\text{b}}}为螺栓倾角。 式中：{P_{\text{1}}}为管片外侧单根钢筋集中力；{P_{\text{2}}}为管片内侧单根钢筋集中力；{\sigma _{{\text{c1}}}}为管片内侧钢筋位置处混凝土应力；{\sigma _{{\text{c2}}}}为管片外侧钢筋位置处混凝土应力；{n_{\text{c}}}为管片内(外)侧环向主筋数量；b为管片厚度；a'为钢筋保护层厚度；Ac为管片横截面面积。
对第1534、1538环管片结构的内力进行分析，管片环宽度为1.6 m，同一环管片上理论计算弯矩值会在一定的范围波动，其与监测弯矩对比结果如图 9，10所示。
![]()
图 9 1529环管片实测弯矩与计算弯矩Figure 9. Measured and calculated bending moments of segments of No. 1529 ring![]()
图 10 1538环管片实测弯矩与计算弯矩Figure 10. Measured and calculated bending moments of segments of No. 1538 ring由图 9，10可知：现场实测得到的隧洞弯矩与理论计算较为接近。1529环根据现场实测钢筋应变反算管片弯矩值在212.2~228.5 kN，在监测后期管片的弯矩值基本稳定在220 kN·m左右。1538环根据现场实测钢筋应变反算管片弯矩值在175.4~193.6 kN·m，1538环管片弯矩值稳定在180 kN·m左右。
4. 参数敏感性分析
4.1 断层破碎带倾角
假定隧道埋深40 m，断层破碎带宽度为30 m，水深10 m，分别对断层破碎带倾角为20°，40°，60°和80°条件下隧道纵向沉降进行分析，如图 11所示。在断层破碎带区域隧道沉降先急剧增大，后缓慢增加、最后急剧减小，即曲线整体呈现三段变化规律：激增段、缓增段和骤减段。在断层破碎带与正常围岩界面附近隧道不均匀沉降急剧增加。
![]()
图 11 不同断层破碎带倾角隧道纵向沉降图Figure 11. Longitudinal settlements of tunnel with different inclination angles of fault fracture zone4.2 断层破碎带宽度
假定隧道埋深40 m，断层破碎带倾角为60°，分别对断层破碎带宽度为20，30，40，50，60 m条件下隧道纵向沉降进行分析，如图 12所示。随着断层破碎带宽度的增大，断层破碎带范围内隧道的最大纵向沉降逐渐增大并趋于稳定，最大沉降出现位置逐渐远离断层破碎带中部。对于8.3 m外径海底盾构隧道，倾斜断层破碎带对延伸侧1倍破碎带宽度范围内隧道的沉降影响较大，当断层破碎带宽度超过50 m时，隧道的最大纵向沉降基本保持不变。
![]()
图 12 不同断层破碎带宽度隧道纵向沉降图Figure 12. Longitudinal settlements of tunnel with different widths of fault fracture zone不同断层破碎带宽度对隧道纵向弯矩影响如图 13所示。随着断层破碎带宽度增加，在断层破碎带和正常围岩界面附近，隧道纵向弯矩基本不变，在断层破碎带内部隧道的纵向弯矩逐渐减小。对于8.3 m外径海底盾构隧道，当破碎带宽度超过40 m，断层破碎带中部几乎无弯矩。
![]()
图 13 不同断层破碎带宽度隧道弯矩图Figure 13. Bending moments of tunnel with different widths of fault fracture zone4.3 断层破碎带弹性模量
假定隧道埋深40 m，断层破碎带宽度为30 m，倾角为60°，分别对断层破碎带与正常围岩弹性模量比值为1∶2，1∶4，1∶6，1∶8进行分析，如图 14所示。随着断层破碎带与正常围岩弹性模量比值的减小，隧道沉降趋势基本不变，但不均匀沉降迅速增大。对于外径为8.3 m海底盾构隧道，当宽度为30 m的断层破碎带与正常围岩弹性模量比值小于1∶4时，隧道的沉降量超过预警值10 mm[20]。
![]()
图 14 不同断层破碎带弹性模量隧道纵向沉降图Figure 14. Longitudinal settlements of tunnel with different elastic moduli of fault fracture zone5. 结论
本文针对断层破碎带海底盾构隧道纵向沉降问题，基于太沙基松动土压力理论，结合泰勒级数展开公式，对断层破碎带海底盾构隧道纵向沉降及内力进行分析，得到以下3点结论。
(1) 通过分析海底盾构隧道穿越断层破碎带地层全过程，提出了可考虑断层破碎带宽度和倾角的统一荷载模型和理论公式。
(2) 针对复杂上覆荷载条件下Timoshenko梁难以直接求解问题，利用泰勒级数展开公式提出了高精度泰勒公式分段展开法，结合Timoshenko梁理论，推导建立了可用于复杂荷载作用下海底盾构隧道管片纵向沉降及内力系列解析解。工程实例表明本文理论推导的系列解析解能够较为准确地计算管片结构内力。
(3) 计算结果表明，断层破碎带内隧道的沉降曲线表现为激增段、缓增段和骤减段。断层破碎带对延伸侧1倍破碎带宽度范围内隧道的沉降影响较大；当断层破碎带宽度超过6倍洞径时，隧道的沉降峰值基本保持不变。
-
![]()
图 1 盾构隧道在外荷载下的纵向变形
Figure 1. Longitudinal deformations of a shield tunnel subjected to.external loads
![]()
图 4 在外荷载下盾构隧道纵向响应计算模型
Figure 4. Model for longitudinal responses of shield tunnel to external loads
![]()
图 7 新建隧道上穿和下穿既有盾构隧道计算模型
Figure 7. Model for existing shield tunnel due to over-crossing tunneling and under-crossing tunneling
![]()
图 8 上穿工程剖面图
Figure 8. Sectional view of existing shield tunnel due to over-crossing tunneling
![]()
图 9 1号线双线隧道纵向位移实测值与计算值对比
Figure 9. Comparison between measured and computed displacements of tunnel of Metro Line 1
![]()
图 10 1号线右线隧道环间变形计算值对比
Figure 10. Comparison of calculated deformations of rings of right line tunnel of Metro Line 1
![]()
图 11 下穿工程剖面图
Figure 11. Sectional view of existing shield tunnel due to under-crossing tunneling
![]()
图 12 4号线内圈隧道竖向位移实测值与计算值对比
Figure 12. Comparison between measured and calculated vertical displacements of inner tunnel of Metro Line 4
![]()
图 13 4号线内圈隧道环间错台量计算值对比
Figure 13. Comparison of calculated dislocations of rings of inner tunnel of Metro Line 4
![]()
图 14 4号线内圈隧道剪力计算值对比
Figure 14. Comparison of calculated shearing forces of inner tunnel of Metro Line 4
表 1 既有盾构隧道结构参数
Table 1 Structural parameters of existing shield tunnel
管片弹性模量Ec/MPa 管片泊松比 {\nu _{\text{c}}} 环间螺栓数量nb 螺栓直径Db/mm 螺栓长度lb/mm 螺栓弹性模量Eb/MPa 3.45×104 0.2 17 30 400 2.06×105 
下载: 导出CSV
表 2 主要地层物理参数
Table 2 Physical parameters of main soil layers
土层 重度 {\gamma _{\text{s}}} /(kN·m-3) 含水率/% 压缩模量Es0.1-0.2/MPa 泊松比 {\nu _{\text{s}}} 3-3粉砂 19.6 24.8 14.0 0.28 3-5粉砂夹粉质粉土 19.7 23.6 15.0 0.27 3-7砂质粉土 19.2 29.5 7.0 0.34 7-2粉质黏土 19.7 26.5 12.0 0.32
下载: 导出CSV
表 3 主要土层物理参数
Table 3 Physical parameters of main soil layers
土层 厚度/m 重度 {\gamma _{\text{s}}} /(kN·m-3) 压缩模量Es0.1-0.2/MPa 泊松比 {\nu _{\text{s}}} ④淤泥质黏土 8.4 16.7 2.09 0.33 ⑤1a砂质粉土 4.5 18.2 8.21 0.24 ⑤1黏土 4.3 17.8 3.36 0.26 ⑤3粉质黏土 5.8 18.1 4.66 0.29
下载: 导出CSV
-
[1] 张志伟, 梁荣柱, 李忠超, 等. 盾尾非对称推力作用下盾构隧道纵向变形分析[J]. 岩土力学, 2023, 44(1): 88-98. ZHANG Zhiwei, LIANG Rongzhu, LI Zhongchao, et al. Analysis of longitudinal deformation of shield tunnel subjected to shield tail asymmetric thrust[J]. Rock and Soil Mechanics, 2023, 44(1): 88-98. (in Chinese)
[2] LIANG R Z, XIA T D, HONG Y, et al. Effects of above-crossing tunnelling on the existing shield tunnels[J]. Tunnelling and Underground Space Technology, 2016, 58: 159-176. doi: 10.1016/j.tust.2016.05.002
[3] LIANG R Z, KANG C, XIANG L M, et al. Responses of in-service shield tunnel to overcrossing tunnelling in soft ground[J]. Environmental Earth Sciences, 2021, 80(5): 1-15.
[4] ZHANG Z G, HUANG M S. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil[J]. Computers and Geotechnics, 2014, 56: 121-132. doi: 10.1016/j.compgeo.2013.11.008
[5] YU J, LI H, HUANG M S, et al. Timoshenko-beam-based response of existing tunnel to single tunneling underneath and numerical verification of opening and dislocation[J]. Computers and Geotechnics, 2022, 147: 104757. doi: 10.1016/j.compgeo.2022.104757
[6] 陈仁朋, 刘慕淳, 孟凡衍, 等. 基坑开挖旁侧盾构隧道结构横向受力与变形研究[J]. 岩土工程学报, 2023, 45(1): 24-32. doi: 10.11779/CJGE20211420 CHEN Renpeng, LIU Muchun, MENG Fanyan, et al. Circumferential forces and deformations of shield tunnels due to lateral excavation[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(1): 24-32. (in Chinese) doi: 10.11779/CJGE20211420
[7] CHENG H Z, CHEN R P, WU H N, et al. A simplified method for estimating the longitudinal and circumferential behaviors of the shield-driven tunnel adjacent to a braced excavation[J]. Computers and Geotechnics, 2020, 123: 103595. doi: 10.1016/j.compgeo.2020.103595
[8] 魏新江, 洪文强, 魏纲, 等. 堆载引起临近地铁隧道的转动与错台变形计算[J]. 岩石力学与工程学报, 2018, 37(5): 1281-1289. WEI Xinjiang, HONG Wenqiang, WEI Gang, et al. Rotation and shearing dislocation deformation of subway tunnels due to adjacent ground stack load[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1281-1289. (in Chinese)
[9] LIU B, YU Z W, HAN Y H, et al. Analytical solution for the response of an existing tunnel induced by above-crossing shield tunneling[J]. Computers and Geotechnics, 2020, 124: 103624. doi: 10.1016/j.compgeo.2020.103624
[10] LIU B, YU Z W, ZHANG R H, et al. Effects of undercrossing tunneling on existing shield tunnels[J]. International Journal of Geomechanics, 2021, 21(8): 04021131. doi: 10.1061/(ASCE)GM.1943-5622.0002102
[11] 魏纲, 洪文强, 魏新江, 等. 基坑开挖引起邻近盾构隧道转动与错台变形计算[J]. 岩土工程学报, 2019, 41(7): 1251-1259. doi: 10.11779/CJGE201907009 WEI Gang, HONG Wenqiang, WEI Xinjiang, et al. Calculation of rigid body rotation and shearing dislocation deformation of adjacent shield tunnels due to excavation of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1251-1259. (in Chinese) doi: 10.11779/CJGE201907009
[12] HUANG S F, CHEN Z B, XIE Y N, et al. A variational approach to the analysis of excavation-induced vertical deformation in a segmental tunnel[J]. Tunnelling and Underground Space Technology, 2022, 122: 104342. doi: 10.1016/j.tust.2021.104342
[13] 张治国, 程志翔, 张孟喜, 等. 考虑衬砌渗透性的盾构下穿既有隧道纵向结构错台变形研究[J]. 中国公路学报, 2022, 35(11): 180-194. ZHANG Zhiguo, CHENG Zhixiang, ZHANG Mengxi, et al. Dislocation deformation of existing longitudinal tunnel structure induced by shield tunneling by under-crossing considering influence of lining permeability[J]. China Journal of Highway and Transport, 2022, 35(11): 180-194. (in Chinese)
[14] KOIZUMI J, MURAKAMI H, SAINO K. Modelling of longitudinal structure of shield tunnel[J]. Journal of Japanese Society for Civil Engineering, 1988: 79-88. (in Japanese))
[15] HUANG W M, WANG J C, YANG Z X, et al. Analytical analysis of the longitudinal response of shield tunnel lining considering ring-to-ring interaction[J]. Computers and Geotechnics, 2022, 146: 104705. doi: 10.1016/j.compgeo.2022.104705
[16] KIENDL J, AURICCHIO F, HUGHES T J R, et al. Single-variable formulations and isogeometric discretizations for shear deformable beams[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 284: 988-1004. doi: 10.1016/j.cma.2014.11.011
[17] WU H N, SHEN S L, LIAO S M, et al. Longitudinal structural modelling of shield tunnels considering shearing dislocation between segmental rings[J]. Tunnelling and Underground Space Technology, 2015, 50: 317-323. doi: 10.1016/j.tust.2015.08.001
[18] SHIBA Y, KAWASHIMA K, OBINATA N, et al. Evaluation procedure for seismic stress developed in shield tunnels based on seismic deformation method[J]. Doboku Gakkai Ronbunshu, 1989, 1989(404): 385-394. doi: 10.2208/jscej.1989.404_385
[19] LIANG R Z. Simplified analytical method for evaluating the effects of overcrossing tunnelling on existing shield tunnels using the nonlinear Pasternak foundation model[J]. Soils and Foundations, 2019, 59(6): 1711-1727.
[20] WU B, LIU W, SHI P, et al. A case study of newly tunnels over-crossing the existing subway tunnels[J]. International Journal of Distributed Sensor Networks, 2022, 18(3): 15501329221087183.
[21] 王如路, 袁强, 梁发云, 等. 道路填土引发软土地铁盾构隧道变形案例及整治技术[J]. 岩土工程学报, 2023, 45(1): 112-121. doi: 10.11779/CJGE20211459 WANG Rulu, YUAN Qiang, LIANG Fayun, et al. Case study and treatment technology for deformed shield tunnel in soft soils induced by road construction[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(1): 112-121. (in Chinese) doi: 10.11779/CJGE20211459
[22] 梁荣柱, 宗梦繁, 康成, 等. 考虑隧道剪切效应的隧道下穿对既有盾构隧道的纵向影响[J]. 浙江大学学报(工学版), 2018, 52(3): 420-430, 472. LIANG Rongzhu, ZONG Mengfan, KANG Cheng, et al. Longitudinal impacts of existing shield tunnel due to down-crossing tunnelling considering shield tunnel shearing effect[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(3): 420-430, 472. (in Chinese)
[23] SAGASETA C. Analysis of undraind soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301-320.
-
期刊类型引用(3)
1. 邹弈，朱碧堂，吴颖彪，周宇航. 断层破碎带黏性夹泥岩体与基岩接触界面大型直剪试验研究. 华东交通大学学报. 2025(01): 45-51 . 
百度学术
2. 杨会林. 隧道穿越碎裂大涌水岩体变形破坏机理及处治对策. 铁道建筑技术. 2024(07): 121-124 . 百度学术
3. 王志岗，陶连金，史明，刘建功，石城，张海祥，郭文远，谢霖. 穿越活动断裂带的城市地铁隧道抗断性能及损伤状态量化指标研究. 应用基础与工程科学学报. 2024(06): 1772-1786 . 百度学术
其他类型引用(6)
-
其他相关附件
计量
- 文章访问数: 414
- HTML全文浏览量: 57
- PDF下载量: 143
- 被引次数: 9
