Stability analysis of slopes based on dynamic strength reduction- improved vector sum method
-
摘要: 在边坡稳定性分析中,极限平衡法与矢量和法均假定边坡失稳是由剪切破坏造成的,因此难以正确求解坡体上部存在拉裂区这类复杂边坡的安全系数,应用整体强度折减法虽能求得前述复杂边坡的安全系数,却难以搜索得到包含坡体上部拉裂区的完整滑动面。针对上述问题,采用动态强度折减法来搜索边坡滑动面,并提出了可兼顾边坡张拉破坏与剪切破坏的改进矢量和法,从而可更好地求解边坡稳定性问题。算例表明,应用所提出的方法不仅能搜索得到完整的边坡滑动面,而且求得的安全系数与整体强度折减法基本相同。所提出的方法适用于土质、岩质以及土岩组合等各类型边坡的稳定性分析,且受主滑方向、网格尺寸、模型尺寸的影响较小,有助于推动边坡稳定性分析方法的进一步完善。Abstract: In the slope stability analysis, both the limit equilibrium method and the vector sum method assume that the slope instability is caused by shear failure, accordingly, it is difficult to correctly solve the safety factor of the complex slope with tensile failure at the upper part, while the global strength reduction method can obtain the safety factor, it is difficult to search for the complete sliding surface containing the tensile failure zone in the upper part of the slope. In view of the above problems, the dynamic strength reduction method is adopted to search for the sliding surface of slope, and an improved vector sum method which can take into account the tension failure and shear failure is proposed, so that the slope stability problem can be solved better. The results of three cases show that the dynamic strength reduction method can completely reflect the sliding surface of slopes, and the safety factor obtained by the improved vector sum method is basically the same as that by the global strength reduction method. The proposed method is applicable to the stability analysis of various types of slopes, such as soil, rock and soil-rock combinations, and is less affected by the main sliding direction, mesh size and model size, which helps to promote the further improvement of slope stability analysis methods.
-
-
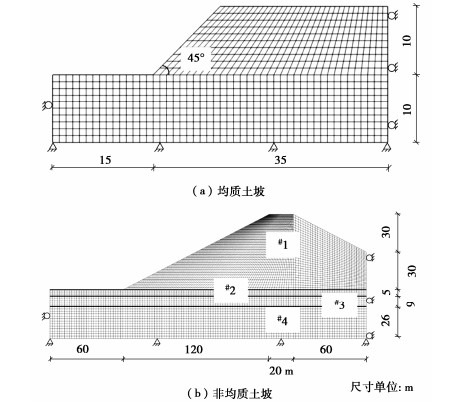
表 1 土质边坡土体物理力学指标的取值
Table 1 Physico-mechanical indices of soil slopes
土休 黏聚力/kPa 内摩擦角/(°) 重度/ (kN·m-3) 均质土坡 20.00 20.0 20.00 非均质土坡 #1土层 49.00 29.0 20.38 #2土层 0 30.0 17.64 #3土层 7.84 20.0 20.38 #4土层 0 30.0 17.64 表 2 土质边坡计算结果对比
Table 2 Comparison of calculated results of soil slopes
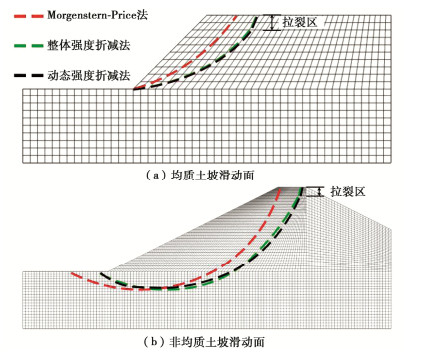
计算方法 均质土坡 非均质土坡 安全系数 相对误差/% 安全系数 相对误差/% 整体强度折减法 1.293 — 1.363 — Morgenstern-Price 1.271 -1.70 1.440 +5.65 本文方法(1) 1.277 -1.24 1.410 +3.45 本文方法(2) 1.275 -1.39 1.410 +3.45 本文方法(3) 1.278 -1.16 1.410 +3.45 传统矢量和法(1) 1.291 -0.15 1.234 -9.46 传统矢量和法(2) 1.284 -0.70 1.234 -9.46 传统矢量和法(3) 1.293 0 1.233 -9.54 应力代数和法 1.275 -1.39 1.412 +3.60 注:本表以整体强度折减法的计算结果为基准进行比较;(1)、(2)、(3)分别表示以极限抗滑力方向、滑动力方向、滑入点指向滑出点方向作为边坡的主滑方向(其中,均质土坡主滑方向与水平方向的夹角分别为28.21°,26.13°,29.25°;非均质土坡主滑方向与水平方向的夹角分别为24.98°,25.10°,21.41°)。 表 3 岩质边坡岩土体物理力学指标
Table 3 Physico-mechanical indices of rock slope
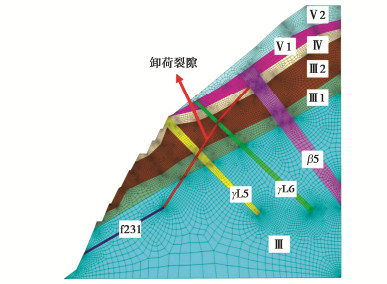
介质 弹性模量/GPa 泊松比 黏聚力/MPa 内摩擦角/(°) 天然重度/(kN·m-3) 抗拉强度/MPa f231 2.0 0.28 0.9 22.8 25.8 0 卸荷裂隙 2.0 0.28 2.0 36.0 26.2 0 V2 2.0 0.27 1.8 21.8 22.1 0 V1 4.0 0.27 2.0 26.5 24.5 1.00 IV 6.0 0.26 7.0 38.6 25.8 3.35 III2 7.5 0.23 17.5 51.3 26.2 6.00 III1 8.0 0.24 15.0 50.2 26.2 5.50 III 9.0 0.22 20.0 52.5 26.5 7.00 表 4 岩质边坡计算结果对比
Table 4 Comparison of calculated results of rock slopes
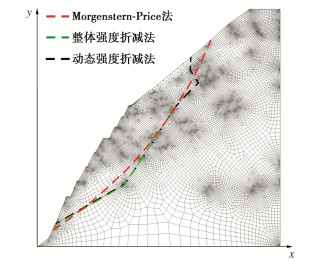
计算方法 岩质边坡 安全系数 相对误差/% 整体强度折减法 1.659 — Morgenstern-Price 12.800 +671.55 本文方法(1) 1.657 -0.12 本文方法(2) 1.660 +0.06 本文方法(3) 1.652 -0.42 传统矢量和法(1) 1.854 +11.75 传统矢量和法(2) 1.841 +10.97 传统矢量和法(3) 1.773 +6.87 应力代数和法 1.980 +19.35 注:(1)、(2)、(3)对应的边坡主滑方向与水平方向的夹角分别为34.09°,36.96°,51.08°。 -
[1] 吴志轩, 张大峰, 孔郁斐, 等. 基-填界面开挖台阶对顺坡填筑高边坡稳定性影响研究[J]. 工程力学, 2019, 36(12): 90-97. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201912011.htm WU Zhixuan, ZHANG Dafeng, KONG Yufei, et al. Study on stability influence of high slope foundation-fill interfacial excavation steps[J]. Engineering Mechanics, 2019, 36(12): 90-97. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201912011.htm
[2] SARKAR S, CHAKRABORTY M. Stability analysis for two-layered slopes by using the strength reduction method[J]. International Journal of Geo-Engineering, 2021, 12(1): 1-22. doi: 10.1186/s40703-020-00130-3
[3] 杨文辉, 章定文, 闫茜, 等. 深浅根混种法加固边坡稳定性的数值分析[J]. 东南大学学报(自然科学版), 2020, 50(1): 161-168. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX202001021.htm YANG Wenhui, ZHANG Dingwen, YAN Qian, et al. Numerical analysis on stability of slope reinforced by combination of deep and shallow roots[J]. Journal of Southeast University (Natural Science Edition), 2020, 50(1): 161-168. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX202001021.htm
[4] 郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381-3388. doi: 10.3321/j.issn:1000-6915.2004.19.029 ZHENG Yingren, ZHAO Shangyi. Application of strength reduction fem in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.19.029
[5] 陈国庆, 黄润秋, 周辉, 等. 边坡渐进破坏的动态强度折减法研究[J]. 岩土力学, 2013, 34(4): 1140-1146. doi: 10.16285/j.rsm.2013.04.040 CHEN Guoqing, HUANG Runqiu, ZHOU Hui, et al. Research on progressive failure for slope using dynamic strength reduction method[J]. Rock and Soil Mechanics, 2013, 34(4): 1140-1146. (in Chinese) doi: 10.16285/j.rsm.2013.04.040
[6] 陈国庆, 黄润秋, 石豫川, 等. 基于动态和整体强度折减法的边坡稳定性分析[J]. 岩石力学与工程学报, 2014, 33(2): 243-256. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201402006.htm CHEN Guoqing, HUANG Runqiu, SHI Yuchuan, et al. Stability analysis of slope based on dynamic and whole strength reduction methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 243-256. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201402006.htm
[7] 侯世伟, 马士贺, 李宏男, 等. 基于局部强度阶梯折减法的边坡渐进破坏研究[J]. 防灾减灾工程学报, 2020, 40(1): 72-78. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202001010.htm HOU Shiwei, MA Shihe, LI Hongnan, et al. Research on progressive slope failure based on stepwise reduction method of local strength[J]. Journal of Disaster Prevention and Mitigation Engineering, 2020, 40(1): 72-78. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202001010.htm
[8] 王述红, 朱承金, 张紫杉, 等. 基于动态强度折减DDA法的边坡多滑面稳定性分析[J]. 煤炭学报, 2019, 44(4): 1084-1091. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201904013.htm WANG Shuhong, ZHU Chengjin, ZHANG Zishan, et al. Stability analysis of multi-slip surface of slope based on dynamic strength reduction DDA method[J]. Journal of China Coal Society, 2019, 44(4): 1084-1091. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201904013.htm
[9] 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时X射线CT扫描和边坡坝基抗滑稳定分析的新方法[J]. 岩土工程学报, 2008, 30(1): 1-20. http://www.cgejournal.com/cn/article/id/12718 GE Xiurun. Deformation control law of rock fatigue failure, real-time X-ray CT scan of geotechnical testing, and new method of stability analysis of slopes and dam foundations[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(1): 1-20. (in Chinese) http://www.cgejournal.com/cn/article/id/12718
[10] 孙建生. "矢量和法"抗滑稳定计算模型的力学概念错误[J]. 岩土工程学报, 2021, 43(5): 975-980. doi: 10.11779/CJGE202105024 SUN Jiansheng. Mechanical concept errors in anti-sliding stability computational model of "vector sum method"[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 975-980. (in Chinese) doi: 10.11779/CJGE202105024
[11] 王伟, 陈国庆, 郑水全, 等. 考虑张拉-剪切渐进破坏的边坡矢量和法研究[J]. 岩土力学, 2019, 40(增刊1): 468-476. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2019S1070.htm WANG Wei, CHEN Guoqing, ZHENG Shuiquan, et al. Study on the vector sum method of slope considering tensile-shear progressive failure[J]. Rock and Soil Mechanics, 2019, 40(S1): 468-476. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2019S1070.htm
[12] 张海涛, 罗先启, 沈辉, 等. 基于矢量和的滑面应力抗滑稳定分析方法[J]. 岩土力学, 2018, 39(5): 1691-1698, 1708. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201805019.htm ZHANG Haitao, LUO Xianqi, SHEN Hui, et al. Vector-sum-based slip surface stress method for analysing slip mass stability[J]. Rock and Soil Mechanics, 2018, 39(5): 1691-1698, 1708. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201805019.htm
[13] DIEDERICHS M S, KAISER P K, EBERHARDT E. Damage initiation and propagation in hard rock during tunnelling and the influence of near-face stress rotation[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(5): 785-812.
[14] 周辉, 张传庆, 冯夏庭, 等. 隧道及地下工程围岩的屈服接近度分析[J]. 岩石力学与工程学报, 2005, 24(17): 3083-3087. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200517012.htm ZHOU Hui, ZHANG Chuanqing, FENG Xiating, et al. Analysis of rock mass stability in tunnel and underground engineering based on yield approach index[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3083-3087. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200517012.htm
[15] 郭明伟, 葛修润, 李春光, 等. 基于矢量和方法的边坡稳定性分析中整体下滑趋势方向的探讨[J]. 岩土工程学报, 2009, 31(4): 577-583. http://www.cgejournal.com/cn/article/id/13220 GUO Mingwei, GE Xiurun, LI Chunguang, et al. Study on potential sliding direction in slope stability analysis based on vector sum method[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 577-583. (in Chinese) http://www.cgejournal.com/cn/article/id/13220
[16] 刘素锦, 郭明伟, 李春光. 三维边坡整体主滑方向的确定[J]. 岩土力学, 2018, 39(S2): 37-44. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2018S2006.htm LIU Sujin, GUO Mingwei, LI Chunguang. Determination of main sliding direction for three-dimensional slope[J]. Rock and Soil Mechanics, 2018, 39(S2): 37-44. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2018S2006.htm
[17] 陈栋, 李红军, 朱凯斌. 基于新主滑趋势方向的矢量和边坡稳定分析方法[J]. 岩土力学, 2021, 42(8): 2207-2214, 2238. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202108016.htm CHEN Dong, LI Hongjun, ZHU Kaibin. Vector sum analysis method for slope stability based on new main sliding trend direction[J]. Rock and Soil Mechanics, 2021, 42(8): 2207-2214, 2238. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202108016.htm
[18] 孙建生. 基于有限元应力载荷宏观刚性滑裂面极限平衡抗滑稳定计算理论[J]. 岩石力学与工程学报, 2018, 37(4): 862-875. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804009.htm SUN Jiansheng. Theoretical model of stability calculation of macro-rigid sliding planes with FEM stress load based on limit equilibrium[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 862-875. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804009.htm
[19] 彭少文, 贺金明, 孙冠军, 等. 高陡边坡深部卸荷张拉裂缝的成因机制探讨[J]. 人民长江, 2015, 46(14): 32-35. https://www.cnki.com.cn/Article/CJFDTOTAL-RIVE201514010.htm PENG Shaowen, HE Jinming, SUN Guanjun, et al. Discussion on genetic mechanism of large-depth unloading tension fracture in high and steep slope[J]. Yangtze River, 2015, 46(14): 32-35. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-RIVE201514010.htm
-
其他相关附件



 下载:
下载: