Micromechanics-based stress-dilatancy relationship for granular materials
-
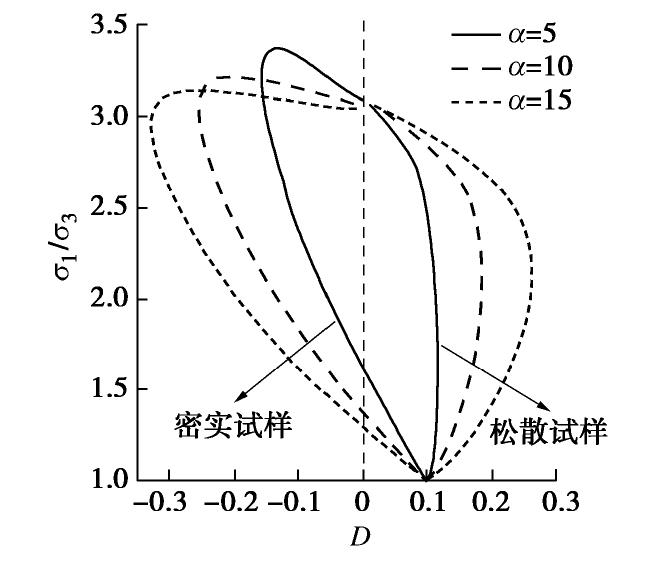
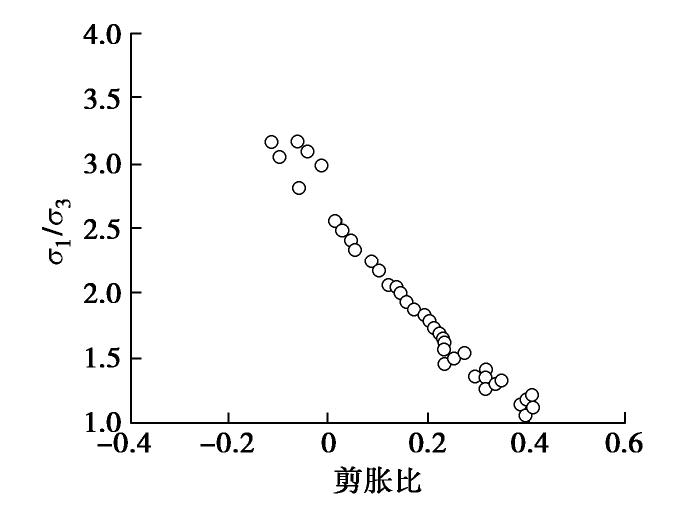
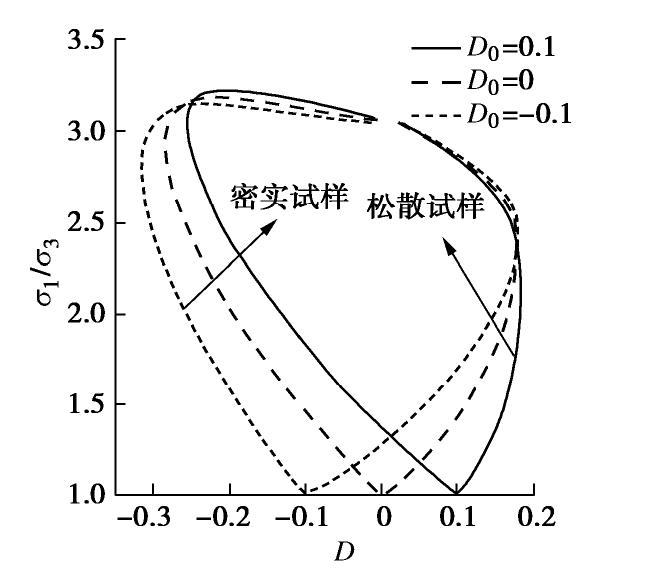
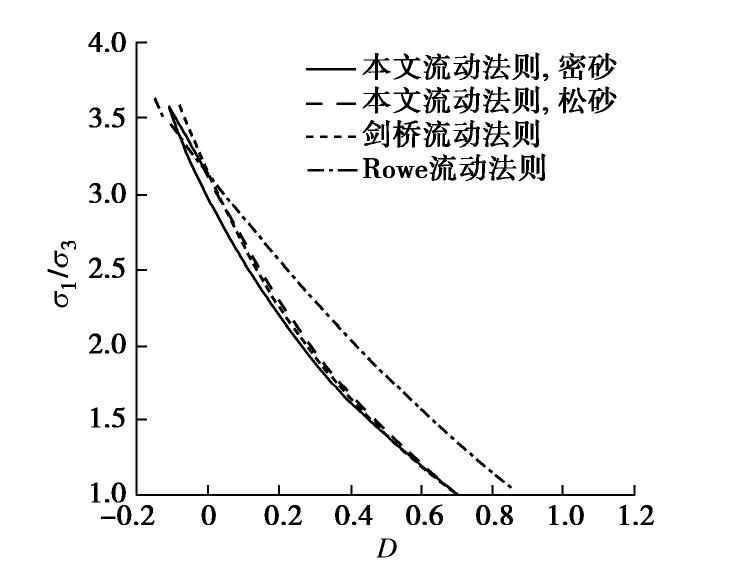
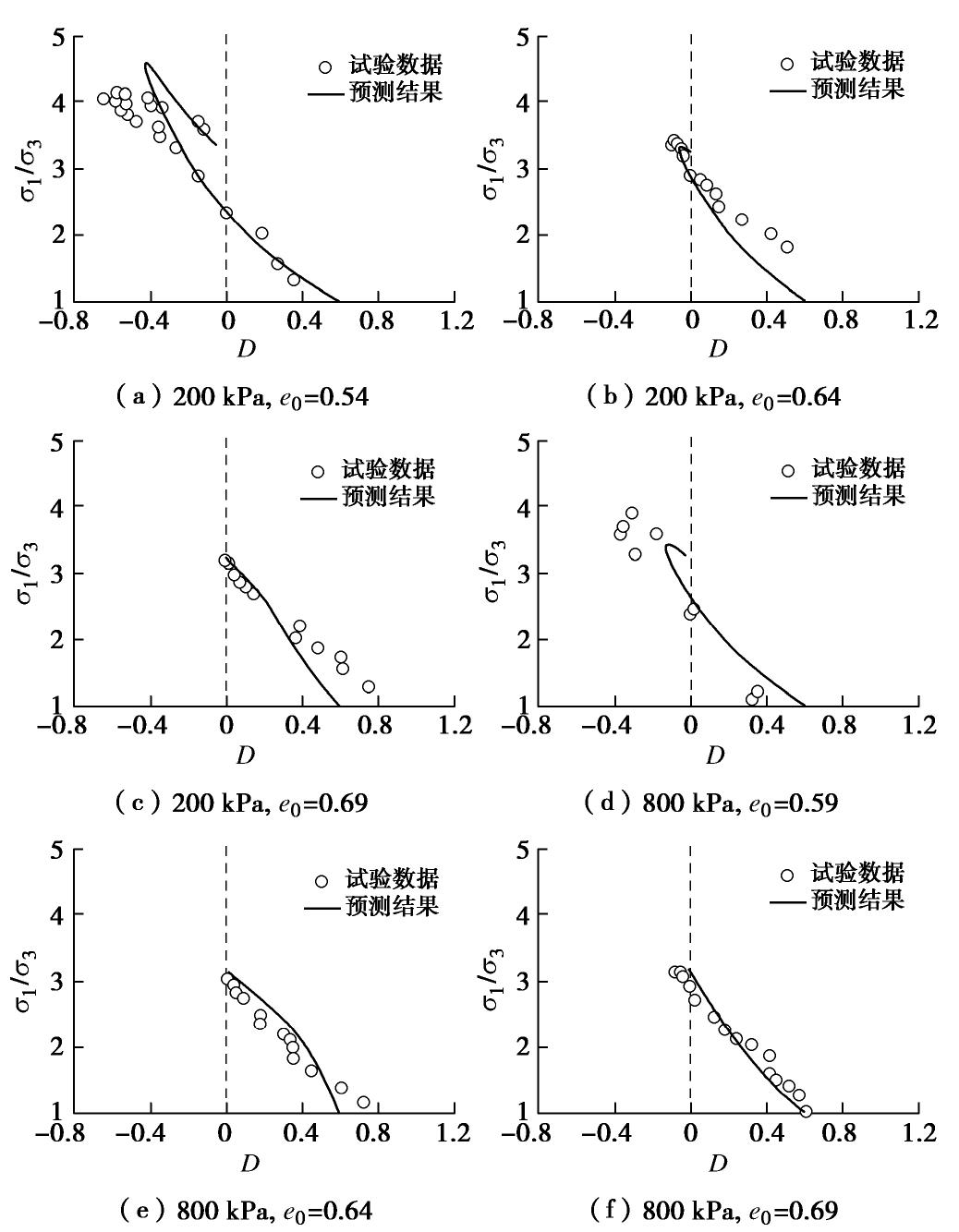
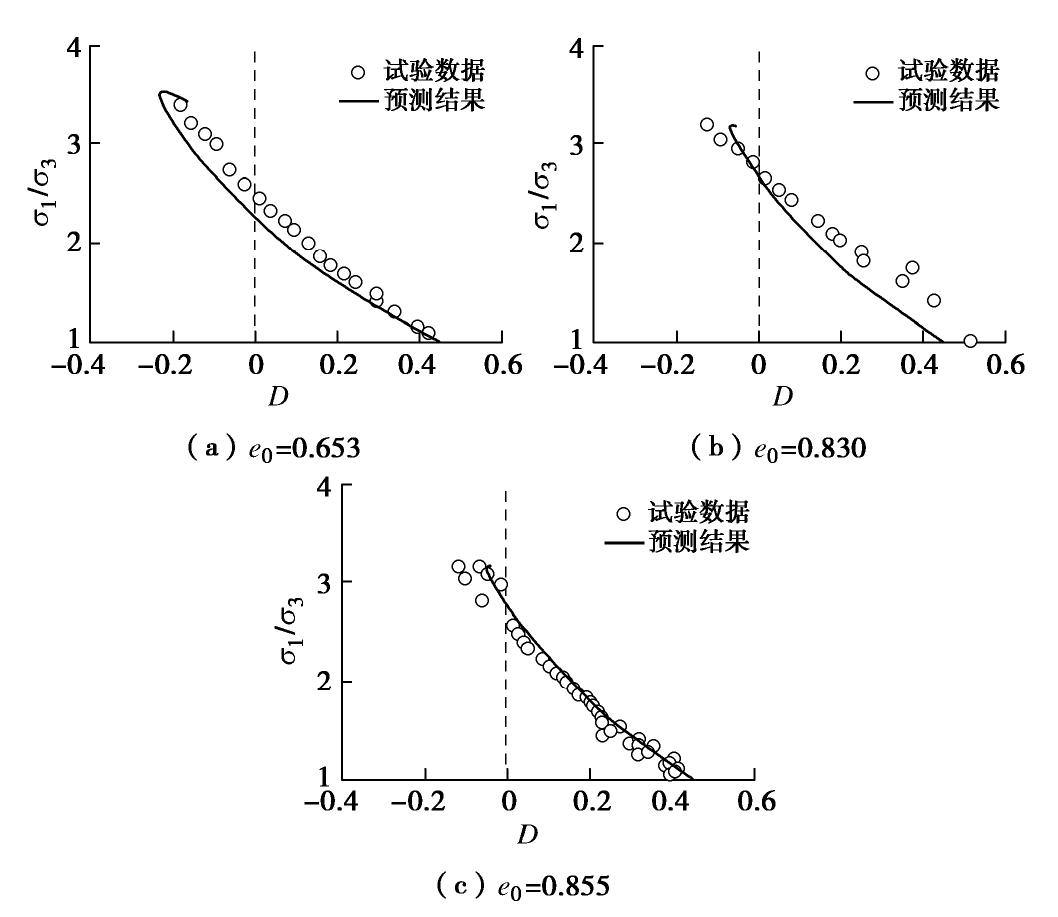
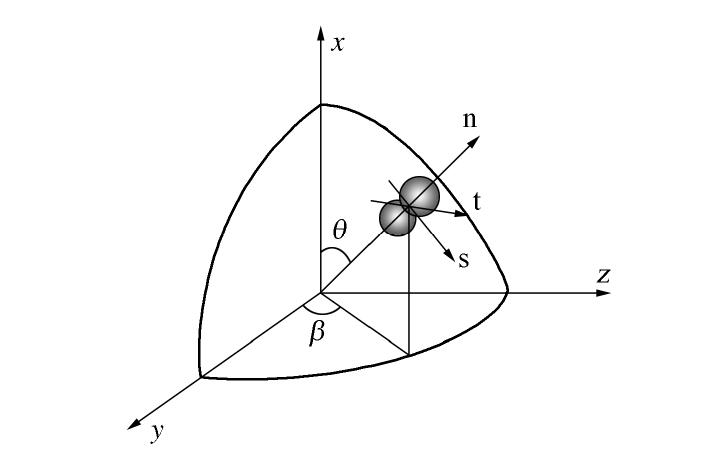
摘要: 从微观力学角度出发,基于真应力张量推导了散体中平均接触力与平均接触位移的计算公式,并通过宏-微观能量守恒得到了考虑散体各向异性组构及其演化的应力-剪胀关系；详细分析了剪胀参数的物理意义及对剪胀性的影响,并与经典的剑桥流动法则、Rowe剪胀方程以及室内试验结果进行了比较分析。研究结果表明,提出的应力-剪胀关系宏微观物理意义明确,考虑了材料密实状态和微观各向异性组构及其演化对应力-剪胀关系的影响,可以很好地模拟散粒体的初始剪胀（缩）行为,并可反映峰值应力比滞后于最大剪胀比的现象。同时提出的应力-剪胀方程还可以描述材料在相变点处应力比不等于临界应力比的现象,与已有室内试验结果一致,能够较好地预测散体材料三轴条件下的各向异性应力-剪胀关系。Abstract: From the perspective of micromechanics, the formulas for the average contact force and contact displacement in the granular are derived based on the true stress tensor, then the stress-shear dilatancy relationship considering the fabric anisotropy and its evolution is obtained through the macro-micro energy conservation. In addition, the physical meaning of dilatancy parameters and their influence on dilatancy are analyzed. Finally, the proposed formulation is compared with the classical Cambridge flow law, Rowe dilatancy equation and test results to calibrate its reasonableness and applicability. The proposed stress-dilatancy relationship with clear physical meaning can describe the initial dilatancy (contraction) behavior for granular materials, considering the anisotropic evolution of fabric and the influence of the density on the dilatancy. Moreover, the proposed stress-dilatancy equation can reflect that the stress ratio at the phase transition point is less than the critical stress ratio and the peak stress ratio emerges behind the maximum dilatancy ratio. It is in good agreement with the test results and can better predict the anisotropic stress-dilatancy relationship of granular materials.
-
-
![]()
图 5 不同流动法则下应力比-剪胀比关系对比图
Figure 5. Comparison of different stress-dilatancy relationships
![]()
图 6 Ottawa砂应力-剪胀关系的试验结果与预测结果对比图
Figure 6. Comparison of predicted and test results for Ottawa sand
-
[1] SCHOFIELD A, WROTH P. Critical State Soil Mechanics[M]. London: McGraw-Hill, 1968.
[2] NOVA R, WOOD D M. A constitutive model for sand in triaxial compression[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1979, 3(3): 255-278. doi: 10.1002/nag.1610030305
[3] LAGIOIA R, PUZRIN A M, POTTS D M. A new versatile expression for yield and plastic potential surfaces[J]. Computers & Geotechnics, 1996, 19(3): 171-191.
[4] ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proceedings of the Royal Society of London, Series A. Mathematical and Physical Sciences, 1962, 269(1339): 500-527.
[5] GUO P J, STOLLE D F. The extension of Rowe’s stress-dilatancy model to general stress condition[J]. Soils and Foundations, 2004, 44(4): 1-10. doi: 10.3208/sandf.44.4_1
[6] 蔡正银, 李相菘. 砂土的剪胀理论及其本构模型的发展[J]. 岩土工程学报, 2007, 29(8): 1122-1128. doi: 10.3321/j.issn:1000-4548.2007.08.002 CAI Zheng-yin, LI Xiang-song. Development of dilatancy theory and constitutive model of sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1122-1128. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.08.002
[7] WAN R, GUO P. A pressure and density dependent dilatancy model for granular materials[J]. Soils and Foundations, 1999, 39(6): 1-11. doi: 10.3208/sandf.39.6_1
[8] LI X S, DAFALIAS Y F. Constitutive modeling of inherently anisotropic sand behavior[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(10): 868-880. doi: 10.1061/(ASCE)1090-0241(2002)128:10(868)
[9] LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460. doi: 10.1680/geot.2000.50.4.449
[10] MANZARI M T, DAFALIAS Y F. A critical state two-surface plasticity model for sands[J]. Géotechnique, 1997, 47(2): 255-272. doi: 10.1680/geot.1997.47.2.255
[11] GAJO A, MUIR WOOD D. Severn-Trent sand: a kinematic-hardening constitutive model: the qp formulation[J]. Géotechnique, 1999, 49(5): 595-614. doi: 10.1680/geot.1999.49.5.595
[12] WANG R, DAFALIAS Y F, FU P, et al. Fabric evolution and dilatancy within anisotropic critical state theory guided and validated by DEM[J]. International Journal of Solids and Structures, 2019, 188-189(3): 210-222.
[13] TOBITA Y. Fabric tensors in constitutive equations for granular materials[J]. Soils and Foundations, 1989, 29(4): 91-104. doi: 10.3208/sandf1972.29.4_91
[14] ZHAO J, GUO N. Unique critical state characteristics in granular media considering fabric anisotropy[J]. Géotechnique, 2013, 63(8): 695-704. doi: 10.1680/geot.12.P.040
[15] YIN Z Y, CHANG C S. Stress-dilatancy behavior for sand under loading and unloading conditions[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2013, 37(8): 855-870.
[16] LIU Y, CHANG C S. Relationship between element-level and contact-level parameters of micromechanical and upscaled plasticity models for granular soils[J]. Acta Geotechnica, 2020, 15(7): 1779-1798. doi: 10.1007/s11440-019-00895-7
[17] XIAO Y, ASCE M, LONG L, et al. Effect of particle shape on stress-dilatancy responses of medium-dense sands[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2018, 145(2): 04018105.
[18] LIANG J, LU D, DU X, et al. A 3D non-orthogonal elastoplastic constitutive model for transversely isotropic soil[J]. Acta Geotechnica, 2021, in press.
[19] TSEGAYE A B, BENZ T, NORDAL S. Formulation of non-coaxial plastic dissipation and stress-dilatancy relations for geomaterials[J]. Acta Geotechnica, 2020, 15(10): 2727-2739. doi: 10.1007/s11440-020-00968-y
[20] 杨骏堂, 刘元雪, 郑颖人, 等. 剪胀型土剪胀特性的大数据深度挖掘与模型研究[J]. 岩土工程学报, 2020, 42(3): 513-522. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003018.htm YANG Jun-tang, LIU Yuan-xue, ZHENG Ying-ren et al. Deep mining of big data and model tests on dilatancy characteristics of dilatant soils[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 513-522. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003018.htm
[21] LIAO C L, CHANG T P, YOUNG D H, et al. Stress-strain relationship for granular materials based on the hypothesis of best fit[J]. International Journal of Solids and Structures, 1997, 34(31/32): 4087-4100.
[22] 刘洋, CHANG C S, 张铎, 等. 散粒介质三维应力-组构解析与破坏分析[J]. 岩土工程学报, 2014, 36(3): 401-408. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403002.htm LIU Yang, CHANG C S, ZHANG Duo, et al. Analytical solution of stress-fabric relationship and failure of granularmaterials in three dimensions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 401-408. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403002.htm
[23] CHANG C S, MISRA A. Packing structure and mechanical properties of granulates[J]. Journal of Engineering Mechanics, 1990, 116(5): 1077-1093. doi: 10.1061/(ASCE)0733-9399(1990)116:5(1077)
[24] ODA M, KONISHI J, NEMAT-NASSER S. Some experimentally based fundamental results on the mechanical behaviour of granular materials[J]. Géotechnique, 1980, 30(4): 479-495. doi: 10.1680/geot.1980.30.4.479
[25] ODA M, NEMAT-NASSER S, KONISHI J. Stress-induced anisotropy in granular masses[J]. Soils and Foundations, 1985, 25(3): 85-97. doi: 10.3208/sandf1972.25.3_85
[26] WAN R G, GUO P J. Stress dilatancy and fabric dependencies on sand behavior[J]. Journal of Engineering Mechanics, 2004, 130(6): 635-645. doi: 10.1061/(ASCE)0733-9399(2004)130:6(635)
[27] BEEN K, JEFFERIES M. Stress dilatancy in very loose sand[J]. Canadian Geotechnical Journal, 2004, 41(5): 972-989. doi: 10.1139/t04-038
[28] LIU D Y, LOURENÇO S D N. Stress-dilatancy behaviour of a polymer-coated sand[J]. Acta Geotechnica, 2021, 16(2): 647-652. doi: 10.1007/s11440-020-01022-7
[29] REGIER K. The stress-dilatancy behaviour of sands: pressure and density dependencies in both monotonic and cyclic loading regimes[M]. Calgary: University of Calgary, 1997.
[30] PRADHAN T B, TATSUOKA F, SATO Y. Experimental stress-dilatancy relations of sand subjected to cyclic loading[J]. Soils and Foundations, 1989, 29(1): 45-64. doi: 10.3208/sandf1972.29.45
-
期刊类型引用(25)
1. 张志哺. 干湿-冻融循环下公路切坡玄武岩力学特性及损伤机制研究. 公路. 2025(03): 41-49 . 
百度学术
2. 黄彦华，李明旭，武世岩，杨超. 基于连续-离散耦合方法的边坡稳定性模拟研究. 中南大学学报(自然科学版). 2025(04): 1502-1513 . 百度学术
3. 张科，李娜. 干湿循环作用下岩桥破裂演化及前兆异常定量识别研究. 工程地质学报. 2024(01): 64-73 . 百度学术
4. 刘帅，杨更社，潘振兴. 冻融环境下“三段式”岩质边坡锁固段损伤破坏及灾变机制研究. 岩石力学与工程学报. 2024(11): 2781-2795 . 百度学术
5. 黎俊华. 基于极限平衡法的边坡稳定性分析. 采矿技术. 2023(01): 39-44 . 百度学术
6. 王建明，崔新男，陈忠辉，陈冲. 露天矿含后缘裂隙岩质边坡岩体卸荷断裂机理与稳定性研究. 岩土工程学报. 2023(02): 345-353 . 本站查看
7. 郭朋瑜，闫兴田，吉锋，易林立. 四川茂县新磨村滑坡启动机制物理模拟试验研究. 工程地质学报. 2023(01): 154-164 . 百度学术
8. 林之岳，黎俊华，王道林. 基于爆破振速演变规律的采场安全分析. 黄金. 2023(03): 5-11 . 百度学术
9. 冷先伦，王川，盛谦，宋文军，陈健，张占荣，陈菲. 基于透明相似模型试验的主控裂隙边坡变形破坏演化机制研究. 岩土力学. 2023(05): 1283-1294+1308 . 百度学术
10. 冉孟坤，韦港荣，熊春发，卢超波，秦梓航. 广西某高速公路基于切线角理论的隧道变形监测预警应用研究. 四川地质学报. 2023(02): 302-306+312 . 百度学术
11. 刘先林，范杰，朱觉文，李明智，朱星. 单轴压缩下岩桥脆性断裂的临界慢化特征. 水利水电技术(中英文). 2022(03): 166-175 . 百度学术
12. 朱星，唐垚. 锁固段边坡模型破坏前兆特征. 地球科学. 2022(06): 1957-1968 . 百度学术
13. 杨泓全，范杰，黄成年，刘先林，朱星. 中部锁固岩桥脆性断裂特征试验研究. 科学技术与工程. 2022(15): 6255-6263 . 百度学术
14. 杨奎斌，朱彦鹏. 考虑后缘裂缝影响的均质土坡滑动面形式及搜索研究. 应用基础与工程科学学报. 2022(05): 1216-1227 . 百度学术
15. 王闯，董金玉，刘汉东，黄志全，赵亚文，杨兴隆. 三段式锁固型岩质边坡动力响应特性及破坏机制振动台模型试验研究. 地球科学. 2022(12): 4428-4441 . 百度学术
16. 郑强强，徐颖，胡浩，钱佳威，宗琦，谢平. 单轴荷载作用下砂岩的破裂与速度结构层析成像. 岩土工程学报. 2021(06): 1069-1077 . 本站查看
17. 陈永峰，张海东，赵广臣. 不同加载速率下端部节理岩桥变形破坏及裂隙扩展试验研究. 长江科学院院报. 2021(07): 66-72 . 百度学术
18. 张海东，陈永峰，赵广臣，张清华. 单轴压缩下预制端部节理岩桥变形破坏及裂隙扩展机制研究. 煤矿安全. 2021(09): 78-84 . 百度学术
19. 范杰，朱星，霍冬冬，胡桔维，刘俊峰. 基于数字图像相关和声发射的岩质锁固段破坏试验研究. 科学技术与工程. 2021(36): 15581-15590 . 百度学术
20. 李巧刚，张树东，吴斌. 矿区大型滑坡体力学机理及地质演化模式研究. 煤炭科学技术. 2020(03): 214-220 . 百度学术
21. 乔趁，李长洪，王宇，颜丙乾. 冻融循环作用下中部锁固岩桥破坏试验研究. 岩石力学与工程学报. 2020(06): 1094-1103 . 百度学术
22. 王建明，陈忠辉，周子涵，陈帅，孙小欢. 不同卸荷速率下节理岩桥变形破坏及裂隙扩展演化试验研究. 矿业科学学报. 2020(04): 382-392 . 百度学术
23. 袁新华. 单轴压缩下中部锁固岩桥变形破坏模式及演化机制研究. 中国安全生产科学技术. 2020(09): 116-121 . 百度学术
24. 李冬冬，刘汉东. 风脉寺滑坡前缘阻滑体不同产状稳定性研究. 华北水利水电大学学报(自然科学版). 2018(06): 8-12 . 百度学术
25. 姜彤，雷家华. 基于图像相关分析的锁固型滑坡模型试验方法. 华北水利水电大学学报(自然科学版). 2018(06): 41-45 . 百度学术
其他类型引用(32)
下载:
计量
- 文章访问数: 331
- HTML全文浏览量: 32
- PDF下载量: 198
- 被引次数: 57
