适用于弹黏塑性本构模型的修正切面算法

李舰; 蔡国庆; 尹振宇

doi:10.11779/CJGE202002006

适用于弹黏塑性本构模型的修正切面算法 English Version

李舰^{1, 2,},
蔡国庆^{1, 2},
尹振宇^3, ,

1.
北京交通大学城市地下工程教育部重点实验室,北京　100044
2.
北京交通大学土木建筑工程学院,北京　100044
3.
香港理工大学土木与环境工程学系,香港

基金项目:

中央高校基本科研业务费专项资金项目 2019JBM083

详细信息

作者简介:
李舰（1985— ）,男,博士,讲师,主要从事土的本构模型及其数值计算方面的研究工作。E-mail：jianli@bjtu.edu.cn

通讯作者:
尹振宇, E-mail：zhenyu.yin@polyu.edu.hk

中图分类号: TU43
计量
- 文章访问数: 378
- HTML全文浏览量: 28
- PDF下载量: 191
出版历程
- 收稿日期: 2019-07-06
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-01-31

Modified cutting-plane integration scheme for elasto-viscoplastic models

LI Jian^{1, 2,},
CAI Guo-qing^{1, 2},
YIN Zhen-yu^3, ,

1.
Key Laboratory of Urban Underground Engineering of Ministry of Education, Beijing Jiaotong University, Beijing 100044, China
2.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
3.
Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Hong Kong, China

摘要

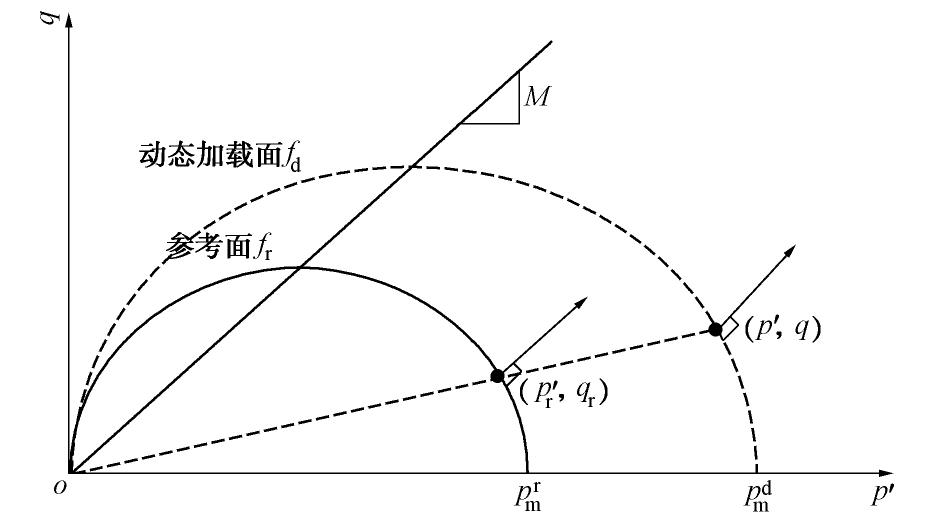
摘要: 针对弹黏塑性本构模型将原始切面算法进行了修正。该弹黏塑性本构模型结合了修正剑桥模型和过应力理论。首先对弹黏塑性本构模型的应力-应变关系式进行了调整,基于过应力理论给出了动态加载面硬化参数的演化方程。其次,利用切面算法对整理后应力-应变关系式进行了数值实现。在弹性试算过程中,该算法假设黏塑性应变率为常数,以此确保时间增量引起的当前应力点与动态加载面间的偏离。在塑性修正过程中,对动态加载面函数进行泰勒级数展开,依此获得黏塑性应变率增量。再次,提出了一种自动分步方法,有效地稳定了大应变步情况下算法的计算精度和收敛性。最后,对变应变率的固结试验和三轴剪切不排水试验进行了模拟,分析了修正切面算法的计算能力。
- 黏塑性 /
- 本构模型 /
- 切面算法 /
- 半隐式算法 /
- 数值积分
Abstract: The elasto-viscoplastic model can be regarded as a combination of the modified Cam-clay model and the overstress theory. Firstly, the stress-strain formulas for the model are rearranged, in which an evolution equation for the hardening parameter of dynamic loading surface is deduced based on the overstress theory. Secondly, the rearranged stress-strain formulas are numerically implemented by the cutting-plane integration scheme. In an elastic prediction process, the viscoplastic strain rate is assumed to be constant, which guarantees the deviation of the current stress state from dynamic loading surface due to time increments. In a plastic corrector process, a Taylor series approximation of the dynamic loading function is used to obtain the increment of viscoplastic multiplier rate. Thirdly, an adaptive substepping method is proposed to maintain the accuracy and convergence of the proposed algorithm at a large loading step. Finally, the performances of the modified cutting-plane algorithm are analyzed by the calculated results of step-changed oedometer tests and undrained triaxial tests.
- viscoplasticity /
- constitutive model /
- cutting-plane algorithm /
- semi-implicit scheme /
- numerical integration

HTML全文

0. 引言

国内外岩土工程稳定性分析及设计计算目前仍广泛采用单一安全系数法。安全系数在国内被定义为“使结构或地基的抗力标准值与作用标准值的效应之比不低于于某一规定安全系数的设计方法^[1-2]”,与梅耶霍夫等著名学者的定义“总安全系数可以定义为土工结构或基础的极限抗力与免受危险、损失或不可接受风险而施加的荷载或荷载影响之比^[3]”一致,也与比琳多（bѐlidor）及库仑（Coulomb）等最早提出安全系数概念的学者们的定义^[3]一致。按定义,安全系数K计算公式应表达为

$K = \sum R / \sum S$ ,

(1)

式中,R及S分别为抗力及荷载。

式（1）可称为安全系数的显式表达,历史悠久,国内外广泛应用于基于极限平衡法的岩土结构稳定性分析验算。K还有隐式表达形式,如国际上应用比较广泛的毕肖普（Bishop）法及国内应用较多的不平衡推力法,如图1,2及下式所示^[4]：

$K = \frac{\sum \frac{1}{m_{θ}_{i}} [c_{i_{^{}}} l_{i} \cos θ_{i} + (G_{i} - U_{i} \cos θ_{i}) \tan φ_{i}]}{\sum (G_{i} \sin θ_{i} + Q_{i} \cos θ_{i})}$ ,

(2)

$m_{θ i} = \cos θ_{i} + \frac{\tan φ_{i} \sin θ_{i}}{K}$ 。

(3)

图 1 条分法边坡稳定分析简图

Figure 1. Slope stability analysis by slice method

下载: 全尺寸图片幻灯片

图 2 不平衡推力法边坡稳定分析简图

Figure 2. Slope stability analysis by unbalanced thrust method

下载: 全尺寸图片幻灯片

式中 K为边坡稳定安全系数；c_i为第i条块滑动面黏聚力（kPa）； $φ_{i}$ 为第i条块滑动面内摩擦角（°）；l_i为第i条块滑动面长度（m）；θ_i为第i条块滑动面倾角（°）；U_i为第i条块单位宽度水压力（kN/m）；G_i为第i条块单位宽度自重（kN/m）；Q_i为第i条块地震力等水平荷载（kN/m）；i为计算条块号,从后方起编；n为条块数量。

$F_{i} = F_{i - 1} ψ + K G_{t i} - G_{n i} \tan φ_{i} - c_{i} l_{i}^{}$ 。

(4)

式中 F_i,F_i-1为第i、第i-1滑块剩余下滑力（kN）；ψ为推力传递系数；G_ti,G_ni为第i滑块自重沿滑动面切向、法向分力（kN）。

K不管是显式表达还是隐式表达,都应该遵守式（1）所示的规则,即稳定安全系数应为抗力之和 $\sum R$ 除以荷载之和 $\sum S$ 。本文为说明问题,把 $\sum R$ 分为R₁与R₂,把 $\sum S$ 分为S₁与S₂两部分（R₁与R₂、S₁与S₂可能相关也可能不相关）,则式（1）可转换为

$K_{0} = （ R_{1} ＋ R_{2} ） / （ S_{1} ＋ S_{2} ）$ 。

(5)

这种较为严谨的表达方式在国内外岩土工程中似乎并没有得到严格遵守。以岩土工程技术标准^[4~11]为代表,不少稳定安全系数计算公式在表达时都没有严格遵守上述安全系数的定义,存在着荷载与抗力在分子分母中错位及丢失现象。这些现象可归纳为如下6类：抗力的一部分（R₂）作为加项或减项被放到了分母,或/和荷载的一部分（S₂）作为减项被放到了分子,组合后产生了5类错位现象,本文称为第1～5类错位,分别如式（6）～（10）所示；式（11）则表示有部分抗力R₂及/或荷载S₂没被计入公式,本文称为丢失现象。

$K_{1} = R_{1} / (\sum S - R_{2})$ ,

(6)

$K_{2} = R_{1} / (\sum s - R_{2})$ ,

(7)

$K_{3} = (\sum R - S_{2}) / S_{1}$ ,

(8)

$K_{4} = （ R_{1} - S_{2} ） / （ S_{1} - R_{2} ）$ ,

(9)

$K_{5} = （ R_{1} - S_{2} ） / （ S_{1} ＋ R_{2} ）$ ,

(10)

$K_{6} = R_{1} / S_{1}$ 。

(11)

本文即对岩土工程稳定安全系数计算公式中这些抗力与荷载的错位与丢失现象进行总结归纳,对因此产生的不良影响进行分析探讨,继而提出如何提高公式计算结果准确性的建议。

1. 公式中荷载与抗力的错位丢失现象

（1）条分法是岩土结构稳定分析最为常用方法之一,有多种理论分析模型及相应计算公式。以瑞典条分法为例,为简单起见,暂不考虑地震力、水压力及地面附加荷载等作用,此时稳定安全系数计算公式如图1及下式所示：

$K = \frac{\sum G_{n i} \tan φ_{i} + \sum c_{i} l_{i}}{\sum G_{t i}}$ 。

(12)

最危险滑动面的滑弧圆心点O不管位于坡体以内还是以外,有些情况下都会有一部分条块产生抗滑力。令滑弧竖向半径对应着第m条块,如图1所示,式（12）的分母此时由 $\sum_{i = 1}^{m - 1} G t i$ 及 $\sum_{i = m}^{n} G t i$ 两项组成,前一项为第1～（m-1）条块产生的滑动力,对应的滑弧半径R_i与竖向夹角 $θ_{i}$ 为正值,在式（5）中用S₁表示；后一项为第m～n条块产生的抗滑力,对应的 $θ_{i}$ 为负值。有的标准将后一项作为滑动力与前一项相加,有的则相减,大多数没说怎么办。后一项本质上是抗力,在式（5）中用R₂表示,正确位置应该放在分子与其他抗力相加：

$K = \frac{\sum G_{n i} \tan φ_{i} + \sum c_{i} l_{i} + \sum_{i = m}^{n} G_{t i}}{\sum_{i = 1}^{m - 1} G_{t i}}$ 。

(13)

放在分母就会产生错位现象,与前一项相减则产生如式（6）所示第1类错位,相加则产生如式（7）所示第2类错位,分别如下式所示（此时S₁即为 $\sum S$ ）：

$K = \frac{\sum G_{n i} \tan φ_{i} + \sum c_{i} l_{i}}{\sum_{i = 1}^{m - 1} G_{t i} - \sum_{i = m}^{n} G_{t i}}$ ,

(14)

$K = \frac{\sum G_{n i} \tan φ_{i} + \sum c_{i} l_{i}}{\sum_{i = 1}^{m - 1} G_{t i} + \sum_{i = m}^{n} G_{t i}}$ 。

(15)

在国内外,Bishop法、Junbu法、Morgenstern-Price法、Spencer法、Sarma法、不平衡推力法等各种条分法^[12]与瑞典法一样,广泛应用于边坡、危岩、各种岩土体支挡结构（如桩墙、加筋土、土钉墙及重力式挡墙等）的整体稳定分析验算,如图3所示,第1,2类错位现象在这些条分法中普遍存在,不再赘述。

图 3 条分法整体稳定分析的各种应用

Figure 3. Various applications of slice method

下载: 全尺寸图片幻灯片

（2）岩土结构中有锚杆（包括土钉）作用时,有标准^[5]提供稳定安全系数分析验算简图及公式如下所示,式中T_tj及T_nj分别为第j根锚杆抗拔承载力T_j作用于滑动面的切向及法向分力（kN）：

$K = \frac{\sum G_{n i} \tan φ_{i} + \sum T_{n j} \tan φ_{j} + \sum c_{i} l_{i}}{\sum G_{t i} - \sum T_{t j}}$ 。

(16)

式（16）将锚杆提供的抗力T_j（在式（5）中用R₂表示）作为减项放在了分母,产生了第1类错位现象。这类公式在有预应力锚杆及土钉参与的岩土锚固结构^[5-8]中常见,如图4～8所示。

图 4 边坡锚固条分法稳定分析简图

Figure 4. Anchorage slope stability analysis by slice method

下载: 全尺寸图片幻灯片

图 5 基坑锚固条分法稳定分析简图

Figure 5. Stability analysis of anchorage foundation pits by slice method

下载: 全尺寸图片幻灯片

图 6 边坡锚固斜面法稳定分析简图

Figure 6. Stability analysis of anchorage slopes by plane method

下载: 全尺寸图片幻灯片

图 7 基础锚固稳定分析简图

Figure 7. Stability analysis of anchorage foundations

下载: 全尺寸图片幻灯片

图 8 危岩体锚固稳定分析简图

Figure 8. Stability analysis of anchorage unstable rock masses

下载: 全尺寸图片幻灯片

锚固坡体及基坑采用斜平面法稳定分析时,有标准^[5]提供K计算公式为

$K = \frac{\sum T_{n j} \tan φ + G_{n} \tan φ + c A}{G_{t} - \sum T_{t j}}$ 。

(17)

锚杆加固承受斜向荷载E_a的基础时,有标准^[5]提供K计算公式为

$K = \frac{f (E_{a} \sin θ + T \cos β)}{E_{a} \cos θ - T \sin β}$ 。

(18)

采用局部锚杆加固危岩时（图8）,有标准^[4]提供K计算公式为

$K = \frac{\sum T_{t j} + f \sum T_{n j}}{G_{t} - f G_{n} - c A}$ ,

(19)

式中,f为摩擦系数。

（3）第1类错位现象在重力式挡土墙抗水平滑移稳定安全系数计算公式中也司空见惯（图9）,如不少标准^{[4, 9]}中提供的K计算公式为

$K = \frac{f (G_{n} + E_{an})}{E_{at} - G_{t}}$ 。

(20)

图 9 挡墙抗水平滑移稳定分析简图

Figure 9. Stability analysis of retaining walls against horizontal sliding

下载: 全尺寸图片幻灯片

（4）考虑水压力作用时,有标准^[4]提供K计算公式如图1及下式所示：

$K = \frac{\sum (G_{i} - U_{i} \cos θ_{i}) \tan φ_{i} + \sum c_{i} l_{i}}{\sum G_{i} \sin θ_{i}^{}}$ 。

(21)

这种水压力对于岩土结构来说是滑动力,即荷载,在式（5）中用S₂表示,应该放在分母,而式（21）将之放在分子,产生了如式（8）所示第3类错位现象。这类错位现象在涉及水侧向压力、水上浮力及地震力等荷载的稳定分析验算时常见,例如有标准^[4]提供边坡斜面法稳定分析时K计算公式为（图10）

$K = \frac{(G \cos θ - Q \sin θ - U) \tan φ + c l}{G \sin θ + Q cos θ}$ 。

(22)

图 10 边坡斜面滑移稳定分析简图

Figure 10. Slope stability analysis by plane method

下载: 全尺寸图片幻灯片

（5）锚杆抗力与水压力等往往会同时发生,采用条分法时与 $θ_{i}$ 负值所对应的抗力也可能同时发生,综合在一起再合并同类项后会产生式（9）,（10）所示的第4类及第5类错位现象,不再赘述。

（6）式（11）所示的荷载与抗力丢失现象以某标准^[10]中的克朗兹（Kranz）法为典型。Kranz分析方法如下所示：当块体处于平衡状态时,利用力多边形（也可采用公式计算方法）求得锚杆承受的最大拉力R_max,其水平分力R_h,max与锚杆抗拔力特征值的水平分力之比定义为稳定安全系数（图11）。

图 11 锚固结构Kranz法稳定分析简图

Figure 11. Stability analysis of anchorage structures by Kranz method

下载: 全尺寸图片幻灯片

Kranz法稳定安全系数定义为锚杆抗拔力极限值与设计值之比,从安全系数角度来看丢失了块体滑动力及抗滑力等重要的荷载及抗力,且极限平衡分析时没有计取支护结构因嵌入地层而得到的被动土压力。这源于锚定板挡墙的分析方法或许尚没有成熟到可列入技术标准,本文不再讨论（图12）。

图 12 抗浮锚杆整体稳定分析简图

Figure 12. Overall stability analysis of anti-floating anchors

下载: 全尺寸图片幻灯片

（7）在涉及水上浮力时,有标准^[5]提供抗浮锚杆整体稳定安全系数计算公式为

$K = \frac{W + G^{'}}{F_{W}}$ 。

(23)

式中 $G^{'}$ 为基础下抗浮锚杆范围内岩土体总重力（kN）,计算时采用有效重力；W为结构自重及其他永久荷载标准值之和（kN）； $F_{W}$ 为地下水浮力标准值（kN）。

式（23）中岩土体取有效重力 $G^{'}$ ,即为重力标准值 $G_{k}$ 减去水浮力 $F_{W}$ ,则式（23）可转化为如下形式：

$K = (G_{k} + W - F_{W}) / F_{W}$ 。

(24)

可见,公式中水浮力被重复扣减了,尚不属于第3类错位现象,本文不再讨论。

2. 荷载与抗力错位对计算结果的影响

稳定安全系数计算公式中荷载与抗力的错位显然会对计算结果有影响,下面进行简单计算分析。

（1）第1类错位现象

为了清晰表达,令ΣS=1.0、R₁=mΣS及R₂=nR₁。以m=0.7为例,按式（5）计算得到的K₀、式（6）计算得到的K₁及相对误差δ₁随n的变化情况如图13所示。

图 13 　m=0.7时K₀,K₁及δ₁随n的变化

Figure 13. Variation of K₀, K₁ and δ₁ with n while m = 0.7

下载: 全尺寸图片幻灯片

变化规律：随着n的增加,K₀及K₁一开始均增大,但K₁增速很快,两者相差越来越大,因为K₀为准确的安全系数,故K₁相对于K₀而言虚高；当R₂大于ΣS后,K₁变为负值。m为其他值时图形大同小异,即这种变化规律不随m而改变。K₁为负值显然不被安全系数规则所允许,安全系数最低为0,不可能为负值,说明用式（6）计算安全系数存在着较大缺陷。工程中通常把稳定安全系数目标值设定为1.30,令K₁为1.30不变,K₀及δ₁随n的变化情况如表1和图14所示。

表 1 K₁=1.30时K₀及δ₁随n的变化

Table 1. Variation of K₀ and δ₁ with n while K₁ = 1.30

n	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	0.99	3.5
K₀	1.30	1.27	1.24	1.22	1.20	1.18	1.17	1.16	1.15	1.14	1.13	1.05
δ₁/%	0	3	5	7	9	10	11	12	13	14	15	23

下载: 导出CSV

| 显示表格

图 14 　K₁=1.30时K₀随n的变化

Figure 14. Variation of K₀ with n while K₁ = 1.30

下载: 全尺寸图片幻灯片

从图14和表1可知,K₁不变时K₀随着n的增加一直低于K₁且相差越来越大,n=3.5时K₁仍有机会为1.30,看起来安全系数足够,但实际上K₀已经低至1.05,安全风险很大。并非危言耸听：图4～7所示岩土结构中,设置有预应力锚杆且发挥主要作用时实际安全系数较低、安全储备不足的机率很大,即第1种错位现象存在着安全隐患,可能会导致设计计算结果安全度不够。

（2）第2类错位现象

仍令ΣS=1.0,R₁=mΣS及R₂=nR₁。m=0.7时,K₀、按式（6）计算得到的K₂及相对误差δ₂随n的变化情况如图15所示。

图 15 　m=0.7时K₀,K₂及δ₂随n的变化

Figure 15. Variation of K₀, K₂ and δ₂ with n while m = 0.7

下载: 全尺寸图片幻灯片

变化规律为：随着n的增加K₀增大而K₂减小,K₂一直低于K₀。m为其他值时图形大同小异,即这种变化规律不随m而改变。把K₂设定为1.30时,K₀及δ₂随n的变化情况及K₀设定为1.30时K₂随n的变化情况如表2和图16,17所示。

表 2 　K₂=1.30时K₀及δ₁随n的变化

Table 2. Variation of K₀ and δ₁ with n while K₂ = 1.30

n	0	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5
K₀	1.30	1.46	1.65	1.86	2.10	2.40	2.76	3.24	3.78	4.57	5.55
δ₂/%	0	-11	-21	-30	-38	-46	-53	-60	-66	-72	-77

下载: 导出CSV

| 显示表格

图 16 　K₂=1.30时K₀随n的变化

Figure 16. Variation of K₀ with n while K₂ = 1.30

下载: 全尺寸图片幻灯片

图 17 　K₀=1.30时K₂随n的变化

Figure 17. Variation of K₂ with n while K₀ =1.30

下载: 全尺寸图片幻灯片

从图15～17及表2可知,随着n的增加,K₂不变时K₀加大或K₀不变时K₂减小,K₂一直低于K₀且相差越来越大,K₂保守的程度越来越大,即第2类错位现象偏于保守,K₂相对于K₀而言虚低,可能会给工程造成较大浪费。高大边坡采用条分法稳定分析时,要达到技术标准规定的目标安全系数有时很难,边坡越高安全系数提高越困难,每提高一点可能需要大量的削方或锚固工作量；而高大边坡滑弧圆点往往在坡体内、如图1所示,部分坡脚岩土体会产生抗滑力,计算公式中应该让这部分抗力发挥应有的作用,以减少不必要的浪费。

第1类及第2类错位公式产生的后果可用一个极端算例加以说明。如图18所示,仅考虑土体自身,没有其他外力作用,假定土的抗剪强度指标c,φ均为0（即水）,水面平静时,滑动力 $\sum_{i = 1}^{m - 1} G t i$ 与抗滑力 $\sum_{i = m}^{n} G t i$ 相等,按式（13）所示正确公式计算,实际安全系数为1,临界稳定。但是：①按式（14）、即第1类错位公式,计算结果安全系数为无穷大,即计算结果虚高。这可能会导致工程安全程度不足,尤其在淤泥等软弱土层中,不少工程经验表明,淤泥等软弱土层中更容易发生稳定破坏,有些即与第1类错位公式计算结果虚高相关；②按式（15）、即第2类错位公式,计算结果安全系数为0,即计算结果虚低,可能会造成较严重浪费,尤其在高大边坡中,时常发生按正确公式计算结果安全系数满足目标值,但按错位公式计算结果不满足而导致工程量大幅增加现象。

图 18 平静水面稳定分析简图

Figure 18. Diagram of stability analysis of calm water surface

下载: 全尺寸图片幻灯片

（3）第3类错位现象

令ΣR=1.0,S₁=mΣR及S₂=nΣR（与第1,2类不同,第3类错位现象中S₂与S₁关联性不强,故n亦设定为与R相关）。m=0.7时,K₀、按式（6）计算得到的K₃及相对误差δ₃随n的变化情况如图19所示。

图 19 　m=0.7时K₀,K₃及δ₃随n的变化

Figure 19. Variation of K₀, K₃ and δ₃ with n while m = 0.7

下载: 全尺寸图片幻灯片

变化规律为：随着n的增加K₀及K₃均减少,K₃在高于1.0时数值比K₀高,在低于1.0时比K₀低且相差越来越大,当S₂大于ΣR后K₃为负值。m为其他值时图形大同小异,即这种变化规律不随m而改变。与K₁一样,K₃不应该为负值,如果为负值说明用式（8）计算安全系数存在着理论缺陷。K₃设定为1.30时K₀及δ₃随n的变化情况如表3和图20所示。

表 3 K₃=1.30时K₀及δ₃随n的变化

Table 3. Variation of K₀ and δ₃ with n while K₃ = 1.30

n	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	0.99
K₀	1.30	1.27	1.23	1.19	1.16	1.13	1.10	1.08	1.05	1.02	1.00
δ₃/%	0	3	6	9	12	15	18	21	24	27	30

下载: 导出CSV

| 显示表格

图 20 K₃=1.30时K₀随n的变化

Figure 20. Variation of K₀ with n while K₃ = 1.30

下载: 全尺寸图片幻灯片

从图19,20及表3可知,K₀随着n的增加在减小,在大于1.0时一直低于K₃且相差越来越大,n=0.8时K₃仍有机会为1.30,但此时准确的安全系数K₀=1.05,安全风险很大,与第1种错位现象类似,K₃虚高。S₂通常为地震力及水压力等荷载,与ΣR相比不大,导致K₀大幅降低的概率不大,但式（21）,（22）所示水为水头较大的承压水时,就有可能导致计算结果安全系数虚高较多,且不少技术标准^[4]允许此类工况时目标安全系数可适当降低,例如为1.15,那么在地震力、暴雨导致的地下水压力增加及公式误差的共同作用下,对岩土结构造成的安全风险就不可轻视了。

（4）如式（9）所示的第4类公式错位现象为第3类与第1类作用相加,安全系数计算结果进一步虚高,岩土结构安全风险进一步加大；式（10）所示第5类公式错位现象为第3类与第2类的作用抵减,R₂作用较大时与第2类相似,S₂作用较大时与第3类相似,R₂与S₂相互作用结果进一步加大了计算结果的不确定性。不再细分赘述。

3. 改进措施

明确了问题所在,对稳定安全系数计算公式的改进也就水到渠成：把式（6）～（10）等公式中错位的荷载与抗力按式（5）归位即可。如果不便直接归位,可先不考虑安全系数、列出极限平衡公式如下式所示：

$\begin{array}{l} \sum R - \sum S = 0, \\ \sum M_{R} - \sum M_{S} = 0 。 \end{array}}$

(25)

式中,MR,MS分别为抗滑力矩及下滑力矩,再按式（1）写出安全系数计算公式,公式中分子及分母均只有加项、没有减项就正确了。

这样,这些计算公式可以修正并概化为一个统一公式,如下式所示：

$K_{0} = \frac{f \sum G n i + \sum_{i = m}^{n} G t i + \sum c i l i + f \sum T n j + \sum T t j + f E an}{\sum_{i = 1}^{m - 1} G t i + E at + E q + f \sum U i}$ ,

(26)

式中,E_q为地震力,f有时需要用tanϕ表达,地面及地下有垂直向下的附加荷载时可视为加大了岩土体的自重。

式（26）是概化公式,适用于图2及图6～10所示力平衡类稳定分析法,采用图1,图3～5所示力矩平衡类稳定分析法时需加上作用力臂。按照国家技术标准管理体系,文献[1, 2]为通用标准,文献[4～11]为专用标准,通用标准为专用标准的上位标准,即专用标准应遵守通用标准,从前述分析可知,式（6）～（11）违背了这一原则。而改进后的式（26）遵守通用技术标准[1-2]要求,符合安全系数应有的概念及规则,计算结果准确程度明显提高,且同一公式在不同工况下及不同设计参数下的计算结果之间具有了可比性。

4. 讨论与说明

（1）岩土结构稳定分析有多种理论模型,仅条分法就有瑞典法、Bishop法、Junbu法、Morgenstern-Price法、Spencer法、Sarma法、不平衡推力法等多种,本文无意讨论各种模型的合理性,讨论的是按不同模型编写的安全系数计算公式有时存在着荷载与抗力错位这种不符合安全系数定义甚至也不符合模型原理的现象以及后果。

（2）荷载与抗力错位在极限平衡状态,即安全系数为1时不产生不良影响,安全系数不为1时才产生。

（3）安全系数可以很小,接近0,但无论如何都不能为负,公式计算结果为负则不符合安全系数定义,说明计算公式存在着不合理之处。

（4）受到水浮力作用时,传统方法取岩土体有效重力进行稳定计算,如图1,10及下式所示：

$K = \frac{{G^{'}}_{n} f + c l}{{G^{'}}_{t}} = \frac{(G - F_{w}) \cos θ f + c l}{(G - F_{w}) \sin θ}$ 。

(27)

把无水浮力作用、即式中 $F_{w}$ 为0时的安全系数记为 $K_{00}$ ,假设岩土体完全被地下水浸泡时c,f不变,令水浮力 $F_{w}$ =nG,则式（24）可表达为

$K_{4} = \frac{K_{00} G \sin θ - n G f \cos θ}{G \sin θ - n G \sin θ} = \frac{K_{00} - n f ctan θ}{1 - n}$ 。

(28)

在fctanθ=0.9工况时,设K00=1.30,则式（28）可表示为

$K 4 = \frac{1.30 - 0.9 n}{1 - n}$ 。

(29)

与式（9）对比可知,式（29）即为第4类错位公式。按概化公式（26）,分子分母中均不应出现减项,故应将式（28）分子分母中的水浮力Fw位置互换,即水浮力作为抗力（减少了下滑力）时放在分子、作为荷载（减少了抗滑力）时放在分母,正确的计算公式应为

$K_{0} = \frac{K_{00} G \sin θ + n G s in θ}{G \sin θ + n G f \cos θ} = \frac{1.30 + n}{1 + 0.9 n}$ 。

(30)

当n从0逐步提高,即水浮力从0逐渐增大时,式（29）,（30）计算结果如表4所示。

表 4 K4及K0随n的变化

Table 4. Variation of K4 and K0 with n

n	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	0.99
K₄	1.30	1.34	1.40	1.47	1.57	1.70	1.90	2.23	2.90	4.90	40.9
K0	1.30	1.28	1.26	1.25	1.24	1.23	1.23	1.22	1.22	1.22	1.21

下载: 导出CSV

| 显示表格

可见,在其他条件不时,随着岩土体受到水浮力增加,式（29）所示错位公式计算得到的稳定安全系数越来越高,而式（30）所示正确公式计算得到的安全系数则越来越低,显然后者更符合工程实际。

（5） $\sum R / \sum S$ 得到的结果为安全系数,称为计算安全系数或实际安全系数等,技术标准中规定的安全系数低限值称为目标安全系数（或安全系数目标值）、规定安全系数或设计安全系数等。有人将目标安全系数称为安全系数,将计算安全系数称为稳定系数,稳定系数可以为负。这种看法显然不准确,不管叫安全系数还是稳定系数, $\sum R / \sum S$ 得到的结果都不应该为负, $\sum R - \sum S$ 的结果才允许出现负值。

（6）以式（28）为例,有人认为,f是个不确定性很大的参数,不可放在荷载（分母）中。认为恰好相反,不确定性大更应该将之放在正确的位置,以避免计算结果产生更大的不确定性。

（7）有人认为,计算公式因技术标准、行业等而不同,已经形成习惯、约定俗成,多年来没有异议,无需改变。认为,稳定分析模型及目标安全系数等可因人、技术标准及行业而不同,但安全系数定义不能不同、安全系数计算公式须符合安全系数定义这一原则不能不同；在计算公式符合安全系数定义这一前提下,各种分析模型的合理性及适用性才能得到更准确的验证,才能够进行统一评判与横向比较。计算公式中的荷载与抗力错位现象,不管是国内还是国外,不管是显式还是隐式,都广泛存在,其中一些计算公式在业内也有过争议,很多商业软件公司在编写稳定验算程序时对式（13）等所示错位现象也有过提示,但均不系统且没有形成结论。这些公式错位现象以前没有被重视,并不代表不需要重视,不需要改进。和国外相比,国内淤泥等软土中的基坑工程以及高大边坡工程越来越多,越是这些困难的条件,错位公式的不良影响越大,按错位公式计算结果导致的安全系数虚高或虚低,对工程都是极为不利的。

（8）另外,文中从相关技术标准引用公式时,对部分公式进行了适当简化及对符号进行了统一调整,故有时看起来与标准不完全一致,但不产生实质影响。

5. 结论

（1）岩土结构稳定分析时,计算公式中的安全系数不管显性表达还是隐性表达,均应为抗力之和除以荷载之和。

（2）国内外相关标准中稳定安全系数计算公式存在着5类抗力与荷载错位现象,还存在着抗力及/或荷载丢失、荷载被重复扣减等现象。

（3）条分法稳定安全系数计算公式在某些情况下会把产生抗滑力的条块作为荷载计入分母中,如果与滑动力相减则形成第1类错位现象,相加则产生第2类错位现象；锚固工程稳定分析时锚杆抗力的切向分量有时被放在了分母与滑动力相减,亦形成第1类错位现象。

（4）有的稳定安全系数计算公式把水压力等荷载放在了分子与抗力相减,产生了第3类错位现象。第3类分别与第1,2类作用叠加,产生了第4,5类错位现象。

（5）第1类与第3类错位造成稳定安全系数计算结果虚高,导致工程有时安全储备不足,尤其是在软弱土层中；第2类错位造成安全系数虚低,可能会导致较大浪费,尤其是高大边坡工程。第4,5类错位加大了计算结果的不确定性,其中第4类会进一步造成安全系数虚高。

（6）这些错位的计算公式可修正并概化为一个统一公式。

图 1 EVP-MCC模型的动态加载面和参考面

Figure 1. Dynamic loading surface and reference surface of EVP-MCC model

下载: 全尺寸图片幻灯片

图 2 变应变率固结试验计算结果

Figure 2. Calculated results of step-changed oedometer tests

下载: 全尺寸图片幻灯片

图 3 3种算法变应变率固结试验

Figure 3. Comparison of calculation errors and total iteration number of three kinds of algorithms for step-changed oedometer tests

下载: 全尺寸图片幻灯片

图 4 变应变率三轴剪切不排水试验

Figure 4. Calculated results of deviatoric stress and pore-water pressure for step-changed undrained triaxial tests

下载: 全尺寸图片幻灯片

图 5 两种算法变应变率三轴试验

Figure 5. Comparison of calculation errors and total iteration number of two kinds of algorithms for step-changed undrained triaxial tests

下载: 全尺寸图片幻灯片

表 1 Saint-Herblain黏土模型参数和状态变量初值

Table 1 Values of parameters and state constants of Saint-Herblain clay

$p_{m0}^{r}$ /kPa	e₀	$μ$	κ	λ	M	Cα_ae
39	2.26	0.2	0.038	0.48	1.2	0.034

下载: 导出CSV

参考文献(21)

[1]	YIN Z Y, ZHU Q Y, YIN J H, et al. Stress relaxation coefficient and formulation for soft soils[J]. Géotechnique Letters, 2014, 4(1): 45-51. doi: 10.1680/geolett.13.00070
[2]	YAO Y P, KONG L M, ZHOU A N, et al. Time-dependent unified hardening model: three-dimensional elastoviscoplastic constitutive model for clays[J]. Journal of Engineering Mechanics, 2015, 141(6): 0414162.
[3]	尹振宇, 朱启银, 朱俊高. 软黏土蠕变特性试验研究：回顾与发展[J]. 岩土力学, 2013, 24(增刊2): 1-17. YIN Zhen-yu, ZHU Qi-yin, ZHU Jun-gao. Experimental investigation on creep behavior of soft clays: Review and development[J]. Rock and Soil Mechanics, 2013, 24(S2): 1-17. (in Chinese)
[4]	韩剑, 姚仰平, 尹振宇. 超固结度对超固结饱和黏土不排水蠕变特性的影响研究[J]. 岩土工程学报, 2018, 40(3): 426-430. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201803007.htm HAN Jian, YAO Yang-ping, YIN Zhen-yu. Influences of overconsolidation ratio on undrained creep behavior of overconsolidated saturated clay[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 426-430. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201803007.htm
[5]	YIN Z Y, CHANG C S, KARSTUNEN M, et al. An anisotropic elastic-viscoplastic model for soft clays[J]. International Journal of Solids and Structures, 2010, 47(5): 665-677. doi: 10.1016/j.ijsolstr.2009.11.004
[6]	YIN Z Y, KARSTUNEN M, CHANG C S, et al. Modeling time-dependent behavior of soft sensitive clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1103-1113. doi: 10.1061/(ASCE)GT.1943-5606.0000527
[7]	殷建华. 等效时间和岩土材料的弹黏塑性模型[J]. 岩石力学与工程学报, 1999, 18(2): 124-128. YIN Jian-hua. Equivalent time and elastic visco-plastic modelling of geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(2): 124-128. (in Chinese)
[8]	王立忠, 但汉波. K₀固结软黏土的弹黏塑性本构模型[J]. 岩土工程学报, 2007, 29(9): 1344-1354. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200709011.htm WANG Li-zhong, DAN Han-bo. Elastic viscoplastic constitutive model for K₀-consolidated soft clays[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1344-1354. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200709011.htm
[9]	李兴照, 黄茂松, 王录民. 流变性软黏土的弹黏塑性边界面本构模型[J]. 岩石力学与工程学报, 2007, 26(7): 1393-1401. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200707012.htm LI Xing-zhao, HUANG Mao-song, WANG Lu-min. Bounding surface elasto-viscoplastic constitutive model for rheological behaviors of soft clays[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1393-1401. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200707012.htm
[10]	尹振宇. 天然软黏土的弹黏塑性本构模型：进展及发展[J]. 岩土工程学报, 2011, 33(9): 1357-1369. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201109011.htm YIN Zhen-yu, Elastic viscoplastic models for natural soft clay: review and development[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1357-1369. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201109011.htm
[11]	孔令明, 罗汀, 姚仰平. 率相关本构模型的临界状态描述[J]. 岩土力学, 2015, 36(9): 2442-2450. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201509003.htm KONG Ling-ming, LUO Ting, YAO Yang-ping. Description of critical state for rate-dependent constitutive models[J]. Rock and Soil Mechanics, 2015, 36(9): 2442-2450. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201509003.htm
[12]	ORTIZ M, SIMO J C. An analysis of a new class of integration algorithms for elastoplastic constitutive relations[J]. International Journal for Numerical Methods in Engineering, 1986, 23(3): 353-366.
[13]	PERZYNA P. Fundamental problems in viscoplasticity[J]. Advances in Applied Mechanics, 1966, 9: 243-377.
[14]	KATONA M G. Evaluation of viscoplastic cap model[J]. Journal of Geotechnical Engineering, 1984, 110(8): 1106-1125.
[15]	BORJA R I. Cam-clay plasticity: part II implicit integration of constitutive equation based on a nonlinear elastic stress predictor[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 88: 225-240.
[16]	STOLLE D F E, VERMEER P A, BONNIER P G. Time integration of a constitutive law for soft clays[J]. Communications in Numerical Methods in Engineering, 1999, 15(8): 603-609.
[17]	HIGGINS W, CHAKRABORTY T, BASU D. A high strain-rate constitutive model for sand and its application in finite-element analysis of tunnels subjected to blast[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(15): 2590-2610.
[18]	YIN Z Y, LI J, JIN Y F, et al. Estimation of robustness of time integration algorithms for elasto-viscoplastic modeling of soils[J]. International Journal of Geomechanics, 2019, 19(2): 04018197.
[19]	SHENG D, SLOAN S W, GENS A, et al. Finite element formulation and algorithms for unsaturated soils: part I theory[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(9): 745-765.
[20]	WANG W, DATCHEVA M, SCHANZ T, et al. A sub-stepping approach for elastoplasticity with rotational hardening[J]. Computational Mechanics, 2006, 37(3): 266-278.
[21]	SLOAN S W. Substepping schemes for the numerical integration of elastoplastic stress-strain relations[J]. International Journal for Numerical Methods in Engineering, 1987, 24(5): 893-911.