悬浮长芯劲性搅拌桩复合地基固结解析解

杨涛; 戴基彤; 王恒栋

doi:10.11779/CJGE202002005

悬浮长芯劲性搅拌桩复合地基固结解析解 English Version

1.
上海理工大学土木系,上海　200093
2.
上海市政工程设计研究总院(集团)　有限公司,上海　200092

基金项目:

国家重点研究发展计划项目 2016YFC0802405

详细信息

作者简介:
杨涛（1962— ）,男,博士,教授,从事地基加固技术与复合地基理论研究工作。E-mail：shyangtao@163.com

中图分类号: TU473
计量
- 文章访问数: 364
- HTML全文浏览量: 67
- PDF下载量: 147
出版历程
- 收稿日期: 2019-05-07
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-01-31

Analytical solutions for consolidation of a composite ground with floating stiffened deep cement mixing columns with long core piles

1.
Department of Civil Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
2.
Shanghai Municipal Engineering Design Institute (Group) Co., Ltd., Shanghai 200092, China

摘要

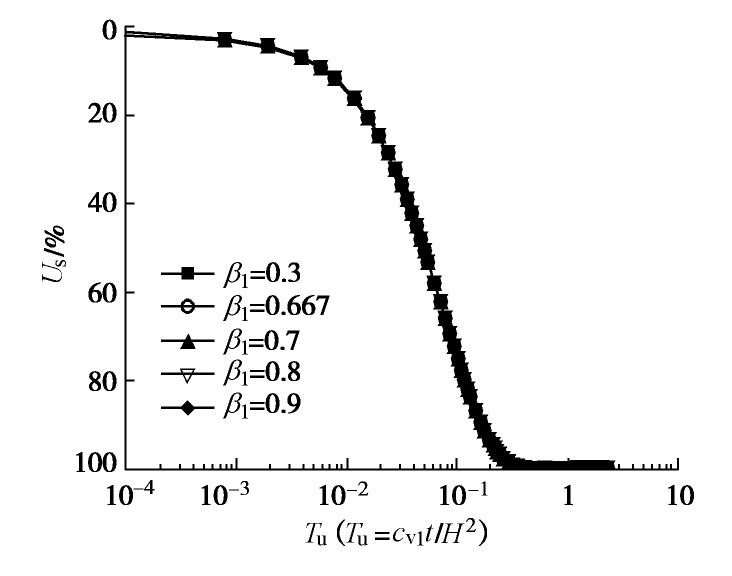
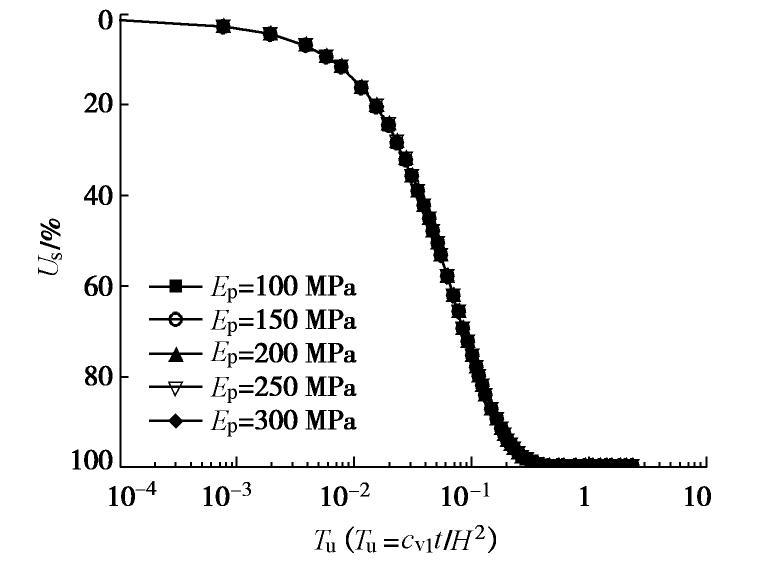
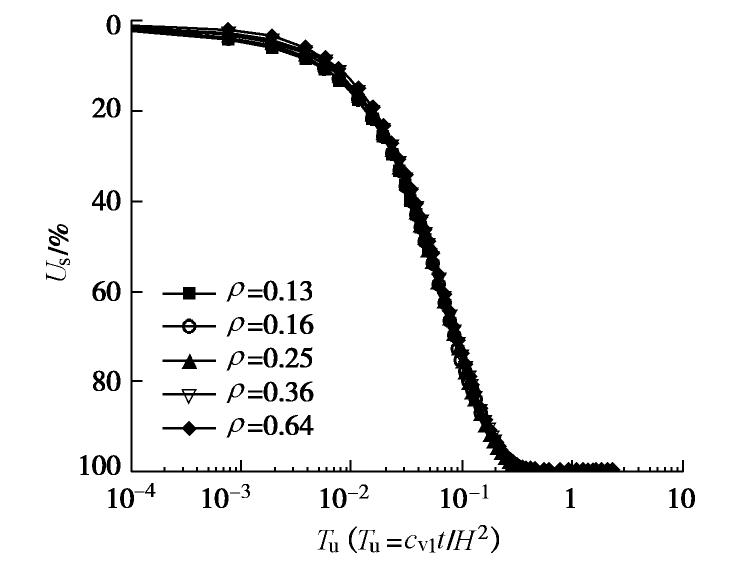
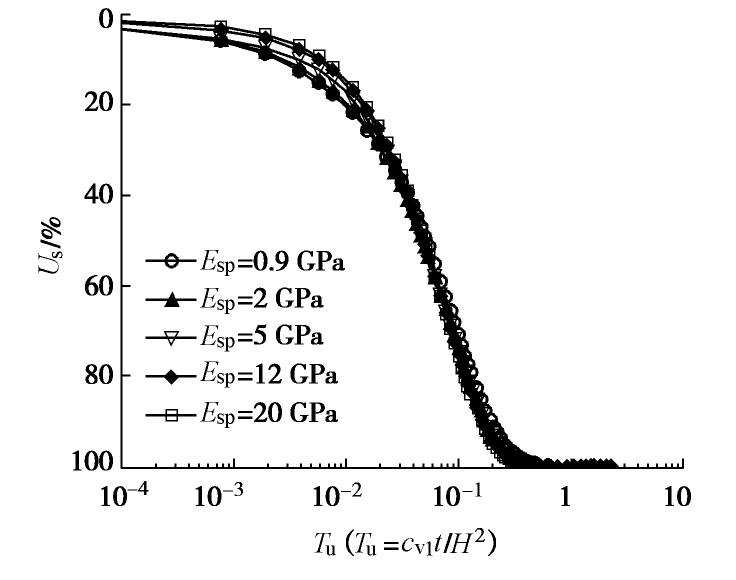
摘要: 推导出瞬时加荷情况下悬浮长芯劲性搅拌桩复合地基的固结方程和相应的定解条件,利用三层地基一维固结理论,建立了相应的固结解析解,包括桩间土和下卧层土中超静孔隙水压力解答和复合地基整体平均固结度解答。通过固结速率解析解与有限元数值解的比较,证明了解析解的合理性。利用解析解进行复合地基固结速率影响因素分析,研究了悬浮长芯劲性搅拌桩复合地基的固结性状。结果表明：悬浮长芯劲性搅拌桩复合地基的固结速率主要受桩的贯入比和下卧层刚度的影响。复合地基的固结速率随桩的贯入比和下卧层土压缩模量的增加而增大。搅拌桩壳长度、厚度和刚度以及芯桩截面含心率的变化对复合地基固结速率没有影响。增加芯桩的压缩模量只会使固结前期复合地基的固结速率略微减小,不会影响固结后期复合地基的固结速率。
- 长芯劲性搅拌桩 /
- 复合地基 /
- 固结 /
- 解析解 /
- 含芯率
Abstract: The consolidation equations and the corresponding solution conditions of the composite ground with floating stiffened deep cement mixing (SDCM) columns with long core piles are derived under an instant loading. On the basis of one-dimensional consolidation theory of a third-layer soil ground, the corresponding analytical consolidation solutions are developed, including the average excess pore water pressures within the surrounding soil and underlying soil and the overall average degree of consolidation of the composite ground. The correctness and accuracy of the proposed analytical solutions are verified by comparison of the consolidation rates by the proposed analytical solution and the FEM. Some main factors are analyzed to investigate the consolidation behavior of this type of composite ground using the proposed analytical solution. The results show that the consolidation rate of the composite ground depends mainly on the penetration ratio of the SDCM columns with long core piles and the stiffness of the underlying soil. It increases with increasing penetration ratio of the pile and the constrained modulus of the underlying soil. The variations in the length, thickness and stiffness of the deep cement mixing (DCM) column sockets as well as the area core ratio of the concrete core piles have little effect on the consolidation rate of the composite ground. An increase in the modulus of the core pile decreases slightly the consolidation rate of the composite ground at the early stage of consolidation process, and it affects insignificantly the consolidation rate at the later stage of consolidation.
- SDCM column with long core pile /
- composite ground /
- consolidation /
- analytical solution /
- area core ratio

HTML全文

0. 引言

由于土体参数的不确定性,边坡工程中越来越多地使用可靠度分析方法进行边坡稳定性评估,相较于传统确定性分析方法,依据可靠度分析方法得到边坡的失效概率,可以获取边坡的整体风险水平,使边坡的设计更加安全可靠,能够更真实地评价边坡安全性水平^[1]。

在岩土工程的可靠度分析中,较为常见的可靠度分析方法有一阶可靠度法（the first-order reliability method, FORM）、高阶可靠度法、响应面法、蒙特卡洛模拟（Monte Carlo simulation, MCS）等。Low^[2]运用FORM对香港红磡一处岩质边坡分析了可靠性；蒋辽等^[3]运用MCS分析得到暴雨工况下一处工程边坡的失效概率；Ji等^[4]在原始空间中导出基于HL-RF递归算法的FORM的简易算式,提升了对隐式极限状态方程类边坡可靠度分析的简便性和适用性。

在实际工程问题中,由于边坡分层或土体参数的不确定性等原因,单体边坡往往会沿多个潜在失稳滑面破坏^[5-8],即存在多个失效模式,此时采用单一临界确定性滑面或临界概率滑面对边坡可靠度进行分析往往会极大地低估失效概率。为了降低这类安全风险,研究边坡系统可靠度至关重要。Low等^[9]采用一阶可靠度法结合Ditlevsen的上下限法对多层土坡进行系统可靠度分析；Ji等^[8]基于分层响应面法,选取代表性滑面并据此建立二阶响应面方程,再采用FORM结合Ditlevsen上下限法进行系统可靠度分析；Cho^[10]采用多点一阶可靠度方法（multi-point FORM）计算边坡系统可靠度。FORM对于单一失效模式的边坡可靠度分析精度足够且效率高,但是面对多失效模式的问题时需要搜索确定多个最可能失效点MPPs^[11]（most probably failure points）,使用相对困难,且对于具有高度非线性的极限状态函数问题,FORM求解可靠度的精度不高。

另一方面,曾鹏等^[12]采用拟牛顿近似二阶法凭借少于FORM的计算量得到与经典二阶法(SORM)相当的系统失稳概率计算精度。杨智勇等^[13]提出了基于广义子集模拟的边坡系统可靠度分析方法及代表性滑面识别方法。李静萍等^[14]建立了基于大量潜在滑面的多重响应面,计算系统失效概率,并识别其中的代表性滑面。

1. 蒙特卡洛模拟及WUS法

1.1 蒙特卡洛模拟（MCS）

蒙特卡洛模拟（MCS）是一种基于大数定律的抽样方法,其失效概率计算等效于失效样本点在全部样本点中出现的频率,原理简单,计算便捷,能够得到相对精确的可靠度指标。

常规MCS往往需要大量的样本数据进行分析计算,尤其是在面对小概率失效问题时,计算量较大。工程边坡问题的失效概率范围一般为10^-6～10^-3,直接采用常规MCS进行分析时往往需要10⁴(10/P_f)以上的样本量才能保证计算精度。当单个样本点需要进行的极限平衡分析过程较为复杂,或者问题为隐式形式的极限状态方程,没有直接的方程式表达,需要进行有限元模型计算分析时,10⁴的样本量会带来庞大的计算量^[15]。针对该缺点,众多学者提出了各类MCS改进方法：Ching等^[16]运用重要性抽样方法（Importance sampling, IS）在大量潜在滑动面的基础上对边坡可靠度进行了有效评估；吴振君等^[17]用拉丁超立方抽样（Latin hypercube sampling, LHS）方法代替MCS的随机抽样,考虑边坡参数的变异性和相关性进行边坡可靠度分析；Echard等^[18]提出主动学习可靠度算法AK-MCS,将克里金模型与MCS结合,兼顾了可靠度计算精度和效率；Bichon等^[19]提出了有效的全局可靠度分析方法,在不确定性空间全域中构建了克里金代理模型,高效地获得精确的可靠度结果。

对于多失效模式的边坡可靠度的计算,MCS具有良好的适用性。Fauriat等^[20]基于AK-MCS提出考虑系统可靠度理论的AK-SYS,进一步提高了对多失效模式问题的适用性。蒋水华等^[21]采用随机响应面法,结合Hermite多项式和MCS有效地识别边坡代表性滑面和计算边坡可靠度。张天龙等^[22]引入了基于主动学习径向基函数（ARBF）代理模型的高效分析方法结合MCS计算边坡系统失效概率。对于MCS处理多失效模式的边坡可靠度问题,主要考虑两个方面：①如何进一步减小MCS计算量,尤其当问题涉及有限元模拟及复杂极限平衡分析时；②如何有效的识别出边坡的多个失效模式,代表性滑面的有效搜索识别对后续边坡维护与治理具有重要参考意义。

1.2 WUS概率密度权重法原理

Rashki等^[23]提出了WUS（weighted uniform simulation）概率密度权重法,是一种改进的的MCS可靠度计算方法,因其在进行MCS时用均匀分布代替随机变量的原有分布类型进行抽样,样本点可以快速布满不确定性空间全域,快速逼近MPP点,所以其能在保证结果足够精确的情况下,大大提高可靠度分析的计算效率,降低计算成本。同时该方法还能在此基础上得到MPP最可能失效点,便于对问题进行进一步的研究分析,这是常规MCS所无法完成的。该算法应用方面,Ghohani Arab等^[24]采用逐层递增取值区间、低差异序列样本分布、局部MPP优化搜索等方法对WUS法进行了改进,进一步提高了计算效率。

基于重要性抽样原理,WUS法将其中的抽样方式改为均匀分布抽样^[25],失效概率P_f改写为

$P_{f} = \int \frac{I (x) f (x)}{U (x)} U (x) d x$ ,

(1)

式中,U(x)为均匀分布概率密度函数,当样本点在取值区间时,其概率密度为1除以取值区间的长度。I(x)为二值变量,当x在失效域时I(x)为1,在安全域时I(x)为0：

$U (x) = {\begin{matrix} \frac{1}{L} & (x \in D) \\ 0 & (x \notin D) \end{matrix}$ 。

(2)

式中,L为随机变量取值区间的长度。

由于重要性抽样需要先验信息如通过FORM获取的设计点或者最大概率密度点等,并且在处理高维问题时存在困难^[26],WUS法运用蒙特卡洛积分思想,将重要性抽样拓展到多个随机变量的高维问题中, $P_{f}$ 可进一步写为

$P_{f} = \frac{\prod L_{j}}{N} \cdot \sum_{i = 1}^{N} I (x_{i}) f_{X} (x_{i}) = \frac{\sum_{i = 1}^{N} I (x_{i}) f (x_{i})}{\frac{N}{\prod L_{j}}}$ ,

(3)

其中,∏L_j为M个随机变量的取值区间长度乘积,N为样本数量,又因为

$\int f_{X} (x) d x ≅ (\frac{\prod L_{j}}{N} \cdot \sum_{i = 1}^{N} f (x_{i})) = 1$ ,

(4)

最终得到 $P_{f}$ 为

$P_{f} ≅ \frac{\sum_{i = 1}^{N} I (x_{i}) f (x_{i})}{\frac{\prod L_{j}}{N} \cdot \sum_{i = 1}^{N} f (x_{i}) \cdot \frac{N}{\prod L_{j}}} = \frac{\sum_{i = 1}^{N} I (x_{i}) f (x_{i})}{\sum_{i = 1}^{N} f (x_{i})}$ ,

(5)

式中, $f (x_{i})$ 为联合概率密度函数,当j个随机变量互相独立时,

$f (x_{i}) = f (x_{1 i}, x_{2 i}, \dots, x_{M i}) = f_{1} (x_{1 i}) \cdot f_{2} (x_{2 i}) \dots f_{M} (x_{M i}) 。$

(6)

1.3 WUS密度权重法步骤

（1）运用MCS的原理,产生大量原随机变量分布类型的数据,用来确定产生大致的样本取值区间。

（2）在样本取值区间内,按照随机均匀分布重新生成均匀分布的M个随机变量的N个随机样本点。

（3）定义随机均匀分布样本点的权重因子W_i为每个样本点x_i的所有随机变量(x₁,x₂,…,x_M)的概率密度函数f_j(x_ji)乘积：

$W_{i} = f_{1} (x_{1 i}) \cdot f_{2} (x_{2 i}) \dots f_{M} (x_{M i})$ ,

(7)

式中,i=1,2,…,N,j=1,2,…,M。

（4）失效概率P_f则定义为失效区域内样本点的权重因子值之和与全域内所有样本点的权重因子值之和的比值：

$P_{f} = \frac{\sum_{i = 1}^{N} I \cdot W_{i}}{\sum_{i = 1}^{N} W_{i}}$ 。

(8)

在WUS方法中,最可能失效点MPP则相应被定义为失效区域内,权重因子W_i值最大的样本点处。

1.4 代表性滑面识别

祁小辉等^[27]提出了边坡最危险滑动面随机分析方法,能够有效地确定边坡最危险滑动面空间分布特征。边坡的破坏经常呈现多种失效模式的情况,换而言之,边坡可靠性分析中存在出现多个最可能失效点MPP的可能性。前述研究中的研究方法多概括为先识别代表性滑面,并以此为基础采用响应面法等方法计算可靠度,而因为MCS可以直接得出可靠度,所以识别代表性滑面更多是为了给后续边坡防治提供依据^[14]。原始WUS法只是求得单个MPP,即只识别出单一失效模式,无法考虑边坡多种失效模式问题。

本文研究拟在原始WUS法基础之上进一步更新算法机制,将所有失效样本点按照权重因子W_i大小降序排列。在确定权重因子W_i值最大的样本点作为第一个MPP点之外,依据权重因子W_i的定义,考虑到其值较小的样本点发生的可能性较小,为进一步减少计算次数,设定进行比较的权重因子W_i的阈值 $ε_{0}$ ,剔除较小点。经过多个算例的比较,发现不同算例因其随机变量个数的不同,其权重因子W_i的范围有较大区别。依据经验设置权重因子W_i的阈值 $ε_{0}$ 为最大权重因子的平方 $W_{\max}^{2}$ 时,对于尤其是随机变量个数较多或者失效概率较大的算例,可以极大地减少相互比较次数。对于这些权重因子W_i相对较大的失效样本点,根据Li等^[28]提出的识别代表性滑面的方法,计算其与上一个保留的MPP点的相关性系数,并设定相关性系数阈值 $ρ_{0}$ 为0.2,作为与上一个MPP点不相关的界限,当计算所得相关性系数大于0.2时,该样本点被认为冗余失效模式^[13]。由该算法自动比对搜索得到符合要求的多个MPP点,即对应多个代表性滑面。

1.5 计算流程

根据滑动面上的抗剪强度与滑动力的比值或者抗剪力矩与滑动力矩的比值定义 $F_{s}$ ,但安全系数 $F_{s}$ 的求解很多情况下为对隐式的极限状态方程的求解,基于此,各种数值模拟手段被使用,如利用基于强度折减的有限元法、有限差分法等。在没有 $F_{s}$ 具体表达式的情况下,边坡稳定分析的极限状态函数^[8]被定义为

$g (x) = F_{s} - 1$ 。

(9)

通过对原始WUS算法的修改,在样本量足够的情况下,修正WUS能高效地得到系统失效概率并且有效地摒弃冗余失效模式而得到较为准确的多失效模式所对应的多个MPP点。基于Excel VBA平台,本文利用简化毕肖普法进行边坡稳定性分析,基于jupyter notebook平台,进行WUS的python代码编写。python与excel良好的交互性为数据的高效联动提供了便利,具体流程如图1所示。主要步骤如下：

图 1 修正WUS法分析系统可靠度的计算流程图

Figure 1. Flow chart for system reliability analysis of slopes by modified WUS

下载: 全尺寸图片幻灯片

（1）Jupyter notebook平台生成土体参数随机变量在取值区间内均匀分布的样本点,保存成xlsx格式,并导入Excel VBA编写的简化毕肖普法程序,修改VBA宏代码完成安全系数F_s的批量计算并保存成F_s.xlsx格式。

（2）WUS程序读入不同样本量下的F_s.xlsx,根据各样本点的随机变量的概率密度函数计算权重因子W_i及其极限状态函数g(x)=F_s-1,进而计算边坡系统失效概率。

（3）针对所有极限状态函数g(x)=F_s-1<0的失效样本点,按照权重因子W_i对其降序排列,确定权重因子W_i最大的样本点为第一个MPP点x_p=1(x₁,x₂,…,x_M),首先判断降序排列中的权重因子W_i大小是否大于设定阈值 $ε_{0}$ ,符合条件进而降序选取失效样本点计算与之前保留的所有MPP点x_p(x₁,x₂,…,x_M)的相关性系数ρ_p,q (p=1,2,…,q),如果所有相关性系数ρ_p,q都小于设定阈值 $ρ_{0}$ ,即代表当前样本点与与之前保留的所有MPP点都不相关,记录该样本点,重复计算直至降序排列中的权重因子W_i小于设定阈值 $ε_{0}$ 。

（4）完成不同样本量的WUS边坡系统可靠度流程计算,直至失效概率收敛。

2. 算例分析

2.1 两层不排水饱和黏土边坡

算例1：如图2所示,运用修正WUS法计算两层不排水饱和黏土边坡的边坡系统可靠度,验证提出的方法应对多失效破坏模式边坡的适用性。Ji等^[8]、Low等^[9]、Ching等^[16]、蒋水华等^[21]、杨智勇等^[13]均对该边坡进行了系统可靠度分析。

图 2 两层黏土边坡代表性滑动面

Figure 2. Representative sliding surfaces of two-layer clay slope

下载: 全尺寸图片幻灯片

两层黏土层均考虑将不排水剪切强度作为随机变量,具体参数如表1所示。基于Excel VBA平台,本篇研究运用简化毕肖普法对算例分别进行样本量为100～500的边坡稳定性批量分析。所有样本均通过基于python平台的jupyter notebook程序生成,同时基于该程序,将批量边坡稳定性分析结果导入并进行修正WUS可靠度分析,得到不同样本量下可靠度指标 $β$ 以及最可能失效点MPP结果如表2所示。

表 1 土体不确定性强度参数（算例1）

Table 1. Uncertain strength properties of soil (Case 1)

随机变量	分布类型	均值/kPa	变异系数
黏土1 c_u	对数正态分布	120	0.3
黏土2 c_u	对数正态分布	160	0.3

下载: 导出CSV

| 显示表格

表 2 MPP点随样本数量变化情况（算例1）

Table 2. Change of MPPs with sample size (Case 1)

样本数量	可靠度指标β	MPP (c_u1/c_u2)
100	2.25	(47.24, 251.34)	(76.39, 71.19)
200	2.69	(44.58, 160.79)	(102.70, 49.77)
300	2.59	(50.34, 125.51)	(72.45, 52.79)
400	2.66	(48.96, 119.39)	(77.43, 57.43)
500	2.68	(47.95, 177.87)	(75.67, 61.73)

下载: 导出CSV

| 显示表格

从表2中不难发现在5次计算中,都存在2组MPP,且所有样本量情况下相应2组MPP所对应的临界滑动面都区别较大,说明该两层土边坡存在两种不同的失效模式,当样本量为500时,2组MPP点（47.95,177.87 kPa）以及（75.67,61.73 kPa）对应的临界滑动面如图2中弧线所示,其中,处于Clay-1层且临界滑动面较小的为MPP点（47.95,177.87 kPa）计算所得,其不排水剪切强度c_u1较小；而贯穿整个边坡、滑动面较大的为MPP点（75.67,61.73 kPa）计算所得,其不排水剪切强度c_u2较小。

算例1使用不同方法计算所得可靠度指标 $β$ 随样本量的变化趋势如图3所示,可以看出可靠度指标 $β$ 在2.6附近上下波动,其中使用MCS所得的折线图显示当样本量达到7000之后可靠度指标 $β$ 大致收敛,而使用修正WUS法当样本量达到400后,可靠度指标 $β$ 即趋于稳定,且两种方法最终结果吻合较好。当样本量为500时,各样本点如图4所示均匀分布在二维不确定性取值空间内。其中,蓝色点为未发生破坏点,红色点为发生破坏点,而红色曲线为示意极限状态面。不难发现,红色点主要分布在不确定性取值空间前侧区域及右前侧部分区域,即分别对应两层土边坡不排水剪切强度c_u较小的情况。权重因子W_i的大小如图4中呈现的柱状图所示,柱状图越高表示该点权重因子W_i越大,可以直观地看到权重因子W_i较大的样本点对应了图4中左侧及后侧两随机变量概率密度函数f_j(x_ji)的较大的位置,这些点对失效概率P_f的影响也更大。因均匀分布抽样,样本点覆盖全域,修正WUS法能快速逼近MPP点,2组MPP点如图4所示为红色柱状图较高且相关性较弱的两点。

图 3 可靠度指标β随样本数量变化情况（算例1）

Figure 3. Change of reliability index β with sample size (Case 1)

下载: 全尺寸图片幻灯片

图 4 样本点权重因子柱状示意图（算例1）

Figure 4. Columnar diagram of sample weight index (Case 1)

下载: 全尺寸图片幻灯片

本文同样对该算例进行3次样本量为500的修正WUS可靠度计算,与其他方法的结果对比如表3所示,采用本文提出的WUS方法开展3次计算模拟所得的失效概率均值 $μ_{P_{f}}$ 为0.42%,方差 $σ_{P_{f}}$ 为0.058%,结果与其他方法较为一致,但是满足精度所需的样本量大为减少,尤其相比MCS大大降低,简单实用。

表 3 不同方法边坡的系统可靠度结果比较（算例1）

Table 3. Comparison of different system reliability analysis results of slopes (Case 1)

计算方法	失效概率P_f	MPP (c_u1/c_u2)	样本数量	来源
WUS	$μ_{P_{f}}$ = 0.42%, $σ_{P_{f}}$ = 0.058%	(47.95, 177.87)(75.67, 61.73)	500	本文
MCS	$μ_{P_{f}}$ = 0.44%, $σ_{P_{f}}$ = 0.067%±0.405%	——	1000020000	Ching等^[16]Ji等^[8]
重要性抽样方法	$μ_{P_{f}}$ = 0.41%, $σ_{P_{f}}$ = 0.027%	—	1000	Ching等^[16]
GSS广义子集模拟	0.44%		1643	杨智勇等^[13]
分层响应面法	{0.402%, 0.411%}	—	—	Ji等^[8]

下载: 导出CSV

| 显示表格

2.2 芝加哥国会街切坡

算例2：边坡进一步设置有4层不同土体性质的土层,顶层为砂层,下面部分为黏土层,如图5所示。Chowdhury等^[7]、Ji等^[8]、Ching等^[16]都对该算例进行了研究,3层黏土层的不排水剪切强度均设为正态分布形式的土层随机变量,具体参数设置如表4所示。

图 5 芝加哥国会街切坡代表性滑动面

Figure 5. Representative sliding surfaces of Congress Street Cut

下载: 全尺寸图片幻灯片

表 4 土体不确定性强度参数（算例2）

Table 4. Uncertain strength properties of soil (Case 2)

随机变量	分布类型	均值/kPa	变异系数
c_u1	正态分布	55	0.37
c_u2	正态分布	43	0.19
c_u3	正态分布	56	0.24

下载: 导出CSV

| 显示表格

基于修正WUS法分析该边坡系统可靠度的过程与算例1保持一致,系统失效概率P_f随样本量的变化趋势如图6所示,可以看出算例2系统边坡失效概率P_f在0.35附近上下浮动,整体较为平稳。

图 6 失效概率P_f随样本数量变化情况（算例2）

Figure 6. Change of probability of failure P_f with sample size (Case 2)

下载: 全尺寸图片幻灯片

表5给出了修正WUS法计算100～500不同样本量下的样本点所得的边坡系统可靠度指标 $β$ 及对应的3组MPP点。其中,样本量为300,500时,3组MPP所对应的临界滑动面区别较大,如图5所示分别分布在3个不同的黏土层,说明该四层土边坡存在3种不同的失效模式,分别对应三层黏土层的不排水剪切强度c_u较小的情况。值得注意的是其他样本量情况下的WUS可靠度分析并没有同时得到3种不同的代表性滑动面,3组MPP点搜索临界滑动面结果只呈现黏土层2及黏土层3中的临界滑动面,其中黏土层3中的MPP点搜索频率更高,而黏土层1中临界滑动面并没有得到有效搜索,分析其原因可能是该样本量下生成的样本点并没有覆盖黏土层1中的临界滑动面情况,修正WUS在样本量较少的情况下对代表性滑面的搜索存在一定局限性。

表 5 MPP点随样本数量变化情况（算例2）

Table 5. Change of MPPs with sample size (Case 2)

样本数量	可靠度指标β	MPP (c_u1/c_u2 /c_u3)
100	0.32	(43.33, 36.05, 48.72)	(110.10, 47.72, 24.05)	(38.60, 44.87, 39.79)
200	0.37	(63.01, 34.28, 37.86)	(40.18, 41.04, 39.92)	(34.67, 36.44, 53.61)
300	0.35	(58.15, 31.30, 44.63)	(46.62, 52.08, 36.64)	(29.65, 35.54, 70.51)
400	0.38	(49.28, 36.93, 41.30)	(34.53, 46.96, 35.31)	(39.55, 37.42, 71.50)
500	0.34	(42.38, 36.90, 49.77)	(39.05, 44.96, 34.13)	(14.86, 49.61, 48.61)

下载: 导出CSV

| 显示表格

不同可靠度分析方法计算该算例的系统可靠度结果对比如表6所示,修正WUS计算所得系统失效概率P_f的均值 $μ_{P_{f}}$ 为34%,标准差 $σ_{P_{f}}$ 为2%,精度满足工程实际要求,但相较于常规MCS,其计算量大大减少,并且在样本量较大时能同时识别出3个代表性滑面,这对类似边坡工程滑坡治理有重要参考意义。

表 6 不同方法边坡的系统可靠度结果比较（算例2）

Table 6. Comparison of different system reliability analysis results of slopes (Case 2)

计算方法	失效概率P_f	MPP (c_u1/c_u2/c_u3)	样本数量	来源
WUS	$μ_{P_{f}}$ = 34%, $σ_{P_{f}}$ = 2%	(42.38, 36.90, 49.77)(39.05, 44.96, 34.13)(14.86, 49.61, 48.61)	500	本文
Slide V6.0 MCS	±36.76%	—	10000	Ji等^[8]
分层响应面法	{31.22%, 41.84%}	—	—	Ji等^[8]
Ditlevsen上下限法	{27.4%, 44.7%}	—	—	Chowdhury等^[7]

下载: 导出CSV

| 显示表格

2.3 不排水软土地基上的黏性土路堤

算例3：如图7同样取自Chowdhury等^[7]的研究,Ji等^[8]对其进行分层响应面法的可靠度分析计算。上层为填土路堤,下层为软黏土地基层,其所有土体不确定性强度参数如表7所示。

图 7 软土地基上的黏性土路堤代表性滑动面

Figure 7. Representative sliding surfaces of embankment resting on soft clay foundation

下载: 全尺寸图片幻灯片

表 7 土体不确定性强度参数（算例3）

Table 7. Uncertain strength properties of soil (Case 3)

随机变量	位置	分布类型	均值	变异系数
内聚力c/kPa	路堤	正态分布	10	0.20
内聚力c/kPa	软黏土基层	正态分布	40	0.20
摩擦角φ/(°)	路堤	正态分布	12	0.25

下载: 导出CSV

| 显示表格

根据计算流程,对该算例进行样本量为100～500的可靠度计算及多MPP点搜索,得到的系统失效概率P_f在0.30～0.40上下浮动（图8）,当样本数量达到400之后,曲线波动逐渐平缓。进一步对稳定性计算结果进行分析,如图9所示,当样本量为500时,均匀分布产生的样本点覆盖三维不确定性取值空间全域。根据简化毕肖普法结果对样本点标注,红色及橘黄色点为安全系数F_s小于1.0,黄色及绿色点为安全系数F_s大于1.0,示意极限状态面橘色点和黄色点之中间（图9红色曲面）。可以直观地看出路堤失效破坏发生在取值空间的底部、左侧以及后方,即3个土体参数随机变量值较小处,安全系数F_s大致呈阶梯状递增。图9表明,高维问题中失效区域与安全区域交界处多有交错,失效区域形状较为复杂。

图 8 失效概率P_f随样本数量变化情况（算例3）

Figure 8. Change of probability of failure P_f with sample size (Case 3)

下载: 全尺寸图片幻灯片

图 9 样本点分布（算例3）

Figure 9. Distribution of samples (Case 3)

下载: 全尺寸图片幻灯片

100～500不同样本量下,算例3经修正WUS法分析所得的的系统可靠度指标 $β$ 及对应的2组MPP点如表8所示。根据算法设定,相关性系数大于0.2的样本点被视作冗余失效模式而被排除,每一次分析的MPP点结果均为2个,表明该路堤算例有两种失效模式,其对应的代表性滑面如图7所示,第一类临界滑动面圆弧位于上层路堤底部,第二类临界滑动面贯穿路堤上下层,圆弧位于地基层底部。按表8沿样本数量递增方向分析MPP点搜索结果,发现2组MPP点区别明显而各自则较为聚集收敛,搜索结果较好；一类为路堤土层的土体强度较低的情况,一类为地基层土体强度参数偏低的情况,与代表性滑面相对应。

表 8 MPP点随样本数量变化情况（算例3）

Table 8. Change of MPPs with sample size (Case 3)

样本数量	可靠度指标β	最可能失效点MPP (c_路堤/φ_路堤/c_基层)
100	0.24	(8.58,11.88, 31.60),	(11.42,16.04, 10.80)
200	0.52	(10.86,10.45,29.99),	(11.57, 15.35, 9.98)
300	0.46	(9.68, 8.07, 36.63)	(10.10, 15.90,13.09)
400	0.37	(9.68, 8.19, 44.93)	(10.68,15.03, 10.97)
500	0.35	(9.29, 8.53, 41.68)	(10.04,18.34, 13.65)

下载: 导出CSV

| 显示表格

修正WUS法与其他边坡系统可靠度方法分析算例3的结果对比如表9所示,本文方法经过3次计算模拟500组样本量下的系统失效概率P_f均值 $μ_{P_{f}}$ 为32.38%,标准差 $σ_{P_{f}}$ 为2.58%,结果与其他方法基本一致,但是计算量较小且能够有效识别两个代表性滑动面。

表 9 不同方法边坡的系统可靠度结果比较（算例3）

Table 9. Comparison of different system reliability analysis results of slopes (Case 3)

计算方法	失效概率P_f	MPP (c_路堤/φ_路堤/c_基层)	样本数量	来源
WUS	$μ_{P_{f}}$ = 32.38%, $σ_{P_{f}}$ = 2.58%	(7.69, 10.09, 40.13)(11.46, 13.19, 12.19)	500	本文
Slide V6.0 MCS	±36.1%	—	2000	Ji等^[8]
分层响应面法	{31.22%, 41.84%}	—	—	Ji等^[8]
Ditlevsen上下限法	{27.4%, 44.7%}	—	—	Chowdhury 等^[7]

下载: 导出CSV

| 显示表格

2.4 ACADS 1(c)算例

算例4：如图10所示,为澳大利亚计算机辅助设计协会赞助支持的一系列边坡稳定性分析算例之一,是极限状态方程为隐式的3层土边坡算例,其砂土层的内摩擦角为38°,其黏土层的4个土体强度参数如表10所示,均为独立随机变量。Ji等^[8]运用分层响应面法对其进行可靠度分析,Zhang等^[29]则将Hassan等^[6]的搜索代表滑动面方法与MCS以及均值一次二阶矩法（the mean first-order reliability method）结合分析边坡系统失效概率,Zhu等^[30]利用基于机器学习的高斯过程回归方法对该算例进行了分析,Tun等^[31]则运用遗传算法计算了三维边坡的系统失效概率。

图 10 ACADS 1(c)边坡代表性滑动面

Figure 10. Representative sliding surfaces of ACADS 1(c) problem

下载: 全尺寸图片幻灯片

表 10 土体不确定性强度参数（算例4）

Table 10. Uncertain strength properties of soil (Case 4)

随机变量		分布类型	均值	变异系数
黏聚力c/kPa	黏土1	正态分布	5.3	0.3
黏聚力c/kPa	黏土2	正态分布	7.2	0.3
摩擦角φ/(°)	黏土1	正态分布	23	0.2
摩擦角φ/(°)	黏土2	正态分布	20	0.2

下载: 导出CSV

| 显示表格

运用修正WUS法分析的系统可靠度指标 $β$ 结果随样本数量变化如图11所示,系统可靠度指标 $β$ 围绕2.16在2.1～2.2浮动,当样本量超过250后,浮动趋于平缓。100～500组样本量下算例4的MPP点搜索结果如表11所示,共有3个MPP点对应图10中3个代表性滑动面。第一类MPP点为黏土层2黏聚力 $c_{2}$ 以及摩擦角 $φ_{2}$ 偏小的情况；第二类MPP点为黏土层1黏聚力 $c_{1}$ 以及摩擦角 $φ_{1}$ 偏小的情况；第三类则为两黏土层强度参数均较小的情况。

图 11 可靠度指标β随样本数量变化情况（算例4）

Figure 11. Change of reliability index β with sample size (Case 4)

下载: 全尺寸图片幻灯片

表 11 MPP点随样本数量变化情况（算例4）

Table 11. Change of MPPs with sample size (Case 4)

样本数量	可靠度指标β	最可能失效点MPP (c₁ /φ₁ / c₂ /φ₂ )
100	2.14	(14.27, 3.49, 12.33, 4.84)	(8.56, 5.74, 10.68, 14.30)	(8.65, 10.73, 8.77, 9.04)
200	2.12	(21.40, 5.47, 12.84, 2.27)	(4.34, 4.32, 14.77, 7.80)	(5.39, 10.53, 5.12, 4.37)
300	2.16	(20.50, 4.60, 11.40, 4.62)	(6.58, 5.26, 23.17, 5.83)	(6.14, 6.02, 4.33, 7.55)
400	2.12	(21.56, 7.20, 11.27, 4.95)	(5.22, 4.58, 18.31, 4.46)	(12.23, 5.54, 6.04, 13.98)
500	2.17	(17.73, 4.93, 10.58, 7.91)	(6.54, 2.21, 28.87, 5.85)	(9.38, 6.92, 9.56, 12.29)

下载: 导出CSV

| 显示表格

同样对该算例进行3组样本量为500的WUS法分析,得到的边坡系统失效概率P_f均值 $μ_{P_{f}}$ 为1.49%,标准差 $σ_{P_{f}}$ 为0.21%,与其他方法的分析结果对比如表12所示,不难发现结果吻合较好,表明修正WUS法针对高维问题（4个随机变量）以及隐式极限状态函数的多层土边坡系统可靠度分析同样具有较好的适用性,同时,具有计算量小、简单高效且能搜索代表性滑面的优点。

表 12 不同方法边坡的系统可靠度结果比较（算例4）

Table 12. Comparison of different system reliability analysis results of slopes (Case 4)

计算方法	失效概率P_f	MPP (c₁ /φ₁ / c₂ /φ₂)	样本数量	来源
WUS	$μ_{P_{f}}$ = 1.49%, $σ_{P_{f}}$ = 0.21%	(17.73, 4.93, 10.58, 7.91)(6.54, 2.21, 28.87, 5.85)(9.38, 6.92, 9.56, 12.29)	500	本文
MCS	1.33%	—	50000	Zhang等^[29]
Slide V6.0 MCS	±1.40%1.22%	——	200001000000	Ji等^[8]Zhu等^[30]
分层响应面法	{1.08%, 1.30%}	—	—	Ji 等^[8]

下载: 导出CSV

| 显示表格

3. 结论

本文根据修正WUS法所提供的可靠度分析算法,针对分层土边坡的多失效模式情况,修正了搜索MPP点的算法部分,对4个边坡系统可靠度进行了分析,得出以下4点结论。

（1）4个算例表明WUS法对于边坡系统可靠度分析有很好的适用性,原理简单,高效实用。对高维、隐式极限状态方程下的多层边坡问题分析精度较高。

（2）比较重要性抽样方法计算边坡可靠度,WUS法不需要提供先验信息且对于高维问题的可靠性分析同样使用简单。不同于常规MCS,该方法极大地减少了样本数量,对于边坡可靠性分析,MCS通常需要10⁴以上的样本量,而WUS法仅需500组左右即可满足精度要求,降低了MCS复杂极限平衡分析或者有限元分析所需庞大的计算量。

（3）在改进了MPP搜索算法后,修正WUS法可以有效地自动识别出多层边坡的多个代表性滑动面,为边坡后期维护防治提供参考。但是其在样本量不足时,会出现代表性滑动面搜索不全的情况,存在一定局限,需进一步研究。

（4）Python平台赋予了该套方法更多拓展的可能性,通过Python平台与MS-Excel的结合,完成可靠度分析；同样还可以充分利用有限元软件如ABAQUS等的Python接口^[32],边坡稳定性分析交由数值模拟软件完成,简便地进行复杂岩土工程问题可靠度分析。

图 1 复合地基固结模型

Figure 1. Consolidation model for composite ground

下载: 全尺寸图片幻灯片

图 2 有限元模型

Figure 2. FEM model

下载: 全尺寸图片幻灯片

图 3 解析解和有限元解的比较

Figure 3. Comparison between analytical results and FEM results

下载: 全尺寸图片幻灯片

图 4 β对固结速率的影响

Figure 4. Influences of β on consolidation rate

下载: 全尺寸图片幻灯片

图 5 　m对固结速率的影响

Figure 5. Influences of m on consolidation rate

下载: 全尺寸图片幻灯片

图 6 β₁对固结速率的影响

Figure 6. Influences of β₁ on consolidation rate

下载: 全尺寸图片幻灯片

图 7 E_p对固结速率的影响

Figure 7. Influences of E_p on consolidation rate

下载: 全尺寸图片幻灯片

图 8 ρ对固结速率的影响

Figure 8. Influence of ρ on the consolidation rate

下载: 全尺寸图片幻灯片

图 9 E_sp对固结速率的影响

Figure 9. Influences of E_sp on consolidation rate

下载: 全尺寸图片幻灯片

图 10 E_s3对固结速率的影响

Figure 10. Influences of E_s3 on consolidation rate

下载: 全尺寸图片幻灯片

参考文献(22)

[1]	ZHENG G, GU X L, LING G R. Development and practice of composite DMM column in China[C]//Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering. Osaka, 2005: 1295-1299.
[2]	HAN J. Recent research and development of ground column technologies[J]. Ground Improvement,2015,168(4): 1-19.
[3]	凌光容, 安海玉, 谢岱宗, 等. 劲性搅拌桩的试验研究[J]. 建筑结构学报, 2001, 22(2): 92-96. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB200102017.htm LING Guang-rong, AN Hai-yu, XIE Dai-zong, et al. Experimental study on concrete core mixing pile[J]. Journal of Building Structure, 2001, 22(2): 92-96. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB200102017.htm
[4]	董平, 陈征宙, 秦然. 砼芯水泥土搅拌桩在软土地基中的应用[J]. 岩土工程学报, 2002, 24(2): 204-207. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200202017.htm DONG Ping, CHEN Zheng-zhou, QIN Ran. Use of concrete-cored DCM pile in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 204-207. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200202017.htm
[5]	吴迈, 赵欣, 窦远明, 等. 水泥土组合桩室内试验研究[J]. 工业建筑, 2004, 34(11): 45-48. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ200411011.htm WU Mai, ZHAO Xin, DOU Yuan-ming, et al. Experimental study of stiffened DCM pile in laboratory[J]. Industrial Construction, 2004, 34(11): 45-48. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ200411011.htm
[6]	VOOTTIPRUEX P, SUKSAWAT T, BERGADO D T, et al. Numerical simulations and parametric study of SDCM and DCM piles under full scale axial and lateral loads[J]. Computers and Geotechnics, 2011, 38: 318-329. doi: 10.1016/j.compgeo.2010.11.006
[7]	吴迈, 窦远明, 王恩远. 水泥土组合桩荷载传递试验研究[J]. 岩土工程学报, 2004, 26(3): 432-435. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200403034.htm WU Mai, DOU Yuanming, WANG Enyuan. A study on load transfer mechanism of stiffened DCM pile[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(3): 432-435. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200403034.htm
[8]	丁永君, 李进军, 刘峨, 等. 劲性搅拌桩的荷载传递规律[J]. 天津大学学报(自然科学与工程技术版), 2010, 43(6): 530-536. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201006012.htm DING Yong-jun, LI Jin-jun, LIU E, et al. Load transfer mechanism of reinforced mixing pile[J]. Journal of Tianjin University (Science and Technology), 2010, 43(6): 530-536. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201006012.htm
[9]	顾士坦, 施建勇, 王春秋, 等. 劲性搅拌桩芯桩荷载传递规律理论研究[J]. 岩土力学, 2011, 32(8): 2473-2478. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201108038.htm GU Shi-tan, SHI Jian-yong, WANG Chun-qiu, et al. Theoretical study of core pile load transfer regularity of reinforced mixing pile[J]. Rock and Soil Mechanics, 2011, 32(8): 2473-2478. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201108038.htm
[10]	WONGLERT A, JONGPRADIST P. Impact of reinforced core on performance and failure behavior of stiffened deep cement mixing piles[J]. Computers and Geotechnics, 2015, 69: 93-104.
[11]	WONGLERT A, JONGPRADIST P, JAMSAWANG P, et al. Bearing capacity and failure behaviors of floating stiffened deep cement mixing column under axial load[J]. Soils and Foundations, 2018, 58(2): 446-461.
[12]	WANG C, XU Y F, DONG P. Plate load tests of composite foundation reinforced by concrete-cored DCM pile[J]. Geotechnical and Geological Engineering, 2014, 32(1): 85-96.
[13]	VOOTTIPRUEX P, BERGADO D T, SUKSAWAT T, et al. Behavior and simulation of deep cement mixing (DCM) and stiffened deep cement mixing (SDCM) piles under full scale loading[J]. Soils and Foundations, 2011, 51(2): 307-320.
[14]	WANG C, XU YF, DONG P. Working characteristics of concrete-cored deep cement mixing piles under embankments[J]. Journal of Zhejiang University (Applied Physics & Engineering), 2014, 15(6): 419-431.
[15]	叶观宝, 蔡永生, 张振. 加芯水泥土桩复合地基桩土应力比计算方法研究[J]. 岩土力学, 2016, 37(3): 672-678. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201603009.htm YE Guan-bao, CAI Yong-shen, ZHANG Zhen. Research on calculation of pile-soil stress ratio for composite foundation reinforced by stiffened deep mixed piles[J]. Rock and Soil Mechanics, 2016, 37(3): 672-678. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201603009.htm
[16]	YE G B, RAO F R, ZHANG Z, et al. Calculation method for settlement of stiffened deep mixed column-supported embankment over soft clay[C]//Proceedings of Geoshanghai 2018 International Conference. Shanghai, 2018: 22-29.
[17]	杨涛, 唐凤. 变荷载下劲性搅拌桩复合地基固结分析[J]. 建筑结构学报, 2017, 38(9): 160-166. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201709019.htm YANG Tao, TANG Feng. Consolidation analysis of composite ground with stiffened deep cement mixing columns under time- dependent loading[J]. Journal of Building Structures, 2017, 38(9): 160-166. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201709019.htm
[18]	陈华顺, 孙元奎, 李挺. 长芯劲性桩桩侧摩阻力计算方法探讨[J]. 水运工程, 2011(5): 40-44. https://www.cnki.com.cn/Article/CJFDTOTAL-SYGC201105009.htm CHEN Huai-shun, SUN Yuan-kui, LI Ting. Calculation method for side friction of stiffened piles with long core pile[J]. Port & Waterway Engineering, 2011(5): 40-44. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SYGC201105009.htm
[19]	程博华. 基于破坏模式的长芯劲性搅拌桩竖向承载力计算方法研究[J]. 铁道建筑技术, 2016(6): 102-106. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJS201606029.htm CHENG Bo-hua. Study on calculation method of vertical bearing capacity of long core strength mixing pile based on failure mode[J]. Railway Construction Technology, 2016(6): 102-106. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJS201606029.htm
[20]	杨涛, 戴基彤, 王恒栋. 刚性基础下T形劲性搅拌桩复合地基固结解析解[J]. 工业建筑, 2018, 48(9): 105-110. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201809017.htm YANG Tao, DAI Ji-tong, WANG Heng-dong. Analytical solution for consolidation of a composite ground with T-shaped stiffened deep cement mixing columns under rigid foundation[J]. Industrial Construction, 2018, 48(9): 105-110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201809017.htm
[21]	YANG T, YANG J Z, NI J. Analytical solution for the consolidation of a composite ground reinforced by partially penetrated impervious column[J]. Computers and Geotechnics, 2014, 57: 30-36.
[22]	谢康和. 成层地基一维固结理论研究最新进展[C]//第二届岩土力学与工程学术讨论会论文集. 杭州: 浙江大学出版社, 1995: 1-9. XIE Kang-he. The new development of one-dimensional consolidation theory of layered soil ground[C]//Proceedings of 2nd Conference on Soil Mechanics and Geotechnical Engineering. Hangzhou: Zhejiang University Press, 1995: 1-9. (in Chinese)