基于相似变换法的半无限空间饱和土一维热固结解析解

韩涛; 周扬; 卢萌盟

doi:10.11779/CJGE20240206

基于相似变换法的半无限空间饱和土一维热固结解析解 English Version

韩涛^{1, 2, 3,},
周扬^{1, 3, ,},
卢萌盟¹

1.
中国矿业大学力学与土木工程学院, 江苏徐州 221116
2.
中国矿业大学深地工程智能建造与健康运维全国重点实验室, 江苏徐州 221116
3.
深地科学与工程云龙湖实验室, 江苏徐州 221116

基金项目:

国家自然科学基金项目 52178373

详细信息

作者简介:
韩涛(1981— )，男，山东淄博人，博士，副研究员，从事岩土特殊施工、岩土体热力耦合方面的研究工作。E-mail: hantaocumt@163.com

通讯作者:
周扬, E-mail：tod2006@126.com

中图分类号: TU431
计量
- 文章访问数: 268
- HTML全文浏览量: 25
- PDF下载量: 61
出版历程
- 收稿日期: 2024-03-07
- 网络出版日期: 2024-08-20
- 刊出日期: 2025-04-30

Analytical solutions for 1-D thermo-consolidation process of semi-infinite saturated soil using similarity transformation method

HAN Tao^{1, 2, 3,},
ZHOU Yang^{1, 3, ,},
LU Mengmeng¹

1.
School of Mechanics & Civil Engineering, China University of Mining & Technology, Xuzhou 221116, China
2.
State Key Laboratory of Intelligent Construction and Healthy Operation and Maintenance of Deep Underground Engineering, China University of Mining & Technology, Xuzhou 221116, China
3.
YunLong Lake Laboratory of Deep Underground Science and Engineering, Xuzhou 221116, China

摘要

摘要: 针对半无限空间饱和土在表面外荷载及变温作用影响下的一维热固结过程，考虑两类传热及渗流边界条件，给出了温度及超静孔压耦合演化过程的基本方程。引入组合变量对耦合方程进行了解耦，应用相似变换法获得了组合变量在半整数次幂函数边界条件下的通解，并基于该通解构建了任意幂级数形式荷载及边界条件下温度与超静孔压的解析解答。通过文献进行了对比验证，随后应用本解答计算分析了半无限空间饱和土在表面正弦温度及热流边界作用下土中温度及超静孔压的耦合响应特性，结果表明：土体变形功项对传热方程贡献很小，对温度及超静孔压演化的影响基本可以忽略；固结方程中温度化率项系数为正值时，温度变化会引起相反趋势的超静孔压变化，而该系数为负值时，温度变化则会引起相同趋势的超静孔压变化。
- 热固结 /
- 半无限空间 /
- 饱和土 /
- 解析解 /
- 相似变换
Abstract: For a 1-D thermo-consolidation process of semi-infinite saturated soil induced by external loads and changing temperature at the surface, basic equations are proposed to describe the coupled evolvement of temperature and excessive porewater pressure, and two types of heat transfer and seepage boundary conditions are considered. The combination variables are introduced to decouple the governing equations, and their general solutions under the boundary conditions in the form of half-integer power functions are developed by applying the similarity transformation method. After expanding the external loads and the boundary conditions into power series, the analytical solutions for the temperature and the excessive porewater pressure can be obtained using these general solutions directly. After their verification by certain solution in the literature, our solutions are then employed to calculate and analyze the coupled response characteristics of soil temperature and excessive porewater pressure for semi-infinite saturated soil under the effects of sinusoidal temperature and heat flux at the soil surface. The results show that, the term of soil deformation work contributes very little to the heat transfer equation, and its impact on the evolution of temperature and excessive porewater pressure can basically be ignored. When the coefficient for the term of temperature changing rate in the consolidation equation is positive, temperature changes will cause changes in the excessive porewater pressure with the opposite trend, and when the coefficient is negative, temperature changes will cause changes in the excessive porewater pressure with the same trend.
- thermo-consolidation /
- semi-infinite space /
- saturated soil /
- analytical solution /
- similarity transformation method

HTML全文

0. 引言

饱和岩土体非等温条件下的热-水-力耦合问题在地热能开发利用、核废料处置、供热管道设计等领域均会遇到。非等温条件下超静孔压演化过程与传统太沙基固结存在显著差异，Paaswel^[1]提出了热固结概念用于描述非等温条件下岩土体的固结过程，目前相关研究已成为岩土涉热工程领域的重要热点。

许多学者围绕岩土体热固结过程的理论模型及计算开展了大量研究^[2-11]。Zhou等^[3]考虑不可逆过程效应、固结水流对流、孔隙率变化影响等诸多复杂因素，建立了饱和多孔介质热-水-力耦合过程的理论模型，推导了模型简化条件下的解析解及复杂条件下的有限元解。Mctigue^[4]忽略固结对传热影响而仅考虑温度对固结作用，建立了饱和岩土体单向耦合热固结模型；针对半无限区域表面恒定温度及热流情形，通过将温度解答代入固结方程求解，推导了热固结过程解析解。Blond等^[5]、白冰^[6]、吴瑞潜等^[7]也针对单向耦合热固结模型，采用将已有温度解代入固结方程的方式，分别推导了半无限空间、有限空间岩土体热固结过程的解析解答。当考虑固结对传热影响后，热固结模型为双向耦合，此时模型解析求解更为困难。针对双向耦合热固结模型，Bai^[8]采用Laplace变换及Gauss- Legendre数值反变换对半无限空间土体在周期性温度波动下的热固结问题进行了求解；王路君等^[9]通过Laplace-Hankel变换，结合数值反变换与精细积分技术，获得了衰变热源作用下层状饱和多孔介质热固结问题解答；钮家军等^[10]通过势函数与分离变量法，推导了饱和单层土体在三类边界条件下热固结过程的三角级数形式解答；随后，钮家军等^[11]又通过正（余）弦变换及其逆变换，建立了半无限空间土体在两类边界条件下热固结过程的精确积分解。

半无限空间土体热固结理论对于季节性地表边界作用下土体热力响应研究十分重要。目前，双向耦合情形下半无限空间土体热固结问题的求解基本都采用积分变换及其数值反变换方式，解答相对复杂，不便于应用，迫切需要新的解析方法给出形式简洁的解答。文献[12，13]针对半无限空间传热问题建立了一种相似变换方法，该方法通过引入相似变量，将偏微分方程转化为常微分方程，通过求解常微分方程获得原偏微分方程的通解，该方法特别适用于半无限空间相关问题的解析求解。因此本文针对半无限空间饱和土在外荷载及表面渗流、传热边界作用下的一维热固结过程，给出考虑双向耦合作用的热固结模型基本方程，通过引入组合变量并应用相似变换方法，建立该模型解析解答，并对热固结过程中的耦合效应进行计算分析。

1. 半无限空间饱和土热固结模型

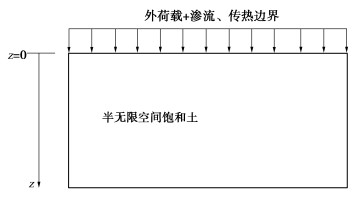
图 1所示为半无限空间饱和土在外荷载（应力）及表面渗流、传热边界作用下一维热固结过程示意图。图 1中上表面外荷载随时间变化记为F_s(t)，渗流、传热边界条件后续给出；初始时刻土体超静孔压为均匀分布F_s(0)，温度为均匀分布T_ini，本节给出该一维热固结过程基本控制方程。

图 1 半无限空间饱和土-维热固结过程示意图

Figure 1. Schematic diagram for 1-D thermo-consolidation process of semi-infinite saturated soil

下载: 全尺寸图片幻灯片

对于固结部分的控制方程，主要简化及假设如下：①忽略土颗粒和水的压缩性，仅考虑其热膨胀性；②热渗效应仅在土体渗透性极小时才会有明显影响^[3]，本文不考虑；③土中孔压适用太沙基有效应力原理，固结水流服从达西定律。

在上述简化及假设基础上，可以推导获得固结部分的控制方程为^{[3, 7, 13]}

$\frac{{\partial P}}{{\partial t}} - \frac{{\partial {F_{\text{s}}}\left( t \right)}}{{\partial t}} + A\frac{{\partial T}}{{\partial t}} = {C_{\text{g}}}\frac{{{\partial ^2}P}}{{\partial {z^2}}}。$

(1)

式中：P为超静孔压；T为温度；z为位置坐标；t为时间；C_g为固结系数，C_g = k_gE_s/γ_w， k_g为渗透系数，γ_w为水的重度，E_s为土体压缩模量。

式（1）中温度变化率项的系数A及其他相关参数为

$A = \beta - {E_{\text{s}}}\bar a\text{，}$

(2)

$\beta = \frac{E}{{1 - 2v}}{a_{{\text{sm}}}}\text{，}$

(3)

${E_{\text{s}}} = \frac{{1 - v}}{{1 + v}}\frac{E}{{1 - 2v}}\text{，}$

(4)

$\bar a = n{a_{\text{w}}} + (1 - n){a_{\text{s}}}。$

(5)

式中：β为土体热应力系数；E_s为土体压缩模量； $\bar a$ 为土骨架和水的热膨胀系数平均值，E为土体变形模量； $\nu$ 为泊松比；n为孔隙率；a_w为水的热膨胀系数；a_s为土骨架热膨胀系数；a_sm为土体热膨胀系数，一般可以取 ${a_{{\text{sm}}}} = \bar a$ 。

对于传热部分方程，主要简化及假设如下：①根据Onsager倒易关系，不考虑孔压梯度引起的传热；②过程中温增不大^[2-3]，热力学温度近似有T_ini+∆T ≈ T_ini；③忽略固结水流引起的热对流作用。

在上述简化及假设基础上，可以推导获得传热部分的控制方程为^[2-3]

${C_{\text{v}}}\frac{{\partial T}}{{\partial t}} + {T_{{\text{ini}}}}\beta \frac{{\partial {\varepsilon _{zz}}}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}}。$

(6)

式中：T为温度；C_v为土体体积热容； $\lambda$ 为土体导热系数；左侧第二项为土体变形功项。

为了消除式（6）中的ε_zz，引入土体一维线性热弹性本构^[3]：

${\sigma '_{zz}} = {E_s}{\varepsilon _{zz}} - \beta (T - {T_{{\text{ini}}}})。$

(7)

式中： ${\sigma '_{zz}}$ 为土体z方向有效应力，应力、应变均以拉为正，而孔压则以压为正。

利用式（7）及有效应力原理可知：

$\frac{{\partial {\varepsilon _{zz}}}}{{\partial t}} = \frac{1}{{{E_{\text{s}}}}}\frac{{\partial P}}{{\partial t}} + \frac{\beta }{{{E_{\text{s}}}}}\frac{{\partial T}}{{\partial t}} - \frac{1}{{{E_{\text{s}}}}}\frac{{\partial {F_{\text{s}}}(t)}}{{\partial t}}。$

(8)

将式（8）代入式（6）后变形得到

$\left( {{C_{\text{v}}} + \frac{{{T_{{\text{ini}}}}{\beta ^2}}}{{{E_{\text{s}}}}}} \right)\frac{{\partial T}}{{\partial t}} + \frac{{{T_{{\text{ini}}}}\beta }}{{{E_{\text{s}}}}}\left[ {\frac{{\partial P}}{{\partial t}} - \frac{{\partial {F_{\text{s}}}(t)}}{{\partial t}}} \right] = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}}。$

(9)

式（1），（9）构成半无限空间饱和土热固结过程温度、超静孔压耦合演化的基本方程。

为了将式（1），（9）齐次化，引入新变量：

$\bar P(z, t) = P(z, t) - {F_{\text{s}}}(t)。$

(10)

将新变量代入式（1），（9）中得到

$\frac{{\partial \bar P}}{{\partial t}} + A\frac{{\partial T}}{{\partial t}} = {C_{\text{g}}}\frac{{{\partial ^2}\bar P}}{{\partial {z^2}}}\text{，}$

(11)

${\bar C_{\text{v}}}\frac{{\partial T}}{{\partial t}} + B\frac{{\partial \bar P}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}}。$

(12)

式中：

$\left.\begin{array}{l}{\overline{C}}_{\text{v}}={C}_{\text{v}}+B\beta \text{ }\text{，}\\ B=\frac{{T}_{\text{ini}}\beta }{{E}_{\text{s}}}\text{ }。\end{array}\right\}$

(13)

对比B的定义式与式（6）中的土体变形功项可知，该系数是描述土体变形功对传热方程影响的一个重要参数。

对于变量 $\bar P$ 与T，初始条件可以表示为

$\left.\begin{array}{l}\overline{P}(z, 0)=0\text{ }\text{，}\\ T(z, 0)={T}_{\text{ini}}\text{ }。\end{array}\right\}$

(14)

表面z = 0处的渗流及传热边界条件主要考虑两类，分别为给定超静孔压及温度的边界Ⅰ，以及给定水流、热流的边界Ⅱ，具体形式为

$\left.\begin{array}{l} P(0, t)={f}_{1}(t)\text{ }\text{，}\\ T(0, t)={f}_{2}(t)\text{ }\text{，}\end{array}\right\}$

(15)

$\left.\begin{array}{l}{\frac{\partial P}{\partial z}|}_{z=0}={g}_{1}(t)\text{ }\text{，}\\ {\frac{\partial T}{\partial z}|}_{z=0}={g}_{2}(t)\text{ }。\end{array}\right\}$

(16)

式中：f₁(t)，f₂(t)，g₁(t)，g₂(t)均为关于时间的任意函数。

对于变量 $\bar P$ 与T，上述两类边界可以表示为

$\left.\begin{array}{l}\overline{P}(0, t)={f}_{1}(t)-{F}_{\text{s}}(t)\text{，}\\ T(0, t)={f}_{2}(t)\text{，}\end{array}\right\}$

(17)

$\left.\begin{array}{l} {\frac{\partial \overline{P}}{\partial z}|}_{z=0}={g}_{1}(t)\text{ }\text{，}\\ {\frac{\partial T}{\partial z}|}_{z=0}={g}_{2}(t)\text{ }。\end{array}\right\}$

(18)

2. 热固结模型解析求解

2.1 组合变量解耦

定义如下形式组合变量：

$\varOmega = \bar P + bT。$

(19)

利用该组合变量，将式（11），（12）中 $\bar P$ 消除后得到

$\frac{{\partial \varOmega }}{{\partial t}} + (A - b)\frac{{\partial T}}{{\partial t}} = {C_{\text{g}}}\frac{{{\partial ^2}\varOmega }}{{\partial {z^2}}} - b{C_{\text{g}}}\frac{{{\partial ^2}T}}{{\partial {z^2}}}\text{，}$

(20)

$B\frac{{\partial \varOmega }}{{\partial t}} + ({\bar C_{\text{v}}} - bB)\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}}。$

(21)

式（20）乘以 $\lambda$ 加上式（21）乘以bC_g得到：

$\begin{align} (\lambda + b{C_{\text{g}}}B)& \frac{{\partial \varOmega }}{{\partial t}} + \left[ {b{C_{\text{g}}}({{\bar C}_{\text{v}}} - bB) + \lambda (A - b)} \right]\frac{{\partial T}}{{\partial t}} \\ &\;\; = \lambda {C_{\text{g}}}\frac{{{\partial ^2}\varOmega }}{{\partial {z^2}}}。 \end{align}$

(22)

为了消除式（22）中的温度变化率项以实现解耦，b需要满足：

$B{C_{\text{g}}}{b^2} + (\lambda - {C_{\text{g}}}{\bar C_{\text{v}}})b - \lambda A = 0。$

(23)

式（23）是关于b的二次方程，它有两个形式的解（b₁取+）：

${b_{1, 2}} = \frac{{ - (\lambda - {C_{\text{g}}}{{\bar C}_{\text{v}}}) \pm \sqrt {{{(\lambda - {C_{\text{g}}}{{\bar C}_{\text{v}}})}^2} + 4\lambda AB{C_{\text{g}}}} }}{{2B{C_{\text{g}}}}}。$

(24)

式（24）给出的两个解可能是两个实数、两个共轭复数，也可能退化为同一个实数，下面先考虑 ${b_1} \ne {b_2}$ 的情形，此时式（19）定义了如下两个不同的组合变量：

${\varOmega }_{i}=\overline{P}+{b}_{i}T\text{ }（i=1, 2）。$

(25)

两个组合变量的控制方程为

$\left.\begin{array}{l} \frac{\partial {\varOmega }_{i}}{\partial t}={C}_{i}\frac{{\partial }^{2}{\varOmega }_{i}}{\partial {z}^{2}}\text{，}\\ {C}_{i}=\frac{\lambda {C}_{\text{g}}}{\lambda +{b}_{i}{C}_{\text{g}}B}（i=1, 2）。\end{array}\right\}$

(26)

两个组合变量的初始条件为

${\varOmega }_{i}(z, 0)=\overline{P}(z, 0)+{b}_{i}{T}_{\text{ini}}={b}_{i}{T}_{\text{ini}}（i=1, 2）。$

(27)

定义如下新变量消除初始条件

${\overline{\varOmega }}_{i}={\varOmega }_{i}-{b}_{i}{T}_{\text{ini}}（i=1, 2）。$

(28)

于是，变量 ${\bar \varOmega _i}$ 的控制方程及初始条件为

$\frac{\partial {\overline{\varOmega }}_{i}}{\partial t}={C}_{i}\frac{{\partial }^{2}{\overline{\varOmega }}_{i}}{\partial {z}^{2}}（i=1, 2） \text{，}$

(29)

${\bar \varOmega _i}(z, 0) = 0。$

(30)

根据式（17），（18）， ${\bar \varOmega _i}$ 的两类边界条件分别为

${\bar \varOmega _i}(0, t) = {f_1}(t) - {F_{\text{s}}}(t) + {b_i}{f_2}(t) - {b_i}{T_{{\text{ini}}}}\text{，}$

(31)

${\left. {\frac{{\partial {{\bar \varOmega }_i}}}{{\partial z}}} \right|_{z = 0}} = {g_1}(t) + {b_i}{g_2}(t) 。$

(32)

2.2 相似变换通解

对于半无限空间中形如式（29）的控制方程，文献[12, 13]建立的相似变换法可以较方便的应用。定义如下形式的相似变量：

$\left.\begin{array}{l}{\psi }_{i}=\frac{{\overline{\varOmega }}_{i}(z, t)}{{t}^{n/2}}\text{，}\\ {\eta }_{i}=\frac{z}{2\sqrt{{C}_{i}t}}（i=\text{ }1, 2）。\end{array}\right\}$

(33)

式中：n为任意非负整数。

将相似变量代入式（29）后推导可得常微分方程为^[12]

${{\psi }^{″}}_{i}+2{\eta }_{i}{{\psi }^{\prime }}_{i}-2n{\psi }_{i}=0\text{ }（i=1, 2）。$

(34)

常微分方程式（34）的通解为^[12]

${\psi }_{i}({\eta }_{i})={A}_{i, n}{\text{i}}^{n}\text{erfc}({\eta }_{i})+{B}_{i, n}{\text{i}}^{n}\text{erfc}(-{\eta }_{i})（i=1, 2）。$

(35)

式中：A_{i, n}，B_{i, n}为任意常数， ${{\text{i}}^n}{\text{erfc}}\left( \cdot \right)$ 为高斯误差函数的累次积分函数，

$\left.\begin{array}{l}{\text{i}}^{-1}\text{erfc(}\varepsilon \text{)}=\frac{2}{\sqrt{\text{π}}}\text{exp}(-{\varepsilon }^{2})\text{，}\\ {\text{i}}^{0}\text{erfc(}\varepsilon \text{)}=\text{erfc(}\varepsilon \text{)}\text{，}\end{array}\right\}$

(36)

${{\text{i}}^n}{\text{erfc(}}\varepsilon {\text{)}} = \mathop \smallint \nolimits_\varepsilon ^\infty {{\text{i}}^{n - 1}}{\text{erfc(}}x{\text{)}}dx。$

(37)

通过相似变换通解式（35），可以获得偏微分方程式（29）如下形式的通解：

$\begin{align} {\bar \varOmega _i}{\text{(}}z, t{\text{)}} = & \mathop \sum \nolimits_{n = 0}^\infty {t^{n/2}}\left[ {{A_{i, n}}{{\text{i}}^n}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_i}t} }}} \right) + } \right. \\& \qquad {B}_{i, n}{\text{i}}^{n}\text{erfc}\left(-\frac{z}{2\sqrt{{C}_{i}t}}\right)]\text{ }（i=1, 2）。\end{align}$

(38)

2.3 模型解析解答

根据 ${{\text{i}}^n}{\text{erfc}}\left( \cdot \right)$ 的定义式可知，通解式（38）中每个级数的第一项均满足初始时刻为0的条件，因此可以取变量 ${\bar \varOmega _i}$ 为

${\overline{\varOmega }}_{i}\text{(}z, t\text{)}={{\displaystyle \sum }}_{n=0}^{\infty }{A}_{i, n}{t}^{n/2}{\text{i}}^{n}\text{erfc}\left(\frac{z}{2\sqrt{{C}_{i}t}}\right)（i=1, 2）。$

(39)

将F_s(t)，f₁(t)，f₂(t)，g₁(t)，g₂(t)均展开为时间的幂级数，并代入式（31），（32），可以得到变量 ${\bar \varOmega _i}$ 所要满足的两类幂级数形式的边界条件为

${f}_{1}(t)-{F}_{\text{s}}(t)+{b}_{i}{f}_{2}(t)-{b}_{i}{T}_{\text{ini}}={{\displaystyle \sum }}_{n=0}^{m}{c}_{i, n}{t}^{n}（i=1, 2） \text{，}$

(40)

${g}_{1}(t)+{b}_{i}{g}_{2}(t)={{\displaystyle \sum }}_{n=0}^{m}{d}_{i, n}{t}^{n}（i=1, 2）。$

(41)

式中：c_{i, n}，d_{i, n}为幂级数的系数。

函数 ${\text{i}}^{n}\text{erfc}(·)$ 在0处的值为

${{\text{i}}^n}{\text{erfc(}}0{\text{)}} = \frac{1}{{{2^n}\varGamma \left( {\frac{n}{2} + 1} \right)}}。$

(42)

式中：Γ(·)为伽马函数。

对式（39）及其梯度在z = 0处取值，并与式（40）、（41）进行幂级数系数对比，可以确定边界条件Ⅰ即式（40）对应的解答为

$\begin{array}{l} {\bar \varOmega _i}(z, t) = \\\; {{\displaystyle \sum }}_{n=0}^{m}{c}_{i, n}\varGamma (n+1){(4t)}^{n}{\text{i}}^{2n}\text{erfc}\left(\frac{z}{2\sqrt{{C}_{i}t}}\right)（i=1, 2）。 \end{array}$

(43)

边界条件Ⅱ即式（41）对应的解答为

$\begin{align}{\bar \varOmega _i}(z, t) = & \mathop \sum \nolimits_{n = 0}^m ( - {d_{i, n}})\varGamma (n + 1)\sqrt {{C_i}} {(4t)^{\left( {2n + 1} \right)/2}} \cdot \\ &\qquad {\text{i}}^{2n+1}\text{erfc}\left(\frac{z}{2\sqrt{{C}_{i}t}}\right)（i=1, 2）。\end{align}$

(44)

根据式（28），可以确定组合变量 ${\varOmega _i}(z, t)$ ，随后可得温度及超静孔压解答：

$T(z, t) = \frac{{{\varOmega _1}(z, t) - {\varOmega _2}(z, t)}}{{{b_1} - {b_2}}}\text{，}$

(45)

$P(z, t) = \frac{{{b_1}{\varOmega _2}(z, t) - {b_2}{\varOmega _1}(z, t)}}{{{b_1} - {b_2}}} + {F_{\text{s}}}(t)。$

(46)

式（45），（46）适用于 ${b_1} \ne {b_2}$ 的情形，也包括b₁，b₂为两个共轭复数时。实际上，当b₁，b₂为两个共轭复数，式（29）中系数C₁，C₂也是两个共轭复数，函数 ${{\text{i}}^n}{\text{erfc}}\left( \cdot \right)$ 会保持复数的共轭性， ${\bar \varOmega _1}(z, t)$ ， ${\bar \varOmega _2}(z, t)$ 也是两共轭复数，因此式（45），（46）得到的温度和超静孔压均为实数。

当 ${(\lambda - {C_{\text{g}}}{\bar C_{\text{v}}})^2} + 4\lambda AB{C_{\text{g}}} = 0$ 时（此时A<0），b₁和b₂为相同实数统一记为b₀，通过上面的推导只能得到一个组合变量Ω₀的解答。利用该已有的组合变量，式（11），（12）可以变形为

$\left( {1 - \frac{A}{{{b_0}}}} \right)\frac{{\partial \bar P}}{{\partial t}} = {C_{\text{g}}}\frac{{{\partial ^2}\bar P}}{{\partial {z^2}}} - \frac{A}{{{b_0}}}\frac{{\partial {\varOmega _0}}}{{\partial t}}\text{，}$

(47)

$({\bar C_{\text{v}}} - B{b_0})\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}} - B\frac{{\partial {\varOmega _0}}}{{\partial t}}。$

(48)

式（47），（48）中 $\partial \bar P/\partial t$ 与 $\partial T/\partial t$ 的系数必有一个为正值，不妨设式（48）中为正，则式（48）为半无限空间中含热源的一维热传导问题，许多方法可以应用，这里直接采用格林函数法给出解答^[14]。

对于边界条件Ⅰ，温度解答为

$\left.\begin{array}{l}T(z, t)={T}_{\text{ini}}{{\displaystyle \int }}_{0}^{\infty }{G}_{1}\text{(}z, t|{z}^{\prime }, 0\text{)}d{z}^{\prime }-\\ {{\displaystyle \int }}_{0}^{t}{{\displaystyle \int }}_{0}^{\infty }\varepsilon \frac{\partial {\varOmega }_{0}({z}^{\prime }, \tau )}{\partial \tau }{G}_{1}(z, t|{z}^{\prime }, \tau )d{z}^{\prime }d\tau +\\ \xi {{\displaystyle \int }}_{0}^{t}{f}_{2}(\tau )\frac{\partial {G}_{1}(z, t|0, \tau )}{\partial z}d\tau \text{，}\\ \xi =\frac{\lambda }{{\overline{C}}_{\text{v}}-B{b}_{0}}\text{，}\\ \varepsilon =\frac{B}{{\overline{C}}_{\text{v}}-B{b}_{0}}。\end{array}\right\}$

(49)

式中：格林函数为^[14]

$\begin{align} {G_1}(z, t|z', \tau ) = & \frac{1}{{{{\left[ {4\pi \xi (t - \tau )} \right]}^{1/2}}}}\left\{ {\exp \left[ { - \frac{{{{(z - z')}^2}}}{{4\xi (t - \tau )}}} \right]} \right. - \\& \left. {{\text{exp}}\left[ { - \frac{{{{(z + z')}^2}}}{{4\xi (t - \tau )}}} \right]} \right\}。 \end{align}$

(50)

对于边界条件Ⅱ，温度解答为

$\begin{align} T(z, t) =& {T_{{\text{ini}}}}\mathop \smallint \nolimits_0^\infty {G_2}(z, t|z', 0)dz' - \\&\;\; \mathop \smallint \nolimits_0^t \mathop \smallint \nolimits_0^\infty \varepsilon \frac{{\partial {\varOmega _0}(z', \tau )}}{{\partial \tau }}{G_2}(z, t|z', \tau )dz'd\tau -\\& \;\; \xi \mathop \smallint \nolimits_0^t {g_2}(\tau ){G_2}(z, t|0, \tau )d\tau 。\end{align}$

(51)

式中：格林函数为^[14]

$\begin{align}& {G_2}(z, t|z', \tau ) = \frac{1}{{{{\left[ {4\pi \xi (t - \tau )} \right]}^{1/2}}}}\left\{ {\exp \left[ { - \frac{{{{(z - z')}^2}}}{{4\xi (t - \tau )}}} \right] + } \right.\\ & \qquad \qquad \left. {{\text{exp}} \left[ { - \frac{{{{(z + z')}^2}}}{{4\xi (t - \tau )}}} \right]} \right\}。 \end{align}$

(52)

随后，超静孔压的解答可以通过组合变量定义式（19）得到。

2.4 恒定边界条件特例 $({b_1} \ne {b_2})$

（1）恒定边界条件Ⅰ

考虑外荷载为瞬时荷载P_c，土体表面超静孔压f₁(t)=0，表面温度f₂(t)=T_s。根据式（40）可知，展开后的幂级数仅有1项，系数为

${c}_{i, 0}={b}_{i}({T}_{\text{s}}-{T}_{\text{ini}})-{P}_{\text{c}}（i=1, 2）。$

(53)

利用2.3节中解答可得

${\overline{\varOmega }}_{i}(z, t)={c}_{i, 0}\text{erfc}\left(\frac{z}{2\sqrt{{C}_{i}t}}\right)（i=1, 2）。$

(54)

于是温度及超静孔压解答为

$T(z, t) = {T_{{\text{ini}}}} + \frac{{{c_{1, 0}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_1}t} }}} \right) - {c_{2, 0}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_2}t} }}} \right)}}{{{b_1} - {b_2}}}\text{，}$

(55)

$P(z, t) = \frac{{{b_1}{c_{2, 0}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_2}t} }}} \right) - {b_2}{c_{1, 0}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_1}t} }}} \right)}}{{{b_1} - {b_2}}} + {P_{\text{c}}}。$

(56)

（2）恒定边界条件Ⅱ

考虑外荷载为瞬时荷载P_c，土体表面水流边界g₁(t)=q_w，表面热流边界g₂(t)=q_h。根据式（41），展开后的幂级数仅有1项，系数为

${d}_{i, 0}={q}_{\text{w}}+{b}_{i}{q}_{\text{h}}\quad （i=1, 2）。$

(57)

利用2.3节的解答，可以得到

${\overline{\varOmega }}_{i}(z, t)=(-{d}_{i, 0})\sqrt{{C}_{i}}{(4t)}^{1/2}\text{ierfc}\left(\frac{z}{2\sqrt{{C}_{i}t}}\right)\quad （i=1, 2）。$

(58)

于是，温度及超静孔压解答为

$\begin{align} & T(z, t) = {T_{{\text{ini}}}} - \\ & {(4t)^{1/2}}\frac{{{d_{1, 0}}\sqrt {{C_1}} {\text{ierfc}}\left( {\frac{z}{{2\sqrt {{C_1}t} }}} \right) - {d_{2, 0}}\sqrt {{C_2}} {\text{ierfc}}\left( {\frac{z}{{2\sqrt {{C_2}t} }}} \right)}}{{{b_1} - {b_2}}}\text{，} \end{align}$

(59)

$\begin{align} & P(z, t) = {P_{\text{c}}} + \\ & {(4t)}^{1/2}\frac{{b}_{2}{d}_{1, 0}\sqrt{{C}_{1}}\text{ierfc}\left(\frac{z}{2\sqrt{{C}_{1}t}}\right)-{b}_{1}{d}_{2, 0}\sqrt{{C}_{2}}\text{ierfc}\left(\frac{z}{2\sqrt{{C}_{2}t}}\right)}{{b}_{1}-{b}_{2}}。 \end{align}$

(60)

3. 单向耦合模型解析解

前面传热部分分析考虑了土体变形功项，因而式（12）中包含了超静孔压变化率，模型是双向耦合的。实际热固结计算中，忽略固结过程对传热影响的单向耦合模型也应用较多^[5-7]，本节考虑单向耦合情形。

单向耦合模型中传热控制方程由式（12）退化为

$\frac{{\partial T}}{{\partial t}} = \alpha \frac{{{\partial ^2}T}}{{\partial {z^2}}}。$

(61)

式中：热扩散率 $\alpha$ = $\lambda$ /C_v。

该情形相当于双向耦合模型中B退化为0，于是关于b的方程式（23）退化为一次方程，仅有一组解答为

${b_{\text{c}}} = \frac{{A\alpha }}{{\alpha - {C_{\text{g}}}}}。$

(62)

此时相当于有T以及 ${\varOmega _{\text{b}}} = \bar P + {b_{\text{c}}}T$ 两个组合变量，引入：

${\bar \varOmega _{\text{b}}} = {\varOmega _{\text{b}}} - {b_{\text{c}}}{T_{{\text{ini}}}}\text{，}$

(63)

$\bar T = T - {T_{{\text{ini}}}}。$

(64)

变量 ${\bar \varOmega _{\text{b}}}$ 与 $\bar T$ 所满足的控制方程为

$\frac{{\partial {{\bar \varOmega }_{\text{b}}}}}{{\partial t}} = {C_{\text{g}}}\frac{{{\partial ^2}{{\bar \varOmega }_{\text{b}}}}}{{\partial {z^2}}}\text{，}$

(65)

$\frac{{\partial \bar T}}{{\partial t}} = \alpha \frac{{{\partial ^2}\bar T}}{{\partial {z^2}}}。$

(66)

变量 ${\bar \varOmega _{\text{b}}}$ 与 $\bar T$ 初始条件均为0，所需满足的边界条件Ⅰ及边界条件Ⅱ分别为

$\left.\begin{array}{l}{\overline{\varOmega }}_{\text{b}}(0, t)={f}_{1}\text{(}t\text{)}-{F}_{\text{s}}\text{(}t\text{)}+{b}_{\text{c}}{f}_{2}\text{(}t\text{)}-\left[{b}_{\text{c}}{T}_{\text{ini}}-{F}_{\text{s}}(0)\right]\text{，}\\ \overline{T}(0, t)={f}_{2}\text{(}t\text{)}-{T}_{\text{ini}}\text{，}\end{array}\right\}$

(67)

$\left.\begin{array}{l} {\frac{\partial {\overline{\varOmega }}_{\text{b}}}{\partial z}|}_{z=0}={g}_{1}(t)+{b}_{\text{c}}{g}_{2}(t)\text{，}\\ {\frac{\partial \overline{T}}{\partial z}|}_{z=0}={g}_{2}(t)。\end{array}\right\}$

(68)

式（67），（68）展开为幂级数形式如下

$\left.\begin{array}{l}{\overline{\varOmega }}_{\text{b}}(0, t)={{\displaystyle \sum }}_{n=0}^{m}{\overline{c}}_{1, n}{t}^{n}\text{，}\\ \overline{ T}(0, t)={{\displaystyle \sum }}_{n=0}^{m}{\overline{c}}_{2, n}{t}^{n}\text{，}\end{array}\right\}$

(69)

$\left. \begin{array}{l}{\frac{\partial {\overline{\varOmega }}_{\text{b}}}{\partial z}|}_{z=0}={{\displaystyle \sum }}_{n=0}^{m}{\overline{d}}_{1, n}{t}^{n}\text{，}\\ {\frac{\partial \overline{T}}{\partial z}|}_{z=0}={{\displaystyle \sum }}_{n=0}^{m}{\overline{d}}_{2, n}{t}^{n}。\end{array}\right\}$

(70)

利用相似变换通解，经过与第2节类似的推导，可以得到单向耦合模型解析解答。对于边界条件Ⅰ，温度及超静孔压解答为

$T(z, t) = \mathop \sum \nolimits_{n = 0}^m {\bar c_{2, n}}\varGamma (n + 1){(4t)^n}{{\text{i}}^{2n}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {\alpha t} }}} \right) + {T_{{\text{ini}}}}\text{，}$

(71)

$\begin{align} P(z, t) =& \mathop \sum \nolimits_{n = 0}^m {\bar c_{1, n}}\varGamma (n + 1){(4t)^n}{{\text{i}}^{2n}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_{\text{g}}}t} }}} \right) - \\ & {b_{\text{c}}}\mathop \sum \nolimits_{n = 0}^m {\bar c_{2, n}}\varGamma (n + 1){(4t)^n}{{\text{i}}^{2n}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {\alpha t} }}} \right) + \\ & \qquad\qquad {F_{\text{s}}}(t) - {F_{\text{s}}}(0)。\end{align}$

(72)

对于边界条件Ⅱ，温度及超静孔压解答为

$\begin{align} T(z, t) =& \mathop \sum \nolimits_{n = 0}^m ( - 1){\bar d_{2, n}}\varGamma (n + 1)\sqrt \alpha {(4t)^{\left( {2n + 1} \right)/2}} \cdot \\&\; {{\text{i}}^{2n + 1}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {\alpha t} }}} \right) + {T_{{\text{ini}}}}\text{，}\end{align}$

(73)

$\begin{align} & P(z, t) = \mathop \sum \nolimits_{n = 0}^m ( - {\bar d_{1, n}})\varGamma (n + 1)\sqrt {{C_{\text{g}}}} {(4t)^{\left( {2n + 1} \right)/2}} \cdot \\&\; {{\text{i}}^{2n + 1}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {{C_{\text{g}}}t} }}} \right) + {b_c}\mathop \sum \nolimits_{n = 0}^m {\bar d_{2, n}}\varGamma \left( {n + 1} \right)\sqrt \alpha {(4t)^{\left( {2n + 1} \right)/2}} \cdot \\&\qquad \qquad {{\text{i}}^{2n + 1}}{\text{erfc}}\left( {\frac{z}{{2\sqrt {\alpha t} }}} \right) + {F_{\text{s}}}(t) - {F_{\text{s}}}(0)。\end{align}$

(74)

4. 算例分析

4.1 对比验证

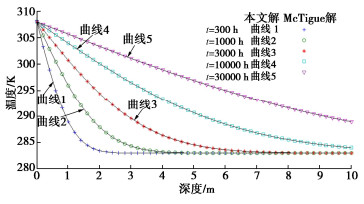
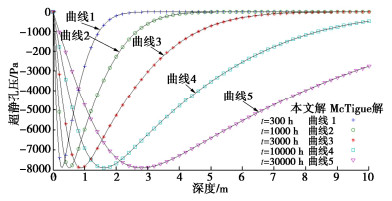
McTigue^[4]给出了半无限空间岩土体热固结过程单向耦合模型的解析解，该解答形式简单，本节利用其对2.3节中解析解作对比验证。对比算例中土体初始温度为283 K，表面温度为308 K，无外荷载作用，表面超静孔压为0。土体导热系数为1.3 W/(m·K)，比热为3000 J/(kg·K)，密度为1300 kg/m³；土体变形模量E为5×10⁶ Pa，泊松比v为0.3，固结系数C_g为10^-8 m²/s；土体热膨胀系数按 ${a_{{\text{sm}}}} = \bar a$ 确定，孔隙率为0.3，骨架热膨胀系数为2.5×10^-5 K^-1，孔隙水的热膨胀系数为2×10^-4 K^-1。

通过2.3节解答及McTigue^[4]解答对该算例进行了计算，为了使2.3节双向耦合模型接近McTigue所采用的单向耦合模型以实现对比，式（12）中无量纲参数B取了很小的值0.01。解析解编程采用Matlab进行，其中 ${{\text{i}}^n}{\text{erfc}}\left( \cdot \right)$ 函数可以方便的调用mfun(‘erfc’, n, z)命令。图 2，3分别给出了两组解析解在不同时刻温度及超静孔压分布的对比情况，两组解答计算结果的一致性验证了本文解析解。

图 2 两组解答温度分布对比

Figure 2. Comparison of temperature distributions for two solutions

下载: 全尺寸图片幻灯片

图 3 两组解答超静孔压分布对比

Figure 3. Comparison of excessive porewater pressure distributions for two solutions

下载: 全尺寸图片幻灯片

4.2 耦合效应分析

本文双向耦合热固结模型控制方程式（11），（12）中，温度变化对固结部分的影响主要通过温度变化率的系数A作用，而超静孔压变化对传热部分的影响则主要通过超静孔压变化率的系数B作用，本节将研究A，B参数对热固结过程中温度、超静孔压耦合发展情况的影响。

算例中半无限空间土体初始温度为283 K，无外荷载作用，考虑式（15），（16）所描述的两类边界条件，其中的具体函数为

$\left.\begin{array}{l}{f}_{1}(t)=0\text{ }\text{，}\\ {f}_{2}(t)=283+20\text{sin}\left(\frac{2\pi }{8760}\cdot t\right)\text{ }\text{，}\end{array}\right\}$

(75)

$\left.\begin{array}{l}{g}_{1}(t)=0\text{，}\\ {g}_{2}(t)=10\text{sin}\left(\frac{2\pi }{8760}t\right)。\end{array}\right\}$

(76)

式中：t为时间（h）。

土体基本物性参数均与4.1节相同，而采用不同参数计算时会另作说明。经试算，式（75），（76）边界条件展开为幂级数10项即可收敛，随后可以应用2.3节中解答对温度场、超静孔压场进行计算。

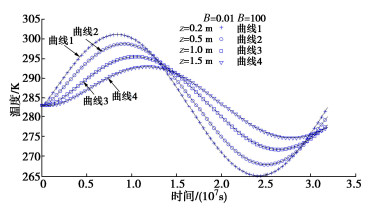
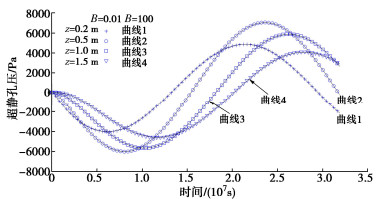
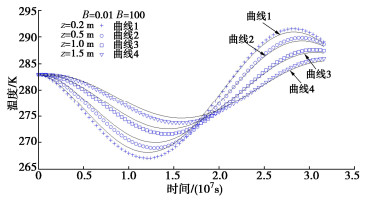
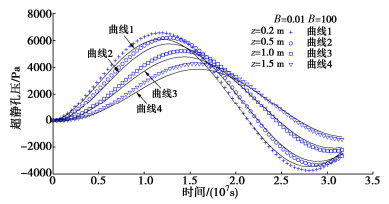
图 4，5给出了边界条件Ⅰ下不同深度处温度、超静孔压随时间变化的曲线。温度从初始的283 K开始呈现升高—降低—升高的典型波动趋势；随着深度的增加，温度波动的幅值逐渐减小，而出现峰值的时间有所推后，这是温度波传播过程中典型的衰减和延迟性质。超静孔压的变化则是从初始的0开始，呈现降低—升高—降低的波动趋势，总体与温度的波动相反；图中4个深度超静孔压波动辐值最高出现在z=0.5 m，而不是更接近地表的z=0.2 m，这是由于地表超静孔压为0，太接近地表反而限制了超静孔压的波动。对比B为0.01，100两种情形发现，B值的变化对温度、超静孔压的发展基本没有影响。

图 4 边界Ⅰ不同深度温度随时间变化

Figure 4. Variation of temperature with time at different depths for type Ⅰ boundary condition

下载: 全尺寸图片幻灯片

图 5 边界Ⅰ不同深度超静孔压随时间变化

Figure 5. Variation of excessive porewater pressure with time at different depths for type Ⅰ boundary condition

下载: 全尺寸图片幻灯片

图 6，7给出了边界条件Ⅱ下不同深度处温度、超静孔压随时间变化的曲线。由于式（76）给出的表面热流是先从地表向外流动的，温度变化主要呈降低—升高—降低的波动趋势，随着深度的增加，温度波动仍体现衰减和延迟特征。超静孔压则呈升高—降低—升高的波动趋势，同样与温度的波动相反；随着深度的增加，超静孔压的波动也出现了衰减和延迟，这是不透水边界与图 4，5中透水边界的区别。B=100时的结果与B=0.01时基本无差异（未作曲线）；而B=1000时与B=0.01时结果相比有一些可见的差异，温度及超静孔压的波动幅度均有所减小。

图 6 边界Ⅱ不同深度温度随时间变化

Figure 6. Variation of temperature with time at different depths for type Ⅱ boundary condition

下载: 全尺寸图片幻灯片

图 7 边界Ⅱ不同深度超静孔压随时间变化

Figure 7. Variation of excessive porewater pressure with time at different depths for type Ⅱ boundary condition

下载: 全尺寸图片幻灯片

图 4~7中选取不同B是为了研究式（12）中土体变形功对传热及固结过程的影响；若直接根据4.1节参数及式（13），可以确定B=4.07×10^-2。从计算结果看，B值的变化对温度、超静孔压发展的影响较小，这一结论也可以从式（12）左侧两项的量级分析中获得。式（12）左侧温度变化率项的系数为C_v+Bβ, 其中C_v的大小是3.9×10⁶ J/(m³·K)，而Bβ的大小即使在B=100时也仅为0.09×10⁶ J/(m³·K)，是远小于C_v的；同时，孔压变化率项的系数B (即使取100)也远小于C_v，这就造成了图 4~7中B的变化对计算结果的影响较小。根据式（3），（4），（13），B不会超过0.3，B，Bβ相对于C_v都是很小的；因此，除非超静孔压变化率很高（10² Pa/s量级），土体变形功项对温度、超静孔压的影响基本都可以忽略。

文献[]对参数A进行过分析，指出按式（2）及 ${a_{{\text{sm}}}} = \bar a$ 取值时（上面算例即是如此），A始终为正值，而也有文献未按此确定a_sm及A，得到的A可能为负值^[3]。下面具体计算分析A的正、负对温度、超静孔压耦合演化过程的影响。

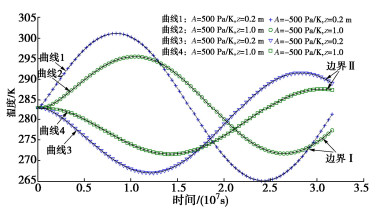
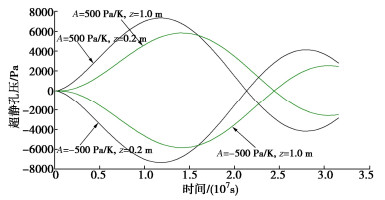
算例参数也均与4.1节相同，通过设置不同A来分析温度变化率项对热固结过程的影响。图 8给出了两种边界情况下不同深度处温度随时间变化的曲线，图中温度变化趋势与图 4，6中的结果是一致的；参考文献[13]中总结的A的取值，选择了A为500，-500 Pa/K两种情形，图中结果表明，A的变化对两种情形下温度场的演化基本没有影响。

图 8 边界Ⅰ与边界Ⅱ下不同深度温度随时间的变化

Figure 8. Variation of temperature at different depths for type Ⅰ and type Ⅱ boundary conditions

下载: 全尺寸图片幻灯片

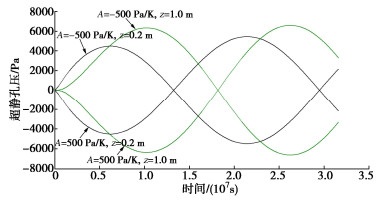
图 9给出了边界Ⅰ情形下不同深度超静孔压随时间的变化情况。在A=500 Pa/K时，超静孔压随时间的变化总体与温度随时间的变化呈相反趋势，这与图 4~7中的结果是一致的。然而，在A=-500 Pa/K时，超静孔压随时间的变化总体与温度变化呈相同的趋势；以z=1.0 m位置为例，t<10⁷ s，超静孔压及温度总体呈升高趋势，而在10⁷ s<t<2.6×10⁷ s，超静孔压与温度总体呈降低趋势，最后在t>2.6×10⁷ s，超静孔压及温度转变为升高趋势。

图 9 边界Ⅰ不同深度超静孔压随时间的变化

Figure 9. Variation of excessive porewater pressure at different depths for type Ⅰ boundary condition

下载: 全尺寸图片幻灯片

图 10给出了边界Ⅱ情形下不同深度超静孔压随时间的变化情况。与图 8中温度变化对比可知，在A= 500 Pa/K时，超静孔压的变化总体与温度变化呈相反趋势，而在A=-500 Pa/K时，超静孔压的变化总体与温度变化呈相同趋势，这与图 9中的结果是一致的。

图 10 边界Ⅱ不同深度超静孔压随时间的变化

Figure 10. Variation of excessive porewater pressure at different depths for type Ⅱ boundary condition

下载: 全尺寸图片幻灯片

A的正负对超静孔压与温度耦合演化的影响特征可以通过对式（11）的分析进一步阐明。对比式（11）与传统固结方程可知，温度变化项的影响相当于给固结过程增加了一个源项-A∂T/∂t，温度变化即通过该源项引起相应的超静孔压变化。当A>0时，∂P/∂t与∂T/∂t前面的符号相反，温度变化引起的超静孔压变化与之呈相反趋势；当A<0时, ∂P/∂t与∂T/∂t前面的符号相同，温度变化引起的超静孔压变化与之呈相同趋势，这便是图 8~10中所展示的结果。

从式（11）也可以看出，若将A = 500 Pa/K情形下该式的解答记为P(z, t)，由于A的变化对温度解答基本没有影响，A=-500 Pa/K情形下该式的解答则为-P(z, t)，即A = -500 Pa/K情形下的超静孔压与A = 500 Pa/K情形下的超静孔压是关于直线P = 0对称的，这与图 9，10中展示的结果一致。

5. 结论

针对半无限空间土体在外荷载及表面两类渗流、传热边界条件下的热固结问题，给出了描述温度、超静孔压双向耦合演化过程的基本方程，并基于相似变换方法建立了幂级数形式荷载及渗流、传热边界条件下温度与超静孔压的解析解答。多数情形下，解答可以直接用 ${{\text{i}}^n}{\text{erfc}}\left( \cdot \right)$ 函数的代数组合形式给出，应用十分方便。

（1）温度波动从地表向深处传播有明显的衰减和延迟特性，而超静孔压传播则随渗流边界条件不同而有所差异。地表为不透水边界时，超静孔压波动随深度增加也具有衰减和延迟特性；地表为透水边界时则有所不同，超静孔压波动幅度最大值出现在距地表一定深度处。

（2）传热控制方程中土体变形功项的贡献很小，模型计算基本可以忽略土体变形功对温度、超静孔压演化过程的影响。

（3）固结控制方程中温度变化率项对温度、超静孔压的耦合演化有显著影响，其特征主要决定于该项的系数A。当系数A为正时，温度变化将引起相反趋势的超静孔压变化；当系数A为负时，温度变化将引起相同趋势的超静孔压变化。

图 1 半无限空间饱和土-维热固结过程示意图

Figure 1. Schematic diagram for 1-D thermo-consolidation process of semi-infinite saturated soil

下载: 全尺寸图片幻灯片

图 2 两组解答温度分布对比

Figure 2. Comparison of temperature distributions for two solutions

下载: 全尺寸图片幻灯片

图 3 两组解答超静孔压分布对比

Figure 3. Comparison of excessive porewater pressure distributions for two solutions

下载: 全尺寸图片幻灯片

图 4 边界Ⅰ不同深度温度随时间变化

Figure 4. Variation of temperature with time at different depths for type Ⅰ boundary condition

下载: 全尺寸图片幻灯片

图 5 边界Ⅰ不同深度超静孔压随时间变化

Figure 5. Variation of excessive porewater pressure with time at different depths for type Ⅰ boundary condition

下载: 全尺寸图片幻灯片

图 6 边界Ⅱ不同深度温度随时间变化

Figure 6. Variation of temperature with time at different depths for type Ⅱ boundary condition

下载: 全尺寸图片幻灯片

图 7 边界Ⅱ不同深度超静孔压随时间变化

Figure 7. Variation of excessive porewater pressure with time at different depths for type Ⅱ boundary condition

下载: 全尺寸图片幻灯片

图 8 边界Ⅰ与边界Ⅱ下不同深度温度随时间的变化

Figure 8. Variation of temperature at different depths for type Ⅰ and type Ⅱ boundary conditions

下载: 全尺寸图片幻灯片

图 9 边界Ⅰ不同深度超静孔压随时间的变化

Figure 9. Variation of excessive porewater pressure at different depths for type Ⅰ boundary condition

下载: 全尺寸图片幻灯片

图 10 边界Ⅱ不同深度超静孔压随时间的变化

Figure 10. Variation of excessive porewater pressure at different depths for type Ⅱ boundary condition

下载: 全尺寸图片幻灯片

参考文献(14)

[1]	PAASWELL R E. Temperature effects on clay soil consolidation[J]. Journal of the Soil Mechanics and Foundations Division, 1967, 93(3): 9-22. doi: 10.1061/JSFEAQ.0000982
[2]	BIOT M A. Thermoelasticity and irreversible thermodynamics[J]. Journal of Applied Physics, 1956, 27(3): 240-253. doi: 10.1063/1.1722351
[3]	ZHOU Y, RAJAPAKSE R K N D, GRAHAM J. A coupled thermoporoelastic model with thermo-osmosis and thermal-filtration[J]. International Journal of Solids and Structures, 1998, 35(34/35): 4659-4683.
[4]	MCTIGUE D F. Thermoelastic response of fluid-saturated porous rock[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B9): 9533-9542. doi: 10.1029/JB091iB09p09533
[5]	BLOND E, SCHMITT N, HILD F. Response of saturated porous media to cyclic thermal loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(11): 883-904. doi: 10.1002/nag.301
[6]	白冰. 循环温度荷载作用下饱和多孔介质热-水-力耦合响应[J]. 工程力学, 2007, 24(5): 87-92. doi: 10.3969/j.issn.1000-4750.2007.05.015 BAI Bing. Thermo-hydro-mechanical responses of saturated porous media under cyclic thermal loading[J]. Engineering Mechanics, 2007, 24(5): 87-92. (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.05.015
[7]	吴瑞潜, 谢康和, 程永锋. 变荷载下饱和土一维热固结解析理论[J]. 浙江大学学报(工学版), 2009, 43(8): 1532-1537. WU Ruiqian, XIE Kanghe, CHENG Yongfeng. Analytical theory for one-dimensional thermal consolidation of saturated soil under time-dependent loading[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(8): 1532-1537. (in Chinese)
[8]	BAI B. Fluctuation responses of saturated porous media subjected to cyclic thermal loading[J]. Computers and Geotechnics, 2006, 33(8): 396-403. doi: 10.1016/j.compgeo.2006.08.005
[9]	王路君, 艾智勇. 衰变热源作用下饱和多孔介质热固结问题的扩展精细积分法[J]. 力学学报, 2017, 49(2): 324-334. WANG Lujun, AI Zhiyong. Epim for thermal consolidation problems of saturated porous media subjected to a decaying heat source[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 324-334. (in Chinese)
[10]	钮家军, 凌道盛, 王秀凯, 等. 饱和单层土体一维热固结精确解[J]. 岩土工程学报, 2019, 41(9): 1715-1723. doi: 10.11779/CJGE201909016 NIU Jiajun, LING Daosheng, WANG Xiukai, et al. Exact solutions for one-dimensional thermal consolidation of single-layer saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1715-1723. (in Chinese) doi: 10.11779/CJGE201909016
[11]	钮家军, 王秀凯, 凌道盛, 等. 半无限空间饱和土一维热固结精确积分解[J]. 岩土工程学报, 2021, 43(8): 1426-1433. doi: 10.11779/CJGE202108007 NIU Jiajun, WANG Xiukai, LING Daosheng, et al. Exact integral solutions for one-dimensional thermal consolidation of semi-infinite saturated soils[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(8): 1426-1433. (in Chinese) doi: 10.11779/CJGE202108007
[12]	ZHOU Y, ZHANG L Y, XU C, et al. Analytical solution for classical one-dimensional thaw consolidation model considering unfrozen water effect and time-varying load[J]. Computers and Geotechnics, 2020, 122: 103513. doi: 10.1016/j.compgeo.2020.103513
[13]	周扬, 武子寒, 许程, 等. 高温下饱和冻土一维融化热固结模型及解答[J]. 岩土工程学报, 2021, 43(12): 2190-2199. doi: 10.11779/CJGE202112005 ZHOU Yang, WU Zihan, XU Cheng, et al. One-dimensional thaw thermo-consolidation model for saturated frozen soil under high temperature and its solution [J]. Chinese Journal of Geotechnical Engineering, 2021, 43(12): 2190-2199. (in Chinese) doi: 10.11779/CJGE202112005
[14]	COLE K D, BECK J V, HAJI-SHEIKH A, et al. Heat Conduction Using Green's Functions[M]. 2nd ed. Boca Raton: CRC Press, 2010.

施引文献

资源附件(1)

其他相关附件
- PDF格式
  17-202505-G24-0206一文审稿意见与作者答复点击下载(1560KB)

图(10)

计量

文章访问数: 268
HTML全文浏览量: 25
PDF下载量: 61
被引次数: 0

0. 引言
1. 半无限空间饱和土热固结模型
2. 热固结模型解析求解
2.1 组合变量解耦
2.2 相似变换通解
2.3 模型解析解答
2.4 恒定边界条件特例({b_1} \ne {b_2})({b_1} \ne {b_2})
3. 单向耦合模型解析解
4. 算例分析
4.1 对比验证
4.2 耦合效应分析
5. 结论

基于相似变换法的半无限空间饱和土一维热固结解析解 English Version

作者简介: 韩涛(1981— )，男，山东淄博人，博士，副研究员，从事岩土特殊施工、岩土体热力耦合方面的研究工作。E-mail: hantaocumt@163.com

通讯作者: 周扬, E-mail：tod2006@126.com

计量

出版历程

Analytical solutions for 1-D thermo-consolidation process of semi-infinite saturated soil using similarity transformation method

0. 引言

1. 半无限空间饱和土热固结模型

2. 热固结模型解析求解

2.1 组合变量解耦

2.2 相似变换通解

2.3 模型解析解答

2.4 恒定边界条件特例(b1≠b2)({b_1} \ne {b_2})

3. 单向耦合模型解析解

4. 算例分析

4.1 对比验证

4.2 耦合效应分析

5. 结论

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 半无限空间饱和土热固结模型

2. 热固结模型解析求解

2.1 组合变量解耦

2.2 相似变换通解

2.3 模型解析解答

2.4 恒定边界条件特例({b_1} \ne {b_2})({b_1} \ne {b_2})

3. 单向耦合模型解析解

4. 算例分析

4.1 对比验证

4.2 耦合效应分析

5. 结论

作者简介:
韩涛(1981— )，男，山东淄博人，博士，副研究员，从事岩土特殊施工、岩土体热力耦合方面的研究工作。E-mail: hantaocumt@163.com

通讯作者:
周扬, E-mail：tod2006@126.com

2.4 恒定边界条件特例 $({b_1} \ne {b_2})$

2.4 恒定边界条件特例 $({b_1} \ne {b_2})$