Model tests and simulation analyses of starting characteristics of muck in slurry-discharge pipelines of slurry shield in sandy pebble stratum
-
摘要: 泥水盾构在砂卵石地层掘进的过程中，由于排浆管路中存在大量不规则卵石，排浆管路输送尤为复杂。设计了环流试验装置，并基于计算流体动力学与离散单元法（CFD-DEM）耦合方法建立了三维瞬态数值模型，对不同形状、粒径、管路倾角、弯头及管径下的卵石起动特性进行了探究。在模型试验中，羧甲基纤维素钠（CMC）浆液被选为载液，透明亚克力管被选为载体；在CFD-DEM耦合模型中，分别通过流变测试和三维扫描技术考虑了浆液的流变性和不规则卵石的形状。结果表明：①当异形卵石粒径和管路倾角相同时，卵石的起动速度大小顺序呈现椭球状＞扁平状＞近球状；②当异形卵石形状和管路倾角时，卵石的起动速度随等容粒径的增大先增大后减小再增大；③对于球形卵石，在水平管路中，卵石的起动速度随粒径的增大先增大后减小再增大，在倾斜和竖直管路中，卵石的起动速度随粒径的增大而减小；④卵石的起动速度随管径的增大而增大；⑤卵石起动速度较大的位置主要出现在较大角度（如60°，90°）的弯头位置处，这是因为当管路倾角≥60°时，在弯头位置处将会出现漩涡区，漩涡区流速与主流区流速相反，阻碍卵石运动，因此在铺设管路时，应尽量减少倾斜角度较大（≥60°）管路的铺设，多采用水平管路或倾斜角度较小（≤45°）的管路。Abstract:During the excavation process of slurry shield tunneling in sandy pebble stratum, the discharge pipeline transport is particularly complex due to a large number of irregular pebbles in the slurry-discharge pipelines. In this study, a circulating current test device is designed, and a three-dimensional transient numerical model is established using the computational fluid dynamics-discrete element method (CFD-DEM) coupling method. The start-up characteristics of the pebbles under different shapes, particle sizes, inclination angles of pipelines, elbow and pipeline diameters are investigated, respectively. In the model tests, the sodium carboxymethyl cellulose (CMC) slurry is used as the carrier liquid, and the transparent acrylic tube is used as the carrier. In the CFD-DEM coupling model, the rheological properties of slurry and the shape of irregular pebbles are considered through the rheological testing and three-dimensional scanning technology, respectively. The results indicated that: (1) Under the same particle size of irregular pebbles and inclination angle of pipelines, the starting velocity of the pebbles follows an order of ellipsoidal shape > flat shape > nearly spherical shapes; (2) Under the same shape of irregular pebbles and inclination angle of pipelines, the starting velocity of pebbles first increases, then decreases, and then increases with the increase of the isometric particle size. (3) For the spherical pebbles, in a horizontal pipeline, the starting velocity of the pebbles first increases, then decreases, and then increases with the increase of the particle size. In the inclined and vertical pipelines, the starting velocity of the pebbles decreases with the increase of the particle size. (4) The starting velocity of the pebbles increases with the increase of the pipe line diameter. (5) The positions with higher starting velocity of pebbles mainly appear at the elbow positions with larger angles (such as 60°and 90°). This is because when the inclination angle of pipelines is≥60°, a vortex zone will appear at the elbow position. The velocity in the vortex zone is opposite to the velocity in the mainstream zone, which hinders the movement of the pebbles. Therefore, when laying pipelines, it is necessary to minimize the laying of large-angle-inclined and vertical pipelines as much as possible, and it is recommended to use more horizontal pipelines or pipelines with small inclination angles (≤45°).
-
Keywords:
- slurry shield /
- large irregular pebbles /
- critical starting velocity /
- model test /
- CFD-DEM coupling
-
0. 引言
泥水盾构法因其安全性能好、施工效率高而被广泛应用于地下隧道工程的施工中[1-4]。泥水盾构在砂卵石地层掘进过程中，由渣石和泥浆组成的渣浆通过排浆管路泵送至地面分离设备进行筛分、旋流和压滤处理，由于排浆管路中存在大量由开挖面切削下的不规则大粒径卵石，渣浆的运输变得尤为复杂，如果浆液流速较低，不能满足卵石输送所需的最低流速，则会发生卵石大量聚集的现象，从而造成管路堵塞，严重或可导致盾构机停机[5-6]。因此，必须足够重视卵石在排浆管路中的起动特性，即关注卵石在管路中的起动速度。影响卵石起动速度的因素主要包含卵石形状、粒径、管径、管路倾角和浆液密度、黏度等，因此，为了明确渣石在排浆管路中的起动特性，拓宽管道输送理论并为现场管路铺设提供参考，对上述关键影响因素下的渣石起动特性进行探究尤为重要。
目前，许多学者针对管道输送固体颗粒问题进行了研究，主要研究方向包含3种：①理论公式；②试验研究；③数值仿真。首先，在理论公式方面，国外学者Durand[7]、Wasp[8]、Shook[9]及Mehment等[10]提出了各自的临界流速公式，其适用范围多针对于颗粒体积分数低于0.30，颗粒粒径小于10 mm的情况；国内学者费祥俊[11]和刘德忠[12]根据大量试验数据，亦分别给出了临界流速公式，其费祥俊公式可用于含有较大粒径的粒径，刘德忠公式则多适用于粒径≤0.05 mm的浆体以及粒径＞0.05的高浓度浆体。在试验研究方面，刘明潇等[13]通过水槽试验分析了粗、细颗粒（粒径＜10 mm）间相互作用，并指出颗粒的粗细比、粒径极差以及当量粒径等非均匀因子对颗粒推移影响显著；周知进等[14]采用理论分析与试验研究的方法，针对垂直远距离水力输送条件下粗颗粒的运动进行研究，得到了在相同的颗粒级配下，输送水流速度随着卵石体积分数的增大而增大；Ravelet等[15]根据试验研究发现，水平管道中颗粒粒径与密度对颗粒的运动形态密切相关。在数值仿真方面，陶贺等[16]基于数值模拟的方法，通过DEM探究了椭球形颗粒在移动床中的运动规律，并指出在颗粒流动过程中，滑动摩擦系数对颗粒流型影响较大；Akhshik等[17]使用计算流体动力学与离散单元法（CFD-DEM）耦合的方法，研究粒子形状对钻井中运输机制的影响，并指出粒子形状在流体-固体相互作用中起着非常重要的作用。
综上所述，目前对于管道中渣石起动特性的研究多集中于理论计算公式，且公式局限于粒径小于10 mm的颗粒；即使采用试验研究的，其试验装置也多针对于水平管路且载液多采用牛顿非黏性流体；因此，当前研究存在明显不足。本文自主设计了包含水平、倾斜和竖直管路的环流试验装置，并以20~100 mm的异形和球形卵石为研究对象，试验载液选择CMC黏性溶液，并结合CFD-DEM耦合仿真技术，对多种关键影响因素（渣石形状、粒径、管径、管路倾角、弯头等）下的泥水盾构排浆管路的渣石起动特性进行探究，以丰富泥水盾构环流管道输送技术与理论，并为未来类似工程提供合理参考与借鉴。
1. 试验方法
1.1 试验材料
泥水盾构的泥浆一般由两部分组成：一部分是泥浆制备的原料，如黏土和膨润土；另一部分是添加剂和水[18]。羧甲基纤维素钠（CMC）一般作为泥浆添加剂，可提高泥浆黏度。泥水盾构的泥浆应具有高稳定性、合适的密度、黏度和良好的流动性，一般情况下，环流管道中的泥浆密度范围为1.05~1.30 g/cm3，浆液的黏度范围为20~35 s（苏氏漏斗测量）[19]，为了更好地模拟泥浆，试验中浆液采用“CMC+工业盐+水”进行配置，经不断测试，当CMC质量分数为1%时，溶液透明度较好，可以清楚地观测卵石运动，并在此基础上，向溶液中添加工业盐，调节溶液密度为1.15 g/cm3，并经苏氏漏斗测量，浆液黏度为22.05 s。表 1为试验浆液和泥浆的参数对比。
表 1 试验浆液与泥浆参数对比Table 1. Physical and mechanical parameters of soils材料 浆液黏度/s 浆液密度/(g·cm-3) CMC溶液 22.05 1.15 泥浆 20~35 1.05~1.3 由表 1可知，采用“CMC+工业盐+水”配置的浆液代替实际泥浆进行试验具有合理性和可靠性。
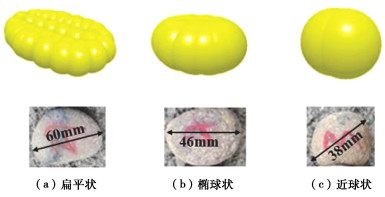
北京市南水北调配套工程团城湖至第九水厂（二期）工程起始段的地层富含砂卵石，对来自泥水分离厂的卵石进行随机取样，卵石的密度区间为2000~2900 kg/m3，且卵石多为不规则异形卵石，包含扁平状、椭球状和近球状。本文依据现场渣石实际情况，将卵石分为3类，即0~25 mm为小粒径卵石，25~50 mm为中等粒径卵石，50~100 mm为大粒径卵石。
从卵石本身特性角度出发，不同形状和粒径的卵石在管道中具有不同的起动速度，因此，本文采用形状系数、扁平度和饱满度描述卵石的形状，采用等容粒径描述卵石的粒径，以研究不同形状和粒径的卵石在管道中起动特性。卵石的形状系数、扁平度、饱满度和等容粒径分别为
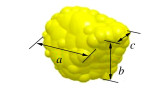
Sf=c√ab， (1) σ=a+b2c， (2) Π=(M1M0)13=(V1V0)13=D1D0， (3) DV=(6VS/π )1/3。 (4) 式中：Sf为卵石的形状系数；σ为卵石的扁平度，a，b，c分别为图 1所示的3个轴向上的长度，a为最长轴长度，c为最短轴长度。当Sf小于0.4时，卵石扁平；当Sf介于0.4~0.8时，卵石为椭球形；当Sf大于0.8时，卵石为近球形。Π为卵石的饱满度，M1为卵石实际质量，M0为标准椭球体质量，V0为标准椭球体卵石质量，D0为标准椭球体卵石等容粒径，当0.9≤Π≤1.1时，卵石为标准椭球体，当Π＜0.9时，卵石为近似椭球体，当Π＞1.1时，卵石为条形；DV是卵石的实测等容粒径，VS为卵石的真实体积。图 2（a）和表 2给出了不同形状卵石的实物图和几何参数。图 2（b）和表 3显示了不同等容粒径异形卵石的实物图和几何参数。图 2（c）和表 4给出了不同粒径球形卵石的实物图和几何参数。
表 2 不同形状卵石几何参数表Table 2. Geometric parameters of pebbles with different shapes标号 密度/
(g·cm-3)形状系数 扁平度 饱满度 等容粒径/
mm29 2.116 0.256 3.958 1.21 36.28 33 2.296 0.351 3.000 1.07 37 2.224 0.471 2.150 1.10 4 2.180 0.548 1.841 1.10 7 2.184 0.635 1.600 1.07 9 2.040 0.728 1.375 1.05 6 2.228 0.803 1.276 1.08 3 2.064 0.904 1.109 1.06 表 3 不同等容粒径卵石几何参数表Table 3. Table of geometric parameters of pebbles with different isometric sizes标号 密度/
(g·cm-3)等容粒径/mm 扁平度 饱满度 形状系数 31 2.893 30.59 2.129~2.222 0.97~1.10 0.470~0.474 36 2.790 38.55 27 2.612 41.71 16 2.664 51.18 18 2.767 59.53 24 2.707 62.85 21 2.786 64.42 表 4 不同球形卵石几何参数表Table 4. Geometric parameters of pebbles with different shapes标号 密度/(g·cm-3) 粒径/mm 右1 2.400 25 右2 2.440 30 右3 2.390 40 右4 2.450 50 右5 2..410 60 右6 2.400 70 右7 2.390 80 1.2 试验装置
采用自主设计的环流试验装置来研究卵石在管道中的起动特性，试验共分为两次进行，由于第一次试验为非完全闭环管道环路，在第一次试验过程是通过消防软管与泥浆泵进行浆液循环。因此，在第二次试验中，对试验装置进行了优化，采用管路闭环的结构，提高试验效率。两次试验装置采用的管径不同，分别为150，100 mm，如图 3，4所示，装置管道采用亚克力管，以便观察卵石的起动状态，水平管道和倾斜（竖直）管道之间采用PVC弯头进行平滑连接，弯头角度根据试验工况（管路倾角为15°，30°，45°，60°和90°）进行更换；CMC浆液由图 3中的1-浆液箱提供，其几何尺寸为1.0 m×1.0 m×0.5 m，为使得CMC在浆液箱中均匀溶解，采用高速搅拌器（图 3中的2）进行搅拌，该搅拌器可提供860 rpm的最大速度；CMC浆液通过动力泵（图 3中的5）流入环流系统，泵的转速由变频器（图 3中的13）控制，其调频范围为0~50 Hz，进而可改变管道内的浆液流速；使用电磁流量计（图 3中的6）测量管内流量，可换算为浆液流速；系统内蝶阀（图 3中的4）、泵与电磁流量计之间采用标准法兰盘连接，并在设备与法兰盘之间用橡胶密封垫连接，保证装置的气密性良好。试验前，使管道中充满浆液，关闭蝶阀，以防止浆液回流，通过投料口将卵石置入管道中，然后关闭投料口球阀，进而进行卵石起动速度的测定。
2. CFD-DEM耦合建模
由泥水盾构机和破碎机破碎的卵石随泥浆进入排浆管道，最后由多级泥浆泵泵送至隧道外。由于浆液和卵石之间的相互作用，流动过程极其复杂，而且浆液和卵石被认为是一种流固两相介质。在本研究中，基于多相流理论，采用CFD-DEM耦合方法，并使用建模软件FLUENT和EDEM建立了三维流体-颗粒两相模型。在两相模型中，浆液和卵石分别被视为流体相和颗粒相。
2.1 理论基础
（1）CFD流体相模型
浆液为均匀的流体相，因此，浆液流动过程中遵循质量守恒定律和动量守恒定律，不考虑浆液和石渣之间的热传递，故不考虑能量守恒方程。
连续性方程：
∂αfρf∂t+∇(αfρfUf)=0。 (5) 动量方程（Navier-Stokes方程）：
∂∂t(αfρfUf)+∇(αfρfUfUf)=−∇αfτ+αfρfg+Fpf。 (6) 式中：ρf为液体密度；t为时间；αf为流体相体积分数；Uf为速度矢量；pf为颗粒体积力；Fpf为通过的所有颗粒施加在流体上的力；τ为浆液黏性力。
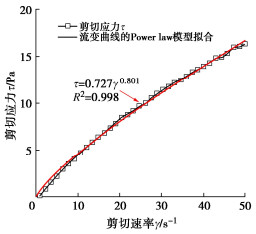
图 5为CMC浆液的流变测试结果。本研究在流变测试中加入了180 s预剪切，加载模式包含180 s的预剪切和60 s的下降剪切，转子为CCT-40同轴转子。由图 5可知，CMC浆液流变曲线符合幂律模型，浆液的稠度系数为0.727 Pa.sn，幂律指数为0.801。
由于管道直径较大，石块不规则，因此，排浆管中的泥浆为典型的湍流，研究表明，Standard-ω更适应于近壁面流动，适用于绕流运动；因此在卵石起动速度模拟分析时，流体流动模型采用Standard-ω湍流模型。
（2）DEM颗粒相模型
液体中不规则的卵石被视为颗粒相，卵石的运动和碰撞可以通过牛顿第二定律，并使用离散元方法解决。在任何时间t，每个粒子的控制方程可以描述如下：
midUp,idt=mig+n∑j=1(Fc,ij+Fd,ij)+(Fc,iω+Fd,iω)+Ff,i ， (7) Iidωidt=n∑j=1Tij+Tiω。 (8) 式中：mi，Up,i，Ii和ωi分别为渣石i的质量、速度、惯性运动和角速度；Fc,ij，Fd,ij和Tij分别为渣石i和其他渣石间的渣石接触力、黏性阻尼力和扭矩；Fc,iω，Fd,iω和Tiω分别为渣石i与排浆管路内壁面之间的接触力、黏性阻尼力和扭矩；Ff,i为流体相作用在渣石i上的力，此外，本研究利用Hertz-Mindlin无滑移接触模型来描述颗粒与管壁之间的接触，并在Yang等[20]的基础上逐步放小接触摩擦系数，并通过模型试验进行标定验证来确定了一组合适的接触参数。
（3）耦合作用力
石渣与泥浆之间的作用力主要有浮力FB、拖曳力FD和压力梯度力Fp组成，其计算公式分别如下：
FB=−ρfρpg， (9) FD=18μeρpd2pCDRep24(Uf−Up)， (10) Fp=−1ρp∇pf。 (11) 式中：Up为渣石的速度；μe为流体的黏度；ρp为渣石的密度；dp为渣石的粒径；Rep为颗粒雷诺数；CD为阻力系数。计算公式分别如下：
Rep=ρdpμ|Uf−Up|， (12) CD=a1+a22Re+a3Re。 (13) 式中：Uf为浆液速度；Re为流体雷诺数；a1，a2，a3为雷诺数常量。
a1,a2,a3={0,24,00<Re<0.13.690,22,0.09030.1<Re<11.222,29.1667,−3.88891<Re<100.6167,46.50,−116.6710<Re<1000.3644,98.33,−2778100<Re<10000.357,148.62,−475001000<Re<50000.46,−490.546,5787005000<Re<100000.5191,−1662.5,5416700Re⩾10000。 (14) 2.2 边界条件
在FLUENT和EDEM耦合过程中，入口边界设置为速度入口，出口边界设置为压力出口，相当于默认出口连接大气压，进行包括重力效应在内的瞬态三维模拟，Z方向定义为重力方向，重力加速度设置为g=9.81 m/s2。在CFD模型中，管道采用了多面体网格，这可以提高模拟的准确性和效率，在DEM模型中，在距离入口一段距离处建立一个颗粒工厂，以生产不同尺寸和形状的颗粒，在FLUENT-EDEM耦合计算中，为了保证颗粒运动信息的动态准确性，FLUENT的时间步长需为EDEM的整数倍，比例为1∶1~100∶1。一般情况下，在EDEM中设置瑞利时间步长为20%左右，本文模拟时，FLUENT中的时间步长设置为EDEM中的100倍，数据保存间隔为0.1 s。表 5给出了其他相关仿真参数。
表 5 FLUENT和EDEM仿真参数表Table 5. Parameters of FLUENT and EDEM simulation参数 渣石 亚克力管 渣石-渣石 亚克力管-渣石 剪切模量/Pa 2.212×1010 3.16×109 — — 泊松比 0.13 0.32 — — 密度/(kg·cm-3) 2000~2800 1190 — — 恢复系数 — — 0.05 0.05 静摩擦系数 — — 0.25 0.25 滚动摩擦系数 — — 0.01 0.01 3. 结果与分析
在临界流速下颗粒运动状态方面，具有代表性的是Thomas[21]、Durand[7]及费祥俊[11]的研究，根据卵石特性，并结合上述学者对临界流速的定义，试验中对于水平管路中起动速度（临界流速）定义为卵石由静止到刚好开始进行缓慢滑动时的流速；对于倾斜及竖直管路中起动速度（临界流速）定义为卵石从管路弯头处缓慢爬升完整段管路长度的最小流速。弯头处起动速度（临界流速）卵石顺利通过弯头的最小流速。
3.1 不同管路倾角下，卵石形状对起动速度的影响
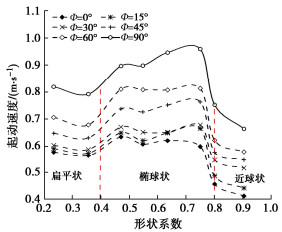
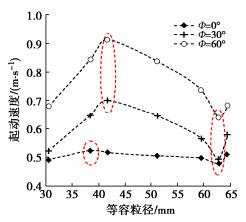
图 6为试验获得不同管路倾角下卵石起动速度随形状系数的变化曲线图。由图 6可知，在相同的卵石粒径与管路倾角下，椭球状卵石的起动速度大于扁平状卵石的起动速度，近球状卵石的起动速度最低，这是因为在水平和倾斜管路中，近球体卵石的运动基本上是滚动的，在开始前需要克服滚动摩擦阻力，与扁平卵石和椭球卵石的滑动摩擦阻力相比，近球状卵石的滚动摩擦阻力相对较低，因此，近球状卵石起动速度最小。
![]()
图 6 不同管路倾角下，卵石起动速度随形状系数变化图（模型试验结果，D=150 mm）Figure 6. Change of starting speed of pebble with shape coefficient under different pipe inclination angles在竖直管路中卵石的运动不再受到管壁摩擦力的作用，其表现为在管道中随机翻滚与飘动，对于近球状卵石，由于其形状近似球体，在卵石随机运动过程中迎流面积基本不发生变化，受力均匀，因此更容易运动；对于椭球状和扁平状卵石，其在卵石随机运动过程中迎流面积不断发生变化，扁平状卵石相对于椭球状卵石来说，其存在的最大迎流面积大于椭球状卵石存在的最大迎流面积，当某一瞬间，卵石的最大迎流截面垂直于来流方向时，扁平状卵石更容易起动；因此，在竖直管路中，出现了起动速度大小顺序为椭球状卵石＞扁平状卵石＞近球状卵石。
针对水平和倾斜管路中出现的椭球卵石的起动速度高于扁平卵石的情况，后续通过数值模拟进行说明。
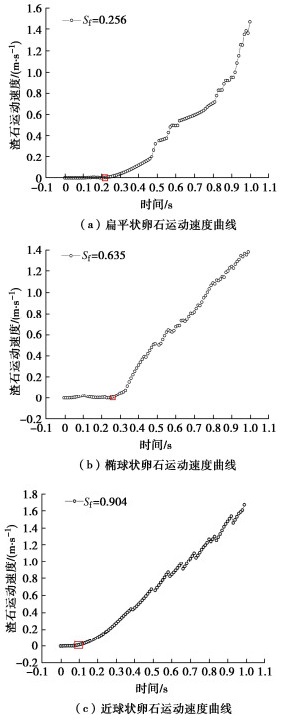
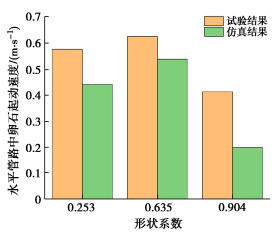
图 7为具有典型形状的扁平状卵石（Sf=0.256）、椭球状卵石（Sf=0.635）以及近球状卵石（Sf=0.904）的仿真模型图，在数值模拟中，通过编程设置了浆液流速随时间变化的函数为v=2t，将卵石运动速度随时间变化曲线中的拐点视为卵石起动时刻点，即可得到卵石的起动速度如图 8所示；仿真模拟以水平管路为例，不同形状系数卵石的起动速度仿真结果见图 9。
![]()
图 8 不同形状卵石运动速度随时间变化曲线图Figure 8. Curves of movement speed of pebble with different shapes with time![]()
图 9 不同形状卵石起动速度试验结果与数值模拟结果对比（D=150 mm）Figure 9. Comparison between test and numerical results of starting speed of pebbles with different shapes由图 8可知，扁平状卵石、椭球状卵石和近球状卵石的起动速度分别为0.440，0.540，0.200 m/s。由图 9可知，基于CFD-DEM耦合方法的模拟获得的结果与模型试验结果基本一致，误差较小，吻合良好，表明数值模型可以很好地描述卵石流动特性。
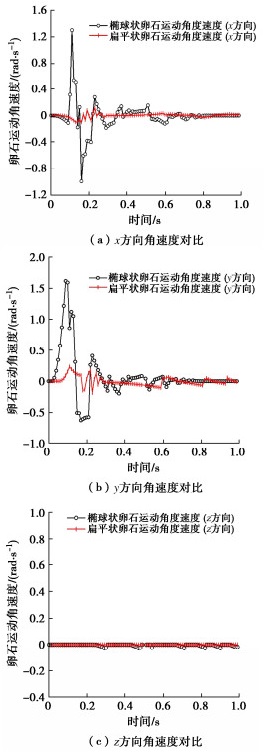
针对水平和倾斜管路中出现的椭球卵石的起动速度高于扁平卵石的情况，现通过数值模拟，分析了扁平状卵石和椭球状卵石起动前x，y，z 3个方向角速度的变化情况，如图 10所示。
![]()
图 10 扁平状与椭球状卵石运动过程中角速度变化情况Figure 10. Variation of angular velocity during movement of flat pebble and ellipsoidal pebble由图 10可知，扁平状卵石起动前在x，y，z 3个方向的角速度均较小，几乎为0，因此，扁平状卵石起动前几乎不做旋转运动，当浆液流速达到其起动速度后，沿管轴直线运动；而椭球状卵石在x，y方向均有较大的角速度，约为扁平状卵石起动前角速度的5倍，说明椭球状卵石在起动之前要做一定程度的旋转运动，需要浆液提供更大的能量才能运动起来。因此，椭球状的起动速度大于扁平状的起动速度。
3.2 不同管路倾角下卵石粒径对起动速度的影响
（1）异形卵石起动速度
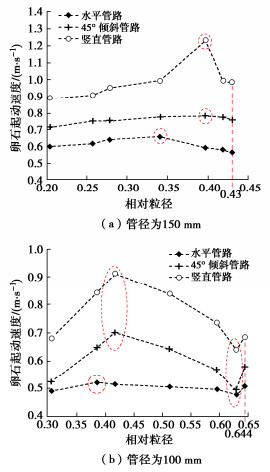
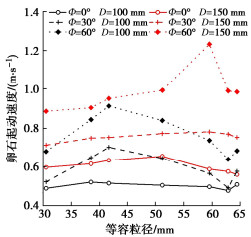
图 11为试验获得的当管路管径为150 mm时，不同管路倾角下，异形卵石起动速度随等容粒径的变化曲线图。图 12为试验获得的当管路管径为100 mm时，不同管路倾角下，同组异形卵石起动速度随等容粒径的变化曲线图。由图 11可知，当管径为150 mm时，卵石在水平、倾斜和竖直管路中均呈现起动速度随着等容粒径的增大先增大后减小的现象；当管径为100 mm时，卵石的起动速度则呈现出随着等容粒径的增大先增大后减小再增大的现象，同组卵石在两次管径下的试验结果存在差异，因此，采用无量纲分析法，本文提出“相对粒径”的概念，即卵石的等容粒径与管径的比值。
![]()
图 11 不同管路倾角下异形卵石起动速度随等容粒径变化图(D=150 mm)Figure 11. Variation of starting speed of pebble with equal volume particle size (D=150 mm)![]()
图 12 不同管路倾角下异形卵石起动速度随等容粒径变化图(D=100 mm)Figure 12. Variation of starting speed of pebble with isometric particle size (D=100 mm)图 13为两次试验管径，不同管路倾角下，卵石起动速度随相对粒径的变化曲线图。由图 13可知，同组试验卵石在100 mm管道中的相对粒径最大值为0.644，而在150 mm管道中的相对粒径最大值仅为0.430，因此并未出现起动速度转而增大的拐点，当在该组卵石的基础上继续增大卵石等容粒径时，则将会出现卵石起动速度先增大后减小再增大的现象。
![]()
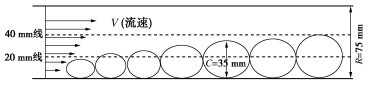
图 13 不同管路倾角下卵石起动速度随相对粒径变化图Figure 13. Variation of starting speed of pebbles with relative particle size under different inclination angles of另外，由图 11，12可知，起动流速曲线的拐点与管道的倾角有关，当管道倾角小于15°时，在管径为150 mm的管道中，曲线存在下降的拐点处对应的渣石的相对粒径为0.34；在管径为100 mm的管道中，曲线存在两个拐点，分别为起动速度开始出现下降和增大的点，拐点处的相对粒径分别为0.39，0.64。当管道倾角大于15度时，在管径为150 mm的管道中，曲线存在下降的拐点处对应的渣石的相对粒径为0.40，在管径为100 mm的管道中，曲线存在两个拐点，起动速度开始出现下降和增大的拐点处的相对粒径分别为0.42，0.63。因此，可以得到，当管道倾角小于15°时，起动速度开始出现下降的拐点处卵石的相对粒径约为0.34；当管道倾角大于15°时，起动速度开始出现下降的拐点处卵石的相对粒径约为0.40；当卵石的相对粒径约大于0.64时，起动速度转而又出现增大。出现拐点的原因是因为：当卵石的等容粒径增加时，卵石质量随之增加，需要更多的能量来克服其自身的重力和与管壁的摩擦，因此起动速度逐渐增加；然而，当卵石的等容粒径增加到某一点（拐点）时，卵石更接近管道中心，因此，由于浆液流体的横截面速度分布从管道中心到管道壁逐渐减小，作用在卵石上的流体的平均动量更大，如图 14所示，因此，起动速度开始减小；后期，随着卵石粒径进一步增大，虽然越来越靠近管道中心，但质量增大明显，需要更大的动力才能起动，此时，影响卵石起动的主要因素为卵石质量。值得注意的是，卵石临界起动速度的拐点与管道内的速度分布有关。
![]()
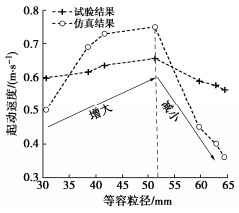
图 14 基于不同等容粒径的水平管路卵石受力Figure 14. Stresses on pebbles of horizontal pipeline based on different isometric particle sizes图 15为不同粒径卵石起动速度试验结果与仿真结果的对比。由图 15可知，同形状系数，不同等容粒径卵石的起动速度试验结果与数值仿真模拟结果变化规律是一致的，也说明了数值仿真方法的有效性。
![]()
图 15 不同粒径卵石起动速度试验结果与数值模拟结果对比（D=150 mm）Figure 15. Comparison between test and numerical results of starting speed of pebbles with different particle sizes (D=150 mm)（2）球形卵石起动速度
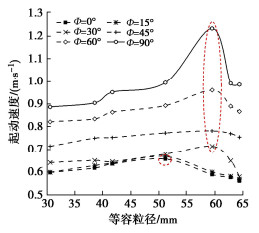
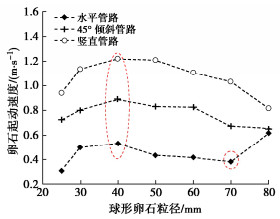
图 16为不同管路倾角下，球形卵石起动速度随粒径的变化曲线图。由图 16可知，随着球形卵石粒径的增大，在水平管路中起动速度呈现先增大后减小再增大的趋势，临界起动速度曲线拐点分别出现在卵石粒径40 mm（相对粒径为0.4）和70 mm（相对粒径为0.70）处；在倾斜和竖直管路中起动速度呈现先增大后减小的趋势，临界速度曲线拐点出现在40 mm（相对粒径为0.40）处。
![]()
图 16 不同管路倾角下球形卵石起动速度随粒径变化图Figure 16. Variation of starting speed of spherical pebbles with particle size under different inclination angles of pipes3.3 管径对卵石起动速度的影响
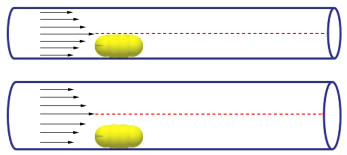
试验时考虑了管径对卵石起动速度的影响，图 17为管径100，150 mm下，卵石在水平、倾斜及竖直管道中的起动速度情况对比。
![]()
图 17 不同管径下卵石起动速度随等容粒径变化图Figure 17. Variation of pebble starting speed with isometric particle size under different pipe diameters (vertical pipeline)由图 17可知，随着管径的增大卵石的起动速度增大，这是与圆管横截面流速分布息息相关的，假设管径不同的两个圆管内的浆液流速是相同的，对于同一块卵石，其受力如图 18所示。由图 18可知，当管径不同的两个圆管内的浆液流速相同时，同一卵石在管径大的圆管内迎流面上的流速分布相对较小，即卵石受到的向前运动的平均动量较小。同时，管径增大，使得横截面速度差减小，卵石受到的近壁面升力减小，即从管道底部悬浮起来的难度也将更大，因此，对于管径较大的圆管，流体需要进一步增加流速才能使卵石运动起来。
![]()
图 18 同一卵石在同一流速不同管径管路中迎流面受力情况示意图Figure 18. Stresses on upstream face of same pebble in pipelines with same flow velocity and different pipe diameters3.4 管道弯头对卵石起动速度的影响
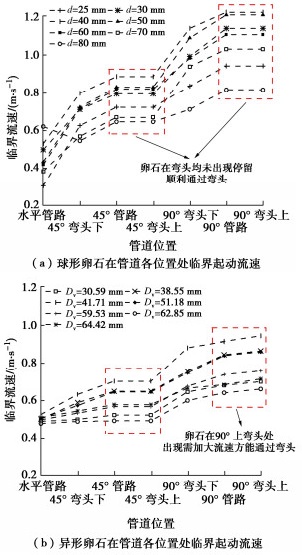
管道弯头作为管路的连接处，由于其位置的特殊性，弯头连接处卵石的受力也存在着特殊性，对卵石的运动亦有着显著的影响，因此，在第二次环流试验过程中，分别针对球形卵石（图 2（c））和异形卵石（图 2（b）），对其在弯头（W1、W2、W3和W4）处以及水平、倾斜以及竖直管路中的起动速度进行了测定。图 19（a）为球形卵石在环流管道各位置处的起动流速变化曲线图，图 19（b）为异形卵石在管道各位置处的起动流速变化曲线图。
![]()
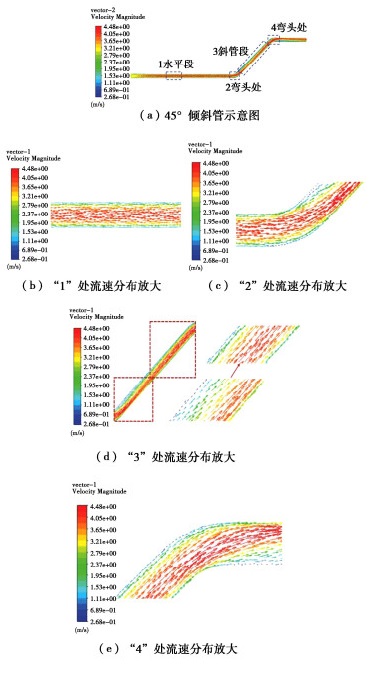
图 19 球形和异形卵石在管道各位置处临界起动流速Figure 19. Critical starting velocities of spherical and irregular pebbles at each position of pipeline由图 19可知，对于异形卵石各部位起动速度有如下关系：W4＞竖直管路＞W3＞W2=45°倾斜管路＞W1＞水平管路；对于球形卵石各部位起动速度有如下关系：W4=竖直管路＞W3＞W2=45°倾斜管路＞W1＞水平管路。为说明发生以上现象的原因，利用FLUENT软件，对水平管路、45°管路、60°管路及竖直管路的横截面流速分布进行了探究，浆液流速设置为3 m/s，管径为150 mm。
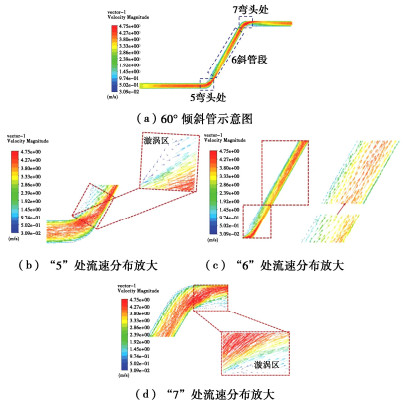
图 20为湍流状态下浆液在水平、45°倾斜管特殊部位流速分布图，图 21为湍流状态下浆液在水平、60°倾斜管特殊部位流速分布图。
![]()
图 20 湍流状态下浆液在水平、45°倾斜管特殊部位流速分布图Figure 20. Distribution of flow velocity of slurry at special parts of horizontal and inclined pipes under turbulent state![]()
图 21 湍流状态下浆液在水平、60°倾斜管特殊部位流速分布图Figure 21. Distribution of flow velocity of slurry at special parts of horizontal and 60°inclined pipes under turbulent state由图 20，21可知：①浆液在圆管中以湍流方式运动时，水平管、倾斜管与竖直管中横截面流速分布整体均呈现由中间向两侧逐渐降低的规律。②浆液在管路连接处（弯头）处会出现流速重分布的现象，横截面流速分布呈现凸面流速大、凹面流速小的规律，且在靠近下弯头处的倾斜管路部分，浆液平均流速降低。③当管路倾角≥60°时，在弯头附近处开始出现漩涡区，漩涡区流速与主流区流速相反，对于渣石运动起阻碍作用，且随着管路倾角的增大，阻碍作用越强。
4. 结论
本文通过模型试验与CFD-DEM方法，探究了渣石形状、粒径、管径、管路倾角、弯头等对泥水盾构排浆管路的渣石起动特性的影响规律，主要得到以下4点结论。
（1）在管路倾角和渣石等容粒径相同的情况下，不同形状渣石的起动速度大小顺序为椭球体＞扁平状＞近球体。
（2）针对不同粒径渣石，通过提出的“相对粒径”的概念，得出：①对于球形卵石，在水平管路中，卵石的起动速度随粒径的增大先增大后减小再增大，当卵石的相对粒径大于0.40时，卵石的起动速度开始下降，当卵石的相对粒径大于0.70时，卵石的起动速度再次增大；在倾斜和竖直管路中，卵石的起动速度随粒径的增大而减小，当卵石的相对粒径为0.40时，卵石起动速度开始下降。②对于异形卵石，对于同一形状系数卵石，在任意管径管道中，均呈现随着等容粒径的增大先增大后减小再增大的规律；临界流速曲线的拐点与管道的倾角有关，当管道倾角小于15°时，临界流速开始出现下降时拐点处卵石的相对粒径约为0.34；当管道倾角大于15°时，临界流速开始出现下降时拐点处卵石的相对粒径约为0.40；当卵石的相对粒径约大于0.64时，临界流速会呈现再次增大。
（3）同一卵石的临界起动速度随着管道管径的增大而增大。
（4）在环流管道中，卵石的起动速度随着管路倾角的增大而增大，且起动速度较大的位置主要出现在较大角度弯头（≥60°）位置处，因此在铺设管路时，应尽量减少倾斜及竖直管路的铺设，多采用水平管路或倾斜角度较小（≤45°）管路。
-
![]()
图 6 不同管路倾角下，卵石起动速度随形状系数变化图（模型试验结果，D=150 mm）
Figure 6. Change of starting speed of pebble with shape coefficient under different pipe inclination angles
![]()
图 8 不同形状卵石运动速度随时间变化曲线图
Figure 8. Curves of movement speed of pebble with different shapes with time
![]()
图 9 不同形状卵石起动速度试验结果与数值模拟结果对比（D=150 mm）
Figure 9. Comparison between test and numerical results of starting speed of pebbles with different shapes
![]()
图 10 扁平状与椭球状卵石运动过程中角速度变化情况
Figure 10. Variation of angular velocity during movement of flat pebble and ellipsoidal pebble
![]()
图 11 不同管路倾角下异形卵石起动速度随等容粒径变化图(D=150 mm)
Figure 11. Variation of starting speed of pebble with equal volume particle size (D=150 mm)
![]()
图 12 不同管路倾角下异形卵石起动速度随等容粒径变化图(D=100 mm)
Figure 12. Variation of starting speed of pebble with isometric particle size (D=100 mm)
![]()
图 13 不同管路倾角下卵石起动速度随相对粒径变化图
Figure 13. Variation of starting speed of pebbles with relative particle size under different inclination angles of
![]()
图 14 基于不同等容粒径的水平管路卵石受力
Figure 14. Stresses on pebbles of horizontal pipeline based on different isometric particle sizes
![]()
图 15 不同粒径卵石起动速度试验结果与数值模拟结果对比（D=150 mm）
Figure 15. Comparison between test and numerical results of starting speed of pebbles with different particle sizes (D=150 mm)
![]()
图 16 不同管路倾角下球形卵石起动速度随粒径变化图
Figure 16. Variation of starting speed of spherical pebbles with particle size under different inclination angles of pipes
![]()
图 17 不同管径下卵石起动速度随等容粒径变化图
Figure 17. Variation of pebble starting speed with isometric particle size under different pipe diameters (vertical pipeline)
![]()
图 18 同一卵石在同一流速不同管径管路中迎流面受力情况示意图
Figure 18. Stresses on upstream face of same pebble in pipelines with same flow velocity and different pipe diameters
![]()
图 19 球形和异形卵石在管道各位置处临界起动流速
Figure 19. Critical starting velocities of spherical and irregular pebbles at each position of pipeline
![]()
图 20 湍流状态下浆液在水平、45°倾斜管特殊部位流速分布图
Figure 20. Distribution of flow velocity of slurry at special parts of horizontal and inclined pipes under turbulent state
![]()
图 21 湍流状态下浆液在水平、60°倾斜管特殊部位流速分布图
Figure 21. Distribution of flow velocity of slurry at special parts of horizontal and 60°inclined pipes under turbulent state
表 1 试验浆液与泥浆参数对比
Table 1 Physical and mechanical parameters of soils
材料 浆液黏度/s 浆液密度/(g·cm-3) CMC溶液 22.05 1.15 泥浆 20~35 1.05~1.3 
下载: 导出CSV
表 2 不同形状卵石几何参数表
Table 2 Geometric parameters of pebbles with different shapes
标号 密度/
(g·cm-3)形状系数 扁平度 饱满度 等容粒径/
mm29 2.116 0.256 3.958 1.21 36.28 33 2.296 0.351 3.000 1.07 37 2.224 0.471 2.150 1.10 4 2.180 0.548 1.841 1.10 7 2.184 0.635 1.600 1.07 9 2.040 0.728 1.375 1.05 6 2.228 0.803 1.276 1.08 3 2.064 0.904 1.109 1.06
下载: 导出CSV
表 3 不同等容粒径卵石几何参数表
Table 3 Table of geometric parameters of pebbles with different isometric sizes
标号 密度/
(g·cm-3)等容粒径/mm 扁平度 饱满度 形状系数 31 2.893 30.59 2.129~2.222 0.97~1.10 0.470~0.474 36 2.790 38.55 27 2.612 41.71 16 2.664 51.18 18 2.767 59.53 24 2.707 62.85 21 2.786 64.42
下载: 导出CSV
表 4 不同球形卵石几何参数表
Table 4 Geometric parameters of pebbles with different shapes
标号 密度/(g·cm-3) 粒径/mm 右1 2.400 25 右2 2.440 30 右3 2.390 40 右4 2.450 50 右5 2..410 60 右6 2.400 70 右7 2.390 80
下载: 导出CSV
表 5 FLUENT和EDEM仿真参数表
Table 5 Parameters of FLUENT and EDEM simulation
参数 渣石 亚克力管 渣石-渣石 亚克力管-渣石 剪切模量/Pa 2.212×1010 3.16×109 — — 泊松比 0.13 0.32 — — 密度/(kg·cm-3) 2000~2800 1190 — — 恢复系数 — — 0.05 0.05 静摩擦系数 — — 0.25 0.25 滚动摩擦系数 — — 0.01 0.01
下载: 导出CSV
-
[1] 徐涛, 史庆锋, 章定文, 等. 泥水盾构开挖面泥膜渗透特性与压力传递机制[J]. 岩土工程学报, 2023, 45(9): 1878-1887. doi: 10.11779/CJGE20220866 XU Tao, SHI Qingfeng, ZHANG Dingwen, et al. Permeability characteristics of filter cake and pressure transfer on face during slurry shield tunnelling[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(9): 1878-1887. (in Chinese) doi: 10.11779/CJGE20220866
[2] 干聪豫, 方应冉, 刘泓志, 等. 复杂多变地层泥水盾构排浆管路振动特性分析[J]. 噪声与振动控制, 2023, 43(1): 275-280. doi: 10.3969/j.issn.1006-1355.2023.01.046 GAN Congyu, FANG Yingran, LIU Hongzhi, et al. Analysis of vibration characteristics of slurry discharge pipelines of a slurry shield in complex and changeable stratums[J]. Noise and Vibration Control, 2023, 43(1): 275-280. (in Chinese) doi: 10.3969/j.issn.1006-1355.2023.01.046
[3] 李承辉, 贺少辉, 刘夏冰. 粗粒径砂卵石地层中泥水平衡盾构下穿黄河掘进参数控制研究[J]. 土木工程学报, 2017, 50(增刊2): 147-152. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2017S2023.htm LI Chenghui, HE Shaohui, LIU Xiabing. Study on main parameters control of tunneling through the yellow river by a slurry balance shield in sandy gravel stratum with some large-size grains[J]. China Civil Engineering Journal, 2017, 50(S2): 147-152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2017S2023.htm
[4] 王振飞, 张成平. 泥水盾构开挖面失稳破坏的颗粒流模拟研究[J]. 中国铁道科学, 2017, 38(3): 55-62. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201703009.htm WANG Zhenfei, ZHANG Chengping. Research on particle flow simulation for excavation face instability of slurry shield[J]. China Railway Science, 2017, 38(3): 55-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201703009.htm
[5] 霍滨, 徐朝辉, 胡相龙, 等. 砂卵石地层泥水盾构施工技术难点及控制措施分析: 以兰州地铁穿黄隧道工程为例[J]. 隧道建设, 2018, 38(5): 846-850. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201805023.htm HUO Bin, XU Zhaohui, HU Xianglong, et al. Analysis of technical difficulties and control measures for slurry shield boring in sandy cobble strata: a case study of Yellow River-corssing tunnel of Lanzhou metro[J]. Tunnel Construction, 2018, 38(5): 846-850. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201805023.htm
[6] 黄波, 李晓龙, 陈长江. 大直径泥水盾构复杂地层长距离掘进过程中的泥浆管路磨损研究[J]. 隧道建设, 2016, 36(4): 490-496. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201604020.htm HUANG Bo, LI Xiaolong, CHEN Changjiang. Study of abrasion of slurry pipe of large-diameter slurry shield boring in complex strata[J]. Tunnel Construction, 2016, 36(4): 490-496. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201604020.htm
[7] DURAND R. The hydraulic transportation of coal and solid mate-rials in pipes[C]// Colloq of National Coal Board, London, 1952: 39-52.
[8] WASP E J, KENNY J P, GANDHI R L. Solid-Liquid Flow Slurry Pipeline Transportation[M]. Clausthal Ger: Trans Tech Publications, 1977.
[9] SHOOK C A. Pipelining solids: the design of short distance pipelines[C]// Proc Symp on Pipeline Transport of Solids, Toronto: Cana Soc Chem Engin, 1969.
[10] MEHMET A K, MUSTAFA G. Critical flow velocity in slurry transporting horizontal pipelines[J]. Canadian Metallurgical Quarterly, 2001, 127(9): 763-771.
[11] 费祥俊. 浆体的物理特性与管道输送流速[J]. 管道技术与设备, 2000(1): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-GDGS200001000.htm FEI Xiangjun. The physical property of slurry and its velocity of pipeline transportation[J]. Pipeline Technique and Equipment, 2000(1): 1-4. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDGS200001000.htm
[12] 刘德忠. 矿浆管道水力输送的试验研究[J]. 泥沙研究, 1983(4): 85-88. https://www.cnki.com.cn/Article/CJFDTOTAL-NSYJ198304009.htm LIU Dezhong. Experimental study on hydraulic transportation of slurry pipeline[J]. Journal of Sediment Research, 1983(4): 85-88. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NSYJ198304009.htm
[13] 刘明潇, 孙东坡, 王鹏涛, 等. 双峰型非均匀沙粗细颗粒相互作用对推移质输移的影响[J]. 水利学报, 2015, 46(7): 819-827. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201507009.htm LIU Mingxiao, SUN Dongpo, WANG Pengtao, et al. Interactions between the coarse and fine particles and their influences on the bimodalnon-uniformbed load transport[J]. Journal of Hydraulic Engineering, 2015, 46(7): 819-827. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201507009.htm
[14] 周知进, 刘爱军, 夏毅敏, 等. 颗粒组分特性对扬矿硬管输送速度的影响[J]. 中南大学学报(自然科学版), 2011, 42(9): 2692-2697. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201109027.htm ZHOU Zhijin, LIU Aijun, XIA Yimin, et al. Influence of particles component properties on transporting speed in lifting pipeline[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2692-2697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201109027.htm
[15] RAVELET F, BAKIR F, KHELLADI S, et al. Experimental study of hydraulic transport of large particles in horizontal pipes[J]. Experimental Thermal and Fluid Science, 2013, 45: 187-197.
[16] 陶贺, 金保昇, 钟文琪. 不同物性对椭球形颗粒在移动床中流动特性影响的模拟研究[J]. 中国电机工程学报, 2011, 31(5): 68-75. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201105013.htm TAO He, JIN Baosheng, ZHONG Wenqi. Effect of particle properties on the flow behaviors of ellipsoidal particles in the moving bed[J]. Proceedings of the CSEE, 2011, 31(5): 68-75. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201105013.htm
[17] AKHSHIK S, BEHZAD M, RAJABI M. CFD-DEM simulation of the hole cleaning process in a deviated well drilling: The effects of particle shape[J]. Particuology, 2016, 25: 72-82.
[18] 金大龙, 袁大军, 郑浩田, 等. 高水压条件下泥水盾构开挖面稳定离心模型试验研究[J]. 岩土工程学报, 2019, 41(9): 1653-1660. doi: 10.11779/CJGE201909009 JIN Dalong, YUAN Dajun, ZHENG Haotian, et al. Centrifugal model tests on face stability of slurry shield tunnels under high water pressures[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1653-1660. (in Chinese) doi: 10.11779/CJGE201909009
[19] 刘方. 砂卵石地层泥水平衡盾构泥浆性能及掘进面稳定性研究[D]. 重庆: 重庆交通大学, 2019. LIU Fang. Study on the Slurry Performance and Face Stability of SPB Shield Tunnel in Cobble-rich Soil[D]. Chongqing: Chongqing Jiaotong University, 2019. (in Chinese)
[20] YANG D, XIA Y M, WU D, et al. Numerical investigation of pipeline transport characteristics of slurry shield under gravel stratum[J]. Tunnelling and Underground Space Technology, 2018, 71: 223-230.
[21] THOMAS D G. Transport characteristics of suspensions: part Ⅵ, minimum transport velocity for large Particle size uspensions in round horizontal pipes[J]. American Institute of Chemical Engineers Journal, 1962, 8(3): 373-378.
-
期刊类型引用(1)
1. 陈爱玲，王越，李瑞石，任振，王又增. 泥水环流系统排渣状态模糊评估技术研究. 建筑机械化. 2025(04): 51-54 . 
百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 362
- HTML全文浏览量: 54
- PDF下载量: 52
- 被引次数: 1
