基于IDA方法的综合管廊纵向地震易损性分析研究

李锦强; 钟紫蓝; 申家旭; 张卜; 张亚波; 杜修力

doi:10.11779/CJGE20230397

基于IDA方法的综合管廊纵向地震易损性分析研究 English Version

北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124

基金项目:

国家自然科学基金面上项目 52378470

国家自然科学基金面上项目 51978020

中国博士后科学基金项目 2021M700311

国家重点研发计划项目 2022YFC3003603

详细信息

作者简介:
李锦强（1995—)，男，博士研究生，主要从事地下结构抗震方面的研究工作。E-mail: lijinqiangs@163.com

通讯作者:
钟紫蓝, zilanzhong@bjut.edu.cn

中图分类号: TU435;TU990.3
计量
- 文章访问数: 350
- HTML全文浏览量: 69
- PDF下载量: 72
出版历程
- 收稿日期: 2023-05-07
- 网络出版日期: 2023-12-19
- 刊出日期: 2024-07-31

Longitudinal seismic fragility analysis of utility tunnel structures based on IDA method

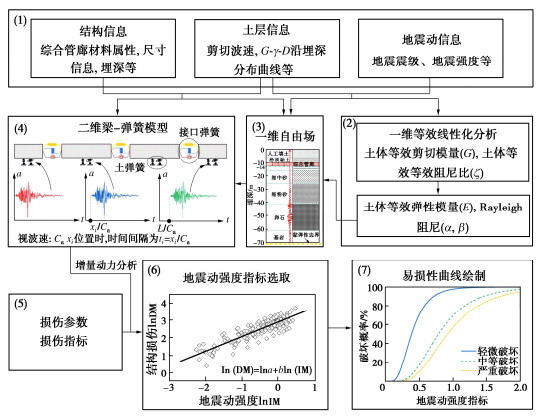
Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China

摘要

摘要: 为了提出一种基于非线性增量动力分析（incremental dynamic analysis, IDA）的长线型综合管廊纵向地震性能评价的易损性分析方法，以单舱综合管廊为研究对象建立了简化梁-弹簧模型，合理地考虑了管廊接口的力学性能和管廊-土相互作用，将筛选的17组地震动统一调幅至不同强度水平后作为输入开展一维自由场分析以获取管廊底板位置处的地震动时程，最后开展了考虑地震动行波效应的综合管廊地震响应分析。基于IDA分析结果对地震动强度指标进行优选，最终建立了以管廊底板位置处峰值速度和地表峰值速度为地震动强度指标，以管廊接口张开量为损伤指标的易损性曲线，得到了不同地震烈度水平下综合管廊的失效概率。给出的典型Ⅱ类场地中管廊地震易损性曲线和失效概率可以作为评价该类地下结构抗震性能的有效工具，为长线型综合管廊在不同地震动强度下的损伤预测提供可靠依据。
- 综合管廊 /
- 梁-弹簧模型 /
- 增量动力分析 /
- 易损性分析 /
- 失效概率
Abstract: This study aims to propose a fragility analysis method for evaluating the longitudinal seismic performance of long-line utility tunnels based on nonlinear incremental dynamic analysis (IDA). To this end, a simplified beam-spring model is established, to reasonably consider the mechanical properties of the joint and the soil-tunnel interaction. A series of 17 sets of ground motion records are selected and uniformly scaled to different intensity levels as the input of one-dimension free filed analyses to obtain the ground motions at the bottom slab of a utility tunnel. Finally, the seismic analysis of the utility tunnel considering wave passage effects is conducted. Based on the IDA results, the optimal intensity measure is selected. With the damage measure of the peak joint opening, the fragility curves of the utility tunnel are established using the peak velocity at the bottom slab of the tunnel and the peak velocity at the ground surface as the intensity measures, respectively. The failure probability of the utility tunnel under different earthquake intensity levels is also obtained. The proposed fragility curves and failure probability of the utility tunnel in typical site Ⅱ can provide an effective tool to estimate the seismic performance of this type of underground structures and a reliable basis for predicting damage under different earthquake intensity levels.
- utility tunnel /
- beam-spring model /
- incremental dynamic analysis /
- fragility analysis /
- failure probability

HTML全文

0. 引言

岩石作为天然地质材料，含有大量多尺度且随机分布的初始空隙，在荷载作用下产生的力学响应极为复杂^[1]。三轴压缩试验已表明，荷载作用初期，初始空隙的闭合将引起初始宏观非线性变形和弹性模量的变化，随着荷载持续作用，脆性岩石将表现出屈服硬化、应变软化和残余强度变形特征。由于脆性岩石强度破坏过程无明显征兆，产生的破坏后果严重，因此，建立能够较准确地预测其全应力–应变过程的模拟方法已成为岩石力学特性研究的长期热点。

自伺服试验机得出岩石全应力–应变曲线以后，基于经典弹塑性理论建立的本构模型已不再适用于模拟岩石变形破坏全过程。近年来，基于应变等效性假设和有效应力原理，将强度统计方法和连续介质损伤理论相结合，提出了统计损伤概念^[2]，在此基础上，众多学者建立了不同表达形式的统计损伤本构模型，并对其合理性和可行性进行了广泛研究，其内容主要包括是否考虑损伤阈值^[3-4]、应力状态^[5-6]和微元体强度随机分布^[7-8]的影响，强度破坏准则^[9-10]和模型参数的确定方法^[11-12]是否合理，以及损伤模型的局限性^[13-14]等，这些问题的研究较好地完善了统计损伤本构理论，然而，该类模型在模拟围压效应和强度脆性跌落方面存在严重缺陷，使其不能够较准确地模拟脆性岩石全应力–应变曲线，这正是本文研究的核心内容。

为此，本文在探讨脆性岩石及其组成物质基本变形特征基础上，将岩石细观化为由软物质和硬物质两部分材料串联组成，提出宏细观物质变形分析模型以及软物质和硬物质的变形分析方法，建立能够考虑围压效应和强度脆性跌落的统计损伤本构模型，给出参数的确定方法，使其能够较准确地预测脆性岩石三轴压缩全应力–应变曲线，以期提高该类模型在岩石工程结构变形分析与计算方面的应用价值。

1. 脆性岩石三轴压缩基本变形特征

MTS815电液伺服岩石力学实验系统广泛使用以来，获得了大量岩石三轴压缩偏应力与轴向应变全过程试验曲线，其典型特征曲线^[15]，见图 1，具有明显阶段性变形特征和围压效应，尽管并非所有岩石都能够反映这些特征，但这不意味着岩石全应力–应变过程客观上就缺少这些特征^[16]。

图 1 大理岩三轴压缩试验曲线^[15]

Figure 1. Triaxial compression test curves of marble^[15]

下载: 全尺寸图片幻灯片

岩石基本变形特征与其围压水平密不可分，随着围压的增大，应力特征值不断增大，峰后强度脆性跌落程度不断减弱，与此同时，发生闭合的初始空隙数量不断增多，初始宏观非线性上凹程度不断降低，弹性模量逐渐增大，当所有初始空隙能够仅在围压作用下完成闭合时，初始宏观变形由非线性转为线性，弹性模量不再随围压增大而变化，而是基本保持不变，称此特征为“围压效应”。孔隙率低的岩石，围压效应微弱，可忽略之，但孔隙率高的岩石，围压效应显著，不能忽略。

岩石先进行仅围压作用，待变形稳定以后再进行恒围压增轴压作用，在此过程岩石与其各组成物质变形协调，其中，初始孔隙率较大或变形力学参数较小的部分物质能够在低应力作用下发生较大变形甚至完成变形，使岩石发生不可恢复的非线性变形，将此类基本变形特征的组成物质细观化为“软物质”；初始孔隙率较小或变形力学参数较大的部分物质在低应力作用下产生弹性微变形，当其所受应力未达到损伤阈值时仅发生弹性变形，超过损伤阈值时发生的变形部分不可恢复，将此类基本变形特征的组成物质细观化为“硬物质”。岩石基本变形特征受其内部细观结构的控制，将其视为由软物质和硬物质两部分细观化材料串联组成，因此需对岩石宏细观物质之间的变形关系进行分析。

2. 岩石宏细观物质变形分析模型

沿某主应力 ${\sigma _i}$ （i=1，2，3）作用方向取出岩石代表性柱状单元（RCU）并进行细观化处理，提出宏细观物质变形分析模型，见。假设RCU、硬物质和软物质在 ${\sigma _i}$ 加载前的长度分别为 $l_i^{}$ ， $l_i^{\text{r}}$ 和 $l_i^{\text{v}}$ ， ${\sigma _i}$ 加载后的变形量分别为 $\Delta l_i^{}$ ， $\Delta l_i^{\text{r}}$ 和 $\Delta l_i^{\text{v}}$ ，软物质初始长度占比（ $l_i^{\text{v}}$ / $l_i^{}$ ）为参数 $\gamma$ 。根据应变分析基本方法，可得

${\varepsilon _i} = (1 - \gamma )\varepsilon _i^{\text{r}} + \gamma \varepsilon _i^{\text{v}} \text{，}$

(1)

图 2 宏细观物质变形分析模型

Figure 2. Deformation analysis model for macro- and meso-materials

下载: 全尺寸图片幻灯片

式中， $\varepsilon _i^{\text{v}}$ ， $\varepsilon _i^{\text{r}}$ 为软物质和硬物质的应变。

2.1 软物质变形分析方法

由于软物质持续产生的变形源于持续增大的应力，基于瞬时应变分析方法^[17]可得软物质变形分析表达式，即

$\varepsilon _i^{\text{v}} = 1 - \exp ( - {\sigma _i}/{E_{\text{v}}}) \text{，}$

(2)

式中， ${E_{\text{v}}}$ 为软物质弹性模量。 $\varepsilon _i^{\text{v}}$ 随 ${\sigma _i}$ 的增大而增大并表现为负指数变化规律，由于 ${E_{\text{v}}}$ 数量级较小，软物质能够在低应力作用下产生较大变形甚至完成变形。

2.2 硬物质变形分析方法

硬物质变形分析与计算取决于所受应力是否达到损伤阈值，需引入损伤力学理论进行研究。

（1）已有损伤模型局限性分析

损伤模型是建立硬物质变形分析方法的关键。目前，已有损伤模型使统计损伤本构模型在模拟强度脆性跌落方面存在严重缺陷，要弄清楚该问题，有必要对模型构建基本方法进行简要梳理。基于应变等效性假设可得损伤模型的基本表达式^[2]，即

${\sigma _i} = {\sigma '_i}(1 - D) 。$

(3)

由于未损伤材料有效应力 ${\sigma '_i}$ 与变形服从广义虎克定律，于是，损伤本构模型基本表达式可为

$\{ \sigma \} = [C]\{ \varepsilon \} (1 - D) \text{，}$

(4)

式中， $\{ \sigma \}$ ， $\{ \varepsilon \}$ 为名义应力张量和名义应变张量，[C]为弹性矩阵，D为损伤变量。由于岩石属于非均质材料，微元体强度F各不相同，因此，假设F服从Weibull分布，D为F破坏的累积效应^[8]，

$D = \int_0^F {P(F){\text{d}}F} = 1 - \exp [ - {(F/{F_0})^m}] \text{，}$

(5)

式中，P(F)为概率密度函数，m，F₀为分布参数。于是，统计损伤本构模型基本表达式可为

$\{ \sigma \} = [C]\{ \varepsilon \} \exp [ - {(F/{F_0})^m}] 。$

(6)

该模型参数仅包括[C]，m和F₀。[C]为基本力学参数，它们不因模型的变化而改变，而是取决于岩石物理性质，可由岩石力学试验获得；m，F₀的确定方法主要有峰值点法^[11]、反演分析法^[12]和线性拟合法^[18]等。峰值点法物理意义明确且计算简单，得到了广泛应用，即

${\left. {{\sigma _1}({\varepsilon _1})} \right|_{{\varepsilon _1} = {\varepsilon _{1{\text{c}}}}}} = {\sigma _{1{\text{c}}}} \text{，}$

(7)

${\left. {\frac{{\partial {\sigma _1}}}{{\partial {\varepsilon _1}}}} \right|_{{\sigma _1} = {\sigma _{1{\text{c}}}},\;{\varepsilon _1} = {\varepsilon _{1{\text{c}}}}}} = 0 \text{，}$

(8)

式中， ${\sigma _{1{\text{c}}}}$ ， ${\varepsilon _{1{\text{c}}}}$ 为试验曲线峰值处最大主应力及其对应的应变。

联立式（7），（8）可得m和F₀的确定方法，然后将所求参数代入式（6）可得理论模型曲线，这就是构建统计损伤本构模型的基本方法。

由此可知，m和F₀的变化仅取决于 ${\sigma _{1{\text{c}}}}$ 和 ${\varepsilon _{1{\text{c}}}}$ ，特定围压下m和F₀具有唯一性，这就导致特定围压下理论曲线有且仅有一条。为了分析参数变化对理论曲线产生的影响，根据式（4），（5）可知强度脆性跌落仅取决于D，而D的变化仅与m和F₀有关，见图 3，4。随着F的增大，D由0递增至1，D–F曲线呈S型，其中，随着m的增大，D–F曲线形状不变并绕点A作逆时针转动，损伤变化率（∂D/∂F）和强度脆性跌落程度不断增大；随着F₀的增大，D–F曲线形状不变并向F增大方向移动，∂D/∂F和强度脆性跌落程度存在不断减小的趋势。因此，当前理论曲线峰后变化规律本质上取决于m和F₀，然而，特定围压下有且仅有一条的理论曲线无法起到模拟具有随机性的试验曲线峰后变化的作用，究其原因，峰值点法无法对理论曲线峰后变化规律起到约束作用，尽管有文献出现理论曲线与试验曲线峰后吻合良好的实例，但这仅仅表明具有唯一性和随机性的理论曲线与试验曲线之间峰后恰巧接近而已，实际上不具有普适性。

图 3 m和F₀对D的影响

Figure 3. Effects of m and F₀ on D

下载: 全尺寸图片幻灯片

图 4 m和F₀对理论模型曲线的影响

Figure 4. Effects of m and F₀ on theoretical model curves

下载: 全尺寸图片幻灯片

（2）考虑初始损伤的双参数型硬物质损伤模型

由于两类细观化材料属于串联结构，硬物质弹性模量远大于软物质，因此可知软物质变形基本发生在初始空隙压密变形阶段，岩石宏观线弹性及其以后变形过程仅为硬物质产生，而且硬物质弹性模量与岩石相等。根据损伤理论可将硬物质视为由未损伤、初始损伤和后继损伤3种材料并联组成，见，它们所受应力分别为有效应力 ${\sigma '_i}$ 、残余应力 ${\sigma _{\text{r}}}$ 和0，作用面积分别为A_u，A_s和A_d，总作用面积为A_t。

图 5 硬物质损伤模型

Figure 5. Damage model for hard materials

下载: 全尺寸图片幻灯片

根据竖向力学平衡分析方法，可建立考虑初始损伤的硬物质损伤模型，即

${\sigma _i} = {\sigma '_i}(1 - {D_{\text{d}}} - {D_{\text{s}}}) + {\sigma _{\text{r}}}{D_{\text{s}}} \text{，}$

(9)

式中， ${D_{\text{d}}}$ ， ${D_{\text{s}}}$ 为硬物质的初始损伤变量和后继损伤变量。由于目前统计损伤本构理论框架已渐趋完善，因此，延续已有损伤模型表达范式与峰值点法优越性，使拟建理论模型能够较准确地模拟试验曲线峰后变化过程，是解决模型局限性的最佳途径。为此，在式（9）基础上引入双参数λ和η，建立考虑初始损伤和强度脆性跌落的双参数型硬物质损伤模型，即

${\sigma _i} = {\sigma '_i}(1 - {D_{\text{d}}} - \lambda {D_{\text{s}}}) + \eta {\sigma _{\text{r}}}{D_{\text{s}}} 。$

(10)

由于弹性模量的变化是损伤典型的宏观表现^[3-4]，因此，根据岩石类材料损伤变量与弹性模量之间的关系，可得 ${D_{\text{d}}}$ 的确定方法，即

${D_{\text{d}}} = 1 - {E_{\text{d}}}/{E_{\text{u}}} \text{，}$

(11)

式中， ${E_{\text{d}}}$ ， ${E_{\text{u}}}$ 为损伤和无损状态下硬物质的弹性模量。由于硬物质含有大量多尺度且不同形态的微裂纹和孔隙，而微裂纹，尤其是孔隙的完全闭合要极高压应力，很难测得 ${E_{\text{u}}}$ ，因此，基于大量三轴压缩试验资料对 ${E_{\text{d}}}$ 和 ${\sigma _3}$ 之间的关系进行统计表达，即

${E_{\text{d}}}/{E_{\text{c}}} = a + b\exp [ - ({\sigma _3}/{\sigma _{\text{c}}})/k] \text{，}$

(12)

式中，a，b，k为试验参数， ${\sigma _{\text{c}}}$ ， ${E_{\text{c}}}$ 为单轴压缩下岩石峰值应力和弹性模量。当 ${\sigma _3}$ 趋于极大值时，基于极限方法可认为空隙近似完全闭合， ${E_{\text{d}}}$ 在数值上趋于 ${E_{\text{u}}}$ ，则 ${E_{\text{u}}}$ 的计算表达式可为

${E_{\text{u}}} = a{E_{\text{c}}} 。$

(13)

（3）硬物质统计损伤本构模型

假设未损伤材料应力–应变关系服从广义虎克定律，即

${\sigma '_i} = {E_{\text{u}}}\varepsilon _i^{\text{r}} + \mu ({\sigma '_j} + {\sigma '_k}) \text{，}$

(14)

式中，μ为硬物质的泊松比。由于三轴压缩下岩石轴向发生破裂并丧失承载力，侧向约束变形并提高承载力，因此可忽略侧向损伤即认为有效应力 ${\sigma '_j}$ 和 ${\sigma '_k}$ 分别与名义应力 ${\sigma _j}$ 和 ${\sigma _k}$ 相等，于是式（14）可表达为

${\sigma '_i} = {E_{\text{u}}}\varepsilon _i^{\text{r}} + \mu ({\sigma _j} + {\sigma _k}) \text{，}$

(15)

于是，将式（15）代入式（10）可得硬物质变形分析表达式，

$\varepsilon _i^{\text{r}} = \frac{{{\sigma _i} - \xi {D_{\text{s}}} - \mu ({\sigma _j} + {\sigma _k})(1 - {D_{\text{d}}})}}{{(1 - {D_{\text{t}}}){E_{\text{u}}}}} \text{，}$

(16)

其中，

$\xi = \eta {\sigma _{\text{r}}} - \lambda \mu ({\sigma _j} + {\sigma _k}) \text{，}$

(17)

${D_{\text{t}}} = {D_{\text{d}}} + \lambda {D_{\text{s}}} 。$

(18)

由于微元体力学特性受应力状态和损伤阈值的双重影响，因此可认为三轴压缩下微元体服从M-C强度破坏准则^[14]，

$F = {E_{\text{d}}}\varepsilon _1^{\text{r}} + (2\mu - \alpha ){\sigma _3} - \kappa \text{，}$

(19)

其中，

$\alpha = (1 + \sin {\varphi _{\text{y}}})/(1 - \sin {\varphi _{\text{y}}}) \text{，}$

(20)

$\kappa = 2{c_{\text{y}}}\cos {\varphi _{\text{y}}}/(1 - \sin {\varphi _{\text{y}}}) 。$

(21)

式中， ${\varphi _{\text{y}}}$ ， ${c_{\text{y}}}$ 为临界损伤状态下硬物质的内摩擦角与黏聚力。当硬物质处于临界损伤状态以下时，微元体未发生破坏，D_s=0；当硬物质处于临界损伤状态以上时，微元体不断发生破坏，D_s由0递增直至硬物质发生完全损伤破坏，D_t=1。于是，D_s可表述为

${D}_{\text{s}}=\left\{\begin{array}{l}0&（F < 0）\\ 1-\mathrm{exp}[-{(}{F/F_0)^m}]&（0\le F < {F}_{\text{s}}）\\ (1-{D}_{\text{d}})/\lambda \text{}&（{F}_{\text{s}}\le F）\end{array} \right.\text{，}$

(22)

式中， ${F_{\text{s}}}$ 为 ${D_{\text{s}}}$ 恰增至(1- ${D_{\text{d}}}$ )/ $\lambda$ 时的微元体强度值。由于硬物质发生损伤可视为连续过程，因此，根据分段函数端点的连续性可得 ${F_{\text{s}}}$ 的计算表达式，

${F_{\text{s}}} = {F_0}{\left( { - \ln \frac{{{D_{\text{d}}} + \lambda - 1}}{\lambda }} \right)^{1/m}} 。$

(23)

3. 岩石全应力–应变曲线模拟方法

当硬物质处于弹性状态（F < 0）时，岩石变形由两类细观化物质组成，将式（2）代入式（1）可得

$\varepsilon _i^{\text{r}} = \frac{{{\varepsilon _i} - \gamma [1 - \exp ( - {\sigma _i}/{E_{\text{v}}})]}}{{1 - \gamma }} 。$

(24)

当硬物质处于损伤变形阶段（0≤F < ${F_{\text{s}}}$ ）时，软物质变形基本结束，exp( $- {\sigma _i}/{E_{\text{v}}}$ )→0，岩石变形与硬物质变形等同，由式（24）可得

$\varepsilon _i^{\text{r}} = ({\varepsilon _i} - \gamma )/(1 - \gamma ) 。$

(25)

当硬物质处于完全损伤变形阶段（ ${F_{\text{s}}}$ ≤F）时，岩石进入残余强度变形阶段。由式（16），（22）可得

${\sigma }_{1}=\left\{\begin{array}{l}\frac{{E}_{\text{d}}\{{\varepsilon }_{1}-\gamma [1-\mathrm{exp}(-{\sigma }_{1}/{E}_{\text{v}})]\}}{1-\gamma }+2\mu {\sigma }_{3}(1-{D}_{\text{d}})\text{(}F < 0\text{)}\\ \frac{{E}_{\text{u}}(1-{D}_{\text{t}})({\varepsilon }_{1}-\gamma )}{1-\gamma }+\xi {D}_{\text{s}}+2\mu {\sigma }_{3}(1-{D}_{\text{d}})\text{(}0\le F < {F}_{\text{s}}\text{)}\\ \frac{(1-{D}_{\text{d}})\eta {\sigma }_{\text{r}}}{\lambda }\text{(}{F}_{\text{s}}\le F\text{)}\end{array}\right.。$

(26)

由于三轴压缩下岩石实测偏应力 ${\sigma _{{\text{1t}}}}$ –实测轴向应变 ${\varepsilon _{{\text{1t}}}}$ 试验曲线与 ${\sigma _{\text{1}}}$ - ${\varepsilon _{\text{1}}}$ 理论曲线存在差异，因此需对 ${\sigma _{{\text{1t}}}}$ - ${\varepsilon _{{\text{1t}}}}$ 与 ${\sigma _{\text{1}}}$ - ${\varepsilon _{\text{1}}}$ 之间的关系进行转化：

${\sigma _{\text{1}}} = {\sigma _{{\text{1t}}}} + {\sigma _{\text{3}}} \text{，}$

(27)

${\varepsilon _{\text{1}}} = {\varepsilon _{{\text{1t}}}} + {\varepsilon _{\text{0}}} \text{，}$

(28)

其中，

${\varepsilon _0} = \frac{{(1 - \gamma )[1 - 2\mu (1 - {D_{\text{d}}})]{\sigma _3}}}{{{E_{\text{u}}}(1 - {D_{\text{d}}})}} + \gamma [1 - \exp ( - {\sigma _3}/{E_{\text{v}}})] 。$

(29)

式中， ${\varepsilon _0}$ 为仅围压作用下岩石发生的应变。于是，将式（27），（28）代入式（26）可得三轴压缩下脆性岩石全应力–应变曲线模拟方法，即

${\sigma _{{\text{1t}}}} = \left\{ \begin{gathered} \frac{{{E_{\text{d}}}}}{{1 - \gamma }}\{ {\varepsilon _{{\text{1t}}}} - \gamma '[1 - \exp ( - \frac{{{\sigma _{{\text{1t}}}}}}{{{E_{\text{v}}}}})]\} \;\,\,\;\quad {\text{ (}}F < 0{\text{)}} \hfill \\ \frac{{{E_{\text{u}}}(1 - {D_{\text{t}}})}}{{1 - \gamma }}({\varepsilon _{{\text{1t}}}} - \gamma ') + (\xi - \xi '){D_{\text{s}}}\quad {\text{(}}0 \leqslant F < {F_{\text{s}}}{\text{)}} \hfill \\ \frac{{(1 - {D_{\text{d}}})\eta {\sigma _{\text{r}}}}}{\lambda } - {\sigma _3}\quad \;\quad \;\quad \quad \quad \quad \;{\text{(}}{F_{\text{s}}} \leqslant F{\text{)}} \hfill \\ \end{gathered} \right. \text{，}$

(30)

其中，

$\gamma ' = \gamma \exp ( - {\sigma _3}/{E_{\text{v}}}) \text{，}$

(31)

$\xi ' = \lambda [1 - 2\mu (1 - {D_{\text{d}}}){\sigma _3}/(1 - {D_{\text{d}}})] 。$

(32)

4. 参数的确定方法

由前述分析可知，m和F₀仍然由峰值点法进行确定。根据式（26），联立式（7），（8）可得m和F₀的确定方法，

$m = \frac{{{F_{{\text{sc}}}}(1 - {D_{\text{d}}} - \lambda {D_{{\text{sc}}}})}}{{(1 - {D_{\text{d}}})(1 - {D_{{\text{sc}}}})[\xi (1 - \gamma ) - \lambda {E_{\text{u}}}({\varepsilon _{1{\text{c}}}} - \gamma )]\ln (1 - {D_{{\text{sc}}}})}} \text{，}$

(33)

${F_0} = {F_{{\text{sc}}}}{[ - \ln (1 - {D_{{\text{sc}}}})]^{ - 1/m}} \text{，}$

(34)

其中，

${F_{{\text{sc}}}} = {E_{\text{d}}}({\varepsilon _{1{\text{c}}}} - \gamma )/(1 - \gamma ) + (2\mu - \alpha ){\sigma _3} - \kappa \text{，}$

(35)

${D_{{\text{sc}}}} = \frac{{(1 - \gamma )[{\sigma _{1{\text{c}}}} - 2\mu {\sigma _3}(1 - {D_{\text{d}}})] - {E_{\text{u}}}(1 - {D_{\text{d}}})({\varepsilon _{{\text{1c}}}} - \gamma )}}{{\xi (1 - \gamma ) - \lambda {E_{\text{u}}}({\varepsilon _{1{\text{c}}}} - \gamma )}} 。$

(36)

此外，参数还包括E_v，E_d， $\gamma$ ，D_d， $\lambda$ 和 $\eta$ ，下面简要介绍其确定方法。首先，当轴向应力低于损伤阈值时，初始空隙压密变形阶段试验数据需满足式（30）第一式，可根据拟合分析方法获得E_v；然后，线弹性及其以后变形过程为硬物质所产生，根据式（30）第一式可知线弹性变形反向延长线在 ${\varepsilon _{{\text{1t}}}}$ 轴上的截距为 $\gamma '$ ，将E_v代入式（30）可得 $\gamma$ ；最后，线弹性直线斜率理论表达式为E_d/(1- $\gamma$ )，基于已知 $\gamma$ 和斜率试验值可得E_d，再将E_d代入式（11）可得D_d。 $\lambda$ 和 $\eta$ 的作用未知，待参数分析以后给出其确定方法。

5. 模型验证

为了表明本文模型和方法能够较准确地模拟出围压效应和强度脆性跌落过程，下面基于大理岩试验资料^[15]分别进行验证。

5.1 围压效应验证

由于围压效应发生在岩石初始宏观变形阶段，因此，根据式（30）第一式进行验证。该理论表达式不包含 $\lambda$ 和 $\eta$ ，根据本文模型和参数确定方法可得相关参数值，见表 1，将其代入理论表达式可获得三轴压缩下大理岩初始宏观变形理论曲线，见图 6，与此同时，也可获得此变形阶段内大理岩宏观与其细观化物质理论曲线之间的关系，见图 7。

表 1 围压效应模型参数

Table 1. Model parameters of confining pressure effect

${\sigma _{\text{3}}}$ /MPa	$\gamma$ /10^-2	${E_{\text{d}}}$ /GPa	${E_{\text{v}}}$ /MPa	D_d
1.38	0.54	10.37	4.73	0.42
2.76	0.47	12.42	6.00	0.31
5.52	0.53	13.69	5.26	0.24
6.89	0.64	16.54	4.27	0.08

下载: 导出CSV

| 显示表格

图 6 初始变形阶段理论曲线与试验数据的比较

Figure 6. Comparison between theoretical curves and test data at initial deformation stage

下载: 全尺寸图片幻灯片

图 7 初始变形阶段宏细观物质理论曲线的关系(

${\sigma _{\text{3}}}$ =2.76 MPa)

Figure 7. Relationship between macro- and meso-theoretical curves at initial deformation stage (

${\sigma _{\text{3}}}$ =2.76 MPa)

下载: 全尺寸图片幻灯片

（1）不同围压作用下轴向荷载作用初期变形阶段理论曲线与大理岩初始空隙压密和线弹性等变形阶段试验数据吻合良好，表明本文模型和方法在反映围压效应方面具有较强的适用性。

（2）大理岩轴向宏观变形可由软物质和硬物质两部分细观变形加权构成，权重分别为 $\gamma$ 与1- $\gamma$ ，克服了将岩石等同颗粒骨架且忽略初始空隙闭合给岩石宏观变形造成的不利影响，具有明显的优越性。

（3）软物质变形是引起大理岩初始宏观变形为非线性的主因，其变形的结束即为初始空隙压密变形阶段的终点，由此可确定出空隙闭合应力，表明本文模型和方法能够阐释出岩石宏观与其细观化物质之间的理论变形关系。

5.2 强度脆性跌落验证

由于强度脆性跌落发生在岩石损伤变形破坏阶段，因此根据式（30）第二、三式进行验证。为了表明仅考虑初始损伤的硬物质损伤模型即式（9）的缺陷，以及在此基础上考虑强度脆性跌落的双参数型硬物质损伤模型即式（10）的优越性，下面分别进行探讨。

（1）考虑初始损伤的本构模型

由于分别基于式（9），（10）建立的统计损伤本构模型的区别仅在于理论表达式是否包含 $\lambda$ 和 $\eta$ ，因此，将 $\lambda$ 和 $\eta$ 均赋值为1，两者模型相同，根据本文模型和方法可获得仅考虑初始损伤的大理岩轴向变形理论曲线及其损伤演化曲线，见图 8。

图 8 理论曲线与试验数据的比较(λ=η=1)

Figure 8. Comparison between theoretical curves and test data (λ=η=1)

下载: 全尺寸图片幻灯片

a）该模型能够较准确地模拟出大理岩峰前轴向变形试验曲线，包括初始空隙压密、线弹性和屈服硬化等阶段，但在模拟应变软化和残余强度变形等阶段存在缺陷，尤其在强度脆性跌落过程中理论曲线与试验曲线之间的应变差值较大，无法将两者近似等同。

b）D_s– ${\varepsilon _{{\text{1t}}}}$ 和D_t– ${\varepsilon _{{\text{1t}}}}$ 曲线形状基本呈S型，两者纵向间距为D_d。当轴向应力未达到损伤阈值时，D_s，D_t分别等于为0，D_d并保持不变；当轴向应力达到损伤阈值时，其内部损伤开始累积，D_s，D_t不断增大；当轴向应力达到残余应力时，D_s，D_t分别等于1-D_d，1并保持不变，表明该损伤演化曲线能够较准确地阐释出大理岩阶段性变形特征。

c）随着 ${\sigma _3}$ 的增大，D_d不断减小，损伤阈值和残余应力不断增大，增大 ${\sigma _3}$ 对大理岩发生轴向损伤变形破坏具有有效抑制作用。

（2）考虑强度脆性跌落的本构模型

为了解决峰后理论曲线严重偏离于试验曲线的不足，建立了考虑强度脆性跌落的本构模型，但该模型含有未知 $\lambda$ ， $\eta$ ，无法给出大理岩轴向变形峰后理论曲线，因此将在参数分析基础上探讨其作用并给出其确定方法，然后对该模型进行验证，具体过程如下。

为了探讨 $\lambda$ 的作用，将 $\eta$ 赋值为1，根据本文模型和方法可获得不同 $\lambda$ 下损伤阈值后轴向变形理论曲线以及损伤演化理论曲线，见，可以看出：λ的变化对不同 ${\sigma _3}$ 下峰前变形理论曲线变化规律不起作用，仅对峰后理论曲线变化规律起作用，随着 $\gamma$ 的增大，强度脆性跌落程度和损伤变化率不断增大，残余应力不断减小，损伤演化曲线形状基本保持为S型并绕点A作逆时针转动。

图 9 不同λ下理论曲线变化规律(η=1)

Figure 9. Variation of theoretical curves under different λ (η=1)

下载: 全尺寸图片幻灯片

同理，为了探讨 $\eta$ 的作用，将λ赋值为1，根据本文模型和方法可获得不同 $\eta$ 下损伤阈值后轴向变形理论曲线以及损伤演化理论曲线，见，可以看出：η的变化对不同 ${\sigma _3}$ 下峰前变形理论曲线变化规律不起作用，仅对峰后理论曲线变化规律起作用，随着η的增大，强度脆性跌落程度不断减小，残余应力和损伤变化率不断增大，损伤演化曲线形状基本保持为S型并向轴向应变减小方向移动。

图 10 不同η下理论曲线变化规律(λ=1)

Figure 10. Variation of theoretical curves under different η (λ=1)

下载: 全尺寸图片幻灯片

由此可知， $\lambda$ ， $\eta$ 具有m，F₀对轴向变形理论曲线以及损伤演化理论曲线的等效作用，在m，F₀保持不变的前提下可通过改变 $\lambda$ ， $\eta$ 的方式以达到模拟强度脆性跌落过程的目的，表明参数引入量及其引入方式合理且可行。由于 $\lambda$ ， $\eta$ 对峰后理论曲线变化规律起控制作用，而峰后变形特征表征指标主要指脆性指标和残余应力，在此基础上可给出λ和η的确定方法。

根据岩石脆性特征定量评价方法^[19]，峰后应力降绝对速率B_pa和峰后应力降相对速率B_pr可表示为

${B_{{\text{pa}}}} = ({\sigma _{1{\text{c}}}} - {\sigma _{\text{r}}})/({\varepsilon _{1{\text{r}}}} - {\varepsilon _{{\text{1c}}}}) \text{，}$

(37)

${B_{{\text{pr}}}} = ({\sigma _{1{\text{c}}}} - {\sigma _{\text{r}}})/{\sigma _{{\text{1c}}}} \text{，}$

(38)

式中， ${\varepsilon _{1{\text{r}}}}$ 为轴向应力恰降至 ${\sigma _{\text{r}}}$ 时的应变。于是考虑峰前与峰后变化特征的脆性指标B_n可建立为

${B_{\text{n}}} = {B_{{\text{pr}}}} \cdot \frac{2}{{\text{π }}}\arctan {B_{{\text{pa}}}} 。$

(39)

显然，B_n在[0，1]变化，脆性程度随B_n增大而增大，于是根据式（37）~（39）可得

${\varepsilon _{{\text{1r}}}} = {\varepsilon _{{\text{1c}}}} + ({\sigma _{{\text{1c}}}} - {\sigma _{\text{r}}}){\tan ^{ - 1}}\frac{{{\text{π }}{B_{\text{n}}}{\sigma _{{\text{1c}}}}}}{{2({\sigma _{{\text{1c}}}} - {\sigma _{\text{r}}})}} 。$

(40)

由式（1），（19）可得偏应力恰跌至σ_r时F_s，

${F_{\text{s}}} = {E_{\text{d}}}({\varepsilon _{{\text{1r}}}} - \gamma )/(1 - \gamma ) + (2\mu - \alpha ){\sigma _3} - \kappa 。$

(41)

于是结合式（23），（41）可得λ的确定方法，

$\lambda =\frac{1-{D}_{\text{d}}}{1-\mathrm{exp}\{{}-{[({E}_{\text{d}}({\varepsilon }_{\text{1r}}-\gamma )/(1-\gamma )+(2\mu -\alpha ){\sigma }_{3}-\kappa )/{F}_{0}]}^{m}\text{}\}}。$

(42)

由三轴压缩条件下岩石基本变形特征分析可得

$\mathop {\lim }\limits_{{\varepsilon _1} \to {\varepsilon _{1{\text{r}}}}} {\sigma _1} = {\sigma _{\text{r}}} 。$

(43)

于是将式（26）第三式代入式（43）可得η的确定方法，即

$\eta = \lambda /(1 - {D_{\text{d}}}) 。$

(44)

根据λ和η的确定方法可获取相应的参数，见，然后，将其代入式（30）可得不同 ${\sigma _3}$ 作用下大理岩全应力–应变理论曲线，见图 11，可以看出：本文模型和方法不仅能够较准确地反映围压效应，也能够较准确地模拟出强度脆性跌落过程，消除了已有模型峰后理论曲线变化的随机性，较好地缓解了峰后变形理论曲线与试验数据的严重偏离程度，从而表明本文模型和方法具有一定的合理性与可行性。

表 2 不同

${\sigma _3}$ 下模型参数λ和η

Table 2. Model parameters λ and η under different σ₃

${\sigma _3}$ /MPa	λ	η
1.38	0.58	1.002
2.76	0.69	0.996
5.52	0.76	0.995
6.89	0.92	0.997

下载: 导出CSV

| 显示表格

图 11 全应力–应变理论曲线与大理岩试验数据的比较

Figure 11. Comparison between theoretical curves of complete stress-strain and test data of marble

下载: 全尺寸图片幻灯片

6. 结论

（1）岩石可视为由软物质和硬物质两种细观化材料的串联结构，在此基础上建立了宏细观物质变形分析模型，其中软物质服从负指数变形规律，硬物质可根据统计损伤理论构建本构模型。

（2）m，F₀能够使模型较准确地模拟轴向峰前变形过程，但在模拟轴向峰后变形过程时带有强烈的随机性；λ，η对轴向峰前变形理论曲线变化规律不起作用，但对峰后变形理论曲线变化规律起控制作用，具有m，F₀对轴向变形理论曲线以及损伤演化理论曲线的等效作用。

（3）建立了能够考虑围压效应和强度脆性跌落的脆性岩石全应力–应变曲线统计损伤模拟方法，给出了参数的确定方法，通过模型验证与分析表明本文模型和方法具有一定的合理性与可行性，完善了岩石统计损伤本构理论。

图 1 综合管廊纵向地震易损性分析流程图

Figure 1. Procedures of longitudinal seismic fragility analysis for utility tunnel

下载: 全尺寸图片幻灯片

图 2 场地信息及综合管廊结构示意图

Figure 2. Schematic diagram of site information and utility tunnel

下载: 全尺寸图片幻灯片

图 3 综合管廊-土体相互作用数值模型示意图

Figure 3. Schematic diagram of utility tunnel-soil interaction model

下载: 全尺寸图片幻灯片

图 4 土体动剪切模量比和动阻尼比曲线

Figure 4. Curves of dynamic shear modulus and damping ratio

下载: 全尺寸图片幻灯片

图 5 损伤指标回归分析

Figure 5. Regression analysis of damage measures

下载: 全尺寸图片幻灯片

图 6 地震动强度指标离散性对比

Figure 6. Comparison of description of different IMs

下载: 全尺寸图片幻灯片

图 7 最大接口张开量d_max与IM线性拟合结果

Figure 7. Linear regression of d_max and IM

下载: 全尺寸图片幻灯片

图 8 综合管廊地震易损性曲线

Figure 8. Seismic fragility curves of utility tunnel

下载: 全尺寸图片幻灯片

图 9 地震易损性曲线对比

Figure 9. Comparison of seismic fragility curves

下载: 全尺寸图片幻灯片

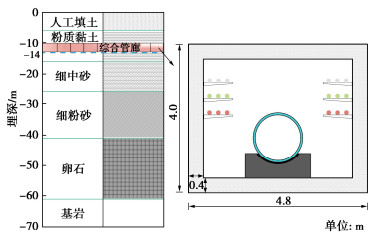
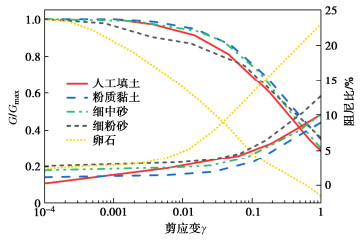
表 1 土层物理参数表

Table 1 Geotechnical properties of soil layers

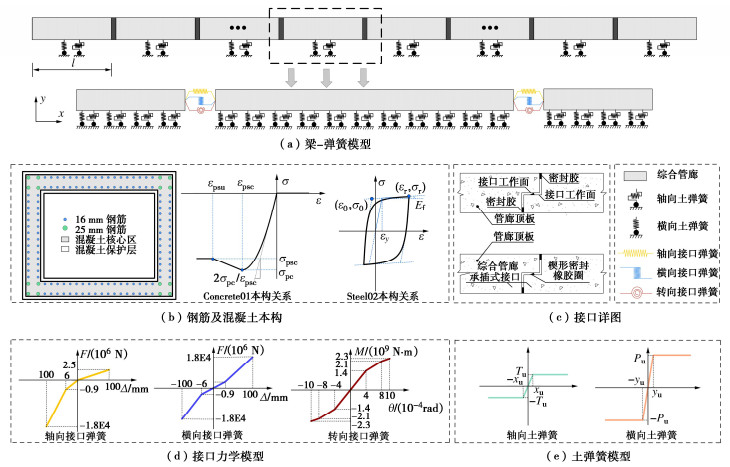
土层	土质	土层厚度H/m	密度ρ/(kg·m^-3)	剪切波速v_s/(m·s^-1)
1	人工填土	6.0	1750	180
2	粉质黏土	10.0	1900	250
3	细中砂	10.0	2000	300
4	细粉砂	15.0	2000	320
5	卵石	20.0	2280	500

下载: 导出CSV

表 2 钢筋及混凝土材料参数

Table 2 Material parameters of steel rebars and concrete

材料	密度γ_u/(kg·m^-3)	弹性模量E_u/GPa	屈服强度f_y/MPa	硬化系数	轴心抗压强度f_c0/MPa	轴心抗拉强度f_t/MPa	峰值压应变ε_c0	极限压应变ε_cu
钢筋	7850	200	426	0.001	—	—	—	—
混凝土	2500	32.5	—	—	19.1	2.39	0.0020	0.0038

下载: 导出CSV

表 3 轴向和横向土弹簧参数

Table 3 Parameters for longitudinal and transverse soil springs

轴向土弹簧			横向土弹簧
T_u/kN	x_u/mm	k_l/(kN·mm^-1)	P_u/kN	y_u/mm	k_t/(kN·mm^-1)
960	10.0	96	120960	420.0	288

下载: 导出CSV

表 4 地震动记录信息

Table 4 Information of ground motion records

序号	震级	时间	地震名称	台站	PGA/g	PGV/(mm·s^-1)
1	6.69	1994	Northridge-01	LA - Wonderland Ave	0.10	76
1	6.69	1994	Northridge-01	LA - Wonderland Ave	0.16	146
2	7.62	1999	Chi-Chi_ Taiwan	CHY102	0.04	68
2	7.62	1999	Chi-Chi_ Taiwan	CHY102	0.05	56
3	7.62	1999	Chi-Chi_ Taiwan	HWA035	0.08	11
3	7.62	1999	Chi-Chi_ Taiwan	HWA035	0.07	67
4	7.62	1999	Chi-Chi_ Taiwan	KAU034	0.06	20
4	7.62	1999	Chi-Chi_ Taiwan	KAU034	0.01	25
5	7.62	1999	Chi-Chi_ Taiwan	TAP086	0.04	97
5	7.62	1999	Chi-Chi_ Taiwan	TAP086	0.05	80
6	7.62	1999	Chi-Chi_ Taiwan	TCU088	0.53	34
6	7.62	1999	Chi-Chi_ Taiwan	TCU088	0.52	14
7	7.62	1999	Chi-Chi_ Taiwan	TTN028	0.02	37
7	7.62	1999	Chi-Chi_ Taiwan	TTN028	0.02	27
8	6.05	1994	Northridge-02	Lake Hughes #12A	0.01	3
8	6.05	1994	Northridge-02	Lake Hughes #12A	0.02	4
9	5.9	1999	Chi-Chi_ Taiwan-02	ILA015	0.01	8.5
9	5.9	1999	Chi-Chi_ Taiwan-02	ILA015	0.01	10
10	6.2	1999	Chi-Chi_ Taiwan-05	HWA002	0.03	31
10	6.2	1999	Chi-Chi_ Taiwan-05	HWA002	0.03	34
11	6.3	1999	Chi-Chi_ Taiwan-06	TTN042	0.03	26
11	6.3	1999	Chi-Chi_ Taiwan-06	TTN042	0.01	23
12	6.9	2008	Iwate_ Japan	IWTH18	0.13	42
12	6.9	2008	Iwate_ Japan	IWTH18	0.04	36
13	6.9	2008	Iwate_ Japan	MYGH03	0.08	25.5
13	6.9	2008	Iwate_ Japan	MYGH03	0.09	27.3
14	5.39	2008	14383980	Mount Wilson Obsv	0.02	9.0
14	5.39	2008	14383980	Mount Wilson Obsv	0.02	8.6
15	5.89	2004	Oroville-01	Oroville Seismograph Station	0.09	21
15	5.89	2004	Oroville-01	Oroville Seismograph Station	0.07	23
16	5.19	2004	Anza (Horse Canyon)-01	Anza - Pinyon Flat	0.10	20
16	5.19	2004	Anza (Horse Canyon)-01	Anza - Pinyon Flat	0.12	50
17	5.45	2007	40204628	Hamilton Field	0.01	4.5
17	5.45	2007	40204628	Hamilton Field	0.01	5

下载: 导出CSV

表 5 综合管廊损伤状态定义

Table 5 Definition of damages states for utility tunnel

性能水准	评价指标范围/mm	评价指标中位值/mm
基本完好	d_max≤2	—
轻微破坏	2＜d_max≤10.5	6.3
中等破坏	10.5＜d_max≤15.0	12.8
严重破坏	d_max＞15.0	15.0

下载: 导出CSV

表 6 PGV转PGA系数^[36]

Table 6 Ratios of PGV to PGA

震级(M_w)	震源-场地距离/km
震级(M_w)	0~20	20~50	50~100
6.5	940	1020	1090
7.5	1400	1270	1550
8.5	1800	1880	1930

下载: 导出CSV

表 7 不同地震动强度下综合管廊的失效概率

Table 7 Failure probabilities of utility tunnel at corresponding seismic intensity levels

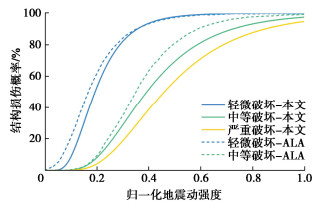
地震动强度	PGA/g	PGV/(mm·s^-1)	场地类别	失效概率/%
地震动强度	PGA/g	PGV/(mm·s^-1)	场地类别	基本完好	轻微破坏	中等破坏	严重破坏
多遇地震动	0.20	286	Ⅱ	78.5	20.0	0.8	0.7
设计地震动	0.40	572	Ⅱ	28.9	50.5	7.6	13.0
罕遇地震动	0.62	887	Ⅱ	7.9	40.8	12.2	39.1

下载: 导出CSV

参考文献(36)

[1]	钱七虎. 建设城市地下综合管廊, 转变城市发展方式[J]. 隧道建设, 2017, 37(6): 647-654. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201706001.htm QIAN Qihu. To transform way of urban development by constructing underground utility tunnel[J]. Tunnel Construction, 2017, 37(6): 647-654. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201706001.htm
[2]	CHEN J, JIANG L Z, LI J, et al. Numerical simulation of shaking table test on utility tunnel under non-uniform earthquake excitation[J]. Tunnelling and Underground Space Technology. 2012, 30: 205-216. doi: 10.1016/j.tust.2012.02.023
[3]	梁建文, 李东桥, 王长祥, 等. 考虑预应力影响的壳-弹簧模型及其在预制地下管廊纵向抗震分析中的应用[J]. 地震工程与工程振动, 2021, 41(4): 13-22. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202104002.htm LIANG Jianwen, LI Dongjiao, WANG Changxiang, et al. Shell-spring model for longitudinal seismic analysis of precast utility tunnels considering prestress[J]. Earthquake Engineering and Engineering Dynamics. 2021, 41(4): 13-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202104002.htm
[4]	TANG G Y, FANG Y M, ZHONG Y, et al. Numerical study on the longitudinal response characteristics of utility tunnel under strong earthquake: a case study[J]. Advances in Civil Engineering, 2020: 8813303.
[5]	钟紫蓝, 申轶尧, 郝亚茹, 等. 基于IDA方法的两层三跨地铁地下结构地震易损性分析[J]. 岩土工程学报, 2020, 42(5): 916-924. doi: 10.11779/CJGE202005014 ZHONG Zilan, SHEN Yiyao, HAO Yaru, et al. Seismic fragility analysis of two-story and three-span metro station structures based on IDA method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 916-924. (in Chinese) doi: 10.11779/CJGE202005014
[6]	ZHONG Z L, SHEN Y Y, ZHAO M, et al. Seismic performance evaluation of two-story and three-span subway station in different engineering sites[J]. Journal of Earthquake Engineering, 2021, 26(14): 1-31.
[7]	ZHONG Z L, FILIATRAULT A, AREF A. Numerical simulation and seismic performance evaluation of buried pipelines rehabilitated with cured-in-place-pipe liner under seismic wave propagation[J]. Earthquake Engineering & Structural Dynamics, 2017, 46(5): 811-829.
[8]	LI J Q, ZHONG Z L, WANG S R, et al. Seismic fragility analysis of water supply pipelines retrofitted with corrosion-protection liner buried in non-uniform site[J]. Soil Dynamics and Earthquake Engineering. 2024, 176: 108333. doi: 10.1016/j.soildyn.2023.108333
[9]	禹海涛, 李心熙, 袁勇, 等. 沉管隧道纵向地震易损性分析方法[J]. 中国公路学报. 2022, 35(10): 13-22. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202210002.htm YU Haitao, LI Xinxi, YUAN Yong, et al. Seismic vulnerability analysis method for longitudinal response of immersed tunnels[J]. China Journal of Highway and Transport, 2022, 35(10): 13-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202210002.htm
[10]	LONG X H, MA Y T, MIAO Y, et al. Longitudinal seismic fragility analysis of long tunnels under multiple support excitation[J]. Soil Dynamics and Earthquake Engineering. 2023, 164: 107608. doi: 10.1016/j.soildyn.2022.107608
[11]	城市轨道交通结构抗震设计规范: GB50909—2014[S]. 北京: 中国计划出版社, 2014. Code for Seismic Design of Urban Rail Transit Structures: GB50909—2014[S]. Beijing, China Planning Press, 2014. (in Chinese)
[12]	SILVIA M, FRANK M, MICHAEL H S, et al. OpenSees command language manual[Z]. Berkeley: Earthquake Engineering Center, University of California, 2009.
[13]	城市综合管廊工程技术规范: GB50838—2015[S]. 北京: 中国计划出版社, 2015. Technical Code for Urban Utility Tunnel Engineering: GB50838—2015[S]. Beijing, China Planning Press, 2015. (in Chinese)
[14]	ZHAO J, SRITHARAN S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. Aci Structural Journal, 2007, 104(2): 133-141.
[15]	FILIPPOU F C, POPOV E P, BERTERO V V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints[R]. Berkeley: Earthquake Engineering Research Center, University of California, 1983.
[16]	冯立, 丁选明, 王成龙, 等. 考虑接缝影响的地下综合管廊振动台模型试验[J]. 岩土力学, 2020, 41(4): 1295-1304. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202004021.htm FENG Li, DING Xuanming, WANG Chenglong, et al. Shaking table model test on seismic responses of utility tunnel with joint[J]. Rock and Soil Mechanics, 2020, 41(4): 1295-1304. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202004021.htm
[17]	胡正一. 非一致地震激励下预制装配式综合管廊结构纵向地震响应及易损性研究[D]. 北京: 北京工业大学, 2022: 11-31. HU Zhengyi. Study on Longitudinal Seismic Response and Vulnerability of Composite Utility Tunnel Structure under Non-Uniform Seismic Excitation[D]. Beijing: Beijing University of Technology, 2022: 11-31. (in Chinese)
[18]	城市轨道交通岩土工程勘察规范: GB50307—2012[S]. 北京: 中国计划出版社, 2014. Code for Geotechnical Investigation of Urban Rail Transit: GB50307—2012[S]. Beijing, China Planning Press, 2012. (in Chinese)
[19]	油气输送管道线路工程抗震技术规范: GB/T50470—2017[S]. 北京: 中国计划出版社, 2017. Seismic Technical Code for Oil and Gas Transmission Pipeline Engineering: GB/T50470—2017[S]. Beijing, China Planning Press, 2017. (in Chinese).
[20]	TSINIDIS G. Response characteristics of rectangular tunnels in soft soil subjected to transversal ground shaking[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research. 2017, 62: 1-22.
[21]	FEMA. Seismic Performance Assessment of Buildings: Volume 1 Methodology[R]. Washington D C: Federal Emergency Management Agency, 2012.
[22]	FEMA. Seismic Performance Assessment of Buildings Volume 2- Implementation Guide[R]. Washington D C: Federal Emergency Management Agency, 2012.
[23]	BULLOCK Z, LIEL A B, PORTER K A, et al. Site-specific liquefaction fragility analysis: cloud, stripe, and incremental approaches[J]. Earthquake Engineering & Structural Dynamics. 2021, 50(9): 2529-2550.
[24]	CHEN Z Y, WEI J S. Correlation between ground motion parameters and lining damage indices for mountain tunnels[J]. Natural Hazards. 2013, 65(3): 1683-1702. doi: 10.1007/s11069-012-0437-5
[25]	钟紫蓝, 史跃波, 李锦强, 等. 考虑土体动力特征参数相关性的工程场地随机地震反应分析[J]. 岩土力学, 2022, 43(7): 2015-2024. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202207027.htm ZHONG Zilan, SHI Yuebo, LI Jinqiang, et al. Stochastic seismic response analysis of engineering site considering correlations of critical soil dynamic parameters[J]. Rock and Soil Mechanics, 2022, 43(7): 2015-2024. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202207027.htm
[26]	杜修力, 许紫刚, 许成顺, 等. 基于等效线性化的土–地下结构整体动力时程分析方法研究[J]. 岩土工程学报, 2018, 40(12): 2155-2163. doi: 10.11779/CJGE201812001 DU Xiuli, XU Zigang, XU Chengshun, et al. Time-history analysis method for soil-underground structure system based on equivalent linear method[J]. Chinese Journal of Geotechnical Engineering, 2018, 40 (12): 2155-2162. (in Chinese) doi: 10.11779/CJGE201812001
[27]	DU X L, ZHAO M. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 937-946. doi: 10.1016/j.soildyn.2010.04.004
[28]	VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 491-514.
[29]	城市轨道交通设计规范: DGJ08109—2004[S]. 上海: 同济大学出版社, 2017. Urban Rail Transit Design Standard: DGJ08109—2004[S]. Shanghai: Tongji University Press, 2017. (in Chinese)
[30]	黄忠凯, 张冬梅. 地下结构地震易损性研究进展[J]. 同济大学学报, 2021, 49(1): 49-59. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ202101007.htm HUANG Zhongkai, ZHANG Dongmei. Recent advance in seismic fragility research of underground structures[J]. Journal of Tongji University, 2021, 49(01): 49-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ202101007.htm
[31]	ARGYROUDIS S A, PITILAKIS K D. Seismic fragility curves of shallow tunnels in alluvial deposits[J]. Soil Dynamics and Earthquake Engineering, 2012, 35: 1-12. doi: 10.1016/j.soildyn.2011.11.004
[32]	钟紫蓝, 冯立倩, 史跃波, 等. 序列型地震作用下地铁车站损伤分析[J]. 岩土工程学报, 2023, 45(8): 1586-1594. doi: 10.11779/CJGE20220788 ZHONG Zilan, FENG Liqian, SHI Yuebo, et al. Seismic damage assessment of subway station subjected to mainshock aftershock sequences[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(8): 1586-1594. (in Chinese)' doi: 10.11779/CJGE20220788
[33]	HAZUS-MHMR1. Multi-hazard Loss Estimation Model: Manual Advanced Engineering Building Module Methodology Earthquake Technical and User's[R]. Washington D C: Federal Emergency Management Agency, 2003.
[34]	SALMON M, WANG J, JONES D, et al. Fragility formulations for the BART system[C]// Proceedings of the 6th US Conference on Lifeline Earthquake Engineering, TCLEE, Long Beach, 2003.
[35]	American Lifelines Alliance. Seismic Fragility Formulations for Water Systems: Part 1 Guideline[M]. Reston: ASCEFEMA, 2005: 1-103.
[36]	POWER M, ROSIDI D, KANESHIRO J. Strawman: "Screening, Evaluation, and Retrofit Design of Tunnels" Report Draft[R]. New York: National Centre for Earthquake Engineering Research, 1996.

施引文献(10)

期刊类型引用(6)

1.	马殷军，杜腾飞，栾恩铭，张寿红，董江龙. 环境温度对青海湖地区含盐土水热变化规律试验研究. 水利与建筑工程学报. 2025(01): 55-60+79 . 百度学术
2.	徐云山，肖子龙，孙德安，李建平. 游离氧化铁赋存形式对脱吸湿条件下红黏土热传导性能的影响. 岩土工程学报. 2025(04): 811-819 . 本站查看
3.	肖慈宇，张海燕，詹建潮，卜继斌. 渣土余泥免烧轻质高强陶粒的制备及应用. 硅酸盐通报. 2025(04): 1428-1437 . 百度学术
4.	孔纲强，常洪林，王天赐，杨庆. 区域尺度地埋管地源热泵与能源地下结构开采浅层地热能评价综述. 岩土力学. 2024(05): 1265-1283 . 百度学术
5.	唐少容，殷磊，杨强，柯德秀. 微胶囊相变材料改良粉砂土的导热系数及预测模型. 中国粉体技术. 2024(03): 112-123 . 百度学术
6.	褚召祥，王一鸣，李晓昭，董凯军，顾晓滨，贾国圣. 岩土热导率预测正三棱柱-准内切球单元结构模型. 岩土工程学报. 2024(12): 2580-2590 . 本站查看

其他类型引用(4)

资源附件(1)

其他相关附件
- PDF格式
  07-202408-G23-0397⼀⽂审稿意⻅与作者答复点击下载(1432KB)

图(9) / 表(7)

计量

文章访问数: 350
HTML全文浏览量: 69
PDF下载量: 72
被引次数: 10

0. 引言
1. 脆性岩石三轴压缩基本变形特征
2. 岩石宏细观物质变形分析模型
2.1 软物质变形分析方法
2.2 硬物质变形分析方法
3. 岩石全应力–应变曲线模拟方法
4. 参数的确定方法
5. 模型验证
5.1 围压效应验证
5.2 强度脆性跌落验证
6. 结论

0. 引言
1. 脆性岩石三轴压缩基本变形特征
2. 岩石宏细观物质变形分析模型
2.1 软物质变形分析方法
2.2 硬物质变形分析方法
3. 岩石全应力–应变曲线模拟方法
4. 参数的确定方法
5. 模型验证
5.1 围压效应验证
5.2 强度脆性跌落验证
6. 结论

参考文献(36)

施引文献

资源附件(1)

基于IDA方法的综合管廊纵向地震易损性分析研究 English Version

作者简介: 李锦强（1995—)，男，博士研究生，主要从事地下结构抗震方面的研究工作。E-mail: lijinqiangs@163.com

通讯作者: 钟紫蓝, zilanzhong@bjut.edu.cn

计量

出版历程

Longitudinal seismic fragility analysis of utility tunnel structures based on IDA method

0. 引言

1. 脆性岩石三轴压缩基本变形特征

2. 岩石宏细观物质变形分析模型

2.1 软物质变形分析方法

2.2 硬物质变形分析方法

3. 岩石全应力–应变曲线模拟方法

4. 参数的确定方法

5. 模型验证

5.1 围压效应验证

5.2 强度脆性跌落验证

6. 结论

期刊类型引用(6)

其他类型引用(4)

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 脆性岩石三轴压缩基本变形特征

2. 岩石宏细观物质变形分析模型

2.1 软物质变形分析方法

2.2 硬物质变形分析方法

3. 岩石全应力–应变曲线模拟方法

4. 参数的确定方法

5. 模型验证

5.1 围压效应验证

5.2 强度脆性跌落验证

6. 结论

作者简介:
李锦强（1995—)，男，博士研究生，主要从事地下结构抗震方面的研究工作。E-mail: lijinqiangs@163.com

通讯作者:
钟紫蓝, zilanzhong@bjut.edu.cn