Measurement of distribution of rock joint stiffness based on active ultrasonic excitation
-
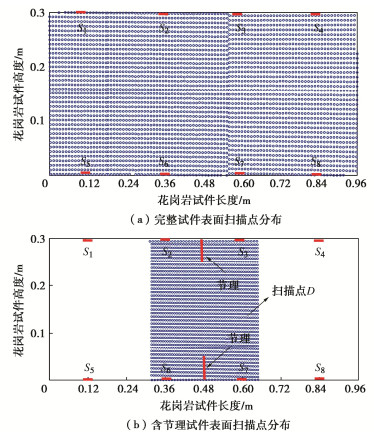
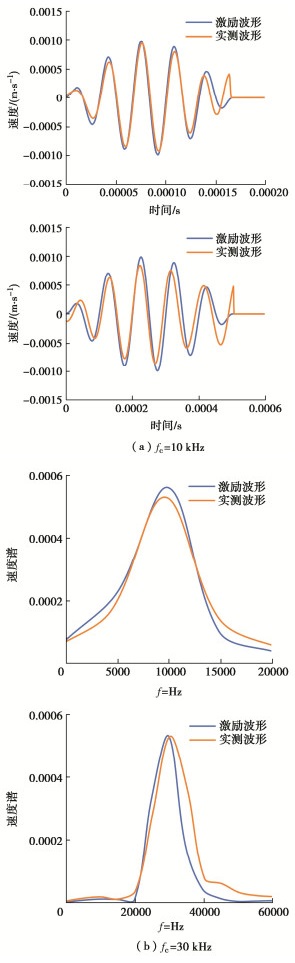
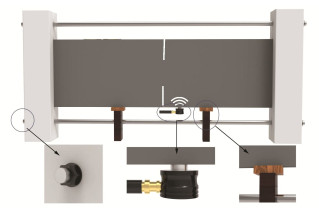
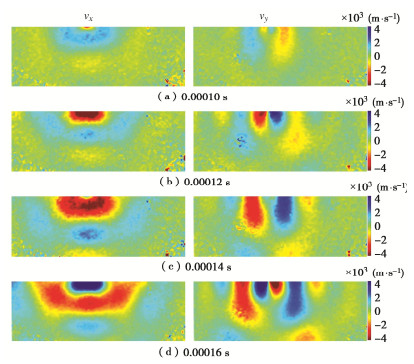
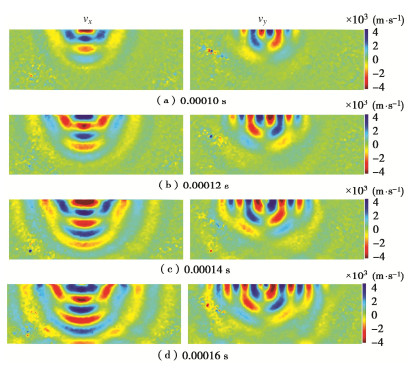
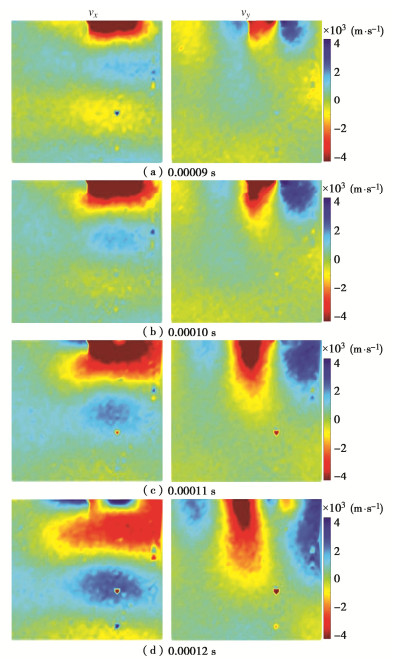
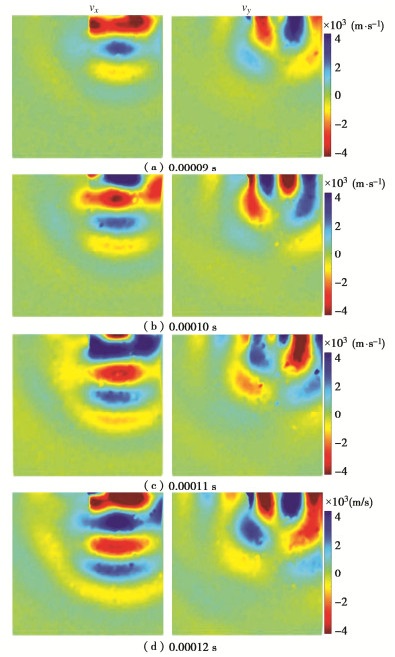
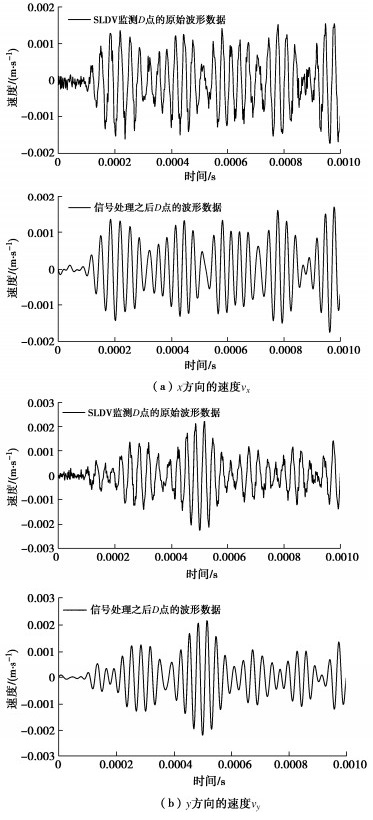
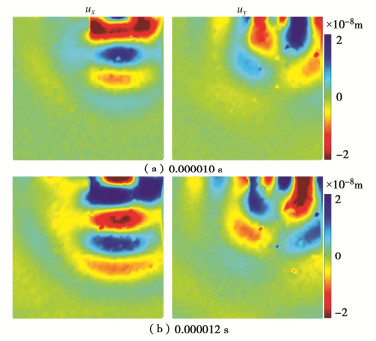
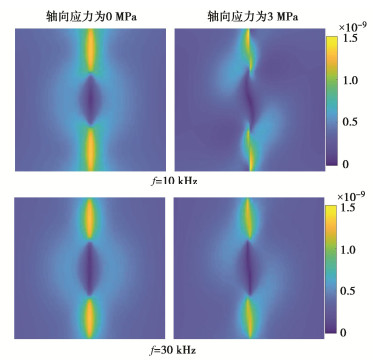
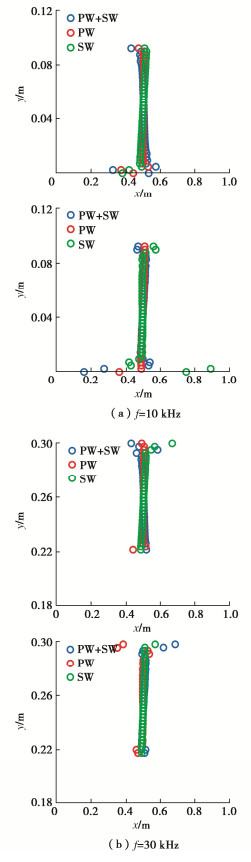
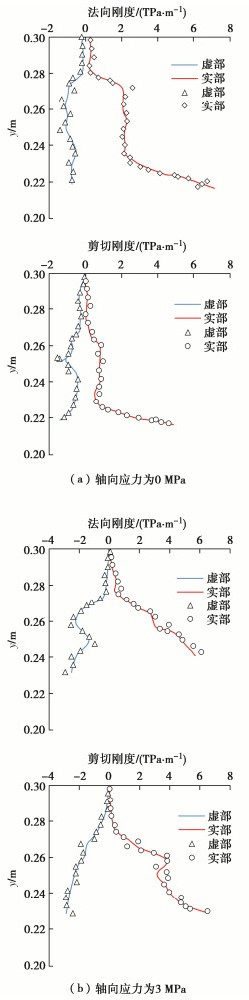
摘要: Goodman提出采用节理刚度表征复杂岩石节理面的拓扑行为并为其提供定量值,而无需对节理面的粗糙度、接触面积等参数进行详细测量分析。然而目前对岩石节理刚度的测量仍存在局限,因此,在试验室环境下采用压电陶瓷换能器对完整平板试件和含节理平板试件进行弹性波激励,同时采用三维扫描激光多普测振仪监测平板内弹性波的传播数据。将采集的波场信号数据进行滤波、插值、积分等一系列处理,并基于Schoenberg线性滑移模型计算节理刚度分布,实现岩石节理接触行为的全局参数表征,同时进一步验证了岩石节理全场超声表征的可行性。全场波形数据清晰地揭示了岩石节理界面接触行为,为后续深入探索岩石节理几何形状、孔径、界面性质及其地震特征之间的相互关系奠定了基础。Abstract: Goodman proposed to use the joint stiffness to characterize the topological behaviors of complex rock joint interfaces and provide quantitative values for them, without measuring and analyzing the geometric parameters such as roughness and contact area of joint interfaces in detail. However, it is difficult to measure the stiffness of rock joints at present. Therefore, the piezoelectric ceramic transducer is used to excite the elastic waves of the intact granite plate specimen and the cracked granite plate specimen in the laboratory environment. At the same time, the scanning laser Doppder Vibrometer is used to monitor propagation data of the elastic waves in the plate. On this basis, the collected signal data of wave fields are processed by filtering, interpolation, integration, etc., and the distribution of joint stiffness is calculated based on the Schoenberg linear sliding model. Then, the joint stiffness is used to parameterize the contact behaviors of rock joints, which further proves the feasibility of ultrasonic characterization of whole rock joints. By using the full-field waveform data, the interface contact behaviors of rock joints are clearly revealed, which lays a foundation for further exploring the relationship among rock joint geometry, pore sizes, interface properties and seismic characteristics.
-
Keywords:
- rock joint /
- contact behavior /
- elastic wave /
- shear stiffness /
- normal stiffness
-
0. 引言
粗粒料作为土石坝工程的主要填筑材料,其变形特性显著影响大坝的安全性[1]。粗粒料的剪胀特性是其重要的力学特性之一,剪胀方程是对粗粒料剪胀性的数学描述,构建的是剪胀比与应力比之间的数学关系,亦是构建粗粒料本构模型的重要基础。因此,构建粗粒料的剪胀方程一直都是建立其本构模型的研究重点。相对于黏土和砂土[2-4],粗粒料显著的颗粒破碎特性使其剪胀特性更加复杂[5],所以,构建合理描述粗粒料剪胀性的剪胀方程需要考虑颗粒破碎的影响。
近年来,国内外学者对粗粒料的剪胀方程已经做了诸多研究,其中,以Rowe剪胀方程和剑桥模型剪胀方程两者的改进形式为主[5-14]。但是,就目前的这些剪胀方程而言,大部分都不能较好地预测粗粒料的剪胀行为,小部分的剪胀方程虽然可以较好地描述粗粒料的剪胀行为,却由于其本身的数学形式较为复杂,无法推出相应的塑性势函数,那么就不能进一步地利用分数阶非正交性流动法则进行本构模型的构建。分数阶非正交性流动法则是指基于塑性势函数可以得到加载方向或根据屈服函数得到塑性流动方向,其中加载方向与流动方向的夹角由分数阶导数的阶数确定[15]。目前,分数阶微积分已经被证明是一个解决力学建模难题的有力数学工具,为此,笔者拟构建一个考虑颗粒破碎的适用于粗粒料且数学形式简单的剪胀方程,可以推出相应的塑性势函数,为后续建立一个考虑颗粒破碎的粗粒料的分数阶本构模型做准备。
在本构模型中引入颗粒破碎参数存在参数过多且将颗粒破碎参数引入本构模型的函数规律适用性不强的缺陷。颗粒破碎本质上是能量转换的过程,用颗粒破碎耗能反映粗粒料的颗粒破碎与应力变形之间的内在联系切实可行。Ueng等[6]在Rowe剪胀方程[16]中引入了颗粒破碎耗能,建立了适用于粗粒料的能量平衡方程。但是,依据该能量平衡方程计算出的颗粒破碎耗能随着颗粒破碎量的增大会出现负数以及减小的情况,违反了热力学定律。其原因在于没有考虑颗粒破碎对摩擦系数的影响。换句话说,在该能量平衡方程中,将临界状态应力比作为摩擦系数是不合理的。因此,贾宇峰等[11]、米占宽等[8]、郭万里等[5]均对摩擦系数进行了修正,使得计算出的颗粒破碎耗能遵循热力学定律,并推导出了各自的剪胀方程。然而,由于这些剪胀方程形式复杂,无法推出塑性势函数,那么就使得分数阶本构模型的构建成为幻想。
颗粒破碎本质上是能量转换的过程,因此,对于微观上堆石料颗粒破碎耗能的研究应基于宏观上其颗粒破碎的研究。笔者首先对三轴剪切过程中粗粒料的颗粒破碎变化规律进行了研究。然后根据该颗粒破碎变化规律,对Ueng等[6]提出的能量平衡方程中的摩擦系数进行了修正,实现了三轴剪切过程中堆石料颗粒破碎耗能的合理计算。在此基础上,发展了一个适用于粗粒料的剪胀方程,其形式简单,与剑桥模型剪胀方程类似,可以推出相应的塑性势函数。
1. 颗粒破碎变化规律
为研究三轴剪切过程中粗粒料的颗粒破碎变化规律,总结了两种类型粗粒料在三轴剪切过程中的颗粒破碎试验数据[17-18],如表 1所示[19]。
表 1 颗粒破碎试验数据Table 1. Particle breakage data粗粒料 围压/kPa 轴向应变/% 破碎指标BE/% 建筑碎
石料[14]200 4.58 10.60 200 9.72 14.40 200 12.90 15.60 500 3.88 11.60 500 7.96 18.70 500 14.40 23.10 1000 3.17 12.20 1000 9.40 26.00 1000 15.80 32.00 1500 2.05 13.20 1500 6.31 30.20 1500 17.20 41.40 玄武岩
堆石料[15]1000 2.16 9.40 1000 7.84 16.10 1000 15.10 21.90 1500 2.41 10.20 1500 8.24 19.70 1500 15.60 25.70 2000 2.47 9.90 2000 8.61 20.30 2000 15.10 27.20 通过分析表 1中的颗粒破碎试验数据发现,破碎指标BE、围压σ3及轴向应变ε1之间的关系可以用下式进行表示:
BE=βarctan(αε1)σ3/paω+σ3/pa。 (1) 利用式(1)对表 1中颗粒破碎数据进行拟合,结果如表 2所示。
表 2 式(1)的拟合结果Table 2. Fitting results of Eq. (1)粗粒料 β α ω 决定系数R2 建筑碎石料 0.417 19.5 5.42 0.962 玄武岩堆石料 0.260 21.4 5.18 0.980 从表 2中可以看出,利用式(1)对两种粗粒料的颗粒破碎数据进行拟合的决定系数为0.962,0.980,可见拟合效果较好。为了进一步地展示式(1)的拟合效果,图 1绘出了式(1)对于颗粒破碎指标BE的拟合值与其实测值。
2. 颗粒破碎耗能的合理计算
2.1 粗粒料的能量平衡方程
Ueng等[6]在Rowe剪胀方程中引入了颗粒破碎耗能,建立了考虑考虑破碎耗能的能量平衡方程,其表达式为
pdεv+qdεs=Mpdεs+(2q−3p)Mdεv/9+dEb, (2) 式中,pdεv+qdεs为总输入能增量dEw,(2q−3p)Mdεv/9为土体剪胀耗能增量dEd,dEb为颗粒破碎耗能增量,Mpdεs为土体摩擦耗能增量dEf,M为摩擦系数,其值为临界状态应力比Mc。
颗粒破碎耗能无法通过试验直接得到,只能通过式(1)进行计算。从式(2)中可知,需确定临界状态应力比Mc才能进行颗粒破碎耗能的计算。三轴试验结束时,试验粗粒料经常没有达到临界状态,无法根据试验直接确定Mc。因此,Guo等[7]和米占宽等[8]均采用Prevost等[20]提出的应力比与广义剪应变的关系式确定粗粒料的临界状态应力比,笔者亦如此。该关系式为
η=βaβbε2s+εsε2s+1 ,Mc=βaβb ,} (3) 式中,βa,βb为拟合参数,εs为广义剪应变,η为应力比。
以粗粒料C[21]为例,粗粒料C为砂岩,试验干密度为2.12 g/cm3,最大粒径为60 mm,试验围压为300,600,900,1200 kPa,其大型三轴固结排水剪切试验的应力应变曲线如图 2所示。
利用式(3)可以确定粗粒料C的临界状态应力比Mc为1.64。进一步地,根据式(2)可以计算出粗粒料C各个围压下的颗粒破碎耗能,结果如图 3所示。从图 3中可以看出,计算出的颗粒破碎耗能Eb在试验的开始阶段出现了小于0的情况,而且在试验的后续过程中出现了减小的情况。鉴于颗粒破碎是不可逆的单向过程,颗粒破碎耗能不可能为负数或减小,所以计算出的颗粒破碎耗能违反了热力学定律。
颗粒破碎是不可逆的单向过程,在三轴试验过程中颗粒破碎率不可能为负数,且当粗粒料进入临界状态后不再发生颗粒破碎[5, 22]。不仅如此,根据式(1)可知,颗粒破碎率与围压和轴向应变均表现出了正相关的非线性关系。颗粒破碎是颗粒破碎耗能的宏观表现,所以,颗粒破碎耗能应满足4个条件:①其值不可能为负数;②其值在剪切过程中随着轴向应变的增加而增大;③其值在相同轴向应变的情况下随着围压的增大而增大;④当粗粒料进入临界状态时,颗粒破碎耗能达到最大值,其增量为0。
从式(2)可以看出,p,q,dεv,dεs,M的正确取值是决定颗粒破碎耗能求解是否合理的保证,而p,q,dεv,dεs可以直接根据试验确定,所以摩擦系数M的取值是不合理的。也就是说,将三轴试验过程中的摩擦系数取为定值Mc,使得计算出的摩擦耗能偏大。为此,需要对式(2)中的摩擦系数进行修正。
2.2 摩擦系数的修正
如前所述,颗粒破碎耗能的合理求解取决于摩擦系数的正确取值。颗粒破碎本质上是能量转换的过程,对于微观上粗粒料颗粒破碎耗能的研究应基于宏观上其颗粒破碎的研究。也就是说,粗粒料颗粒破碎耗能的计算应与其颗粒破碎的变化规律相关联。因此,摩擦系数如何取值应与粗粒料颗粒破碎的变化规律相结合。
在三轴试验过程中,颗粒破碎改变了土颗粒的表面积和颗粒之间的接触状态,在宏观上表现为土体的摩擦系数的增大[5, 22]。在三轴试验的初始阶段,土颗粒之间的相对运动较小,此时,摩擦系数和颗粒破碎率较小。在试验过程中,土体变形显著,土颗粒之间发生翻越和滑移,摩擦系数增大,同时,颗粒破碎率也是增大的。当土体达到临界状态时,不再发生颗粒破碎,即颗粒破碎耗能增量dEb=0,而且体变增量dεv=0,由式(1)可知,此时M=Mc。
基于以上分析可知,试验过程中摩擦系数与颗粒破碎率随着轴向应变增加的变化规律是相似的。因此,基于式(3),构造了摩擦系数M与轴向应变ε1之间的关系,其表达式为
M=βarctan(αε1)。 (4) 构造的式(4)与式(1)类似,不过忽略了围压的影响,因为在整个试验过程中围压σ3为常数,故而认为,摩擦系数M的变化仅与轴向应变ε1有关。
当轴向应变ε1→+∞时,可以认为试验粗粒料达到了临界状态,且arctan(αε1)=π /2,此时M=Mc,结合式(4)可以推出β=2Mc/π。值得注意的是,从数学角度来说,arctan(αε1)只能向π /2趋近,为此,设定当arctan(αε1)=π /2×0.9时,认为试验粗粒料达到了临界状态,此时αε1c=6.31。所以,α可以通过6.31/ε1c进行估算。其中,ε1c为土体达到临界状态时的轴向应变。
通过上述分析,式(4)可以进一步写为
M=2Mcπ arctan(αε1)。 (5) 3. 颗粒破碎耗能的计算
如前所述,基于粗粒料三轴剪切过程中的颗粒破碎规律,实现了摩擦系数的修正。根据式(2),(5)可以计算出颗粒破碎耗能。计算之前,还需要确定参数α。虽然α可以通过6.31/ε1c进行估算,但是由于试验结束时粗粒料C尚未进入临界状态,无法确定临界状态轴向应变ε1c,因此这种估算方法并不实用。取ε1c为30%,则α=6.31/ε1c=21.0(原因将在第6节给出),然后对粗粒料C各围压下的颗粒破碎耗能进行了重新计算,结果如图 4所示。
从图 4中可以看出,在整个试验过程中,颗粒破碎耗能未出现小于0的情况,与围压、轴向应变均表现出了正相关的非线性关系,而且当试验粗粒料到达临界状态时,M=Mc,由式(2)可知,此时dEb=0。所以,重新计算出的颗粒破碎耗能满足了其理论上遵循的4个条件,所以,采用本文修正后的摩擦系数计算出的颗粒破碎耗能是合理的。
4. 剪胀方程
4.1 剪胀方程的提出
笔者在重新计算粗粒料C的颗粒破碎耗能时,发现剪胀耗能在总的外力做功里所占的比例较小,基本上可以忽略不计,如图 5所示。所以,为了能够得到形式更为简单的剪胀方程,忽略了剪胀耗能增量dEd,那么式(2)可以改写为
pdεv+qdεs=Mpdεs+dEb。 (6) 忽略弹性应变,dεpv/dεps=dεv/dεs,将其代入式(6)可得
dg=dεpvdεps=dεvdεs=M−η+dEbpdεs。 (7) 应用式(7)描述堆石料的剪胀行为时,需要先确定dEb/dεs。米占宽等[8]和贾宇峰等[11]分别找到了Eb与轴向应变和剪应变的表达式,再通过微分求得dEb/dε1和dEb/dεs。这样的处理方式使得最终的剪胀方程不仅参数过多而且数学形式极其复杂。郭万里等[14]将dEb/pdεs作为一个整体,通过总结出其与摩擦系数M的线性关系得到了最终的剪胀方程。沿此思路,笔者发现dEb/pdεs与M之间亦存在着较为明显的线性关系:
dEbpdεs=A−BM, (8) 式中,A,B为颗粒破碎耗能参数,与材料性质相关。
以粗粒料C为例,利用式(8)拟合不同围压下dEb/pdεs与M之间的试验点,结果如图 6所示。
从图 6中可以看出,式(8)的拟合曲线与粗粒料C的试验值吻合的较好,且拟合的决定系数为0.970,可见,式(8)可以较好地描述dEb/pdεs与M之间的关系。进一步地,将式(8)代入式(7)可以得到简化后的剪胀方程:
dg=K−η, (9) 式中,K=A+(1−B)M。
将利用式(8)拟合dEb/pdεs与M之间关系得到的A,B代入式(9),得到本文剪胀方程的预测曲线,同时点绘了剪胀比与应力比的试验点,如图 7所示。注意到,不同围压下的应力比与剪胀比之间的部分试验点重合,为了区分这些试验点,在图 8中,将600,1000,2200 kPa围压下的试验点分别沿着横坐标向右平移0.3,0.6,0.9个单位。
从图 7中可以看出,无论在低应力水平还是高应力水平下,式(9)对于剪胀比的预测曲线与其试验值较为吻合,说明本文得出的剪胀方程可以较好地模拟粗粒料的剪胀行为。
4.2 剪胀方程的适用性验证
为了进一步验证本文剪胀方程的适用性,整理了粗粒料D的大型三轴CD剪切试验数据[23]。粗粒料D为板岩,试验干密度为2.07 g/cm3,最大粒径为60 mm,试验围压为300,600,1000,2200 kPa,其大型三轴固结排水剪切试验的应力应变曲线如图 9所示。
首先,利用式(3)确定粗粒料D的临界状态应力比Mc为1.69,取α为21.0。然后根据式(2)可以计算出粗粒料D的颗粒破碎耗能,结果如图 10所示。
从图 9中可以看出,计算出的颗粒破碎耗能未出现小于0或者减小的情况,且与围压、轴向应变表现了正相关的非线性关系,满足了热力学定律。可见,通过本文对摩擦系数的修正,实现了颗粒破碎耗能的合理计算。
进一步地,利用式(8)拟合粗粒料D的dEb/dεs与M之间的试验值,如图 11所示。然后,将利用式(8)拟合得到的A,B代入式(9)得到本文剪胀方程的预测曲线,并与剪胀比与应力比之间的试验值进行对比,如图 8所示。注意到,不同围压下的应力比与剪胀比之间的部分试验点重合,为了区分这些试验点,在图 8中,将600,900,1200 kPa围压下的试验点分别沿着横坐标向右平移0.3,0.6,0.9个单位。
从图 11中可以看出,式(8)的拟合值与dEb/pdεs与M之间的试验值吻合较好,其中拟合的决定系数为0.992,可见,式(8)可以较为准确地描述粗粒料的dEb/dεs与M之间的关系。从图 8中可以看出,本文剪胀方程的预测曲线与剪胀比的试验值较为接近。也就是说,本文的剪胀方程可以较好地模拟粗粒料的剪胀行为。
5. 关于α取值的讨论
如前所述,由于无法根据试验确定ε1c,因此,由α=6.31/ε1c估算α值的方法并不实用。已有研究表明,粗粒料进入临界状态的剪应变大致在15%~30%。对于粗粒料而言,三轴试验结束时其体应变的1/3一般较小,轴向应变与剪应变在数值上较为接近。鉴于此,笔者认为粗粒料进入临界状态时的轴向应变亦约在15%~30%,如图 12所示。从图 12中可知:当ε1c为15%时,α为42.1;当ε1c为23%时,α为27.4;当ε1c为30%时,α为21.0。可见,α的常用取值范围为21.0~42.1。
从式(5),(6)可知,参数α如何取值影响了摩擦系数M的大小,进一步地会影响计算出的颗粒破碎耗能数值。以粗粒料C为例,分别将α取为42.1,27.4,并计算出相应的颗粒破碎耗能,如图 13所示。从图 13,14中可以看出,α值越大,计算出的颗粒破碎耗能越小。无论α值为42.1还是27.4,计算出的颗粒破碎耗能均满足热力学定律。
注意到,构建一个形式简单且适用于粗粒料的剪胀方程为笔者的最终目标。颗粒破碎耗能的合理计算只是笔者构建粗粒料剪胀方程的桥梁,即在实现颗粒破碎耗能的合理计算之后,笔者关心的是剪胀方程对粗粒剪胀行为的模拟效果,而非颗粒破碎耗能数值上的大小。为了明晰α值对于本文剪胀方程质量的影响,继续以粗粒料C为例,将α取为42.1和27.4,利用式(8)分别拟合不同α值下的dEb/dεs与M之间的试验点,如图 14所示。
式(8)对于dEb/pdεs与M之间关系的描述效果决定了式(9)对于粗粒料剪胀行为的模拟效果。从图 14中可以看出,当α为42.1,27.4,21.0时,式(8)对于粗粒料C的dEb/dεs与M之间的试验点的拟合决定系数分别为0.961,0.973,0.970,可见式(8)对于dEb/pdεs与M之间关系的描述效果都很好,只是颗粒破碎耗能参数A,B的数值上会有略微的差异。因此,α的取值对于式(9)对于粗粒料剪胀行为的模拟效果影响较小,正如图 7,15所示。显然,当α为42.1,27.4,21.0时,式(9)对于剪胀比的预测曲线与其试验点均较为接近,即α在其常用范围内取值对于式(9)的模拟效果影响甚微,可以忽略不计。
6. 结论
(1)提出了一个可以描述颗粒破碎指标与轴向应变及围压之间关系的经验公式,试验表明,该公式可以较好地描述三轴剪切过程中粗粒料的颗粒破碎变化规律。
(2)依据上述的颗粒破碎变化规律,对Ueng等[6]提出的能量平衡方程中的摩擦系数进行了修正。利用修正后的摩擦系数计算出的颗粒破碎耗能满足了热力学定律。
(3)剪胀耗能在总的输入功里占比甚微,将修正后的能量平衡方程中的剪胀耗能忽略,同时总结出了dEb/pdεs与M之间的线性关系,得到了本文最终的剪胀方程。经验证,该剪胀方程可以较为准确地模拟粗粒料的剪胀行为。
(4)本文提出的考虑颗粒破碎的剪胀方程数学形式简单,类似于剑桥模型的剪胀方程,可以推出其塑性势函数,为后续考虑颗粒破碎的分数阶弹塑性模型的构建中分数阶非正交性流动法则的引入提供了基础。
-
-
[1] CRAWFORD B R, TSENN M C, HOMBURG J M, et al. Incorporating scale-dependent fracture stiffness for improved reservoir performance prediction[J]. Rock Mechanics & Rock Engineering, 2017, 50: 3349-3359.
[2] MCLASKEY G C, THOMAS A M, GLASER S D, et al. Fault healing promotes high-frequency earthquakes in laboratory experiments and on natural faults[J]. Nature, 2012, 491(7422): 101-104. doi: 10.1038/nature11512
[3] PYRAK-NOLTE L J, NOLTE D D. Frequency dependence of fracture stiffness[J]. Geophysical Research Letters, 2013, 19(3): 325-328.
[4] GOODMAN R E, TAYLOR R L, BREKKE T L A. A model for the mechanics of jointed rock[J]. ASCE Soil Mechanics and Foundation Division Journal, 1968, 99(5): 637-659.
[5] 唐志成, 王晓川. 不同接触状态岩石节理的剪切力学性质试验研究[J]. 岩土工程学报, 2017, 39(12): 2312-2319. doi: 10.11779/CJGE201712021 TANG Zhicheng, WANG Xiaochuan. Experimental studies on mechanical behaviour of rock joints with varying matching degrees[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2312-2319. (in Chinese) doi: 10.11779/CJGE201712021
[6] LANG P S, PALUSZNY A, ZIMMERMAN R W. Evolution of fracture normal stiffness due to pressure dissolution and precipitation[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 88: 12-22. doi: 10.1016/j.ijrmms.2016.06.004
[7] PYRAK-NOLTE L J, NOLTE D D. Approaching a universal scaling relationship between fracture stiffness and fluid flow[J]. Nature Communications, 2016, 7: 10663. doi: 10.1038/ncomms10663
[8] PETROVITCH C L, PYRAK-NOLTE L J, NOLTE D D. Combined scaling of fluid flow and seismic stiffness in single fractures[J]. Rock Mechanics & Rock Engineering, 2014, 47(5): 1613-1623.
[9] QIAO Y D, ZHANG C, ZHANG L. Numerical simulation of fluid-solid coupling of fractured rock mass considering changes in fracture stiffness[J]. Energy Science & Engineering, 2019, 10: 519-536.
[10] HEDAYAT A, PYRAK-NOLTE L J, BOBET A. Precursors to the shear failure of rock discontinuities[J]. Geophysical Research Letters, 2015, 41(15): 5467-5475.
[11] 刘日成, 尹乾, 杨瀚清, 等. 恒定法向刚度边界条件下三维粗糙节理面循环剪切力学特性[J]. 岩石力学与工程学报, 2021, 40(6): 1092-1109. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106002.htm LIU Richeng, YIN Qian, YANG Hanqing, et al. Cyclic shear mechanical properties of 3D rough joint surface under constant normal stiffness(CNS) boundary conditions[J]. Chinese Journal of Rock mechanics and Engineering, 2021, 40(6): 1092-1109. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106002.htm
[12] KULATILAKE P, SHREEDHARAN S, SHERIZADEH T, et al. Laboratory estimation of rock joint stiffness and frictional parameters[J]. Geotechnical & Geological Engineering, 2016, 34(6): 1-13.
[13] JIANG Y, XIAO J, TANABASHI Y, Et al. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(2): 275-286.
[14] NASSIR M A, WAN SETTARI R, et al. Joint stiffness and deformation behaviour of discontinuous rock[J]. The Journal of Canadian Petroleum Technology, 2010, 49(9): 78-86. doi: 10.2118/140119-PA
[15] LI J, QIU Z, ZHONG H, et al. Parametric study on near-wellbore fracture geometry for wellbore strengthening in anisotropic formation[J]. Journal of Petroleum Science and Engineering, 2019, 184: 106549.
[16] HEDAYAT A, PYRAK-NOLTE L J, BOBET A. Detection and quantification of slip along non-uniform frictional discontinuities using digital image correlation[J]. Geotechnical Testing Journal, 2014, 37(5): 1-14.
[17] LUBBE R, WORTHINGTON M H. A field investigation of fracture compliance[J]. Geophysical Prospecting, 2006, 54(3): 319-331. doi: 10.1111/j.1365-2478.2006.00530.x
[18] ACOSTA-COLON A, PYRAK-NOLTE L J, NOLTE D D. Laboratory-scale study of field of view and the seismic interpretation of fracture specific stiffness[J]. Geophysical Prospecting, 2010, 57(2): 209-224.
[19] Schoenberg, Michael. Elastic wave behavior across linear slip interfaces[J]. Journal of the Acoustical Society of America, 1998, 68(5): 1516-1521.
[20] 邓华锋, 熊雨, 肖瑶, 等. 基于单试件法的节理岩体抗剪强度参数分析[J]. 岩土工程学报, 2020, 42(8): 1509-1515. doi: 10.11779/CJGE202008016 DENG Huafeng, XIONG Yu, XIAO Yao, et al. Shear strength parameters of jointed rock mass based on single test sample method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1509-1515. (in Chinese) doi: 10.11779/CJGE202008016
[21] POURAHMADIAN F, GUZINA B B. On the elastic-wave imaging and characterization of fractures with specific stiffness[J]. International Journal of Solids & Structures, 2015, 71: 126-140.
[22] WANG P, WANG S, ZHANG Z, et al. Reconstruction of fracture geometry in material medium by elastic wave[J]. Construction and Building Materials, 2021, 287(2): 123001.
[23] WANG P, WANG S, YANG T. Spatial distribution of mechanical parameters along a fracture interface[J]. Soil Dynamics and Earthquake Engineering, 2022, 157(5): 107222.
[24] NGUYEN T P, GUZINA B B. Generalized linear sampling method for the inverse elastic scattering of fractures in finite bodies[J]. Inverse Problems, 2019, 35(10): 516-532.
-
期刊类型引用(8)
1. 介玉新. Rowe剪胀方程及一种新的推导方法. 水力发电学报. 2024(01): 109-123 .  百度学术
百度学术
2. 蔡新合,陈子玉,李国英. 考虑颗粒破碎能耗的堆石料剪胀方程及其应用. 水利水运工程学报. 2024(03): 127-135 .  百度学术
百度学术
3. 王步雪岩,孟庆山,钱建固. 基于体积变化的珊瑚砂砾破碎率研究. 岩土力学. 2024(07): 1967-1975 .  百度学术
百度学术
4. 蔡新合,朱雨萌,李国英. 基于广义塑性理论框架的堆石料变形计算. 水利水运工程学报. 2024(04): 127-139 .  百度学术
百度学术
5. 程诗芸,彭杨旭,张紫怡,郝晨曦,丰家俊,郭鸿. 土颗粒破碎机理的研究进展. 安徽建筑. 2023(01): 141-143 .  百度学术
百度学术
6. 王柳江,刘啸宇,刘斯宏,扎西顿珠,沈超敏. 改进hhu-SH模型及其在面板堆石坝工程中的应用. 河海大学学报(自然科学版). 2023(02): 64-72 .  百度学术
百度学术
7. 陈榕,武智勇,郝冬雪,高宇聪. 高应力下石英砂三轴剪切颗粒破碎演化规律及影响. 岩土工程学报. 2023(08): 1713-1722 .  本站查看
本站查看
8. 迟世春,郭宇,马锡钰,贾宇峰. 颗粒流变破碎与堆石料流变应变计算. 水力发电. 2023(10): 77-84+91 .  百度学术
百度学术
其他类型引用(8)
-
其他相关附件



 下载:
下载: