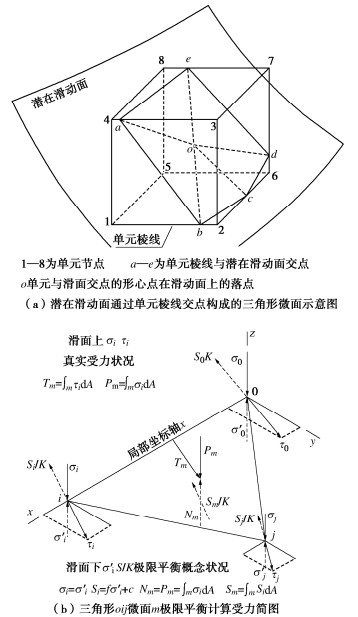
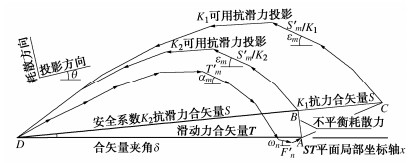
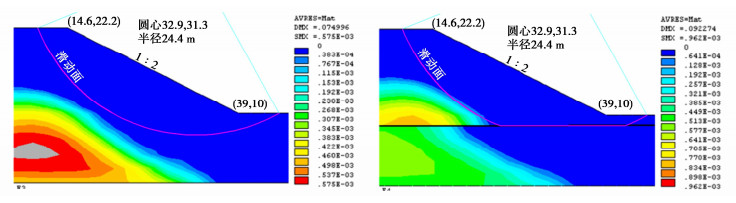
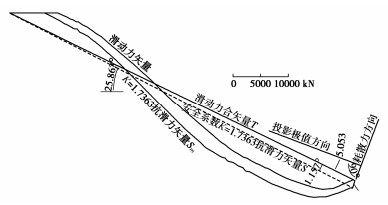
Theoretical model for limit equilibrium anti-sliding stability of stress vectors on three-dimensional sliding surface based on projection direction extreme principle
-
摘要: 根据投影方向极值原理揭示的复杂滑动面切向应力合矢量非共线不平衡特征，且其滑动势能比在平衡研究投影方向具有极大、耗散方向势能极小，针对三维滑动面节点应力状态差异使微面内的切向滑动力与抗滑力作用方向存在微小差异，构建三维复杂滑动面切向应力合成矢量在投影-耗散正交极值方向的塑性极限平衡抗滑稳定计算理论模型。完成理论模型的三维拓展，并给出理论模型具体计算方法步骤。通过典型稳定算题的微面切向滑动力与抗滑力势能比极值特性曲线和计算极值点的吻合程度证明理论模型的合理可靠性。并且依典型算例探讨了有限元应力场影响因素的变化对理论模型解的敏感性。矢量理论模型是抗滑稳定力学基础理论创新性的研究成果，具有重大理论发展推进作用和工程实际使用经济价值。Abstract: According to the projection direction extreme principle, in which the unbalance characteristics of non-collinear forces formed by tangential stress vectors on the complex sliding surface are revealed and the sliding potential energy ratio of the unbalance stress vectors in the equilibrium direction has the maximum, and minimum potential energies in the dissipation direction, in view that the difference of the stress state of the joints on the three-dimensional sliding surface leads to slight difference between direction of the tangential sliding force and that of the anti-sliding force in the micro-element plane, a theoretical model for calculating the stability of a three-dimensional complex sliding surface against sliding in the plastic limit equilibrium is proposed in the direction of the projection-dissipation orthogonal extreme. The three-dimensional expansion for the theoretical model is completed, and the concrete calculation steps of the theoretical model are given. The reasonable reliability of the model is proved by the curve of the extreme value of potential energy ratio between tangential sliding force and anti-sliding force on the sliding surface of typical stability problems and the degree of agreement between the calculated extreme point and the model. The sensitivity of the change of the factors affecting the finite element stress field to the solution of the theoretical model is also discussed. The vector theoretical model is an innovative research on the basic mechanics theory of anti-slide stability, which is of important theoretical development and practical economic value.
-
0. 引言
岩石节理、断层的界面特性对天然气和地热资源的能源开采、地震学、水文地质学、环境保护等科学技术领域都至关重要[1-3]，其中岩石节理、断层界面的特征主要包括粗糙度、接触面积、孔径分布等。Goodman等[4]引入节理刚度作为一个有效参数来捕获复杂节理界面的拓扑行为并为其提供定量值，而无需对节理界面几何特征参数进行详细测量分析。研究发现节理刚度与应力分布直接相关，可用于岩质边坡、地下结构的稳定性分析[5-6]；同时节理水力特性与节理刚度的时空变化之间存在很强的相关性，可用于地热、石油等地质资源的开采[7-9]；其次节理剪切刚度的变化可以作为岩石节理发生剪切破坏的前兆[10-11]。因此，确定岩石节理刚度分布具有重要的工程应用价值。
目前，国内外专家学者对岩石节理刚度的测量计算开展了大量研究。Kulatilake等[12]使用从不同地理位置和地层中获取的岩石制备相对光滑节理和锯切节理试件，通过单轴压缩和直剪试验估算岩石节理法向刚度和剪切刚度，建立了现场节理刚度估算的经验关系数据库。Jiang等[13]开发了自动伺服控制直剪装置和计算机控制系统，以自适应恒定法向刚度边界条件下法向应力的变化，通过假设恒定的法向刚度条件来确定节理剪切刚度。Nassir等[14]基于常规节理面参数和约束荷载，提出了节理峰前剪切刚度模型。同时，建立了用于评估节理岩石变形行为的本构矩阵。Li等[15]研究了剪切破坏时测量岩石节理剪切刚度的可行性，并分析了剪切破坏和剪切刚度之间的关系。
上述测量计算方法的刚度值表示整个岩石节理界面的平均刚度，但是岩石节理是非均质的，不同位置的刚度往往不同，平均值无法表征节理不同位置的接触行为。对此，Hedayat等[16]对石灰岩试样进行直剪试验，同时测量穿过节理传输和反射的纵波和横波。根据透射波振幅与反射波振幅计算激励位置的节理剪切刚度。Lubbe等[17]在不同围压下，使用脉冲反射技术测量节理法向刚度和剪切刚度，发现两者之比取决于节理填充流体。Acosta等[18]分析了不同测量尺度对节理刚度测量结果的影响。上述测量计算方法只适用于垂直于节理的入射波，同时要求节理界面是平面。
针对目前节理刚度测量计算的局限性，本文在试验室环境下通过压电陶瓷换能器对花岗岩平板试件进行激励，同时采用扫描激光多普勒测振仪非接触式监测试件平面内的波形传播数据，将数据信号处理后，根据线性滑移模型描述弹性波作用下的岩石节理本构响应[19]，计算节理刚度沿节理几何形状的分布，从而实现岩石节理接触行为的全局参数表征，验证岩石节理全场超声表征的可行性。
1. 波形运动数据监测
1.1 试验装置
节理全场超声表征试验采用尺寸为0.96 m×0.30 m×0.03 m的花岗岩平板试件，试件密度为2750 kg/m3，泊松比为0.23，杨氏模量为62.6 GPa。在S1至S8共8个位置处（如图 1）采用压电换能器分别进行S波和P波激励，频率为10，30 kHz；激励的同时使用扫描激光多普勒测振仪（SLDV）进行非接触式采集试件表面的波形运动数据，平面应力假设条件下整个试件厚度方向波形运动恒定[20]。完整试件的扫描范围是0.96 m×0.30 m，扫描点分布如图 1（a）所示。为了更好地关注节理周围的波形运动，将含节理试件扫描范围缩小为0.34 m×0.32 m区域，扫描点分布如图 1（b）所示。
为了保证波形数据测量的精度，要求每段波形占据10~20个扫描点，采用的波长约为10 cm，扫描点在x方向和y方向的空间分辨率均约为1 cm，所以每段波形占据10个扫描点，符合测量精度要求。对压电换能器产生的激励波形和试件中实际传播的波形进行比较，理论速度vy的波形和SLDV测得的激励位置S3附近的实际粒子速度vy，在时域和频域上的结果如图 2所示。对比发现换能器的信号波形和试件中实际传播的信号波形一致，表明压电换能器与试件耦合良好。
1.2 试验步骤
首先对轴向应力为0 MPa的完整试件进行全场超声表征试验，测量数据可计算由于节理产生的散射波场（散射波场=总场-自由场），其中含节理试件的数据为总场，完整试件的数据为自由场。接着在试件顶部和底部边缘中间位置制造3 cm长的缺口，然后以三点弯曲方式压裂形成两条非贯通节理。最后将试件安装到图 3所示的固定装置，载荷框架由两个铝制块组成，铝制块的两端均带有螺纹钢，通过拧紧螺纹钢上的螺母对节理施加轴向应力。试件在0 MPa和3 MPa轴向应力作用下分别产生宏观节理和微观节理，微观节理肉眼不可见。采用相同方式对3 MPa轴向应力状态下的含节理试件进行全场超声表征试验。
2. 数据可视化处理
试验共在8个不同位置进行激励，因为篇幅有限，仅以激励作用于S2和S3位置时试件中的波形运动为例。从激励开始到扫描结束整个过程共持续0.001 s，激励频率为10 kHz时完整试件的所有扫描点在4个不同时刻的速度场vx和vy如图 4所示。
![]()
图 4 10 kHz激励作用于S2时完整试件不同时刻的速度场vx和vyFigure 4. Velocity fields vx and vy at different moments of intact granite specimen with excitation acting of 10 kHz on S2激励频率为30 kHz时完整试件的所有扫描点在4个不同时刻的速度场vx和vy如图 5所示。
![]()
图 5 30 kHz激励作用于S2时完整试件不同时刻的速度场vx和vyFigure 5. Velocity fields vx and vy at different moments of intact granite specimen with excitation acting of 30 kHz on S2激励频率为10 kHz时含节理试件的所有扫描点在4个不同时刻的速度场vx和vy如图 6所示。
![]()
图 6 10 kHz激励作用于S3时含节理试件不同时刻的速度场vx和vyFigure 6. Velocity fields vx and vy at different moments of fractured granite specimen with excitation acting of 10 kHz on S3激励频率为30 kHz时含节理试件的所有扫描点在4个不同时刻的速度场vx和vy如图 7所示。
![]()
图 7 30 kHz激励作用于S3时含节理试件不同时刻的速度场vx和vyFigure 7. Velocity fields vx and vy at different moments of fractured granite specimen with excitation acting of 30 kHz on S33. 波形信号处理
首先设计带通滤波器对原始速度场进行滤波处理，带通滤波器只允许特定频段的信号通过，抑制低于或高于该频段的信号和噪声，从而适应频率为10 kHz和30 kHz的激励波形。含节理试件表面扫描点D的原始速度曲线以及经过带通滤波器处理之后的速度变化曲线如图 8所示。
![]()
图 8 扫描点D记录的原始速度以及经过带通滤波器处理之后的速度Figure 8. Original recorded velocities and velocity fields after bandpass filtering at scanming point D将滤波后的速度场积分转换成可微分的位移波场数据，计算节理界面的牵引力时位移场需要满足二次可微[21]，接着采用具有λs/10×λs/10窗口的中值滤波器消除位移波场中突然出现尖峰的信噪比极低的扫描点，并采用具有相同大小窗口的均值滤波器进行滤波处理，最后进行一维傅里叶级数近似，获得时间和空间可微分的平滑位移波场。信号处理之后试件表面散射场的位移ux和uy如图 9所示。
4. 节理面接触行为
4.1 节理几何形状重建
从激励开始到扫描结束整个过程共持续了0.001 s，SLDV每间隔0.000002 s采集一次试件表面的波形运动数据，共采集了500组数据。弹性波与岩石节理发生相互作用时产生不连续现象，弹性波在不含节理区域传播时波形连续。因此，为了获得节理的几何形状，在每个时间间隔之间计算x方向和y方向位移场分布的跳跃。然后，在整个时间范围内对x方向和y方向位移跳跃的绝对值进行积分，其中累积位移跳跃最大的点暴露了节理的真实几何形状，通过编译代码运算之后的检测结果如图 10所示。
为了提高检测精度，在时间间隔段进行傅里叶变换得到频域波形数据，对频域上的波形数据进行分析。首先选择检测窗口window_size = 5，循环次数等于列数减去window_size加1，在每个检测窗口检测频域上所有大于jump_lim的点，跳跃极限jump_lim取0.5×10-9；如果窗口不存在跳跃点，则采用pchip插值进行处理。如果存在跳跃，则将跳跃两侧的位移取平均值。计算梯度，接着按行依次计算duxx的值，按列依次求duxy的值，按行依次求duxy的值，按列依次求duyy的值，取所有计算结果的绝对值，并在每个检测窗口检测所有大于extreme_val的点，设置extr_val = 1×10-8；如果不存在异常点，则采用pchip插值进行处理。如果存在异常点，则将两侧的值取平均值。最后对整理好的每行每列数据在x方向和y方向进行积分，绝对值最小值即裂缝点的位置。通过编译代码运算之后轴向应力为0 MPa时节理几何形状的检测结果如图 11所示。节理几何形状的重建为计算节理刚度沿节理几何形状分布奠定基础。
4.2 节理刚度分布计算
岩石节理、断层界面凹凸不平且存在局部相互接触，为弹性波揭示节理的几何形状和残余接触行为提供了可能[22-23]。因此，通过线性滑移模型描述弹性波作用下岩石节理本构响应：
n⋅C:∇u=K(ξ)⋅[[u]],ξ∈Γ。 (1) 式中：u为位移场；n=n−为节理的单位法线；C:=λI2⊗I2+2μI4，其中μ和λ为拉梅常数，Im(m=2,4)为m阶对称恒等张量，等式左侧整体表示节理界面牵引力，[[u]]:=u|Γ+−u|Γ−为节理界面跳跃位移，K(ξ)∈C2×2是描述节理ξ∈Γ刚度的对称张量[24]。因此，线性滑移模型通过节理刚度描述了节理界面牵引力和跳跃位移之间的局部线性关系。
基于重建的节理几何形状，将二次可微分的位移波场数据转换成节理界面牵引力和跳跃位移，然后通过傅里叶变换到频域，最后根据线性滑移模型计算每个节理点频域上切向（法向）牵引力和切向（法向）跳跃位移之比从而获得节理剪切（法向）刚度沿节理几何形状分布。依次计算8个不同位置激励作用下的节理刚度并取平均值，试件顶部位置节理刚度分布结果如图 12所示。图中虚线和实线分别表示频率f为10 kHz和30 kHz的节理刚度分布。
由图 12可以看出激励频率为10 kHz和30 kHz时节理刚度计算结果变化趋势一致。朝节理尖端方向节理界面之间的孔径减小，接触面积增大，节理剪切刚度和法向刚度均逐渐增大。观察发现轴向应力作用下节理界面闭合，增大了节理界面接触面积，导致节理的法向刚度和剪切刚度整体增大。同时，该方法可以重构试件中多条节理的几何形状和刚度分布。试验成功获得岩石节理刚度分布，实现了节理接触行为的全局参数表征。文中计算节理刚度的方法与激励频率无关，对于不同尺度级别的节理、断层可采用不同频率的弹性波。当岩石节理、断层距离激励声源较近时可采用频率较大的弹性波；当岩石节理、断层距离激励声源较远时，可采用频率较小的弹性波，从而使探测距离达到几百米。因此提出的岩石节理几何形状的重建以及节理刚度分布的计算方法对岩石节理、断层均适用。
5. 结论
在试验室环境下实现了岩石试件中节理的全场超声表征，得到以下3点结论。
（1）通过三维扫描激光多普勒测振仪监测压电换能器激励作用下平板试件的波形传播数据，基于线性滑移理论重构试件中多条节理几何形状以及刚度分布，实现岩石节理接触行为的表征。
（2）朝节理尖端方向节理界面之间的孔径减小，接触面积增大，节理剪切刚度和法向刚度均逐渐增大，通过节理刚度分布可判断节理的开裂区域以及扩展方向；不同轴向荷载作用下节理刚度变化明显著，可通过节理刚度实现节理界面受力分析；不同激励频率条件下节理刚度计算结果变化趋势一致。
（3）后续将开展复杂加载路径下岩石节理刚度分布的演化规律及机制研究，通过节理刚度分布的时空变化实现不同条件下岩石节理、断层界面不同位置接触状态的实时动态监测分析。
-
![]()
图 1 滑动面任意点的真实应力状况与极限平衡受力计算简图
Figure 1. Real stress states of any point on slip surface and calculation of limit equilibrium forces
![]()
图 2 滑面通过单元三角形微面矢量极限平衡计算简图
Figure 2. Calculation of vector limit equilibrium on triangle micro-plane of sliding surface over element
![]()
图 3 三角形微面矢量力在合矢量平面的投影示意图
Figure 3. Projection sketch of vector forces of triangular micro-plane in resultant vector plane
![]()
图 5 有限元网格及水平位移云图
Figure 5. Finite element meshes and nephogram of horizontal displacement
![]()
图 6 椭球滑动面对称面处无软夹层情况、有软夹层情况等效塑性应变云图
Figure 6. Equivalent plastic strain nephogram of ellipsoidal sliding surface without and with soft strata on symmetric plane
![]()
图 8 随投影方向角变化的安全系数、势能、势能比曲线
Figure 8. Curves of factor of safety, potential energy and potential energy ratio with respect to projection direction
![]()
图 9 楔体算例1与算例2有限元剖分网格图
Figure 9. Finite element meshes of wedges (example 1 and example 2)
![]()
图 10 楔体1对称材料、楔体1非对称材料、楔体2结构面单元的等效塑性应变云俯视图
Figure 10. Top views of equivalent plastic strain nephogram for wedge 1 (symmetric material), wedge 1 (asymmetric material) and wedge 2 in soft rock elements
![]()
图 11 楔体算例2合矢量平面内的矢量平衡图
Figure 11. Vector equilibrium of wedge 2 in resultant vector plane
![]()
图 12 楔体算例2随投影方向变化的安全系数、势能曲线
Figure 12. Variation of curves of factor of safety and potential energy of wedge 2 with projection direction
表 1 椭球滑动面土层力学参数
Table 1 Mechanical parameters of soil on ellipsoidal surface
参数 内摩擦角φ/(°) 黏聚力c/(kN·m-2) 重度/(kN·m-3) 弹性模量E/kPa 泊松比μ 剪胀角/(°) 土层 20 28.74 18.84 5.0×104 0.30 4 软层 10 0. 18.84 2.0×103 0.25 2 
下载: 导出CSV
表 2 椭球滑动面两种情况抗滑稳定计算结果
Table 2 Calculated results of stability of ellipsoidal sliding surface in two cases
计算方法 情况1无软夹层 情况2有软夹层 安全系数 与本文Kλ相比/% 安全系数 与本文Kλ相比/% Zhang-X极限平衡法[6] 2.122 -2.08 1.553 -14.13 Hungr简化Bishop法[6] 2.167 +0.04 1.620 -9.41 陈祖煜极限平衡法[2-3] 2.187 +0.96 1.640 -8.08 郑宏滑面极限平衡法[7-8] 2.140 -1.22 1.706 -3.89 Lam通用极限平衡法[9] — 1.603 -10.57 Huang极限平衡法[10] — 1.665 -6.46 Jiang主滑向极限平衡法[11] 2.127 -1.84 1.766 -0.37 极限分析上限法[3, 12] 2.262 +4.24 1.717 -3.23 应力数值解代数和法[13] — 1.607 -10.30 有限元应力主滑向极限平衡法[14] 2.226 +2.69 1.730 -2.46
下载: 导出CSV
表 3 矢量理论模型计算结果
Table 3 Calculation results of vector theoretical model
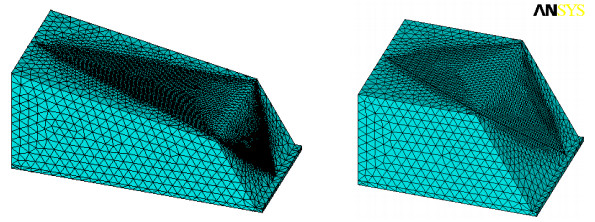
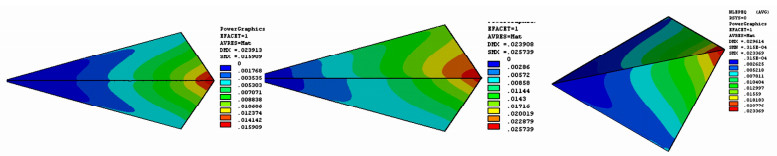
参数 本文矢量理论解 滑动力合矢量倾角和合矢量夹角δ 投影极值方向倾角和投影极值方向角θ 应力代数和法安全系数 滑面通过单元数和三角形微面数 情况1无软夹层 Kλ=2.1661，K=2.0546，λ=0.9485 倾角24.5607°，夹角δ=2.8630° 倾角32.8839°，θ=-8.3232° 代数和法K=2.1006，与本文Kλ相比为-3.12% 单元1606个，微面6420个 情况2有软夹层 Kλ=1.7725，K=1.7363，λ=0.9796 倾角25.8634°，夹角δ=1.1573° 倾角20.8109°，θ=-5.0528° 代数和法K=1.7404，与本文Kλ相比为-1.84% 单元1684个，微面6776个
下载: 导出CSV
表 4 楔体几何形体特征
Table 4 Geometric features of wedges
部位 楔体算例1 楔体算例2 倾向/(°) 倾角/(°) 倾向/(°) 倾角/(°) 左结构面 115 45 120 40 右结构面 245 45 240 60 顶面 180 10 180 0 坡面 180 60 180 60 楔体坡高/m 64.89 98.4
下载: 导出CSV
表 5 模型物理力学参数
Table 5 Physical and mechanical parameters of models
算例工况 内摩擦角φ/(°) 黏聚力c/(kN·m-2) 重度/(kN·m-3) 弹性模量E/kPa 泊松比 剪胀角/(°) 楔体1对称工况左右结构面 20 50 25.48 1.0×105 0.25 4 弹性岩体 25.48 5.0×106 0.20 楔体1非对称工况左结构面 20 50 25.48 1.0×105 0.25 4 右结构面 10 30 25.48 1.0×105 0.25 3 楔体2左右结构面相同 30 50 26.0 1.0×105 0.25 4 弹性岩体 26.0 5.0×106 0.20
下载: 导出CSV
表 6 楔体抗滑稳定算例计算结果
Table 6 Calculated results of anti-sliding stability of wedges
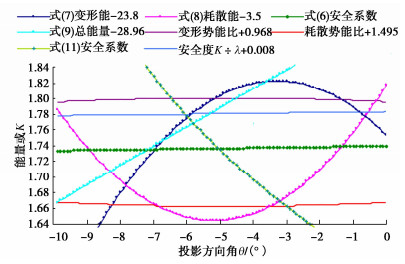
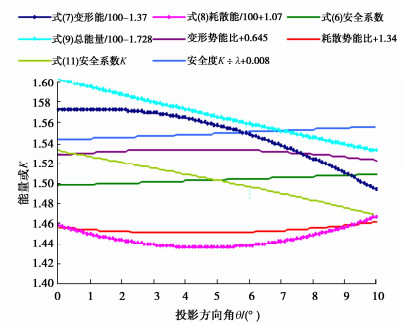
计算方法 楔体1材料对称 楔体1材料非对称 楔体2交线倾向11.3380° 安全系数 投影倾角/(°) 与本文比较/% 安全系数 投影倾角/(°) 与本文比较/% 安全系数 投影倾角/(°) 与本文比较/% 楔体极限平衡[15, 16] 1.5578 22.9098 +10.17 1.1815 22.9098 -7.91 1.6400 28.9964 +4.30 陈祖煜简化极限平衡法[2] 1.556 22.9098 +10.06 1.167 22.9098 -9.25 — 郑宏滑面严格平衡法[8] — 1.636 +4.07 极限平衡法[11] — 1.629 +3.66 主滑向应力代数和[14] — 1.497 -4.84
下载: 导出CSV
表 7 矢量理论模型计算结果
Table 7 Calculation results of vector theoretical model
参数 楔体1材料对称 楔体1材料非对称 楔体2交线倾向11.3380° 安全系数 投影倾角 安全系数 投影倾角 安全系数 投影倾角 本文矢量理论模型解 Kλ=1.3994 40.2520° Kλ=1.2750 28.7662° Kλ=1.5694 42.2410° 安全系数K和程度系数λ K=1.3365 λ=0.9551 K=1.2384 λ=0.9713 K=1.5034 λ=0.9580 合矢量夹角δ和投影倾向 δ=2.5649° 倾向0° δ=1.6438° 倾向1.6267° δ=2.3986° 倾向16.7218° 滑动力矢量倾角和倾向 倾角39.7084° 倾向0° 倾角29.1022° 倾向3.1532° 倾角44.0963° 倾向10.4716° 代数和法安全系数K K=1.3392 -4.50% K=1.2375 -3.03% K=1.4978 -4.78% 滑面通过单元和微面数 单元11616个 微面46493个 单元6936个 微面28014个
下载: 导出CSV
表 8 单元剖分尺寸对理论模型解的影响
Table 8 Influences of element size on solution of theoretical model
单元类型及尺寸 3 m四面体 3 m六面体 4 m六面体 5 m六面体 安全度系数Kλ 1.5711（+0.108%） 1.5694（0.0%） 1.5703（+0.057%） 1.5712（+0.115%） 安全系数K 1.5055 1.5034 1.5045 1.5054 程度系数λ 0.9582 0.9580 0.9581 0.9581 三角形微面数 28014 16417 10742 结构面单元数 13673 6936 4056 2646 单元总数 135732 342623 190545 127207 注：括号内数字为相对于3 m六面体单元的安全度系数Kλ变化率。
下载: 导出CSV
表 9 弹性模量变化对理论模型解的影响
Table 9 Influences of change of elastic modulus on solution of theoretical model
变化部位 弹性模量乘数 0.50 0.75 1.00 1.25 1.50 仅结构面 安全度系数Kλ 1.6042（+2.06%） 1.5858（+0.92%） 1.5712 1.5592（-0.77%） 1.5497（-1.39%） 程度系数λ 0.9623 0.9599 0.9581 0.9566 0.9553 仅岩体 安全度系数Kλ 1.5330（-2.49%） 1.5555（-1.01%） 1.5712 1.5825（+0.71%） 1.5920（+1.31%） 程度系数λ 0.9535 0.9562 0.9581 0.9595 0.9608 结构面
及岩体安全度系数Kλ 1.5711 1.5711 1.5712 1.5711 1.5712 程度系数λ 0.9581 0.9581 0.9581 0.9581 0.9584 注：括号内数字为相对于弹性模量乘数1.00的安全度系数Kλ变化率。
下载: 导出CSV
表 10 泊松比变化对理论模型的影响
Table 10 Influences of Poisson's change on solution of theoretical model
部位 泊松比μ μ=0.15 0.20 0.25 0.30 0.350 结构面 安全度系数Kλ 1.5849（+0.86%） 1.5787（+0.75%） 1.5712（0.0%） 1.5619（-0.60%） 1.4827（-1.29%） 程度系数λ 0.9601 0.9593 0.9581 0.9571 0.9559 岩体 安全度系数Kλ 1.5577（-0.87%） 1.5712（0.0%） 1.5856（+0.91%） 1.6016（+1.90%） 1.6171（+2.84%） 程度系数λ 0.9570 0.9581 0.9593 0.9609 0.9622 两者同比例 泊松比乘数 0.75μ 0.8μ 1.0μ 1.2μ 1.4μ 安全度系数Kλ 1.5685（-0.17%） 1.5689（-0.15%） 1.5712（0.0%） 1.5750（+0.24%） 1.5805（+0.59%） 程度系数λ 0.9584 0.9584 0.9581 0.9581 0.9583 注：括号内数字为相对于结构面泊松比μ=0.25、岩体泊松比μ=0.20的安全度系数Kλ变化率。
下载: 导出CSV
表 11 剪胀角变化对理论模型解影响
Table 11 Influences of change of dilatancy angle on theoretical model
剪胀角 0° 2° 4° 6° 8° 安全度系数Kλ 1.5800（+0.56%） 1.5753（+0.26%） 1.5712（0.0%） 1.5681（-0.20%） 1.5646（-0.42%） 安全系数K 1.5207 1.5126 1.5054 1.4997 1.4935 程度系数λ 0.9625 0.9602 0.9581 0.9564 0.9546 注：括号内数字为相对于剪胀角4°的安全度系数Kλ变化率。
下载: 导出CSV
表 12 不同塑性准则对理论模型解的影响
Table 12 Influences of different plastic criteria on solution of theoretical model
塑性准则 等底面积D-P 外接圆D-P 弹性 安全度系数Kλ 1.5712 1.4200（-10.64%） 1.2960（-21.23%） 安全系数K 1.5054 1.3315 1.1801 程度系数λ 0.9581 0.9397 0.9106 滑动力合矢量/(104 kN) 292.525 306.053（+4.42%） 321.222（+8.93%） 滑动力合矢量倾角/(°) 44.1091 48.5751 51.6391 抗滑力合矢量/(104 kN) 439.202 405.907（-8.20%） 379.014（-10.63%） 合矢量夹角/(°) 2.3900 3.5533 5.1188 极值方向倾角/(°)
极值方向倾向/(°)42.3137
16.560146.8366
20.854551.4313
19.4447注：括号内数字为相对于等底面积D-P准则的变化率。
下载: 导出CSV
-
[1] DUNCAN J M. State of the art: limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering, 1996, 122(7): 577-596. doi: 10.1061/(ASCE)0733-9410(1996)122:7(577)
[2] 陈祖煜, 弥宏亮, 汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525-529. http://cge.nhri.cn/article/id/10783 CHEN Zuyu, MI Hongliang, WANG Xiaogang. A three-dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525-529. (in Chinese) http://cge.nhri.cn/article/id/10783
[3] 陈祖煜. 土质边坡稳定分析: 原理·方法·程序[M]. 北京, 中国水利水电出版社, 2003. CHEN Zuyu. Soil Slope Stability Analysis: Theory, Methods and Programs[M]. Beijing: China Water Power Press, 2003: 335-376. (in Chinese)
[4] 孙建生. 基于有限元应力载荷宏观刚性滑裂面极限平衡抗滑稳定计算理论[J]. 岩石力学与工程学报, 2018, 37(4): 862-875. SUN Jiansheng. Theoretical model of stability calculation of macro-rigid sliding planes with FEM stress load based on limit equilibrium[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 862-875. (in Chinese)
[5] 孙建生. 投影方向极值原理的滑裂面应力矢量极限平衡抗滑稳定计算理论[J]. 计算力学学报, 2023, 40(1): 93-104. SUN Jiansheng. Theoretical model of limit equilibrium anti-sliding stability of stress vector on sliding planes based on projection direction extreme principle[J]. Chinese Journal of Computational Mechanics, 2023, 40(1): 93-104. (in Chinese)
[6] XING Z. Three-dimensional stability analysis of concave slopes in plan view[J]. Journal of Geotechnical Engineering, 1988, 114(6): 658-671. doi: 10.1061/(ASCE)0733-9410(1988)114:6(658)
[7] 郑宏. 严格三维极限平衡法[J]. 岩石力学与工程学报, 2007, 26(8): 1529-1537. doi: 10.3321/j.issn:1000-6915.2007.08.002 ZHENG Hong. A rigorous three-dimensional limit equilibrium method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1529-1537. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.08.002
[8] ZHENG H. Eigenvalue problem from the stability analysis of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 647-656. doi: 10.1061/(ASCE)GT.1943-5606.0000071
[9] LAM L, FREDLUND D G. A general limit equilibrium model for three-dimensional slope stability analysis[J]. Canadian Geotechnical Journal, 1993, 30(6): 905-919. doi: 10.1139/t93-089
[10] HUANG C C, TSAI C C. New method for 3D and asymmetrical slope stability analysis[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(10): 917-927. doi: 10.1061/(ASCE)1090-0241(2000)126:10(917)
[11] JIANG Q H, ZHOU C B. A rigorous method for three-dimensional asymmetrical slope stability analysis[J]. Canadian Geotechnical Journal, 2018, 55(4): 495-513. doi: 10.1139/cgj-2017-0317
[12] CHEN Z Y, WANG X G, HABERFIELD C, et al. A three-dimensional slope stability analysis method using the upper bound theorem[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 369-378. doi: 10.1016/S1365-1609(01)00012-0
[13] STIANSON J R, FREDLUND D G, CHAN D. Three-dimensional slope stability based on stresses from a stress-deformation analysis[J]. Canadian Geotechnical Journal, 2011, 48(6): 891-904. doi: 10.1139/t11-006
[14] 苏振宁. 三维边坡稳定有限元极限平衡法研究及应用[D]. 大连: 大连理工大学, 2021. SU Zhennin. Research and Application of Finite Element Limit Equilibrium Method for Three-Dimensional Slope Stability[D]. Dalian: Dalian University of Technology, 2021. (in Chinese)
[15] HOEK E, BRAY J D. Rock Slope Engineering[M]. 3rd ed. Boca Raton: CRC Press, 1981.
[16] 陈祖煜. 岩质边坡稳定分析: 原理·方法·程序[M]. 北京: 中国水利水电出版社, 2005. CHEN Zuyu. Rock Slope Stability Analysis: Theory, Methods and Programs[M]. Beijing: China Water & Power Press, 2005. (in Chinese)
[17] CHEN Z Y, MI H L, ZHANG F M, et al. A simplified method for 3D slope stability analysis[J]. Canadian Geotechnical Journal, 2003, 40(3): 675-683. doi: 10.1139/t03-002
[18] 赵尚毅, 郑颖人, 刘明维, 等. 基于Drucker-Prager准则的边坡安全系数定义及其转换[J]. 岩石力学与工程学报, 2006, 25(增刊1): 2730-2734. ZHAO Shangyi, ZHENG Yingren, LIU Mingwei, et al. Definition and transformation of slope safety factor based on Drucker-Prager criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S1): 2730-2734. (in Chinese)
[19] 孙建生. 挡土墙土压力研究的错误倾向[J]. 岩土工程学报, 2016, 38(7): 1324-1329. doi: 10.11779/CJGE201607021 SUN Jiansheng. Error tendency for studying earth pressure on retaining walls[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1324-1329. (in Chinese) doi: 10.11779/CJGE201607021
[20] 孙建生. "矢量和法" 抗滑稳定计算模型的力学概念错误[J]. 岩土工程学报, 2021, 43(5): 975-980. doi: 10.11779/CJGE202105024 SUN Jiansheng. Mechanical concept errors in anti-sliding stability computational model of "vector sum method"[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 975-980. (in Chinese) doi: 10.11779/CJGE202105024
[21] 孙建生. 关于"稳定安全系数计算公式中荷载与抗力错位影响探讨"的质疑[J]. 岩土工程学报, 2021, 43(11): 2146. doi: 10.11779/CJGE202111024 SUN Jiansheng. Query about "Discussion of dislocation phenomena of resistance and load in formula for stability safety factor"[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2146. (in Chinese) doi: 10.11779/CJGE202111024
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 298
- HTML全文浏览量: 44
- PDF下载量: 95
- 被引次数: 1
