Delayed crushing time for particles of rockfill materials
-
摘要: 堆石料颗粒的延迟破碎是指颗粒受力一定时间后发生的破碎。给出颗粒延迟破碎时间是采用离散元法模拟堆石料流变进行定量分析的前提。从断裂力学出发，将颗粒内部缺陷概化为一币形裂纹，给出了颗粒瞬时破碎强度与裂纹半长的关系。将颗粒瞬时强度作为随机变量，采用Logistic函数描述其分布，并运用求解随机变量函数概率分布的方法，求出裂纹半长的概率分布。然后将颗粒岩石加工成板试样，通过双扭松弛试验，测量其亚临界裂纹扩展速度。在此基础上对颗粒裂纹扩展方程进行积分，得到裂纹贯通（即颗粒延迟破碎）的时间表达式。以裂纹半长为随机变量，求出颗粒延迟破碎时间的概率分布。云南红石岩堰塞坝工程白云岩颗粒的分析结果表明，在相同应力水平下，大颗粒延迟破碎时间长且离散性大，小颗粒延迟破碎时间短且离散性小。这与堆石料室内流变试验稳定快而现场堆石坝流变持续时间长的宏观现象相吻合。颗粒延迟破碎时间的给出为采用离散元模拟堆石料流变，提升堆石料流变本构模型，解决堆石料室内流变试验的时间尺寸效应奠定了基础。Abstract: The delayed crushing of rockfill particles is specifically referring to the crushing of particles after loading for a certain period time, which is the basis for the rheological deformation calculation using the discrete element method (DEM). Based on the fracture mechanics, the internal defects of particles are generalized into a coin-shaped crack, and the relationship between the instantaneous crushing strength of particles and the half-length of the crack is developed. The Logistic function is used to describe the distribution of particle strength as a random variable, and the probability distribution of half-length of crack is obtained by using the method of solving the probability distribution of random variable function. The rockfill particle is processed into a plate specimen, and its sub-critical crack propagation velocity is measured using a bi-torsional relaxation test. On this basis, the formula for crack propagation of particles is integrated to obtain the time expression for crack penetration (i.e. delayed particle crushing). The probability distribution of delayed crushing time of particles can be calculated using the half-length of the crack as a random variable. The results of dolomite particles in Hongshiyan landslide dam in Yunnan Province show that under the same stress level, large particles have long delayed crushing time and large standard deviation, while small particles have short delayed crushing time and small standard deviation. This is consistent with the macro-phenomenon that the rheological deformation of rockfill materials converges quickly in laboratory tests, while the rheological deformation of rockfill dam lasts a long time in field. The development of delayed crushing time of particles provides conditions for simulating the rheological behaviors of rockfill using the DEM, improving the rheological constitutive model for rockfill materials, and solving the time size-effects of rockfill rheology for laboratory tests.
-
0. 引言
流变变形是堆石坝主要变形，也是影响坝体安全、评价大坝安全性的主要指标。观测资料显示，坝体竣工后发生的流变变形可持续几年、十几年甚至更长时间。堆石料流变变形与其颗粒的延迟破碎密切相关。实际工程中，堆石料颗粒受力有3种情况：①颗粒受力大于瞬时强度，颗粒发生瞬时破碎，形成堆石体的瞬时变形。②颗粒受力介于瞬时强度和长期强度之间，不会发生瞬时破碎，但在颗粒长期受力过程的某个时间点上发生破碎，引起堆石体的流变变形。③颗粒受力小于长期强度，颗粒不破碎，堆石体不发生流变变形。可见堆石料流变与颗粒破碎时间有关。
近些来离散元模拟逐渐成为研究堆石料结构性、尺寸效应以及本构模型的主要方法之一[1-4]。其中单颗粒破碎特性是堆石料离散元数值模拟定量分析的基础。已有试验表明[5-6]单颗粒破碎强度表现出明显的离散性和尺寸效应。Mcdowell[7]曾对0.5，1.0，2.0 mm粒径的石英砂进行单轴压缩实验，并采用σ表示颗粒的破碎强度，σ=F/d2，F为颗粒破碎力，d为颗粒粒径，发现颗粒强度服从Weibull分布。Ovalle等[8]采用4参数Weibull公式描述岩石骨料破碎强度的尺寸效应。Rozenblat等[9]认为在大多数情况下，单个颗粒破碎强度分布可以用Weibull分布、对数正态分布以及Logistic分布函数来拟合，其中Logistic分布函数拟合效果好且公式简便。Deluzarche等[10]、Alaei等[11]针对典型碎石料颗粒建立了块(Clump)模型，利用相关破碎准则对颗粒接触力进行破碎判断，实现了预设破碎模式的计算。Alonso等[12]在Clump模型的劈裂破碎准则中引入裂缝长度来体现破碎（包括延时破碎）的尺寸效应特征，但没有给出破碎时间表达式。胡训健等[13]将等效晶质模型和应力腐蚀模型结合，建立了考虑晶体粒径分布的分均值性流变颗粒流模型。笔者[14]基于应力腐蚀理论构建了基于亚临界裂缝扩展的堆石流变细观模型，编写了模拟室内堆石流变试验的颗粒流程序，并结合室内试验确定了模型参数。通过颗粒流数值试验揭示了堆石料流变变形过程中的颗粒破碎规律和断裂力学原理。现有颗粒延时破碎的研究主要关注裂纹扩展过程、破坏模式和破碎强度，对于颗粒破碎时间及其尺寸效应的研究较少。
为此，本文基于断裂力学理论，将颗粒内部缺陷概化为一币形裂纹，通过单粒破碎试验确定了颗粒瞬时破碎强度与裂纹半长的关系式。采用Logistic函数描述颗粒瞬时强度的分布，并通过求解随机变量函数概率分布的方法，确定初始裂纹半长的概率分布。然后通过同颗粒材质的薄板双扭试验，测量亚临界裂纹扩展速度。以裂纹半长为随机变量，求出不同应力水平下颗粒延迟破碎时间的概率分布函数。
1. 堆石料颗粒内部概化裂纹半长
堆石颗粒内部存在着尺寸、方位、密度分布并不一致的微缺陷，但这些微缺陷既无法量测，也难以简单描述。格林菲斯理论认为，材料内部存在许多细微裂隙，在力的作用下，这些裂隙的周围，特别是缝端，会产生应力集中现象。材料的破坏从缝端开始，经过裂隙扩展、贯通，最后导致材料完全破坏。将材料中含有大量方向杂乱的微裂隙，概化为一个张开的椭圆形裂缝，进而推导出格里菲斯强度公式。堆石颗粒多为空间不规则形状，其颗粒破碎属于接触力作用下的三维力学问题。颗粒内部存在着各种缺陷可概化为一个三维的币形裂纹，在受力劈裂过程中，裂纹尖端的应力强度因子查《应力强度因子手册》[15]为
$$ {K_ \text{I}} = 2{\sigma _\theta }Y\sqrt {a/\mathtt{π} } 。 $$ (1) 式中：σθ为垂直加载轴的颗粒张拉劈裂应力；π为圆周率；Y为形状因子，为缝径比a/R的函数，a为概化裂纹半长，R为粒径的一半。
形状因子Y在《应力强度因子手册》中以图表方式给出，不方便公式使用。Srivastava等[16]在研究球形岩石颗粒内部存在一币型裂纹时，给出了参数Y的表达式。当a/R≤0.6时：
$$ Y\left( {\frac{a}{R}} \right) = 1 + 1.5433{\left( {\frac{a}{R}} \right)^3} - 2.387{\left( {\frac{a}{R}} \right)^5} + 2.3818{\left( {\frac{a}{R}} \right)^6} + \\ 3.2711{\left(\frac{a}{R}\right)}^{7}-6.447{\left(\frac{a}{R}\right)}^{8}-0.2107{\left(\frac{a}{R}\right)}^{9}。 $$ (2) 当a/R为0.6，0.7，0.8，0.9时，Y取值为1.27016，1.32240，1.47210，1.81071。
Chau等[17]推导了球形岩石颗粒受压时的应力解析解，认为除边缘外，在加载轴上垂直加载轴的拉应力近似呈均匀分布，为$ {\sigma _\theta } $=βF/πR2，β为加载轴上张拉应力归一化系数。显然$ {\sigma _\theta } $与颗粒表征强度F/d2=σ存在联系，即
$$ \sigma = \mathtt{π} {\sigma _\theta }/4\beta 。 $$ (3) 进行颗粒瞬时破碎强度试验时，在劈裂应力σ作用下颗粒被快速压碎。若初始裂纹半长为$ {a_0} $，则裂纹尖端的应力强度因子需达到断裂韧度KIC才能实现，故有
$$ \sigma = \frac{{\mathtt{π} {K_\text{IC}}}}{{8\beta Y}}\sqrt {\mathtt{π} /{a_0}} 。 $$ (4) 初始裂纹半长$ {a_0} $为
$$ {a_0} = \frac{{{\mathtt{π} ^3}K_{_{IC}}^2}}{{64{\beta ^2}{Y^2}{\sigma ^2}}} 。 $$ (5) 岩石颗粒的断裂韧度KIC可先将大粒径的岩石颗粒加工成板，进行岩石的双扭松弛试验，直接加载至破坏以测量其断裂韧度。因为形状因子Y为缝径比a/R的函数，故初始裂纹半长$ {a_0} $并不能直接给出显式表达式，可采用隐函数形式表达：
$$ {a_0} = f({K_\text{IC}},\sigma ) 。 $$ (6) 式中：σ为颗粒劈裂时的应力，即颗粒的瞬时破碎强度，由单粒压缩试验确定。利用式（5），可通过迭代求取初始半裂纹半长$ {a_0} $。对颗粒进行强度试验，得到颗粒瞬时强度σ，先假设初始裂纹半长，求取形状因子Y，代入式（5）后，求出新的裂纹半长，若前后两次裂纹半长满足精度要求，则终止迭代。
2. 颗粒延时破碎时间
考虑含有初始裂纹半长为$ {a_0} $的堆石颗粒裂纹扩展情况。Charles[18]根据亚临界裂纹扩展理论，给出岩石内部裂纹扩展速度V与应力强度因子KI的关系：
$$ V = AK_ \text{I}^n 。 $$ (7) 式中：A, n为亚临界裂纹扩展参数，通过双扭试验测定。裂纹扩展速度V、裂纹半长a与时间t的关系为
$$ V = \text{d}a/\text{d}t 。 $$ (8) 联立式（1），（7），（8）可得
$$ V = \frac{{\text{d}a}}{{\text{d}t}} = \frac{{A{Y^n}{2^n}\sigma _\theta ^n{a^{n/2}}}}{{{\mathtt{π} ^{n/2}}}} 。 $$ (9) 式（9）分别对裂纹半长a和时间t进行积分，得到裂纹半长与时间的关系为
$$ t = \frac{{{\mathtt{π} ^{n/2}}}}{{(n - 2){2^{n - 1}}A{Y^n}}} \cdot \frac{{a_0^{(2 - n)/2}}}{{\sigma _\theta ^n}}\left[ {1 - \left( {\frac{a}{{{a_0}}}} \right)_{}^{(2 - n)/2}} \right] 。 $$ (10) 随着荷载的持续施加，裂纹不断扩展，当裂纹尖端应力强度因子达到断裂韧度时，裂纹迅速贯通颗粒，裂纹半长变为颗粒半径，远大于初始裂纹半长a0。并且n的数值远大于2，(a/a0)的指数为负，故式（10）右侧括号第二项的数值近似为0，式（10）可简化为
$$ {t_ \text{f}} = \frac{2}{{(n - 2)}} \cdot \frac{{{\mathtt{π} ^{n/2}}a_0^{(2 - n)/2}}}{{A{Y^n}{2^n}\sigma _\theta ^n}} 。 $$ (11) 式中：tf为颗粒受劈裂应力σθ作用时的延迟破碎时间。
颗粒瞬时破碎时，在瞬时破碎强度σ作用下，裂纹尖端的应力强度因子为断裂韧度，即$ {K_\text{IC}} = $ $ 2\sigma Y\sqrt {a/\mathtt{π} } $，故$ 1/(2Y\sqrt {a/\mathtt{π} } ) = \sigma /{K_\text{IC}} $。将该式代入式（11）得
$$ {t_ \text{f}} = \frac{{2a_0^{}}}{{(n - 2)AK_\text{IC}^n}}{\left( {\frac{\sigma }{{\sigma _\theta ^{}}}} \right)^n} 。 $$ (12) 这就是断裂韧度为KIC、初始裂纹半长为$ a_0^{} $、瞬时破碎强度为$ \sigma $的岩石颗粒，在劈裂应力$ \sigma _\theta ^{} $作用下，颗粒破碎所需要的流变时间，即颗粒延迟破碎时间表达式。其中，颗粒瞬时强度σ由单粒强度试验确定，参数A，n由双扭松弛试验确定，断裂韧度KIC由双扭极限加载试验确定。
3. 单粒强度试验与双扭试验
为了验证颗粒延迟破碎时间公式的有效性，进行了单粒强度试验与双扭试验。试验材料来源于云南省鲁甸地震形成的红石岩堰塞坝堆积体，为白云岩颗粒。
3.1 单粒强度试验
单粒强度试验采用的颗粒形状大致相似、粒状饱满、棱角分明。粒径由小到大依次为20~24，24~28，28~32，32~36，36~40，40~44，44~48，48~52，52~56，56~60，120，180，240，300 mm共14个粒组。
采用σ =F/d2整理颗粒破碎强度，F为颗粒破碎力，d为颗粒粒径。Rozenblat等[9]指出Logistic函数适合描述颗粒强度分布：
$$ {P_ \text{s}} = 1 - {\left[ {1 + {{\left( {\frac{\sigma }{{{\sigma _{50}}}}} \right)}^S}} \right]^{ - 1}} 。 $$ (13) 式中：Ps为颗粒破碎概率；σ为颗粒瞬时破碎强度；$ {\sigma _{50}} $为该粒组颗粒均值特征强度；S为强度离散性的参数。
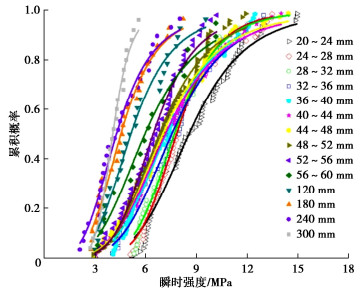
将堆石颗粒所有瞬时破碎强度σ从小到大排列，计算颗粒破碎概率，采用Logistic分布函数进行拟合，如图 1所示。所有的粒组拟合参数如表 2所示。结合图 1和表 1可以看到，Logistic分布函数能够很好地描述颗粒瞬时破碎强度的分布规律，各粒组瞬时强度的拟合曲线与试验数据的拟合度基本在0.98以上[19]。并且，各粒组均值特征强度σ50随着粒径的增大而减小，体现出明显的尺寸效应。
![]()
图 1 各粒组瞬时强度的Logistic分布图Figure 1. Logistic distribution of instantaneous strength for various grain groups表 1 各粒组瞬时强度Logistic分布参数Table 1. Logistic distribution parameters of instantaneous strength for various grain groups粒组/mm 20~24 24~28 28~32 32~36 36~40 40~44 44~48 48~52 52~56 56~60 120 180 240 300 σ50/MPa 8.55 7.82 7.69 7.53 7.20 7.15 6.99 6.80 6.44 5.94 5.12 4.53 4.27 4.05 S 5.09 6.55 6.07 4.62 4.47 4.17 4.24 4.57 5.13 3.70 4.18 4.26 3.89 7.61 R2 0.983 0.989 0.991 0.984 0.991 0.995 0.99 0.990 0.985 0.979 0.981 0.979 0.984 0.989 表 2 亚临界裂纹扩展参数及断裂韧度Table 2. Subcritical crack parameters and fracture toughnesses编号 A n 编号 KIC/(MN·m-3/2) DT-1 5.50×10-11 66.82 DT-6 1.25 DT-2 5.13×10-10 57.09 DT-7 1.20 DT-3 1.12×10-12 56.71 DT-8 1.18 DT-4 1.10×10-10 45.35 DT-9 1.21 DT-5 2.19×10-10 60.48 DT-10 1.17 均值 1.8×10-10 57.29±6.98 均值 1.20±0.028 3.2 双扭试验
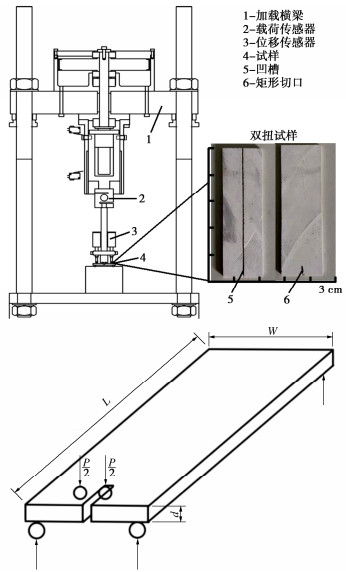
双扭试验采用大连理工大学研制的YSB-Ⅰ型岩石双扭试验仪，见图 2。加载框架为高强度反力框架，配备20，1 kN载荷传感器各一个，一个±2.5 mm的位移传感器，位移加载速率范围为0.01~50 mm/min。
![]()
图 2 双扭试验装置及双扭试样受力示意图Figure 2. Schematic diagram of device and specimen loading of double-torsion tests双扭试验首先将岩块料加工成长度为150 mm、宽度为50 mm、厚度为4.8 mm的薄片状试样，并在试样中央加工一条凹槽。槽宽2 mm、槽深约试样厚度的1/3，最后在试样一端切割一矩形切口，保证试验过程中裂纹沿着试样中央扩展。试样见图 2。
试样放置在配有4粒钢珠的平台上，通过控制加载头的位移进行加载，加载头下方有两粒对称钢珠保证试样受力为点荷载，加载示意图如图 2所示。
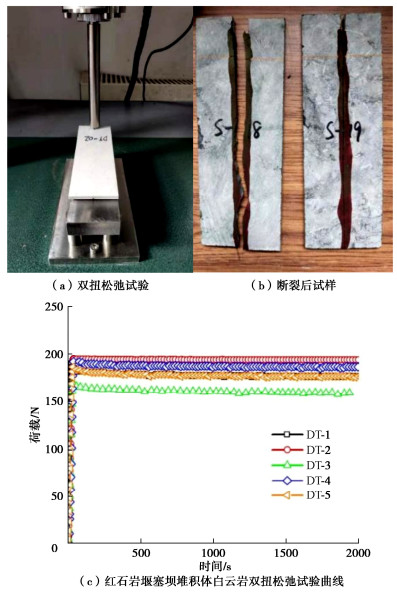
先将试样放置在加载台上并严格对中，采用位移控制进行加载，以0.05 mm/min的加载速率进行预裂；预裂完毕后以0.5 mm/min的加载速率加载到临界荷载值附近，保持加载头位移不变进行双扭松弛试验，见图 3（a）；松弛试验完成后以5 mm/min的加载速率加载直至裂纹扩展引起试样断裂，断裂后试样见图 3（b）；试验过程中记录荷载、位移随时间的变化，绘制双扭松弛试验的力与位移曲线，见图 3（c）。
Williams等[20]指出应力强度因子和裂纹扩展速度为
$$ {K_ \text{I}} = P{W_ \text{m}}\sqrt {\frac{{3(1 + \nu )}}{{W{d^3}{d_{\text{n}}}}}} \text{，} $$ (14) $$ V = \frac{{ \text{d}a}}{{\text{d}t}} = - \frac{{W{d^3}Ey}}{{6W_ \text{m}^2{P^2}(1 + \nu )}}\frac{{\text{d}P}}{{\text{d}t}}。 $$ (15) 式中：P为施加荷载；Wm为加载力臂；$ \nu $为泊松比；W，d，dn分别为试样的宽度、厚度以及凹槽的厚度；a为裂纹半长；E为岩石材料杨氏模量；y为竖向位移；dP/dt为荷载变化率。
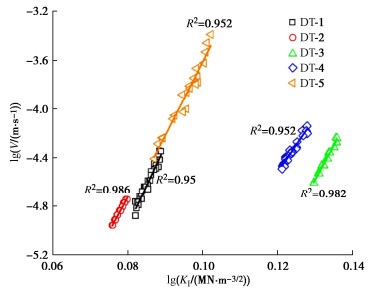
采用式（14），（15）计算松弛试验过程中应力强度因子和裂纹扩展速度，将计算结果绘制在双对数图表中，并采用式（7）对试验数据进行拟合，如图 4所示。
使用双扭试验仪进行双扭断裂加载试验，采用恒定加载速率法测量试样断裂韧度，将断裂加载试验中最大荷载值PC代入下式：
$$ {K_\text{IC}} = {P_ \text{C}}{W_ \text{m}}\sqrt {\frac{{3(1 + \nu )}}{{W{d^3}{d_ \text{n}}}}} 。 $$ (16) 通过双扭松弛试验（DT-1~DT-5）和双扭断裂加载试验（DT-6~DT-10）求出各组试验亚临界裂纹扩展参数拟合结果及断裂韧度计算结果如表 2所示。测得的白云岩材料亚临界裂纹扩展参数A的均值为1.8×10-10，n的均值为57.29，断裂韧度KIC为1.2 MN/m3/2。
参数A，n的测量值有一定离散性，原因是试验试件由红石岩堰塞坝堆积体岩块加工而成。而红石岩堰塞坝堆积体是鲁甸地震引起两岸山体滑坡所致，试验岩块取自堆积体表面。可以设想岩块颗粒来自近千米高差的山顶，岩石的风化程度不一，力学特性差异较大，在滑坡翻滚而下的过程中损伤程度不一，其力学性质的离散性是必然的。如颗粒强度的变异系数为33%~78%。在岩块加工成板状试样的过程中，有的岩块可以成样，有的则难以成样，直接破碎。可以看出红石岩堰塞坝岩石颗粒的强度低，容易破碎。因此与其他工程新鲜岩石相比，试验得到的红石岩堰塞坝岩石颗粒裂纹扩展速度参数偏大。
4. 颗粒内部裂纹半长的概率分布函数
白云岩颗粒材料的断裂韧度试验表明，断裂韧度变异系数仅为2.3%，可以将断裂韧度视为材料常数。白云岩堆石颗粒的强度试验表明其具有一定的离散性，并服从Logistic概率分布函数，可将其视为随机变量。式（6）给出了颗粒中初始裂纹半长是断裂韧度和瞬时破碎强度的函数。这样，颗粒中初始裂纹半长a0自然也是一随机变量，可依据概率论中求解随机变量的函数概率分布方法，求出初始裂纹半长的概率分布。由于含缺陷颗粒强度与内部裂纹半长具有强相关关系，由式（6）可知函数$ {a_0} = f(\sigma ) $为严格单调函数，$ f(\sigma ) $处处可导且恒有$ f'(\sigma ) < 0 $，且瞬时强度σ服从Logistic分布，则裂纹半长的分布函数为
$$ {F_{{a_0}}}({a_0}) = {F_\sigma }(h({a_0})) = {\left[ {1 + {{\left( {\frac{{{K_\text{IC}}{\mathtt{π} ^{1.5}}}}{{8Y\beta {\sigma _{50}}{a_0}^{0.5}}}} \right)}^S}} \right]^{ - 1}} 。 $$ (17) 式中：h(a0)为f(σ)的反函数。
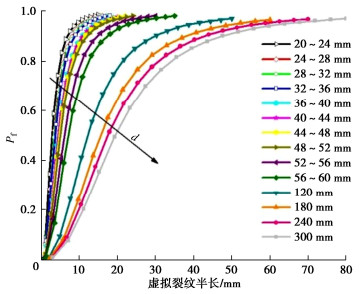
将试验测得参数代入式（17），可以得到不同粒径下初始裂纹半长分布函数，见图 5。从图 5中可以看出即使是在同一粒径下裂纹半长分布具有一定离散性；不同粒径颗粒内部裂纹分布存在明显的粒径相关性。
![]()
图 5 白云岩颗粒内部虚拟裂纹初始半长的分布函数Figure 5. Half-length distribution of initial virtual crack of dolomite particles5. 颗粒延迟破碎时间的概率分布函数
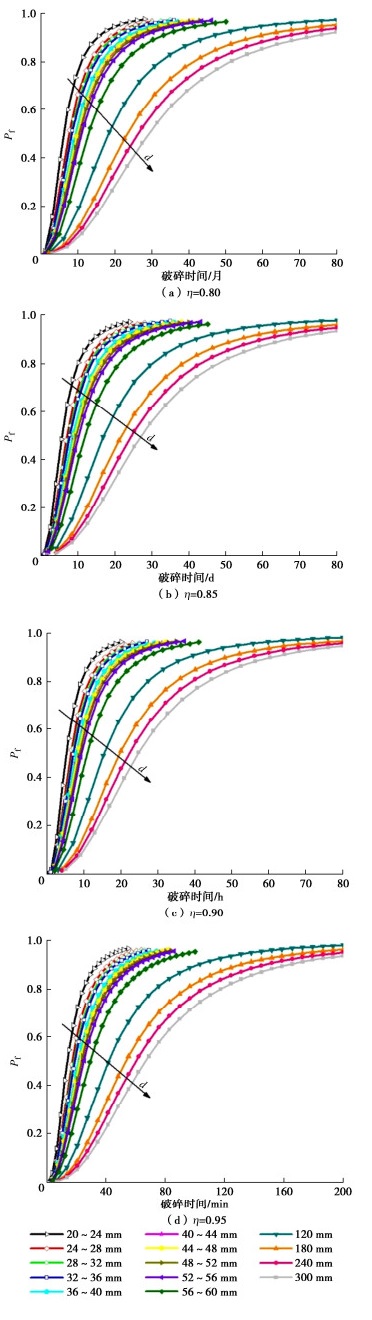
第4节讨论了堆石颗粒内部初始裂纹半长的分布函数。本节将根据式（12）讨论颗粒延时破碎时间的概率分布。在式（12）中断裂韧度KIC为常量；裂纹初始半长为a0为随机变量，其概率分布函数见上节。定义应力σθ与颗粒瞬时强度σ之比为颗粒受力的应力水平η，即η=σθ/σ。采用求解随机变量函数概率分布的方法，可得到不同应力水平颗粒延迟破碎时间的累计分布函数：
$$ {F_ \text{t}}(t) = {\left[ {1 + {{\left( {\frac{{{K_\text{IC}}{\mathtt{π} ^{1.5}}}}{{8Y\beta {\sigma _{50}}\sqrt t {\eta ^n}{{\left( {\frac{{(n - 2)AK_\text{IC}^n}}{2}} \right)}^{0.5}}}}} \right)}^S}} \right]^{ - 1}} 。 $$ (18) 从式（18）可以看出延迟劈裂时间主要受σ50，η的影响，其他参数均与岩石材料性质有关，在本研究中均为常量。分别对不同粒径颗粒在施加应力水平η为0.8，0.85，0.9，0.95作用下的延迟破碎时间进行计算，结果如图 6。可以看出，同一种堆石颗粒材料延迟破碎时间主要受粒径和应力水平影响。当施加的应力水平为0.8时，延迟破碎时间主要分布在几个月到几十个月范围内。当施加的应力水平达到0.95时，延迟破碎时间会在几分钟到200 min。可见延迟破碎时间对施加的应力水平非常敏感。对于同一应力水平作用下，颗粒粒径越大延迟破碎时间越长，离散性也越大，表现出明显的粒径相关性。
![]()
图 6 不同应力水平下各粒组白云岩延迟破碎时间预测Figure 6. Prediction of delayed crushing time of various dolomite particle groups under different stress levels6. 裂纹半长及延迟破碎时间的粒径相关性
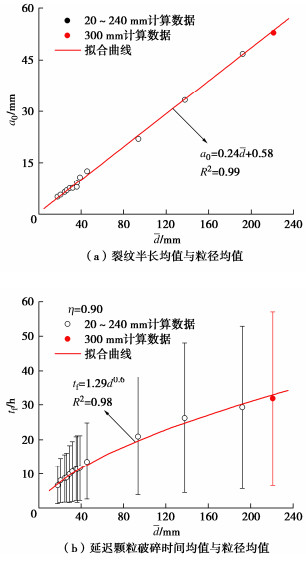
裂纹半长及延迟破碎时间与粒径的关系见图 7及表 3。由图 7（a）可见，裂纹半长均值与颗粒粒径呈良好的线性关系。图 7（b）示出了白云岩颗粒在应力水平0.9时延迟破碎时间与粒径呈幂函数关系。采用300 mm粒径颗粒的试验结果进行验证，其中裂纹半长和延迟劈裂破碎时间的预测值和计算值的相对误差为1.4%，3.5%。从图 7（b）还可以看出，随着粒径的增大，颗粒破碎时间的标准差逐渐增大。说明大颗粒岩石延迟破碎时间的离散性比小颗粒大。
![]()
图 7 白云岩颗粒参数的尺寸相关性曲线Figure 7. Size correlation curves of parameters of dolomite particles表 3 参数的尺寸相关性模型Table 3. Models for size correlation of parameters参数名称 经验模型 R2 300 mm粒径颗粒预测误差/% 裂纹半长/mm $ {a_0} = 0.24\overline d + 0.58 $ 0.99 1.4 延迟破碎时间/h $ {t_ \text{f}} = 1.29{\overline d ^{0.6}} $ 0.98 3.5 在相同应力水平下，大颗粒延迟破碎时间长且离散性大，小颗粒延迟破碎时间短且离散性小。大、小粒径颗粒延迟破碎时间的这种差异导致了室内缩尺堆石料与原型足尺堆石料流变演化规律及稳定时间的不一致。把这种现象称为堆石料流变的时间缩尺效应。室内缩尺料流变试验一般在7 d左右变形就已稳定，有的稳定时间为2~3 d。但现场堆石坝的流变变形持续时间可维持几年甚至十几年。沈珠江[21-22]曾经指出，通过坝体观测变形的反馈分析确定堆石料流变参数是唯一可行的途径，对反映时间因素的流变参数建议采用反馈值，而非试验值。这也说明室内流变试验的时间参数并不反映坝体堆石料的实际情况。
这是因为室内试验的缩尺料颗粒小且级配窄，在承受恒载的条件下，颗粒的延迟破碎时间短且离散性小。即堆石料在较短的时间内延迟破碎完毕，变形随即趋于稳定。而堆石坝现场，足尺堆石料粒径大且级配宽，小颗粒部分会在短时间内延迟破碎完毕，但大颗粒的延迟破碎时间长且离散性大。故实际堆石坝的流变需要较长的时间才能趋于稳定。
7. 结论
基于断裂力学理论，将堆石料颗粒内部缺陷概化为一币形裂纹，推导了堆石料颗粒瞬时强度与裂纹半长的关系式，并结合亚临界裂纹拓展理论推导了堆石料颗粒的延迟破碎时间公式。在此基础上，通过红石岩堰塞坝堆积体白云岩颗粒的单粒强度试验和双扭试验，求出各种应力水平下白云岩颗粒内部裂纹半长和延迟破碎时间的概率分布函数。
（1）云南红石岩堰塞坝工程白云岩颗粒的瞬时强度具有明显的离散性并且服从Logistic分布。各粒组均值特征强度σ50随着粒径的增大而减小，体现出明显的尺寸效应。
（2）云南红石岩堰塞坝工程白云岩颗粒的裂纹半长具有明显的尺寸效应，其与颗粒平均粒径呈线性关系a0=0.24d+0.58。
（3）在相同应力水平下，大颗粒延迟破碎时间长且离散性大，小颗粒延迟破碎时间短且离散性小。大、小粒径颗粒延迟破碎时间的这种差异导致了室内缩尺堆石料与原型足尺堆石料流变演化规律及稳定时间的不一致，即堆石料流变的时间缩尺效应。这与堆石料室内流变试验稳定快而现场堆石坝流变持续时间长相吻合。云南红石岩堰塞坝工程白云岩颗粒延迟破碎时间与颗粒平均粒径呈指数关系tf=1.29d0.6。
颗粒延迟破碎时间的给出为离散元模拟堆石料流变变形，研究符合现场实际的堆石料流变本构模型与参数提供了前提条件。
-
![]()
图 1 各粒组瞬时强度的Logistic分布图
Figure 1. Logistic distribution of instantaneous strength for various grain groups
![]()
图 2 双扭试验装置及双扭试样受力示意图
Figure 2. Schematic diagram of device and specimen loading of double-torsion tests
![]()
图 5 白云岩颗粒内部虚拟裂纹初始半长的分布函数
Figure 5. Half-length distribution of initial virtual crack of dolomite particles
![]()
图 6 不同应力水平下各粒组白云岩延迟破碎时间预测
Figure 6. Prediction of delayed crushing time of various dolomite particle groups under different stress levels
![]()
图 7 白云岩颗粒参数的尺寸相关性曲线
Figure 7. Size correlation curves of parameters of dolomite particles
表 1 各粒组瞬时强度Logistic分布参数
Table 1 Logistic distribution parameters of instantaneous strength for various grain groups
粒组/mm 20~24 24~28 28~32 32~36 36~40 40~44 44~48 48~52 52~56 56~60 120 180 240 300 σ50/MPa 8.55 7.82 7.69 7.53 7.20 7.15 6.99 6.80 6.44 5.94 5.12 4.53 4.27 4.05 S 5.09 6.55 6.07 4.62 4.47 4.17 4.24 4.57 5.13 3.70 4.18 4.26 3.89 7.61 R2 0.983 0.989 0.991 0.984 0.991 0.995 0.99 0.990 0.985 0.979 0.981 0.979 0.984 0.989 
下载: 导出CSV
表 2 亚临界裂纹扩展参数及断裂韧度
Table 2 Subcritical crack parameters and fracture toughnesses
编号 A n 编号 KIC/(MN·m-3/2) DT-1 5.50×10-11 66.82 DT-6 1.25 DT-2 5.13×10-10 57.09 DT-7 1.20 DT-3 1.12×10-12 56.71 DT-8 1.18 DT-4 1.10×10-10 45.35 DT-9 1.21 DT-5 2.19×10-10 60.48 DT-10 1.17 均值 1.8×10-10 57.29±6.98 均值 1.20±0.028
下载: 导出CSV
表 3 参数的尺寸相关性模型
Table 3 Models for size correlation of parameters
参数名称 经验模型 R2 300 mm粒径颗粒预测误差/% 裂纹半长/mm 0.99 1.4 延迟破碎时间/h 0.98 3.5
下载: 导出CSV
-
[1] 马刚, 周伟, 常晓林, 等. 颗粒劣化效应的堆石料流变细观数值模拟[J]. 岩土力学, 2012, 33(增刊1): 257-264. MA Gang, ZHOU Wei, CHANG Xiaolin, et al. Meso-numerical simulation of rheological behavior of rockfill materials due to particle deterioration effect[J]. Rock and Soil Mechanics, 2012, 33(S1): 257-264. (in Chinese)
[2] MA G, ZHOU W, NG T T, et al. Microscopic modeling of the creep behavior of rockfills with a delayed particle breakage model[J]. Acta Geotechnica, 2015, 10(4): 481-496. doi: 10.1007/s11440-015-0367-y
[3] WANG Y J, SONG E X, ZHAO Z H. Particle mechanics modeling of the effect of aggregate shape on creep of durable rockfills[J]. Computers and Geotechnics, 2018, 98: 114-131. doi: 10.1016/j.compgeo.2018.02.013
[4] ZHAO Z H, SONG E X. Particle mechanics modeling of creep behavior of rockfill materials under dry and wet conditions[J]. Computers and Geotechnics, 2015, 68: 137-146. doi: 10.1016/j.compgeo.2015.04.008
[5] LOBO-GUERRERO S, VALLEJO L E. Application of weibull statistics to the tensile strength of rock aggregates[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(6): 786-790. doi: 10.1061/(ASCE)1090-0241(2006)132:6(786)
[6] 米晓飞, 迟世春. 堆石颗粒强度的尺寸效应研究[J]. 水利与建筑工程学报, 2019, 17(4): 182-187, 197. doi: 10.3969/j.issn.1672-1144.2019.04.032 MI Xiaofei, CHI Shichun. Size effects of rockfill particle strength[J]. Journal of Water Resources and Architectural Engineering, 2019, 17(4): 182-187, 197. (in Chinese) doi: 10.3969/j.issn.1672-1144.2019.04.032
[7] MCDOWELL G R. On the yielding and plastic compression of sand[J]. Soils and Foundations, 2002, 42(1): 139-145. doi: 10.3208/sandf.42.139
[8] OVALLE C, FROSSARD E, DANO C, et al. The effect of size on the strength of coarse rock aggregates and large rockfill samples through experimental data[J]. Acta Mechanica, 2014, 225(8): 2199-2216. doi: 10.1007/s00707-014-1127-z
[9] ROZENBLAT Y, PORTNIKOV D, LEVY A, et al. Strength distribution of particles under compression[J]. Powder Technology, 2011, 208(1): 215-224. doi: 10.1016/j.powtec.2010.12.023
[10] DELUZARCHE R, CAMBOU B. Discrete numerical modelling of rockfill dams[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(11): 1075-1096. doi: 10.1002/nag.514
[11] ALAEI E, MAHBOUBI A. A discrete model for simulating shear strength and deformation behaviour of rockfill material, considering the particle breakage phenomenon[J]. Granular Matter, 2012, 14(6): 707-717. doi: 10.1007/s10035-012-0367-7
[12] ALONSO E E, TAPIAS M, GILI J. Scale effects in rockfill behaviour[J]. Géotechnique Letters, 2012, 2(3): 155-160. doi: 10.1680/geolett.12.00025
[13] 胡训健, 卞康, 谢正勇, 等. 细观结构的非均质性对花岗岩强度及变形影响的颗粒流模拟[J]. 岩土工程学报, 2020, 42(8): 1540-1548. doi: 10.11779/CJGE202008020 HU Xunjian, BIAN Kang, XIE Zhengyong, et al. Influence of meso-structure heterogeneity on granite strength and deformation with particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1540-1548. (in Chinese) doi: 10.11779/CJGE202008020
[14] 邵磊, 迟世春, 王振兴. 基于裂缝扩展的堆石料流变细观模型[J]. 岩土工程学报, 2013, 35(1): 66-75. SHAO Lei, CHI Shichun, WANG Zhenxing. Rheological model for rockfill based on sub-critical crack expansion theory[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 66-75. (in Chinese)
[15] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1993. Chinese Aeronautical Establishment. Handbook of Stress Intensity Factors[M]. Beijing: Science Press, 1993. (in Chinese)
[16] SRIVASTAVA K N, DWIVEDI J P. The effect of a penny-shaped crack on the distribution of stress in an elastic sphere[J]. International Journal of Engineering Science, 1971, 9(4): 399-420. doi: 10.1016/0020-7225(71)90060-7
[17] CHAU K T, WEI X X, WONG R H C, et al. Fragmentation of brittle spheres under static and dynamic compressions: experiments and analyses[J]. Mechanics of Materials, 2000, 32(9): 543-554. doi: 10.1016/S0167-6636(00)00026-0
[18] CHARLES R J. Static fatigue of glass. Ⅱ[J]. Journal of Applied Physics, 1958, 29(11): 1554-1560. doi: 10.1063/1.1722992
[19] 王腾腾. 堆石颗粒延迟劈裂破碎时间效应研究[D]. 大连: 大连理工大学, 2022. WANG Tengteng. Study on Time Effect of Delayed Fracturing of Rockfill Particles[D]. Dalian: Dalian University of Technology, 2022. (in Chinese)
[20] WILLIAMS D P, EVANS A G. A simple method for studying slow crack growth[J]. Journal of Testing and Evaluation, 1973, 1(4): 264-270. doi: 10.1520/JTE10015J
[21] 沈珠江. 土石料的流变模型及其应用[J]. 水利水运科学研究, 1994(4): 335-342. SHEN Zhujiang. Rheological model of soil and stone and its application[J]. Hydro-Science and Engineering, 1994(4): 335-342. (in Chinese)
[22] 沈珠江. 鲁布革心墙堆石坝变形的反馈分析[J]. 岩土工程学报, 1994, 16(3): 1-13. SHEN Zhujiang. Feedback analysis of deformation of Lubuge core rockfill dam[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 1-13. (in Chinese)
-
期刊类型引用(1)
1. 崔哲森，徐振洋，范立鹏，王雪松，李政. 循环冲击荷载下爆堆孔隙分布特征. 西安科技大学学报. 2025(02): 393-403 . 
百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 258
- HTML全文浏览量: 33
- PDF下载量: 77
- 被引次数: 1
