考虑竖向地震作用的大型地下框架结构易损性分析

邱大鹏; 陈健云; 王文明; 曹翔宇

doi:10.11779/CJGE20221053

考虑竖向地震作用的大型地下框架结构易损性分析 English Version

邱大鹏^{1, 2,},
陈健云³,
王文明^{1, 2, ,},
曹翔宇⁴

1.
山东建筑大学土木工程学院, 山东济南 250101
2.
建筑结构加固改造与地下空间工程教育部重点实验室, 山东济南 250101
3.
大连理工大学建设工程学部, 辽宁大连 116024
4.
南京水利科学研究院, 江苏南京 210029

基金项目:

国家重点研发计划项目 2020YFC1511905

国家自然科学基金项目 52208397

国家自然科学基金项目 51908340

山东省自然科学基金青年基金项目 ZR2021QE126

山东建筑大学博士科研基金项目 X20026Z0101

详细信息

作者简介:
邱大鹏(1992—)，男，博士，副教授，主要从事地下结构抗震性能与韧性提升研究。E-mail: qiudapeng20@sdjzu.edu.cn

通讯作者:
王文明, E-mail: wangwenmingmr@sdjzu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 396
- HTML全文浏览量: 74
- PDF下载量: 101
出版历程
- 收稿日期: 2022-08-24
- 网络出版日期: 2023-03-16
- 刊出日期: 2023-11-30

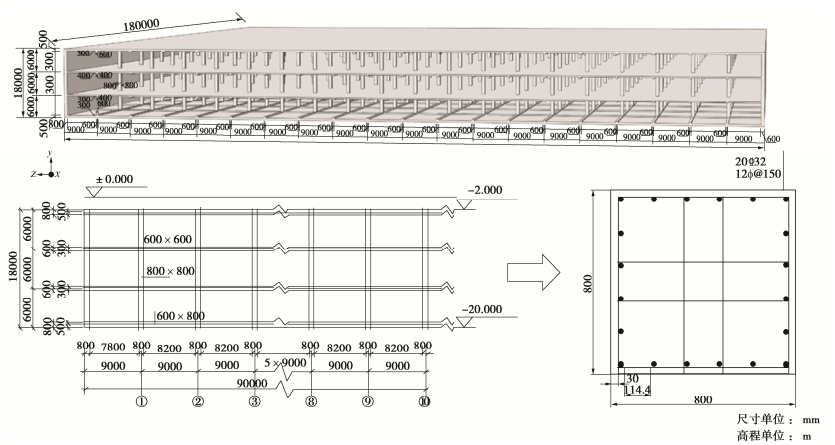
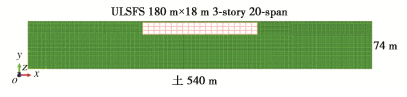
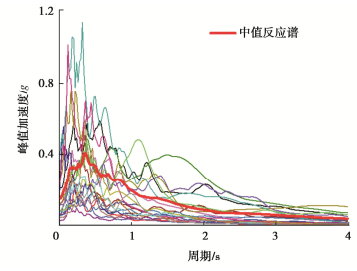
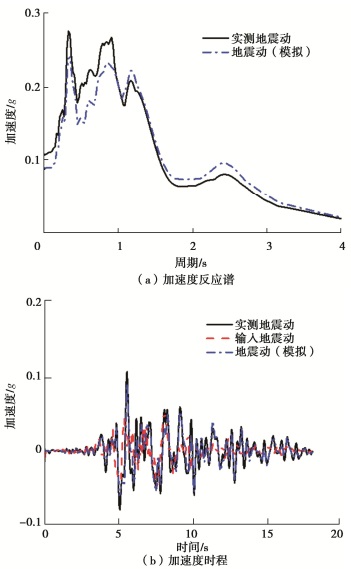
Fragility analysis of underground large-scale frame structures considering seismic effects of vertical earthquakes

QIU Dapeng^{1, 2,},
CHEN Jianyun³,
WANG Wenming^{1, 2, ,},
CAO Xiangyu⁴

1.
School of Civil Engineering, Shandong Jianzhu University, Jinan 250101, China
2.
Key Laboratory of Building Structural Retrofitting and Underground Space Engineering (Shandong Jianzhu University), Ministry of Education, Jinan 250101, China
3.
Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China
4.
Nanjing Hydraulic Research Institute, Nanjing 210029, China

摘要

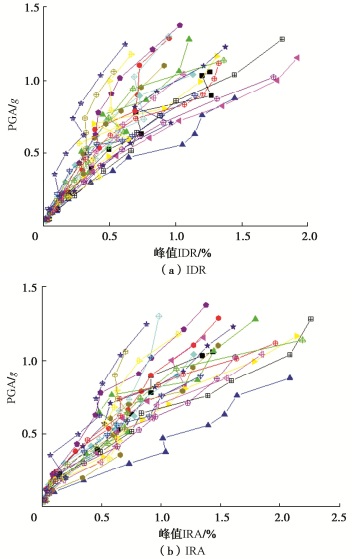
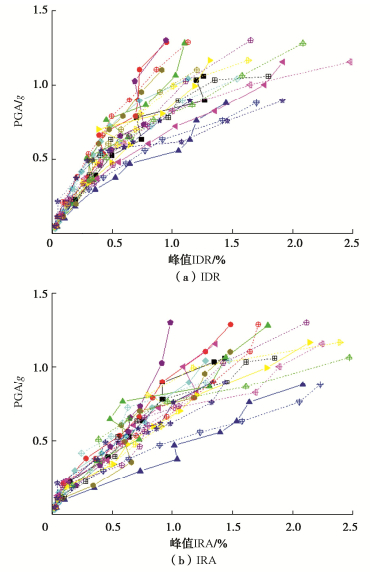
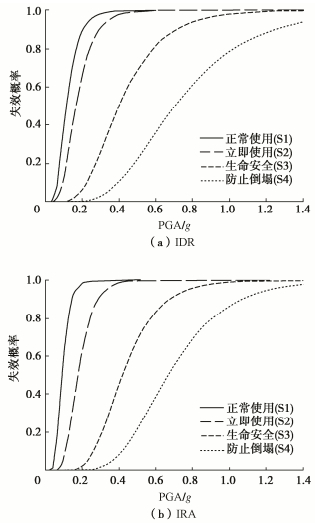
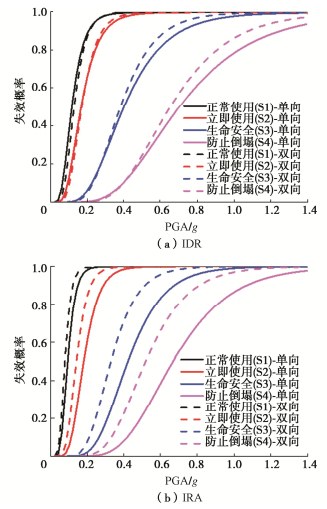
摘要: 基于增量动力分析（IDA）方法，探究了单一水平向地震及水平向与竖向地震联合作用下大型地下框架结构地震响应的IDA曲线，揭示了竖向地震对结构不同危险位置响应的影响规律；针对结构的层间水平变形与弯曲变形，提出分别选择层间位移角与层间梁柱转角作为性能评价指标，阐明了竖向地震对结构抗震性能的影响机理，得到了单向和双向地震分别作用下结构的地震易损性曲线。研究表明：竖向地震作用对结构基于层间位移角的地震易损性影响较小，但会增大外侧结构的局部弯曲变形并降低结构基于弯曲变形的抗震性能，基于层间梁柱转角的地震易损性明显提高，建议综合层间位移角与层间梁柱转角对双向地震动作用下大型地下结构的地震易损性进行全面地评估。
- 大型地下框架结构 /
- 增量动力分析 /
- 抗震性能 /
- 竖向地震 /
- 易损性分析
Abstract: The increase dynamic analysis (IDA) curves of seismic responses of the underground large-scale frame structure (ULSFS) are investigated during the single horizontal earthquakes and horizontal-vertical earthquakes, respectively. The influence mechanism of vertical earthquakes on the seismic responses of different vulnerable positions is revealed. Aiming at the interlayer drift deformation and flexural deformation in the ULSFS, the interlayer drift ratio (IDR) and interlayer rotation angle (IRA) are employed as the seismic performance evaluation indexes. Therefore, the influence mechanism of vertical earthquakes on structural seismic performance is further revealed. The seismic fragility curves of the ULSFS are achieved during horizontal earthquakes and horizontal-vertical earthquakes, respectively. The results show that the vertical earthquakes have small seismic influences on the seismic fragility of the ULSFS based on the IDR. However, the vertical earthquakes enlarge the local flexural deformation of the ULSFS and decrease the seismic performance of the ULSFS based on the IRA. The seismic fragility considerably increases after considering the vertical seismic effects. The IDR aiming at the horizontal drift deformation and the IRA aiming at the interlayer flexural deformation are advised to be employed to assess the seismic fragility of large underground structures during both horizontal and vertical earthquakes comprehensively.
- underground large-scale frame structure /
- increase dynamic analysis /
- seismic performance /
- vertical earthquake /
- fragility analysis

HTML全文

0. 引言

土工膜由于具有防渗性优越、适应变形能力强、施工便捷和造价低廉等优点，已广泛应用于堤坝、库盆、水池、垃圾填埋场等水利工程和环境岩土工程^[1-2]。土工膜在实际工程（比如水库防渗）中作为防渗体应用时，受到覆盖层自重、水压力、界面摩擦力、结构变形引起的拉力等荷载作用，蓄水后除瞬时变形外还会产生蠕变变形。当水位消落时，土工膜所受荷载随之减小，开始出现蠕变恢复现象。

目前，国内外学者开展了不少包括土工膜在内的高分子聚合物蠕变特性试验研究。Nishigata等^[3]对膜下垫层出现不均匀沉降引起的土工膜蠕变进行了研究，发现当蠕变应变超过12%时，会较快导致土工膜蠕变破坏，并认为经过蠕变作用的土工膜抗拉强度较初始值降低40%。Koerner等^[4]根据复合土工膜蠕变试验，发现断裂即将发生之前土工膜可以保持相当大的变形，并认为在工程设计中土工膜拉伸强度应有1.5倍折减。王广月等^[5]开展了4级荷载下复合土工膜蠕变试验，发现长期拉伸作用下复合土工膜表现出横向收缩特性，且颈缩量的大小与荷载成正比；当所受荷载低于60%极限荷载时，材料强度仍然保持在70%左右，可视为可靠且不影响工程稳定性。杨武等^[6]研究了不同厚度复合土工膜蠕变特性，发现蠕变稳定时的应变随膜厚增加呈线性减小，相同恒载下膜厚每增加0.1 mm，稳定应变量较小约6%。此外，亦有学者开展了土工格栅方面的蠕变研究，可供参考借鉴。

相较于高分子聚合物材料加载蠕变研究，对其开展蠕变恢复特性的研究相对较少。Leaderman等^[7]以20 min为一周期，对聚氯乙烯试样进行了蠕变与蠕变恢复循环试验，发现聚氯乙烯蠕变与蠕变恢复符合玻尔兹曼叠加原理。Hao等^[8]对聚丙烯复合材料进行了72 h蠕变和24 h蠕变恢复试验研究，通过试验发现聚丙烯复合材料在高温下有较高的蠕变恢复率，温度上升后聚合物蠕变抗力减弱。敬凌霄^[9]对聚酯织物增强膜进行7 h蠕变和7 h蠕变恢复试验，发现聚酯织物膜蠕变与蠕变恢复大小与应力水平呈线性关系，与时间呈指数关系。汪泽幸等^[10]对蠕变后的PVC涂层膜进行应力卸载试验，发现蠕变恢复受卸载应力大小与加、卸载速率影响，但加、卸载速率仅影响蠕变恢复量。

总体而言，目前对于土工膜蠕变特性的研究主要集中于加载蠕变阶段，对荷载降低时的蠕变恢复研究很少，而实际工程中土工膜所受荷载常处于加载或卸载状态，使土工膜呈现蠕变变形或蠕变恢复特性。基于此，本文开展了土工膜加载蠕变及卸载后的蠕变恢复试验，获得不同荷载水平下土工膜的蠕变和蠕变恢复规律，对土工膜的蠕变和蠕变恢复初始模量变化进行比较分析，改进建立了考虑黏弹性特性的蠕变数学模型，并对土工膜蠕变变形及蠕变恢复试验数据进行模拟验证，相关成果可为工程设计提供理论指导。

1. 试验材料与方案

试验选用厚度分别为0.5，1.0，1.5 mm的高密度聚乙烯（HDPE）土工膜。根据《土工合成材料试验规程》（SL/T235—2012），对密度为0.94 g/cm³的3种厚度试验土工膜进行单向拉伸试验，测得土工膜基本力学指标，见表 1。土工膜加、卸载蠕变试验参照国家规范GB/T1040—2018采用窄条法，试样尺寸为160 mm×50 mm，其中试样蠕变变形测量范围为100 mm ×50 mm，两端预留30 mm夹持长度用以固定土工膜。

表 1 HDPE土工膜拉伸力学特性

Table 1. Properties of geomembranes

厚度/mm	屈服强度/(N·mm^-1)	屈服应变/%	断裂强度/(N·mm^-1)	断裂应变/%
0.5	5.71	12.49	5.04	506.38
1.0	10.35	22.36	11.45	416.15
1.5	15.75	17.00	15.68	610.32

下载: 导出CSV

| 显示表格

本试验采用3种不同厚度土工膜（0.5，1.0，1.5 mm）和6级荷载（10%，20%，30%，40%，50%，60%屈服强度），设置3×6组试验方案。荷载大小采用荷载水平进行量化，即所施加荷载大小占土工膜屈服强度的百分比。本次蠕变与蠕变恢复试验均在室温（23~25℃）条件下进行，在土工膜加载试验持续100 h时，卸除荷载，并记录土工膜回弹变形过程。

2. 试验结果与分析

2.1 蠕变与蠕变恢复试样变形特性

图 1为不同荷载水平下不同厚度HDPE土工膜试样蠕变曲线。由图可见，在蠕变试验过程中，土工膜在加载后产生瞬时变形，随后在蠕变第一阶段迅速增加，且蠕变速率逐渐趋缓。在100 h的试验时间内，所受荷载水平较低的试样蠕变速率趋于零，蠕变变形达到稳定值，而荷载水平较高时部分试样持续以相对恒定速率蠕变，蠕变变形持续增加，不再出现稳定值。以1.0 mm厚土工膜为例，在荷载水平10%，20%，30%时，土工膜蠕变较快地稳定于0.42%，1.03%，2.21%，稳定应变随荷载水平增大而升高。当荷载水平上升至40%及以上时，在100 h试验时间内土工膜进入了恒速蠕变阶段（第二阶段蠕变）。其中，40%，50%，60%荷载水平下土工膜的蠕变速率分别为0.006，0.010，0.014 mm/h，蠕变速率随荷载水平升高近似呈线性增加，在蠕变试验结束时蠕变应变分别为4.35%，7.41%，8.87%。

图 1 不同厚度HDPE土工膜蠕变曲线

Figure 1. Curves of creep of HDPE geomembranes

下载: 全尺寸图片幻灯片

图 2为不同荷载水平下不同厚度HDPE土工膜试样蠕变恢复曲线。由图可知，不同厚度土工膜蠕变恢复变化规律相似，卸载后土工膜在初始阶段变形迅速减小，随后曲线缓慢下降，并趋于稳定。在100 h的卸载时间内，只有10%，20%荷载水平下的土工膜蠕变变形完全恢复，即无残余变形；其余荷载水平下，土工膜均出现了残余变形，且荷载水平越大，土工膜残余变形量亦越大。以1.0 mm厚土工膜为例，当所卸除的荷载水平低于20%时，土工膜蠕变变形完全恢复至零；但当荷载水平达到30%时，完全卸载后的土工膜依旧有0.28%残余变形，残余变形占总变形量比例为12.67%；当荷载水平分别为40%，50%，60%时，土工膜残余应变分别为0.68%，1.26%，1.65%，占总应变量比例分别为15.63%，17.01%，18.60%。表明经历高荷载水平蠕变后的土工膜的黏弹性变形减小，而不可恢复的残余变形比例增大。

图 2 不同厚度HDPE土工膜蠕变恢复曲线

Figure 2. Curves of creep recovery of HDPE geomembranes

下载: 全尺寸图片幻灯片

2.2 蠕变与蠕变恢复曲线对照分析

将不同荷载水平下土工膜蠕变恢复曲线“上下翻转”，并与土工膜蠕变曲线进行比较。以1.0 mm厚土工膜为例，对蠕变与蠕变恢复曲线进行比较展示，如图 3所示。在10%，20%荷载水平下，蠕变曲线与蠕变恢复曲线近乎重合，表明在低荷载水平下HDPE土工膜中晶区几乎不发生任何变化，主要无定形区中分子链的键长、键角被拉伸所引起，当撤除外力后分子链变形能够恢复^[11-12]，宏观上表现为卸载后土工膜蠕变变形的完全恢复。当荷载水平升至30%，40%时，在加载与卸载后10 h内土工膜蠕变曲线与恢复曲线重合，随后恢复曲线进入应变无明显变化的稳定阶段，土工膜蠕变恢复变形与蠕变变形的差值随时间增长而增大，即土工膜出现了残余变形，表明此时土工膜内无定形区分子链沿蠕变方向拉伸，进而造成晶区开始发生缓慢滑移^{[11, 13]}，宏观上表现为土工膜蠕变趋近于稳定应变，但在卸载后存在少量不可恢复的残余变形。当荷载水平处于50%，60%时，土工膜的恢复曲线与蠕变曲线即使在初始阶段亦不再重合，恢复曲线在初始阶段应变变化量明显大于蠕变曲线初始阶段应变量，并且恢复曲线快速达到应变稳定阶段。

图 3 1.0 mm厚HDPE土工膜蠕变与恢复曲线对比

Figure 3. Comparison of creep and recovery curves of 1.0 mm-thick HDPE geomembrane

下载: 全尺寸图片幻灯片

为了进一步分析荷载水平对土工膜蠕变及蠕变恢复特性的影响，选取若干典型时刻，对应变-荷载关系进行分析。限于篇幅，仅给出1.5 mm厚土工膜的结果，见图 4。在土工膜蠕变与蠕变恢复试验中，其变形均随载荷水平的增加逐渐增大，在相对较低荷载水平下不同典型时刻的蠕变变形随荷载水平呈线性增大趋势，但在较高荷载水平时，应变有显著增大。其中，0.5，1.5 mm厚土工膜各时刻的应变–荷载关系曲线在40%荷载水平后增长明显，1.0 mm厚土工膜各时刻的应变–荷载关系曲线在30%荷载水平后增长明显。对比加、卸载时的应变–荷载曲线，土工膜蠕变恢复过程各特定时刻曲线在高荷载水平下更为集中，加载试验中前0.5 h时土工膜应变量约占总应变量的40%左右，而卸载试验中前0.5 h时土工膜应变量达到总应变量的60%左右。

图 4 1.5 mm厚HDPE土工膜等时应变–荷载曲线

Figure 4. Isochronous stress-strain relation curves of 1.5 mm-thick HDPE geomembrane

下载: 全尺寸图片幻灯片

2.3 蠕变与蠕变恢复初始模量特性

以土工膜初始模量为例，进一步分析探究土工膜在蠕变与蠕变恢复过程中力学性质的变化规律。Cheng等^[14]和Liu等^[15]为避免蠕变试验加载瞬时变形记录误差，取蠕变60 s时应变计算不同荷载水平下土工膜蠕变初始模量。本文按此方法分别计算蠕变与蠕变恢复初始模量，不同厚度土工膜初始模量随荷载水平变化规律如图 5所示。

图 5 不同荷载水平下HDPE土工膜蠕变与蠕变恢复初始模量

Figure 5. Creeps and initial modulis of HDPE geomembranes under different load levels

下载: 全尺寸图片幻灯片

0.5~1.5 mm厚土工膜初始模量变化趋势相似，当荷载水平达到40%（出现第二阶段恒定速率蠕变）时，1.0 mm厚土工膜蠕变与恢复初始模量均迅速下降，且恢复初始模量下降幅度大于蠕变初始模量下降幅度，模量下降幅度均大于100 MPa。0.5，1.5 mm厚土工膜在荷载水平达到50%时，蠕变与恢复初始模量均迅速下降约120 MPa。表明土工膜在出现第二阶段恒定速率蠕变时，土工膜内材料晶区发生分子链的解缠与滑移^[10]，导致部分晶区在蠕变过程中转变为无定形区，与部分学者对高分子聚合物晶区和无定形区初始模量进行的试验测定^[16-17]与分子动力学模拟^[11]所得到晶区初始模量比无定形区初始模量至少大70 MPa的结果相吻合。

表 2给出了不同厚度土工膜蠕变与蠕变恢复初始模量平均值及其对比关系，其中E_s，E_s'分别为蠕变第二阶段蠕变速率为0（较低荷载水平）时的土工膜蠕变与蠕变恢复初始模量平均值，E_u和E_u'分别为蠕变第二阶段为恒定蠕变速率（较高荷载水平）时的土工膜蠕变与蠕变恢复初始模量平均值。对比E_u/E_s可知，当荷载水平较高时，土工膜蠕变初始模量约为荷载水平较低时的0.6倍，表明较高荷载水平使土工膜蠕变初始模量下降。对比E_s'/E_s，E_u'/E_u可知，当荷载水平较低时土工膜蠕变与蠕变恢复初始模量变化不大，而当经过较高荷载水平蠕变后，土工膜蠕变恢复初始模量约为0.71倍的蠕变初始模量。对比E_u'/E_s可知，较高荷载水平下蠕变恢复初始模量仅为0.43倍较低荷载水平下的相应值，表明蠕变恢复初始模量同时受荷载水平与蠕变过程的双重影响，其中荷载水平使蠕变初始模量有约40%下降（E_u/E_s），而经之前的蠕变过程进一步使土工膜蠕变恢复初始模量下降约30%（E_u'/E_u）。

表 2 土工膜蠕变与恢复初始模量

Table 2. Comparison of initial moduli under different load levels

膜厚/mm	较低荷载水平/MPa		较高荷载水平/MPa		E_s'/E_s	E_u'/E_u	E_u/E_s	E_u'/E_s
膜厚/mm	E_s	E_s'	E_u	E_u'	E_s'/E_s	E_u'/E_u	E_u/E_s	E_u'/E_s
0.5	432.43	387.49	274.58	164.08	0.90	0.60	0.63	0.38
1.0	387.53	381.91	194.90	155.17	0.99	0.80	0.50	0.40
1.5	287.17	276.45	194.40	145.80	0.96	0.75	0.68	0.51
平均值	—	—	—	—	0.95	0.71	0.60	0.43

下载: 导出CSV

| 显示表格

3. 土工膜蠕变及蠕变恢复模型

3.1 模型的改进

恒定荷载下，土工膜蠕变常用模型有三元件和四元件黏弹性模型^[18]，其表达式分别为

，

$\varepsilon = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}(1 - {{\text{e}}^{ - t{E_2}/{\eta _1}}}) \text{，}$

(1)

，

$\varepsilon = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}(1 - {{\text{e}}^{ - t{E_2}/{\eta _1}}}){\text{ + }}\frac{{{\sigma _0}}}{{{\eta _2}}}t \text{，}$

(2)

式中， $\varepsilon$ 为蠕变应变， ${\sigma _0}$ 为恒定蠕变应力， ${E_1}$ ， ${E_2}$ 为弹性模量， ${\eta _1}$ ， ${\eta _2}$ 为黏性模量。

当处于初始时刻（t趋于0）时，两式均有瞬时应变 $\varepsilon = {\sigma _0}/{E_1}$ ；当时间足够长时，式（1）中的应变趋于稳定，应变速率为0，稳定应变为 $\varepsilon = {\sigma _0}({E_1} + {E_2})/$ ${E_1}{E_2}$ ，式（2）则进入应变速率为 ${\sigma _0}/{\eta _2}$ 的蠕变阶段。这与试验得到的不同荷载水平下HDPE土工膜蠕变试验曲线有着相同规律，即式（1），（2）可分别模拟较低荷载水平下的蠕变稳定过程和较高荷载水平下恒速蠕变过程。

为了更好反映土工膜在不同荷载水平下的蠕变过程，将三元件与四元件模型组合得到改进的黏弹性联合元件模型，如图 6所示。其中黏壶元件由应力控制元件激活（虚线框内），当土工膜处于较低荷载水平时，应力控制元件使黏壶元件不发挥效用。

图 6 土工膜联合元件模型

Figure 6. Composite element model for geomembrane

下载: 全尺寸图片幻灯片

联合式（1），（2）推导可得不同荷载水平下土工膜黏弹性蠕变方程：

，

${\varepsilon _{\text{c}}}(t) = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}(1 - {{\text{e}}^{ - t{E_2}/{\eta _1}}}){\text{ + }}\frac{{{\text{(sgn(}}{\sigma _0} - {\sigma _{\text{s}}}{\text{) + 1)}}{\sigma _0}}}{{2{\eta _2}}}t{\text{ }} \text{，}$

(3)

（ ） （ ） ，

$\text{sgn(}x\text{)=}\left\{\begin{array}{c}\text{ }1\text{ }（x\ge 0）\\ -1\text{ }（x < 0）\end{array} \text{，} \right.$

(4)

式中， ${\varepsilon _{\text{c}}}$ 为蠕变应变， ${\sigma _0}$ 为恒定蠕变应力， ${\sigma _{\text{s}}}$ 为发生恒速蠕变时的蠕变应力，其余变量解释同前。

经过“上下翻转”得到的土工膜蠕变恢复曲线与三元件模型有着相同的规律，即在荷载变化瞬间产生瞬时应变，随后应变速率随时间趋于零，应变最终达到稳定值。当在t₁时刻撤除荷载时，土工膜蠕变应变恢复过程为

${\varepsilon _{\text{r}}} = {\varepsilon _{\text{c}}}({t_1}) - \left[ {\frac{{{\sigma _0}}}{{{{E'}_1}}} + \frac{{{\sigma _0}}}{{{{E'}_2}}}(1 - {{\text{e}}^{ - (t - {t_1})E'_2/\eta' _1}})} \right]{\text{ (}}t \geqslant {t_1}{\text{)}} \text{，}$

(5)

式中， ${\varepsilon _{\text{r}}}$ 为蠕变恢复应变， ${\sigma _0}$ 为卸载应力， ${E'_1}$ ， ${E'_2}$ 为蠕变恢复弹性模量， ${\eta '_1}$ 为蠕变恢复黏性模量。

3.2 模型参数求解与模型验证

本文建议的蠕变联合元件模型与蠕变恢复模型共有7个参数，其中弹性模量 $E_1^{}$ ， ${E'_1}$ 可通过蠕变与蠕变恢复试验数据直接获得；将不同厚度土工膜在各荷载水平下的蠕变与蠕变恢复试验数据分别代入式（4），（5）进行寻优迭代求解，可得蠕变与蠕变恢复模型其余参数。以1.0 mm厚土工膜参数为例，确定的计算参数见。由表可见，随着荷载水平的增加，蠕变模型参数 ${E_2}$ ， ${\eta _2}$ 均不断减小，表明当土工膜受荷载水平逐渐上升时变形表现得更加明显；而参数 ${\eta _1}$ 随着荷载水平上升呈现为先增大后减小的趋势，表明在10%荷载水平下Kelvin体发挥作用较小，即土工膜在10%荷载水平下黏弹性特征相对不明显；在20%荷载水平下 ${\eta _1}$ 上升使土工膜表现为较强抗蠕变能力，随着荷载水平上升 ${E_2}$ ， ${\eta _2}$ 持续减小，表明Kelvin体黏弹性发挥的作用逐渐提高，土工膜蠕变表现得更加明显。蠕变恢复模型参数 ${E'_2}$ ， ${\eta '_1}$ 均随荷载水平升高不断减小，表明蠕变恢复过程中土工膜黏弹性随荷载水平升高逐渐凸显。

表 3 1.0 mmHDPE土工膜蠕变及蠕变恢复模型参数

Table 3. Parameters of creep deformation and recovery model of 1.0 mm-thick HDPE geomembrane

荷载水平/%	蠕变				蠕变恢复
荷载水平/%	E₁/MPa	E₂/MPa	${\eta _1}$ _/(MPa·h)	${\eta _2}$ _/(MPa·h)	${E'_1}$ /MPa	${E'_2}$ /MPa	${\eta '_1}$ /(MPa·h)
10	406.62	711.11	531.86	—	406.62	720.38	1852.12
20	381.84	475.39	1656.88	—	385.75	478.60	1762.96
30	374.15	244.93	784.05	—	353.37	306.75	682.31
40	205.54	262.52	611.81	53866.31	190.53	331.86	627.10
50	192.61	164.97	381.58	28712.66	131.71	249.36	209.89
60	186.56	176.94	450.14	26936.52	143.26	228.82	387.86

下载: 导出CSV

| 显示表格

图 7为不同荷载水平下不同厚度HDPE土工膜蠕变与蠕变恢复模型拟合曲线。由图可知，改进蠕变模型能较好反映不同荷载水平下土工膜蠕变过程，即较低荷载水平下能较好模拟土工膜最终蠕变应变量，在较高荷载水平下能较好模拟恒定应变速率的蠕变第二阶段。由三元件模型所得到的蠕变恢复模型，对较高荷载水平下土工膜蠕变恢复初期（0~10 h）模拟有所偏差，但模型能较好反映蠕变恢复第二阶段变形过程，并能准确模拟残余变形。

图 7 不同厚度HDPE土工膜试验值与模型曲线对比

Figure 7. Comparison of test and simulated curves for HDPE geomembranes with different thicknesses

下载: 全尺寸图片幻灯片

4. 结论

本文开展了不同荷载水平下HDPE土工膜加载蠕变与卸载蠕变恢复特性试验，对加、卸载后土工膜蠕变性能的变化进行了较为深入研究，并采用改进的联合元件模型对土工膜的蠕变变形与蠕变恢复过程进行了模拟分析，得到4点结论。

（1）HDPE土工膜的蠕变变形随时间不断增长，所受荷载水平越高，蠕变变形越大。荷载水平较低时，土工膜会较快地进入稳定蠕变阶段，随着荷载水平的升高，土工膜将进入较长时间的恒定速率蠕变阶段，恒定速率将随荷载水平的上升而增大。以1.0 mm厚土工膜为例，在荷载水平10%，20%，30%时最终蠕变应变分别稳定于0.42%，1.03%，2.21%，稳定应变随荷载水平增大而升高；在40%，50%，60%荷载水平下，土工膜进入恒速蠕变阶段，其速率分别为0.006，0.010，0.014 mm/h，蠕变速率随荷载水平升高近似呈线性增加。

（2）对于蠕变恢复阶段的HDPE土工膜，在卸掉荷载的初始阶段其应变曲线迅速下降，随后缓慢下降并趋于稳定；所受荷载水平越高，蠕变恢复后土工膜产生的残余变形与其占比逐渐增大。以1.0 mm厚土工膜为例，当所荷载水平低于20%时，卸载后土工膜蠕变变形可完全恢复；当荷载水平上升至30%，40%，50%，60%时，卸载后土工膜出现残余应变，残余应变分别为0.68%，1.26%，1.65%，占总应变量比例分别为12.67%，15.63%，17.01%，18.60%。

（3）土工膜初始模量受荷载水平与蠕变过程的双重影响。较低荷载水平对土工膜初始模量影响较小；当土工膜荷载水平上升至40%~50%时，初始模量将显著下降超100 MPa，且土工膜进入第二阶段蠕变，开始出现恒定速率蠕变；较高荷载水平下蠕变恢复初始模量同时受荷载水平与蠕变过程的叠加影响，其中荷载水平使蠕变初始模量有约40%下降，而经蠕变过程后进一步使蠕变恢复初始模量下降约30%。

（4）改进的蠕变联合元件模型将三元件、四元件模型相结合，能较好反映不同荷载下土工膜的黏弹性蠕变过程，即能较好表征较低荷载水平下土工膜达到最终的稳定蠕变量及较高荷载水平下第二阶段的恒速蠕变增长特性。蠕变恢复模型能较好反映不同荷载水平下土工膜蠕变恢复过程，并能准确预测土工膜最终残余应变值。

图 1 ULSFS的构造及框架柱配筋示意图

Figure 1. Structural diagram of ULSFS and reinforcements of framework columns

下载: 全尺寸图片幻灯片

图 2 土-结构有限元模型

Figure 2. Finite element models for soil and structure

下载: 全尺寸图片幻灯片

图 3 所选地震动加速度反应谱

Figure 3. Acceleration response spectra of ground motions

下载: 全尺寸图片幻灯片

图 4 实测地震动与模拟地震动

Figure 4. Recorded and simulated ground motions

下载: 全尺寸图片幻灯片

图 5 水平向地震作用下Ⅱ类场地中ULSFS的IDA曲线

Figure 5. IDA curves of ULSFS during horizontal earthquakes in site Ⅱ

下载: 全尺寸图片幻灯片

图 6 水平向与竖向地震作用下Ⅱ类场地中ULSFS的IDA曲线

Figure 6. IDA curves of ULSFS during horizontal and vertical earthquakes in site Ⅱ

下载: 全尺寸图片幻灯片

图 7 结构抗震性能曲线及“最远点法”示意图

Figure 7. Diagram of seismic performance curve and farthest point method

下载: 全尺寸图片幻灯片

图 8 ULSFS抗震性能曲线

Figure 8. Seismic performance curves of ULSFS

下载: 全尺寸图片幻灯片

图 9 水平向地震作用下Ⅱ类场地条件中ULSFS的易损性曲线

Figure 9. Fragility curves of ULSFS during horizontal earthquakes in site Ⅱ

下载: 全尺寸图片幻灯片

图 10 双向地震作用下Ⅱ类场地条件中ULSFS的易损性曲线

Figure 10. Fragility curves of ULSFS during bi-directional earthquakes in site Ⅱ

下载: 全尺寸图片幻灯片

表 1 ULSFS本构与材料属性

Table 1 Material constitutive models of ULSFS

材料	混凝土								钢筋
材料	密度 ${\rho _{{\text{c1}}}}$ /(kg·m^-3)	弹性模量 ${E_{{\text{s1}}}}$ /GPa	泊松比	扩张角 ${\psi _{\text{c}}}$ /(°)	偏心率η	${K_{{\text{t1}}}}$	拉伸屈服强度 ${\sigma _{{\text{t1}}}}$ /MPa	压缩屈服强度 ${\sigma _{{\text{c1}}}}$ /MPa	密度 ${\rho _{\text{r}}}$ /(kg·m^-3)	弹性模量 ${E_{{\text{sr}}}}$ /GPa	屈服强度 ${\sigma _{\text{r}}}$ /MPa
数值	2400	32.5	0.20	15	0.1	0.666	3	30	7800	200	400

下载: 导出CSV

表 2 实际场地各土层参数

Table 2 Parameters of soil layers in actual site

土层	土壤类型	埋深/m	密度/(kg·m^-3)	泊松比	内摩擦角/(°)	黏聚力/kPa	剪切波速/(m·s^-1)
1	回填土	0~4	1870	0.33	20	20	181
2	粉质黏土	4~12	1900	0.28	18	40	193
3	粉质黏土	12~20	1900	0.28	20	25	405
4	粉质黏土	20~34	1850	0.30	20	10	247
5	粉质黏土	34~42	1850	0.28	20	20	271
6	黏土	42~54	1900	0.25	30	30	303
7	砾石	54~74	1950	0.20	20	1	427

下载: 导出CSV

表 3 所选地震动信息

Table 3 Data of selected ground motions

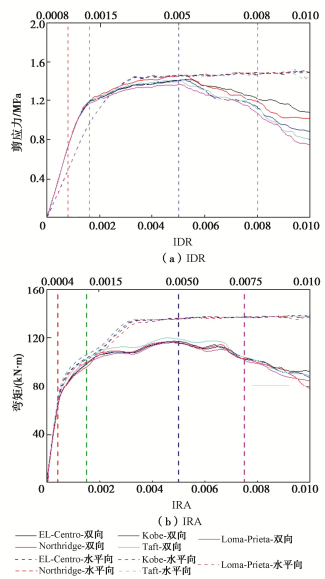
编号	地震动名称	震级M_w	${v_{{\text{s20}}}}$ / (m·s^-1)	Rrup/km	编号	地震动名称	震级M_w	${v_{{\text{s20}}}}$ /(m·s^-1)	Rrup/km
GM-1	"Imperial Valley-02"	6.95	213.44	6.09	GM-11	"San Fernando"	6.61	385.69	112.52
GM-2	"Northwest Calif-02"	6.6	219.31	91.22	GM-12	"Managua_Nicaragua-01"	6.24	288.77	4.06
GM-3	"Kern County"	7.36	316.46	117.75	GM-13	"Loma Prieta"	6.93	304.08	67.52
GM-4	"Kern County"	7.36	385.43	38.89	GM-14	"Loma Prieta"	6.93	331.21	50.99
GM-5	"Northern Calif-03"	6.5	219.31	27.02	GM-15	"Loma Prieta"	6.93	333.85	22.68
GM-6	"Parkfield"	6.19	289.56	9.58	GM-16	"Northridge-01"	6.69	269.29	68.62
GM-7	"Borrego Mtn"	6.63	316.46	222.42	GM-17	"Northridge-01"	6.69	301.23	41.17
GM-8	"San Fernando"	6.61	280.56	55.20	GM-18	"Kobe_Japan"	6.90	312.14	0.96
GM-9	"San Fernando"	6.61	316.46	22.77	GM-19	"Chi-Chi_Taiwan-05"	6.20	330.55	54.76
GM-10	"San Fernando"	6.61	303.79	193.91	GM-20	"Chi-Chi_Taiwan-06"	6.30	297.86	61.03

下载: 导出CSV

表 4 ULSFS抗震性能评价指标及状态阈值

Table 4 Seismic performance evaluation indexes and thresholds of ULSFS

项目	性能指标	基本完好	轻微破坏	中等破坏	严重破坏	塌毁
未考虑竖向地震	IDR-本文	$\theta < 0.10\%$	$0.10\% \leqslant \theta < 0.15\%$	$0.15\% \leqslant \theta < 0.40\%$	$0.40\% \leqslant \theta < 0.75\%$	$0.75\% \leqslant \theta$
	IDR-文章^[4]	$\theta < 0.12\%$	$0.12\% < \theta < 0.25\%$	$0.25\% \leqslant \theta < 0.40\%$	$0.40\% \leqslant \theta < 0.6\%$	$0.60\% \leqslant \theta$
	IDR-文章^[9]	$\theta < 0.08\%$	$0.08\% < \theta < 0.29\%$	$0.29\% \leqslant \theta < 0.60\%$	$0.60\% \leqslant \theta < 0.95\%$	$0.95\% \leqslant \theta$
	IDR-文章^[10]	$\theta < 0.12\%$	$0.12\% \leqslant \theta < 0.32\%$	$0.32\% \leqslant \theta < 0.73\%$	$0.73\% \leqslant \theta < 1.29\%$	$1.29\% \leqslant \theta$
	IRA-本文	$\theta < 0.05\%$	$0.05\% \leqslant \theta < 0.125\%$	$0.125\% \leqslant \theta < 0.40\%$	$0.40\% \leqslant \theta < 0.75\%$	$0.75\% \leqslant \theta$
考虑竖向地震动	IDR-本文	$\theta < 0.08\%$	$0.08\% \leqslant \theta < 0.12\%$	$0.12\% \leqslant \theta < 0.33\%$	$0.33\% \leqslant \theta < 0.65\%$	$0.65\% \leqslant \theta$
	IDR-文章^[8]	$\theta < 0.05\%$	$0.05\% \leqslant \theta < 0.21\%$	$0.21\% \leqslant \theta < 0.46\%$	$0.46\% \leqslant \theta < 0.72\%$	$0.72\% \leqslant \theta$
	IRA-本文	$\theta < 0.04\%$	$0.04\% \leqslant \theta < 0.1\%$	$0.1\% \leqslant \theta < 0.33\%$	$0.33\% \leqslant \theta < 0.63\%$	$0.63\% \leqslant \theta$

下载: 导出CSV

表 5 地震强度指标与结构性能评价指标平均标准偏差

${\beta _{\text{D}}}$ between ${\text{IM}}$ and ${u_{\text{d}}}$

${\beta _{\text{D}}}$	${\text{PGA}}$	${\text{PBA}}$	${\text{PGV}}$
${\text{IDR}}$	0.35	0.41	0.38
${\text{IRA}}$	0.39	0.36	0.43

下载: 导出CSV

表 6 Ⅱ场地条件下ULSFS地震失效概率50%所对应PGA

Table 6 PGAs corresponding to failure probability of ULSFS with value of 50% in site Ⅱ

失效概率（50%）	单向地震-IDR	单向地震-IRA	双向地震-IDR	双向地震-IRA
正常使用（S1）	0.11g	0.09g	0.13g	0.08g
立即使用（S2）	0.17g	0.18g	0.17g	0.15g
生命安全（S3）	0.40g	0.42g	0.38g	0.33g
防止倒塌（S4）	0.70g	0.67g	0.65g	0.52g

下载: 导出CSV

参考文献(25)

[1]	HASHASH Y M A, HOOK J J, SCHMIDT B, et al. Seismic design and analysis of underground structures[J]. Tunnelling and Underground Space Technology, 2001, 16(4): 247-293. doi: 10.1016/S0886-7798(01)00051-7
[2]	PENZIEN J. Seismically induced racking of tunnel linings[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(5): 683-691.
[3]	杜修力, 马超, 路德春, 等. 大开地铁车站地震破坏模拟与机理分析[J]. 土木工程学报, 2017, 50(1): 53-62, 69. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201701007.htm DU Xiuli, MA Chao, LU Dechun, et al. Collapse simulation and failure mechanism analysis of the Daikai subway station under seismic loads[J]. China Civil Engineering Journal, 2017, 50(1): 53-62, 69. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201701007.htm
[4]	庄海洋, 任佳伟, 王瑞, 等. 两层三跨框架式地铁地下车站结构弹塑性工作状态与抗震性能水平研究[J]. 岩土工程学报, 2019, 41(1): 131-138. doi: 10.11779/CJGE201901014 ZHUANG Haiyang, REN Jiawei, WANG Rui, et al. Elasto-plastic working states and seismic performance levels of frame-type subway underground station with two layers and three spans[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 131-138. (in Chinese) doi: 10.11779/CJGE201901014
[5]	马超. 地铁车站结构地震塌毁过程模拟及破坏机理分析[D]. 北京: 北京工业大学, 2017. MA Chao. Collapse Procedure Simulation and Failure Mechanism Analysis on subway Stations under Seismic Loads[D]. Beijing: Beijing University of Technology, 2017. (in Chinese)
[6]	LI W T, CHEN Q J. Seismic damage evaluation of an entire underground subway system in dense urban areas by 3D FE simulation[J]. Tunnelling and Underground Space Technology, 2020, 99: 103351. doi: 10.1016/j.tust.2020.103351
[7]	许成顺, 李洋, 杜修力, 等. 上覆土竖向惯性力对浅埋地下框架结构地震损伤反应影响离心机振动台模型试验研究[J]. 土木工程学报, 2019, 52(3): 100-110, 119. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201903010.htm XU Chengshun, LI Yang, DU Xiuli, et al. Dynamic centrifuge tests for influence of vertical inertia force of overburden soil on earthquake damage response of shallow-buried underground frame structures[J]. China Civil Engineering Journal, 2019, 52(3): 100-110, 119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201903010.htm
[8]	DU X L, JIANG J W, EL NAGGAR M H, et al. Interstory drift ratio associated with performance objectives for shallow-buried multistory and span subway stations in inhomogeneous soil profiles[J]. Earthquake Engineering & Structural Dynamics, 2021, 50(2): 655-672.
[9]	杜修力, 蒋家卫, 许紫刚, 等. 浅埋矩形框架地铁车站结构抗震性能指标标定研究[J]. 土木工程学报, 2019, 52(10): 111-119, 128. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201910012.htm DU Xiuli, JIANG Jiawei, XU Zigang, et al. Study on quantification of seismic performance index for rectangular frame subway station structure[J]. China Civil Engineering Journal, 2019, 52(10): 111-119, 128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201910012.htm
[10]	ZHONG Z L, SHEN Y Y, ZHAO M, et al. Seismic fragility assessment of the Daikai subway station in layered soil[J]. Soil Dynamics and Earthquake Engineering, 2020, 132: 106044. doi: 10.1016/j.soildyn.2020.106044
[11]	ZHUANG H Y, YANG J, CHEN S, et al. Statistical numerical method for determining seismic performance and fragility of shallow-buried underground structure[J]. Tunnelling and Underground Space Technology, 2021, 116: 104090. doi: 10.1016/j.tust.2021.104090
[12]	HE Z M, CHEN Q J. Vertical seismic effect on the seismic fragility of large-space underground structures[J]. Advances in Civil Engineering, 2019, 2019: 1-17.
[13]	刘晶波, 兰兴欢, 谭辉. 地下与地上钢筋混凝土矩形结构抗震性能对比研究[J]. 地震工程学报, 2019, 41(2): 271-277. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201902001.htm LIU Jingbo, LAN Xinghuan, TAN Hui. Comparative study on the seismic performances of underground vs. above-ground reinforced concrete structures with rectangular cross sections[J]. China Earthquake Engineering Journal, 2019, 41(2): 271-277. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201902001.htm
[14]	QIU D P, CHEN J Y, XU Q. 3-D numerical analysis on seismic responses of the underground large scale frame structure under near-fault ground motions[J]. Tunnelling and Underground Space Technology, 2019, 91: 103020.
[15]	LUDWIG W. ABAQUS User' s Guide, Version 6.14[R]. Rhode Island: Abaqus Inc., 2014.
[16]	建筑抗震设计规范: GB50011—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for Seismic Design of Buildings: GB50011—2010[S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[17]	钟紫蓝, 申轶尧, 郝亚茹, 等. 基于IDA方法的两层三跨地铁地下结构地震易损性分析[J]. 岩土工程学报, 2020, 42(5): 916-924. doi: 10.11779/CJGE202005014 ZHONG Zilan, SHEN Yiyao, HAO Yaru, et al. Seismic fragility analysis of two-story and three-span metro station structures based on IDA method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 916-924. (in Chinese) doi: 10.11779/CJGE202005014
[18]	廖振鹏, 刘晶波. 离散网格中的弹性波动(Ⅰ)[J]. 地震工程与工程振动, 1986, 6(2): 1-16. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199002000.htm LIAO Zhenpeng, LIU Jingbo. Elastic wave motion in discrete grids[J]. Earthquake Engineering and Engineering Vibration, 1986, 6(2): 1-16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199002000.htm
[19]	QIU D P, CHEN J Y, XU Q. Improved pushover analysis for underground large-scale frame structures based on structural dynamic responses[J]. Tunnelling and Underground Space Technology, 2020, 103: 103405.
[20]	Pacific Earthquake Engineering Research Center. PEER strong motion database[R]. Berkeley: California Berkeley, 2005.
[21]	冯鹏, 强翰霖, 叶列平. 材料、构件、结构的"屈服点"定义与讨论[J]. 工程力学, 2017, 34(3): 36-46. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201703005.htm FENG Peng, QIANG Hanlin, YE Lieping. Discussion and definition on yield points of materials, members and structures[J]. Engineering Mechanics, 2017, 34(3): 36-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201703005.htm
[22]	QIU D P, CHEN J Y, FU H Q. Research on the comprehensive evaluating index of seismic performance of underground large-scale frame structures[J]. Structures, 2022, 37: 645-660.
[23]	CHEN Z Y, FAN Y, JIA P. Influence of buried depth on seismic capacity of underground subway stations through performance-based evaluation[J]. Structures, 2021, 32: 194-203.
[24]	CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533.
[25]	NIBS. HAZUS-MH: Technical Manuals[S]. 2004.

施引文献(8)

期刊类型引用(5)

1.	晏静，吴道勇，吴诗雨. 基于数字图像处理的盐溶液过饱和比与结晶压力测量方法. 硅酸盐通报. 2023(03): 1081-1085 . 百度学术
2.	万旭升，谭冬雪，路建国，晏忠瑞，何佑彪，钟闻华. 低温盐侵蚀环境下砂浆孔隙水相变特性研究. 冰川冻土. 2022(02): 545-554 . 百度学术
3.	应赛，周凤玺，文桃，曹亚鹏. 盐渍土冻结过程中的特征温度研究. 岩土工程学报. 2021(01): 53-61 . 本站查看
4.	王策，沐方元，刘东浩，马金铭，吉植强. 硫酸盐渍土盐胀结晶试验研究进展. 低温建筑技术. 2021(11): 120-124 . 百度学术
5.	吴松波，万旭升，杨婷婷，颜梦宇，刘力，钟昌茂. 混合侵蚀和冻融循环条件下混凝土力学机制试验研究. 南京理工大学学报. 2020(04): 493-500 . 百度学术

其他类型引用(3)

资源附件(2)

其他相关附件
- PDF格式
  13-202312-G22-1053一文审稿意见与作者答复点击下载(11246KB)
- PDF格式
  13-202312-G22-1053一文审稿意见与作者答复点击下载(11246KB)

图(10) / 表(6)

计量

文章访问数: 396
HTML全文浏览量: 74
PDF下载量: 101
被引次数: 8

0. 引言
1. 试验材料与方案
2. 试验结果与分析
2.1 蠕变与蠕变恢复试样变形特性
2.2 蠕变与蠕变恢复曲线对照分析
2.3 蠕变与蠕变恢复初始模量特性
3. 土工膜蠕变及蠕变恢复模型
3.1 模型的改进
3.2 模型参数求解与模型验证
4. 结论

考虑竖向地震作用的大型地下框架结构易损性分析 English Version

作者简介: 邱大鹏(1992—)，男，博士，副教授，主要从事地下结构抗震性能与韧性提升研究。E-mail: qiudapeng20@sdjzu.edu.cn

通讯作者: 王文明, E-mail: wangwenmingmr@sdjzu.edu.cn

计量

出版历程