Characteristic temperatures of saline soil during freezing
-
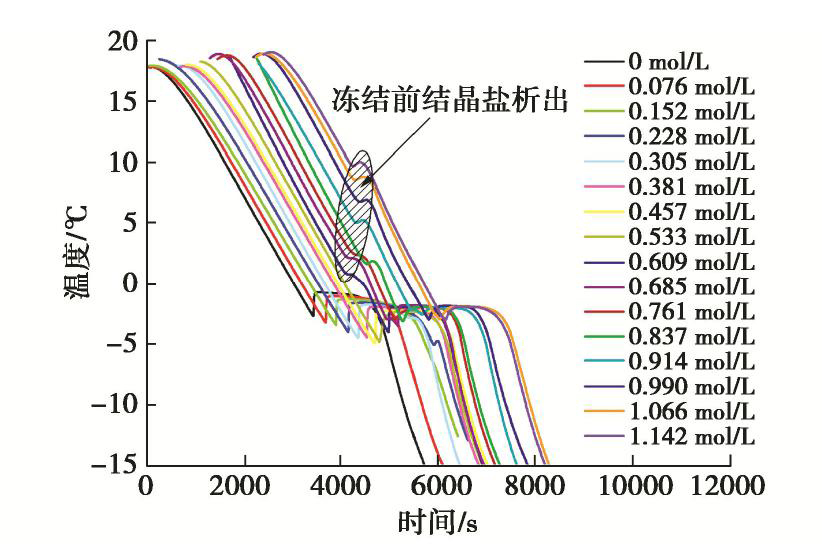
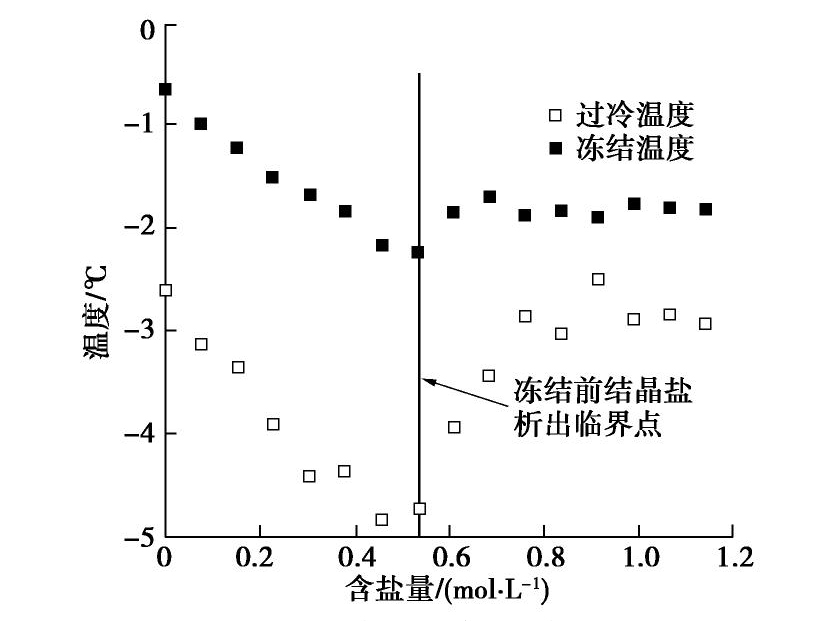
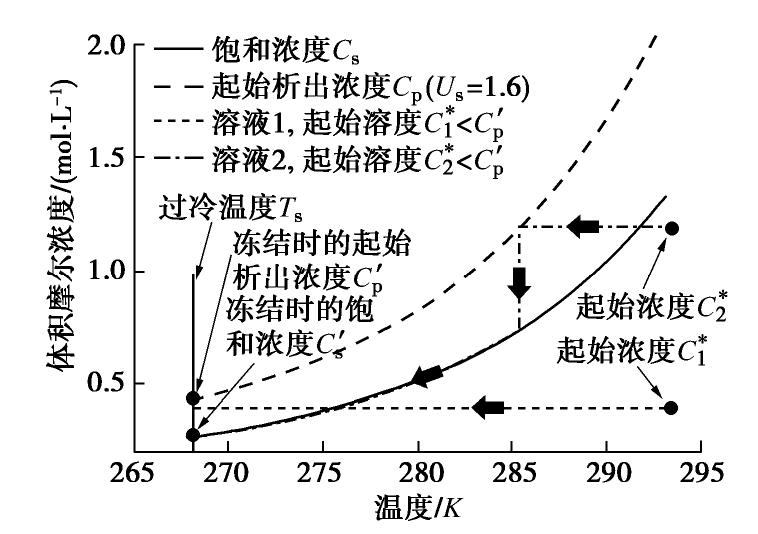
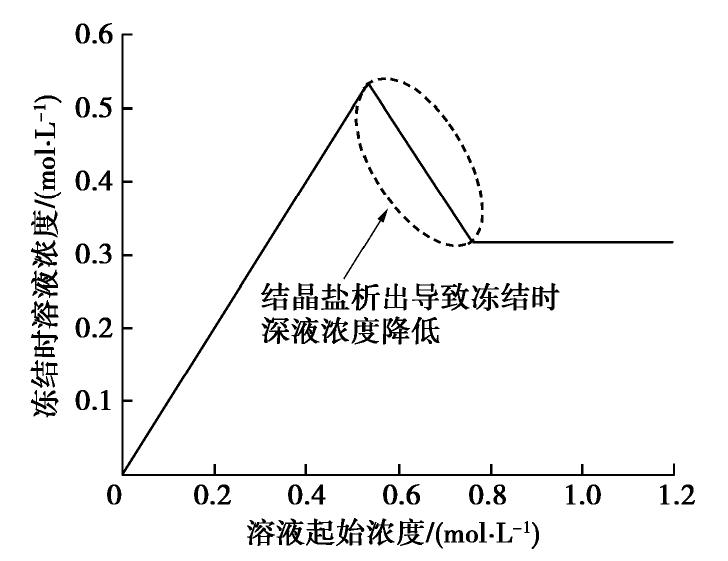
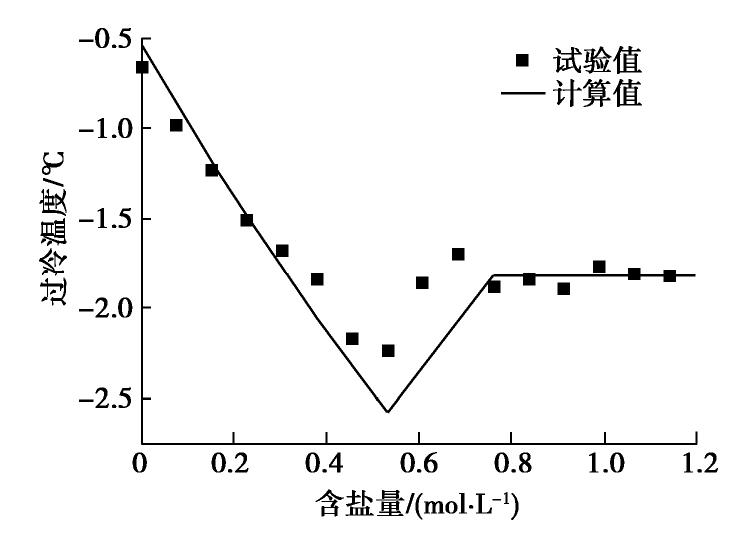
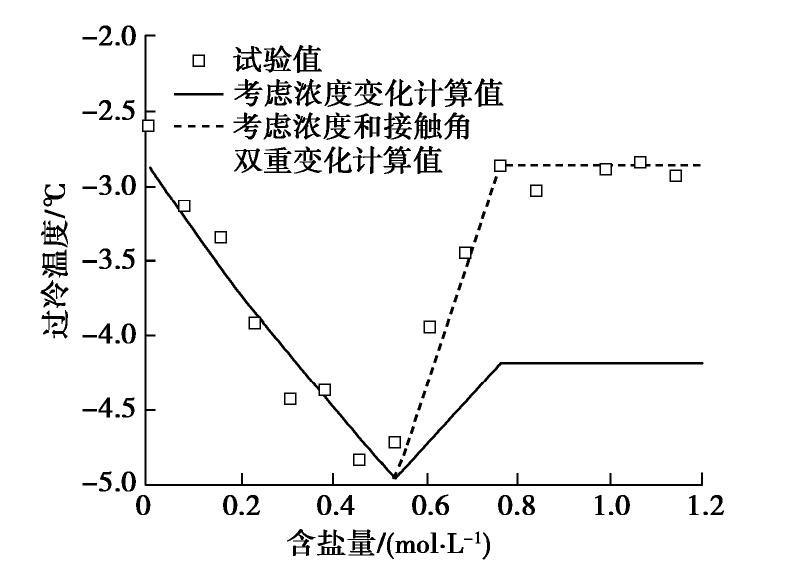
摘要: 盐渍土在降温冻结过程中出现过冷温度和冻结温度两种特征温度,分别表示在降温过程中孔隙溶液中晶核形成和孔隙溶液与冰晶共存时的临界温度,对判断土体的冻结状态有着重要的意义。首先,通过不同含盐量的土体冻结试验,得到了相应的过冷温度和冻结温度;然后,基于热力学与经典成核理论给出了盐渍土冻结过程中的两种特征温度的理论计算模型,并与试验结果进行对比,验证了该模型的有效性;最后,分析了盐渍土特征温度的影响因素,重点考察了孔隙溶液中结晶盐析出对冻结温度和过冷温度的影响。结果表明,提出的模型可以实现对盐渍土冻结特征温度的有效预测。通过冻结特征温度随含盐量的关系曲线,可以得到结晶盐析出时的含盐量。冻结时孔隙溶液的浓度与冻结温度存在负相关关系,结晶盐的析出引起冻结时孔隙溶液浓度下降,从而使冻结温度升高。而结晶盐析出导致孔隙溶液浓度降低和土颗粒与冰晶接触角减小的双重影响,是盐渍土过冷温度的升高的原因。Abstract: The characteristic temperatures appearing in freezing process of saline soil include the freezing temperature and the supercooling temperature. The former is the point at which chemical potentials of ice and liquid achieve equilibrium, and the latter is the point of ice nucleation. The characteristic temperatures are important for the analysis of the freezing state of soil. In the beginning, the characteristic temperatures are obtained through the freezing tests on the saline soil with different salt contents. And then, a model for calculating the characteristic temperatures is provided based on the thermodynamics and the classical nucleation theory. The model is proved to be reliable by comparing the calculated data with the test data. Finally, the influence factors for the model are analyzed, and especially the influences of salt precipitation on the characteristic temperatures are considered. The results show that the proposed model can effectively predict the characteristic temperatures of the saline soil. The salt content corresponding to the salt precipitation can be acquired by the relationship curve between the characteristic temperatures and the salt contents of the saline soil. The freezing temperature has a negative correlation with the concentration of pore solution, and the salt precipitation will induce the depression of the concentration of pore solution so as to increase the freezing temperature. The reason for the increase of the supercooling temperature of the saline soil is the double-effect of the depression of solution concentration and the decrease of contact angle between ice and soil particles.
-
Keywords:
- saline soil /
- freezing temperature /
- supercooling temperature /
- salt precipitation
-
0. 引言
防波堤是用于阻挡波浪侵袭、保证海港内设施安全的重要建筑物,常规的防波堤有沉箱结构、复合式结构和半圆形结构等结构形式[1-2]。然而在遇到软土地基、深水、大波浪荷载等复杂条件时,常规防波堤结构可能不再适用,结构失稳破坏的现象时有发生[3-4]。针对上述问题,国内近年开始应用新型的箱筒型基础防波堤结构[5-7]。该结构由基础和上部挡浪墙组成,基础部分通常由4个圆桶通过连接墙和盖板组成整体,依靠复杂的结构与土相互作用抵御风暴波浪作用。
目前国内外对于单桶基础已有较多的研究。在承载力方面,张金来等[8]、Bransby等[9]、Wang等[10]、黎冰等[11]通过数值模拟、离心试验以及理论推导,研究了桶基尺寸、长径比、埋深、土层性质对单桶基础水平、竖向和弯矩承载力的影响;并考虑土压力、摩擦力的发挥过程以及环向各点土压力大小的不同,基于极限平衡法提出了承载力计算方法。在破坏机理方面,Liu等[12]、刘润等[13]、范庆来等[14]通过数值模拟研究了单桶基础在V–H–T空间的屈服面,以及破坏模式;Zhang等[15]通过离心试验提出单桶基础的动力破坏形式包括地基动液化和长期动荷载引起的结构沉降两种形式。在结构变位方面,Zhu等[16]、Cox等[17]通过模型试验得出了长期循环荷载作用下单桶基础倾角、沉降的计算公式。
在三桶基础和箱筒型基础的研究方面。Kim等[18]提出三桶基础相对于单桶基础具有较大的刚度,并得出了三桶基础承载力和群桶效应系数的规律。蔡正银等[5]通过数值模拟提出箱筒型基础结构在下沉过程中,筒壁周边存在着下沉、相对隆起和下压变形区,并分析了挤土效应对稳定性的影响。杨立功等[19]、王元战等[20]通过数值法研究了波浪力作用下,筒壁上主动、被动、静止土压力以及正负摩阻力的分布范围,并提出了土压力简化计算法。肖忠等[6]、蒋敏敏等[7]通过数值模拟、离心试验等方法对天津港软土层中箱筒型基础结构的失稳和承载特性进行了研究。肖忠等[21-22]基于极限平衡法和数值模拟,提出了箱筒型基础结构稳定性分析计算法。
中国沿海广泛分布了黏土地基,港口工程的发展必然要求建设大量防波堤,箱筒型基础防波堤结构已经在天津、连云港等港口工程中得以应用,并初步显现出对于软黏土、大波浪荷载条件的适应性[5-7]。然而现有的关于桶形基础的研究主要集中于单桶基础、三桶基础,箱筒型基础结构的基础部分相比于以往的结构具有更多的分隔部分,复杂的结构与土相互作用,必然导致其破坏模式和承载特性与单桶基础、三桶基础不同。部分针对箱筒型基础结构的研究主要集中于土压力、稳定性的数值研究,对失稳破坏模式和承载特性的试验研究仍不足。本文针对天津港箱筒型基础防波堤,在离心试验中对结构施加不同的水平力和弯矩组合,研究地基土体强度、波浪力作用高度等因素影响下,箱筒型基础结构的静力失稳破坏模式和承载力等性质,为结构优化设计提供参考和依据。
1. 试验设计
1.1 试验设备和试验装置
本试验在南京水利科学研究院50 g·t臂式离心机中进行,最大有效半径为2.5 m,最高加速度250g,相应的最大负载为200 kg。模型箱净空尺寸的长、宽、高为685,350,450 mm。
采用自行研制的离心机水平静力加载设备[7]对箱筒型基础结构施加波浪力,该设备由电机、齿轮箱、导向支座和荷重传感器构成,如图1所示。该设备以等应变速率对防波堤施加静推力,推力最大值为15 kN(在原型尺度达165 MN),同时通过导向支座,避免传力杆在离心超重力场中产生过大挠曲。
1.2 箱筒型基础结构和地基土体的模拟
箱筒型基础防波堤为钢筋混凝土结构,由箱筒型基础和上部挡浪墙组成,箱筒型基础由4个圆桶通过连接墙连成整体,基础圆桶的上面为盖板,盖板以上为圆桶形挡浪墙。基础圆桶直径为12 m、高度9 m、壁厚0.3 m,盖板边长27 m、厚度0.5 m,上部圆桶形挡浪墙的直径为12 m。
模型箱筒型基础结构采用铝合金制作,根据离心试验相似原理结构尺寸缩小为原型的1/N,N为离心试验比尺,本试验中设为105。箱筒型基础结构的桶壁受地基土压力和摩阻力作用,为受弯结构[5,19],在本研究中根据抗弯刚度相似原理设计桶壁的厚度[23]为
tm=tpN3√Ep/Em, (1) 式中,tm和tp分别为模型和原型结构的壁厚,Em和Ep分别为模型和原型材料的弹性模量。模型箱筒型基础防波堤结构如图2所示。
本文离心模型试验中模拟了厚度为20 m的黏土地基,模型地基土层厚度大于2倍基础圆桶高度,能够保证结构的变位不受模型箱边界的影响。将天津港现场取回的黏土,在模型箱中制成泥浆,通过离心模型固结仪对模型箱中的重塑土体施加不同的压力,如图3所示,排水固结后得到不同强度的黏土地基[24],固结后通过微型静力触探仪测得地基土体的平均强度如表1所示。黏土层下方为一层砂土,是固结时的排水层。
表 1 离心试验方案Table 1. Centrifuge test programs试验编号 波浪力作用高度e/m 土体不排水强度Su/ kPa S1 4.5 23.9 S2 10.5 22.9 S3 13.5 23.6 S4 10.5 37.4 S5 10.5 44.5 1.3 试验程序和试验方案
离心试验程序如下:①首先在1g条件下,通过离心模型固结仪在模型箱中对土体施加固结压力,制作均匀的黏土地基。②已有研究表明,负压下沉或压入下沉方法对结构的稳定和承载特性不产生影响[16],本研究采用静力压入法,将模型结构压入固结后的黏土地基中,直至盖板底面与海床面齐平。③将模型箱置于离心超重力场中再次固结,模拟结构下沉施工后,由于结构重量引起的地基固结过程,直至结构沉降稳定。④对箱筒型基础结构施加水平力和弯矩,模拟波浪的作用,直至结构达到失稳破坏条件。
采用Goda法计算天津港工程区域结构上的设计波浪力[1],并考虑曲墙上波浪力的折减[6],得出箱筒型基础结构上的设计波浪力Hd为8465 kN,海床面处的设计弯矩Md为37730 kN·m。本研究的加载方式与Zhu等[16]和Kim等[18]的方法相同,通过将水平力H作用于不同的高度e(e为水平力作用点至海床面的距离),实现了不同水平荷载和弯矩的组合,如图4所示,图中弯矩M=He。
本文试验方案如下:试验模拟了3种不同的波浪力作用高度,4.5 m代表天津港工程区域的波浪作用高度,10.5 m和13.5 m代表波浪力作用高度较大的情况;同时模拟了3种不同强度的地基土体条件,不排水抗剪强度约23 kPa代表了天津港工程现场地基土体强度较小的情况,不排水抗剪强度37.4 kPa和44.5 kPa代表了土体强度更高的情况。具体试验参数如表1所示。
模型试验的布置如图5所示。通过调整静力加载装置作用高度,模拟不同波浪力作用高度e。箱筒型基础结构的位移通过3个激光位移传感器测量,2个沉降V1和V2,1个水平位移H3,并计算结构的转角
θ 、水平位移量u、竖向位移量v。转角以向港侧转动为正、水平位移量以向港侧为正、竖向位移量以沉降为正。2. 结构的荷载位移特性
2.1 结构位移
箱筒型基础结构的归一化弯矩M/Md(Md为前文计算的设计弯矩)与转角
θ 的关系如图6所示,其中图6(a)为不同地基土体强度的结果,图(b)为不同波浪力作用高度的结果。从弯矩–转角结果可见,在不同土体强度和波浪力作用高度下,结构均发生向港侧的转动。由图6(a)可见,土体强度越高对结构转动的约束越强,在相同弯矩下转角越小。由图(b)可见,相同弯矩下波浪力作用高度越大转角越小,表明波浪作用高度增大,相同弯矩时转角越小。弯矩–转角曲线可分为两个阶段,如图6(a)所示,弯矩小于临界值时,弯矩–转角关系近似为弹性;弯矩大于临界值后,转角随着弯矩的增大迅速增大,直至结构产生较大的转角而失稳破坏。Zhu等[16]和Villalobos等[25]提出了单桶基础承载力确定方法,即在荷载–位移曲线上分别对曲线第一阶段弹性变位阶段和第二阶段失稳阶段采用直线拟合,在汇交点作水平线,该水平线与荷载位移曲线的交点为承载力,该方法同样被证明适用于确定三桶基础的承载力[18,26]。根据这一方法,在箱筒型基础结构的弯矩–转角图中确定弯矩承载力MR,如图6(a)所示。同时从图6可见,各组试验对应于弯矩承载力时的转角介于1.6°~2.8°之间。
箱筒型基础结构盖板底面中心(图4中O点)的归一化水平荷载H/Hd与水平位移量u的关系如图7所示。由图7水平位移结果可见,在波浪荷载作用下,防波堤盖板底面中心发生向港侧的水平位移,仅有在S1试验中波浪力较小时有向海侧的水平位移。土体强度越高对结构的水平位移约束越强,在相同水平荷载下水平位移量越小。相同水平荷载下波浪力作用高度越大结构盖板底面中心的水平位移越大,表明波浪作用高度增大,相同水平荷载时水平位移量越大。
与弯矩–转角曲线类似,箱筒型基础结构的水平荷载–水平位移曲线也呈现为弹性变位和失稳破坏两个阶段,如图7所示。根据上述承载力确定方法,同样可在水平荷载–水平位移图中得出水平承载力HR,如图7(a)所示。从试验结果可见,受土体强度、波浪力作用高度等因素的影响,对应于水平承载力HR时,结构的水平位移量变化范围较大,介于3~238 mm之间。
箱筒型基础结构盖板底面中心(O点)的归一化弯矩M/Md与竖向位移量v的关系如图8所示。由图8可见,在波浪荷载作用下,盖板底面中心发生向下的竖向位移。箱筒型基础结构的竖向位移与转角、水平位移有着不同的规律,在土体强度较低时(Su约为23 kPa,S1、S2和S3试验),弯矩–竖向位移曲线仍有弹性变位和失稳破坏两个阶段;土体强度为37.4 kPa时(S4试验),弯矩–竖向位移曲线近似为线性关系;土体强度为44.5 kPa时(S5试验),竖向位移随着弯矩增大至一定值后,又呈现减小的趋势,表明土体强度增大至44.5 kPa,结构不会由于竖向位移引起失稳破坏。相同弯矩下波浪力作用高度越大结构盖板底面中心的竖向位移量越小,表明波浪作用高度增大,相同弯矩时竖向位移量越小。
2.2 转动中心位置
结构的转动中心是加载过程的转动圆心,转动中心对于分析结构位移规律具有重要作用[16,27]。根据箱筒型基础结构的转角、水平位移和竖向位移结果,计算出转动中心深度随着归一化弯矩M/Md的变化如图9所示。从结果可见:在弯矩较小时,转动中心位于海床面以上,随着弯矩的增大,转动中心不断向下移动,弯矩大于1.2~1.8Md时,转动中心逐渐移动至海床面以下。在不同的土体强度、波浪力作用高度下,弯矩在达到承载力MR时,各组试验的转动中心均逐渐趋于桶底边缘附近,约9 m深度处,表明在达到弯矩承载力MR时,箱筒型基础结构将绕着基础桶底端向港侧转动而失稳。
3. 结构失稳破坏模式和承载力特性
3.1 失稳破坏模式
箱筒型基础结构与单桶基础的结构形式有较大的差异,基础部分具有多个分隔部分,如图2(b)所示,且具有更小的高径比,本研究中结构高径比为0.33,箱筒型基础结构的失稳破坏规律必然与单桶基础有较大的不同。文献[6]根据荷载位移曲线拐点稳定性判别标准,得出S1试验的水平承载力为1.82Hd,本文根据Zhu等[16]和Villalobos等[25]的承载力确定方法得出的水平承载力为1.83Hd,与数值模拟结果较一致,表明该方法可用于确定箱筒型基础结构的承载力。
根据荷载位移曲线得出了不同土体强度、波浪力作用高度下,荷载为承载力时,箱筒型基础结构盖板底面中点O(如图4所示)的位移结果如表2所示,位移量大于表2中限值时,结构将会由于承载力不足而失稳破坏。从结果可见,由于受土体强度、波浪力作用高度等参数的影响,箱筒型基础结构具有明显不同的失稳变位特性。
表 2 承载力时箱筒型基础结构中心的位移量Table 2. Displacements of center of composite bucket foundation under bearing capacity试验编号 转角θ/(°) 水平位移量u/mm 竖向位移量v/mm S1 2.0 3 209 S2 1.6 108 166 S3 1.6 238 128 S4 2.5 185 147 S5 2.8 157 14 由表2可见,土体强度为23.9 kPa,波浪力作用高度为4.5 m时(S1试验),箱筒型基础结构的转角和竖向位移较大,而水平位移较小,失稳变位模式为转动和竖向位移的模式。土体强度约23 kPa,波浪力作用高度增大为10.5 m和13.5 m时(S2和S3试验),结构的转角、水平位移和竖向位移均有较大值,失稳变位模式为转动、水平位移和竖向位移的模式。
波浪力作用高度为10.5 m,土体强度为22.9 kPa和37.4 kPa(对应于S2和S4试验),结构的失稳变位模式为转动、水平位移和竖向位移的模式。当土体强度增大至44.5 kPa(S5试验),承载力时结构竖向位移极小,失稳变位模式为转动和水平位移的模式。
3.2 承载力特性
根据前述的承载力确定方法,得出了不同土体强度、波浪力作用高度下,箱筒型基础结构的水平承载力HR和弯矩承载力MR,并将HR/Hd和MR/Md结果(Hd和Md分别为前文定义的设计波浪力和设计弯矩)绘制在M-H平面内,如图10所示。从图10可见,受土体强度、波浪力作用高度的影响,箱筒型基础结构具有不同的水平承载力HR和弯矩承载力MR的组合。
由图10可见,在土体强度相同时(Su约23 kPa),黏土地基中箱筒型基础结构的弯矩承载力随着水平承载力的增大而呈线性降低,即弯矩承载力越大水平承载力越小,趋势线如图中的实线。Zhu等[16]和LeBlanc等[28]对砂土中刚性桩和单桶基础的承载力规律进行了研究,表明在相对密度相同时(土体状态一致)结构的弯矩承载力MR随着水平承载力HR的增大而呈线性降低,与本文的黏土中箱筒型基础结构的承载特性有相似的规律。根据离心试验结果,一定土体强度下,天津港箱筒型基础防波堤结构弯矩承载力与水平承载力间的关系可合理表示为
MRMd=−0.854HRHd+4.92。 (2) 在波浪力作用高度相同、土体强度不同时,弯矩承载力随着水平承载力的增大而呈线性增长关系,且地基土体强度越大,水平承载力和弯矩承载力均越大,表明土体强度增大,明显增强了箱筒型基础结构的承载力。一定波浪力作用高度下,天津港箱筒型基础防波堤结构弯矩承载力与水平承载力间的关系可表示为
MRMd=3.179HRHd-0.745。 (3) 此外,本文离心试验中土体强度是均一的,如考虑地基土体强度沿着深度线性增大的情况,由于深层土体强度较高,产生的嵌固效应将增强,会导致结构承载力略增大[29]。
4. 结论
本文通过离心试验研究了箱筒型基础防波堤失稳破坏模式和承载力特性,并研究了土体强度、波浪力作用高度对其影响规律,得到以下主要结论:
(1)箱筒型基础结构的荷载与转角、水平位移曲线有弹性变位和失稳破坏两个阶段。而竖向位移受土体强度的影响呈现不同的规律,土体强度约23 kPa,荷载–竖向位移曲线也呈现弹性变位和失稳破坏两阶段;土体强度为37.4 kPa,荷载–竖向位移为线弹性关系;土体强度为44.5 kPa,竖向位移先增大后减小。
(2)随着弯矩的增大,结构的转动中心从海床面以上逐渐向地基中移动,在达到弯矩承载力时,转动中心的深度大致位于桶底端。
(3)土体强度约23 kPa,波浪力作用高度为4.5 m,结构失稳时的变位模式为转动和竖向位移的模式;土体强度不变,波浪力作用高度增大为10.5 m和13.5 m时,结构失稳时的变位模式为转动、水平位移和竖向位移的模式。波浪力作用高度为10.5 m,土体强度为22.9 kPa和37.4 kPa,结构的失稳变位模式为转动、水平位移和竖向位移的模式;波浪力作用高度不变,土体强度增大至44.5 kPa时,失稳变位模式为转动和水平位移的模式。
(4)土体强度相同时,箱筒型基础结构的弯矩承载力随着水平承载力的增大呈线性降低关系;波浪力作用高度相同时,弯矩承载力随着水平承载力的增大呈线性增长关系。
-
表 1 土的物理性质指标
Table 1 Physical properties of soil
土粒相对质量密度 液限wL/% 塑限wP/% 塑性指数Ip 2.71 26.8 17.6 9 表 2 土样含盐量
Table 2 Salt contents of samples
编号 含盐量/(mol·L-1) 编号 含盐量/(mol·L-1) 1 0 9 0.610 2 0.076 10 0.685 3 0.152 11 0.761 4 0.228 12 0.838 5 0.305 13 0.914 6 0.381 14 0.990 7 0.457 15 1.066 8 0.533 16 1.142 表 3 溶液参数表
Table 3 Parameters of electrolyte solution
盐种类 β(0)MX β(1)MX β(2)MX CϕMX Na2SO4 0.1939 1.4285 -0.5954 -0.008222 -
[1] 徐攸在. 盐渍土地基[M]. 北京: 中国建筑工业出版社, 2012. XU You-zai. Saline Soil Foundation[M]. Beijing: China Architecture & Building Press, 2012. (in Chinese)
[2] WU D, LAI Y, ZHANG M. Heat and mass transfer effects of ice growth mechanisms in a fully saturated soil[J]. International Journal of Heat and Mass Transfer, 2015, 86: 699-709. doi: 10.1016/j.ijheatmasstransfer.2015.03.044
[3] KONIORCZYK M, GAWIN D. Modelling of salt crystallization in building materials with microstructure: poromechanical approach[J]. Construction & Building Materials, 2012, 36: 860-873.
[4] ESPINOSA R M, FRANKE L, DECKELMANN G. Model for the mechanical stress due to the salt crystallization in porous materials[J]. Construction and Building Materials, 2008, 22(7): 1350-1367. doi: 10.1016/j.conbuildmat.2007.04.013
[5] ESPINOSA R M, FRANKE L, DECKELMANN G. Phase changes of salts in porous materials: crystallization, hydration and deliquescence[J]. Construction & Building Materials, 2008, 22(8): 1758-1773.
[6] SCHERER G W. Crystallization in pores[J]. Cement & Concrete Research, 1999, 29(8): 1347-1358.
[7] SCHERER G W. Stress from crystallization of salt[J]. Cement & Concrete Research, 2004, 34(9): 1613-1624.
[8] WANG C, LAI Y, YU F, et al. Estimating the freezing-thawing hysteresis of chloride saline soils based on the phase transition theory[J]. Applied Thermal Engineering, 2018, 135: 22-33. doi: 10.1016/j.applthermaleng.2018.02.039
[9] KHVOROSTYANOV V I, CURRY J A. Thermodynamic theory of freezing and melting of water and aqueous solutions[J]. The Journal of Physical Chemistry A, 2004, 108(50): 11073-11085. doi: 10.1021/jp048099+
[10] WU D, LAI Y, ZHANG M. Heat and mass transfer effects of ice growth mechanisms in a fully saturated soil[J]. International Journal of Heat and Mass Transfer, 2015, 86: 699-709. doi: 10.1016/j.ijheatmasstransfer.2015.03.044
[11] 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 科学出版社, 2001. XU Xue-zu, WANG Jia-cheng, ZHANG Li-xin. Frozen Soil Physics[M]. Beijing: Science Press, 2001. (in Chinese)
[12] LAI Y, WU D, ZHANG M. Crystallization deformation of a saline soil during freezing and thawing processes[J]. Applied Thermal Engineering, 2017, 120: 463-473. doi: 10.1016/j.applthermaleng.2017.04.011
[13] KONRAD J M. Temperature of ice lens formation in freezing soils[C]//Proceedings of 5th International Conference on Permafrost. Trondheim, Norway: Tapir Publishers. 1988: 384-389.
[14] STYLE R W, PEPPIN S S L, COCKS A C F, et al. Ice-lens formation and geometrical supercooling in soils and other colloidal materials[J]. Physical Review E, 2011, 84(4): 041402.
[15] 万旭升, 赖远明, 廖孟柯. 硫酸盐渍土未相变含水率与温度关系研究[J]. 岩土工程学报, 2015, 37(12): 2175-2181. doi: 10.11779/CJGE201512006 WAN Xu-sheng, LAI Yuan-ming, LIAO Meng-ke. Relationship between temperature and water content of sodium saline soils without phase transformation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(12): 2175-2181. (in Chinese) doi: 10.11779/CJGE201512006
[16] 邴慧, 马巍. 盐渍土冻结温度的试验研究[J]. 冰川冻土, 2011, 3(5): 1106-1113. https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT201105020.htm BING Hui, MA Wei. Experimental study on freezing point of saline soil[J]. Journal of Glaciology and Geocryology, 2011, 3(5): 1106-1113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT201105020.htm
[17] BING Hui, MA Wei. Laboratory investigation of the freezing point of saline soil[J]. Cold Regions Science & Technology, 2011, 67(1): 79-88.
[18] 张婷, 杨平. 不同因素对浅表土冻结温度的影响[J]. 南京林业大学学报(自然科学版), 2009, 34(4): 136-138. doi: 10.3969/j.issn.1000-2006.2009.04.029 ZHANG Ting, YANG Ping. Effect of different factors on the freezing temperature of shallow top soil[J]. Journal of Nanjing Forestry University (Natural Science Edition), 2009, 33(4): 132-134. (in Chinese) doi: 10.3969/j.issn.1000-2006.2009.04.029
[19] 李毅, 崔广心, 吕恒林. 有压条件下湿黏土结冰温度的研究[J]. 冰川冻土, 1996, 18(1): 43-46. LI Yi, CUI Guang-xin, LÜ Heng-lin. A study on freezing point of wet clay under loading[J]. Journal of Glaciolgy & Geocryology, 1996, 18(1): 43-46. (in Chinese)
[20] 周家作, 谭龙, 韦昌富, 等. 土的冻结温度与过冷温度试验研究[J]. 岩土力学, 2015, 36(3): 777-785. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201503027.htm ZHOU Jia-zuo, TAN Long, WEI Chang-fu, et al. Experimental research on freezing temperature and super-cooling temperature of soil[J]. Rock and Soil Mechanics, 2015, 36(3): 777-785. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201503027.htm
[21] HAN Y, WANG Q, KONG Y, et al. Experiments on the initial freezing point of dispersive saline soil[J]. Catena, 2018, 171: 681-690. doi: 10.1016/j.catena.2018.07.046
[22] WAN X, HU Q, LIAO M. Salt crystallization in cold sulfate saline soil[J]. Cold Regions Science and Technology, 2017, 137: 36-47. doi: 10.1016/j.coldregions.2017.02.007
[23] XIAO Z, LAI Y, YOU Z, et al. The phase change process and properties of saline soil during cooling[J]. Arabian Journal for Science and Engineering, 2017, 42(9): 3923-3932. doi: 10.1007/s13369-017-2542-y
[24] PETROV O, FURÓ I. Curvature-dependent metastability of the solid phase and the freezing-melting hysteresis in pores[J]. Physical Review E, 2006, 73(1): 011608. doi: 10.1103/PhysRevE.73.011608
[25] MORISHIGE K, KAWANO K. Freezing and melting of water in a single cylindrical pore: the pore-size dependence of freezing and melting behavior[J]. The Journal of Chemical Physics, 1999, 110(10): 4867-4872. doi: 10.1063/1.478372
[26] JIANG Q, WARD M D. Crystallization under nanoscale confinement[J]. Chemical Society Reviews, 2014, 43(7): 2066-2079. doi: 10.1039/C3CS60234F
[27] SLIWINSKA-BARTKOWIAK M, GRAS J, SIKORSKI R. Phase transitions in pores: experimental and simulation studies of melting and freezing[J]. Langmuir, 1999, 15(18): 6060-6069. doi: 10.1021/la9814642
[28] 王中平, 王弢. 简述核磁共振冷冻测孔法的原理及应用[J]. 材料导报, 2013, 27(1): 129-133. https://www.cnki.com.cn/Article/CJFDTOTAL-CLDB201301025.htm WANG Zhong-ping, WANG Tao. A brief introduction to the principle and application of nuclear magnetic resonance cryoporometry[J]. Materials Reports, 2013, 27(1): 129-133. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CLDB201301025.htm
[29] WAN X, LAI Y, WANG C. Experimental study on the freezing temperatures of saline silty soils[J]. Permafrost & Periglacial Processes, 2015, 26(2): 175-187.
[30] XIAO Z, LAI Y, ZHANG M. Study on the freezing temperature of saline soil[J]. Acta Geotechnica, 2018, 13(1): 195-205.
[31] KOZLOWSKI T. Some factors affecting supercooling and the equilibrium freezing point in soil-water systems[J]. Cold Regions ence & Technology, 2009, 59(1): 25-33.
[32] STEIGER M. Crystal growth in porous materials—I: The crystallization pressure of large crystals[J]. Journal of Crystal Growth, 2005, 282(3/4): 455-469.
[33] 周凤玺, 应赛, 蔡袁强. 多孔介质中晶体的结晶压力分析[J]. 岩土工程学报, 2019, 41(6): 1158-1163. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201906023.htm ZHOU Feng-xi, YING Sai, CAI Yuan-qiang. Crystallization pressure of crystals in porous media[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(6): 1158-1163. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201906023.htm
[34] PITZER K S. Activity Coefficients in Electrolyte Solutions[M]. Boca Rton: CRC press, 2018.
[35] 万旭升. 硫酸盐渍土盐晶体析出,盐分迁移及寒区路基防盐胀试验研究[D]. 北京: 中国科学院大学, 2015. WAN Xu-sheng. Labotory Investigation on Salt Crystals precipitation of Sulfate Saline Soil and Salt Transfer and Salt-Heaving Mitigation of Embankment in Cold Regions[D]. Beijing: University of Chinese Academy of Sciences, 2015. (in Chinese)
[36] STEIGER M. Crystal growth in porous materials—II: Influence of crystal size on the crystallization pressure[J]. Journal of Crystal Growth, 2005, 282(3/4): 470-481.
[37] MULLIN J W. Crystallization[M]. Oxford: Butterworth- Heinemann, 2001.
[38] FLETCHER N H J. Size effect in heterogeneous nucleation[J]. The Journal of Chemical Physics, 1958, 29(3): 572-576.
[39] 李星星, 王思敬, 肖锐铧, 等. 硫酸钠溶液在降温结晶过程中的盐胀与冻胀[J]. 岩土工程学报, 2016, 38(11): 2069-2077. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201611022.htm LI Xing-xing, WANG Si-jin, XIAO Rui-hua, et al. Saline expansion and frost heave of sodium sulfate solution during cooling crystallization process[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(11): 2069-2077. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201611022.htm
-
期刊类型引用(5)
1. 刘智敏,陈广思,王晓磊,李成凤,刘润. 海上风电筒型基础在水平力和力矩耦合作用下的变形模式研究. 太阳能学报. 2025(03): 697-704 .  百度学术
百度学术
2. 李文轩,范开放,刘永刚,朱洵. 粉砂地基中复合筒型基础水平承载特性研究. 水利水运工程学报. 2023(02): 87-95 .  百度学术
百度学术
3. 吴宜鹏,范庆来,任增乾,陈箫笛. 考虑软土应变软化效应的深埋式大圆筒承载性状分析. 防灾减灾工程学报. 2022(04): 859-865 .  百度学术
百度学术
4. 蔡正银,王清山,关云飞,韩迅,李文轩. 分舱板对海上风电复合筒型基础承载特性的影响研究. 岩土工程学报. 2021(04): 751-759 .  本站查看
本站查看
5. 张连丽,蒋幼梅,林浙,唐成虎. 筒形导管架桩基防波堤结构及其经济分析. 中阿科技论坛(中英文). 2020(11): 44-46 .  百度学术
百度学术
其他类型引用(3)




 下载:
下载: