0.   引言

缩尺模型试验作为对复杂的工程问题研究的重要手段，具有试验成本低、时间省、易操作等优点，其基本原理为相似的结构在相似的影响下，产生相似的结果。盾构隧道作为地下结构，其受外部影响复杂，如地表加载、基坑开挖、桩基施工等^[1-2]，因此常通过缩尺模型试验研究外部影响下盾构隧道响应。盾构隧道是由管片拼装而成的管状结构，在外部影响下不仅发生横断面变形，同时发生纵向挠曲变形。因此在开展盾构隧道变形影响缩尺模型试验时，确保模型盾构隧道的横向刚度与纵向刚度均满足相似要求至关重要。

由于管片接头的存在，相比无接头的匀质圆管而言，盾构隧道的横向刚度与纵向刚度均大幅度降低^[3-5]。对于横向刚度的考虑不同，分别有匀质圆环模型、修正匀质圆环模型、多铰环模型、梁-弹簧模型，其中修正匀质圆环模型因对隧道管片环横向刚度考虑合理，且方便分析计算而成为主要的使用模型^[5]。盾构隧道纵向刚度分析主要有纵向梁-弹簧模型与纵向等效连续化模型为主，其中纵向等效连续化模型因其方便建模计算而得到了广泛的应用^[6]。由于盾构隧道纵缝接头与环缝接头的受力性能不同，因此，管片接头对盾构隧道横向刚度与纵向刚度的降低幅度也不同，对应的横向刚度有效率与纵向刚度有效率也不同^[7-9]。因此若将盾构隧道简化为匀质圆管结构，则无法使简化模型的横、纵向刚度与实际盾构隧道均满足相似要求，当进行缩尺模型试验时，模型盾构隧道的横、纵向刚度将无法同时满足相似关系。

为了使在模型盾构隧道满足横向刚度相似，梁荣柱等^[7]将横型管片环在纵缝接头处切断，然后再用塑料片连接；黄大维等^[10]采用开槽模拟管片纵缝接头，从达到盾构隧道的横向刚度折减的目的；吴庆等^[11]则采用匀质圆管模拟盾构隧道。为了使模型盾构隧道纵向刚度满足要求，文献[12~15]分别采用有机玻璃、聚乙烯片、石膏与硅藻土混合材料、聚乙烯管，制作了外径分别为0.4，0.16，0.25，0.2 m的模型盾构隧道，并采用简支梁法测得了模型隧道的纵向刚度；Li等^[16]采用有机玻璃制作了外径为0.4 m的模型盾构隧道，开展了盾构隧道残余顶推力对盾构隧道的纵向刚度影响。然而，上述的模型盾构隧道并未考虑与原型盾构隧道的横向刚度与纵向刚度相似设计，因此在设计过程中只考虑了横向刚度在匀质圆环模型的基础上进行一定的刚度折减，或只考虑了纵向刚度在匀质圆管的基础上进行一定的刚度折减，而刚度折减幅度与对应的刚度有效率、相关影响参数的关系并未考虑。从现有研究来看，至今暂未设计出横向刚度与纵向刚度均可满足相似要求的模型盾构隧道。

基于现有的模型盾构隧道暂未对其横向刚度与纵向刚度同时进行相似设计，为此，本文提出了一种横向刚度与纵向刚度均可满足相似要求的模型盾构隧道设计方法，并得到了模型盾构隧道纵向刚度计算方法。通过模型试验对模型盾构隧道的横向与纵向刚度进行了测定与验证，成果对模型盾构隧道合理设计、提高模型试验相似度均具有重要的参考与借鉴意义。

1.   模型盾构隧道相似分析及设计

1.1   模型盾构隧道相似分析

结构缩尺模型试验可用于模拟结构的弹性变形与结构破坏特性^[17]。在模拟结构破坏特性时，模型结构材料的应力、应变、强度均需满足相似要求，而在模拟结构的弹性变形时只需要应力、应变满足相似要求。为了方便设计模型试验，通常只模拟结构的弹性变形，模型试验的相似准则与相似比只需要按弹性力学问题进行推导。

模型试验目的是通过缩小试验结构几何尺寸，从而减小试验难度、降低试验成本、节省试验时间，但试验结构的几何尺寸减小势必加大试验误差，甚至导致试验数据的测试元件不便布设^[18]。因此在模型盾构隧道设计时，应根据试验目的及要求选用几何相似比。本文开展模型盾构隧道相似设计分析，并以几何相似比1︰10(模型结构几何尺寸与原型结构几何尺寸之比)为例设计了模型盾构隧道。

用$C$加上物理量的下标表示相似常数，即原型结构物理量与模型结构物理量的比值。模型试验通常以几何相似常数${C_{\text{l}}} = 10$及重度相似常数${C_{\text{γ }}} = 1$为设计基础，根据相似第一定理(相似正定理)、相似第二定理($\Pi$定理)及相似第三定理^{[17, 19-20]}，并按弹性力学问题推导得到了室内模型试验的相似关系及相似常数如表 1所示。

表  1  缩尺模型试验基本物理量的相似常数

Table  1.  Similar constants of fundamental physical quantities for scaled model tests

物理量	相似关系	相似常数		物理量	相似关系	相似常数
几何尺寸	基本量(${C_{\text{l}}}$)	10		弯矩	${C_{\text{M}}} = {C_{\text{γ }}}{C_{\text{l}}}^{\text{4}}$	10000
重度	基本量(${C_{\text{γ }}}$)	1		轴力	${C_{\text{N}}} = {C_{\text{γ }}}{C_{\text{l}}}^{\text{3}}$	1000
应力	${C_\sigma } = {C_{\text{l}}}{C_{\text{γ }}}$	10		剪力	${C_{\text{Q}}} = {C_g}{C_{\text{l}}}^{\text{3}}$	1000
位移	${C_{\text{δ }}} = {C_{\text{l}}}$	10		弯曲刚度	${C_{{\text{EI}}}} = {C_{\text{l}}}^{\text{5}}$	100000
弹性模量	${C_{\text{E}}} = {C_{\text{l}}}$	10		轴向刚度	${C_{{\text{EA}}}} = {C_{\text{l}}}^{\text{3}}$	1000

下载: 导出CSV 

| 显示表格

从表 1可以看出，若要使模型盾构隧道与原型盾构隧道完全满足相似关系，需要采用一种重度与混凝土相同、弹性模量则为混凝土1/10的材料加工管片，同时要确保模型盾构隧道的纵缝接头与环缝接头对其刚度影响均满足相似关系。若采用石膏与重晶石粉等混合材料加工模型盾构隧道管片，因其强度过低，试验过程极易发生脆性破坏，甚至使模型试验过程存在较大安全风险。盾构隧道发生横断面变形过程中，管片纵缝接头受到弯矩、轴力、剪力等荷载的影响；而盾构隧道发生纵向挠曲变形时，环缝接头将受到拉压与剪力等荷载影响。因此，若使模型盾构隧道与原型盾构隧道保持相似关系，则需要使模型与原型盾构隧道的纵缝接头和环缝接的力学性能也保持相似关系，而管片接头的力学性能影响因素复杂，其相似设计难度极大。因此，有必要提出更加合理的模型盾构隧道设计方法。

1.2   模型盾构隧道设计

盾构隧道由管片环拼装而成，管片环由于纵缝接头的存在，其横向刚度相比无纵缝接头的匀质环横向刚度要小，两者的横向刚度比即为横向刚度有效率。由已有研究可知，横向刚度有效率的大小与管片拼装方式(通缝拼装或错缝拼装)、管片环分块数量、管片幅宽、盾构隧道直径等因素有关^[8-9]。盾构隧道由于环缝接头的存在，其纵向刚度相比相同材质与厚度的匀质圆管纵向刚度要小，两者的纵向刚度比即为纵向刚度有效率。盾构隧道的纵向刚度有效率影响因素同样复杂，如环缝接头的连接螺栓数量及预紧力、盾构隧道直径、盾构隧道残余顶推力等^{[7, 14]}。

盾构隧道的横向刚度有效率与纵向刚度有效率影响因素与影响机制不同，因此两者并不相等，甚至相差较大。在缩尺模型盾构隧道设计时，若通过匀质圆管模拟盾构隧道，则无法使模型盾构隧道的横向刚度与纵向刚度均满足相似要求。在模型盾构隧道试验静力学相关模型试验时，盾构隧道的横向与纵向刚度相似将直接关系到盾构隧道的横断面变形与纵向挠曲变形，从而影响盾构隧道与地层的相互作用。从表 1可以看出，要设计出完全满足相似要求的模型盾构隧道，模型盾构隧道的加工材料的选用、隧道结构的构造设计等难度极大。因此，为了使模型盾构隧道的横向刚度与纵向刚度均可按需设计，模型盾构隧道管片环采用修正匀质圆环，其横向抗弯刚度通过管片环的材质及厚度进行控制；管片环之间通过垫有弹簧的螺栓连接，模型盾构隧道的纵向刚度通过垫在螺栓上的弹簧压缩刚度进行控制。

为了方便设计与加工模型盾构隧道，其材料的重度与弹性模量均可不满足相似要求。因为加工模型盾构隧道的材料重度将影响模型盾构隧道的自重，而隧道的自重对隧道的变形影响要远小于周围地层荷载对隧道的变形影响。因此自重不满足相似关系对模型盾构隧道静力学试验结果影响可以忽略；材料的弹性模量将影响模型盾构隧道的横向与纵向刚度，而采用本文提出的模型盾构隧道设计方法，通过设计管片环的厚度来控制模型盾构隧道横向刚度，通过垫在环缝连接螺栓上的弹簧压缩刚度控制模型盾构隧道纵向刚度，材料弹性模量不满足相似关系均可通过上述设计进行调整。

考虑到加工的可行性，基于钢材强度高、韧性好，且加工方便，模型盾构隧道管片环采用钢板卷制而成，如图 1(a)所示。

图  1  模型盾构隧道

Figure  1.  Shield tunnel model

下载: 全尺寸图片 幻灯片

在管片环两端等间隔角度焊接4个角码(间隔角度为90°，也可焊接更多，但试验时内部不方便布设位移计)，管片环之间采用垫有弹簧的螺栓连接(弹簧长度要求不影响安装空间即可，压缩性稳定)，如图 1(b)所示。完成组装的模型盾构隧道如图 1(c)所示，其外径为62 cm。接下来将给出模型盾构隧道横向刚度与纵向刚度相似设计及相关参数的计算方法。

2.   模型盾构隧道横向刚度相似设计

2.1   模型管片环相似设计

若使模型盾构隧道横向刚度满足相似要求，则需要使模型管片环横向刚度满足相似要求。模型管片环在横向变形时包括弯曲变形、轴向变形及剪切变形。由结构力学可知，对于长度远大于厚度的梁，以弯曲变形为主，而模型盾构隧道管片环在横向变形时为曲梁结构，因此最理想的设计方案是使梁结构弯曲变形、轴向变形及剪切变形均满足相似关系。但当在无法同时都满足时，则应使弯曲变形满足相似关系作为设计目标，其他两种变形则不做要求。下面将对弯曲变形相似进行分析。

设原型盾构隧道管片环对应的匀质圆环模型刚度为${(EI)_{{\text{p - h}}}}$，对应的修正匀质圆环模型刚度为${\eta _{\text{h}}}{(EI)_{{\text{p - h}}}}$，其中${\eta _{\text{h}}}$为横向刚度有效率，根据相似关系得到模型盾构隧道修正匀质圆环模型刚度为${(EI)_{{\text{m - h}}}}$为

式中：${(EI)_{{\text{p - h}}}}$为原型盾构隧道管片环对应的匀质圆环模型横向刚度；${\eta _{\text{h}}}$为原型盾构隧道横向刚度有效率；${(EI)_{{\text{m - h}}}}$为模型盾构隧道修正匀质圆环模型横向刚度；${C}_{(EI)}$为刚度相似常数。

根据刚度相似原理，得到原型盾构隧道与模型盾构隧道的管片幅宽、管片厚度及材料弹性模量的关系为

进而得到模型管片环的修正匀质圆环厚度计算公式为

式(2)，(3)中：${b_{\text{p}}}$为原型盾构隧道管片幅宽；${t_{\text{p}}}$原型盾构隧道管片厚度；${E_{\text{p}}}$为原型盾构隧道管片材料弹性模量；${b_{\text{m}}}$为模型盾构隧道管片幅宽；${t_{\text{m}}}$为模型盾构隧道管片厚度；${E_{\text{m}}}$为模型盾构隧道管片材料弹性模量。

式(3)中${b_{\text{p}} }{\text{/}}{b_{\text{m}}}$的大小与几何相似常数$C{}_{\text{l}}$相等；${E_{\text{p}}}{\text{/}}{E_{\text{m}}}$为原型隧道材料弹性模量与模型隧道材料弹性模量的比值，考虑到材料的强度、韧性及方便加工，模型盾构隧道采用钢板加工，因此${E_{\text{p}}}{\text{/}}{E_{\text{m}}}$不取表 1中的${C_{\text{E}}}$，而是${C}_{(EI)}$取值参考表 1。因此最终得到模型管片环的修正匀质圆环厚度计算公式为

式中：${C_{\text{l}}}$为模型盾构隧道的几何相似常数。

2.2   模型管片环结构设计

以上海通缝拼装盾构隧道作为原型盾构隧道，其外径为6.2 m，内径为5.5 m，管片幅宽为1.2 m。管片混凝土强度等级为C55，其弹性模量为35.5 GPa。将模型盾构隧道几何相似常数考虑为10(即${C_{\text{l}}} = 10$，其几何相似比为1︰10)，模型隧道在满足几何相似要求时，其外径为620 mm，管片环幅宽为120 mm。

模型管片环钢板的弹性模量为206 GPa。根据文献[10]反演分析结果，假设盾构隧道的横向刚度有效率0.464，根据式(4)得到模型盾构隧道管片环的厚度${t_{\text{m}}}$为6.998 mm。模型管片环与原型管片环的参数如表 2所示，其中原型管片环横向刚度计算时，需要乘以横向刚度有效率0.464。

表  2  原型管片环与模型管片环的参数对比

Table  2.  Comparison of parameters of prototype and model segment rings

对比参数	幅宽/ mm	弹性模量/ GPa	厚度/ mm	横向刚度/ (kN·m2)
原型管片环	1200	35.5	350	70623.7
模型管片环	120	206	6.998	0.705975

下载: 导出CSV 

| 显示表格

为了方便加工，在市场上选购了厚度7 mm(为厂完标识厚度)的钢板加工模型盾构隧道管片环，并采用对压法对其横向刚度进行测试，如图 2所示(测试时往加载桶内加入称量好的石子)。加载过程中，模型管片环变形与竖向压力的关系如图 3所示。从图 3可以看出，模型管片环的线弹性良好。

图  2  模型管片环横向刚度测试

Figure  2.  Tests on transverse rigidity of model segment ring

下载: 全尺寸图片 幻灯片

图  3  测试结果坐标图

Figure  3.  Coordinate diagram of test results

下载: 全尺寸图片 幻灯片

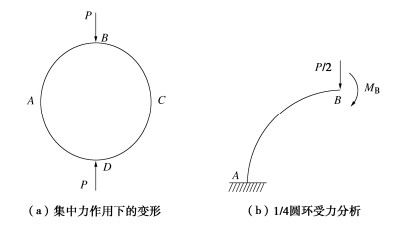
根据结构力学知识，图 2测试对应的结构受力为图 4(a)，利用结构及受力的对称性，将结构简化为图 4(b)所示的1/4圆环受力。利用力法求解，得到了圆环变形与圆环横向刚度的关系为

图  4  圆环在集中力作用下的变形

Figure  4.  Deformations of ring under concentrated force

下载: 全尺寸图片 幻灯片

式中：${{\text{(}}EI{\text{)}}_\varDelta }$为圆环的横向刚度；$P$为圆环所受对压集中力；$R$为圆环的半径；$\varDelta$为圆环的竖向直径变形。

根据式(5)中对压集中力与圆环竖向直径变形的关系，得到模型管片环的横向刚度为0.6486 kN·m²。稍小于表 2中的模型隧道设计横向刚度，导致该现象原因：①与加工模型管片环的钢板弹性模量与理论弹性模量(设计时假设为206 GPa)不一致有关；②与钢板的实际厚度与理论厚度(设计为7 mm)不一致有关，选购时是以厂家标识的厚度，实际厚度有一定出入。若以测试时最大变形所得的横向刚度(0.6486 kN·m²)反算，得到模型盾构隧道管片环的横向刚度有效率为0.426，为可接受的范围值。

3.   模型盾构隧道纵向刚度相似设计

3.1   模型盾构隧道纵向刚度计算

由于角码的螺栓孔与螺栓直径较为接近，其发生剪切错动量非常有限；在进行盾构隧道纵向挠曲变形分析时，不考虑管片环之间的剪切变形。将模型盾构隧道看作由匀质圆管切断为管片环后再次通过环缝连接螺栓连接而成，为此假设盾构隧道纵向挠曲变形由两部分组成：①匀质圆管发生的挠曲变形，②环缝接头张开导致的挠曲变形。接下来对这两部分挠曲变形进行分析。

(1) 匀质圆管的纵向挠曲变形

匀质圆管的截面惯性矩为

式中：$I$为匀质圆管的截面惯性矩；$\alpha$为匀质圆管的内径与外径的比值，即$\alpha = d{\text{/}}D$；$d$为匀质圆管的内径；$D$为匀质圆管的外径。

式中：${(EI)_1}$为匀质圆管的纵向抗弯刚度；E为匀质圆管的弹性模量。

长度为$L$，纵向抗弯刚度为${(EI)_1}$的简支梁在跨中集中荷载$F$作用下发生的最大纵向挠曲变形${S_1}$为

式中：$F$为简支梁跨中位置的集中荷载；$L$为简支梁的长度；${S_1}$为简支梁的最大纵向挠曲变形。

(2) 环缝接头张开导致的纵向挠曲变形

当环缝张开时，环缝接头将发生拉伸变形。假设环缝接头的拉伸量与连接螺栓的拉力成正比，当环缝张开时，环缝接头$i$在拉伸量为${\varDelta _i}$时对应的拉力${F_i}$为

式中：${F_i}$为环缝接头$i$受到的拉力；${K_{\text{S}}}$为环缝接头的拉伸刚度；${\varDelta _i}$为环缝接头$i$的拉伸量。

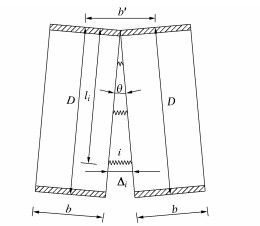
在弯矩作用下，假设两相邻管片环端面绕其顶点发生相对转动。管片环有$n$个环缝接头，当管片环环缝张开角度为$\theta$时，如图 5所示(因张开量很小，张开后两管片中心之间的长度$b'$可近似的认为等为管片幅宽b)，管片环环缝位置的弯矩表达式为

图  5  管片环环缝张开

Figure  5.  Openings of segment ring of shield tunnel

下载: 全尺寸图片 幻灯片

式中：$M$为管片环环缝发生张开时的弯矩；${l_i}$为环缝接头$i$到管片环顶点的垂直距离；n为环缝接头连接螺栓的数量；$\theta$为管片环环缝张开角度。

如图 5所示，当管片环环缝在弯矩$M$作用下的张开角度为$\theta$时，环缝连接螺栓$i$的拉伸量${\varDelta _i}$与管片环环缝张开角度为$\theta$的关系为

由于式中环缝连接螺栓$i$的拉伸量${\varDelta _i}$的单位为mm，而环缝连接螺栓$i$到管片环顶点的垂直距离${l_i}$单位为m，故需要乘以1000。

将式(9)，(11)代入式(10)，得到弯矩$M$与各环缝连接螺栓的拉伸刚度${K_{\text{S}}}$及管片环环缝张开角度为$\theta$的关系为

对于模型盾构隧道，每一环管片环对应有一个环缝。当环缝发生张开变形时，盾构隧道的整体刚度会有所降低。由纵向等效连续化模型可知，长度为b的简支梁在弯矩$M$作用下发生转角为$\theta$时，其纵向抗弯刚度${(EI)_2}$为

式中：${(EI)_2}$为环缝接头张开所导致的纵向抗弯刚度；$b$为管片环的幅宽。

由于管片环环缝张开角度$\theta$较小，根据三角函数关系有$\sin (\theta /2) \approx \theta /2$。将式(12)代入式(13)得到：

即环缝接头张开导致的盾构隧道纵向抗弯刚度${(EI)_2}$的计算式如式(14)所示。纵向抗弯刚度为${(EI)_2}$的简支梁在跨中集中荷载$F$作用下发生的最大纵向挠曲变形${S_2}$为

式中：${S_2}$为纵向抗弯刚度为${(EI)_2}$的简支梁的最大纵向挠曲变形。

(3) 模型盾构隧道纵向抗弯刚度计算

由上述分析可知，长度为$L$的模型盾构隧道在外部荷载作用下发生的最大纵向挠曲变形$S_{1}$为

假设模型盾构隧道理论纵向抗弯刚度为${(EI)_3}$，由纵向等效连续化模型可知，相同纵向抗弯刚度的简支梁在跨中集中荷载$F$作用下发生的最大纵向挠曲变形${S_3}$为

式中：${(EI)_3}$为模型盾构隧道理论纵向抗弯刚度；${S_3}$为简支梁跨中的最大纵向挠曲变形。

根据式(7)，(14)，(17)得到模型盾构隧道纵向抗弯刚度${(EI)_3}$为

式(18)中的${(EI)_1}$，${(EI)_2}$分别见式(7)，(14)。

3.2   模型盾构隧道环缝接头设计

在模型管片环内侧顶部、底部和两侧4个位置设置环缝连接接头，由螺栓、弹簧和角码连接而成，其螺栓的长度为90 mm、直径为8 mm；弹簧直径和长度均为40 mm，弹簧压缩刚度为745 N/mm，也即模型盾构隧道环缝接头的拉伸刚度为745 N/mm；角码边长为50 mm，厚度为5 mm，孔径为13 mm。

已知模型隧道外径为620 mm，内径为606 mm，厚度为7 mm，幅宽为120 mm；隧道环缝接头的拉伸刚度为745 N/mm。顶部环缝接头到管片环顶点的垂直距离${l_1}$为0.02 m，底部环缝接头到管片环顶点的垂直距离${l_2}$为0.586 m；侧部环缝接头到管片环顶点的垂直距离${l_3}$$({l_4})$为0.293 m。将上述参数分别代入式(7)，(14)，则得到匀质圆管的纵向抗弯刚度${(EI)_1}$=1.3056× 10⁸ N·m²，由环缝接头张开导致的纵向抗弯刚度${(EI)_2}$=4.6049×10⁴ N·m²，再将${(EI)_1}$和${(EI)_2}$代入式(18)，得到盾构隧道理论纵向抗弯刚度${(EI)_3}$=4.6033×10⁴ N·m²。

可以看出，由于环缝对模型盾构隧道的纵向刚度削弱影响显著，因此模型盾构隧道的纵向刚度${(EI)_3}$与${(EI)_2}$非常接近，即可近似地认为模型盾构隧道的纵向刚度${(EI)_3}$由环缝接头的张开所导致的刚度${(EI)_2}$所决定。

3.3   模型盾构隧道纵向刚度测试

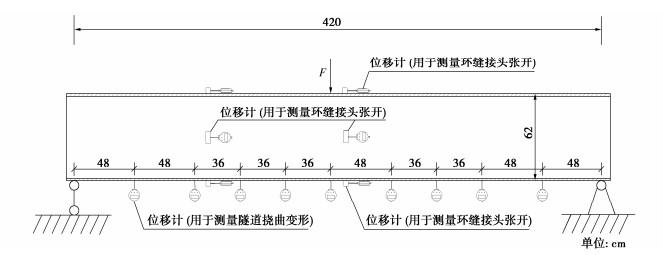
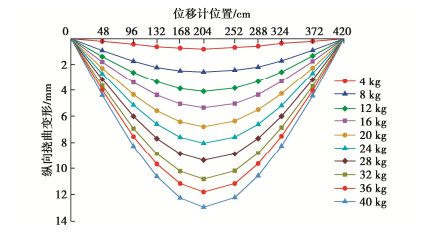
模型盾构隧道由36环模型管片环拼接而成，全长432 cm，在模型盾构隧道第1环管片环的中心位置设置固定铰支座(支承在角钢上，成近似点接触)，在第36环管片环的中心位置设置滑动支座(支承架底部设计有四轮小车)，两支座间的距离为420 cm。其示意图和实物图分别如图 6，7(a)所示。在模型盾构隧道底部第5、第9、第12、第15、第18、第22、第25、第28、第32环管片环的中心位置布设了9个用于测量竖向挠曲变形的位移计(图 6(b))；在第9—10环(模型盾构隧道1/4位置)和第18—19环(模型盾构隧道1/2位置)之间的环缝顶部、底部和两侧4个位置布设了用于测量管片环环缝张开量的位移计(图 8(c))。

图  6  模型试验示意图

Figure  6.  Schematic diagram of model tests

下载: 全尺寸图片 幻灯片

图  7  模型盾构隧道纵向刚度测试

Figure  7.  Tests on longitudinal rigidity of shield tunnel model

下载: 全尺寸图片 幻灯片

图  8  模型盾构隧道纵向挠曲变形

Figure  8.  Longitudinal deformations of shield tunnel model

下载: 全尺寸图片 幻灯片

模型试验采用中间单点加载，加载点位于第18环的管片环中心位置。在加载点处设置加载桶，如图 7(a)所示，采用逐级加载，每次加载4 kg，共加载10次，并记下位移计的读数。

图 8为模型盾构隧道在逐级加载过程中不同测点对应的纵向挠曲变形。从图 8中可以看出，由于螺栓预紧力的存在，在第一次加载导致的最大挠曲变形增量较小，之后每级加载对应的跨中最大变形增量近似相等。随着加载的逐渐增大，模型盾构隧道纵向挠曲变形增量也在逐渐增大，且增幅逐渐趋于稳定。

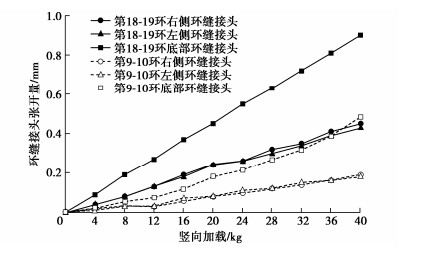
图 9为模型盾构隧道第18—第19环和第9—第10环管片环的环缝接头逐级加载过程中的张开量变化。由图 9可知，环缝接头底部张开量约为侧部接头张开量的两倍，由此可见，前面假设横型管片环的环缝张开时绕顶部转动是合理可行的。随着加载的逐渐增大，管片环的环缝接头张开量近似线性增加；环缝两侧接头张开量接近。

图  9  第18—第19环和第9—第10环环缝接头张开量

Figure  9.  Openings of 18^th-19^th and 9^th-10^th segment ring joints

下载: 全尺寸图片 幻灯片

假设模型盾构隧道实测纵向抗弯刚度为${(EI)_4}$，简支梁在跨中集中荷载$F$作用下发生的实测最大纵向挠曲变形${S_4}$，两者的关系为

式中：${(EI)_4}$为模型盾构隧道实测纵向抗弯刚度；${S_4}$为简支梁跨中实测的最大纵向挠曲变形。

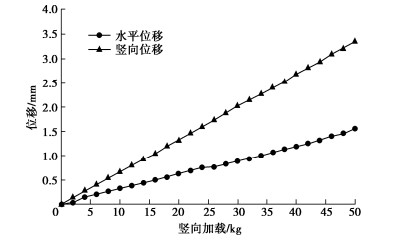
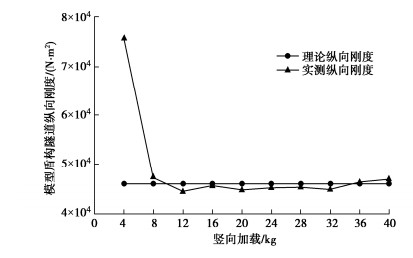
已知简支梁长度$L$为4.2 m，不同加载作用下的最大纵向挠曲变形${S_4}$如图 8中部位置所示，将${S_4}$代入式(19)得到${(EI)_4}$，计算得到模型盾构隧道实测纵向抗弯刚度${(EI)_4}$的结果如图 10所示。从图 10的实测纵向抗弯刚度可以看出，当加载重量为4 kg时，由于螺栓预紧力的存在，模型纵向挠曲变形偏小，进而导致反算得到的纵向抗弯刚度较大；后续加载导致的模型盾构隧道实测纵向抗弯刚度${(EI)_4}$总体变化不大。

图  10  模型盾构隧道理论和实测纵向刚度对比

Figure  10.  Comparison between theoretical and experimental longitudinal rigidities of shield tunnel model

下载: 全尺寸图片 幻灯片

图 10为模型盾构隧道在逐级加载过程中的理论和实测纵向抗弯刚度的对比。由图 10可知，当加载重量为4 kg时，由于螺栓预紧力的存在，导致模型理论纵向抗弯刚度远大于模型实测纵向抗弯刚度；随着模型试验跨中加载重量的增加，实测盾构隧道纵向刚度与盾构隧道理论计算纵向刚度非常接近。

以上提出的模型盾构隧道将模型管片环采用垫有弹簧的连接螺栓连接，通过控制弹簧的压缩刚度来控制模型盾构隧道的纵向刚度。因此当需要设计纵向刚度有效率为${\eta _z}$的模型盾构隧道时，根据相似设计理论以及原型盾构隧道的匀质圆管纵向刚度${(EI)_{\text{p}}}$，即可得到模型盾构隧道的纵向刚度${(EI)_{\text{m}}}$为

式中：${(EI)_{\text{m}}}$模型盾构隧道的纵向刚度；${(EI)_{\text{p}}}$原型盾构隧道的纵向刚度；${\eta _z}$原型盾构隧道的纵向刚度有效率；${C_{(EI)}}$模型盾构隧道与原型盾构隧道的相似常数，其计算见表 1。

考虑到模型盾构隧道的纵向刚度主要由环缝张开变形所决定，因此近似地认为模型盾构隧道的纵向刚度按式(14)计算，由此得到模型盾构隧道的环缝连接螺栓所垫弹簧的压缩刚度计算式为

4.   结论

(1) 提出了一种纵向刚度与横向刚度均可满足相似要求的模型盾构隧道设计方法，即模型盾构隧道管片环采用匀质圆环模型；管片环之间采用垫有弹簧的螺栓连接形成模型盾构隧道。

(2) 模型盾构隧道管片环采用匀质圆环模型时，以横向抗弯刚度满足相似要求进行设计，并采用对压法对其横向刚度进行了测定与验证。

(3) 模型盾构隧道的纵向挠曲变形可考虑为由匀质圆管发生的纵向挠曲变形和由环缝接头张开导致的纵向挠曲变形组成。推导了模型盾构隧道纵向刚度计算方法，并通过简支梁法对模型盾构隧道的纵向刚度进行了测定，对模型盾构隧道理论纵向刚度计算方法进行了验证。

(4) 根据模型盾构隧道与原型盾构隧道纵向抗弯刚度相似关系，得到了垫在管片环环缝连接螺栓上的弹簧刚度与原型盾构隧道纵向刚度之间的关系。