UH model and parameter inversion for crushable sands
-
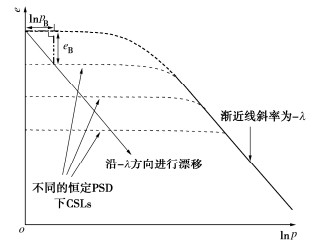
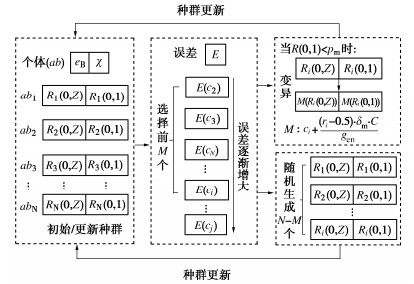
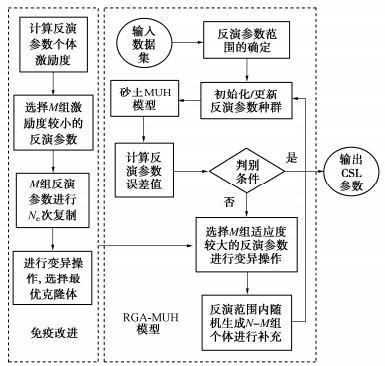
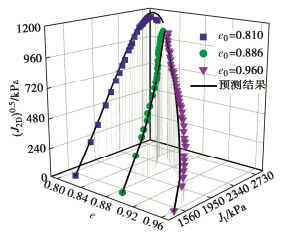
摘要: 颗粒破碎对粒状土临界状态的影响十分显著，研究认为在e-lnp空间内，粒状土的临界状态线会随着破碎的进行向下漂移，而捕捉颗粒破碎量与临界状态线漂移量之间的一一映射关系是一项巨大的挑战。通过引入颗粒破碎参数eB对砂土UH模型进行了修正，并将其嵌入实数编码免疫遗传算法（RIGA）中，构建了RIGA-MUH模型，提出了可获取不同破碎程度下临界状态线的新方法。为得到更加准确的临界状态参数，模型通过调整粒状土临界状态下在误差函数中的权重比进行优化改进，并通过Toyoura砂和Cambria砂的常规排水三轴压缩试验结果，验证模型的稳定性、合理性和准确性。结果表明，该模型可以得到某一颗粒破碎量下精度较高的临界状态线，为提出考虑颗粒破碎的本构方程提供一种新方法。Abstract: The effect of particle breakage on the critical state of granular soils is of great significance. The existing studies have shown that the critical state line (CSL) of granular soils in the e-lnp space shifts downward as a result of particle breakage. However, it remains a big challenge for capturing the degree of particle breakage and the movement of CSL. In this study, the UH model for sands is modified by introducing the particle breakage parameter eB and embedded in the real number encoding immune genetic algorithm (RIGA) to establish the RIGA-MUH model, which proposes a new method that can obtain the CSLs for the sands with varying particle-size distributions. The model is optimized and improved to obtain more accurate critical state parameters by adjusting the weight ratio in the error function under the critical state of granular soils. The stability, rationality and accuracy of the model are verified through the results of conventional drainage triaxial compression tests on the Toyoura sand and Cambria sand. The results show that the proposed model can be used to obtain the CSLs with high accuracy under a certain amount of particle breakage, which provides new insight into the constitutive modeling of crushable sands.
-
0. 引言
杆塔基础是架空输电线路的重要组成部分，用于支撑来自于上部杆塔及导线金具的全部荷载。杆塔运行中，会承受来自导线、金具、以及风等作用。通常情况下，杆塔基础承受垂直荷载与水平荷载，其中顺着线路方向为纵向水平荷载、垂直线路方向为横向水平荷载，因此，实际的杆塔基础主要以承受竖向与横向荷载组合而成的倾斜荷载作用。
关于倾斜荷载作用下桩基承载性能的研究，国内外学者开展了大量的研究工作。以Meyerhof为代表的学者[1-11]通过大量的模型试验，分析了均质及双层地基条件下，倾斜荷载作用下的刚性桩、柔性桩的承载机理，推导出倾斜荷载作用下桩基极限承载力计算的经验方法；日本学者横山幸满[12]基于理论推导，提出地基系数不变时，倾斜荷载作用下桩基承载力的计算，仅仅通过竖、横向承载力的简单叠加是不确切的；范文田[13]基于横山幸满的研究成果，通过理论推导，分析了轴向压力对桩身横向变位及内力的影响；赵明华等[14-16]、侯云秋等[17]、彭文祥等[18]、吴鸣等[19]通过室内模型试验，研究了不同倾斜角度荷载作用下桩基承载机理，并提出桩基承载力与倾角之间的椭圆曲线关系；文松霖[20]通过均质砂土中扩底桩模型的离心机试验，分析了竖向荷载对桩基水平承载性能的影响；吕凡任等[21]通过求解倾斜荷载作用下单桩的位移积分方程，分析了倾斜角度对桩基承载性能的影响，提出倾斜角度对桩基竖向及水平向位移的影响差异；郑刚等[22]借助有限元法，分析了成层地基土中，倾斜荷载作用下桩基土抗力的分布特点及影响因素；王孝兵等[23]采用FLAC有限差分软件，分析了倾斜荷载作用下大直径长桩的受力性状，并提出倾斜角度对桩基位移、桩侧土抗力分布的影响规律；周立朵等[24]基于p–y曲线法，并考虑桩–土相对滑移和竖向力引起的二阶弯矩效应，分析了倾斜荷载作用下群桩的受力变形特征。
以上研究工作大多针对倾斜下压荷载作用下的桩基承载特性开展的相关研究工作，而正如上文分析，实际的输电线路基础不仅承倾斜下压荷载作用，同时还承受倾斜上拔荷载作用，而针对同时包括以上两种荷载工况下的桩基承载性能及差异方面的研究，目前鲜见相关文献报道。
本文选取临近750kV兰平乾输电线路工程的黄土地基作为试验现场，分别开展了2种单一荷载工况、2种组合荷载工况的6组挖孔桩足尺现场试验，通过分析荷载位移曲线规律、极限承载力及桩端土压力分布，研究了复杂荷载工况下挖孔桩的承载特性及差异，为架空输电线路基础承载机理的揭示以及优化设计提供了重要的理论依据。
1. 试验条件及方案设计
1.1 试验场地
本次试验场地位于甘肃省定西市巉口镇西北20 km外的车道岭山，地处陇西黄土高原丘陵区，距离750 kV兰—平—乾线路#192塔位20 m处，如图 1所示。该处常年缺水，地基土体主要以第四系上更新Q3黄土为主。
在现场开展原位试验，获得该试验场地的主要物理力学参数值为：相对质量密度为2.72，密度为1.65 kg/m3，含水率为9.7%，孔隙比e为1.23，液限为31.2%，塑限为20.5%，黏聚力为11.24 kPa，内摩擦角为24.76。根据规范[25]判断，现场地基土为低液限粉质黏土。
1.2 试验基础
本次试验对象为黄土地基输电线路工程中常用的大直径等截面挖孔桩基础，如图 2所示。为了避免基础在受拉（弯）作用下桩身本体破坏，每个试验桩的全截面配筋率均按照1.5%设计。为了分析不同入土深度下，挖孔桩的受力特点，同时结合输电线路基础的受力特点，本次试验共设计6个基础样本，分为4种荷载工况，详见表 1所示。
表 1 试验基础明细表Table 1. Information list of test foundation编号 d/mm ht/mm h0/mm 荷载工况 #1 1000 5000 500 上拔 #2 1000 7500 500 上拔+水平 #3 1000 10000 500 上拔+水平 #4 1000 5000 500 下压+水平 #5 1000 7500 500 下压+水平 #6 1000 7500 500 水平 试验基础采用人工开挖，现场浇筑的方式制作，整个施工流程可概括如下：首先根据基础布置图，定点放线，确定每个试验基础与反力基础的准确位置（图 3（a））；其次根据图 2和表 1所示的基础尺寸进行基坑开挖（图 3（b）），同时制作钢筋笼和地脚螺栓骨架（图 3（c））；待基坑挖至设计深度后，采用机械将钢筋笼吊装于基坑内（图 3（d）），其中上拔基础还包括地脚螺栓；最后进行混凝土浇筑，完成试验基础制作（图 3（e））。浇筑完成后养护28 d后即可开展试验。
1.3 试验加载方案
6个试验基础均采用锚桩法[26]进行现场加载，采用RS-JYC型桩基静载荷测试分析系统实现加载、测试和数据记录，如图 4所示。竖向荷载由千斤顶、上拔螺杆、反力钢梁与钢筋混凝土反力墩组成的传力系统提供；水平荷载由千斤顶、水平箱梁、反力基础组成传力系统提供，其中千斤顶一端施加于试验基础顶部，另一端支撑于具有足够刚度与承载能力的反力基础上。试验过程中采用布设于基础顶部的位移传感器测定基础的竖向与水平向位移。
试验采用慢速荷载维持法，其中竖向荷载与水平向荷载按照7∶1比例同步加载（与竖直方向倾斜8°），每个试验基础均加载至破坏状态，具体加卸载方案、加卸载终止条件详见相关规范[26-27]。
2. 试验结果分析
2.1 变形破坏特征
通过记录每级荷载作用下试验桩不同位置处位移传感器的数据，获得6个挖孔桩的荷载–位移曲线，如图 5所示，其中图 5（a）为各试验桩的竖向荷载与位移关系曲线，图 5（b）为相应的水平荷载与位移关系曲线。
从图 5（a）中可以看出，#1~#3试验桩荷载位移曲线屈服点明显，其曲线特征较好地符合“陡降型”；#4、#5试验桩荷载位移曲线与之相反，屈服点不明显，其特征较好地符合“缓变型”。
究其原因，主要由于试验桩在不同荷载工况下的承载机理及破坏模式差异所致。上拔荷载作用下，试验桩主要依靠其自重与桩土界面间的摩阻力抵抗上拔力。图 6所示为#2试验桩破坏时，地表土体破坏时的照片，透过土体裂缝间隙可清晰地看到桩土界面处脱开的混凝土表面；下压荷载作用下，桩基承载力包括摩阻力与端阻力两部分，沉降量由桩体压缩、桩端土体沉降两部分组成，根据土体性质，桩基可能会发生整体剪切、局部剪切、刺入剪切3种破坏模式[28]中的一种，而无论发生哪种破坏，桩基达到极限状态时的位移量以及桩土体系呈现出的塑性变形特性较上拔荷载作用时更大、更明显。
试验过程中，4个组合荷载工况下的试验桩（#2~#4）加载终止条件均由竖向荷载决定。由图 5（b）可知，除#4外，其余5个试验桩的水平向荷载位移曲线整体均呈“缓变型”曲线特征。
Meyerhof[2, 5]提出倾斜荷载作用下的桩基，可采用桩–土相对刚度Kr表征桩基础抗水平承载能力：
Kr=EpIpEsLt4， (1) 式中，EpIp为桩体的抗弯刚度，Es桩侧土水平变形模量，Lt为桩入土深度。
采用公式（1）推算出3个入土深度相同的试验桩的Kr值，如表 2所示。从表 2中可以看出，入土深度相同时，Kr从大到小的荷载工况依次为：下压+水平（#5）、水平（#6）、上拔+水平（#2）。由此可见，组合荷载工况下的挖孔桩，下压力可有效提高其抗水平承载能力，反之，上拔力会削弱其抗水平承载能力。
表 2 试验桩的Kr值Table 2. Values of Kr of test piles编号 d/mm ht/mm 荷载工况 Kr #2 1000 7500 上拔+水平 0.1111 #5 1000 7500 下压+水平 0.1815 #6 1000 7500 水平 0.1248 2.2 极限承载力
根据规范[26-27]中推荐的方法确定#1、#6试验桩上拔、水平荷载工况下的极限承载力。针对倾斜荷载工况下桩基极限承载力的确定，目前主要有两种方法：倾斜荷载–位移曲线法[13]、倾斜荷载–合成位移曲线法[14]，本文采用倾斜荷载–位移曲线法，即在同一坐标系中做出倾斜荷载与竖向、水平位移曲线，分别确定出对应的极限荷载，然后取其较小值作为桩基极限承载力，如图 7所示。
![]()
图 7 倾斜荷载作用下桩基极限承载力取值示意图Figure 7. Schematic diagram of ultimate bearing capacity of pile under inclined loads由表 3可知，#2~#5四个试验桩的极限承载力均由荷载–竖向位移曲线确定，由此表明：承受组合荷载作用下的输电线路基础，竖向承载力往往是设计中的控制因素。在此需要说明的是，此规律仅限于基础露头h0较小、且高配筋率条件下。当h0较大且配筋率较小时，水平荷载在自由段范围内产生较大的初始弯矩，基础承受明显的“弯剪效应”，此时，基础往往受到水平承载力控制，设计中除校核桩顶水平位移之外，还需校核基础的构件承载力。
表 3 试验桩的极限承载力Table 3. Ultimate bearing capacities of test piles序号 Qvu svu/mm Qhu shu/mm Qu 1 450 2.52 — — 450 2 848 3.91 919 3.87 848 3 1060 3.76 1072 10.00 1060 4 730 50.00 848 7.51 730 5 923 50.00 1060 8.92 923 6 — — 315 10.00 315 注：①陡降型曲线，取陡降起始点；缓变型曲线，取允许位移对应的荷载值，其中允许位移取值分别为：上拔25 mm，下压50 mm（0.05d）、水平10 mm。②Qvu和svu、Qhu和shu、Qu分别为竖向极限荷载值及相应位移、水平极限荷载值及相应位移、极限承载力值。 同时，对于相同尺寸与入土深度的试验桩，下压+水平组合荷载下的#5桩较上拔+水平组合荷载下的#2桩承载力高出9%，如上节分析可知，主要由于不同荷载工况下，桩基承载力的组成存在差异所致。
2.3 桩端土压力
为了测试桩端阻力，在#4，#5桩的桩底不同位置处布置3个土压力盒。通过记录每级荷载作用下土压力盒的测试数据，绘制出桩端土压力与下压荷载之间的关系曲线，如图 8所示。
![]()
图 8 下压荷载与桩端土压力关系曲线Figure 8. Relationship between compression load and soil pressure at pile end从图 8中可以看出，桩端土压力随下压荷载的增加呈非线性增加趋势，其两者之间的关系曲线为
f=A⋅p2+B⋅p， (2) 式中f为桩端土压力（kPa）；p为下压荷载强度（kPa）；A、B分别为拟合参数，A单位为1/kPa，B量纲为1，见表 4。
表 4 参数A、B的取值Table 4. Values of parameters A and B基础编号 测点号 A/kPa-1 B 拟合方差 qpk/kPa #4 1 0.0004 -0.011 0.98 336 2 0.0006 -0.079 0.99 445 3 0.0005 0.028 0.99 458 #5 1 0.0004 -0.104 1.00 431 2 0.0006 -0.258 0.99 526 3 0.0005 -0.211 0.99 443 将#4、#5桩的极限荷载代入式（2），即可求出各个测点的桩端土压力值qpk，如表 4所示。
为了分析水平荷载对桩端土压力的影响，分别绘制出30%，60%，90%极限荷载时，不同位置测点处土压力的分布曲线，如图 9所示。
从图 9可知，#4桩中#3测点土压力最大，较#1、#2测点分别大22%、2%（90%极限荷载时），水平力引起的偏心作用明显；#5桩中#1~#3测点土压力的分布规律不明显，水平力引起的偏心作用不明显。这主要由于#4、#5桩的刚度差异而导致的运动方式不同所致。经计算#4、#5桩的变形系数αh分别为2.05、3.08，根据文献[35]，判定出#4为刚性桩、#5为弹性桩。其中#4桩在水平力作用下会绕桩体上某一点发生转动，导致桩端平面产生转动趋势，产生偏心效应，如图 10（a）所示；而#5桩会产生如图 10（b）所示的运动方式，此时，桩端界面不会产生转动趋势，因此桩端土压力的分布等同于轴心受压时的受力特征，偏心效应不明显。
![]()
图 10 水平荷载作用下桩的变形模式[35]Figure 10. Deformation modes of piles under horizontal loads[35]3. 结论
本文开展了4种荷载工况，6个挖孔桩真型基础承载性能的现场试验，分析了输电线路挖孔桩基础在复杂荷载工况下的荷载值位移曲线、极限承载力及桩端土压力分布，得到以下3点结论。
（1）不同性质竖向荷载作用下的挖孔桩，其荷载–竖向位移曲线形态特征呈现明显差异，具体表现为：上拔荷载作用下曲线型式呈“陡降型”，屈服点明显；下压荷载作用下曲线型式呈“缓变型”，屈服点不明显，这主要由于挖孔桩在不同性质竖向荷载作用下的承载机理及破坏模式差异所致。
（2）采用Meyerhof公式，分别推算出承受不同荷载组合、相同截面尺寸的挖孔桩桩土相对刚度Kr值，分析结果表明：下压+水平组合荷载工况下挖孔桩的Kr最大，其次为水平荷载工况，上拔+水平组合荷载作用时Kr最小。由此表明，下压力可有效提高了挖孔桩的抗水平承载能力，反之，上拔力会削弱挖孔桩的抗水平承载能力。
（3）试验结果表明：桩端土压力与下压荷载之间较好地服从二次多项式的函数关系。不同类别的挖孔桩，水平荷载的作用对桩端土压力分布的影响也存在差异。刚性桩由于其在水平力作用下产生了绕桩体的转动，导致桩端土压力偏心作用明显，相反，弹性桩产生的该偏心作用不明显。
-
![]()
图 1 CSL随PSD漂移及颗粒破碎参数示意图
Figure 1. Schematic diagram of shifting CSL with varying PSDs and particle breakage parameter
![]()
图 4 Toyoura砂的三轴试验结果和预测结果对比
Figure 4. Comparison between triaxial test results and predicted results for Toyoura sand
![]()
图 6 第一阶段稳定解与最终解预测结果对比
Figure 6. Comparison of predicted results between first-stage stable solution and final solution
![]()
图 7 RGA-MUH模型和RIGA-MUH模型稳定性分析对比
Figure 7. Comparison of stability analysis between RGA-MUH model and RIGA-MUH model
![]()
图 10 Cambria砂中高围压组试验结果与模型预测结果对比
Figure 10. Comparison between test results and model predictions for Cambria sand subjected to medium and high confining pressures
![]()
图 11 Cambria砂高围压组试验结果与模型预测结果对比
Figure 11. Comparison between test results and model predictions for Cambria sand subjected to high confining pressure
![]()
图 13 Cambria砂不同颗粒破碎指标Br下的CSL截距
Figure 13. Intercepts of CSL of Cambria sands with different particle breakage index Br
表 1 Toyoura砂UH模型参数
Table 1 UH model parameters of Toyoura sand
M χ ν Z m λ κ N 1.25 0.55 0.3 0.943 1.8 0.135 0.04 1.973 
下载: 导出CSV
表 2 RGA-MUH模型超参数
Table 2 Hyperparameters of RGA-MUH model
参数名称 RGA参数取值 种群规模N 50 变异概率pm 0.7 选择操作后个体数M 25 最大迭代次数G 100 变异系数δm 0.5
下载: 导出CSV
表 3 RIGA-MUH模型免疫超参数分析试验方案及结果
Table 3 Experimental protocols and results of immune hyperparameter analysis of RIGA-MUH model
试验号 激励度系数α 克隆次数Nc 相似度阈值δs 试验结果 1 1(0.3) 1(3) 1(0.1) 0.621 2 1 2(6) 2(0.2) 0.603 3 1 3(9) 3(0.3) 0.610 4 2(0.6) 1 2 0.623 5 2 2 3 0.594 6 2 3 1 0.622 7 3(0.9) 1 3 0.597 8 3 2 1 0.596 9 3 3 2 0.597
下载: 导出CSV
表 4 各参数方差分析
Table 4 Analysis of variance for each parameter
方差来源 平方和 自由度 均方差 F值 激励度系数α 0.000494 2 0.000247 5.501 克隆次数Nc 0.000457 2 0.000229 5.100 相似度阈值δs 0.000284 2 0.000142 3.163 空列误差 0.0000897 2 0.0000449 总和 0.00132 8
下载: 导出CSV
表 5 RIGA-MUH模型参数
Table 5 Parameters of RIGA-MUH model
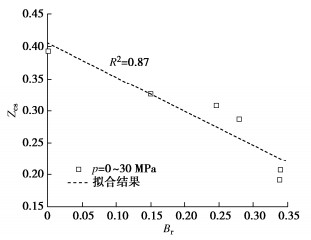
M ν Z m λ κ N 1.45 0.1 0.61 3 0.112 0.0102 1.5578
下载: 导出CSV
表 6 不同围压下颗粒破碎指标Br
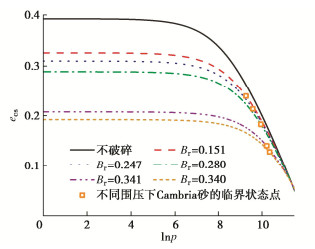
Table 6 Values of Br under different confining pressures
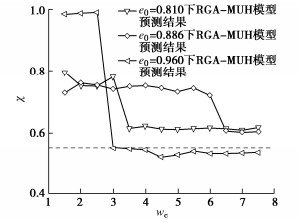
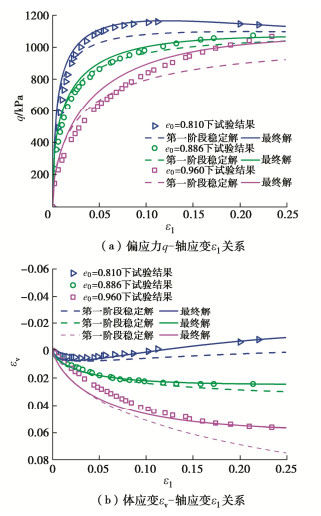
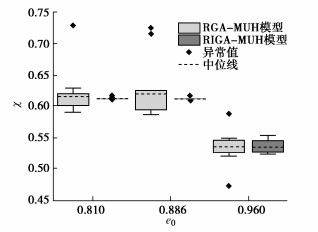
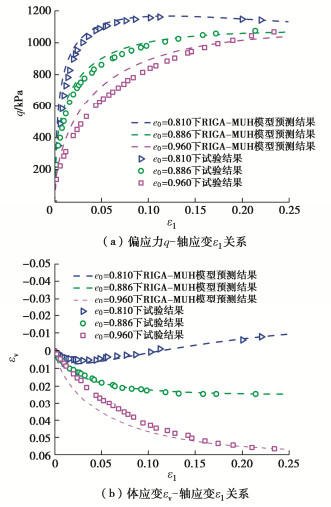
围压/kPa 5800 8000 11500 15000 17200 Br 0.151 0.247 0.280 0.341 0.340
下载: 导出CSV
表 7 RIGA-MUH模型和RGA-MUH模型预测结果
Table 7 Predicted results of RIGA-MUH and RGA-MUH models
参数名称 围压/MPa 5.8 8.0 11.5 15.0 17.2 RIGA χ 0.886 0.899 0.883 0.866 0.843 eB 0.072 0.090 0.114 0.215 0.237 RGA χ 0.827 0.883 0.926 0.883 0.816 eB 0.115 0.151 0.088 0.228 0.266
下载: 导出CSV
-
[1] 张家铭, 蒋国盛, 汪稔. 颗粒破碎及剪胀对钙质砂抗剪强度影响研究[J]. 岩土力学, 2009, 30(7): 2043-2048. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200907035.htm ZHANG Jiaming, JIANG Guosheng, WANG Ren. Research on influences of particle breakage and dilatancy on shear strength of calcareous sands[J]. Rock and Soil Mechanics, 2009, 30(7): 2043-2048. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200907035.htm
[2] TONG C X, BURTON G J, ZHANG S, et al. Particle breakage of uniformly graded carbonate sands in dry/wet condition subjected to compression/shear tests[J]. Acta Geotechnica, 2020, 15(9): 2379-2394. doi: 10.1007/s11440-020-00931-x
[3] TONG C X, ZHAI M Y, LI H C, et al. Particle breakage of granular soils: changing critical state line and constitutive modelling[J]. Acta Geotechnica, 2022, 17(3): 755-768. doi: 10.1007/s11440-021-01231-8
[4] WOOD D M, MAEDA K. Changing grading of soil: effect on critical states[J]. Acta Geotechnica, 2008, 3(1): 3-14. doi: 10.1007/s11440-007-0041-0
[5] HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177-1192. doi: 10.1061/(ASCE)0733-9410(1985)111:10(1177)
[6] DAOUADJI A, HICHER P Y, RAHMA A. An elastoplastic model for granular materials taking into account grain breakage[J]. European Journal of Mechanics - A/Solids, 2001, 20(1): 113-137. doi: 10.1016/S0997-7538(00)01130-X
[7] BANDINI V, COOP M R. The influence of particle breakage on the location of the critical state line of sands[J]. Soils and Foundations, 2011, 51(4): 591-600. doi: 10.3208/sandf.51.591
[8] LI G, LIU Y J, DANO C, et al. Grading-dependent behavior of granular materials: from discrete to continuous modeling[J]. Journal of Engineering Mechanics, 2015, 141(6): 276-285.
[9] 兰鹏, 李海潮, 叶新宇, 等. PINNs算法及其在岩土工程中的应用研究[J]. 岩土工程学报, 2021, 43(3): 586-592. doi: 10.11779/CJGE202103023 LAN Peng, LI Haichao, YE Xinyu, et al. PINNs algorithm and its application in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 586-592. (in Chinese) doi: 10.11779/CJGE202103023
[10] HOLLAND J. Adaptation in Natural and Artificial Systems[M]. Ann Arbor: University of Michigan Press, 1975.
[11] WANG L, TANG D B. An improved adaptive genetic algorithm based on hormone modulation mechanism for job-shop scheduling problem[J]. Expert Systems With Applications, 2011, 38(6): 7243-7250. doi: 10.1016/j.eswa.2010.12.027
[12] 王煦法, 张显俊, 曹先彬, 等. 一种基于免疫原理的遗传算法[J]. 小型微型计算机系统, 1999, 20(2): 117-120. https://www.cnki.com.cn/Article/CJFDTOTAL-XXWX902.007.htm WANG Xufa, ZHANG Xianjun, CAO Xianbin, et al. An improved genetic algorithm based on immune principle[J]. Mini-Micro Systems, 1999, 20(2): 117-120. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XXWX902.007.htm
[13] HAN H, DING Y S, HAO K R, et al. An evolutionary particle filter with the immune genetic algorithm for intelligent video target tracking[J]. Computers & Mathematics With Applications, 2011, 62(7): 2685-2695.
[14] YAO Y P, HOU W, ZHOU A N. Constitutive model for overconsolidated clays[J]. Science in China Series E: Technological Sciences, 2008, 51(2): 179-191. doi: 10.1007/s11431-008-0011-2
[15] YAO Y P, HOU W, ZHOU A N. UH model: three- dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[16] YAO Y P, LIU L, LUO T, et al. Unified hardening (UH) model for clays and sands[J]. Computers and Geotechnics, 2019, 110: 326-343. doi: 10.1016/j.compgeo.2019.02.024
[17] YAO Y P, WANG N B, CHEN D. UH model for granular soils considering low confining pressure[J]. Acta Geotechnica, 2021, 16(6): 1815-1827. doi: 10.1007/s11440-020-01084-7
[18] 姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报, 2016, 38(12): 2147-2153. doi: 10.11779/CJGE201612002 YAO Yangping, LIU Lin, LUO Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2147-2153. (in Chinese) doi: 10.11779/CJGE201612002
[19] DE BONO J P, MCDOWELL G R. Micro mechanics of the critical state line at high stresses[J]. Computers and Geotechnics, 2018, 98: 181-188. doi: 10.1016/j.compgeo.2018.02.016
[20] RUSSELL A R, KHALILI N. A bounding surface plasticity model for sands exhibiting particle crushing[J]. Canadian Geotechnical Journal, 2004, 41(6): 1179-1192. doi: 10.1139/t04-065
[21] KIKUMOTO M, WOOD D M, RUSSELL A. Particle crushing and deformation behaviour[J]. Soils and Foundations, 2010, 50(4): 547-563.
[22] VERDUGO R, ISHIHARA K. The steady state of sandy soils[J]. Soils and Foundations, 1996, 36(2): 81-91.
[23] YAMAMURO J A, LADE P V. Drained sand behavior in axisymmetric tests at high pressures[J]. Journal of Geotechnical Engineering, 1996, 122(2): 109-119.
[24] 史金权, 肖杨, 刘汉龙, 等. 钙质砂小应变初始剪切模量试验研究[J]. 岩土工程学报, 2022, 44(2): 324-333. doi: 10.11779/CJGE202202014 SHI Jinquan, XIAO Yang, LIU Hanlong, et al. Experimental study on small-strain shear modulus of calcareous sand[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(2): 324-333. (in Chinese) doi: 10.11779/CJGE202202014
[25] XIAO Y, LIU H L, DING X M, et al. Influence of particle breakage on critical state line of rockfill material[J]. International Journal of Geomechanics, 2016, 16(1): 04015031.
[26] WANG L, MENG M Q, LIU H L, et al. Numerical investigation on the effect of grain crushing process on critical state on rockfill material[M]//Challenges and Innovations in Geomechanics. Cham: Springer International Publishing, 2021: 295-302.
[27] HU W, YIN Z Y, SCARINGI G, et al. Relating fragmentation, plastic work and critical state in crushable rock clasts[J]. Engineering Geology, 2018, 246: 326-336.
-
期刊类型引用(4)
1. 王云龙，邢兰昌，魏伟，韩维峰，朱作飞，苏丕波. 基于多场耦合数值模型的含水合物多孔介质声学特性：骨架颗粒排列和形状的影响. 新能源进展. 2025(01): 7-16 . 
百度学术
2. 叶阳升，蔡德钩，安再展，魏少伟，闫宏业，姚建平. 基于机-土耦合模型的铁路路基连续压实质量控制方法. 铁道学报. 2024(03): 1-10 . 百度学术
3. 张涛，吴健，魏骁，杨仲轩. 颗粒表面粗糙度对材料小应变动力特性的影响. 岩土工程学报. 2024(08): 1783-1790 . 本站查看
4. 袁丽，崔振东，张忠良. Stoke固定-自由型共振柱实验系统测试原理及标定方法. 实验技术与管理. 2023(06): 68-73+89 . 百度学术
其他类型引用(2)
-
其他相关附件
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
- 被引次数: 6
