隔离桩对隧道开挖诱发土体竖向位移牵制效应的理论分析

曹利强; 陈湘生; 张顶立; 苏栋

doi:10.11779/CJGE202205015

隔离桩对隧道开挖诱发土体竖向位移牵制效应的理论分析 English Version

曹利强^{1, 2, 3, 4,},
陈湘生^{1, 2, 4, 5, ,},
张顶立³,
苏栋^{1, 2, 4, 5}

1.
深圳大学土木与交通工程学院, 广东深圳 518060
2.
深圳大学未来地下城市研究院, 广东深圳 518060
3.
北京交通大学城市地下工程教育部重点实验室, 北京 100044
4.
深圳大学滨海城市韧性基础设施教育部重点实验室, 广东深圳 518060
5.
深圳市地铁地下车站绿色高效智能建造重点实验室, 广东深圳 518060

基金项目:

国家自然科学基金青年项目 52108376

国家自然科学基金重大项目 52090084

国家自然科学基金重点项目 51938008

国家自然科学基金重点项目 51738002

详细信息

作者简介:
曹利强(1991—)，男，博士后，主要从事城市地下工程施工力学及灾变控制方面的科研工作。E-mail: liqiangcao@bjtu.edu.cn

通讯作者:
陈湘生，E-mail: xschen@szu.edu.cn

中图分类号: TU470
计量
- 文章访问数: 247
- HTML全文浏览量: 46
- PDF下载量: 146
出版历程
- 收稿日期: 2021-07-18
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-04-30

Theoretical investigation of restraint effect of isolation piles on vertical ground displacements due to tunneling under the plane state

CAO Li-qiang^{1, 2, 3, 4,},
CHEN Xiang-sheng^{1, 2, 4, 5, ,},
ZHANG Ding-li³,
SU Dong^{1, 2, 4, 5}

1.
College of Civil and Transportation Engineering, Shenzhen University, Shenzhen 518060, China
2.
Underground Polis Academy, Shenzhen University, Shenzhen 518060, China
3.
Key Laboratory of Urban Underground Engineering of Ministry of Education, Beijing Jiaotong University, Beijing 100044, China
4.
Key Laboratory of Coastal Urban Resilient Infrastructures (MOE), Shenzhen University, Shenzhen 518060, China
5.
Shenzhen Key Laboratory of Green, Efficient and Intelligent Construction of Underground Metro Station, Shenzhen 518060, China

摘要

摘要: 隔离桩作为一种高效的防护措施被广泛应用于城市隧道施工环境效应的控制中。基于两阶段理念建立了可考虑隔离桩与土体之间相对滑移（采用桩侧弹簧与桩端弹簧模拟）的桩-土竖向相互作用的解析模型。基于该模型并引入变形协调关系，利用改进的Loganathan-Poulos（L&P）公式和一般化的竖向位移的Melan解，求解了隔离桩与土体之间的相互作用力（即弹簧内力）。利用叠加原理，进一步求解了隔离桩牵制下隧道开挖引起的地层竖向位移，该结果通过与既有解析方法和现场实测数据对比得到了验证。基于新提出模型的解析结果，分析并揭示了隔离桩对地层竖向位移发挥牵制作用的力学机制。研究表明，隔离桩对土体的牵制作用可以分为向上牵制和向下牵制两个部分，向上和向下牵制作用相结合共同驱使土体竖向位移沿深度方向由原来的隧道开挖引起的不均匀状态转变为相对均匀状态。隔离桩的桩侧与桩端弹簧刚度决定了桩与土体相互作用的程度，其刚度越小则相互作用力越小，桩与土体的相对位移越大，向上与向下牵制效应也越小。相关研究可为隔离桩的设计和效应评估做出理论指导。
- 理论分析 /
- 盾构隧道 /
- 隔离桩 /
- 竖向位移 /
- 牵制效应
Abstract: As an efficient protective measure, the isolation piles are widely used in the control of tunneling-induced environmental effects in urban areas. Based on the two-stage concept, a vertical pile-soil interaction model that can consider the relative slip between the isolation pile and the soil (simulated by the pile shaft spring and the pile tip spring) is established. Based on this model and introducing the displacement compatibility condition, using the modified Loganathan-Poulos (L&P) formula and the Melan solution of the vertical displacement in a general form, the interaction forces between the isolation pile and the soil (i.e., the internal force of the springs) are solved. Using the superposition principle, the ground vertical displacements caused by tunnel excavation under the restraint of isolation piles are further solved. The results are verified by comparing with those of the existing analytical methods and field measured data. Based on the analytical results of the proposed model, the mechanical mechanism of the effects of the isolation piles on the ground vertical displacements is investigated. The studies have shown that the restraint effect of the isolation piles on soil can be divided into two parts, upward part and downward part. The combination of the upward and downward effects together drives the tunneling-induced ground vertical displacements along the depth direction to change from non-uniform state to a relatively uniform one. The spring stiffness of the pile shaft and pile tip determines the degreeof interaction between the pile and the soil. The smaller the stiffness, the smaller the interaction force, the greater the relative displacement between the pile and the soil, and the smaller the upward and downward restraint effects. The related research may provide theoretical guidance for the design and effect evaluation of isolation piles.
- theoretical analysis /
- shield tunnel /
- isolation pile /
- ground vertical displacement /
- restraint effect

HTML全文

0. 引言

盾构在建（构）筑物密集分布的城市环境中掘进时常面临近接施工的严峻工况，隧道开挖诱发的土体变形极易导致结构开裂甚至失效破坏，隔离桩作为一种可靠、高效的防护措施被广泛应用于此类工程中^[1]。尽管隔离桩应用十分广泛，但目前对其如何发挥隔离性能尚未形成统一、系统的理论认识，而这对于评估隔离桩的作用效果并指导其设计至关重要。

国内外学者针对隔离桩如何发挥阻隔效应开展了一系列研究，这些研究不仅针对隧道开挖亦针对基坑开挖。Bilotta等^[2-3]采用离心试验方法研究了不排水黏土中嵌入式连续墙在阻隔隧道开挖产生的地层沉降的作用效果，并进一步利用离心试验和数值模拟方法对隔离墙的阻隔效果进行分析。Rampello等^[4]、Bilotta等^[5]、邹文浩等^[6]采用二维或三维数值模拟方法研究了隧道开挖下隔离桩或隔断墙对地层竖向位移的控制效果并就其影响因素进行分析。郑刚等^[7]、徐长节等^[8]结合现场试验方法并采用数值模拟方法研究了基坑开挖后隔离桩对土体深层位移及既有隧道位移的控制机制。陈仁朋等^[9-10]综合采用离心试验、现场试验及数值模拟方法研究了基坑开挖卸载对邻近隧道的影响及设置隔断墙的作用机理。徐晓兵等^[11]进一步采用室内模型试验研究了基坑开挖过程中隔离桩对基坑侧方近接隧道整体位移和自身变形的控制机制。综合既往研究发现，相关学者主要以某一工程为背景，采用离心试验、常重力模型试验、数值模拟，以及现场试验方法对隔离桩的工作机制展开探究，重点分析不同隔离桩的参数对其阻隔效应的影响，但缺乏对于隔离桩发挥阻隔效应的力学机制的深入研究。基于力学模型的解析理论可以清楚的揭示力学原理并可对隔离桩的阻隔效应进行基本判断，但鲜有此方面的研究。尽管Ledesma等^[12]采用解析方法求解了隔离桩约束下土体的竖向变形，但解析模型较为简化，也未能考虑土体泊松比、内摩擦角对隔离桩发挥阻隔效应的影响。此外，该研究仅针对地表的沉降进行分析，未能考虑桩与周围土体之间的相对滑移，从而也未能通过解析原理阐述并揭示隔离桩发挥“牵制效应”的作用机制。事实上，当隔离桩作为防护结构保护地下既有结构时，探究隔离桩对地层深层竖向位移的牵制效应意义重大。同时，鉴于隔离桩表面的粗糙程度的差异性，其与土体的相对滑动也应被重点考虑。

为此，本文试图建立可以考虑隔离桩与土体间相对滑移的竖向相互作用的解析模型，基于改进的L&P公式并结合一般化的竖向位移的Melan解，求解隔离桩牵制作用下隧道开挖引起的地层竖向位移。基于该力学模型和解析结果，分析并试图从解析角度深入揭示隔离桩对地层竖向位移发挥牵制作用的力学机制，以期为隔离桩的设计和效应评估做出理论指导。

1. 隧道开挖诱发的土体竖向位移

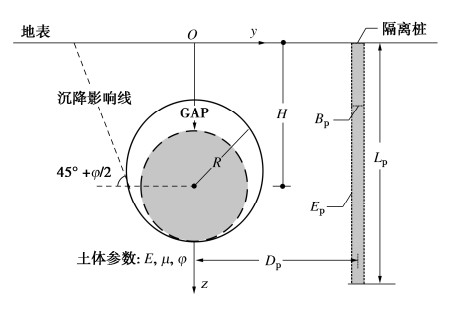
隧道开挖必将诱使土体发生运动，对于盾构隧道而言，当不考虑沿隧道延伸方向的盾构掘进效应（即平面应变状态）时，土体的位移将仅局限于垂直于掘进方向的平面内（， $yOz$ 平面）。

图 1 隧道收敛模式及桩隧的相关参数示意图

Figure 1. Schematic diagram of convergence mode at tunnel opening and related parameters of tunnel and pile

下载: 全尺寸图片幻灯片

展示了隧道开挖后的收敛模式及桩隧的相关参数，坐标为 $yOz$ 系统， $y$ 轴水平向右， $z$ 轴竖直向下；隧道的半径为 $R$ ，隧道的轴线埋深为 $H$ ，隧道开挖后拱顶的竖向收敛位移（即间隙参数^[13-14]）为 ${\text{GAP}}$ ，土体的弹性模量为 $E$ ，泊松比为 $\mu$ ，内摩擦角为 $\varphi$ ；隔离桩的长度为 ${L_{\text{p}}}$ ，宽度为 ${B_{\text{p}}}$ ，弹性模量为 ${E_{\text{p}}}$ ，隔离桩轴线与隧道对称轴线的距离为 ${D_{\text{p}}}$ 。

为研究桩–土间的相互作用，则必须首先厘清隧道开挖诱发的土体位移，然后依据两阶段理念进行分析。目前，有多种不同的方法用来预测、评估隧道开挖诱发的土体平面内位移，如经验方法包括Peck理论及其衍生，以及Celestino理论等；数值仿真方法包括有限元法、有限差分法、边界元法，以及离散元法等；解析法和半解析法包括镜像法、极坐标下的应力函数法、复变函数法、能量方法，以及随机介质理论等。在以上这些方法中，经验方法和（半）解析法均可直接通过输入地层及几何参数快速输出地层的位移预测值，并可方便地对各参数开展参数分析以揭示影响地层位移的力学机理。但是，经验方法如Peck理论、Celestino理论，以及半解析方法中的随机介质理论通常仅可预测隧道拱顶水平线以上的地层位移，而无法预测隧道拱顶水平线以下的位移，因而此类预测方法实际上是并不完备的。镜像法、极坐标下的应力函数法、复变函数法，以及能量方法等均是基于一定假设建立力学模型，并通过推导直接得到地层位移的预测公式。在这些方法中，除能量方法外，其他方法都只能基于弹性介质模型开展分析，但能量方法通常需要更多的假设，因此其应用程度也受到一定限制。应力函数法和复变函数法推导得到的公式较为复杂，不利于将其用于桩–土相互作用机理的理论推导过程。因此，基于镜像原理的Loganathan-Poulos（L&P）公式常成为一个比较好的选择^[15]，L&P公式的预测结果已被证明在黏土中具有较高的精度。地层在坐标 $(y,z)$ 处的竖向位移 ${S_z}(y,z)$ 为

${S_z}(y,z) = {\varepsilon _0}{R^2}\left[ \begin{gathered} \frac{{H - z}}{{{y^2} + {{(H - z)}^2}}} + \frac{{(3 - 4\mu )(H + z)}}{{{y^2} + {{(H + z)}^2}}} \\ - \frac{{2z({y^2} - {{(H + z)}^2})}}{{{{({y^2} + {{(H + z)}^2})}^2}}} \\ \end{gathered} \right] \cdot\\ \;\;\;\;\;\;\;\;\;\;\;\;{\text{exp}}\left[ { - \frac{{1.38{y^2}}}{{{{{\text{(}}H + R{\text{)}}}^2}}} - \frac{{0.69{z^2}}}{{{H^2}}}} \right]\text{，}$

(1)

式中， ${\varepsilon _0}$ 为隧道开挖边界处的地层损失率，

${\varepsilon _0} = \frac{{{V_{\text{s}}}}}{{{\text{π }}{R^2}}} = \frac{{4R \cdot {\text{GAP}} - {\text{GA}}{{\text{P}}^2}}}{{4{R^2}}} \text{，}$

(2)

式中， ${V_{\text{s}}}$ 为隧道开挖边界处的地层损失（即开挖边界的收敛面积）。

研究表明，式（2）在预测黏土地层的竖向位移具有较高的精度，但在预测砂土地层时误差较大。为此，考虑地层的内摩擦角 $\varphi$ 的影响，将式（2）拓展为更为一般的预测公式^[16]：

${S_z}{\text{(}}y,z{\text{)}} = {\varepsilon _0}{R^2}\left[ \begin{gathered} \frac{{H - z}}{{{y^2} + {{(H - z)}^2}}} + \frac{{{\text{(}}3 - 4\mu {\text{)}}(H + z)}}{{{y^2} + {{(H + z)}^2}}} \\ - \frac{{2z({y^2} - {{(H + z)}^2})}}{{{{({y^2} + {{(H + z)}^2})}^2}}} \\ \end{gathered} \right] \cdot\\ \;\;\;\;\;\;\;{\text{exp}}\left[ { - \frac{{1.38{y^2}}}{{{{(H\cot ({{45}^ \circ } + \varphi {\text{/2}}) + R)}^2}}} - \frac{{0.69{z^2}}}{{{H^2}}}} \right] 。$

(3)

2. Melan问题的竖向位移解

以上研究已确定了地层竖向位移的计算方法，当进一步分析桩-土的竖向相互作用时，需首先分析半无限平面弹性介质情况下，作用在平面内一点一个作用力时，引起的弹性介质的应力及位移问题。此问题被称作Melan问题^[17]，Melan首先求解了介质内某一点的应力解，但并未求解竖向位移解。

2.1 Melan问题的原始解

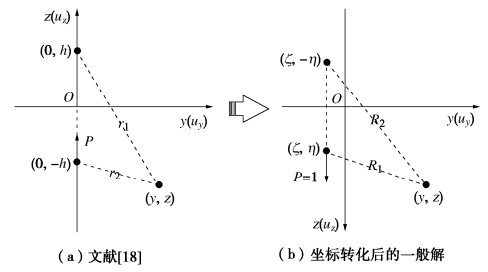
Verruijt等^[18]求解了半平面无限弹性介质中作用一点竖向集中力 $P$ 时，弹性介质的位移。如所示，坐标为 $yOz$ 系统， $y$ 轴水平向右， $z$ 轴竖直向上，水平位移用 ${u_y}$ 表示，竖向位移用 ${u_z}$ 表示，两者的方向分别与 $y$ 轴和 $z$ 轴一致，集中力的作用点为 $(0, - h)$ ，作用方向为竖直向上。

图 2 Melan问题示意图

Figure 2. Schematic diagram of Melan problem

下载: 全尺寸图片幻灯片

地层在坐标 ${\text{(}}y,z{\text{)}}$ 处的竖向位移 ${u_z}$ 为

$\;\;\;\;{u_z} = \frac{P}{{8{\text{π }}G(1 - \mu )}}\left[ {(3 - 4\mu )\ln \frac{{{r_1}}}{{{r_2}}} + \frac{{{y^2}}}{{{r_1}^2}} - \frac{{{y^2}}}{{{r_2}^2}}} \right] - \\ \frac{{P(1 - \mu )}}{{{\text{π }}G}}\ln {r_1} + \frac{{P{{(z - h)}^2}}}{{2{\text{π }}G{r_1}^2}} + \frac{{Phz\left[ {{y^2} - {{(z - h)}^2}} \right]}}{{4{\text{π }}G(1 - \mu ){r_1}^4}} + {u_0} \text{，}$

(4)

式中， $G$ 为土体的剪切模量， ${r_1}$ 为集中力作用点的镜像点与所求竖向位移点的距离， ${r_2}$ 为集中力作用点与所求竖向位移点的距离（图 2（a）），

$\left.\begin{array}{l}{r}_{1}=\sqrt{{y}^{2}+{(z-h)}^{2}}\text{ }\text{，}\\ {r}_{2}=\sqrt{{y}^{2}+{(z+h)}^{2}\text{ }}。\end{array}\right\}$

(5)

2.2 Melan问题的竖向位移的一般解

式（4）的解是特殊情况下的解，即集中力的量值为 $P$ ，作用方向竖直向上，作用点的位置位于竖轴之上。这将为任意位置作用集中力引起的地层竖向位移的求解带来困难。本文将此解进行改造成为一个更为普遍的解，使其等适应任意情况，为此，执行下式所示的转换关系（图 2（b））：

$\left.\begin{array}{l}(0,h)\Rightarrow (\zeta ,\eta )\text{ }\text{，}\\ z\Rightarrow -z\text{ }\text{，}\\ P\Rightarrow 1\text{ }\text{，}\\ G=E/2(1+\mu )\text{，}\text{ }\end{array}\right\}$

(6)

式中，为了与所示的坐标系统保持一致，首先将 $z$ 轴改为竖直向下，其次将集中力 $P$ 改为单位集中力；再次将集中力的作用点改为任意点 $(\zeta ,\eta )$ ，最后将剪切模量转化为用土体弹性模量表示的量以便于统一计算。得到的在点 $(\zeta ,\eta )$ 处作用一个竖直向下的单位集中力时，在另外任意一点 $(y,z)$ 处的竖向位移 ${\bar \mu _z}(\zeta ,$ $\eta ,y,z)$ 为

${\bar \mu _z}(\zeta ,\eta ,y,z) = \frac{{(1 + \mu )}}{{{\text{π }}E}}\left\{ {\frac{{(3 - 4\mu )}}{{4(1 - \mu )}}\ln \frac{{{R_2}}}{{{R_1}}}} \right. +\\ \frac{{{{(y - \zeta )}^2}}}{{4(1 - \mu )}}\left( {\frac{1}{{{R_2}^2}} - \frac{1}{{{R_1}^2}}} \right) - 2(1 - \mu )\ln {R_2} +\\ \left. {\frac{{{{(z + \eta )}^2}}}{{{R_2}^2}} - \frac{{\eta z\left[ {{R_2}^2 - 2{{(z + \eta )}^2}} \right]}}{{2(1 - \mu ){R_2}^4}}} \right\} + {\bar \mu _{z0}} \text{，}$

(7)

式中， ${\bar \mu _{z0}}$ 为与刚体位移相关的任意常数， ${R_1}$ 为集中力作用点与所求竖向位移点的距离， ${R_2}$ 为集中力作用点的镜像点与所求竖向位移点的距离（图 2（b））：

$\left.\begin{array}{l}{R}_{1}=\sqrt{{(y-\zeta )}^{2}+{(z-\eta )}^{2}\text{ }}\text{，}\\ {R}_{2}=\sqrt{{(y-\zeta )}^{2}+{(z+\eta )}^{2}\text{ }。}\end{array}\right\}$

(8)

为确定任意常数 ${\bar \mu _{z0}}$ ，需要假设一个地层中的位移不动点。本文假设地面上距离集中力一定水平距离 $t$ 处的竖向位移为零^[12]，即令 ${\bar \mu _z}(\zeta ,\zeta \pm t,\eta ,0) = 0$ ，可得

${\bar \mu _{z0}} = \frac{{1 - {\mu ^2}}}{{{\text{π }}E}}\ln ({t^2} + {\eta ^2}) - \frac{{(1 + \mu ){\eta ^2}}}{{{\text{π }}E({t^2} + {\eta ^2})}} 。$

(9)

将式（9）代入式（7）可得任意一点的竖向位移：

${\bar \mu _z}(\zeta ,\eta ,y,z) = \frac{{(1 + \mu )}}{{{\text{π }}E}}\left\{ {\frac{{(3 - 4\mu )}}{{4(1 - \mu )}}\ln \frac{{{R_2}}}{{{R_1}}}} \right. + \frac{{{{{\text{(}}y - \zeta {\text{)}}}^2}}}{{4(1 - \mu )}} \cdot\\ \;\;\;\;\;\;\;\;\;\left( {\frac{1}{{{R_2}^2}} - \frac{1}{{{R_1}^2}}} \right) - \frac{{{\eta ^2}}}{{{t^2} + {\eta ^2}}} + (1 - \mu )\ln \frac{{{t^2} + {\eta ^2}}}{{{R_2}^2}} +\\ \;\;\;\;\;\;\;\;\;\frac{{{{{\text{(}}z + \eta {\text{)}}}^2}}}{{{R_2}^2}} - \left. {\frac{{\eta z\left[ {{R_2}^2 - 2{{(z + \eta )}^2}} \right]}}{{2(1 - \mu ){R_2}^4}}} \right\} 。$

(10)

值得注意的是， $t$ 的选择决定了集中力的影响范围。有学者认为 $t{\text{ = }}H$ 即可较好地确保桩土相互作用的影响范围衰减与隧道开挖引起的地层变形保持一致^[12]。因本文中在自由地层变形的计算中考虑了内摩擦角对沉降范围的影响，同时尽可能考虑到影响范围的保守程度，本文取 $t = 4/3 \cdot H\cot ({45^ \circ } + \varphi {\text{/2}})$ 是一个比较合理的估计。

当研究桩–土的相互作用时，需要计算桩与土接触点对另外任意一点竖向位移的影响。因此，在应用式（10）时，作用点和所求点具有同样的横坐标，即 $\zeta {\text{ = }}y$ ，将此关系代入（10）中，可得精简的竖向位移公式为

$f(\eta ,z) = \frac{{(1 + \mu )}}{{{\text{π }}E}}\left[ {\frac{{3 - 4\mu }}{{4(1 - \mu )}}\ln \frac{{z + \eta }}{{\left| {z - \eta } \right|}}} \right. + \frac{{\eta z}}{{2(1 - \mu ){{(z + \eta )}^2}}} +\\ \;\;\;\;\;\;\;\;\; (1 - \mu )\ln \frac{{{t^2} + {\eta ^2}}}{{{{(z + \eta )}^2}}}\left. { - \frac{{{\eta ^2}}}{{({t^2} + {\eta ^2})}} + 1} \right] 。$

(11)

3. 桩–土竖向相互作用分析

对桩–土竖向相互作用的分析是进一步研究隔离桩对土体位移发挥牵制作用的基础。为此，需首先建立相应的力学模型，然后考虑桩与土体的变形协调关系求解二者之间的相互作用力，最后叠加隧道开挖引起的地层竖向位移与桩对土体的作用力引起的地层竖向位移得到考虑隔离桩牵制作用下地层的最终位移。

3.1 桩–土竖向相互作用模型

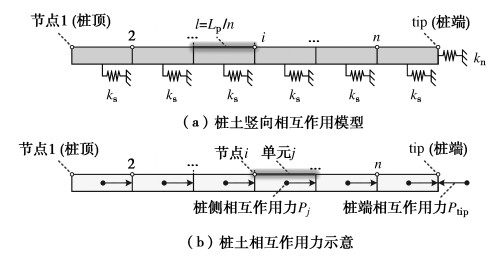
桩–土竖向相互作用模型如所示，桩长为 ${L_{\text{p}}}$ ，桩共分为 $n + 1$ 个节点，节点编号为 $i$ （ $i = 1$ ~ $n + 1$ ），因此共划分为 $n$ 个单元，单元编号为 $j$ （ $j = 1$ ~ $n$ ），单元的长度为 ${L_{\text{p}}}/n$ 。桩与土的相互作用采用线弹性弹簧模拟，桩侧弹簧的刚度为 ${k_{\text{s}}}$ ，连接位置处于各个桩单元的中点处，桩端弹簧的刚度为 ${k_{\text{n}}}$ ，连接位置处于桩端处。

图 3 桩–土相互作用模型及相互作用力示意图

Figure 3. Schematic diagram of pile-soil interaction model and interaction force

下载: 全尺寸图片幻灯片

桩与土体之间的相互作用力即为各弹簧的内力（），桩侧弹簧的伸缩可以模拟桩与桩侧土体的相对滑移；桩端弹簧的伸缩可以模拟桩端与支撑土体的相对位移（即桩端嵌入土体或者桩端不连续抬升）。值得注意的是，中，作用力的示意为土对桩的作用力，且桩侧的作用力 ${P_j}$ 假设竖直向下（实际情况可能有上也有下），桩端土对桩端的作用力 ${P_{{\text{tip}}}}$ 根据平衡条件可知竖直向上。根据作用力与反作用力的关系，桩对土的作用力与土对桩的作用力大小相等、方向相反。

3.2 考虑桩–土相对位移的变形协调关系

隧道开挖后土体发生变形，变形传递到桩位置处时必将牵动桩发生移动、变形，土牵动桩发生运动，但桩同时抵抗这种牵动作用，两者博弈的结果就是达到力学平衡，满足的条件则是变形协调关系，如下式所示：

${w_{{\text{p}}i}} + {w_{{\text{f}}i}} = {w_{{\text{st}}i}} + {w_{{\text{sp}}i}} \text{，}$

(12)

式中， ${w_{{\text{p}}i}}$ 为桩节点 $i$ 处由于土体对桩的作用力导致的桩的竖向位移， ${w_{{\text{f}}i}}$ 为桩节点 $i$ 处的桩土相对位移（由弹簧伸长或压缩量表示）， ${w_{{\text{st}}i}}$ 为桩节点 $i$ 处由于隧道开挖引起的土体的竖向位移， ${w_{{\text{sp}}i}}$ 为桩节点 $i$ 处由于桩对土体的作用力导致的土体的竖向位移。

$\left.\begin{array}{l}{w}_{\text{p}i}={w}_{{}_{\text{T}}}+{\displaystyle \sum _{j=i}^{n}\frac{{N}_{j}{L}_{\text{p}}}{n{E}_{\text{p}}{A}_{\text{p}}}}\text{，}\text{ }{N}_{j}={\displaystyle \sum _{k=1}^{j}{P}_{k}}\text{ (}i\in [1,n+1]\text{)}\text{，}\\ {w}_{\text{f}i}=\left\{\begin{array}{l}\left\{\begin{array}{l}{P}_{j}/{k}_{\text{s}}\text{ }\text{ (}i\in [1,n]\text{，}j=i\text{)}\\ 0\text{ (}i\in [1,n]\text{，}j\ne i)\end{array}\right. \\ -{\displaystyle \sum _{j=1}^{n}{P}_{j}}/{k}_{\text{n}}\text{ (}i=n+1\text{)}\end{array}\right.\text{，}\\ {w}_{\text{st}i}={S}_{z}({D}_{\text{p}},{z}_{i})\text{ (}i\in [1,n+1]\text{)}\text{，}\\ {w}_{\text{sp}i}=f({\eta }_{\text{T}},{z}_{i}){\displaystyle \sum _{j=1}^{n}{P}_{j}}-{\displaystyle \sum _{j=1}^{n}{P}_{j}f({\eta }_{j},{z}_{i})\text{ (}i\in [1,n+1]\text{)}。}\end{array}\right\}$

(13)

式中 ${w_{_{\text{T}}}}$ 为桩端竖向位移； ${N_j}$ 为编号 $j$ 单元的轴力； ${{{N_j}{L_{\text{p}}}} \mathord{\left/ {\vphantom {{{N_j}{L_{\text{p}}}} {n{E_{\text{p}}}{A_{\text{p}}}}}} \right. } {n{E_{\text{p}}}{A_{\text{p}}}}}$ 为编号 $j$ 单元的压缩或伸长量； ${A_{\text{p}}}$ 为单位长度桩的截面积， ${A_{\text{p}}}{\text{ = }}{B_{\text{p}}}$ ；其他符号的意义同前。 ${S_z}({D_{\text{p}}},{z_i})$ 利用式（3）计算， $f(\eta ,z)$ 利用式（11）计算。

3.3 隔离桩牵制作用下土体的竖向位移

将变形协调关系在 $n + 1$ 个节点处展开，可以得到 $n + 1$ 个方程构成的方程组，将第 $n + 1$ 个方程分别代入到前 $1 \sim n$ 方程中，可以将桩端竖向位移 ${w_{_{\text{T}}}}$ 消去，整理相关公式可以得到

$\left[ \delta \right]\left\{ P \right\} = \left\{ \psi \right\} 。$

(14)

式中 $\left\{ P \right\}$ 为桩侧与土体相互作用力列向量， $\left\{ P \right\} = {\left\{ {{P_1},{P_2}, \cdots ,{P_i}, \cdots ,{P_{n - 1}},{P_n}} \right\}^{\text{T}}}$ ； $\left\{ \psi \right\}$ 为土体相对位移列向量， $\left\{ \psi \right\} = {\left\{ {{\psi _1},{\psi _2}, \cdots ,{\psi _i}, \cdots ,{\psi _{n - 1}},{\psi _n}} \right\}^{\text{T}}}$ ； $\left[ \delta \right]$ 为 $n$ 阶类柔度矩阵。

$\left.\begin{array}{l}{\delta }_{ij}=\left\{\begin{array}{l}[\begin{array}{l}\\ \end{array}f\text{(}{\eta }_{j},{z}_{i}\text{)}+f\text{(}{\eta }_{{}_{\text{T}}},{z}_{{}_{\text{T}}}\text{)}-f\text{(}{\eta }_{j},{z}_{{}_{\text{T}}}\text{)}-f\text{(}{\eta }_{{}_{\text{T}}},{z}_{i}\text{)}+\\ \frac{(n-i+1){L}_{\text{p}}}{n{E}_{\text{p}}{A}_{\text{p}}}+\frac{1}{{k}_{\text{n}}}]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ (}1\le j < i\text{)}\\ [\begin{array}{l}\\ \end{array}f\text{(}{\eta }_{j},{z}_{i}\text{)}+f\text{(}{\eta }_{{}_{\text{T}}},{z}_{{}_{\text{T}}}\text{)}-f\text{(}{\eta }_{j},{z}_{{}_{\text{T}}}\text{)}-f({\eta }_{{}_{\text{T}}},{z}_{i})+\\ \frac{(n-j+1){L}_{\text{p}}}{n{E}_{\text{p}}{A}_{\text{p}}}+\frac{1}{{k}_{\text{n}}}+\frac{1}{{k}_{\text{s}}}]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ (}j=i\text{)}\\ [\begin{array}{l}\\ \end{array}f({\eta }_{j},{z}_{i})+f{\eta }_{{}_{\text{T}}},{z}_{{}_{\text{T}}}\text{)}-f\text{(}{\eta }_{j},{z}_{{}_{\text{T}}}\text{)}-f({\eta }_{{}_{\text{T}}},{z}_{i})+\\ \frac{(n-j+1){L}_{\text{p}}}{n{E}_{\text{p}}{A}_{\text{p}}}+\frac{1}{{k}_{\text{n}}}]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ (}i < j\le n\text{)}\end{array}\right. \text{，}\\ {\psi }_{i}={S}_{z}({D}_{\text{p}},{z}_{i})-{S}_{z}({D}_{\text{p}},{z}_{{}_{\text{T}}})\text{，}\\ {z}_{i}=(i-1)\frac{{L}_{\text{p}}}{n}\text{，}\text{ }{z}_{\text{T}}={L}_{\text{p}}\text{，}\\ {\eta }_{j}=(j-1)\frac{{L}_{\text{p}}}{n}+\frac{{L}_{\text{p}}}{2n}\text{，}\text{ }{\eta }_{{}_{\text{T}}}={L}_{\text{p}}+\frac{{L}_{\text{p}}}{2n}。\end{array}\right\}$

(15)

结合式（14），（15），桩侧与土体相互作用力列向量 $\left\{ P \right\}$ 为

$\left\{ P \right\} = {\left[ \delta \right]^{ - 1}}\left\{ \psi \right\} 。$

(16)

求得桩与土体相互作用力后，则可进一步结合式（3），（10）计算土体叠加后的最终竖向位移 ${S_{{\text{Total}}}}(y,$ $z)$ ，

${S_{{\text{Total}}}}(y,z) = {S_z}(y,z) + {\bar \mu _z}({D_{\text{p}}},{\eta _{\text{T}}},y,z)\sum\limits_{j = 1}^n {{P_j} - }\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ }{\displaystyle \sum _{j=1}^{n}{P}_{j}{\overline{\mu }}_{z}({D}_{\text{p}},{\eta }_{j},y,z)}\text{ }。$

(17)

4. 本文方法验证

为了验证本文提出的理论方法的正确性，采用与既有解析方法的结果和现场实测数据进行对比分析。为比较方便，将计算数据进行无量纲化处理。

4.1 与既有解析解对比

既有解析方法^[12]的相关计算参数如下所列： $R{\text{ = }}5{\text{ m}}$ ， $E{\text{ = }}100{\text{ MPa}}$ ， $\mu {\text{ = }}0.5$ ， $\varphi {\text{ = }}0$ ， ${B_{\text{p}}}{\text{ = }}1{\text{ m}}$ ， ${E_{\text{p}}} =$ $200{\text{ GPa}}$ ， $z = 0$ ， $H = 15{\text{ m}}$ ， ${D_{\text{p}}} = 10{\text{ m}}$ ， ${L_{\text{p}}} =$ 10~40 m， ${\varepsilon _0}{\text{ = }}1{\text{% }}$ ，文献中提到的单元数量为固定数量即 $n = 6$ ，但原文并不能考虑 $\mu$ 和 $\varphi$ 的影响。按照此计算参数，并取 ${k_{\text{s}}} = {k_{\text{n}}} = 1 \times {10^{15}}{\text{ N/m}}$ （即桩侧与土体紧密接触，无相对滑移；同时桩端与下侧支撑土体紧密接触，无嵌入或上浮），采用本文的方法可以计算出对应结果，其中在不同桩长情况下地表沉降槽的对比结果如图 4所示。

图 4 与既有解析解对比结果

Figure 4. Comparison between calculated results and existing analytical solutions

下载: 全尺寸图片幻灯片

从图 4可以看出，本文的方法与既有解析方法的计算结果非常接近，因此可以验证本文提出方法的正确性。从图中可以看出，隔离桩的存在客观地改变了地面沉降槽的形状和大小，即沉降槽不再以隧道中心线为轴对称分布，最大沉降出现的位置偏离隧道中心线，隔离桩附近一定范围内的地面沉降小于其自由沉降。

4.2 与现场实测数据对比

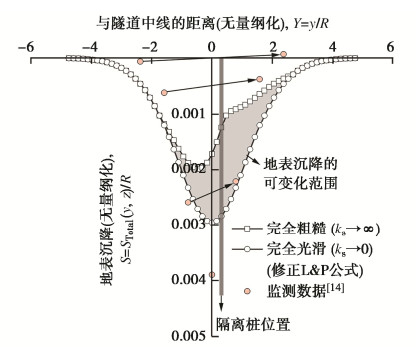
清华园盾构隧道3-2号区间主要穿越粉质黏土地层^[14]，其中DK18+160断面设置了钻孔灌注桩作为隔离措施，该断面的相关几何参数和土体参数如下： $R{\text{ = }}6.32{\text{ m}}$ ， $E{\text{ = }}6{\text{ MPa}}$ ， $\mu {\text{ = }}0.32$ ， $\varphi =$ 18.4°， ${B_{\text{p}}} =$ $0.8{\text{ m}}$ ， ${E_{\text{p}}}{\text{ = }}30{\text{ GPa}}$ ， $z = 0$ ， $H = 14.36{\text{ m}}$ ， ${D_{\text{p}}} = 3{\text{ m}}$ ， ${L_{\text{p}}} =$ $23.68{\text{ m}}$ ， ${\varepsilon _0}{\text{ = }}0.247{\text{% }}$ 。基于上述参数，采用本文方法的计算结果与实测数据的对比如所示，其中为了提高计算精度取 $n = 10$ 。

图 5 与实测数据对比结果

Figure 5. Comparison between calculated results and measured data

下载: 全尺寸图片幻灯片

从图 5中的实测数据可以看出，隔离桩侧的地表沉降均小于以隧道中线为轴的对称位置处的沉降，表现出了隔离桩较为明显的“牵制效应”。对于本文方法，选择两个极端情况进行计算，第一种情况为当桩非常光滑完全不与桩侧土体协调变形；另一种情况为当桩非常粗糙完全与桩侧土体协调变形，不发生相对滑移。第一种情况下，隔离桩完全未发挥“牵制作用”，土体的沉降与自由沉降相同；第二种情况下，隔离桩发挥了最大的“牵制作用”，土体的最终沉降呈现出较为明显的不对称性。按照此计算理论，地表沉降的实际值应位于两者之间，从与实测数据的对比来看，计算结果能较好的解释这种规律。

5. 隔离桩发挥牵制效应的力学机制

采用解析方法研究隔离桩的主要优势在于能清楚的揭示其对土体沉降发挥“牵制效应”的力学机制。开展研究的相关参数如下： $R{\text{ = }}5{\text{ m}}$ ， $E{\text{ = }}100{\text{ MPa}}$ ， $\mu = 0.5$ ， $\varphi = 0$ ， ${B_{\text{p}}} = {\text{1 m}}$ ， ${E_{\text{p}}} = 200{\text{ GPa}}$ ， $H = 15{\text{ m}}$ ， ${D_{\text{p}}} =$ $10{\text{ m}}$ ， ${L_{\text{p}}} = 20{\text{ m}}$ ， ${\varepsilon _0}{\text{ = }}1{\text{% }}$ ， ${k_{\text{s}}}{\text{ = }}{10^{15}}{\text{ N/m}}$ ， ${k_{\text{n}}} =$ ${10^{15}}{\text{ N/m}}$ ， $n = 20$ 。

5.1 桩对土体竖向位移的牵制效应分析

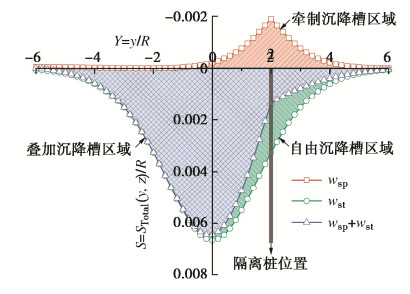
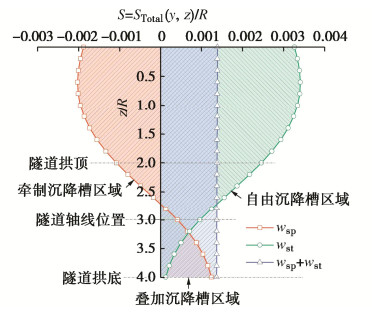
利用以上参数计算得到的地表沉降槽如所示，图中的 ${w_{{\text{sp}}}}$ 为由于桩对土的牵制作用引起的地层竖向位移， ${w_{{\text{st}}}}$ 为由于隧道开挖诱发的地层竖向位移（即地层自由沉降）， ${w_{{\text{st}}}} + {w_{{\text{sp}}}}$ 为地层最终的叠加竖向位移。

图 6 各个因素引起的地表沉降槽

Figure 6. Surface settlement troughs caused by various factors

下载: 全尺寸图片幻灯片

从图 6可以看出，隔离桩通过与土体的相互作用一定程度上牵制了地表土向下运动，这在客观上改变了地表沉降槽的形态，使其从对称沉降转化为非对称沉降，同时有效地抑制了地表的最大沉降。隔离桩所处位置的牵制效应最为明显，远离隔离桩时牵制效应发生衰减直至为零。

图 7为隔离桩的位置处的地层深层竖向位移情况。从图中可以看出，当隔离桩不存在时，地层的沉降由地表向隧道拱底位置变化时，总体上呈现出非线性减小的规律。当隔离桩存在时，隔离桩在隧道水平轴线以上一定位置处以上的区域呈现出对土体沉降的显著抑制作用，即向上的牵制作用。这种牵制作用与地层的自由沉降密切相关，即自由沉降越大则隔离桩对土体沉降的牵制作用越大，体现出“遇强则强”的牵制规律。另一方面，隔离桩在隧道水平轴线以上一定位置处以下的区域呈现出对土体沉降的向下牵制作用，且越向下这种向下牵制作用越强。造成这种现象的原因可能是：隧道水平轴线以上大部分深度的土体的沉降较大，则会带动隔离桩向下运动同时发生压缩变形。因隔离桩与土体相比其变形刚度较大，因此表现出较为明显的刚体运动，如图 7所示，呈现出较为明显的整体沉降（变形情况不甚明显）。因此，当隔离桩的整体沉降大于隧道轴线下方的土体沉降时，则隔离桩将反过来向下牵制并促进土体向下运动，进而增大此处土体的沉降。当相对位移越明显时，这种向下牵制效应越明显。

图 7 隔离桩位置处的地层深层竖向位移

Figure 7. Subsurface ground vertical displacements at pile position

下载: 全尺寸图片幻灯片

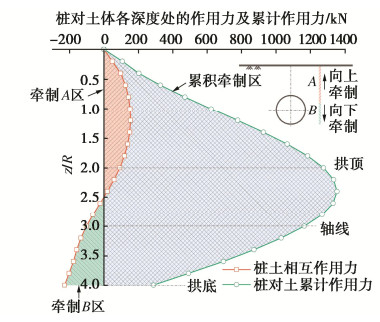
为进一步解释地层沉降呈现出来的规律，计算此位置处的桩–土相互作用力与桩对土的累计作用力，计算结果如图 8所示。从图中可以看出，隧道轴线位置以上某一位置处以上的土体区域中，土体相对于桩向下运动，因此桩对土体产生了向上的牵制作用（图 8中的牵制A区）；以下的土体区域中，由于桩的整体竖向沉降导致桩相对于土体向下运动，因此该区域桩对土体产生了向下的牵制作用（图 8中的牵制B区）。这同样解释了桩位置处土体沿深度方向的“相对均匀化”地层沉降（与桩的整体沉降密切相关）。隔离桩对土体的累计作用力（即桩身轴力的反作用力）呈现出先增大后减小的趋势，但最小值仍然大于零，说明桩一直呈现被土体牵制压缩的状态。

图 8 桩–土间相互作用力

Figure 8. Interaction forces between pile and surrounding soil

下载: 全尺寸图片幻灯片

5.2 桩侧–土刚度对隔离桩发挥牵制效应的影响

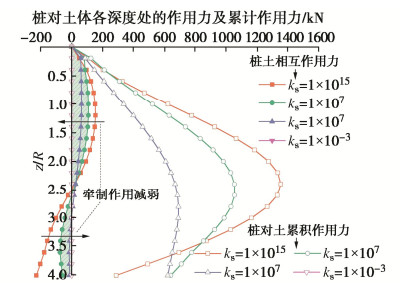
为研究不同桩侧–土刚度对隔离桩发挥牵制效应的影响，选择4组不同侧向弹簧刚度计算桩–土之间的相互作用力和桩位置处的土体竖向位移和桩身沉降，计算结果分别如，所示。侧向弹簧的刚度： ${k_{\text{s}}} = {10^{15}}{\text{ N/m}}$ ， ${k_{\text{s}}} = {\text{5}}$ × ${10^7}{\text{ N/m}}$ ， ${k_{\text{s}}} = {\text{1}}$ × ${10^7}{\text{ N/m}}$ ， ${k_{\text{s}}} =$ ${\text{1}}$ × ${10^{ - 3}}{\text{ N/m}}$ ，其他计算参数保持不变。

图 9 不同桩侧–土刚度情况下桩土之间的相互作用力

Figure 9. Interaction forces between pile and surrounding soil under different stiffnesses at pile shaft-soil interface

下载: 全尺寸图片幻灯片

图 10 不同桩侧–土刚度情况下桩与土体的竖向位移

Figure 10. Vertical displacements of ground and pile under different stiffnesses at pile shaft-soil interface

下载: 全尺寸图片幻灯片

从图 9可以看出，随着桩侧弹簧刚度从接近无限大到接近于零变化时，桩与土体间的相互作用力逐渐减小为零，即相互作用逐渐减弱，则隔离桩对土体的牵制作用在向上牵制区和向下牵制区均呈现出减弱的趋势。

从图 10可以看出，随着桩侧弹簧刚度从接近无限大到接近于零变化时，桩对土体的牵制作用逐渐减小。桩土之间发生相对滑动，弹簧刚度无限大时，桩土协调变形（土体与桩的变形一致，图 10中两条曲线重合）；当弹簧刚度接近于零时，桩土间完全滑移，土体的位移仍为隧道开挖引起的自由竖向位移，桩的位移为整体位移（与桩端处的土体位移相同）且无压缩变形。桩侧弹簧刚度介于无限大与零之间时，桩–土之间的位移介于完全协调与完全不协调之间。

5.3 桩端–土刚度对隔离桩发挥牵制效应的影响

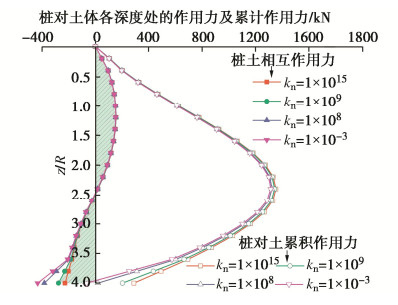
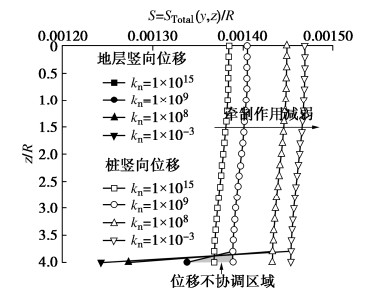
为研究不同桩端–土刚度对隔离桩发挥牵制效应的影响，选择4组不同桩端弹簧刚度计算桩-土之间的相互作用力和桩位置处的土体竖向位移和桩身沉降，计算结果分别如，所示。桩端弹簧的刚度： ${k_{\text{n}}}{\text{ = 1}} \times {10^{15}}{\text{ N/m}}$ ， ${k_{\text{n}}}{\text{ = 1}} \times {10^9}{\text{ N/m}}$ ， ${k_{\text{n}}}{\text{ = 1}} \times {10^8}{\text{ N/m}}$ ， ${k_{\text{n}}}{\text{ = 1}} \times {10^{ - 3}}{\text{ N/m}}$ ，其他计算参数保持不变。

图 11 不同桩端–土刚度情况下桩土之间的相互作用力

Figure 11. Interaction forces between pile and surrounding soil under different stiffnesses at pile tip-soil interface

下载: 全尺寸图片幻灯片

图 12 不同桩端–土刚度情况下桩与土体的竖向位移

Figure 12. Vertical displacements of ground and pile under different stiffnesses at pile tip-soil interface

下载: 全尺寸图片幻灯片

从可以看出，随着桩端弹簧刚度从接近无限大到接近于零变化时，靠近桩端的局部范围内桩与土体间的相互作用力逐渐增大，隔离桩对土体的牵制作用在向下牵制区呈现出加强的趋势。但由于桩端弹簧刚度的不断减小，桩土之间的作用力同样不断减小，当弹簧刚度接近零时，桩端与土不存在相互作用力（值得说明的是，在中，当 ${k_{\text{n}}}{\text{ = 1}} \times {10^{ - 3}}{\text{ N/m}}$ 时，桩对土的累积作用力在桩端处为负值，这是受到桩分段数量的影响造成的误差，当计算数量提高时，此值趋向于零）。

从图 12可以看出，因为桩侧弹簧的刚度很大，因此桩侧与土体协调变形，即未产生相对滑移（土体与桩的变形一致，图 12中两条曲线重合）。但当桩端弹簧的刚度逐渐减小时，桩端位移与桩端土的位移变得不再一致。从图中看出，桩将嵌入到桩端以下的土体中。当失去桩端土的支撑作用后，桩对土体沉降的牵制效应将被削弱。因此，确保桩端与桩端土协调变形可有效地发挥隔离桩的牵制效应。

5.4 隔离桩相关参数对地表沉降槽的影响

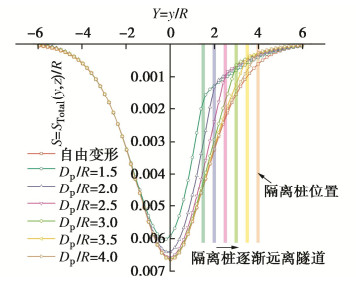
图 13展示了隔离桩与隧道轴线的距离对牵制后的地表沉降槽的影响。由图 13可见，隔离桩离隧道越近，受隔离桩约束的沉降槽范围越大。隔离桩离隧道越近，最大沉降越小，最大沉降偏离隧道中心线的位置越远。因此，条件允许时，隔离桩应靠近隧道设置效果更好。

图 13 隔离桩与隧道轴线的距离对牵制后的地表沉降槽的影响

Figure 13. Effect of distance of tunnel axis from pile axis on ground surface settlement trough

下载: 全尺寸图片幻灯片

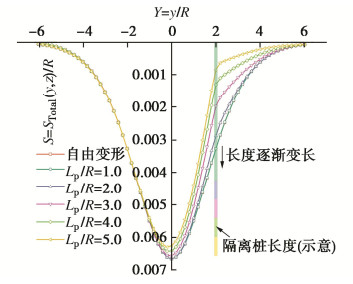
图 14展示了隔离桩的长度对牵制后的地表沉降槽的影响。由图 14可见，隔离桩的桩长越长，受隔离桩约束的沉降槽范围越大。桩长越长，最大沉降越小，最大沉降偏离隧道中心线的位置越远。由以上分析也可知，隧道底部水平线附近的地层竖向变形已经很小，因此当桩端嵌入到隧道拱底处，隔离效果已经很明显，若继续增加桩长并不会显著提升其隔离效果。

图 14 隔离桩的长度对牵制后的地表沉降槽的影响

Figure 14. Effect of pile length on ground surface settlement trough

下载: 全尺寸图片幻灯片

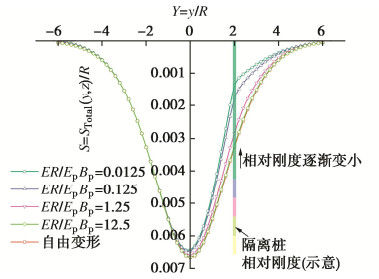
图 15展示了隔离桩的相对刚度对牵制后的地表沉降槽的影响。由图 15可见，隔离桩的相对刚度越小（即在土体刚度不变的情况下，桩的轴向刚度越大），隔离桩所抑制的沉降槽范围就越大。同时，最大沉降越小，最大沉降出现的位置偏离隧道中心线的位置也越远。但是不加限制地增加隔离桩的刚度不会显著提升其牵制作用反而造成经济浪费。

图 15 隔离桩的相对刚度对牵制后的地表沉降槽的影响

Figure 15. Effect of relative stiffness of pile on ground surface settlement trough

下载: 全尺寸图片幻灯片

6. 结论

本文建立了可以考虑隔离桩与土体间相对滑移的相互作用解析模型，基于改进的L&P公式并结合一般化的竖向位移的Melan解，求解了隔离桩牵制作用下隧道开挖引起的地层竖向位移。基于该力学模型和解析结果，分析并揭示了隔离桩对地层竖向位移发挥牵制作用的力学机制，同时得到以下3点结论。

（1）隔离桩对土体的牵制作用可以分为向上牵制和向下牵制两个区域。隧道水平轴线以上一定位置处以上的区域由于土体沉降较大，土体牵动隔离桩向下运动，因此隔离桩对土体施加向上的作用力，表现出向上牵制效应。该区域以下，由于土体的自由沉降较小而隔离桩的沉降较大（刚体沉降为主，压缩变形为辅），则隔离桩牵动土体向下运动，因此隔离桩对土体施加向下的作用力，表现出向下牵制效应。因此，隔离桩对土体竖向位移的牵制作用可以总体概括为：驱使土体位移沿深度方向转变为相对均匀化状态。

（2）隔离桩的桩侧与桩端弹簧刚度决定了桩与土体相互作用的程度，其刚度越小则相互作用力越小，桩与土体的相对位移越大，向上与向下牵制效应越小。对于桩侧弹簧而言，当其刚度接近于零时，桩土间完全滑移，土体的位移仍为隧道开挖引起的自由竖向位移，桩的位移为整体位移且无压缩变形，牵制效应为零；对于桩端弹簧而言，当其刚度接近于零亦即桩端失去土体支撑后，桩将嵌入到土体之中，隔离桩对土体沉降的牵制效应也将被削弱。

（3）隔离桩与隧道轴线的水平距离、隔离桩的长度与隔离桩的刚度的变化都会对隔离桩发挥其牵制能力造成影响。隔离桩离隧道越近，受隔离桩约束的沉降槽范围越大，条件允许时，隔离桩应尽可能设置在近隧道处。隔离桩的桩长越长，受隔离桩约束的沉降槽范围越大，当桩端嵌入到隧道拱底处，牵制效应已经很明显，若继续增加桩长并不会显著提升其隔离效果。隔离桩的轴向刚度越大，受隔离桩约束的沉降槽范围越大，但不加限制的增加隔离桩的刚度不会显著提升其牵制能力反而造成经济浪费。

图 1 隧道收敛模式及桩隧的相关参数示意图

Figure 1. Schematic diagram of convergence mode at tunnel opening and related parameters of tunnel and pile

下载: 全尺寸图片幻灯片

图 2 Melan问题示意图

Figure 2. Schematic diagram of Melan problem

下载: 全尺寸图片幻灯片

图 3 桩–土相互作用模型及相互作用力示意图

Figure 3. Schematic diagram of pile-soil interaction model and interaction force

下载: 全尺寸图片幻灯片

图 4 与既有解析解对比结果

Figure 4. Comparison between calculated results and existing analytical solutions

下载: 全尺寸图片幻灯片

图 5 与实测数据对比结果

Figure 5. Comparison between calculated results and measured data

下载: 全尺寸图片幻灯片

图 6 各个因素引起的地表沉降槽

Figure 6. Surface settlement troughs caused by various factors

下载: 全尺寸图片幻灯片

图 7 隔离桩位置处的地层深层竖向位移

Figure 7. Subsurface ground vertical displacements at pile position

下载: 全尺寸图片幻灯片

图 8 桩–土间相互作用力

Figure 8. Interaction forces between pile and surrounding soil

下载: 全尺寸图片幻灯片

图 9 不同桩侧–土刚度情况下桩土之间的相互作用力

Figure 9. Interaction forces between pile and surrounding soil under different stiffnesses at pile shaft-soil interface

下载: 全尺寸图片幻灯片

图 10 不同桩侧–土刚度情况下桩与土体的竖向位移

Figure 10. Vertical displacements of ground and pile under different stiffnesses at pile shaft-soil interface

下载: 全尺寸图片幻灯片

图 11 不同桩端–土刚度情况下桩土之间的相互作用力

Figure 11. Interaction forces between pile and surrounding soil under different stiffnesses at pile tip-soil interface

下载: 全尺寸图片幻灯片

图 12 不同桩端–土刚度情况下桩与土体的竖向位移

Figure 12. Vertical displacements of ground and pile under different stiffnesses at pile tip-soil interface

下载: 全尺寸图片幻灯片

图 13 隔离桩与隧道轴线的距离对牵制后的地表沉降槽的影响

Figure 13. Effect of distance of tunnel axis from pile axis on ground surface settlement trough

下载: 全尺寸图片幻灯片

图 14 隔离桩的长度对牵制后的地表沉降槽的影响

Figure 14. Effect of pile length on ground surface settlement trough

下载: 全尺寸图片幻灯片

图 15 隔离桩的相对刚度对牵制后的地表沉降槽的影响

Figure 15. Effect of relative stiffness of pile on ground surface settlement trough

下载: 全尺寸图片幻灯片

参考文献(18)

[1]	雷永生. 西安地铁二号线下穿城墙及钟楼保护措施研究[J]. 岩土力学, 2010, 31(1): 223–228, 236. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201001039.htm LEI Yong-sheng. Research on protective measures of City Wall and Bell Tower due to underneath crossing Xi'an Metro Line No. 2[J]. Rock and Soil Mechanics, 2010, 31(1): 223–228, 236. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201001039.htm
[2]	BILOTTA E, TAYLOR R N. Centrifuge modelling of tunnelling close to a diaphragm wall[J]. International Journal of Physical Modelling in Geotechnics, 2005, 5(1): 27–41. doi: 10.1680/ijpmg.2005.050103
[3]	BILOTTA E. Use of diaphragm walls to mitigate ground movements induced by tunnelling[J]. Géotechnique, 2008, 58(2): 143–155. doi: 10.1680/geot.2008.58.2.143
[4]	RAMPELLO S, FANTERA L, MASINI L. Efficiency of embedded barriers to mitigate tunnelling effects[J]. Tunnelling and Underground Space Technology, 2019, 89: 109–124. doi: 10.1016/j.tust.2019.03.027
[5]	BILOTTA E, RUSSO G. Use of a line of piles to prevent damages induced by tunnel excavation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(3): 254–262. doi: 10.1061/(ASCE)GT.1943-5606.0000426
[6]	邹文浩, 徐明. 考虑土体小应变刚度特征时隔断结构保护效果的三维数值分析[J]. 岩土工程学报, 2013, 35(增刊1): 203–209. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S1034.htm ZOU Wen-hao, XU Ming. 3D numerical analysis of mitigation effect of separation pile and diaphragm wall considering small strain stiffness of soils[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S1): 203–209. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S1034.htm
[7]	郑刚, 杜一鸣, 刁钰. 隔离桩对基坑外既有隧道变形控制的优化分析[J]. 岩石力学与工程学报, 2015, 34(增刊1): 3499–3509. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2015S1111.htm ZHENG Gang, DU Yi-ming, DIAO Yu. Optimization analysis of efficiency of isolation piles in controlling the deformation of existing tunnels adjacent to deep excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 3499–3509. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2015S1111.htm
[8]	徐长节, 曾晓鑫, 戚晓锴, 等. 拱形双排隔离桩对既有隧道的保护效果研究[J]. 防灾减灾工程学报, 2018, 38(4): 633–641. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201804007.htm XU Chang-jie, ZENG Xiao-xin, QI Xiao-kai, et al. Study on protective effect of arched double row piles on existing tunnel[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(4): 633–641. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201804007.htm
[9]	陈仁朋, 王诚杰, 鲁立, 等. 开挖对地铁盾构隧道影响及控制措施[J]. 工程力学, 2017, 34(12): 1–13. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201712002.htm CHEN Ren-peng, WANG Cheng-jie, LU Li, et al. Influence of excavation on exist metro shield tunnel and control measures[J]. Engineering Mechanics, 2017, 34(12): 1–13. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201712002.htm
[10]	陈仁朋, AL-MADHAGI ASHRAF, 孟凡衍. 基坑开挖对旁侧隧道影响及隔断墙作用离心模型试验研究[J]. 岩土工程学报, 2018, 40(增刊2): 6–11. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17549.shtml CHEN Ren-peng, ASHRAF A M, MENG Fan-yan. Three-dimensional centrifuge modeling of influence of nearby excavations on existing tunnels and effects of cut-off walls[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 6–11. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17549.shtml
[11]	徐晓兵, 胡琦, 曾理彬, 等. 隔离桩对干砂地基中基坑侧方隧道影响的模型试验研究[J]. 岩石力学与工程学报, 2020, 39(增刊1): 3015–3022. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2020S1042.htm XU Xiao-bing, HU Qi, ZENG Li-bin, et al. Model tests on the effect of isolation pile on existing tunnel with adjacent excavation in dry sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(S1): 3015–3022. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2020S1042.htm
[12]	LEDESMA A, ALONSO E E. Protecting sensitive constructions from tunnelling: the case of world heritage buildings in Barcelona[J]. Géotechnique, 2017, 67(10): 914–925. doi: 10.1680/jgeot.SiP17.P.155
[13]	LEE K M, ROWE R K, LO K Y. Subsidence owing to tunneling: I estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29(6): 929–940. doi: 10.1139/t92-104
[14]	CAO L Q, ZHANG D L, FANG Q, et al. Movements of ground and existing structures induced by slurry pressure-balance tunnel boring machine (SPB TBM) tunnelling in clay[J]. Tunnelling and Underground Space Technology, 2020, 97: 103278. https://www.sciencedirect.com/science/article/pii/S0886779819302950
[15]	LOGANATHAN N, POULOS H G. Analytical prediction for tunneling-induced ground movements in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 846–856. doi: 10.1061/(ASCE)1090-0241(1998)124:9(846)
[16]	LOGANATHAN N, POULOS H G, XU K J. Ground and pile-group responses due to tunnelling[J]. Soils and Foundations, 2001, 41(1): 57–67. https://trid.trb.org/view.aspx?id=685255
[17]	MELAN E. Der spannungszustand der durch eine einzelkraft im innern beanspruchten halbscheibe[J]. ZAMM - Zeitschrift Für Angewandte Mathematik Und Mechanik, 1932, 12(6): 343–346. (in German). doi: 10.1002/zamm.19320120603
[18]	VERRUIJT A, BOOKER J R. Complex variable analysis of Mindlin's tunnel problem. In Developments in theoretical geomechanics[M]// The John Booker Memorial Symposium, Rotterdam: Balkema, 2000.

施引文献(9)

期刊类型引用(3)

1.	罗基伟，王乐明，杨立功，王欢，李建东，左殿军. 水平及岸坡地层中大直径盾构隧道邻近穿越对码头栈桥影响. 中国铁道科学. 2025(01): 120-135 . 百度学术
2.	刘德军，乔可可，商奇，左建平，段抗，董海洋，张成瑞. 复合地层大直径盾构隧道侧穿既有桩基扰动影响研究. 中国矿业大学学报. 2024(06): 1144-1156 . 百度学术
3.	郑镇跡，曹利强，苏栋，陈湘生. 隔离桩对隧道开挖引起沉降的控制效能分析. 深圳大学学报(理工版). 2022(06): 615-621 . 百度学术