土–地下结构相互作用的三维弱耦合有效应力分析法

赵凯; 夏高旭; 王彦臻; 赵丁凤; 庄海洋; 陈国兴

doi:10.11779/CJGE202205009

土–地下结构相互作用的三维弱耦合有效应力分析法 English Version

1.
南京工业大学岩土工程研究所, 江苏南京 210009
2.
中交上海航道勘察设计研究院有限公司, 上海 200120

基金项目:

国家自然科学基金项目 51978335

国家自然科学基金项目 51978334

国家重点研发计划项目 2018YFC1504301

详细信息

作者简介:
赵凯(1982—)，男，教授，博士，主要从事岩土地震工程研究。E-mail: zhaokai@njtech.edu.cn

通讯作者:
王彦臻, E-mail: soledadwang@163.com

中图分类号: TU43
计量
- 文章访问数: 232
- HTML全文浏览量: 32
- PDF下载量: 200
出版历程
- 收稿日期: 2021-06-15
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-04-30

Three-dimensional loosely coupled effective stress method for seismic soil-structure interactions

1.
Institute of Geotechnical Engineering, Nanjing Tech University, Nanjing 210009, China
2.
Shanghai Waterway Engineering Design and Consulting Co., Ltd., Shanghai 200120, China

摘要

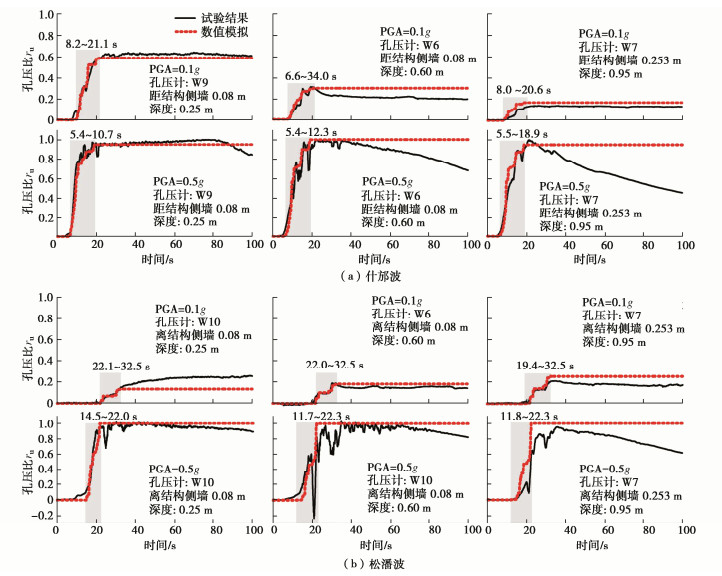
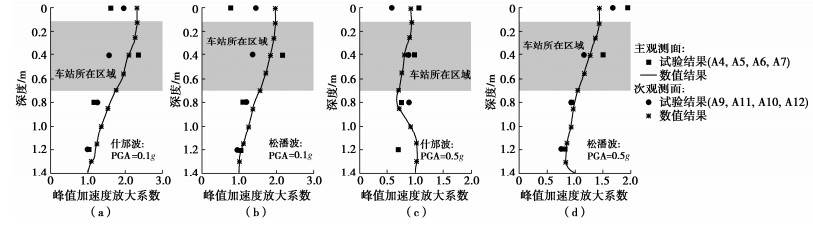
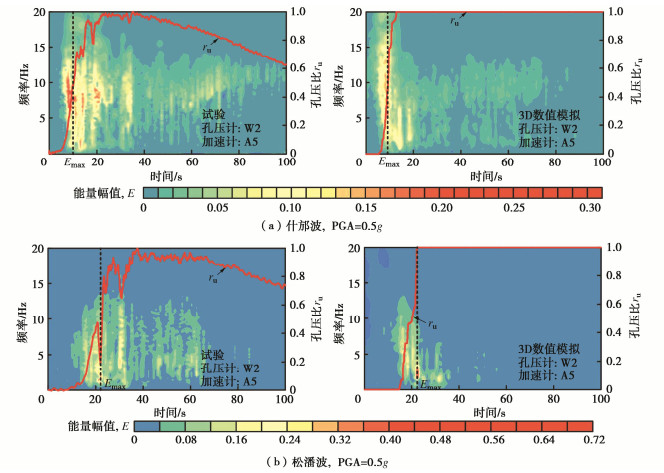
摘要: 地震波传播至土–结构接触界面时会发生反射与透射现象，结构周围土体处于往复剪应力和正应力差耦合的三维循环剪切状态。采用三维等效剪应变算法和加卸载判据将一维Davidenkov非线性滞回模型与剪切–体积应变耦合的孔压增量模型拓展至三维应力空间。考虑循环加载过程中土骨架循环刚度退化与超静孔隙水压力增长的耦合关系，建立了三维应力空间中的弱耦合有效应力分析法。基于ABAQUS显式求解器，实现了该有效应力算法，可应用于大型三维可液化场地中的土–地下结构体系非线性地震反应分析。针对已完成可液化场地三层三跨地铁车站结构试验开展数值模拟，结果表明：超静孔隙水压力的累积导致土的性状变化显著影响土–地下结构动力相互作用，数值模拟得到的土–结构接触界面能量聚焦时刻以及该时刻对应的瞬时卓越频率与振动台试验结果均吻合较好，提出的三维弱耦合有效应力法能较为理想地反映振动台试验中土–地下结构动力相互作用特性。土骨架有效应力水平显著影响超孔压比的发展规律，振动台不完备的密度相似比设计会造成模型结构周围地基土与原型的超孔压比分布规律存在差异。
- 可液化场地 /
- 土–结构动力相互作用 /
- 弱耦合有效应力分析法 /
- 振动台试验
Abstract: Wave reflection and transmission phenomena occur when seismic ground motion propagates to the soil-structure interface, and the surrounding soil is under three-dimensional (3D) cyclic shearing with reciprocating change of shear stress and normal stress difference. The 3D equivalent shear strain algorithm and the loading-unloading criterion are used to extend the 1D Davidenkov hysteretic model in association with an incremental excess pore water pressure (EPWP) model to the 3D stress state. A weakly coupled effective stress method in 3D stress state is established considering the coupling between the cyclic degradation of soil stiffness and the EPWP generation during cyclic loading. Based on the ABAQUS explicit solver, the proposed method is implemented, allowing to perform nonlinear seismic response analysis of soil-structure interactions in 3D liquefiable site. The numerical simulation is carried out against a shaking table test on the subway station in liquefiable site. The results show that the EPWP generation leads to the degradation of soil stiffness, which significantly affects the dynamic soil-structure interactions. The energy-focusing time at the soil-structure interface obtained by numerical simulation and the corresponding instantaneous predominant frequency are in good agreement with the test results. The proposed effective stress method can capture the dynamic soil-structure interaction characteristics in the shaking table tests. However, the effective stress level at soil skeleton significantly affects the EPWP generation. The incomplete density similarity ratio design of the shaking table tests can cause the distribution of the EPWP ratio in the model soil deviated with the prototype.
- liquefiable site /
- seismic soil-structure interaction /
- loosely coupled effective stress method /
- shaking table test

HTML全文

0. 引言

顶管法施工是一种暗挖法工法,能够避免对地下构建筑物的破坏,不影响上方道路交通的正常通行,被广泛应用于压力管道,通信和电力等市政管线的铺设安装,以及微型隧道、地下通道和管幕支护结构的施工当中^[1-4]。合理地确定作用于顶管结构的土压力,对注浆压力及顶推力的控制有着重要作用,是顶管工程结构设计以及施工控制中的基本要求。由于开挖造成的地层运动,会使得结构上方土体间发生相对运动,进而使得作用在结构上的垂直土压力要比上覆土体的自重要小^[5-6]。

松动土压力的相关问题一直以来都是岩土工程中的热点问题,在隧道掘进、埋地管道、路堤加固等诸多工程中都有所涉及。Janssen^[7]分析了侧压力系数与摩擦力的关系,通过连续介质力学理论定量分析了筒仓效应。Marston等^[8]针对沟埋式和上埋式管道的特点,考虑了相对滑动造成土体的摩擦作用,对管道上方的土体进行了散体平衡分析,得到了Marston土压力计算公式,之后学者在此基础之上进行了相关探究^[9-10]。Terzaghi^[11]通过活动门试验,验证了土拱效应的存在,采用极限平衡理论推导出了活动门上方的松动土压力计算公式,并得到了广泛应用和深入研究^[12-14]。目前,基于Terzaghi活动门模型的土压力计算方法在顶管工程实践中得到了广泛应用^[15-16],但基于水平微分土条受力平衡分析还存在着不足,其中对土拱滑移面渐进发展过程的研究相对较少,活动门位置深度关系以及土体特性对土拱滑移面形态的影响也有待进一步深入研究。

本文在Terzaghi松动土压力模型的基础之上,结合顶管施工特点,考虑了主应力轴旋转,通过对水平微分土条的受力分析,通过对应力轴偏转角的合理分析,建立了平衡微分方程。分析了土拱的渐进发展中滑移面的偏转过程,并引入等沉面高度对最终稳定状态下的松动土压力进行了分析计算。通过对比分析,验证了计算模型的合理性,并在此基础之上进行了相关的参数分析。

1. 顶管施工中的模型转化

顶管施工过程中造成的地层损失会使得顶管结构上方土体与两侧土体之间发生相对错动,进而形成滑移破坏面,产生土拱效应^[6]。此时两侧滑移面间的土体应力状态也会发生改变,主应力轴在此过程中发生旋转,可将顶管施工中出现的土拱效应转化为经典的Terzaghi活动门模型来进行分析^[11]。

土拱现象的伴随着土体的滑移错动,从开始滑移到最终到达极限平衡状态,是一个渐进发展的过程。Iglesia等^[17-18]通过离心模型试验对活动门下移过程中的应力屈服状态与应力比和滑移面形状的发展过程进行了相对应的分析。图1给出了浅埋条件下滑移面随活动门位移 $δ$ 的偏转变化情况示意图,在起始阶段土体受到轻微扰动尚处于弹性阶段,土体只发生弹性变形并未产生剪切破坏,故无滑移面生成。随着活动门持续下移,部分土体开始出现屈服现象,此时从活动门两边边缘向中心形成抛物线、三角形或者塔型的滑移面。不少学者对活动门边缘滑移面与竖直方向的角度 $α$ 进行了分析,Evans^[19]、Stone等^[20]取 $α = ψ$ （ $ψ$ 为土体剪胀角）；Iglesia等^[18]认为 $α = φ$ （ $φ$ 为土体摩擦角）；Rui等^[21-23]则取 $α = π/ 4 - φ / 2$ 。夹角 $α$ 的大小受到土体膨胀性、应力状态以及密实度等因素的影响^[24],假设初始滑移面为与活动门边缘夹角取 $α = ψ$ 的斜线。随着活动门的下移,松动土体的范围也随着增大,而滑移面逐渐向竖直方向转动,最终滑移面发展为竖直面,即 $α =0$ ,此时土拱发展成为稳定状态,活动门上所受的竖向应力也不再变化。

图 1 浅埋条件下滑移破坏面发展示意图

Figure 1. Development of failure surface with shallow burial depth

下载: 全尺寸图片幻灯片

利用活动门模型来进行顶管施工过程中的上覆土压力计算,另一个需要明确的参数就是滑移面的宽度范围,如图2所示,许多学者针对极限滑移面的起始位置和发展方向进行了研究,随着管节埋置深度的增加,拱效应也会随之增强,滑移面的宽度范围也会随之增长^[25-26]。汪大海等^[27]通过数值模拟分析了埋深比对滑移面宽度范围的影响,认为滑移面的宽度范围应满足

$\begin{array}{l} 2 B = D (H \leq D), \\ 2 B = D + \frac{2 (H - D)}{3} \tan (π / 4 - φ / 2) (D < H \leq 4 D), \\ 2 B = D [1 + 2 \tan (π / 4 - φ / 2)] (H > 4 D) 。 \end{array}}$

(1)

图 2 滑移面的宽度范围（改自文献[28]）

Figure 2. Widths of failure surface in different theories

下载: 全尺寸图片幻灯片

式中 H为管节埋置深度；B为单侧滑移面距管节对称轴的距离；D为开挖面直径。当 $H / D \leq 1$ 时,滑移面范围符合Korner假设；当 $H / D > 4$ 时,滑移面范围符合Terzaghi假设；当 $1 < H / D \leq 4$ 时,滑移面范围在Korner假设与Terzaghi假设之间,且随上覆土厚度增加而增加。

2. 顶管施工中松动土压力计算

2.1 基本假设

分析模型以Terzaghi活动门模型为基础进行分析计算,模型的基本假设为：①滑移面为直线,滑移面形成时,其与竖直方向夹角为ψ,并最终可发展为竖直面的稳定状态；②滑移面处土体的内摩擦角充分发挥,并达到Mohr-Coulomb极限平衡状态；③水平微分土条上应力状态处于同一个莫尔应力圆；④土体均匀且各向同性。

2.2 水平微分土条受力状态

水平微分土条的受力分析是松动土压力计算的基础,如图3所示,由基本假设③,水平微分土条上任意处的应力可由主应力和主应力旋转角表示：

$τ = (σ_{h} - σ_{3}) \tan θ_{i}$ ,

(2)

$σ_{h} = σ_{1} \cos^{2} θ_{i} + σ_{3} \sin^{2} θ_{i}$ ,

(3)

$σ_{v} = σ_{1} \sin^{2} θ_{i} + σ_{3} \cos^{2} θ_{i}$ ,

(4)

$\bar{σ_{v}} = \int_{0}^{B} σ_{v} d x / B = \frac{σ_{1}}{B} \int_{0}^{B} [1 + (K_{a} - 1) \cos^{2} θ_{i}] d x$ 。

(5)

图 3 水平微分土条应力分布图

Figure 3. Distribution of stresses on horizontal soil element

下载: 全尺寸图片幻灯片

式中 $σ_{1}$ 为大主应力； $σ_{3}$ 为小主应力； $σ_{v}$ 为竖向应力； $σ_{h}$ 为侧向应力； $\bar{σ_{v}}$ 为水平微分土条所受竖向平均应力； $τ$ 为剪应力； $θ_{i}$ 为大主应力与水平方向夹角。则任意位置的侧向土压力系数可表示为

$K = \frac{σ_{h}}{σ_{v}} = \frac{\cos^{2} θ_{i} + K_{a} \sin^{2} θ_{i}}{\sin^{2} θ_{i} + K_{a} \cos^{2} θ_{i}}$ ,

(6)

式中, $K_{a} = σ_{3} / σ_{1} = (1 - \sin φ) / (1 + \sin φ)$ , $φ$ 为内摩擦角。

为了表示出水平微分土条的应力状态关系,Handy^[29]将小应力迹线假设为悬链线,由此将土条内不同位置的应力由主应力和主应力旋转角来表示。徐长节等^[30]则将大主应力迹线分别假设为圆弧形、悬链线形、抛物线形,以对水平土条内的土体应力状态进行分析,并得到上凸形的大主应力迹线计算结果更符合实际情况。汪大海等^[31]通过上凸形的大主应力迹线方法,并将 $θ_{i}$ 假设为线性分布,得到水平土条内的土体应力关系。

以对称轴与活动门表面的交点为原点,水平方向为x轴,竖直方向为z轴,将 $θ_{i}$ 假设为双曲正弦曲线,结合剪切面处（x=B时, $θ_{i} = θ_{s}$ ）和对称轴处（x=0时, $θ_{i} = 0$ ）的边界值,则有

$\cos 2 θ_{i} = \frac{2 e \cdot cos 2 θ_{s}}{e^{2} - 1} \sinh \frac{x}{B}$ ,

(7)

式中, $e$ 为自然常数, $θ_{s}$ 为剪切面处大主应力与水平方向夹角。则竖向平均应力可表示为

$\begin{matrix} \bar{σ_{v}} = \frac{σ_{1}}{2 B} \int_{0}^{B} [K_{a} + 1 + (K_{a} - 1) \cos 2 θ_{i}] d x \\ = \frac{σ_{1}}{2} [K_{a} + 1 + \frac{(e - 1) (K_{a} - 1) \cos 2 θ_{s}}{e + 1}] \end{matrix}$ 。

(8)

图4给出了水平微分土条在滑移面的应力状态以及主应力轴偏转状态示意图,根据单元体在水平方向和竖直方向的受力平衡条件可得

$\begin{matrix} τ_{s} S \cos α - σ_{ns} S \sin α \\ = σ_{1} S \cos (θ_{s} + α) \sin θ_{s} - σ_{3} S \sin (θ_{s} + α) \cos θ \end{matrix}$ ,

(9)

$\begin{matrix} σ_{ns} S \cos α + τ_{s} S \sin α \\ = σ_{1} S \cos (θ_{s} + α) \cos θ_{s} + σ_{3} S \sin (θ_{s} + α) \sin θ_{s} \end{matrix}$ 。

(10)

图 4 水平微分土条滑移面应力状态

Figure 4. Stresses on failure surface of horizontal soil element

下载: 全尺寸图片幻灯片

式中 $τ_{s}$ 为滑移面的剪应力； $σ_{ns}$ 为滑移面的法应力；S为滑移面面积。经整理,滑移面上的剪应力 $τ_{s}$ 和法应力 $σ_{ns}$ 可分别表示为

$σ_{ns} = σ_{1} \cos^{2} (θ_{s} + α) + σ_{3} \sin^{2} (θ_{s} + α)$ ,

(11)

$τ_{s} = (σ_{1} - σ_{3}) \cos (θ_{s} + α) \sin (θ_{s} + α)$ 。

(12)

2.3 水平微分土条的平衡微分方程

由于水平微分土条的受力状态具有对称性,由图5可知,以对称轴与活动门表面的交点为原点,水平方向为x轴,竖直方向为z轴,微分土条的受力具有以下平衡关系：

$P_{z} + F_{s} \cdot \cos α = P_{z} + d P_{z} + F_{ns} \cdot \sin α + W$ 。

(13)

图 5 水平微分土条受力分析图

Figure 5. Forces applied to horizontal soil element

下载: 全尺寸图片幻灯片

式中 $P_{z}$ 为z处微分土条的竖向力； $F_{s}$ 和 $F_{ns}$ 分别为微分土条侧向剪切力和法向力；W为微分土条的重力。

$\begin{array}{l} F_{s} = τ_{s} \cdot s = τ_{s} \cdot \sec α \cdot d z, \\ F_{ns} = σ_{ns} \cdot s = σ_{ns} \cdot \sec α \cdot d z, \\ P_{z} = \bar{σ_{v z}} \cdot B_{z} = (B - z \tan α) \bar{σ_{v z}}, \\ \begin{array}{l} d P_{z} = (B - z \tan α) d \bar{σ_{vz}} - \bar{σ_{v z}} \cdot \tan α \cdot d z, \\ W = γ (B - z \tan α - \frac{dz}{2} \tan α) d z 。 \end{array} \end{array}}$

(14)

式中 $\bar{σ_{vz}}$ 为z位置处微分土条的平均竖向应力。由式（8）,（11）,（12）的关系可做如下代换：

$σ_{1} = \frac{2 (e + 1)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ ,

(15)

$σ_{3} = \frac{2 K_{a} (e + 1)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ ,

(16)

$σ_{ns} = \frac{2 (e + 1) [\cos^{2} (θ_{s} + α) + K_{a} \sin^{2} (θ_{s} + α)]}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ ,

(17)

$τ_{s} = \frac{2 (1 - K_{a}) (e + 1) \cos (θ_{s} + α) \sin (θ_{s} + α)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ 。

(18)

将式（17）,（18）代入式（13）,（14）中,忽略高阶项后整理可得

$\frac{t \bar{σ_{v z}} - γ (B - z \tan α)}{(B - z \tan α)} = \frac{d \bar{σ_{v z}}}{d z}$ ,

(19)

其中,

$\begin{matrix} t = \frac{τ_{s} + \bar{σ_{v z}} \tan α - σ_{ns} \tan α}{\bar{σ_{v z}}} \\ = \frac{2 (1 - K_{a}) (e + 1) \cos (θ_{s} + α) \sin (θ_{s} + α)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} + \tan α - \\ \frac{2 (e + 1) \tan α [K_{a} \cos^{2} (θ_{s} + α) + \sin^{2} (θ_{s} + α)]}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \end{matrix}$ 。

(20)

对式（19）进行求解,则其通解可表示为

$\bar{σ_{v z}} = C_{1} {(B - z \tan α)}^{- t \cdot \cot α} + \frac{γ (B - z \tan α)}{t + \tan α}$ 。

(21)

式（21）的解不包含 $α = 0$ （滑移面发展为竖直面）的情况,当 $α = 0$ 时,由式（13）所得的平衡方程可转化为

$\frac{m \bar{σ_{v z}} - γ B}{B} = \frac{d \bar{σ_{v z}}}{d z}$ ,

(22)

其中,

$m = \frac{τ_{s}}{\bar{σ_{v z}}} = \frac{2 (1 - K_{a}) (e + 1) \cos (θ_{s} + α) \sin (θ_{s} + α)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}}$ ,

(23)

其通解为

$\bar{σ_{v z}} = C_{2} e^{\frac{m z}{B}} + \frac{γ B}{m}$

(24)

2.4 滑移面主应力轴偏转角的确定

土拱的形成和发展与地层的变形有着密切联系,一些学者建立了地层沉降量与滑移面主应力轴偏转角的关系^[32-34]：

$θ_{s} = arccot (\frac{4 λ}{1 - 4 λ^{2}})$ ,

(25)

式中, $λ = δ / 2 B$ 为顶部的相对变形量, $δ$ 为活动门位移,即顶管管节拱顶变形量。根据主应力轴偏转角与滑移破坏面的角度关系,可得滑移面与竖直方向的夹角为

$α = π/ 4 + φ / 2 - θ_{s}$ 。

(26)

结合Evans^[19]的试验数据和上文中 $α$ 值的假设条件,参照文献[31]的相关分析,假设滑移面夹角 $α$ 与相对变形量 $λ$ 的关系为

$α = {\begin{cases} ψ - \frac{\arctan (\frac{4 λ}{1 + 4 λ^{2}})}{π / 4} ψ (0 \leq λ < 0.5) \\ 0 (0.5 \leq λ) \end{cases}$ 。

(27)

滑动破坏面形成时,其与竖直方向的初始夹角为土体的剪胀角 $ψ$ ,随着活动门位移的继续增长,滑移破坏面也向竖直方向发生转动,逐渐发展成为竖直面。图6给出了式（27）的计算结果与实测数据对比,验证了该方法能够更好地反映土拱形态与地层变形之间的关系。

图 6 滑移破坏面与竖直方向夹角随变形发展关系

Figure 6. Normalized displacement versus angle between failure surface and vertical plane

下载: 全尺寸图片幻灯片

2.5 平衡方程的边界条件

如图7所示,在土拱的形成过程中,依据相对变形量 $λ$ 和土拱应力比 $η$ 的关系可分为4个阶段^[17-18],Han等^[35]将此过程简化为线性的3阶段模型,而在此简化模型中最小土拱应力比和稳定土拱应力比是模型的关键参数,并可由此表示出土拱的渐进发展过程。其土拱应力比 $η$ 可表示为

$η = {\bar{σ}}_{v z} / γ H$ 。

(28)

图 7 土拱应力比变化示意图(改自文献[35])

Figure 7. Soil-arching ratio versus normalized displacement

下载: 全尺寸图片幻灯片

在活动门发生位移的过程中,在较小的相对变形条件下,活动门上的应力发生显著下降,达到图7中的最小土拱比。此时,管节上方土体开始发生膨胀及相对错动,但并未达到稳定状态。此时滑移破坏面与竖直方向的夹角为 $ψ$ ,滑移面的高度具有以下可能的关系：

（1） $B \cot ψ \geq H$ ,此时破坏面延伸至地表,边界条件为 $z = H$ 时, ${\bar{σ}}_{vz} = 0$ ,则有

$C_{1} = - \frac{γ (B - H \tan α)}{t + \tan α} \cdot {(B - H \tan α)}^{t \cdot \cot α}$ 。

(29)

（2） $B \cot ψ < H$ ,此时破坏面在地表以下形成封闭三角形,由于滑移面处于初始形成状态,滑移面上方土体不能将上方土压力传递到滑移面以下土体,因此边界条件为 $z = B \cdot \cot ψ$ 时, ${\bar{σ}}_{v z} = 0$ ,则 $C_{1} = 0$ 。

随着相对变形量的增长,最终将会到达稳定状态。对于施工深度较浅的工况,通常可认为滑移破坏面延伸至地表。但随着施工深度的不断增加,上方土体的差异沉降逐渐减小,当上方土体高度增加到某一值时,差异沉降消失,这一平面被称之为等沉面,即等沉面上方土体不在发生相对滑动^[36]。此时如果还将滑移破坏面假设延伸至地表,其计算结果与竖向土压力测量值不一致,其计算结果往往不够准确^[5,10,37-38]。

假设施工过程中超挖及顶进偏差造成的地层损失全部由两侧滑移破坏面之间的土体所填补,如图8所示,滑移破坏面的高度则取决于土体的松动情况。可引入土体体积膨胀系数 $β$ 来反映土体的膨胀性^[6],滑移破坏面的高度可认为存在以下近似关系：

$\begin{array}{l} \frac{π}{4} [D^{2} - d^{2}] = \\ β \cdot [H_{e} (2 B - H_{e} \cdot \tan α) + \frac{{(2 B - D)}^{2} \cot ω}{4} + \frac{4 - π}{4} D^{2}] 。 \end{array}$

(30)

图 8 滑移破坏面高度关系示意图

Figure 8. Sketch of failure surface height

下载: 全尺寸图片幻灯片

式中 $β = Δ V / V_{0}$ ,通常砂土取值为0.1～0.18,黏土的取值为0.18～0.4； $H_{e}$ 为滑移破坏面的高度（等沉面高度）；D为开挖面直径；d为顶管结构物直径。

在土体达到稳定状态时,两侧滑移面交点的高度 $B \cot α$ 与等沉面高度 $H_{e}$ 以及上方土体高度H之间可能存在以下关系：

（1） $B \cot α > H$ 且 $H_{e} > H$ ,即破坏面延伸至地表,边界条件为 $z = H$ 时, ${\bar{σ}}_{v z} = 0$ ,此时C₁可按式（29）计算。若 $α$ =0,则有

$C_{2} = - \frac{γ B}{m} e^{- \frac{m H}{B}}$ 。

(31)

（2） $B \cot α > H_{e}$ 且 $H > H_{e}$ ,此时取等沉面高度为临界高度,边界条件为当 $z = H_{e}$ 时, ${\bar{σ}}_{v z} =$ $γ (H - H_{e})$ ,则有

$\begin{matrix} C_{1} = [γ (H - H_{e}) - \frac{γ (B - H_{e} \cdot \tan α)}{t + \tan α}] \cdot \\ (B - H_{e} \cdot \tan α) t \cdot \cot α, \end{matrix}$

(32)

$C_{2} = [γ (H - H_{e}) - \frac{γ B}{m}] \cdot e^{- \frac{m \cdot H_{e}}{B}}$ 。

(33)

3. 模型验证及参数分析

3.1 模型的对比验证

为验证解析解的合理性,本节内容从竖向土压力和侧向土压力两个方面进行对比验证,分别选用土拱应力比 $η$ 和平均侧向压力系数K_avg进行分析,其中侧向压力系数K_avg可表示为

$K_{avg} = \frac{σ_{h}}{{\bar{σ}}_{v z}} = \frac{2 (\cos^{2} θ_{s} + K_{a} \sin^{2} θ_{s})}{K_{a} + 1 + (e - 1) (K_{a} - 1) \cos 2 θ_{s} / (e + 1)}$ 。

(34)

对于最小土拱应力比的计算,此时的土体处于刚发生相对错动的状态,相对变形量很小,滑移破坏面之间土体的填补作用尚未发挥,因此不考虑等沉面高度的影响。在稳定土拱应力比的计算中,此时活动门的相对变形量较大,且滑移破坏面之间土体的填补作用已发挥,需要考虑等沉面的高度关系。Evans^[19]通过一系列的活动门模型试验,对干砂的松动土压力进行来研究,根据相对变形量的关系,计算出来初始倾斜滑移面状态下的最小土拱应力比和稳定状态下的土拱应力比,其中活动门的宽度D为38.1 mm,土体内摩擦角 $φ$ 为38°,从图9可以看出两种状态下的应力比范围与基本覆盖了模型试验的结果,特别是在深埋条件下,最终稳定状态的计算结果与试验结果具有更好的一致性,这也验证了考虑等沉面高度的必要性。

图 9 干砂试验结果与解析解计算结果对比

Figure 9. Comparison between trapdoor test and calculated results

下载: 全尺寸图片幻灯片

图10给出了采用不同理论计算的地基土侧向压力系数,Terzaghi理论认为侧向土压力系数为经验值,并建议取值为1.0。在考虑主应力轴偏转的基础上,侧向压力系数是随着土体摩擦角的变化而发生改变的。陈若曦等^[12]对侧向压力系数的修正中认为在剪切面上的水平向的应力大于竖直向应力,因此其大主应力轴与水平向的夹角小于竖直方向夹角,因此其侧向压力系数数值随摩擦角的增大而增大,区别于其他理论。本文的提出的平均侧向压力系数计算结果与已有的相关研究结果相近,主要区别在于主应力轴偏转角的设定以及偏转角与相对变形量关系的不同。

图 10 侧向土压力系数对比

Figure 10. Comparison of coefficients of lateral earth pressure under different internal friction angle

下载: 全尺寸图片幻灯片

3.2 松动土压力渐进发展过程

在顶管顶进施工过程中,地层损失主要是由超挖间隙和顶进偏差所造成的,因此正常施工条件下的相对变形量是较小的,其值通常不会超过0.1。图11给出了在相对变形量达到0.05,0.075和0.10时达到稳定状态条件下的土拱应力比发展情况,其中管道的外径为2 m,土体内摩擦角 $φ$ 为35°,随着相对变形量的增长,滑移面的偏转角会向竖直方向偏转,同时滑移面的最终长度也随之增加,因此土拱应力比呈下降趋势。而随着埋深比的增加,等效活动门模型中的活动门宽度也随之增加,进而等沉面高度H_e的增量随着埋深比的增长而减小,而土拱应力比的下降趋势也随之放缓。

图 11 土拱应力比随相对变形量发展

Figure 11. Soil-arching ratio versus normalized displacement

下载: 全尺寸图片幻灯片

本文所提出的计算模型考虑了土拱形成的渐进发展过程,从相对滑移形成的初始状态到最终的稳定状态,其中土体相对运动达到稳定状态后的等沉面高度对地层中的应力分布产生了重要影响,如图12所示。由图12可以看出,在等沉面上方土体的平均竖向应力与静止土压力的分布情况相同,在等沉面下方土体的平均竖向应力明显下降,与现有研究的整体趋势相近,计算结果偏高的主要原因正是由于等沉面的存在使得土体滑移破坏面的长度不同,使得平衡方程的边界条件发生变化。

图 12 顶管上方平均竖向应力沿深度方向分布

Figure 12. Distribution of mean vertical stress along depth

下载: 全尺寸图片幻灯片

3.3 剪胀角的影响

剪胀角的大小对土体滑移破坏面的初始形态具有重要影响,当剪胀角角度较大而且管节所处深度较浅的时候,两侧滑移破坏面在地层中有可能出现封闭的三角形。当剪胀角的角度越小,滑移破坏面则越接近竖直面。

如上所述剪胀角的增大会使得滑移破坏面更加倾向于水平方向,在相对变形量等其它条件不变的情况下,等沉面的高度也不会发生变化,因此倾斜角度更大的滑移破坏面,其发生相对摩擦的面积也会更大,土拱应力比也会越低；式（26）给出了滑移面夹角 $α$ 与应力偏转角 $θ_{s}$ 之间的关系,剪胀角越大则 $α$ 的值越大,相应的 $θ_{s}$ 值越小,则由式（34）计算所得的平均侧向土压力系数越大,如图13所示。

图 13 剪胀角与土拱应力比及平均侧向土压力系数的关系

Figure 13. Influences of dilatancy angle on soil-arching ratio and coefficient of lateral earth pressure

下载: 全尺寸图片幻灯片

3.4 内摩擦角的影响

土体的内摩擦角反映土的摩擦特性,土拱效应的本质正是由于土体之间相互错动产生的摩擦力平衡了部分的竖向应力,因此内摩擦角是影响土拱效应的重要因素。

图14给出了土体内摩擦角 $φ$ 与土拱应力比以及侧向土压力系数的关系。随着 $φ$ 值的增大,土体间的摩擦作用增强,土拱效应随之增强,土拱应力比呈现下降趋势；同时,内摩擦角的增大改变了土体的应力状态,其直接体现在 $K_{a}$ 值的减小,但应力偏转角 $θ_{s}$ 随着内摩擦角 $φ$ 的增大而减小,最终 $K_{a}$ 值对平均侧向土压力系数的影响更为显著,因此平均侧向土压力系数随着内摩擦角的增大而减小。

图 14 内摩擦角与土拱应力比及平均侧向土压力系数的关系

Figure 14. Influences of internal friction angle on soil-arching ratio and coefficient of lateral earth pressure

下载: 全尺寸图片幻灯片

4. 结论

本文对砂土地层中的顶管施工中的土拱形成及发展问题进行了探究,并得到以下4点结论。

（1）在Terzaghi松动土压力模型的基础之上,考虑了主应力轴的旋转,通过假设应力偏转角的方式,构造了水平微分土条的微分方程,并结合土拱的渐进发展状态进行求解,经与室内试验的对比分析,验证了解析解的合理性,可为顶管施工中的土压力计算提供参考依据。

（2）分析了土拱的渐进发展过程,建立了相对变形量与滑移面夹角的关系,随着相对变形量的增大,滑移面将逐步向竖直方向偏转,在相对变形充分的条件下最终偏转为竖直滑移面。结合顶管施工的实际,正常施工条件下的开挖地层损失所形成的相对变形量较小,故破坏面的最终形状为塔型。

（3）在土拱的渐进发展过程中,管节顶部的竖向应力在很小的相对变形量范围内发生了显著下降,达到最小土拱应力比。此时,管节上方土体开始发生膨胀及相对错动,破坏面的高度只取决于滑移面倾角和施工深度之间的关系。随着相对变形量的增大,土体达到稳定状态,此时滑移破坏面的高度则需要考虑上方土体的松动情况,其高度取决于等沉面高度、滑移面倾角和施工深度之间的关系。

（4）土体剪胀角的大小对土体滑移破坏面的初始形态具有重要影响,剪胀角的增大会使得滑移破坏面与水平面的夹角减小,增加了滑移摩擦接触面的长度和水平向的应力；土体的内摩擦角则反映了土体的摩擦特性是影响土拱效应的重要因素,内摩擦角的增大,会使得土体间的摩擦作用增强,减小竖向应力,但同时也改变了土体的应力状态,使得平均侧向土压力系数降低。

图 1 Davidenkov模型骨架曲线图

Figure 1. Davidenkov model skeleton curve

下载: 全尺寸图片幻灯片

图 2 传感器布置

Figure 2. Layout of sensors

下载: 全尺寸图片幻灯片

图 3 地基土–车站结构的三维有限元分析模型

Figure 3. 3D finite element model for soil-subway station structure

下载: 全尺寸图片幻灯片

图 4 输入地震动

Figure 4. Input motions

下载: 全尺寸图片幻灯片

图 5 数值模拟与试验给出的孔压比时程曲线的对比

Figure 5. Comparison between predicted and measured results for time histories of pore pressure ratios

下载: 全尺寸图片幻灯片

图 6 数值模拟与试验给出的土中加速度计A1，A3的加速度时程与Fourier谱的对比

Figure 6. Comparison between predicted and measured results for time histories of acceleration and Fourier spectra for points A1 and A3 in model soil

下载: 全尺寸图片幻灯片

图 7 数值模拟与试验给出的土中峰值加速度放大系数随深度的变化关系

Figure 7. Comparison between predicted and measured results for peak acceleration amplification factors with model soil depth

下载: 全尺寸图片幻灯片

图 8 加速度反应的时-频-能量特性及与孔压比时域发展的相关性

Figure 8. Relationship between time-frequency-energy spectra of accelerations and time histories of EPWP ratio of model soil

下载: 全尺寸图片幻灯片

表 1 黏土与南京细砂的模型参数

Table 1 Model parameters of clay and Nanjing fine sand

土层	密度/(g·cm^-3)	动泊松比	Davidenkov模型					孔压增量模型
土层	密度/(g·cm^-3)	动泊松比	A	B	a₁	a₂	a₃	C₁	C₂	C₃	γ_tv/%	m	n
黏土	1.75	0.49	1.2	0.35	2.5×10^-4	0	0	—	—	—	—	—	—
南京细砂	1.83	0.49	1.02	0.43	4.1×10^-4	0.5	0.45	1.051	0.143	1.25	0.02	0.345	6.689

下载: 导出CSV

表 2 微粒混凝土CDP模型的参数

Table 2 Model parameters of micro-concrete

弹性模量E_o /GPa	拉伸变量ω_t	压缩变量ω_c	泊松比	ψ/(°)	ε	f_bo/f_c	K_c	u
7.5	0	1	0.18	36.31	0.1	1.16	2/3	0.005

下载: 导出CSV

表 3 振动台试验加载工况

Table 3 Schemes of shaking table tests

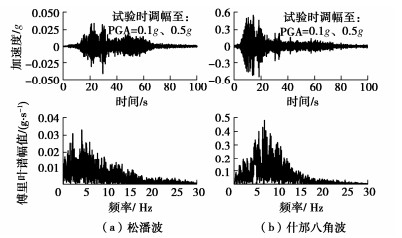
地震动	峰值加速度/g	工况	持时/s
松潘波	0.1	SP-1	100
松潘波	0.5	SP-2	100
什邡八角波	0.1	SF-1	100
什邡八角波	0.5	SF-2	100

下载: 导出CSV

参考文献(22)

[1]	ZHUANG H Y, HU Z H, WANG X J, et al. Seismic responses of a large underground structure in liquefied soils by FEM numerical modelling[J]. Bulletin of Earthquake Engineering, 2015, 13(12): 3645–3668. doi: 10.1007/s10518-015-9790-6
[2]	ELGAMAL A, YANG Z H, PARRA E, et al. Modeling of cyclic mobility in saturated cohesionless soils[J]. International Journal of Plasticity, 2003, 19(6): 883–905.
[3]	YANG Z H, ELGAMAL A, PARRA E. Computational model for cyclic mobility and associated shear deformation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1119–1127. doi: 10.1061/(ASCE)1090-0241(2003)129:12(1119)
[4]	KHOSHNOUDIAN F, SHAHROUR I. Numerical analysis of the seismic behavior of tunnels constructed in liquefiable soils[J]. Soils and Foundations, 2002, 42(6): 1–8. doi: 10.3208/sandf.42.6_1
[5]	BAO X H, XIA Z F, YE G L, et al. Numerical analysis on the seismic behavior of a large metro subway tunnel in liquefiable ground[J]. Tunnelling and Underground Space Technology, 2017, 66: 91–106. doi: 10.1016/j.tust.2017.04.005
[6]	王刚, 张建民, 魏星. 可液化土层中地下车站的地震反应分析[J]. 岩土工程学报, 2011, 33(10): 1623–1627. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14212.shtml WANG Gang, ZHANG Jian-min, WEI Xing. Seismic response analysis of a subway station in liquefiable soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1623–1627. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14212.shtml
[7]	王睿, 张建民. 可液化地基中单桩基础的三维数值分析方法及应用[J]. 岩土工程学报, 2015, 37(11): 1979–1985. doi: 10.11779/CJGE201511006 WANG Rui, ZHANG Jian-min. Three-dimensional elastic-plastic analysis method for piles in liquefiable ground[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 1979–1985. (in Chinese) doi: 10.11779/CJGE201511006
[8]	TROPEANO G, CHIARADONNA A, D'ONOFRIO A, et al. A numerical model for non-linear coupled analysis of the seismic response of liquefiable soils[J]. Computers and Geotechnics, 2019, 105: 211–227. doi: 10.1016/j.compgeo.2018.09.008
[9]	OLSON S M, MEI X, HASHASH Y M A. Nonlinear site response analysis with pore-water pressure generation for liquefaction triggering evaluation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(2): 04019128. doi: 10.1061/(ASCE)GT.1943-5606.0002191
[10]	FINN L. Practical studies of the seismic response of a rockfill dam[J]. Buddhist Christian Studies, 1993, 24: 89–100.
[11]	FINN W, YOGENDRAKUMAR M, YOSHIDA N. Comparative assessment of methods for dynamic effective stress analysis[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1989, 8: 330–339.
[12]	CHEN G X, WANG Y Z, ZHAO D F, et al. A new effective stress method for nonlinear site response analyses[J]. Earthquake Engineering & Structural Dynamics, 2021, 50(6): 1595–1611.
[13]	王彦臻, 赵丁凤, 陈国兴, 等. 一维场地地震反应非线性有效应力分析法及其验证[J]. 岩土工程学报, 2021, 43(3): 502–510. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18573.shtml WANG Yan-zhen, ZHAO Ding-feng, CHEN Guo-xing, et al. A new nonlinear effective stress method for one-dimensional seismic site response analysis and its validation[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 502–510. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18573.shtml
[14]	CHEN G X, CHEN S, ZUO X, et al. Shaking-table tests and numerical simulations on a subway structure in soft soil[J]. Soil Dynamics and Earthquake Engineering, 2015, 76: 13-28.
[15]	CHEN G X, CHEN S, QI C Z, et al. Shaking table tests on a three-arch type subway station structure in a liquefiable soil[J]. Bulletin of Earthquake Engineering, 2015, 13(6): 1675–1701.
[16]	王国波, 郝朋飞, 孙富学. 地铁车站结构端部效应影响范围研究[J]. 岩土工程学报, 2020, 42(8): 1435–1445. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18271.shtml WANG Guo-bo, HAO Peng-fei, SUN Fu-xue. Spatial influence scope of end wall of metro station structures[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1435–1445. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18271.shtml
[17]	陈国兴, 左熹, 王志华, 等. 可液化场地地铁车站结构地震破坏特性振动台试验研究[J]. 建筑结构学报, 2012, 33(1): 128–137. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201201017.htm CHEN Guo-xing, ZUO Xi, WANG Zhi-hua, et al. Shaking table test on seismic failure characteristics of subway station structure at liquefiable ground[J]. Journal of Building Structures, 2012, 33(1): 128–137. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201201017.htm
[18]	CHEN G X, ZHAO D F, CHEN W Y, et al. Excess pore-water pressure generation in cyclic undrained testing[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(7): 04019022.
[19]	DSSC. Abaqus/Standard User's Manual, ABAQUS 6.10 Documentation [CP/DK]. Providence, Rhode Island, 2010.
[20]	陈国兴, 王志华, 左熹, 等. 振动台试验叠层剪切型土箱的研制[J]. 岩土工程学报, 2010, 32(1): 89–97. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract11904.shtml CHEN Guo-xing, WANG Zhi-hua, ZUO Xi, et al. Development of laminar shear soil container for shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 89–97. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract11904.shtml
[21]	王军, 蔡袁强, 李校兵. 循环荷载作用下超固结软黏土软化-孔压模型研究[J]. 岩土力学, 2008, 29(12): 3217–3222. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200812012.htm WANG Jun, CAI Yuan-qiang, LI Xiao-bing. Cyclic softening-pore pressure generation model for overconsolidated clay under cyclic loading[J]. Rock and Soil Mechanics, 2008, 29(12): 3217–3222. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200812012.htm
[22]	邱贤阳, 史秀志, 周健, 等. 基于HHT能量谱的高精度雷管短微差爆破降振效果分析[J]. 爆炸与冲击, 2017, 37(1): 107–113. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201701015.htm QIU Xian-yang, SHI Xiu-zhi, ZHOU Jian, et al. On vibration reduction effect of short millisecond blasting by high-precision detonator based on HHT energy spectrum[J]. Explosion and Shock Waves, 2017, 37(1): 107–113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201701015.htm

施引文献(4)

期刊类型引用(1)

王昌盛，林建好，杨艳，徐家云. 土-结构相互作用体系实模态近似解耦及地震响应分析. 振动与冲击. 2025(05): 184-190 .

百度学术

其他类型引用(3)

资源附件(0)

图(8) / 表(3)

计量

文章访问数: 232
HTML全文浏览量: 32
PDF下载量: 200
被引次数: 4

0. 引言
1. 顶管施工中的模型转化
2. 顶管施工中松动土压力计算
2.1 基本假设
2.2 水平微分土条受力状态
2.3 水平微分土条的平衡微分方程
2.4 滑移面主应力轴偏转角的确定
2.5 平衡方程的边界条件
3. 模型验证及参数分析
3.1 模型的对比验证
3.2 松动土压力渐进发展过程
3.3 剪胀角的影响
3.4 内摩擦角的影响
4. 结论

0. 引言
1. 顶管施工中的模型转化
2. 顶管施工中松动土压力计算
2.1 基本假设
2.2 水平微分土条受力状态
2.3 水平微分土条的平衡微分方程
2.4 滑移面主应力轴偏转角的确定
2.5 平衡方程的边界条件
3. 模型验证及参数分析
3.1 模型的对比验证
3.2 松动土压力渐进发展过程
3.3 剪胀角的影响
3.4 内摩擦角的影响
4. 结论

参考文献(22)

施引文献(4)

资源附件(0)

土–地下结构相互作用的三维弱耦合有效应力分析法 English Version

作者简介: 赵凯(1982—)，男，教授，博士，主要从事岩土地震工程研究。E-mail: zhaokai@njtech.edu.cn

通讯作者: 王彦臻, E-mail: soledadwang@163.com

计量

出版历程

Three-dimensional loosely coupled effective stress method for seismic soil-structure interactions

0. 引言

1. 顶管施工中的模型转化

2. 顶管施工中松动土压力计算

2.1 基本假设

2.2 水平微分土条受力状态

2.3 水平微分土条的平衡微分方程

2.4 滑移面主应力轴偏转角的确定

2.5 平衡方程的边界条件

3. 模型验证及参数分析

3.1 模型的对比验证

3.2 松动土压力渐进发展过程

3.3 剪胀角的影响

3.4 内摩擦角的影响

4. 结论

期刊类型引用(1)

其他类型引用(3)

计量

出版历程

目录

0. 引言

1. 顶管施工中的模型转化

2. 顶管施工中松动土压力计算

2.1 基本假设

2.2 水平微分土条受力状态

2.3 水平微分土条的平衡微分方程

2.4 滑移面主应力轴偏转角的确定

2.5 平衡方程的边界条件

3. 模型验证及参数分析

3.1 模型的对比验证

3.2 松动土压力渐进发展过程

3.3 剪胀角的影响

3.4 内摩擦角的影响

4. 结论

作者简介:
赵凯(1982—)，男，教授，博士，主要从事岩土地震工程研究。E-mail: zhaokai@njtech.edu.cn

通讯作者:
王彦臻, E-mail: soledadwang@163.com