基于分形级配方程的堆石料颗粒破碎SBG模型

丁林楠; 李国英

doi:10.11779/CJGE202202007

基于分形级配方程的堆石料颗粒破碎SBG模型 English Version

丁林楠^{1, 2,},
李国英^{1, 2, ,}

1.
南京水利科学研究院岩土工程研究所, 江苏南京 210024
2.
水利部土石坝破坏机理与防控技术重点实验室, 江苏南京 210024

详细信息

作者简介:
丁林楠(1994—)，男，博士研究生，主要从事粗粒土力学特性方面的研究工作。E-mail: LinnanDing@163.com

通讯作者:
李国英，E-mail: gyli@nhri.cn

中图分类号: TU43
计量
- 文章访问数: 227
- HTML全文浏览量: 25
- PDF下载量: 112
出版历程
- 收稿日期: 2021-04-04
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-01-31

SBG model for particle breakage of rockfills based on fractal gradation equation

DING Lin-nan^{1, 2,},
LI Guo-ying^{1, 2, ,}

1.
Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, China
2.
Key Laboratory of Failure Mechanism and Safety Control Techniques of Earth-Rock Dam of the Ministry of Water Resources, Nanjing 210029, China

摘要

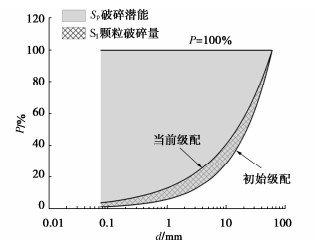
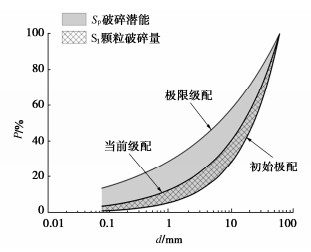
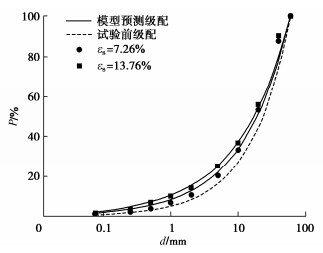
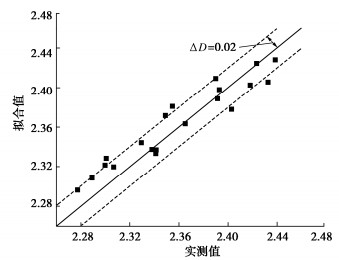
摘要: 准确预测堆石料在受剪过程中颗粒的破碎率以及相应的级配变化，是揭示堆石料在复杂应力状态下强度、渗透、变形等特性的基础。基于分形级配方程，建立了一个实现“应力应变—破碎指标—级配分布（SBG）”转换的模型。引入Einav破碎指标B_E作为衡量颗粒破碎率的指标，对分形级配方程进行变形和积分，推导了颗粒破碎率B_E和分形维数D的数学转换，即“破碎指标—级配分布”的转换。对已有的三轴剪切试验数据进行分析，提出一个可以定量表示颗粒破碎率随剪应变和平均正应力变化的数学模型，模型共有3个参数a，b，c，参数b与土体的临界状态有关，根据临界剪应变可以直接确定。对两组不同的试验数据进行拟合，发现模型预测值与试验值具有较高的吻合度，实现“应力应变—破碎指标”的转换。将以上两种转变联立，成功预测了不同剪应变及平均正应力下堆石料的级配变化。
- 堆石料 /
- 颗粒破碎 /
- 破碎指标 /
- 级配方程
Abstract: Accurately predicting the particle breakage rate and the corresponding gradation changes of rockfills in shearing process is beneficial to revealing their characteristics such as strength, penetration and deformation under complex stress conditions. Based on the fractal gradation equation, a model for realizing the conversion of "stress strain-breakage index-gradation distribution (SBG)" is established. The breakage index B_E is used to measure the particle breakage rate. The fractal gradation equation is deformed and integrated, and the mathematical conversion of particle breakage rate B_E and fractal dimension D is derived, that is, the conversion of "breakage index-gradation distribution". The existing triaxial shear test data are analyzed, and a mathematical model that can quantitatively express the change of particle breakage rate with shear strain and average normal stress is proposed. The model has three parameters a, b and c. The parameter b is related to the critical state of soils and can be directly determined according to the critical shear strain. Two sets of different test data are fitted, and it is found that the predicted values by the model has a high degree of agreement with the test ones, and the conversion of "stress strain-breakage index" is realized. Combining the above two conversions, the gradation changes of rockfills under different shear strains and average normal stresses are successfully predicted.
- rockfill /
- particle breakage /
- breakage index /
- gradation equation

HTML全文

0. 引言

基础频域阻抗是土结动力相互作用研究中描述基础的一种重要方法。目前,关于基础阻抗函数解析解已有大量的研究成果,如：崔春义等^[1]利用桩–土耦合条件推导得到管桩基础的动力阻抗解析解；杨林青等^[2]求解了任意形状基础的频域动力阻抗。频域阻抗只适用于结构线性响应的频域求解,无法用于非线性响应分析和混合试验要求的时域逐步积分求解。为了将该频域阻抗用于土–结相互作用系统动力时程分析,需要将其转换为时域阻抗模型。目前常用的拟合方法有离散有理近似^[3]和连续有理近似函数^[4]两种,有理近似函数的稳定性与精度决定了动力时域分析的稳定性与精度。采用离散时间有理近似函数对基础频域阻抗进行准确拟合主要取决于参数识别方法的有效性。Paronesso等^[5]采用平衡逼近的方法推导了相互作用力与位移的差分方程,并将其表示为离散时间的有理近似函数；Wolf等^[6]、Safak等^[7]、杜修力等^[8]分别利用有理近似函数拟合了基础阻抗,并给出了后验的函数稳定性条件为函数极点的模小于1；Laudon等^[9]采用了Safak等^[7]的方法拟合了频域阻抗,指出该方法虽然可以保证拟合精度,但存在失稳问题；Gash等^[10]将离散时间函数与Newmark-β法结合,评价了滤波器–积分器所需的稳定条件；Sung等^[11]采用最小二乘法对阻抗进行了拟合,分析了土结动力相互作用对结构动力响应的影响。以上研究表明,大多频域阻抗的最优有理近似存在失稳问题,需要一个有效的方法保证识别函数的稳定性。赵建锋等^[12]利用罚函数给失稳的参数组合增加惩罚值,保证了识别程序输出结果的稳定性；赵密等^[3]先在S域中利用连续时间有理近似函数与罚函数法拟合基础阻抗,再通过双线性变换得到Z域的离散时间函数,保证了函数的稳定性。

离散时间有理近似函数的参数识别方法主要存在如下问题：部分方法未对函数的稳定性进行判断,可能导致时域分析失稳；另一部分方法采用后验方式判断辨识函数的稳定性,虽然可以较好地确保稳定性和精度,但由于辨识参数在整个实数域以及参数稳定性判别的复杂性,参数辨识效率较低,在实际中（特别是多自由度基础系统）难以应用。本文从控制理论角度给出了完整的稳定约束条件,并据此提出了一种高效稳定的离散时间有理近似函数参数识别方法。

1. 离散时间有理近似的稳定性

采用解析方法或数值方法求解基础频域动力阻抗^[4]是土结动力相互作用研究中基础的重要描述方法。根据输入与输出物理量不同,频域阻抗函数可以分为两种：广义位移作为输入,广义力作为输出的动力刚度阻抗函数S(ω)；广义力作为输入,广义位移作为输出的动力柔度阻抗函数F(ω)。因此,在频域中基础与无限土体之间力与位移的关系可以表示为

$f (ω) = S (ω) u (ω)$ ,

(1)

式中,f(ω)为广义力,u(ω)为广义位移,S(ω)为基础频域阻抗函数,其可以表示为频率的函数：

$S (ω) = S_{0} [K (ω) + i C (ω)]$ 。

(2)

式中 ω为外荷载频率；S₀为静刚度；i= $\sqrt{(- 1)}$ 为虚数单位；K(ω),C(ω)分别为与频率相关的刚度系数和阻尼系数。采用离散时间有理近似作为时域模型时,其对应的基础频域阻抗S(ω)可描述为

$S (ω) \approx S (z) = S_{0} \frac{b_{0} + b_{1} z^{- 1} + \dots + b_{M} z^{- M}}{1 + a_{1} z^{- 1} + \dots + a_{N} z^{- N}}$ 。

(3)

式中 b_j和a_j分别为分母和分子多项式的待定系数,且均为实数；z=e^iωΔt为Z变换的频域符号,Δt为离散时间步长；M,N分别为分子与分母多项式的阶数,通常根据基础频域阻抗复杂程度选择合适的阶次即可,频域阻抗越复杂需要的阶次越高。该模型的参数识别过程中只需用到离散的频域阻抗值,在采用式（3）进行拟合时,无需K(ω)与C(ω)的具体表达形式,而得到式（3）所示模型后,可以用不同时域模型对其进行等效。为了保证时域模型的稳定性,需要首先保证式（3）所示频域模型的稳定性。根据系统稳定性理论^[13],离散时间有理近似函数的稳定性可由其极点确定：当且仅当其极点全部位于单位圆内,即所有极点的模均小于1时,模型稳定。假设形如式（3）的离散时间有理近似函数的极点为z_j,则其稳定条件可表示为

$| z_{j} | < 1$ 。

(4)

以一个3×3群桩模型为例,假设地基土分为3层,模型如图1所示。其中桩直径d=1 m,桩长L=6 m,土层厚度h=2 m,土泊松比 $ν$ =0.35,土阻尼比β=0.05,桩距S=5 m,桩土密度比 $ρ_{p} / ρ_{s}$ =1.3,混凝土弹性模量E_p=30000 MPa,3层土的桩土弹模比E_p/E_s1=1000,E_p/E_s2=2000、E_p/E_s3=500。土体阻抗由文献[14]的方法计算得到,群桩阻抗由文献[15]的方法计算得到。采用时域递归算法^[12]对其进行描述,假设基础–土界面之间的相互作用力为f,则其可采用前M个时刻的界面位移和前N个时刻的相互作用力描述,其时域力学模型如图2,力学方程如下所示：

图 1 3×3群桩基础模型

Figure 1. Model for foundation with 3×3 pile groups

下载: 全尺寸图片幻灯片

图 2 时域递归模型计算流程

Figure 2. Computational process of time-domain recursive model

下载: 全尺寸图片幻灯片

$f (t) = \sum_{i = 0}^{M} b_{i} u (t - i Δ t) - \sum_{i = 1}^{N} a_{i} f (t - i Δ t)$ 。

(5)

并采用文献[12]给出的修正有理近似函数辨识群桩阻抗进行无约束识别,计算结果如图3所示。由图可知,虽然在频域内有理函数可以精确地与基础阻抗吻合,但由于拟合过程中未考虑函数稳定性问题,因此导致了时程分析发散。因此,对于离散时间有理近似函数,仅令其函数值在频域内精确地拟合基础阻抗函数是不够的,还需要确保时域分析的收敛性才具有应用价值。

图 3 3×3群桩动力响应

Figure 3. Dynamic responses of foundation with 3×3 pile groups

下载: 全尺寸图片幻灯片

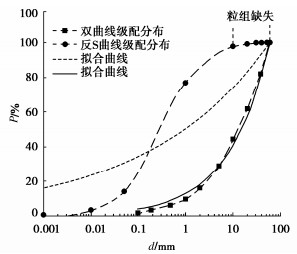
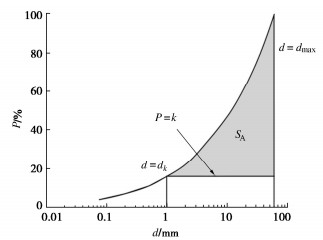
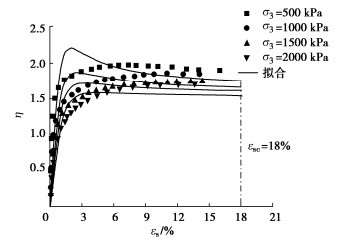
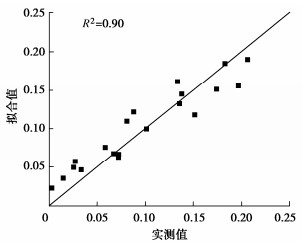
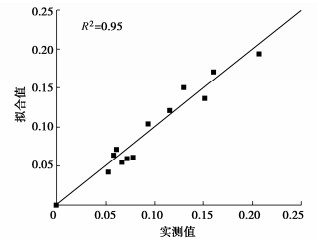
2. 稳定参数识别方法

为了确保基础时域模型的收敛性,现有识别方法先满足频域响应精度,而后进行稳定性判别,当发现不稳定时重新识别参数,直到获得同时满足精度和稳定性条件的参数后停止识别。该方法的缺陷在于无法识别过程和结果不可控。如果预先确定满足稳定性的参数条件,然后在该范围内去寻找满足精度要求的参数将会更有效。

2.1 稳定参数约束条件

由式（4）可知,离散时间有理近似函数稳定的充分必要条件为所有极点的模均小于1,但由式（3）可知,只有该模型的所有参数已知才能得到其根,这就是现有方法无法提前确定稳定参数范围的原因所在。从控制系统角度来看,式（3）所示的多阶系统由多个一阶和二阶系统组成。因此,形如式（3）的离散时间有理近似函数,可用下式等效：

$S (ω) = \frac{\sum_{j = 0}^{m} b_{j} z^{- j}}{\prod_{j = 1}^{l} (1 + x_{1 j} z^{- 1} + x_{2 j} z^{- 2}) \times \prod_{j = 1}^{n - 2 l} (1 + x_{0 j} z^{- 1})}$ ,

(6)

式中,x_1j和x_2j为二阶系统系数,x_0j为一阶系统系数,l为二阶系统总数。

当式（3）等效为式（6）后,辨识多阶系统参数变为了辨识一阶和二阶系统参数。由一阶、二阶系统的根可得到其解析式,也就可以根据式（4）限制（6）中参数的取值范围了。式（6）每个一阶与二阶项的根为

$z_{j} = {\begin{matrix} \frac{- x_{1 j} \pm \sqrt{x_{1 j}^{2} - 4 x_{2 j}}}{2} \\ - x_{0 j} \end{matrix}$ 。

(7)

式中,一阶项根x_0j的取值范围可以简单地确定：

$- 1 < x_{0 j} < 1$ 。

(8)

而二阶项的根需分为实数根与复数根。由于未得到系数x的值时,不能判断一阶和二阶系统个数。因此,当n为偶数时,假设一阶项的个数为0,即n=2l；当n为奇数时,假设一阶项的个数为1,即n-1=2l。而当求出未知系数x后,若二阶项的根为实数根,则可自动变为两个一阶项。因此,二阶系统的参数范围分为实极点和复极点分别讨论。

（1）复极点

由于根为复数根,因此x_1j²-4x_2j<0,式（7）的二阶项根改写为

$z = \frac{- x_{1 j} \pm (\sqrt{4 x_{2 j} - x_{1 j}^{2}}) i}{2}$ 。

(9)

而函数稳定要求极点的模小于1,因此存在：

$\begin{array}{l} \frac{x_{1 j}^{2}}{4} + \frac{4 x_{2 j} - x_{1 j}^{2}}{4} < 1, \\ x_{1 j}^{2} - 4 x_{2 j} < 0 。 \end{array}}$

(10)

进一步化简得到x的取值范围：

$\begin{array}{l} 0 \leq x_{2 j} < 1, \\ - 2 \sqrt{x_{2 j}} \leq x_{1 j} \leq 2 \sqrt{x_{2 j}} 。 \end{array}}$

(11)

由式（11）可知,x_1j的取值范围受x_2j的影响,需要非线性约束,其取值范围如图4所示阴影范围。

图 4 复数根时稳定参数界限

Figure 4. Stability parameter boundary for complex roots

下载: 全尺寸图片幻灯片

（2）实极点

当极点为实数时,极点的模小于1的条件为

$\begin{array}{l} | \frac{- x_{1 j} \pm \sqrt{x_{1 j}^{2} - 4 x_{2 j}}}{2} | < 1, \\ x_{1 j}^{2} - 4 x_{2 j} \geq 0 。 \end{array}}$

(12)

将式（12）进一步化简可得

$\begin{array}{l} x_{1 j} - 2 < \sqrt{x_{1 j}^{2} - 4 x_{2 j}} < 2 + x_{1 j}, \\ - x_{1 j} - 2 < \sqrt{x_{1 j}^{2} - 4 x_{2 j}} < 2 - x_{1 j} 。 \end{array}}$

(13)

而由于根为实数根,在实数范围内实数的偶次平方根必然为非负数,因此式（13）不等式组的右端需大于0,可以得到x_1j的取值范围：

$- 2 < x_{1 j} < 2$ 。

(14)

进而根据式（14）可以判断出式（13）的左端必然成立,将不等式组的左端去掉并对两侧取平方可得

$\begin{array}{l} x_{1 j} - 1 < x_{2 j}, \\ - x_{1 j} - 1 < x_{2 j}, \\ x_{1 j}^{2} - 4 x_{2 j} \geq 0, \\ - 2 < x_{2 j} < 2 。 \end{array}}$

(15)

式（15）的不等式组需要取交集以保证式（13）必然成立,则取值范围可简化为式（16）,为便于理解,取值范围可见图5,图中深色填充部分为式（16）所示取值范围,两条交叉直线分别为x_2j=x_1j-1和x_2j=-x_1j-1,抛物线为4x_2j=x_1j²。

图 5 实数根时稳定参数界限

Figure 5. Stability parameter boundary for real roots

下载: 全尺寸图片幻灯片

$\begin{matrix} x_{1 j} - 1 < x_{2 j} \leq \frac{x_{1 j}^{2}}{4} & 0 \leq x_{1 j} < 2, \\ - x_{1 j} - 1 < x_{2 j} < \frac{x_{1 j}^{2}}{4} & - 2 < x_{1 j} < 0 。 \end{matrix}}$

(16)

（3）稳定参数界限

观察式（11）,（16）和图4,5可以发现,当共轭根分别为复数与实数时,参数x的取值范围以曲线为4x_2j=x_1j²界线分为上下两部分。因此,可将两部分合并,则式（6）所示模型的稳定参数界限如式（17）,其参数范围如图6所示,图中浅色填充部分为复数根的取值范围,深色填充部分为实数根的取值范围。

图 6 稳定参数界限

Figure 6. Boundary of stable parameters

下载: 全尺寸图片幻灯片

$\begin{array}{l} - 2 < x_{1 j} < 2, \\ - 1 < x_{2 j} < 1, \\ x_{1 j} - 1 < x_{2 j} (0 \leq x_{1 j} < 2), \\ - x_{1 j} - 1 < x_{2 j} (- 2 < x_{1 j} < 0) 。 \end{array}}$

(17)

而当拟合动力柔度频响函数时,则需要保证函数零点的模小于1,此时可将分子提取b₀,然后再采用部分分式的方法得到相同的取值界限。

2.2 参数识别

得到了新的有理近似函数形式及其稳定参数取值边界后,如何通过参数识别确保最优的精度是参数寻优问题。优化算法可以分为全局优化算法和局部优化算法,常见的全局优化算法有进化算法、遗传算法、粒子群优化算法等等,而常见的局部算法有单纯形法、序列二次规划算法等等。

本文以Wang等^[16]将遗传算法与单纯形法结合形成的混合算法为基础,采用序列二次规划算法(SQP算法)代替单纯形法,形成遗传–序列二次规划算法,用于求解有理近似函数的待定系数。遗传算法作为全局优化算法,不需要给出合理的初始值,其从多个任意初始值开始寻优,搜索范围大,利于全局择优。而SQP算法作为局部优化算法可以从遗传算法得到的全局最优解中选择初始值,避免了因初值选择不适当而造成的拟合效果不佳。此外,采用SQP算法代替单纯形法可以将无约束优化问题变为有约束优化问题,通过约束方程人为地规定参数的取值范围,更适用于本文建立的稳定参数边界。具体的计算流程如图7所示,预先设定有理近似函数阶次和预期误差（比如均方根小于10%）,当辨识参数对应阻抗函数精度满足预期误差条件时跳出循环；当辨识参数对应精度无法满足预期误差条件时,设定连续10次循环每两次输出结果精度之差均小于0.1%时跳出循环,增加有理近似函数阶次,重复前面的循环,直至辨识精度满足预期误差条件。

图 7 参数识别流程

Figure 7. Flow chart of parameter identification

下载: 全尺寸图片幻灯片

3. 数值算例验证

为了验证上述方法的有效性,本节分别采用3组复杂程度不同的基础阻抗进行对比研究。

（1）算例1：3×3群桩基础

对图2所示的3×3群桩基础的频域阻抗,本文采用文献[12]提出的修正离散时间有理近似函数进行辨识,辨识所用目标函数如下式所示：

$f = \sum_{Ω} ({| \frac{R (Ω) - S (Ω)}{S_{0}} |}^{2})$ ,

(18)

式中, $Ω$ 为外荷载频率ω或其无量纲频率a₀,视函数形式而定,但计算过程中需保持量纲一致,R( $Ω$ )为离散时间有理近似函数,S( $Ω$ )为频域阻抗函数。

为了综合验证本文方法在稳定性、精度和计算效率,对图3所示无约束识别失稳案例采用罚函数法^[12]和本文方法进行对比分析,分别对有理函数m=n=3/4/5/6/7阶进行了分析。为了对辨识模型精度进行定量评价,取频域函数精确解与识别函数之差绝对值积分面积占精确阻抗绝对值积分面积的比值作为误差评价指标,其计算方法如下式所示,其中虚部和实部误差权重均定义为0.5。

$\begin{matrix} E = (\frac{\int_{0}^{ω_{N}} | R {(ω)}_{Re} - S {(ω)}_{Re} | d ω}{\int_{0}^{ω_{N}} | S {(ω)}_{Re} | d ω} \times 0.5 + \\ \frac{\int_{0}^{ω_{N}} | R {(ω)}_{Im} - S {(ω)}_{Im} | d ω}{\int_{0}^{ω_{N}} | S {(ω)}_{Im} | d ω} \times 0.5) \times 100 % \end{matrix}$ 。

(19)

式中 E表示识别模型误差,由实部与虚部的权重各一半；R(ω)_Re,S(ω)_Re,R(ω)_Im和S(ω)_Im分别表示有理函数与阻抗精确值的实部与虚部；ω_N表示频率最大值。辨识结果如表1和图8所示。

表 1 3×3群桩基础辨识效率

Table 1. Identification efficiency of foundation with 3×3 pile groups

阶次	3	4	5	6	7
本文方法/s	1.82	2.24	2.24	2.86	2.92
罚函数法/s	3.53	4.67	8.41	16.17	33.67

下载: 导出CSV

| 显示表格

图 8 6阶有理函数拟合结果

Figure 8. Identification results of six-order rational function

下载: 全尺寸图片幻灯片

由图8（a）,8（b）可以看到,两种方法辨识所得模型均可较精确地描述频域阻抗,采用式（19）计算所得误差小于1%,证明两种方法拥有很高精度。由图8（c）,8（d）可以看到,将EL-centro波作为地震动输入,两种方法均可保证时程计算的稳定性,且时程曲线一致。由表1可知,在计算效率方面上,本文方法明显优于罚函数法。两种方法分别采用3到7阶函数对基础阻抗进行识别,本文方法所需时间均在3 s以内,且效率损失随函数阶数增加并不明显,而罚函数法所需时间在3～34 s,为本文方法的2倍到10倍,且拟合用时随阶数增加几乎成倍增长。原因在于：第一,本文方法给定了参数取值区间,而罚函数法的参数取值范围为整个实数域,取值范围的增大造成了计算效率的降低；第二,本文方法取值区间内可保证函数稳定,但罚函数法需要求解高阶多项式判断稳定性,进一步降低了计算效率。

（2）算例2：5×5群桩基础

为验证阶数对于辨识精度的影响,分别采用不同阶数的有理近似函数对图9和图10所示5×5群桩基础的阻抗进行拟合,其阻抗由文献[17]的图6所得。图中d为桩基础直径,S为桩间距,桩中心距筏板边缘长0.5S。由于此基础动力阻抗对频率变化剧烈,因此利用离散时间的有理近似函数拟合具有挑战性。本文采用式（3）给出的有理函数,取Δt=0.02 s,阶数m=n=3～7阶进行拟合。函数拟合精度采用式（19）进行判断,结果如图10和表2。

图 9 5×5群桩基础模型

Figure 9. Model for foundation with 5×5 pile groups

下载: 全尺寸图片幻灯片

图 10 5×5群桩基础不同阶次拟合精度

Figure 10. Identification accuracy of foundation with 5×5 pile groups in different orders

下载: 全尺寸图片幻灯片

表 2 5×5群桩基础拟合精度与效率

Table 2. Identification accuracy and efficiency of foundation with 5×5 pile groups

阶次	3	4	5	6	7
误差/%	18.80	18.23	13.02	2.03	1.97
时间/s	9.02	8.15	9.81	13.74	16.46

下载: 导出CSV

| 显示表格

由表2和图10可以看到,采用不同阶次的有理函数辨识时,辨识精度随阶数增加逐渐提高,当采用3阶函数拟合时,效果较差,整体误差约有19%,难以拟合复杂阻抗。但当阶数增加到6阶时,整体误差降低到2%,此时有理函数可较精确地吻合频域阻抗。从辨识效率来看,3阶函数时拟合用时约为9 s,7阶时约为16 s,增加了仅一倍,可以看出拟合效率的损失随阶次增加较低。采用同阶次的罚函数法进行拟合由于计算效率过低未得到有效结果,证明本文方法更适用于采用高阶次函数对复杂阻抗函数进行准确辨识。

（3）算例3：水平运动的圆形基础

对于随频率变化更为复杂的阻抗函数,以文献[7]中图7的圆形基础水平运动动力刚度函数为例。基础模型如图11所示,图中Pe^iωΔt和ue^iωΔt分别为基础受到的外荷载与产生的位移。基础参数为：半径r=10 m,剪切波速V_s=100 m/s,土体泊松比 $ν$ =1/3,土体阻尼比 $ζ$ =0.05,土层厚度H=2 m。拟合阶数取m=n=3/5/7/9/11阶,拟合精度采用式（19）进行判断,结果如图12与表3所示。

图 11 水平运动的圆形基础

Figure 11. Circular foundation under horizontal motion

下载: 全尺寸图片幻灯片

图 12 圆形基础不同阶次拟合精度

Figure 12. Identification accuracy of circular foundation in different orders

下载: 全尺寸图片幻灯片

表 3 圆形基础拟合精度与效率

Table 3. Identification accuracy and efficiency of circular foundation

阶次	3	5	7	9	11
误差/%	16.82	12.29	7.49	6.74	6.62
时间/s	4.46	4.19	5.79	7.12	8.66

下载: 导出CSV

| 显示表格

对于此圆形基础阻抗,罚函数法仍无法辨识出有效结果,而本文方法结果如表3与图12所示。由表3可知,随有理函数阶次增加,拟合用时逐渐增加,而拟合精度也逐渐提高,但总体用时低于10 s,误差可降低到7%,通过图12的不同阶次对比可知：增加阶次有利于提高阻函数拟合精度,在达到7阶后,增加阶次对精度提高不明显,此时已可以较好的满足应用需求。

4. 结论

针对基础频响离散时间有理近似函数的参数识别难以同时保证稳定性、精度及计算效率的问题,本文提出了时域绝对稳定的离散有理近似函数参数识别方法。采用不同基础阻抗函数,对本文方法和罚函数拟合方法就稳定性、精度及计算效率等方面进行了对比分析,验证了本文方法的有效性与优势。

（1）从线性系统理论角度将基础阻抗离散有理近似函数看成一阶与二阶系统的组合,并根据其根的稳定条件建立了被辨识参数的稳定界限。据此,采用遗传–序列二次规划算法建立了时域稳定的参数识别方法,保证了识别函数时域模型的绝对稳定性。

（2）对单自由度基础阻抗对比仿真表明,本文方法与既有方法拥有同等精度,但计算效率明显优于既有算法。对于简单阻抗函数,本文方法拟合用时均低于3 s,为同等精度既有方法的10%～50%；对于不同的复杂函数,本文方法用时也均低于20 s,提高了多自由度阻抗函数识别的适用性。

（3）通过对复杂基础阻抗的辨识仿真表明,增加有理函数阶次有利于提高拟合精度,但过高的阶次对提高精度不明显。根据本文仿真结果,7阶有理近似函数能比较好的描述复杂基础阻抗。

（4）本文基于单输入单输出控制理论建立了单自由度基础阻抗的时域模型参数识别方法,对于多自由度体系,动力分析方法与有理近似函数特性相互耦合,其稳定条件更为复杂,将在后续工作中开展进一步研究。

图 1 不同堆石料的拟合结果

Figure 1. Fitting results of different rockfills

下载: 全尺寸图片幻灯片

图 2 不同形状级配的拟合

Figure 2. Fitting of different shape gradations

下载: 全尺寸图片幻灯片

图 3 破碎指标B_r示意图

Figure 3. Diagram of breakage index B_r

下载: 全尺寸图片幻灯片

图 4 破碎指标B_E示意图

Figure 4. Diagram of breakage index B_E

下载: 全尺寸图片幻灯片

图 5 级配面积示意图

Figure 5. Diagram of gradation area

下载: 全尺寸图片幻灯片

图 6 应力比η与剪应变ε_s的关系

Figure 6. Test data and fitting curves of η and ε_s

下载: 全尺寸图片幻灯片

图 7 B_E的实测值与拟合值

Figure 7. Measured and fitting data of B_E

下载: 全尺寸图片幻灯片

图 8 破碎指标B_E的实测值与拟合值

Figure 8. Measured and fitting data of breakage indicator B_E

下载: 全尺寸图片幻灯片

图 9 模型预测的级配与试验级配

Figure 9. Gradation curves from test and prediction

下载: 全尺寸图片幻灯片

图 10 分形维数D的实测值与拟合值

Figure 10. Measured and fitting data of fractal dimension D

下载: 全尺寸图片幻灯片

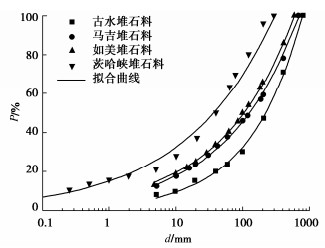
表 1 不同堆石料的拟合参数

Table 1 Fitting parameters of different rockfills

土体类型	d_max/mm	D	R²
古水堆石料	800	2.46	0.99
马吉堆石料	700	2.59	0.99
如美堆石料	600	2.60	0.99
茨哈峡堆石料	300	2.67	0.98

下载: 导出CSV

表 2 三轴剪切过程中的颗粒破碎试验数据^[19]

Table 2 Test data of particle breakage during triaxial shearing^[19]

围压/kPa	剪应变ε_s/%	平均正应力p/kPa	D	B_E/%
0	0	0	2.2742	0
500	1.87	1242	2.2777	0.34
500	4.56	1422	2.3070	3.34
500	8.44	1494	2.3416	7.21
500	12.49	1469	2.3378	6.77
500	16.01	1420	2.3418	7.24
1000	1.75	2046	2.2891	1.48
1000	4.60	2343	2.3294	5.80
1000	7.20	2552	2.3657	10.16
1000	10.66	2534	2.3490	8.09
1000	15.19	2621	2.4026	15.14
1500	1.90	2760	2.3000	2.60
1500	7.34	3504	2.3913	13.55
1500	9.31	3596	2.3929	13.78
1500	12.47	3543	2.4180	17.40
1500	14.35	3602	2.4325	19.66
2000	1.85	3336	2.3009	2.70
2000	4.55	4064	2.3549	8.81
2000	7.26	4484	2.3901	13.39
2000	10.75	4653	2.4235	18.25
2000	13.76	4619	2.4386	20.63

下载: 导出CSV

表 3 颗粒破碎试验数据^[27]

Table 3 Test data of particle breakage^[27]

围压/kPa	剪应变ε_s/%	平均正应力p/kPa	B_E/%
0	0	0	0
200	4.41	570	10.6
200	9.95	580	14.4
200	13.40	560	15.6
500	3.37	1140	11.6
500	7.53	1300	18.7
500	14.30	1320	23.1
1000	2.60	1800	12.2
1000	8.56	2370	26.0
1000	15.20	2480	32.1
1500	1.63	2160	13.2
1500	5.34	3010	30.2
1500	16.30	3570	41.4

下载: 导出CSV

参考文献(27)

[1]	贾宇峰, 王丙申, 迟世春. 堆石料剪切过程中的颗粒破碎研究[J]. 岩土工程学报, 2015, 37(9): 1692–1697. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509024.htm (JIA Yu-feng, WANG Bing-shen, CHI Shi-chun. Particle breakage of rockfill during triaxial tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1692–1697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509024.htm
[2]	TAPIAS M, ALONSO E E, GILI J. A particle model for rockfill behaviour[J]. Géotechnique, 2015, 65(12): 975–994. doi: 10.1680/jgeot.14.P.170
[3]	XIAO Y, LIU H L. Elastoplastic constitutive model for rockfill materials considering particle breakage[J]. International Journal of Geomechanics, 2017, 17(1): 04016041. doi: 10.1061/(ASCE)GM.1943-5622.0000681
[4]	XIAO Y, LIU H L, DING X M, et al. Influence of particle breakage on critical state line of rockfill material[J]. International Journal of Geomechanics, 2016, 16(1): 04015031. doi: 10.1061/(ASCE)GM.1943-5622.0000538
[5]	孔宪京, 刘京茂, 邹德高, 等. 紫坪铺面板坝堆石料颗粒破碎试验研究[J]. 岩土力学, 2014, 35(1): 35–40. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401004.htm KONG Xian-jing, LIU Jing-mao, ZOU De-gao, et al. Experimental study of particle breakage of Zipingpu rockfill material[J]. Rock and Soil Mechanics, 2014, 35(1): 35–40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401004.htm
[6]	MARSAL R J. Large scale testing of rockfill materials[J]. Journal of the Soil Mechanics and Foundations Division, 1967, 93(2): 27–43. doi: 10.1061/JSFEAQ.0000958
[7]	HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177–1192. doi: 10.1061/(ASCE)0733-9410(1985)111:10(1177)
[8]	EINAV I. Breakage mechanics-part I: theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(6): 1274–1297. doi: 10.1016/j.jmps.2006.11.003
[9]	郭万里, 朱俊高, 王青龙, 等. 基于级配方程的粗粒料级配演化预测模型[J]. 中南大学学报(自然科学版), 2018, 49(8): 2076–2082. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201808030.htm GUO Wan-li, ZHU Jun-gao, WANG Qing-long, et al. Mathematical model based on the gradation equation for predicting gradation evolution of coarse-grained soils[J]. Journal of Central South University (Science and Technology), 2018, 49(8): 2076–2082. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201808030.htm
[10]	陈生水, 傅中志, 韩华强, 等. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土工程学报, 2011, 33(10): 1489–1495. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201110003.htm CHEN Sheng-shui, FU Zhong-zhi, HAN Hua-qiang, et al. An elastoplastic model for rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1489–1495. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201110003.htm
[11]	张凌凯, 王睿, 张建民, 等. 考虑颗粒破碎效应的堆石料静动力本构模型[J]. 岩土力学, 2019, 40(7): 2547–2554, 2562. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907008.htm ZHANG Ling-kai, WANG Rui, ZHANG Jian-min, et al. A static and dynamic constitutive model of rockfill material considering particle breakage[J]. Rock and Soil Mechanics, 2019, 40(7): 2547–2554, 2562. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907008.htm
[12]	张季如, 张弼文, 胡泳, 等. 粒状岩土材料颗粒破碎演化规律的模型预测研究[J]. 岩石力学与工程学报, 2016, 35(9): 1898–1905. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201609019.htm ZHANG Ji-ru, ZHANG Bi-wen, HU Yong, et al. Predicting the particle breakage of granular geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(9): 1898–1905. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201609019.htm
[13]	童晨曦, 张升, 李希, 等. 基于Markov链的岩土材料颗粒破碎演化规律研究[J]. 岩土工程学报, 2015, 37(5): 870–877. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505017.htm TONG Chen-xi, ZHANG Sheng, LI Xi, et al. Evolution of geotechnical materials based on Markov chain considering particle crushing[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 870–877. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505017.htm
[14]	吴二鲁, 朱俊高, 黄维, 等. 三轴剪切过程中粗粒料颗粒破碎变化规律研究[J]. 岩土工程学报, 2020, 42(12): 2330–2335. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202012027.htm WU Er-lu, ZHU Jun-gao, HUANG Wei, et al. Evolution law of particle breakage of coarse-grained soil during triaxial shearing[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2330–2335. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202012027.htm
[15]	蔡正银, 李小梅, 关云飞, 等. 堆石料的颗粒破碎规律研究[J]. 岩土工程学报, 2016, 38(5): 923–929. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm CAI Zheng-yin, LI Xiao-mei, GUAN Yun-fei, et al. Particle breakage rules of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 923–929. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm
[16]	刘汉龙, 秦红玉, 高玉峰, 等. 堆石粗粒料颗粒破碎试验研究[J]. 岩土力学, 2005, 26(4): 562–566. doi: 10.3969/j.issn.1000-7598.2005.04.011 LIU Han-long, QIN Hong-yu, GAO Yu-feng, et al. Experimental study on particle breakage of rockfill and coarse aggregates[J]. Rock and Soil Mechanics, 2005, 26(4): 562–566. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.04.011
[17]	高玉峰, 张兵, 刘伟, 等. 堆石料颗粒破碎特征的大型三轴试验研究[J]. 岩土力学, 2009, 30(5): 1237–1240, 1246. doi: 10.3969/j.issn.1000-7598.2009.05.007 GAO Yu-feng, ZHANG Bing, LIU Wei, et al. Experimental study on particle breakage behavior of rockfills in large-scale triaxial tests[J]. Rock and Soil Mechanics, 2009, 30(5): 1237–1240, 1246. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.05.007
[18]	SALIM W, INDRARATNA B. A new elastoplastic constitutive model for coarse granular aggregates incorporating particle breakage[J]. Canadian Geotechnical Journal, 2004, 41(4): 657–671. doi: 10.1139/t04-025
[19]	JIA Y F, XU B, CHI S C, et al. Research on the particle breakage of rockfill materials during triaxial tests[J]. International Journal of Geomechanics, 2017, 17(10): 04017085. doi: 10.1061/(ASCE)GM.1943-5622.0000977
[20]	朱俊高, 郭万里, 王元龙, 等. 连续级配土的级配方程及其适用性研究[J]. 岩土工程学报, 2015, 37(10): 1931–1936. doi: 10.11779/CJGE201510023 ZHU Jun-gao, GUO Wan-li, WANG Yuan-long, et al. Equation for soil gradation curve and its applicability[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1931–1936. (in Chinese) doi: 10.11779/CJGE201510023
[21]	郭万里, 朱俊高, 钱彬, 等. 粗粒土的颗粒破碎演化模型及其试验验证[J]. 岩土力学, 2019, 40(3): 1023–1029. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903022.htm GUO Wan-li, ZHU Jun-gao, QIAN Bin, et al. Particle breakage evolution model of coarse-grained soil and its experimental verification[J]. Rock and Soil Mechanics, 2019, 40(3): 1023–1029. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903022.htm
[22]	TALBOT A N, RICHART F E. The strength of concrete-its relation to the cement, aggregates and water[J]. Illinois Univ Eng Exp Sta Bulletin, 1923, 137: 1–118.
[23]	YANG Z Y, JUO J L. Interpretation of sieve analysis data using the box-counting method for gravelly cobbles[J]. Canadian Geotechnical Journal, 2001, 38(6): 1201–1212. doi: 10.1139/t01-052
[24]	XIAO Y, LIU H L, YANG G, et al. A constitutive model for the state-dependent behaviors of rockfill material considering particle breakage[J]. Science China Technological Sciences, 2014, 57(8): 1636–1646. doi: 10.1007/s11431-014-5601-6
[25]	GUDEHUS G. A comprehensive constitutive equation for granular materials[J]. Soils and Foundations, 1996, 36(1): 1–12. doi: 10.3208/sandf.36.1
[26]	贾宇峰, 迟世春, 杨峻, 等. 粗粒土的破碎耗能计算及影响因素[J]. 岩土力学, 2009, 30(7): 1960–1966. doi: 10.3969/j.issn.1000-7598.2009.07.015 JIA Yu-feng, CHI Shi-chun, YANG Jun, et al. Measurement of breakage energy of coarse granular aggregates[J]. Rock and Soil Mechanics, 2009, 30(7): 1960–1966. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.07.015
[27]	郭万里. 粗粒土颗粒破碎演化规律及本构模型研究[D]. 南京: 河海大学, 2018. GUO Wan-li. Study on the Particle Breakage Evolution and Constitutive Model of Coarse-Grained Soils[D]. Nanjing: Hohai University, 2018. (in Chinese)

施引文献(9)

期刊类型引用(3)

1.	徐荣超，王怡博，张圣哲，孟凡震，李震，高梁，阎震. 轴向及环向变形加载控制方式对花岗岩力学及声发射特性影响的试验研究. 工程地质学报. 2025(01): 123-134 . 百度学术
2.	胡玉波，房敬年，徐荣超，郝小红，阎震，周文朋，李震. 饱水作用对白砂岩损伤破裂及声发射特性的影响. 长江科学院院报. 2024(11): 163-171 . 百度学术
3.	李泓颖，刘晓辉，郑钰，肖文根. 深埋锦屏大理岩渐进破坏过程中的特征能量分析. 岩石力学与工程学报. 2022(S2): 3229-3239 . 百度学术