0.   引言

深埋大断面顶管隧道在施工过程中，要不断经历安装—顶进—止退的循环交替，直至隧道贯通。在顶管顶进时，顶进力在平衡掌子面水土压力的同时，还要克服顶进过程中的各种摩阻力。倘若顶进力过大，会导致顶管机头前方的土压力超过被动土压力而产生地面隆起，破坏周围环境。达到预定进尺之后，在撤回油压千斤顶安装下一环之前，对管节进行止退。一方面如果止退力不足，可能会导致顶管机头回退，出现地面塌陷的危害；另一方面，管节环缝上的纵向力过小会导致环缝止水失效，同时还将导致环缝的抗剪刚度和抗弯刚度大幅减小，从而使得隧道不均匀沉降增加。因此，有必要研究顶管隧道横断面上受到的纵向压力的分布规律和消散规律，从而在施工过程中以及隧道贯通后，纵向力不满足使用要求时采取相应措施。

目前国内关于顶管纵向受力的研究以顶进力的计算^[1-2]、注浆减阻^[3-4]对周围环境的影响^[5]以及环向受力特性^[6-7]为主，较少关注顶管纵向受力。而盾构隧道中对盾构管片的纵向力研究较多^[8]，但因为两者施工工法的区别，纵向力的推导和计算也大不相同，应力松弛等因素^[9-10]并不适用于长期处于运动状态的顶管的纵向力研究。

通过计算求解顶管隧道受力与摩阻力、掌子面压力以及止退反力之间的数学方程，对顶管隧道断面纵向力随时间的变化关系进行初步的研究，并分析各因素对隧道断面纵向力时变规律的影响。

1.   顶管隧道断面纵向力推导

在顶管隧道施工期，顶进和止退交替进行。顶进时，油压千斤顶顶力通过顶环作用于管节，之后在管节间传递，因摩阻力作用，传递的纵向力逐渐减小，直至传递到顶管机头的纵向力与掌子面水土压力保持平衡。当顶进到预定进尺后，安装止退装置并收回千斤顶。因止退装置支撑刚度相对顶管后靠不足，且提供的止退反力小于主动施加的千斤顶顶力，会出现管节回弹的情况，而此时各处摩阻力开始反向并阻止管节回弹。因此纵向力由掌子面向止退装置逐渐减小，直至与止退力平衡。考虑到从顶进交替为止退之后，掌子面的被动土压力逐渐减小至静止土压力，则纵向力进一步减小。

1.1   纵向力空间分布

（1）顶进时纵向力空间分布

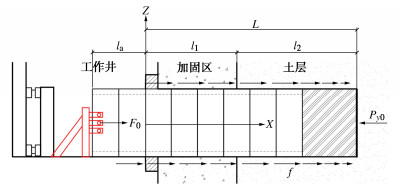
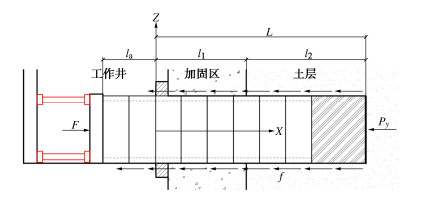
顶管顶进时的纵向受力图如图 1所示，已顶进里程为L，加固区长度为${l_1}$，土层内顶管长度为${l_2}$（包括顶管机），工作井内未进洞顶管长度为l_a。

图  1  顶进时纵向受力图

Figure  1.  Longitudinal forces during jacking of pile

下载: 全尺寸图片 幻灯片

顶进施工时，顶管在油压千斤顶总顶力F，总摩阻力${F_{\text{f}}}$及掌子面压力P_y的共同作用下受力平衡。即

摩阻力${F_{\text{f}}}$的来源包括导向轨、盾尾刷、止水箱、加固区及土层。其中，导向轨上的摩阻力较小，可忽略不计，即不考虑l_a范围内的摩阻力；盾尾刷、止水箱处的摩阻力较大，但因长度较小，可算作加固区洞口处摩阻力。根据实测荷载结果，在管节进洞后测得的初始水压力较小，而随顶进里程增加，各测点水压力几乎呈线性增长，接近土层后，水压力才达到一个较为稳定的区段。然而位于加固区段的管节在施工过程中并不注浆，因此可认为加固区段的泥浆是由土层段流入，但加固区段的泥浆并不充盈，且越靠近洞口，泥浆量越少，仅洞口底部会有少量泥浆流出。因此，相比平均摩阻力，采用线性变化摩阻力更适合实际情况。但不论采用线性变化摩阻力还是平均摩阻力，都不会影响土层段纵向力大小的推导计算。在${l_2}$区段土层内，顶进过程中地层与管节无协同运动，因此在稳定注浆减摩时${l_2}$区段内的单位面积管土摩擦力${f_2}$可保持稳定，因此可假定其为一常数。另外，因管节接近土层时水压力基本稳定，可假定管土摩擦力在加固区—土层交界处不发生突变。

以洞口处为坐标系原点沿顶进方向建立水平坐标系，则${l_1}$区段内的单位面积管土摩擦力${f_1}$可表示为

式中，m无实际物理含义，用于表示${f_1}$的线性变化，n单位为kPa。

设管节外表面周长为B，则顶进时顶管断面纵向力沿坐标轴的分布为

式中，

（2）止退时纵向力空间分布

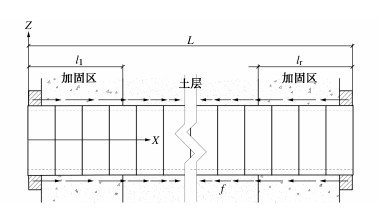
顶管止退时的纵向受力如图 2所示，在撤回油压千斤顶之前将止退装置作用于末端管节，提供被动反力F₀，阻止顶管隧道回退，但顶管依旧有回退趋势，因此摩阻力与顶进施工时反向。

图  2  止退时纵向受力图

Figure  2.  Longitudinal forces at back-stopping

下载: 全尺寸图片 幻灯片

设止退时掌子面压力为${P_{y0}}$，受力平衡时，止退时顶管断面纵向力沿坐标轴的分布为

1.2   止退装置协同变形

止退装置相较顶管隧道纵向刚度较小，因此在止退时，顶管末端仍会产生一定量的回退。考虑到每一环管节安装时，会在千斤顶顶力作用下压紧弹性衬垫并安装环缝螺栓，因此在螺栓的作用下可忽略弹性衬垫回弹量。则由协同变形可知，止退装置纵向位移量等于顶管机头回退量加上管节的弹性回弹量。为方便计算，不妨忽略顶管机头的回退量，即掌子面处无纵向位移，止退装置纵向位移量完全等于管节的弹性回弹量。

如图 3所示，管节弹性模量为E，纵向断面面积为A，顶进时顶管隧道的纵向弹性压缩变形量为

图  3  顶管纵向变形图

Figure  3.  Longitudinal deformations of pipe jacking

下载: 全尺寸图片 幻灯片

止退时顶管隧道的纵向弹性压缩变形量为

则止退管节的弹性回弹量为

设止退装置纵向弹性系数为k，则有

联立上式可得止退时掌子面压力

式中

由此得到止退时掌子面压力${P_0}$关于顶推时掌子面压力${P_y}$、摩阻力${F_{\text{f}}}$、顶进里程L、止退装置纵向弹性系数k及其他各项参数的关系式。当顶管隧道在同一埋深下顶进时，若隧道长度较短，地质条件稳定，且顶进时保持稳定的顶进速度，便可忽略这些因素对掌子面压力${P_{\text{p}}}$的影响，认为其大小仅与隧道埋深及断面面积有关。若埋深不变，便可认为其是一固定值。

1.3   隧道贯通残余纵向力

隧道贯通后，两端卸载，管节沿纵向双向回弹变形。如图 4所示，隧道残余应力主要受摩阻力控制，隧道两端不受纵向力作用，并与洞口进行固接。

图  4  贯通后荷载形式

Figure  4.  Load forms after coalescence

下载: 全尺寸图片 幻灯片

设隧道两侧加固区宽度相同，则断面纵向力分布为

可见，仅由摩阻力控制的隧道断面残余纵向力远小于施工期间。纵向卸载后，环缝刚度会迅速减小，因此在隧道贯通后应尽快进行泥浆置换或固化，以保证结构稳定并控制地面沉降。另外，当环间纵向力不足时，可能出现环缝渗漏水的情况，在隧道贯通后可对环缝进行焊接处理。

考虑到大多实际工程中，接收井一侧加固区厚度要小于始发井一侧，顶管隧道在纵向卸载后，两端的摩阻力并不对称，摩阻力较小的一侧应力得到较大释放，因此需重点关注加固区较短的一侧，假定图 4中坐标起点一侧加固区${l_{\text{l}}}$较短，其长度为另一侧${l_{\text{r}}}$的$\gamma$倍，由式（2）可得，${l_{\text{l}}}$区段内的单位面积管土摩擦力${f_{\text{l}}}$为

后续仍可依据式（13）计算加固区较短一侧的隧道残余纵向力分布。

2.   理论模型的试验验证

2.1   试验概况

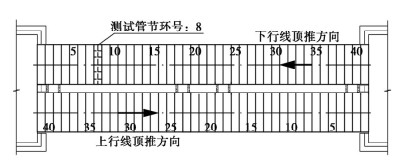
上海地铁14号线静安寺站B区站台层采用如图 5所示两条长度为82 m、断面尺寸为9.9 m×8.7 m的顶管隧道，隧道埋深15.17~15.37 m。其中下行线8，21环，上行线6环，共3环测试管节。下行线中，相比于隧道中间段的第21环管节，前部的第8环管节所顶进的里程更长，更能体现施工全过程的受力变化，而上行线测试第6环管节更偏重结构环向荷载及内力的测试，因此本文将采用下行线第8环管节进行纵向力的试验验证。

图  5  顶管隧道平面图

Figure  5.  Plan of pipe jacking tunnel

下载: 全尺寸图片 幻灯片

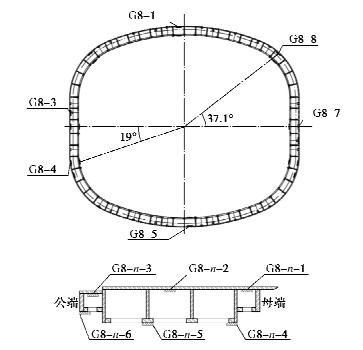
隧道断面如图 6所示，因施工需要，部分截面不满足测点布置需求，因此结构应变监测位置共选取6个截面，分别为顶底部、两侧腰部以及两个角部。每个截面钢板、钢肋内弧面共布置有6组钢板应变计（见图 7）。其中，纵向应变计编号G 8-n-m，其中n为断面编号，m为测点编号。

图  6  顶管断面与测点布置图

Figure  6.  Section of pipe jacking and layout of measuring points

下载: 全尺寸图片 幻灯片

图  7  应变监测图

Figure  7.  Photo of strain monitoring

下载: 全尺寸图片 幻灯片

2.2   模型参数

依据结构设计计算书及地勘报告，将本文理论计算推导所需的主要结构尺寸及地质参数汇总如表 1所示。

表  1  计算参数

Table  1.  Values of parameters

参数	取值
隧道长度L	82 m
管节断面宽度b	9.9 m
管节断面高度h	8.7 m
管节断面面积A	1.24 m2
管节外周长B	31.1 m
掌子面面积A1	74.7 m2
加固区长度l1	8 m
钢管节弹性模量E	2.06×105 N/mm2
止退装置弹性系数k	1.5×106 N/m
隧道顶部埋深D	15.2 m
地下水位高度Hw	0.5 m
平均土重度γ	18 kN/m3
侧向土压力系数	0.55

下载: 导出CSV 

| 显示表格

顶进施工过程中，为控制地表变形，往往使得掌子面总压力略大约该埋深下的静止水土压力，并据此调整千斤顶顶力大小。根据表 1中参数可计算得掌子面静止总压力约为20766 kN，因此可设顶进时掌子面总压力P_y为21000 kN。

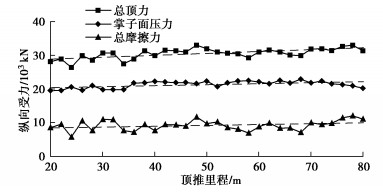
单位面积管土摩擦力难以在施工前通过相关试验进行测定，而依据经验取值可能偏差较大，因此本文根据施工数据记录进行测算。顶管顶进时，隧道纵向受力如图 8所示，包括总顶力、掌子面压力及总摩阻力。随顶进里程的增长，三者均呈现出较小的增长趋势。自8环管节始发至隧道贯通，总顶力变化范围为26500~33100 kN，线性趋势增量3300 kN；掌子面压力变化范围为19600~22900 kN，线性趋势增量1800 kN，理论值取值恰为该范围均值；由此得到总摩阻力变化范围为5800~11900 kN，线性趋势增量1500 kN。

图  8  顶管顶进时纵向受力

Figure  8.  Longitudinal forces during jacking of pipe

下载: 全尺寸图片 幻灯片

由此可计算得，顶管土层内顶进时平均摩阻力为25 kN/m，管节外周长B为31.05 m，由此得到的平均管土摩擦力约为0.8 kPa，远小于《T/CECS 716—2020矩形顶管工程技术章程》中的3~4 kPa。一方面是因为钢顶管外壁涂料表面光滑，管土摩擦系数较小；另一方面是该工程采用了新型的触变泥浆并配备自动压浆系统，形成完整的泥浆套，减摩效果良好。

加固区长度l₁为8 m，盾尾刷及加固区的总摩阻力约为8200 kN。根据前文对单位面积管土摩擦力的假定可得

2.3   纵向力变化规律

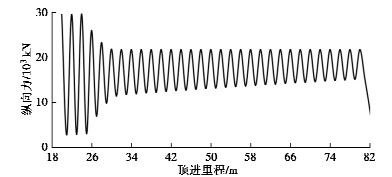
将以上参数代入式（1）~（13）中，可计算得第8环管节纵向力。如图 9所示，管节断面纵向力随顶进里程的变化规律为一条逐渐收敛的波动曲线：①管节始发时纵向受力大小波动最大，峰值29400 kN；②顶进里程达到26 m时8环进入加固区，其纵向力波动范围快速收缩；③顶进里程达34 m时管节进入土层，其顶推时的纵向力大小稳定在21600 kN，止退时的纵向力随顶进里程增长而缓慢增大；④隧道贯通后迅速下降至8300 kN。

图  9  纵向力随顶进里程变化曲线

Figure  9.  Curves of longitudinal force with jacking mileage

下载: 全尺寸图片 幻灯片

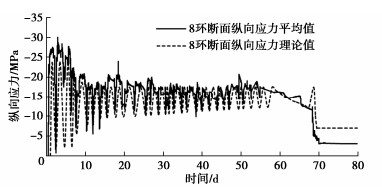
现场试验得到6个测试截面共36个测点的应变数据，其中3个测点损坏，由剩余测点数据计算得到的管节断面纵向应力均值时变曲线如图 10所示，为方便与理论值进行对比，依据施工日期与顶进里程的对应关系，将理论纵向应力时变曲线绘制于同一坐标系中。

图  10  纵向应力时变曲线

Figure  10.  Curves of longitudinal stress with time

下载: 全尺寸图片 幻灯片

当试验管节进入土层后（图 10），最小断面纵向应力均值为-5.55 MPa，最大断面纵向应力均值为-23.92 MPa。整体上看，实测管节断面纵向应力均值时变曲线与理论断面纵向应力值的变化规律基本一致，具有良好的匹配性。主要差异表现为隧道贯通后，残余应力实测均值为-3.08 MPa，与理论值-6.90 MPa相差较大。若考虑实际工程中，接收井一侧的加固区长度约为始发井一侧的1/2，即$\gamma$= 0.5。

代入式（13），（14）中求解并计算得断面纵向残余应力均值为-1.95 MPa，与实测值较为接近，由此可见，该工程中不可忽略两侧加固区长度差异带来的影响。

3.   纵向应力影响因素敏感性分析

顶管止退期间及隧道贯通之后，环间纵向应力及纵向刚度较小，对防水较不利，且易产生不均匀沉降。本文将基于上述理论推导，对顶管管节纵向应力影响因素进行敏感性分析，在工程中对其进行重点控制，以满足施工及使用要求。本文将研究止退装置弹性系数、顶进里程、隧道尺寸、隧道埋深对顶管断面纵向力的影响。

3.1   止退装置弹性系数影响

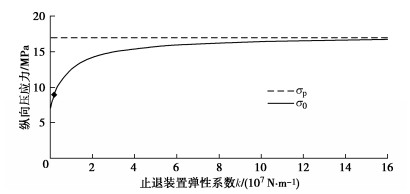
管节断面纵向应力时变在止退时产生较大波动的原因是止退装置纵向弹性系数较小，使得顶管产生一定量的回退，掌子面压力降低，进而使得管节纵向应力降低。图 11为顶进里程为30 m时纵向应力随止退装置弹性系数的变化规律，实际止退装置（k=0.15×10⁷ N/m）作用下的纵向应力${\sigma _0}$约为8.5 MPa，仅为顶推时纵向应力${\sigma _{\text{p}}}$的50%，若将止退装置弹性系数k提升10倍至1.5×10⁷ N/m，则止退时纵向应力${\sigma _0}$提升至13.5 MPa，为顶推时纵向应力的80%；若将止退装置弹性系数k提升20倍至3.0×10⁷ N/m，则止退时掌子面压力${\sigma _0}$提升至15.0 MPa，为顶推时纵向应力${\sigma _{\text{p}}}$的89%；后续若继续提升止退装置弹性系数k则对掌管节断面纵向应力无明显影响。因此，通过优化止退装置结构形式、增大截面积等方式增大其弹性系数10~20倍可明显增强止退效果，增大管节纵向应力。

图  11  纵向应力随止退装置弹性系数变化规律

Figure  11.  Variation laws of longitudinal stress with elastic coefficient of stopping device

下载: 全尺寸图片 幻灯片

3.2   顶进里程影响

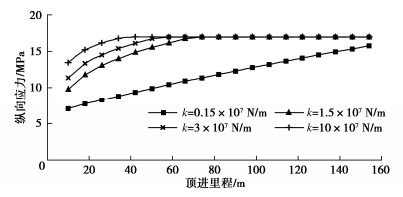
由图 10可知，止退时断面纵向应力随顶进里程增长而增大，并逐渐向顶进时断面纵向应力收敛，趋于稳定。图 12为不同止退装置弹性系数下的管节纵向应力随顶进里程的变化规律，由图 12可知，止退装置弹性系数越大，纵向应力达到稳定所需的顶进里程越小，当k=3×10⁷ N/m时，顶进里程达54 m后，止退时纵向应力与顶进时相同，进入稳定状态；当k=1.5×10⁷ N/m时，顶进里程需达70 m后才进入稳定状态；而实际止退装置作用下顶进里程达到178 m后才能进入稳定状态。由此可知，顶进里程越长，施工时纵向受力越稳定，因此需格外关注顶管施工前中期的结构受力状态。

图  12  纵向应力随顶进里程变化规律

Figure  12.  Variation laws of longitudinal stress with jacking mileage

下载: 全尺寸图片 幻灯片

3.3   隧道尺寸影响

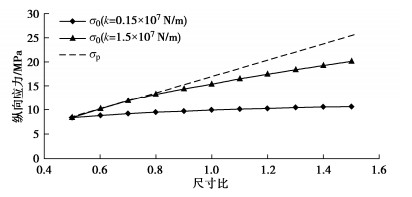
实际工程会依据设计需要选定合适的断面尺寸，假设隧道中轴线埋深与管节厚度不变，当顶管隧道断面尺寸大小发生变化时，会引起管节外周长、截面积、管土总摩阻力的同步线性变化，以及掌子面压力的平方倍数变化。如图 13所示，随顶管隧道尺寸与既有结构的尺寸比例的增长，顶推时管节纵向应力${\sigma _{\text{p}}}$呈线性增长，止退时纵向应力${\sigma _0}$呈乘幂指数增长，指数大小与止退装置弹性系数相关。

图  13  纵向应力随结构尺寸比例变化规律

Figure  13.  Variation laws of longitudinal stress with proportion of structural size

下载: 全尺寸图片 幻灯片

3.4   隧道埋深影响

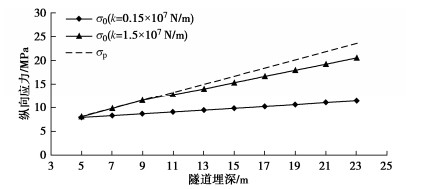
在实际工程中，顶管隧道可能应用于不同埋深情况下，当隧道埋深发生变化时，掌子面压力会同步线性变化。如图 14所示，随隧道埋深的增长，顶推时管节纵向应力${\sigma _{\text{p}}}$及止退时纵向应力${\sigma _0}$均呈线性增长。

图  14  纵向应力随隧道埋深变化规律

Figure  14.  Variation laws of longitudinal stress with buried depth of tunnel

下载: 全尺寸图片 幻灯片

综上所述，实际工程中通过优化止退装置性能，增大止退装置弹性系数可明显增强止退效果，增大断面纵向力。施工过程中，随顶进里程增长，断面纵向力会逐渐趋于稳定。随隧道尺寸及隧道埋深的增大，断面纵向力也会同步增长。

4.   结论与建议

通过理论推导，建立了顶管隧道任意断面纵向力随时间的变化规律，并将其与上海14号线轨道交通静安寺站顶管车站实测纵向力变化规律进行了对比，得到以下几点结论：

（1）管节断面纵向力随时间的变化规律为一条逐渐收敛的波动曲线，并在隧道贯通后迅速降低。理论值与实测值具有良好的匹配性。

（2）止退时土层内管节纵向应力最小为-5.55 MPa，隧道贯通后为-3.08 MPa，使得隧道纵向刚度减小。

（3）止退装置弹性系数、顶进里程、隧道尺寸及隧道埋深是顶管断面纵向力的重要影响因素，且均呈现不同程度的正相关关系。

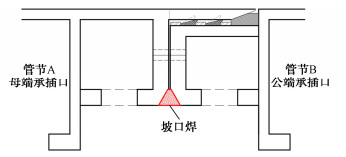
在实际工程中，建议增加止退环数，或者通过优化止退装置结构形式、增大截面积等方式增大其弹性系数，进而增强止退性能，提高顶管环缝防水能力并控制地面沉降。在隧道贯通后，应如图 15所示迅速对管节环缝进行焊接处理，严防渗漏水，并提高纵向刚度，避免产生不均匀沉降。隧道贯通后还应尽快向管壁外泥浆中注入凝固剂，使得浆液固化，以大幅度提高管道与“土体”间的摩阻力，提高管节间纵向力。

图  15  管节环缝环接

Figure  15.  Circumferential seam weld of pipe joint

下载: 全尺寸图片 幻灯片