Numerical study on dynamic crack propagation of brittle materials by discontinuous deformation analysis
-
摘要: 非连续变形分析方法(DDA)属于隐式离散元法，通过引入虚拟节理可以模拟材料从连续到破坏全过程。尝试将DDA方法应用于脆性材料动态裂纹扩展问题。采用基于Voronoi多边形离散的DDA方法进行模拟。由于Voronoi多边形会存在较多短边，采用原始DDA程序计算时短边会优先发生破坏。针对该问题通过引入均布弹簧算法，在一定程度上减轻了过多短边发生破坏的问题。其次，为了能够定量分析动态裂纹扩展，提出了一套参数标定方案。该方案通过单轴压缩试验进行弹性参数标定，通过带切槽半圆盘试验进行强度参数标定。利用标定后的参数模拟的带切槽半圆盘，裂纹扩展路径与试验结果高度一致。最后，基于标定的参数，模拟了几类典型脆性材料的动态裂纹扩展问题，包括自相似裂纹扩展、裂纹分叉和紧凑拉伸试验。模拟结果表明，DDA方法能够较好地再现自相似裂纹扩展时裂纹扩展速度保持不变的规律，可以真实地模拟出脆性材料的裂纹分叉现象，并成功模拟了不同加载速度下紧凑拉伸试验中不同的破坏模式。这些算例验证了DDA方法在模拟脆性材料动态裂纹扩展问题的可行性，为后续相关应用打下了基础。
-
关键词:
- 脆性材料 /
- 非连续变形分析 /
- Voronoi多边形 /
- 动态裂纹扩展 /
- 裂纹扩展速度
Abstract: The discontinuous deformation analysis (DDA), as an implicit discrete element method, can simulate the evolution process from continuum to failure by introducing the virtual joint technology. In this study, the DDA method is modified and applied to the dynamic crack propagation problem of brittle materials. Firstly, the DDA with Voronoi discretization is adopted. Since there are many short edges in the Voronoi discretization, these edges will fail preferentially using the original DDA algorithm. A uniform spring algorthim for the DDA is proposed to solve this issue. Then, a parameter calibration scheme is presented. The uniaxial compression and a semi-circular bend (SCB) with a pre-existing crack are used to calibrate the elastic parameters and the strength parameters, respectively. Based on the calibrated parameters, the predicted crack propagation paths of SCB are highly consistent with the test results. Finally, several dynamic crack propagation problems for brittle materials, such as self-similar crack propagation, crack branching and compact tensile tests, are simulated based on the calibrated parameters. The proposed DDA method can reproduce the phenomenon of crack propagation with the constant speed for the self-similar crack and the crack branching phenomenon under dynamic loading. Meanwhile, different failure patterns for compact tensile tests under different loading speeds are reproduced successfully. The results verify the feasibility of the DDA for dynamic crack propagation of brittle materials, and pave the way for future engineering applications. -
0. 引言
土与结构的相互作用问题是土木和水利等大型工程的一个关键共性问题,例如,大坝中的防渗体与堆石体或地基之间的相互作用、桩基与地基之间的相互作用等。土与结构由于存在明显的刚度差异,导致两种介质之间接触界面（带）的力学特性与远离界面的土体明显不同。实际工程在外力作用下,土与结构两者之间变形差异会导致接触界面（带）出现剪切应变集中、应变软化、法向张开—闭合等,这些现象会导致土与结构间的接触力传递机制复杂,进而显著影响静、动荷载条件下结构的响应[1-2]。因此,土与结构的相互作用分析是揭示工程中结构损伤破坏机理的重要环节,将土与结构作为一个整体进行分析才能更为合理地模拟结构的破坏,但在大型工程分析时将面临着一系列难题：①土与结构间接触几何形状复杂；②土与结构间的接触力学特性复杂；③土与结构间尺度跨越大,计算网格精细剖分难。以上3个难题依次涉及到接触边界约束模拟的问题、接触力学行为模拟（本构模型）的问题以及土与结构间单元跨尺度分析的问题。本文对这些问题的相关研究依次进行了综述和总结,在此基础上介绍了土-界面-结构体系研究的进展及工程应用情况,最后对今后的主要发展方向进行了展望。
1. 土-结构间接触约束模拟
目前在分析土与结构间接触问题时,主要有两种思路：①将接触问题转化为力和位移边界的约束问题进行分析,称为接触边界约束方法。代表性方法有拉格朗日乘子法[3-4]、罚函数法[3-4]、增广（或改进）的拉格朗日乘子法[5]、直接约束法[6]等。②将接触问题等效为特殊单元及其力学特性问题进行分析,称为接触界面单元方法。代表性的方法有Goodman单元和薄层单元等。接触边界约束方法主要用于刚-刚的接触分析,在土-结构接触问题中无法反映界面区域的剪缩、剪胀法向变形,以及滑动前的剪切变形特性。本文主要介绍接触界面单元方法的相关研究。
接触界面单元实现方法与实体单元相近。在非线性有限元静、动力计算时,通过反复迭代接触面（或界面）两侧节点变形,进而计算接触单元应力,并同时判断力和位移是否满足接触边界条件,直至满足接触要求。该过程与非线性有限元求解过程是一致的,因此很方便植入有限元程序中。但为了模拟接触区域的特性,需要采用特殊的单元和合理的本构模型。下面根据计算网格中单元的剖分厚度在总刚中是否有作用来分类,简单介绍接触界面单元的研究情况。
1.1 Goodman单元
Goodman等[7]最早提出了目前被广泛应用的二维四节点界面单元,也就是两条平行直线组成的单元,该单元最早是用于模拟岩石节理问题。由于该单元假定界面应变等于界面相对位移除以界面厚度,同时将弹塑性矩阵除以界面厚度,最终得到的界面刚度中的界面厚度会被消去,所以表现为单元的“无厚度”。详细见下面刚度矩阵K推导的过程,对于实体单元和界面单元都有
K=∫VΒTDΒdV, (1) 式中,B为应变-位移矩阵转换矩阵,与单元的厚度大小有关,D为应力与应变之间的弹塑性矩阵,与单元的厚度大小无关,V为体积。
对于Goodman单元,由于体积微元dV=tdξ（对于二维单元）,B=N/t,则可得
K=1t∫l/2−l/2NTDNdξ, (2) 式中,t为单元的厚度,l为其长度,N为界面相对位移与节点位移之间的转换矩阵,与单元的厚度大小无关。
若
D=tk ,可得Goodman单元的刚度阵表达式K=∫l/2−l/2NTkNdξ。 (3) 在计算的时候,由于矩阵k是根据试验测定的相对位移-应力之间关系确定的,因此式（3）是与计算网格中单元厚度无关的,即无论Goodman单元厚度多大,都不会影响Goodman单元刚度阵的数值。依据Goodman单元的思想还可以构造点界面单元、二维六节点曲线界面单元、三维八节点界面单元等。
Goodman单元早期应用于岩石节理分析时,为了防止两侧节点的嵌入,通常假定法向刚度很大,这一方面会导致法向刚度取值具有任意性,另一方面法向刚度很大可能会导致刚度矩阵病态引发数值求解不稳定。针对Goodman单元数值不稳定的问题,雷晓燕等[8]研究发现采用Newton-Cotes积分相比Gauss积分会消除接触面应力震荡现象。Day等[9]研究认为,积分方法仅是积分点位置和权重的不同,并不是导致应力波动的根本原因,界面区域单元应力梯度大（或单元剖分不够精细）是导致刚度矩阵病态数值求解不稳定（应力波动）的本质原因,而非接触界面单元的特性引起的,并且减小靠近接触面区域的单元尺寸或采用更高精度的单元可以提高数值的稳定性。
目前由于Goodman单元简单易于实现,并且联合界面本构模型,该单元可用于模拟土-结构接触区域的滑移、张开、闭合等,在工程中得到了广泛应用。
1.2 薄层单元
薄层单元本质上与实体单元并没有差异,不同之处在于薄层单元的厚度要足够小。当薄层单元足够小时,单元的应力和应变可以近似表达,此时可等效于Goodman单元,其刚度矩阵可以近似等效为式（2）。采用薄层单元计算时,式（2）中矩阵D根据试验测定的应变-应力关系确定,因此薄层单元的刚度矩阵K与计算网格中单元厚度t的大小有关。
早期采用实体单元模拟接触区域的较大变形时,一般是通过降低接触区域土体的模量来实现。例如,Griffiths[10]采用八节点四边形单元来模拟接触黏结和摩擦滑动行为,同时比较了不同刚度和单元长宽比,研究表明,该单元的性能良好,但长宽比较大时需要更严格的迭代收敛精度。Zienkiewicz[11]采用二维六节点等参单元（一边三个节点,厚度方向上没有设立节点）可以模拟接触面的弯曲。Wilson[12]将相对位移作为独立参数形成刚度矩阵构建了二维八节点薄层单元（厚度方向中心设一个节点）。相比Zienkiewicz[11]提出的单元,Wilson[12]对于描述接触面法向应力和位移梯度变化较大时会更准确。依据Wilson相同的思想,Pande等[13]构建了八节点抛物线三维等参薄层单元。Wilson最初采用相对位移的思想构建薄层单元的主要目的是增加计算的准确性,但Pande等[13]研究发现,是否采用相对位移作为独立参数构建刚度矩阵,计算结果差异并不大。Desai等[1, 14]对“有厚度”薄层单元进行了详细的研究,其采用与土体不同的剪切模量来描述接触面的剪切滑移变形,并且法向刚度取值考虑了土体特性、粗糙度等影响,计算表明,单元长宽比为0.01～0.1时能满足精度要求。
综上,薄层单元在应用时问题之一在于其单元厚度如何确定,其取值与单元长度l是有关的,并非真实条件下土与结构间接触面的厚度h（其约为5～20倍的平均粒径）,也就是说虽然薄层单元的厚度具有一定的物理意义,但并不完全真实。只有当t=h时,薄层单元的厚度物理意义才能明确,并且此时可近似等效于Goodman单元。
2. 土-结构间接触本构模型
与刚-刚接触不同（主要基于库仑摩擦模型）,土-结构间接触特性更复杂。土-结构接触问题的分析精度很大程度上取决于界面区域的力学特性模拟。试验表明,与土体相似,土-结构接触带区域的变形也表现为应力路径相关性、加载硬化/软化、剪胀/剪缩、蠕变等特性[15-18]。从本质上讲,土-结构界面的这些特性是土体变形引起的,应当属于土体单元和本构模拟的范畴。从这一点来看,接触约束方法模拟界面约束似乎更合理[19]。但实际上由于界面区域土体的变形受到结构形状约束和表面粗糙度等因素的影响,该区域土体的特性与远离界面的土体特性（包括压缩和剪切）差异很大,采用接触约束方法很难反映界面区域土体的力学特性。例如,界面区域土体的法向变形机制与远离界面土体的体变机制存在一定的差异,并且大多数的研究表明接触面法向的剪胀变形和法向应力变化及摩擦角会低于土体的,当结构面粗糙度增加后接触面的摩擦角开始接近或等于土体的[20-22]；此外,Desai等[23]试验表明接触区域的液化要比周围土体更容易。因此,接触区域的力学特性需要进行特殊研究,其中清华大学在粗粒土与结构接触面试验研究方面做了大量的工作[22, 24-25]。
接触区域的变形包括该区域的连续土体变形和非连续错动两种变形机制,目前的研究一般在宏观上将两者不进行区分均统称为接触界面变形,并且假定接触区域应变是没有梯度变化的。目前的接触面本构模型大都是研究接触界面变形与应力之间关系。包括非线性弹性模型[26-27]、传统弹塑性模型[28-31]、损伤本构模型[32]、扰动本构模型[33]及状态相关的弹塑性本构模型[34-35]。以上模型仅适用于单调加载条件,对卸载和再加载过程没有给出描述。一些反映循环荷载条件下的接触面也相继提出包括非线性弹性模型[16, 36],理想弹塑性模型[37]及弹塑性本构模型[25, 38-40],这些模型大都可以反映土-结构接触的基本特性。但是目前先进界面本构模型主要针对二维条件[41],且工程应用研究还是较少。
3. 土-界面-结构体系跨尺度计算方法
上述方法和模型在应用时需对土-界面-结构体系整体进行网格离散,但大型工程常常面临土体尺寸和结构尺寸相差百倍、千倍的情况,使得局部小尺度结构破坏和整体响应的高效分析工作面临极大的挑战。若采用全局一致细尺度网格方案,为了满足局部小尺度结构破坏的分析要求,迫使整体结构必须进行精细剖分,进而导致土-结构分析体系单元量剧增、计算成本急剧攀升,难以开展大规模非线性分析。跨尺度分析是兼顾结构局部小尺度破坏和整体宏观响应的高效分析方法和有效途径之一,但其面临的最大困难是不同尺寸单元在交界面处的节点衔接处理,针对不同的处理形式,目前常用的方法主要有子模型法、多节点约束法和单元直接过渡法。
3.1 子模型方法
子模型方法又称切割位移边界法,其主要思想是分别建立结构宏观尺度模型和局部细节模型,然后将在宏观尺度模型上计算所得的截断边界力学物理量施加于子模型,最终获得问题域数值解。这种方法具有鲜明的“二次分析”特点,且没有考虑子模型和整体模型之间的相互作用问题。由于岩土工程弹塑性分析中需要进行迭代计算,如果采用“二次分析”,易产生大量的计算误差累积[42]。
3.2 多节点约束法
多节点约束方法主要用于解决梁单元、壳单元、实体单元之间的相互连接问题,因此该方法在建筑结构和桥梁工程中应用较多[43]。该方法通过在不同单元交界面寻找单元自由度间的内在联系,根据位移、应力、功等平衡条件,建立和求解多点约束方程,从而实现衔接面的平稳过渡和协调。不同学者的研究差异在于如何确定和改进优化不同单元交界面的约束方程。有研究表明,当结构进入塑性时,不同平衡条件下约束方法的计算结果差异较大,会造成分析结果失真[44]。岩土工程中涉及到的均是强非线性问题,多点约束方法在岩土工程的应用合理性有待进一步探讨。并且当梁单元和壳单元用来模拟结构时,采用该类方法很难对土-结构接触区域的复杂接触特性（如剪胀、剪缩等）进行精细模拟。
3.3 单元直接过渡法
（1）基于常规规则形状单元的逐级网格过渡法
有限单元法是仿真计算应用最广的数值方法,其计算单元主要为四边形/六面体及其退化的简单形状（三角形/四面体等）,限制了单元形状构造和空间节点分布。该方法需通过较繁琐的、半自动的人机交互操作,才能实现较为粗糙和缓慢的疏密网格过渡。并且疏密网格过渡时单元尺寸跨越较为缓慢,剖分单元数量大,且会生成形状不规则、精度不高的单元。采用该方法难以高效、高质地建立跨尺度精细分析模型。
（2）基于多边形/多面体单元的网格过渡法
多边形/多面体单元不限制形状构造和节点空间位置分布,放松了对单元离散的限制,故该方法可为疏密网格交界面衔接提供便捷高效的选择。这类方法的最大难点是构造节点丰富的单元类型。目前构造该类单元的方法主要有以下两大类。
a）传统多边形/多面体有限单元：将交界面的非协调节点直接作为多边形/多面体单元节点。根据不同的构造思想,可分为3类：①多胞单元[45],将求解域剖分为胞体组合,基于最小余能原理,推导构造有限单元格式进行求解。该单元几何特征与实物较为相似,故在颗粒增强复合材料仿真领域,拥有独到的优势。②基于位移插值的多边形单元[46],主要采用有理函数插值多边形节点,包括Wachspress提出通过几何投影构造单元形函数及相关改进算法,以及基于自然邻点插值的Laplace方法。③基于重心坐标的多边形单元[47],该方法思路简单,但相关表达式较难显式描述。上述方法理论相对成熟,主要应用于固体力学分析、简单结构断裂过程模拟及计算流体动力学分析等[48]。相较于等参单元,多边形/多面体单元的形函数构造较为复杂,数值积分较为繁琐复杂,甚至需要特殊的积分技巧,尤其三维构造计算繁琐耗时,故该方法发展推广过程较为缓慢[48],目前主要用于简单结构理论机理分析研究。
b）其他方法：通过不同的技术处理疏密网格衔接处的非对称节点,使其满足边界变形、应力协调条件。王勖成等[49]通过修改插值函数法和引入虚拟节点法,构造了5节点二维平面单元。强天弛等[50]、钟红等[51]通过虚拟节点和凝聚自由度技术,实现了一种非对称节点单元的求解方法。但上述方法仍有一定的应用条件,如主从自由度方法中,计算效果与从自由度数的选择相关性大。此外,模型前处理过程较为繁琐耗时、需大量人机交互、易出错,较难实现自动生成分析模型,目前仍未见到此类方法在岩土工程大规模精细分析中的应用。
4. 土-界面-结构体系研究的几点进展及工程应用
鉴于以上土-界面-结构体系精细分析存在的问题,大连理工大学工程抗震研究所对以上3项内容均分别进行了发展和改进,主要取得了以下进展。
4.1 土-结构间非点对点接触模拟
前文所述的接触单元只能满足节点-节点一一对应的情况。但岩土工程中土-结构间的尺度差异一般都比较大,建立非对称节点的界面单元是实现土-结构间网格尺寸高效跨越的一种途径。Qu等[52]、Gong等[53-55]开展了两方面的研究：一是通过在接触面单元两侧设置虚拟节点和凝聚自由度方法,构造了两侧非对称节点接触界面单元,计算结果表明,该方法在保证计算精度的基础上,显著降低网格离散的数量、提高计算效率。二是采用背景网格,借助径向点插值函数计算高斯点相对位移,建立了非点对点的无网格界面模拟方法,实现了界面两侧节点自由分布,该方法可直接连接尺寸不同的网格,为土-结构间相互作用跨尺度分析提供了界面模拟技术（图1）。
4.2 反映颗粒破碎的三维广义塑性接触面模型
为了解决接触面弹塑性模型三维实用化的问题,笔者等引入广义塑性理论开展了三维接触面本构模型研究。广义塑性理论由于其理论框架简单、易实现,在收敛性和稳定性方面有独特的优势,为接触面弹塑性模型的应用提供了理论框架基础。在该理论框架下,将颗粒破碎引入到临界状态理论中,建立了反映颗粒破碎的状态参数与塑性模量、峰值强度、相位变换应力比之间的关系,然后基于边界面理论的思想描述单调和循环荷载下接触面的塑性模量、加载方向和流动方向,最终提出了考虑颗粒破碎的三维土与结构界面弹塑性本构模型。模型可以用一套参数较好地反映三维单调和循环荷载下土与结构界面的法向（剪胀、剪缩、卸载体缩）和切向（硬化和软化）变形特性[56-57]。在界面模型研究的基础上,结合发展的砂土和粗粒土广义塑性本构模型和混凝土塑性损伤模型[37, 58-62],建立了三维土与结构（包括土、界面、混凝土）全弹塑性-损伤静、动力分析模型,实现了土-界面-结构体系的损伤过程及渐进破坏模拟,为土与结构相互作用问题的研究提供了实用、有效的计算方法。
4.3 非线性比例边界多边形/多面体单元（NSBPFEM）
针对复杂岩土结构高质量精细网格生成难、分析方法求解效率有待优化的问题,笔者等采用多边形/多面体网格直接过渡的思想,发展了一套高效的跨尺度分析方法,为大型土-结构体系的精细分析提供了技术手段。
首先采用计算机信息学科的四分树和八分树网格离散技术,对复杂几何体进行高效的跨尺度精细网格离散,实现操作简便、低人力成本、易修改再建的模型前处理,使得复杂工程结构跨尺度精细网格生成/再生成过程在很短时间即可完成,并且生成网格中约60%以上为高质量正方形、正方体单元,较好地解决了大型复杂工程结构跨尺度、精细化、高质量网格高效生成的问题。
针对交界面处的多边形/多面体单元,基于比例边界有限单元法（SBFEM）[63]发展高性能数值算法进行求解。该方法具有数据结构简单、降低计算维度、易于程序实现和修改、高精度半解析等多重优势,已被学者广泛应用于无限域、固体力学、裂纹扩展、液体晃动等领域的弹性问题研究[63-69]。为解决该方法难应用于岩土工程非线性分析的问题,笔者等[70-75]进行了下述改进：
（1）基于比例边界有限元理论（SBFEM）,提出了多边形平均值形函数直接插值复杂多面体环向边界的方法,通过假定径向插值函数,建立弹性平衡方程获得半解析的刚度矩阵,构造了高精度、形状灵活的多面体SBFEM（图2）,克服了传统SBFEM需二次处理边界面的不足（将多边形拆分为三角形和四边形）,使得计算机图形学八分树网格离散技术可直接用于工程结构分析,实现了大型工程的跨尺度精细化建模和分析。
（2）基于边界线/边界面高斯积分和常刚度矩阵的弹性解计算多边形/多面体形函数,避免了传统SBFEM刚度变化时频繁特征值分解导致低效率问题,提出多边形和多面体域内分块积分计算弹塑性矩阵和应力,建立了高效和实用的SBFEM非线性计算方法,克服了传统SBFEM局限于弹性分析的难题,实现了大型复杂土工构筑物的非线性精细化分析。
4.4 工程应用
将以上3项进展集成到大型岩土工程高性能分析软件系统GEODYNA,建立了考虑防渗体-堆石-接触面-无限地基相互作用的全体系精细模型,采用该软件系统,开展了多个土石坝工程的静、动力分析,取得了较好的效果,验证了软件和分析方法的高效性和稳定性。此外,该方法具有良好的通用性,已拓展用于核电工程、建筑结构、地下结构等复杂结构的损伤演化研究,使得重大工程三维渐进破坏规律和机制的研究成为可能[73-84]。
5. 结语
合理考虑土与结构间的相互作用对揭示大型工程中结构损伤破坏机理是十分重要的,将土-结构作为一个体系进行整体分析是精细研究土-结构相互作用的基础,必须协同解决土-结构接触界面约束模拟、土-结构间接触材料特性精准模拟,以及土与结构体系高效建模及分析方法等难题。针对这些问题,大连理工大学工程抗震研究所发展了土-界面-结构全弹塑性-损伤本构模型,并基于比例边界有限元理论和无网格法开发了跨尺度实体和界面单元,实现了土-结构相互作用精细化模拟。鉴于目前土与结构相互作用分析研究现状和中国“三深”、“三极”的发展战略需求,建议今后的发展方向：①继续深入开展土-结构体系跨尺度计算模型及计算理论研究；②重点关注长期服役、深水环境等复杂条件下土-结构接触力学特性及本构模型研究；③融合离散元、比例边界有限元、有限元、无网格等多种数值分析方法,开展土-结构相互作用大变形和非连续机理研究。
-
![]()
图 1 不同边长块体的破坏模型及块体1，2的y方向位移–时间关系
Figure 1. Failure model with different size blocks and y-direction displacement-time curves of blocks 1 and 2
![]()
图 2 单轴压缩试样微破裂角度分布
Figure 2. Distribution of microcrack angle of uniaxial compression specimens
![]()
图 4 巴西劈裂试样微破裂角度分布
Figure 4. Distribution of microcrack angle of Brazilian split specimens
![]()
图 6 SCB的Voronoi多边形离散模型及正则化临界应力强度因子对比
Figure 6. Voronoi discretization model of SCB and comparison of critical normalized stress intensity factors from experimental and numerical tests
![]()
图 7 SCB模拟的裂纹扩展路径与试验对比
Figure 7. Comparison of numerical and experimental crack propagation paths
![]()
图 9 预加载试样自发裂纹产生引发弹性波的速度云图
Figure 9. Elastic waves induced by spontaneous crack in a pre-loaded specimen
![]()
图 11 规则网格的自相似裂纹扩展和不同预荷载下不规则网格的自相似裂纹扩展
Figure 11. Self-similar crack propagation for both regular and irregular discretizations under different pre-loads
![]()
图 15 不同数值方法得到的裂纹扩展速度与时间关系对比图
Figure 15. Comparison of predicted crack velocity versus time by different numerical methods
![]()
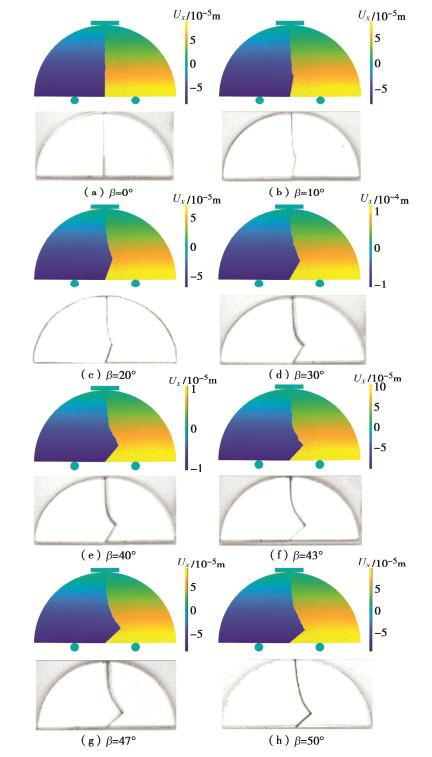
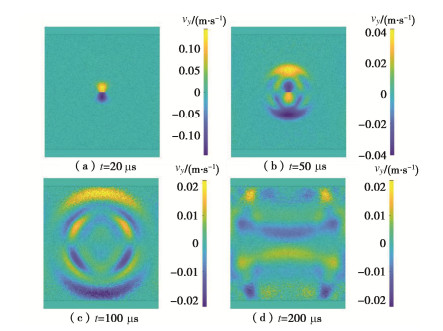
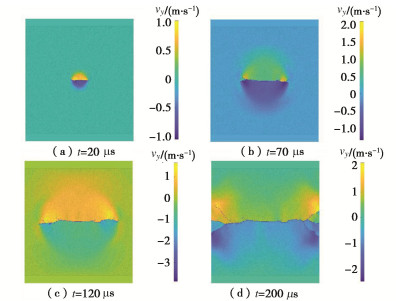
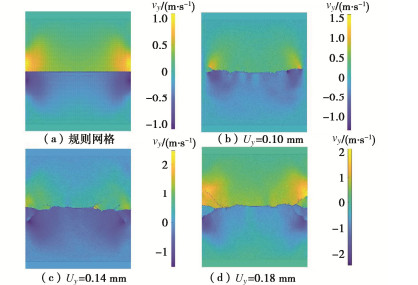
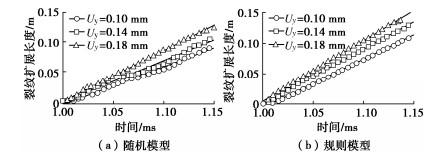
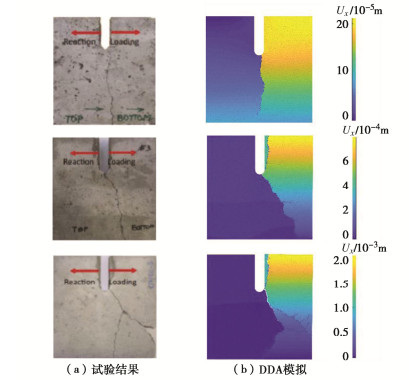
图 16 不同冲击速度下裂纹扩展路径的试验[27]和模拟结果对比
Figure 16. Comparison of experimental and simulation results of crack propagation path under different loading velocities
表 1 DDA微观参数取值
Table 1 Values of DDA microscopic parameters
密度/(kg·m-3) 弹性模量/GPa 泊松比 内摩擦角/(°) 端部摩擦角 黏聚力/MPa 抗拉强度/MPa 法向弹簧刚度/GPa 切向弹簧刚度/GPa 最大位移比 时间步长 1190 4.4 0.38 30 0 70 7 13.2 5.28 1×10-5 0(自动计算时步) 
下载: 导出CSV
表 2 块体数量对岩石材料弹性参数的影响
Table 2 The influence of the number of blocks on the elastic parameters
块体尺寸/mm 块体数量/个 弹性模量/GPa 泊松比 1.0 6129 59.30 0.268 1.5 2672 59.05 0.264 2.0 1593 58.62 0.264 2.5 1051 59.10 0.264 3.0 701 58.61 0.269 4.0 430 58.82 0.273 注：Voronoi离散(R=0.3)。
下载: 导出CSV
表 3 PMMA和模型的宏观参数值
Table 3 Value of macroscopic parameters of PMMA and model
类型 密度/(kg·m-3) 弹性模量/GPa 泊松比 PMMA材料 1190 3.24 0.350 模型 1190 3.28 0.357
下载: 导出CSV
表 4 数值标定荷载与试验荷载对比
Table 4 Comparison of numerical and experimental load
裂纹角度/(°) 数值荷载/kN 试验荷载均值/kN 误差/% 0 2.28 2.38 4.20 10 2.47 2.53 2.37 20 2.28 2.45 6.94 30 2.53 3.03 16.50 40 3.54 3.73 5.09 43 3.58 3.63 1.38 47 4.14 4.13 0.24 50 3.97 4.24 6.37
下载: 导出CSV
-
[1] BELYTSCHKO T, CHEN H, XU J X, et al. Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment[J]. International Journal for Numerical Methods in Engineering, 2003, 58(12): 1873–1905. doi: 10.1002/nme.941
[2] XU X P, NEEDLEMAN A. Numerical simulations of fast crack growth in brittle solids[J]. Journal of the Mechanics and Physics of Solids, 1994, 42(9): 1397–1434. doi: 10.1016/0022-5096(94)90003-5
[3] 梁正召, 李连崇, 唐世斌, 等. 岩石三维表面裂纹扩展机理数值模拟研究[J]. 岩土工程学报, 2011, 33(10): 1615–1622. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201110026.htm LIANG Zheng-zhao, LI Lian-chong, TANG Shi-bin, et al. 3D numerical simulation of growth of surface crack of rock specimens[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1615–1622. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201110026.htm
[4] 马鹏飞, 李树忱, 袁超, 等. 基于SED准则的近场动力学及岩石类材料裂纹扩展模拟[J]. 岩土工程学报, 2021, 43(6): 1109–1117. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202106019.htm MA Peng-fei, LI Shu-chen, YUAN Chao, et al. Simulations of crack propagation in rock-like materials by peridynamics based on SED criterion[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(6): 1109–1117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202106019.htm
[5] CUNDALL P A, HART R D. Numerical modelling of discontinua[J]. Engineering Computations, 1992, 9(2): 101–113. doi: 10.1108/eb023851
[6] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47–65. doi: 10.1680/geot.1979.29.1.47
[7] KOU M M, LIAN Y J, WANG Y T. Numerical investigations on crack propagation and crack branching in brittle solids under dynamic loading using bond-particle model[J]. Engineering Fracture Mechanics, 2019, 212: 41–56. doi: 10.1016/j.engfracmech.2019.03.012
[8] ZHAO G F, XIA K W. A study of mode-I self-similar dynamic crack propagation using a lattice spring model[J]. Computers and Geotechnics, 2018, 96: 215–225. doi: 10.1016/j.compgeo.2017.11.001
[9] SHI G H. Manifold Method of Material Analysis[M]. Minneaplolis: Minesota, 1992: 57–76.
[10] 徐栋栋, 郑宏, 夏开文, 等. 高阶扩展数值流形法在裂纹扩展中的应用[J]. 岩石力学与工程学报, 2014, 33(7): 1375–1387. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201407009.htm XU Dong-dong, ZHENG Hong, XIA Kai-wen, et al. Application of higher-order enriched numerical manifold method to crack propagation[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(7): 1375–1387. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201407009.htm
[11] SHI G H, GOODMAN R E. Discontinuous deformation analysis. a new method for computing stress, strain and sliding of block systems[J]. Internal Medicine Journal, 1988, 44(3): 309–311.
[12] 王士民, 朱合华, 蔡永昌. 非连续子母块体理论模型研究(Ⅰ): 基本理论[J]. 岩土力学, 2010, 31(7): 2088–2094. doi: 10.3969/j.issn.1000-7598.2010.07.012 WANG Shi-min, ZHU He-hua, CAI Yong-chang. A discontinuous sub-block model (Ⅰ): fundamentals[J]. Rock and Soil Mechanics, 2010, 31(7): 2088–2094. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.07.012
[13] 王士民, 朱合华, 蔡永昌. 非连续子母块体理论模型研究(Ⅱ): 实例分析[J]. 岩土力学, 2010, 31(8): 2383–2388. doi: 10.3969/j.issn.1000-7598.2010.08.006 WANG Shi-min, ZHU He-hua, CAI Yong-chang. A discontinuous sub-block model(Ⅱ): case analysis[J]. Rock and Soil Mechanics, 2010, 31(8): 2383–2388. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.08.006
[14] NING Y J, YANG J, AN X M, et al. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework[J]. Computers and Geotechnics, 2011, 38(1): 40–49. doi: 10.1016/j.compgeo.2010.09.003
[15] NING Y J, ZHAO Z Y, SUN J P, et al. Using the discontinuous deformation analysis to model wave propagations in jointed rock masses[J]. CMES-Computer Modeling in Engineering and Sciences, 2012, 89(3): 221–262.
[16] 焦玉勇, 张秀丽, 刘泉声, 等. 用非连续变形分析方法模拟岩石裂纹扩展[J]. 岩石力学与工程学报, 2007, 26(4): 682–691. doi: 10.3321/j.issn:1000-6915.2007.04.004 JIAO Yu-yong, ZHANG Xiu-li, LIU Quan-sheng, et al. Simulation of rock crack propagation using discontinuous deformation analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 682–691. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.04.004
[17] JIAO Y Y, ZHANG X L, ZHAO J. Two-dimensional DDA contact constitutive model for simulating rock fragmentation[J]. Journal of Engineering Mechanics, 2012, 138(2): 199–209. doi: 10.1061/(ASCE)EM.1943-7889.0000319
[18] 徐栋栋, 邬爱清, 李聪, 等. 破裂全过程模拟的改进非连续变形分析方法[J]. 岩土力学, 2019, 40(3): 1169–1178. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903038.htm XU Dong-dong, WU Ai-qing, LI Cong, et al. An improved discontinuous deformation analysis method for simulation of whole fracturing process[J]. Rock and Soil Mechanics, 2019, 40(3): 1169–1178. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903038.htm
[19] XIA M Y, CHEN G Q, YU P C, et al. Improvement of DDA with a new unified tensile fracture model for rock fragmentation and its application on dynamic seismic landslides[J]. Rock Mechanics and Rock Engineering, 2021, 54(3): 1055–1075. doi: 10.1007/s00603-020-02307-9
[20] 张开雨, 夏开文, 刘丰. 基于Voronoi多边形离散的DDA方法模拟岩石破坏[J]. 岩石力学与工程学报, 2021, 40(4): 725–738. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202104007.htm ZHANG Kai-yu, XIA Kai-wen, LIU Feng. Simulation of rock failure by Voronoi-based discontinuous deformation analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(4): 725–738. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202104007.htm
[21] AYATOLLAHI M R, ALIHA M R M, HASSANI M M. Mixed mode brittle fracture in PMMA—An experimental study using SCB specimens[J]. Materials Science and Engineering: A, 2006, 417(1/2): 348–356.
[22] XIA K W, CHALIVENDRA V B, ROSAKIS A J. Observing ideal "self-similar" crack growth in experiments[J]. Engineering Fracture Mechanics, 2006, 73(18): 2748–2755. doi: 10.1016/j.engfracmech.2006.05.001
[23] ZHOU F H, MOLINARI J F, SHIOYA T. A rate-dependent cohesive model for simulating dynamic crack propagation in brittle materials[J]. Engineering Fracture Mechanics, 2005, 72(9): 1383–1410. doi: 10.1016/j.engfracmech.2004.10.011
[24] HA Y D, BOBARU F. Characteristics of dynamic brittle fracture captured with peridynamics[J]. Engineering Fracture Mechanics, 2011, 78(6): 1156–1168. doi: 10.1016/j.engfracmech.2010.11.020
[25] KOSTESKI L, BARRIOS D'AMBRA R, ITURRIOZ I. Crack propagation in elastic solids using the truss-like discrete element method[J]. International Journal of Fracture, 2012, 174(2): 139–161. doi: 10.1007/s10704-012-9684-4
[26] RAMULU M, KOBAYASHI A S. Mechanics of crack curving and branching·a dynamic fracture analysis[J]. International Journal of Fracture, 1985, 27(3/4): 187–201.
[27] WANG T, ZHOU M, LI Y Q, et al. Lattice spring model with angle spring and its application in fracture simulation of elastic brittle materials[J]. Theoretical and Applied Fracture Mechanics, 2020, 106: 102469. doi: 10.1016/j.tafmec.2019.102469
-
期刊类型引用(8)
1. 胡静静，余丁浩，李钢，王睿，张晗，苏璞. 考虑土-结相互作用的大型结构高效地震分析方法. 工程力学. 2024(03): 135-149 . 
百度学术
2. 邓铭江，孙奔博，许佳. 高沥青混凝土心墙坝抗震安全评估研究进展. 水力发电学报. 2023(03): 82-91 . 百度学术
3. 刘京茂，邵伟峰，邹德高，屈永倩，迟福东. 基于弹塑性模型参数反演的高土石坝地震响应预测. 人民长江. 2023(09): 184-190+205 . 百度学术
4. 张亚国，肖书雄，杨赟，李同录. 一种状态变量相关的非饱和接触面弹塑性模型及验证. 岩土工程学报. 2023(10): 2081-2090 . 本站查看
5. 左双英，付丽，陈世万，吴道勇. 基于Interface改进算法的水工隧洞衬砌受力分析. 华中科技大学学报(自然科学版). 2022(01): 99-104 . 百度学术
6. 王雅甜，杨春山，黄福杰. 紧邻既有结构的灌注桩施工力学行为研究. 南昌工程学院学报. 2022(03): 41-46 . 百度学术
7. 邹德高，彭俊，李俊超，陈涛，刘京茂，王建全，陈楷. 沥青混凝土面板堆石坝强震变形模式和极限抗震能力分析. 水电与抽水蓄能. 2022(06): 15-20 . 百度学术
8. 邹德高，刘京茂，汪玉冰，李俊超，李多，陈涛，王锋. 西部某水电站覆盖层地基离心机动力试验数值模拟. 水电与抽水蓄能. 2021(01): 23-27 . 百度学术
其他类型引用(12)
计量
- 文章访问数: 285
- HTML全文浏览量: 39
- PDF下载量: 133
- 被引次数: 20
