DEM investigation on tunnel excavation of deeply-situated composite rock mass with different strength ratios
-
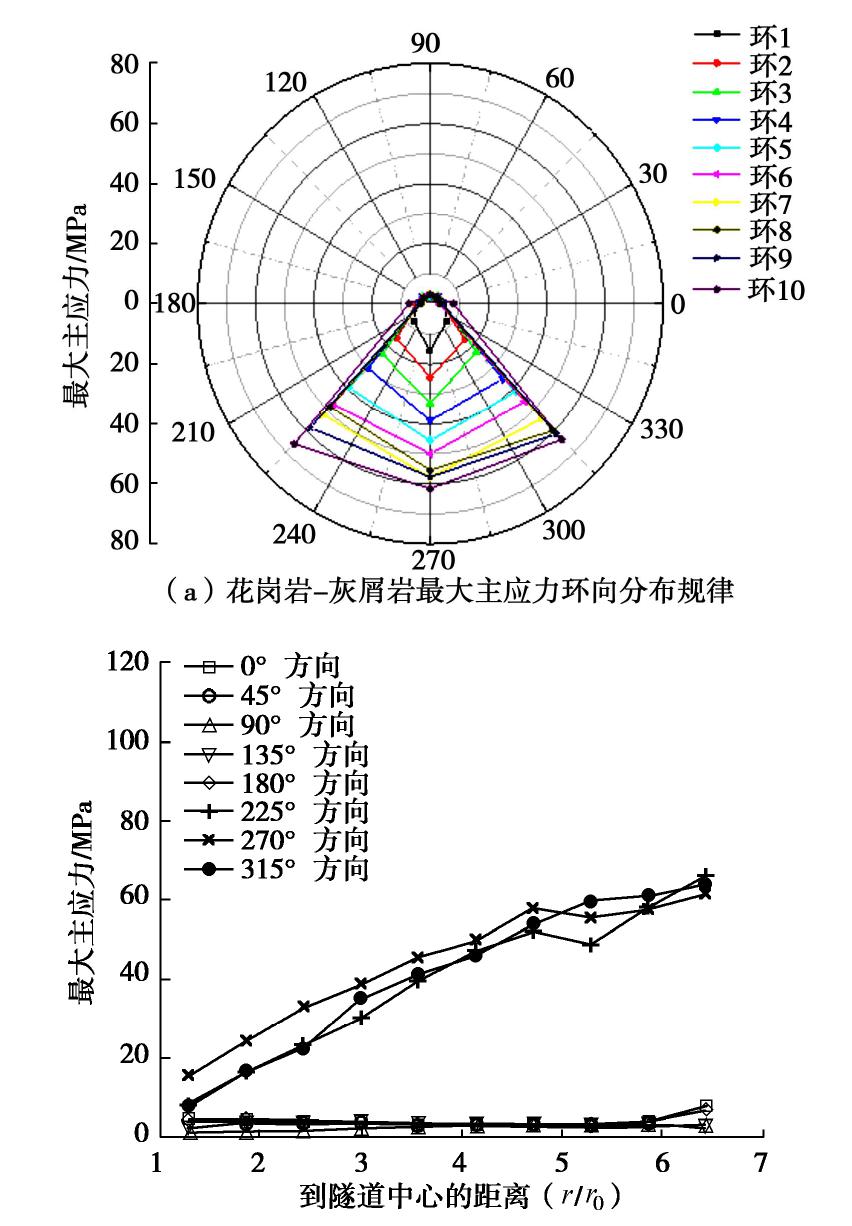
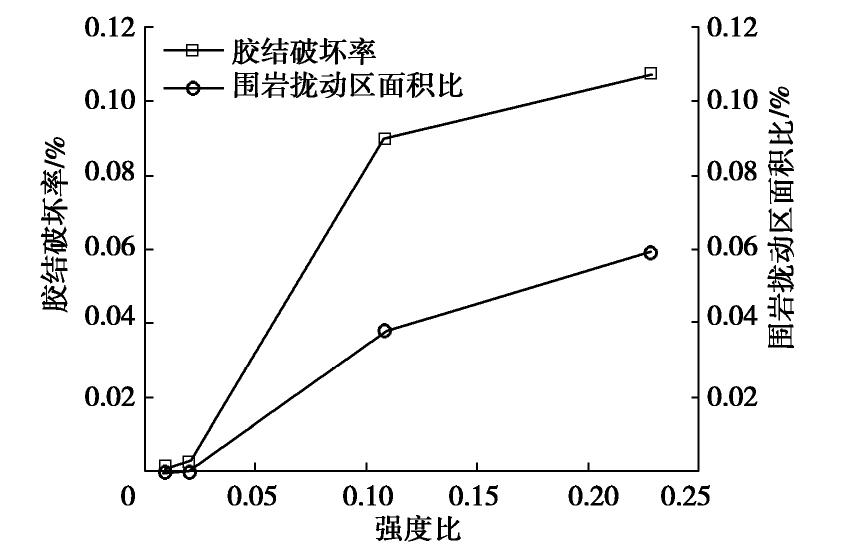
摘要: 深部复合岩体隧道开挖过程中,抗压强度比是影响围岩稳定的重要因素。引入考虑胶结尺寸的微观接触模型,采用二维离散元方法对深部上软下硬复合岩体隧道开挖进行了数值模拟,分析了强度比对围岩胶结破坏、最大主应力及扰动区的影响。结果表明,随着抗压强度比的增大,隧道开挖引起的围岩胶结破坏率与扰动区逐渐增大,胶结破坏形式以拉剪破坏为主；最大主应力沿围岩环向呈下垂的滴水状分布,沿径向在软岩中先减小后增大,在硬岩中逐渐增大；随着抗压强度比的增大,最大主应力沿径向在硬岩区变化幅度减小,在软岩区变化幅度增大。Abstract: The strength ratio is an important factor affecting the stability of the surrounding rock during tunnel excavation of deeply-situated composite rock mass. A size-dependent bond contact model is implemented to the software of the two-dimensional distinct element method (DEM) to simulate the tunnel excavation of deeply-situated up-soft/low-hard composite rock mass. The influences of strength ratio on bond breakage, the maximum principal stress and disturbance zone of the surrounding rock are investigated. The results show that the bond breakage ratio and the disturbed area ratio caused by tunnel excavation gradually increase with the increase of strength ratio of composite rock mass, and the bond breakage is mainly caused by bond tensile failure. The maximum principal stress is distributed in teardrop shape in the circumferential direction of the surrounding rock, while in the radial direction it decreases firstly and then increases in the soft rock and increases in the hard rock. Moreover, in the radial direction, with the increase of the strength ratio, the variation range of the maximum principal stress decreases in the hard rock but increases in the soft rock.
-
0. 引言
中国土壤重金属污染形势严峻，据2014年发布的《全国土壤污染状况调查公报》，无机重金属污染占全部超标点位的82.18%，其中砷点位超标率为2.7%，特别是在长三角、珠三角等区域污染较为突出。砷主要来源于人类工农业生产活动，排放的砷在降雨淋滤作用下进入地下从而造成土壤污染，在迁移的过程中，将发生吸附与解吸、溶解与沉淀、氧化与还原等一系列物理化学作用，其中吸附是重要的控制因素[1]。砷是变价元素，在土中多为As(III)和As(V)两种价态、以无机阴离子基团的形式存在，其中在地表环境主要为五价（H2AsO4-和HAsO42-），而在深部还原环境中主要为三价（H3AsO3）[2]，因此砷在土中的吸附有别于一般重金属阳离子（如Pb(II)、Cd(II)等）：黏土矿物表面一般带负电荷，故Pb(II)等较易被土吸附，而以阴离子基团形式存在的砷只能和矿物中氧化物表面的正电荷相结合，不易被吸附[3]。研究砷的吸附特性和机理对砷污染防治具有重要现实意义。
当前对重金属阳离子吸附的研究较多，而基团阴离子吸附的研究相对较少。Goldberg[4]研究了不同黏土矿物对砷的吸附, 发现吸附量的大小顺序为伊利石 > 高岭石 > 蒙脱石，而Mohapatra等[5]得到吸附量大小顺序为高岭石 > 蒙脱石 > 伊利石，分别为0.86，0.64，0.52 mg/g。通常3种黏土矿物中，蒙脱石对重金属阳离子的吸附能力最强，上述研究表明砷在黏土矿物中的吸附规律与之不同。一般说来，土中的阳离子或正电荷越多，土表面的吸附位就越高，砷越易被吸附，如土壤胶粒、无定型铁铝氧化物等含量越高，对砷的吸附能力越强[6]。Shaw[7]发现土中有机质官能基团（如-COOH，-OH）的存在，会促使砷发生络合和螯合从而产生外层吸附。Lee等[8]研究发现随pH升高砷的吸附性增强，而郭华明等[9]研究了山阴地区地下水中砷富集的影响因素，发现高pH、高磷酸根含量和强还原环境不利于砷的吸附。综上所述，砷在土中的吸附与土的矿物成分、土中正电荷量、溶液pH和氧化还原环境等因素有关，是一个复杂的地球物理化学过程，当前对砷在土中吸附机理的认识尚不深入，尚缺少基团阴离子与重金属阳离子吸附特性的对比试验研究。
当前对土的渗透系数随重金属含量变化的研究也主要关注重金属阳离子。查甫生等[10]研究发现，随铅、锌浓度增加黏土渗透系数逐渐变大；范日东等[11]发现膨润土渗透系数随铅、镉浓度增加而增大；Du等[12]试验发现铅污染土固化体渗透系数随铅浓度增大而增大、随溶液pH降低而增大。已有的研究表明，随重金属阳离子浓度增加，扩散层结合水膜厚度减小，黏土颗粒彼此靠近，土颗粒出现团聚现象导致孔隙变大，另外，重金属离子侵蚀了土颗粒间的联结结构、腐蚀了部分胶体也导致孔隙变大，使得渗透性增强[13]。但目前尚未见到有砷含量对土渗透系数影响的研究。
本文通过批式吸附（Batch）试验对比研究了阴离子基团形式的重金属As(V)和阳离子Pb(II)在粉质黏土中的吸附特性，通过吸附模型分析和微观测试揭示了As(V)吸附机理，通过渗透试验研究了吸附重金属后土的渗透系数。
1. 材料与方法
1.1 试验材料
试验用土属于上海广泛分布的②1层褐黄色粉质黏土，取自某基坑深度1.5~2 m处。X射线荧光光谱分析（XRF）表明土的化学成分以SiO2为主，含量为62.81%，其次为Al2O3含量为13.63%，Fe2O3含量为5.34%，CaO为3.82%，K2O为2.26%，MgO为2.25%，Na2O为1.24%，TiO2为0.78%，MnO2为0.10%，矿物成分主要为石英（64.7%）、白云母（24.0%）和斜绿泥石（11.3%）。土的物理化学性质：相对质量密度为2.71，液限为38.1%，塑限为24.3%，最大干密度为1.65 g/cm3，天然含水率为12.4%，最优含水率为20.4%，阳离子交换量为7.8 cmol/kg，天然pH为7.10。土样经风干后置于105℃的烘箱中烘24 h，粉碎后过0.25 mm筛，储存在密封袋中备用。
试验采用砷酸钠和硝酸铅的分析纯配制重金属溶液，分别将4.165，1.599 g的Na2HAsO4·7H2O和Pb(NO3)2与去离子水在1 L定容瓶中混合得到1000 mg/L的母液。后续试验中所用的不同质量浓度溶液由母液按一定倍数稀释得到。
1.2 吸附试验方法和方案
采用Batch试验研究粉质黏土对Pb(II)和As(V)的吸附特性。将一定体积和浓度的重金属溶液与一定质量的粉质黏土混合于聚丙乙烯管中，置于恒温振荡器中在转速180 r/min下振荡一定时间，在离心机中3000 r/min转速下离心30 min使固液分离，取上清液用电感耦合等离子发射光谱仪（ICP）测重金属浓度，利用差减法获得吸附量qe：
qe=(C0−Ce)Vm， (1) 式中，C0为重金属初始质量浓度（mg/L），Ce为吸附平衡后上清液中重金属浓度（mg/L），V为溶液体积（L），m为土的质量（g）。
研究了土水比、反应时间、重金属浓度、溶液pH和温度等因素对吸附的影响，各试验的具体控制条件如表 1所示。考虑到吸附性的差异，对As(V)和Pb(II)试验时采用了不同的土水比和初始质量浓度。考察土水比的影响时，Pb(II)试验的土水比从4 g/L变化到40 g/L，As(V)的从10 g/L变化到60 g/L；为了考察反应时间的影响，调节振荡时间10~1440 min；为了考察重金属浓度的影响，Pb(II)初始质量浓度取10~300 mg/L，As(V)为10~250 mg/L；为了考察溶液pH的影响，调节溶液初始pH在2.0~10.0；为了考察试验温度的影响，温度取25，35，45℃。
表 1 批式吸附试验方案Table 1. Schemes of batch tests控制条件 土水比/(g·L-1) 初始质量浓度/(mg·L-1) 时间/ min 溶液初始pH 温度/℃ 土水比 Pb(II) 4~40 100 1440 7.0 25 As(V) 10~60 50 反应时间 Pb(II) 6 100 10~1440 7.0 25 As(V) 40 50 重金属浓度 Pb(II) 6 10~300 1440 7.0 25 As(V) 40 10~250 溶液pH Pb(II) 6 100 1440 2.0~10.0 25 As(V) 40 50 温度 Pb(II) 6 150 1440 7.0 25~45 As(V) 40 100 1.3 吸附分析模型
（1）吸附动力学模型
本文使用准二阶动力学模型、颗粒内扩散模型和Elovich模型来研究As(V)和Pb(II)的吸附速率。准二阶动力学模型可用于描述整个吸附过程，其线性形式为[14]
tqt=1k2qe2+tqe， (2) 式中，qt为t时刻吸附量，k2为准二级动力学吸附速率常数（g/mg/min）。
颗粒内扩散模型主要用于描述吸附质在颗粒内部的扩散过程，通过计算颗粒内扩散速率常数来阐述吸附机理并确定控速步骤[15]：
qt=kidt0.5+C， (3) 式中，kid为颗粒内扩散的速率常数，C为与边界层厚度有关的常数。当C=0时，即边界层厚度为零，颗粒内扩散是唯一的控速步骤；当C≠0时，即存在一定程度的边界层控制，吸附速率由液膜扩散和颗粒内扩散共同控制。
Elovich模型描述了在能量异质固体表面上的化学吸附，适用于活化能发生较大变化的过程，其经验公式为[16]
qt=1βln(αβ)+1βlnt， (4) 式中，α为吸附速率常数，β为与吸附剂表面覆盖程度及化学吸附活化能有关的参数（g/mg）。
（2）等温吸附模型
分别使用Langmuir、Freundlich与Dubinin- Radushkevich（D-R）模型拟合等温吸附试验数据。其中Langmuir模型假定吸附剂表面均匀且为单分子层吸附，可以反映吸附容量，线性表达式为
ceqe=ceqmax+1bqmax， (5) 式中，qmax为吸附容量（mg/g），b为和能量相关的常数（L/mg）。Langmuir模型的基本特征可以用无量纲因子RL=1/(1+bc0)来描述，RL为0~1表示吸附是有利的，RL > 1表示吸附不利，RL=1表示吸附可逆，RL=0表示吸附不可逆[17]。
Freundlich模型是描述非均质表面吸附系统的经验表达式：
lgqe=lgKF+1NFlgce， (6) 式中，KF为吸附平衡常数，NF为吸附强度，可用于定量描述吸附难易程度。
D-R模型假定吸附是溶质在孔隙中填充的过程，可用于确定吸附自由能和吸附类型[18]：
lnqe=lnqm−βε2， (7) 式中，qm为单层吸附容量，β为平均吸附能（mol2/kJ2），ε为Polanyi势。一般可以通过下式计算吸附自由能E，从而判定主要的吸附机理：
E=−1√2β。 (8) 若1 < |E|≤8 kJ/mol，表明吸附过程主要是物理吸附；若8 < |E| < 16 kJ/mol，表明化学吸附是主要机制[17]。
（3）吸附热力学模型
根据吉布斯自由能理论[19]：
ΔG0=−RTlnKc， (9) ΔG0=ΔH0−TΔS0， (10) 式中，R为理想气体常数（J/mol/K），T为温度（K）， Kc为分布系数（g/L），ΔG0，ΔH0分别为吉布斯自由能和焓的变化（J/mol），ΔS0为熵的变化（J/mol/K）。
式（9），（10）可以线性化为
lnKc=−ΔH0RT+ΔS0R。 (11) 则ΔH0，ΔS0可由吸附热力学拟合直线的斜率和截距获得。ΔG0，ΔH0和ΔS0可用于分析吸附过程的热力学行为。
1.4 吸附重金属后的微观测试
进行了粉质黏土吸附重金属前后的XRD，SEM，EDS，FTIR测试，从矿物组成、微观形貌、元素组成、官能团等细微观角度进一步阐述吸附机理。
1.5 渗透试验
为了研究重金属含量对渗透系数的影响，配制重金属含量分别为0，500，1000，5000，10000 mg/kg（即相对含量分别为0%，0.05%，0.1%，0.5%，1%）的土样，于渗透仪中测其渗透系数。制样时，称取前述密封保存的干土，根据拟控制的重金属含量称取相应质量比例的重金属，按最优含水率（20.4%）量取蒸馏水，先将砷酸钠或硝酸铅溶解在蒸馏水中，再将溶液与土充分拌合均匀。最终试样为直径3.8 cm、高度为2 cm的土柱，根据最优干密度（1.65 g/cm3）称取所需土，放入制样模具内用液压千斤顶压实得到。不同重金属含量的渗透试验采用蒸馏水，采用自下而上的入渗方式，控制水力梯度为250。量测并记录出流量，待出流速度稳定后（此时试样达到饱和），根据出流速度由达西定律计算得到渗透系数。之后采用重金属含量0.1%的土进行不同pH下的入渗试验，用HCl和NaOH溶液调整入渗的pH分别为3，5，7，9，研究入渗溶液pH对渗透系数的影响。
2. 结果与分析
2.1 吸附试验结果
（1）土水比
不同土水比的试验结果如图 1所示，因As(V)和Pb(II)的吸附量存在数量级上的差别，图中使用“双Y轴”，左边轴为Pb(II)的，右边为As(V)的。可见随着土水比增大，单位质量土上的Pb(II)吸附量减小，而As(V)的吸附量没有明显减小的趋势。究其原因，是Pb(II)在粉质黏土上容易发生吸附，土水比高时土上出现了剩余的吸附点位；而以阴离子团形式存在的As(V)不易在带正电荷的土颗粒表面发生吸附，试验的土水比范围内，土中对应As(V)的吸附点位没有剩余，即仍为饱和吸附状态。
因此，后续研究其他因素对吸附的影响时，对As(V)和Pb(II)采用了不同的土水比，Pb(II)取6 g/L，As(V)取40 g/L。同样原因，As(V)溶液初始质量浓度取50 mg/L，也低于Pb(II)的100 mg/L。
（2）反应时间
吸附量随时间的变化过程如图 2所示，吸附速率随时间逐渐变慢：反应初始阶段黏土表面可用吸附点位较多，吸附较快，随着反应进行吸附点位减少，吸附速度减缓，并在约720 min时达到吸附平衡。除了平衡吸附浓度明显不同，As(V)和Pb(II)的吸附量–时间曲线基本没有差别。
（3）重金属浓度
随重金属初始浓度的增加，吸附量增加（图 3），但Pb(II)增加的速度逐渐变慢，这是因为土水比一定的情况下，可提供的总吸附点位有限，在Pb(II)吸附试验中，吸附已渐趋饱和；As(V)的吸附量随浓度线性增加，说明As(V)在溶液与黏土表面的分配遵循某一比例，这与Pb(II)显不同。
（4）溶液pH
溶液pH对重金属吸附有很大影响（图 4）。pH从2.0变化到6.0，Pb(II)吸附量从3.11 mg/g增加到16.58 mg/g，之后在碱性条件下吸附量变化不明显，故Pb(II)最佳吸附pH为6.0。在酸性条件下Pb(II)吸附量较低，主要因为Pb(II)与土表面的正电荷（Si–OH2+）之间是静电斥力，另外，溶液中H+也会竞争吸附点位，碱性条件下黏土表面带净负电荷，与Pb(II)间转变为静电引力导致吸附量增加。As(V)吸附量在2.0~10.0变化不大，在碱性条件下略有减小，这是因为pH为2.0~7.0时，As(V)主要存在形式是H2AsO−4，pH在7.0~10.0时则主要以HAsO2−4存在[20]，酸性条件下，源自氧化钙溶解的HCO−3与As(V)竞争从而抑制吸附，碱性条件下黏土表面带负电，静电排斥导致吸附减少。As(V)的最佳吸附pH为6.0，对应吸附量为0.48 mg/g。
2.2 吸附机理分析
（1）吸附动力学分析
吸附动力学模型的拟合如图 5所示，参数列入表 2。其中准二阶动力学拟合的R2最接近1，拟合所得最大吸附量qe也与试验值接近，因此准二阶动力学模型能够很好地描述粉质黏土对As(V)和Pb(II)吸附的动力学行为。
表 2 Pb(II)和As(V)的吸附动力学参数Table 2. Parameters of adsorption kinetics of Pb(II) and As(V)重金属 准二级动力学模型 颗粒内扩散模型 Elovich模型 k2/(g·mg-1·min-1) qe/(mg·g-1) R2 kid/(mg·g-1·min-1/2) C/(mg·g-1) R2 α/(mg·g-1·min-1) β/(g·mg-1) R2 Pb(II) 4.13×10-3 16.52 1.000 9.75×10-2 13.27 0.952 2.22×107 1.51 0.929 As(V) 1.38×10-1 0.48 1.000 3.70×10-3 0.37 0.886 1.25×103 37.04 0.974 颗粒内扩散模型拟合结果（图 5（b））表明，Pb(II)的qt与t1/2大致呈线性关系，拟合线没有通过原点，即C≠0，说明颗粒内扩散和液膜扩散都是吸附速率控制因素；而As(V)的拟合线近似过原点，说明颗粒内扩散是主要的速率控制步骤。由拟合的kid（图中斜率）可见，Pb(II)的吸附速率远大于As(V)。
As(V)和Pb(II)吸附的qt–lnt基本呈线性关系（图 5（c）），拟合的R2分别为0.929，0.974，表明Elovich模型可以描述As(V)和Pb(II)的吸附动力学行为，根据模型适用性，说明粉质黏土对As(V)和Pb(II)的吸附均以化学吸附为主。
（2）吸附等温线
Langmuir，Freundlich与D-R模型拟合的吸附等温线如图 6所示，参数列入表 3。Pb(II)的Langmuir拟合R2接近1，随着重金属浓度增加，RL值从0.38降至0.02，表明粉质黏土对Pb(II)吸附有利，吸附趋势上逐渐不可逆；而对As(V)的拟合效果较差（R2仅为0.749），RL从0.83降至0.17，表明粉质黏土对As(V)的吸附性弱于Pb(II)。
![]()
图 6 Langmuir、Freundlich与D-R吸附等温线Figure 6. Adsorption isotherms of Langmuir, Freundlich and D-R models表 3 Pb(II)和As(V)的等温吸附参数Table 3. Parameters of adsorption isotherm of Pb(II) and As(V)重金属 Langmuir模型 Freundlich模型 D-R模型 b/(L·mg-1) qmax/(mg·g-1) R2 KF NF R2 β/(mol2·kJ-2) qm/(mol·g-1) |E|/(kJ·mol-1) R2 Pb(II) 0.16 26.46 0.993 2.54 4.53 0.952 1.74×10-3 2.13×10-4 16.95 0.977 As(V) 0.02 2.83 0.749 0.16 1.89 0.957 4.87×10-3 0.83×10-4 10.13 0.933 图 6（b）中Freundlich模型对Pb(II)和As(V)拟合的R2大于0.95，lgqe–lgce之间均为线性关系，Pb(II)的吸附强度NF拟合值为4.53，明显大于2，表明易于吸附，而砷的NF值为1.89，在1~2属于中等难吸附。
图 6（c）中lnqe–ε2为线性关系，D-R模型拟合得到Pb(II)和As(V)的吸附自由能E分别为16.95，10.13 kJ/mol，表明吸附机制都以化学吸附为主，与前述动力学分析结果一致。
（3）吸附热力学分析
由As(V)和Pb(II)的吸附热力学拟合（图 7）得到模型中的ΔH0，ΔS0和ΔG0值，列入表 4。Pb(II)的ΔH0值为正，说明吸附是吸热过程；As(V)的ΔH0为负，吸附为放热过程。Pb(II)的ΔS0为正，表明吸附过程中系统的自由度增加；而As(V)的ΔS0为负，表明系统的自由度随吸附而降低。Pb(II)的ΔG0随着温度升高而减小，表明温度高有利于吸附；As(V)的ΔG0随着温度的升高而增加，因其吸附过程放热，所以温度高不利于砷的吸附。
表 4 Pb(II)和As(V)吸附的热力学参数Table 4. Thermodynamic parameters of Pb(II) and As(V)重金属 T/K ∆G0/(kJ·mol-1) ∆H0/(kJ·mol-1) ∆S0/(J·mol-1·K-1) R2 Pb(II) 298 -15.29 37.16 176.40 0.949 308 -17.53 318 -18.79 As(V) 298 -7.40 -70.87 -224.70 0.954 308 -6.05 318 -2.86 2.3 吸附重金属后的微观测试结果
粉质黏土吸附Pb(II)和As(V)前后的XRD图谱如图 8所示，分析发现吸附重金属后各特征衍射峰位置无变化，说明吸附Pb(II)和As(V)后并未引入其他晶体杂相；各衍射峰宽无变化，说明结晶程度无变化；按布拉格方程计算的晶格间距无明显变化，说明吸附主要发生在颗粒表面而非晶格内部。
![]()
图 8 粉质黏土吸附重金属前后的XRD图谱Figure 8. XRD patterns of silty clay before and after adsorptionSEM所得的微观形貌特征（图 9）表明，原土具有多孔结构，颗粒棱角较分明，富含晶体缺陷，这些缺陷可提供吸附点位；吸附Pb(II)后，颗粒表面稍显光滑和平坦，部分颗粒出现团聚；吸附As(V)后颗粒更加分散，粒间孔隙变小。图 9同时给出了EDS分析结果，可见原土中主要元素为Si，O，Al，Fe，K，Mg，Ca，Na和Ti，表明土中可交换的阳离子有Al3+，Fe2+，K+，Mg2+，Ca2+和Na+等，吸附重金属后可观察到相应的信号峰，但相比土中原有元素峰值较低，说明量较少。
![]()
图 9 粉质黏土吸附重金属前后的SEM和EDS图Figure 9. SEM and EDS of silty clay before and after adsorption研究了土中与吸附有关的官能团，FTIR图谱如图 10所示，仔细分析发现吸附重金属后官能区吸收峰位置有稍许偏移，如原土中3429 cm处的吸收峰代表羟基（-OH）的伸缩振动[21]，吸附Pb(II)和As(V)后峰值分别移动至3436，3434 cm处，说明该官能团参与了吸附，吸收峰向高频方向偏移，说明吸附重金属引起了土表面电荷分布的变化，诱导效应导致电负性增强。
![]()
图 10 粉质黏土吸附重金属前后FTIR图谱Figure 10. FTIR patterns of silty clay before and after adsorption2.4 渗透试验结果分析
渗透系数随土中重金属含量的变化如图 11所示。随着土中Pb(II)含量增加，渗透系数逐渐增大，特别是当Pb(II)含量超过0.5%后增大较明显，这是因为Pb(II)通过离子交换和浓度作用使双电层厚度减小，土颗粒团聚，土中大孔隙增多[13]。而As(V)对渗透系数的影响则相反，随着土中As(V)含量增加，渗透系数逐渐减小，含有0.5%的As(V)时渗透系数约为原土的1/3，这是因为As(V)以阴离子基团形式存在，促进了表面带负电的土颗粒的分散状态，从而导致渗透系数减小。
![]()
图 11 土中重金属含量对渗透系数的影响Figure 11. Effects of heavy metal content on hydraulic conductivity对0.1%重金属含量的土进行不同pH下的入渗试验，发现渗透系数随入渗溶液酸性增强而增大（图 12），其中Pb(II)的增大明显，而As(V) 的不明显。这是因为酸会溶蚀土中胶体、可溶盐和游离氧化物等成分，削弱土颗粒之间的连接，使孔隙增大；而随着pH增大，Pb(II)易生成沉淀、堵塞孔隙，As(V)则主要由于碱性条件下表面带负电的土颗粒离间斥力增强、颗粒进一步分散，渗透系数减小。
3. 结论
本文主要揭示了As(V)在粉质黏土中的吸附与常见重金属阳离子Pb(II)的异同，研究了各因素对吸附的影响规律，通过吸附动力学、吸附等温线和吸附热力学模型以及微观分析揭示吸附机制，另外研究了土渗透系数随重金属含量和pH的变化规律，得到以下4点结论。
（1）As(V)在粉质黏土上的最大吸附量为0.48 mg/g，远低于铅的16.52 mg/g，As(V)的吸附试验需要更高的土水比；随溶液浓度增加，Pb(II)吸附量逐渐减小，而As(V)吸附量线性增加；随溶液pH增加Pb(II)吸附量增加，而在碱性条件下As(V)吸附量稍有减小。
（2）As(V)和Pb(II)的吸附都符合准二阶动力学模型，都是以化学吸附为主，颗粒内扩散和液膜扩散是Pb(II)吸附速率控制因素，而颗粒内扩散是As(V)吸附的主要控速因素；3种等温吸附模型都适合Pb(II)，而Langmuir模型对As(V) 拟合较差，Pb(II)属于易吸附，而As(V)属于中等难吸附；Pb(II)的吸附是吸热过程，温度高有利于Pb(II)吸附，而As(V)的吸附过程放热，吸附量随温度升高而降低。
（3）微观测试表明，粉质黏土对As(V)和Pb(II)的吸附基本发生在晶格以外；吸附Pb(II)后土颗粒团聚导致孔隙变大，而吸附As(V)后土颗粒进一步分散、孔隙变小；土颗粒表面羟基等官能团参与了吸附过程。
（4）渗透试验结果表明，渗透系数随着土中Pb(II)含量增加而增大，随着土中As(V)含量增加而减小，主要因为阳离子促使土粒团聚，而阴离子促使土粒分散；酸性条件下含As(V)和Pb(II)的土渗透系数均增大。
-
![]()
图 1 立方体抗压强度与层理倾角的关系
Figure 1. Relationship between cubic compressive strength and bedding angle
![]()
图 6 花岗岩-灰屑岩最大主应力分布特征
Figure 6. Distribution characteristics of maximum principal stress in granite-limestone
![]()
图 7 不同抗压强度比与胶结破坏率及扰动区面积比关系曲线
Figure 7. Bond breakage rates and disturbed area ratios under different strength ratios
表 1 岩样微观参数
Table 1 Microscopic parameters of rock specimens
岩石 类型 颗粒部分 胶结部分 ρ颗粒密度/(kg·m-3) kn颗粒法向刚度/(N·m-1) ks颗粒切向刚度/(N·m-1) μ颗粒摩擦系数 β颗粒抗转动系数 hmax最大胶结厚度/m σt胶结拉伸强度/Pa σc胶结压缩强度/Pa Eb胶结弹性模量/N sp胶结延伸率 花岗岩 2700 6.50×1010 4.33×1010 1.0 1.5 1.30×104 1.00×109 3.00×1010 3.75×109 0.15 大理岩 2700 3.10×1010 2.05×1010 1.0 1.5 1.30×104 1.60×109 1.07×1010 1.07×109 0.15 绿片岩 2700 9.00×109 6.00×109 0.3 0.5 1.30×104 1.50×108 2.50×109 2.50×108 0.15 灰屑岩 2700 9.00×108 3.6×108 0.7 0.6 1.30×104 2.18×107 2.30×108 1.10×107 0.15 
下载: 导出CSV
表 2 岩石宏观参数
Table 2 Macroscopic parameters of rocks
参数 弹性模量E/GPa 泊松比μ 巴西劈裂强度σt/MPa 单轴抗压强度σc/MPa 黏聚力c/MPa 内摩擦角φ/(°) 花岗岩 69.0 0.260 16.7 200.00 50.00 48.00 大理岩 30.0 0.210 20.0 101.24 24.60 35.23 绿片岩 3.54 0.360 1.00 19.47 4.47 25.26 灰屑岩 0.29 0.300 0.34 2.15 0.60 29.00
下载: 导出CSV
表 3 DEM试样宏观力学参数
Table 3 Macroscopic mechanical parameters of DEM specimens
参数 弹性模量E/GPa 泊松比μ 巴西劈裂强度σt/MPa 单轴抗压强度σc/MPa 黏聚力c/MPa 内摩擦角φ/(°) 花岗岩 68.070 0.254 18.360 198.200 43.000 40.41 大理岩 29.065 0.243 15.100 105.940 28.200 34.23 绿片岩 3.730 0.359 0.978 22.671 7.900 23.22 灰屑岩 0.295 0.440 0.325 2.040 0.646 30.10
下载: 导出CSV
表 4 不同抗压强度比深部复合岩体
Table 4 Composite rock mass with different strength ratios
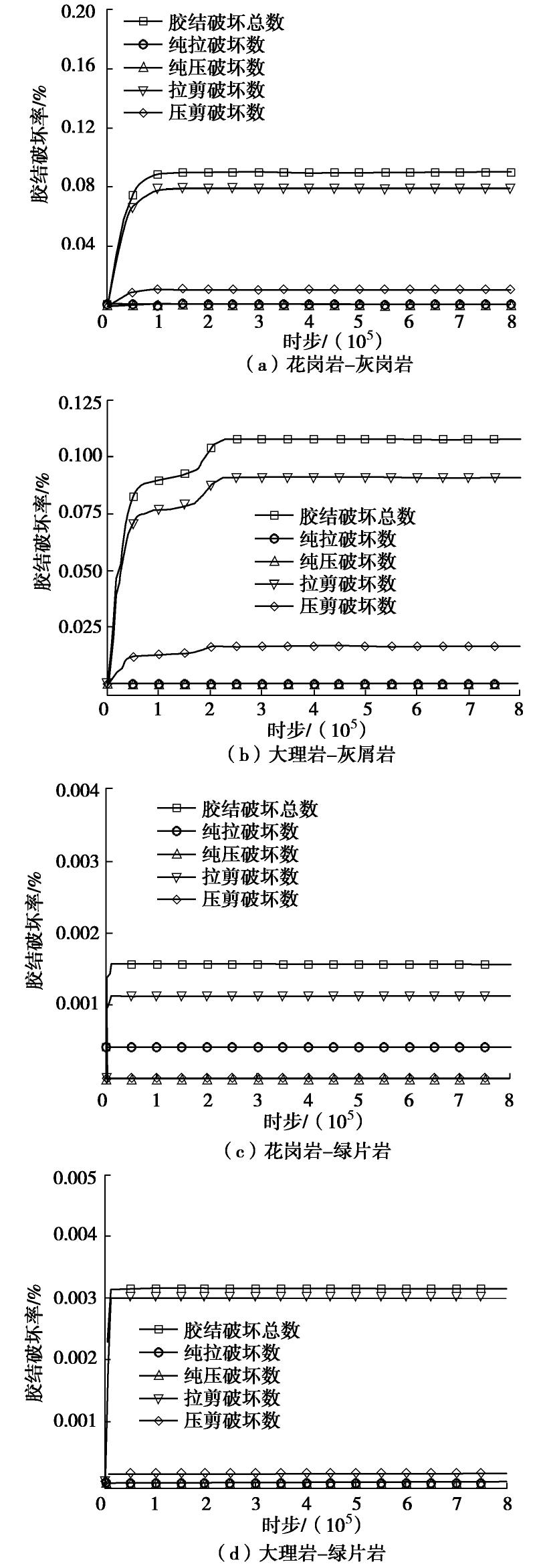
复合岩层组合 上部 下部 抗压强度比（上∶下） 具体比值 组合一 绿片岩 花岗岩 22.671∶198.2 0.114 组合二 灰屑岩 花岗岩 2.04∶198.2 0.010 组合三 绿片岩 大理岩 22.671∶105.94 0.214 组合四 灰屑岩 大理岩 2.04∶105.94 0.019
下载: 导出CSV
表 5 最终胶结破坏率及对应时步
Table 5 Final bond breakage rates and corresponding time steps
组合 花岗岩-灰屑岩 大理岩-灰屑岩 花岗岩-绿片岩 大理岩-绿片岩 时步 123301 213300 4100 9100 胶结破坏率/% 0.0899 0.1070 0.00143 0.00315
下载: 导出CSV
-
[1] 高文艺. 深部复合地层TBM隧道变形时空演化规律研究[D]. 徐州: 中国矿业大学, 2015. GAO Wen-yi. Study on Space-time Evolution Laws of Surrounding Rockmass Deformation in Deep Mixed Strata Tunnel Excavated by TBM[D]. Xuzhou: China University of Mining and Technology, 2015. (in Chinese)
[2] 黄锋, 周洋, 李天勇, 等. 软硬互层岩体力学特性及破坏形态的室内试验研究[J/OL]. 煤炭学报: 1-10[2020-03-17]. doi: 10.13225/j.cnki.jccs.2019.1388. [3] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[4] 蒋明镜. 现代土力学研究的新视野—宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[5] 王志伟, 乔春生, 宋超业. 上软下硬岩质地层浅埋大跨隧道松动压力计算[J]. 岩土力学, 2014, 35(8): 2342-2352. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201408030.htm WANG Zhi-wei, QIAO Chun-sheng, SONG Chao-ye. Calculation method of relaxation pressure of shallow large span tunnel in up-soft/low-hard rock stratum[J]. Rock and Soil Mechanics, 2014, 35(8): 2342-2352. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201408030.htm
[6] JIANG M J, ZHANG N, CUI L, et al. A size-dependent bond failure criterion for cemented granules based on experimental studies[J]. Computers and Geotechnics, 2015, 69: 182-198. doi: 10.1016/j.compgeo.2015.05.007
[7] JIANG M J, LIU W, XI B L, et al. Preliminary DEM analysis on micro-mechanical behavior of the composite cemented granules under complex stress conditions[C]//Proceedings of the 7th International Conference on Discrete Element Methods, 2016, Singapore.
[8] 张春深, 陈祥荣, 侯靖, 等. 锦屏二级水电站深埋大理岩力学特性研究[J]. 岩石力学与工程学报, 2010, 29(10): 1999-2009. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201010009.htm ZHANG Chun-shen, CHEN Xiang-rong, HOU Jing, et al. Study of mechanical behavior of deep-buried marble at jinping hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 1999-2009. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201010009.htm
[9] MARTIN D C. The strength of massive Lac du Bonnet Granite Around Underground Opeanings[D]. Winnipeg: University of Manitoba, 1993.
[10] 黄书岭. 高应力下脆性岩石的力学模型与工程应用研究[D]. 武汉: 中国科学院研究生院(武汉岩土力学研究所), 2008. HUANG Shu-ling. Study on Mechanical Model of Brittle Rock under High Stress Condition and Its Engineering Applications[D]. Wuhan: Graduateschool of the Chinese Academy of Sciences (Wuhan Institute of Geotechnical Mechanics), 2008. (in Chinese)
[11] 吕品. 锦屏水电站绿片岩段扩挖及落底开挖稳定研究[D]. 大连: 大连理工大学, 2011. LÜ Pin. The Research of Enlarged Excavation and Surrounding Rock Stability in The Green Schist Area of Jinping Hydropower Station[D]. Dalian: Dalian University of Technology, 2011. (in Chinese)
[12] CIANTIA M O, CASTELLANZA R, PRISCO C D. Experimental study on the water-induced weakening of calcarenites[J]. Rock Mechanics and Rock Engineering, 2015, 48(2): 441-461. doi: 10.1007/s00603-014-0603-z
[13] PARMA M, NOVA R. Effects of bond crushing on the settlements of shallow foundations on soft rocks[J]. Géotechnique, 2011, 61(3): 247-261. doi: 10.1680/geot.7.00183
[14] 杨开新, 蒋明镜, 陈有亮, 等. 不同岩性下TBM滚刀破岩过程离散元分析[J]. 水资源与水工程学报, 2019, 30(2): 198-204, 211. YANG Kai-xin, JIANG Ming-jing, CHEN You-liang, et al. Discrete element method analysis on rock breaking process induced by TBM cutters under different lithologies[J]. Journal of Water Resources and Water Engineering, 2019, 30(2): 198-204, 211. (in Chinese)
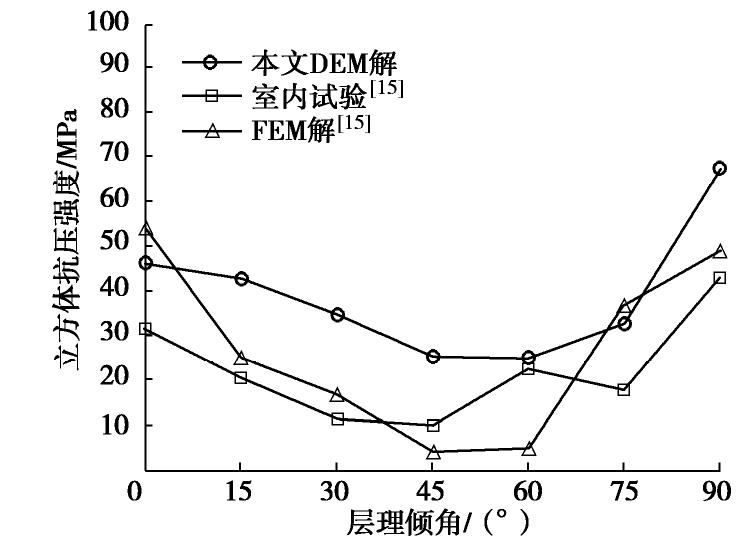
[15] 吴渤. 层状岩体隧道围岩扰动区演化与锚固机理研究[D]. 武汉: 中国地质大学, 2016. WU Bo. Study on disturbance zone evolution and anchoring mechanism of surrounding rock in layered rock tunnel[D]. Wuhan: China University of Geosciences, 2016. (in Chinese)
[16] JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597. doi: 10.1016/S0266-352X(03)00064-8
[17] 陈贺. 岩石宏微观力学特性及高陡岩质边坡的离散元数值模拟[D]. 上海: 同济大学, 2013. CHEN He. Macroscopic and Microscopic Mechanical Properties of Rocks and Discrete Element Numerical Simulation of High-Steep Rock Slopes[D]. Shanghai: Tongji University, 2013. (in Chinese)
[18] 蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002. CAI Mei-feng, Rock Mechanics and Engineering[M]. Beijing: Science Press, 2002. (in Chinese)
[19] 赵瑜, 卢义玉, 陈浩. 深埋隧道三心拱洞室平面应变模型试验研究[J]. 土木工程学报, 2010, 43(3): 68-74. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201003015.htm ZHAO Yu, LU Yi-yu, CHEN Hao. A plane strain modeling study of a three-center arch for deep tunnels[J]. China Civil Engineering Journal, 2010, 43(3): 68-74. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201003015.htm
[20] JIANG M J, YIN Z Y. Analysis of stress redistribution in soil and earth pressure on tunnel lining using the discrete element method[J]. Tunnelling and Underground Space Technology, 2012, 32(6): 251-259.
计量
- 文章访问数: 254
- HTML全文浏览量: 30
- PDF下载量: 236
