Centrifuge modeling of excavation effects on a nearby tunnel in soft clay
-
摘要: 为研究软黏土地层基坑开挖对旁侧隧道的影响,开展了相似比为1∶120的离心模型试验。试验获得了基坑开挖引起的地层不排水抗剪强度、土体孔隙水压力、隧道周围地层水平向土压力、地表沉降、隧道沉降和弯矩响应规律。试验结果表明：①基坑底暴露导致坑底和隧道周围土体超孔压长时间演变,并伴随着隧道周围地层水平向土压力大小和分布形式的持续变化；②基于竖向有效应力衰减程度的土体扰动度评价方法,发现位于坑底下方0.3倍和0.7倍开挖深度处的土体扰动度分别达到了0.33,0.21；③因既有隧道的约束作用,围护墙外侧地表沉降主要位于Peck（1969年）预测的地表沉降Ⅱ区；④基坑开挖完成后,地表沉降、隧道沉降和弯矩持续发展,开挖完成815 d后隧道总沉降达到了开挖期间沉降的1.6倍。固结和蠕变变形是开挖卸载后隧道变形和内力持续发展的主要原因,实际工程中应尽量减少坑底暴露时间。Abstract: The centrifuge modeling with a similarity ratio of 1∶120 is carried out to investigate the impacts of an excavation on a nearby tunnel in soft clayey strata. The responses of undrained shear strength, pore water pressures, horizontal earth pressures around the tunnel, ground settlements, tunnel settlements and bending moments are obtained. The test results show that: (1) The exposure of the excavation base leads to the continuous evolution of the excess pore water pressures of soils below the excavation base and around the tunnel, together with both the magnitude and distribution changes of horizontal earth pressures around the tunnel. (2) Using the effective vertical stress reduction ratio-based equation for soil disturbance degree (SDD), SDD of soils with vertical distances of 0.3 and 0.7 times the excavation depth below the excavation base are 0.33 and 0.21, respectively. (3) Due to the existing tunnel, the ground surface settlements behind the diaphragm wall mainly locate at Zone II predicted by Peck (1969). (4) After excavation, the ground surface settlements, tunnel settlements and bending moments develop continuously. The tunnel settlement at 815 days after excavation is 1.6 times that during excavation stage. The consolidation and creep may be the main reasons for the continuous development of tunnel deformations and internal forces after excavation, implying that the exposure time of the excavation base should be minimized in real projects.
-
Keywords:
- centrifuge modeling /
- excavation /
- tunnel /
- soft clay /
- settlement
-
0. 引言
随着城市快速发展,地下空间开发程度越来越高,各种工程近接施工变得非常普遍。其中,邻近既有隧道的基坑开挖工程是目前常见的近接工程类型之一。基坑开挖对周围土体产生卸荷作用,进而引起既有隧道产生附加内力和变形。中国沿海地区广泛分布着海湖相软黏土,如上海、天津、杭州等地。该区域软黏土具有孔隙比大、压缩性高、强度和渗透性低等特性。因此,该区域基坑开挖对邻近隧道影响问题尤为突出。例如,宁波地铁一号线某区间隧道在邻近大面积基坑开挖影响下出现了管片开裂及渗漏等现象,严重威胁到隧道结构安全[1]。另外,低渗透性软黏土地层中的开挖工程会导致地层工后变形持续发展[2-3]。因此,揭示软黏土地层基坑开挖对周围地层和旁侧隧道的影响机理具有重要意义,特别是长期效应。
目前,国内外学者对此问题的研究以有限元数值分析[1,3-7]和模型试验[8-11]为主。数值分析方面,Chen等[4]通过三维数值分析研究了深基坑开挖过程中隧道变形和内力变化规律,比较了典型保护措施对控制既有隧道变形和内力的有效性。郑刚等[5]建立了考虑土体小应变刚度特性的有限元分析模型,研究了基坑施工对坑外既有隧道变形影响规律,认为坑外隧道变形的影响区可以简化成直角梯形,且坑外变形影响区范围与围护结构水平位移有关。Dolezavola等[6]通过二维有限元模型分析了基坑开挖对下方隧道变形和内力的影响规律。Shi等[7]通过三维有限元模型分析了圆形地下室开挖直径和覆土厚度对下卧隧道变形的影响机理。模型试验方面,Ng等[8]研究了干砂地层基坑开挖对下卧及旁侧隧道内力和沉降的影响。Zheng等[9]研究了干砂地层基坑开挖对下卧隧道内力及周围土压力的影响规律。陈仁朋等[10]通过离心模型试验研究了干砂地层中隔断墙对控制基坑开挖引起的旁侧隧道内力和变形的作用。然而,目前关于软黏土地层基坑开挖对邻近隧道影响的离心模型试验研究还很少见,尤其是基坑底暴露对地层和隧道的长期响应机制分析。
本文开展了软黏土地层邻近既有隧道旁的基坑开挖离心模型试验,获得了隧道结构和周围土体在基坑开挖阶段和开挖完成后的变形和内力演变规律。
1. 离心模型试验方案
因超重力加速度的作用,土工离心机特有的缩尺、缩时效应可以在模型条件下还原较长时间的原型土应力场变化。本次离心模型试验采用的是浙江大学ZJU-400土工离心机,该离心机有效旋转半径为4.5 m,吊篮有效容积1.5 m×1.2 m×1.5 m,容量400 g·t,最大离心加速度150g。本试验采用的离心加速度为120g。离心模型试验中参数相似关系[11]如表1所示。
表 1 离心模型试验参数相似关系（模型/原型）Table 1. Relevant scaling laws in centrifuge models (model/prototype)物理量 相似比 物理量 相似比 重力加速度/(m·s-2) 120 质量密度/(kg·m-3) 1 几何尺寸/m 1×120-1 弹性模量 1 面积/m2 1×120-2 弯矩/(N·m-1) 1×120-3 应变 1 抗弯刚度/(N·m-2) 1×120-4 应力/kPa 1 时间/s 1×120-2 1.1 地基土
本次试验选用马来西亚高岭土[12]制备软黏土地基。地基土制备过程中将高岭土粉末与1.5倍液限的水混合,在真空搅拌器中制成泥浆。随后,经过堆载固结和离心机固结实现饱和高岭土模型地基的制备,最终地基固结度达到90%以上[13]。固结完成后的地基土物理力学性质：相对密度Gs=2.64,液限wL=80.7%,塑限wP=36.5%,渗透系数k=2.0×10-8 m/s,固结系数cv=40 m2/a,内摩擦角φ=23°,等向固结压缩系数
λ =0.244,临界应力状态比M=0.9,回弹系数k=0.053。其中M,λ ,k为修正剑桥模型参数。另外,基坑内土体采用与地基土等密度的ZnCl2重液代替,试验过程中采用排液的方式模拟开挖过程[14]。1.2 模型构件布置
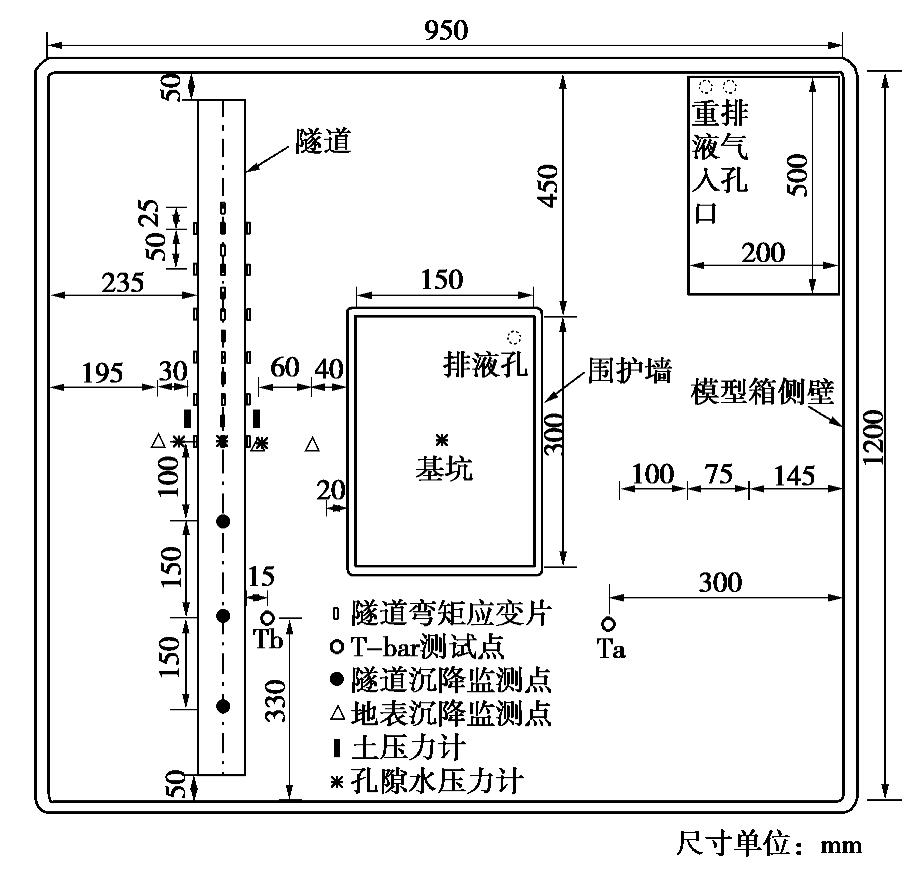
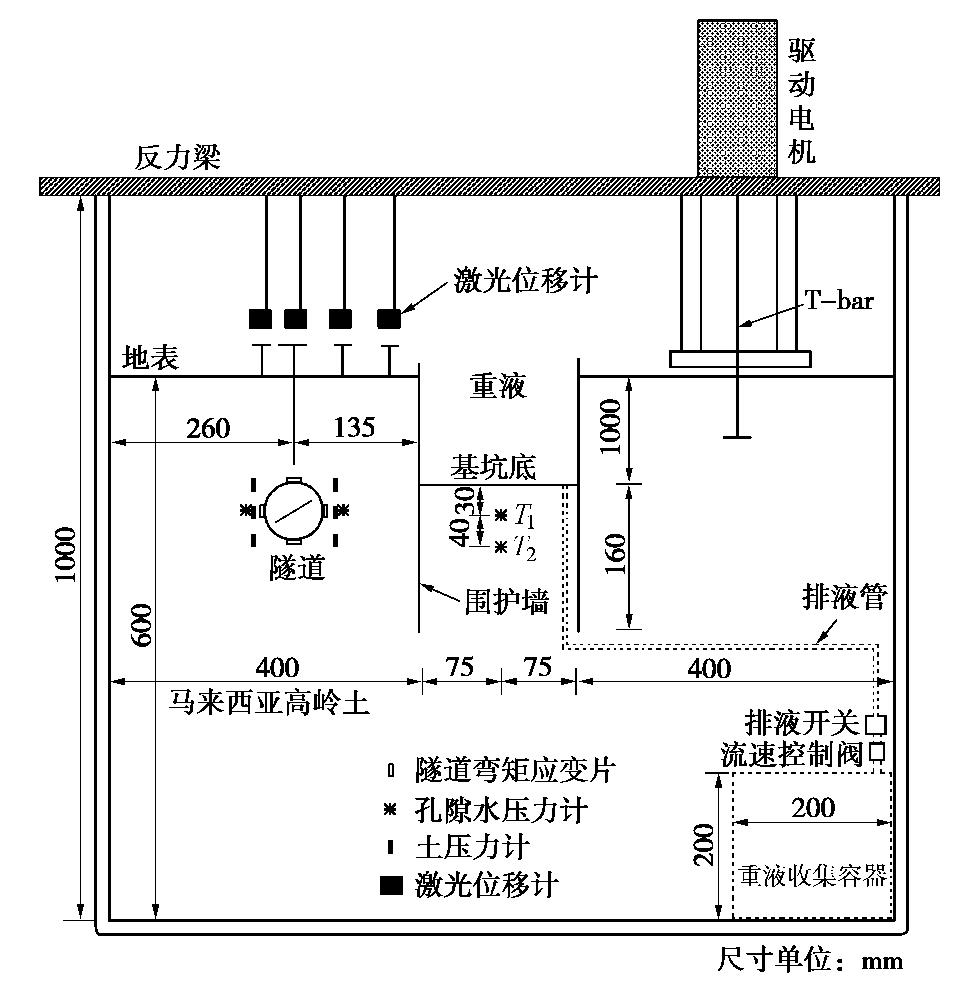
模型平面图与横剖面图如图1,2所示。基坑围护墙采用均质铝板,弹性模量72 GPa,厚度5 mm,对应原型弹性模量为30 GPa,厚度为800 mm（抗弯刚度等效）的混凝土板。模型隧道纵向与基坑长边平行,材料与基坑围护墙一致,对应原型弹性模量为35 GPa,厚度为143 mm（纵向抗弯刚度等效）的混凝土衬砌。以上模型结构与原型结构等效方法与Ng等[8]一致。具体试验模型尺寸和原型尺寸如表2所示。
表 2 试验模型和对应原型尺寸Table 2. Dimensions of test model and corresponding prototype模型 变量名 模型尺寸/mm 原型尺寸/m 围护墙 长×宽 300×150 36×18 围护墙板厚度 5 0.6 开挖深度 100 12.0 插入深度 160 19.2 隧道 与基坑距离 110 13.2 隧道外径 50 6 隧道长度 1100 132 隧道厚度 1 0.12 隧道拱顶埋深 100 12 1.3 传感器布置
如图2所示,试验采用激光位移计测量地表沉降,3个监测点与围护墙距离分别为(4/5)D,2D,(17/5)D,D为隧道直径。距离隧道中间断面5D处布置一个激光监测点用于测量拱顶竖向位移,隧道拱顶出伸出一个直径3 mm壁厚0.5 mm的空心套管,套管顶部黏接一塑料片用于反射激光。隧道纵向中间断面两侧的拱顶、拱腰和拱底高度分别布设土压力盒用以测量水平向土压力,测点距离隧道轴线35 mm。拱顶上方0.7D处和拱腰两侧0.2D处分别布置孔隙水压力计。基坑中心下方30,70 mm处分别布置孔隙水压力计用于监测孔压变化情况。隧道拱顶和拱底每隔0.5D布置一对应变片,拱腰两侧每隔1D布置一对应变片以监测弯矩变化情况。模型固结完成后和开挖完成后,采用T-bar装置下探30 cm（对应原型36 m）分别测试了相应位置土体强度随深度变化情况。
1.4 试验步骤
本次试验拟采用排液法模拟基坑开挖过程（图3）。具体试验步骤如下：
（1）在固结成模的地基土中挖出一凹槽并将模型隧道埋入预设位置,随后回填隧道上方土层并整平。将模型箱吊入固结仪,采用堆载预压固结,预压荷载分为4级（18.5,30.4,43.8,56.8 kPa）,每级荷载持续72 h。
（2）将模型箱吊入离心机内重新在120g加速度下固结,固结后用T-bar测试土体不排水抗剪强度。
（3）将模型箱吊出地面,静压基坑围护墙至预设深度,挖出坑内土体至预定坑底,敷设硅胶袋置基坑内并倒入重液,并安装调试试验所需传感器。
（4）开启离心机,转机到120g,传感器数据采集稳定后,开启电磁阀排液（此时电磁阀在超重力下停止工作）,为实现基坑开挖的模拟,试验过程中采用停机开挖[15]的方式,下文的试验结果也表明停机开挖方式,得到的地层和隧道响应结果较为合理。
（5）重新开启离心机使模型地基重新建立应力场,获取开挖前后各传感器数据。为获得基坑开挖引起的地基土和隧道长期响应,离心加速度到达120g后持续转机2.3 h（对应原型约3.8 a）,然后停机。
2. 试验结果分析
2.1 土体不排水抗剪强度
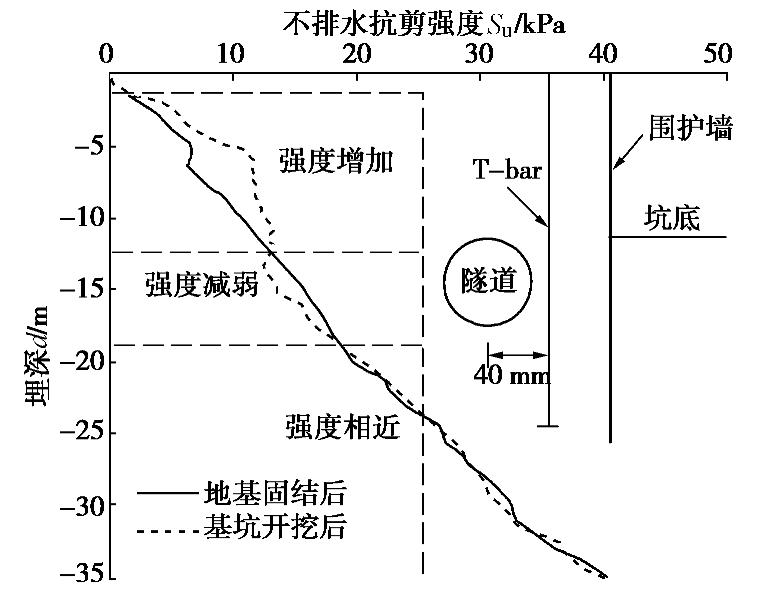
整个试验过程共进行了3次T-bar测试,即固结完成后、基坑开挖前和基坑开挖完成后。其中基坑开挖前T-bar测试数据异常,没有计入数据。
从图4可以看出,固结完成后T-bar测试曲线线性度较好,不排水抗剪强度随深度近似线性增加,梯度约1.1～1.2 kPa/m,这也表明地基土固结情况良好,没有明显分层情况。本试验围护墙采用静压的方式安装,隧道上方的土体较固结完成后的模型土体强度有所增加。从开挖完成面到隧道仰拱深度附近,由于开挖引起的卸荷效应导致土体强度减弱,Su值低于饱和土地基,对埋深19 m以下土层（约拱底以下）,两次测试得到的不排水抗剪强度大小趋于一致。
2.2 基坑底土体超静孔隙水压力
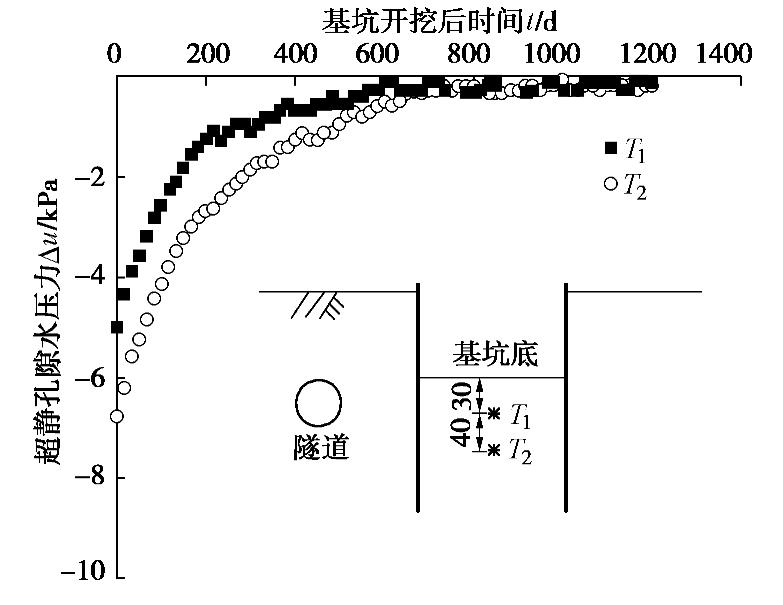
基坑开挖卸荷会引起坑底土体产生负的超静孔隙水压力（以下称超孔压）。开挖完成后,负超孔压随时间发展逐渐消散,导致土体回弹持续发展。
如图5所示,本试验获得了基坑开挖引起的坑底T1和T2位置土体超孔压随时间变化规律。需要指出的是,图6所示的超孔压大小为按照开挖完成后坑底水位确定的静水压力与实测孔压的差值。
![]()
图 5 基坑底T1和T2测点超孔压演变过程Figure 5. Development of excess pore water pressure at T1 and T2基坑刚开挖完成时（t = 0）,T1和T2位置的负超孔压分别为6.8,5 kPa。随后两个测点的土体超孔压逐渐消散。开挖完成100 d时,T2测点超孔压消散了50%且消散速度变慢。此时T1测点超孔压消散了约39%,且在开挖完成150 d时其超孔压消散程度达到了约50%。T1和T2测点土体超孔压消散程度分别在基坑开挖完成后640,380 d时达到了90%。
因此,试验结果表明基坑开挖引起的坑底土体超孔压随埋深增大而减小,而其消散速度则随埋深增大而增大。另外,Xu等[16]等认为可以通过有效应力衰减程度来确定卸载引起的土体应力扰动度（SDD）,并提出SDD计算公式：
SDD=1−σ′vdσ′v0, (1) 式中,
σ′vd 为土体受扰动后的竖向有效应力,σ′v0 为土体初始竖向有效应力,σ′vd=γh−uwd, (2) σ′v0=γ(He+h)−uw0, (3) 其中,γ为土体饱和重度或重液重度,He为基坑开挖深度,h为测点到基坑底的竖向距离,uw0为基坑开挖前的实测孔隙水压力,uwd为基坑开挖完成时的实测孔隙水压力。
根据式（1）～（3）和实测孔压大小计算得到的T1和T2位置的土体扰动度在基坑开挖完成时分别为0.33,0.21。
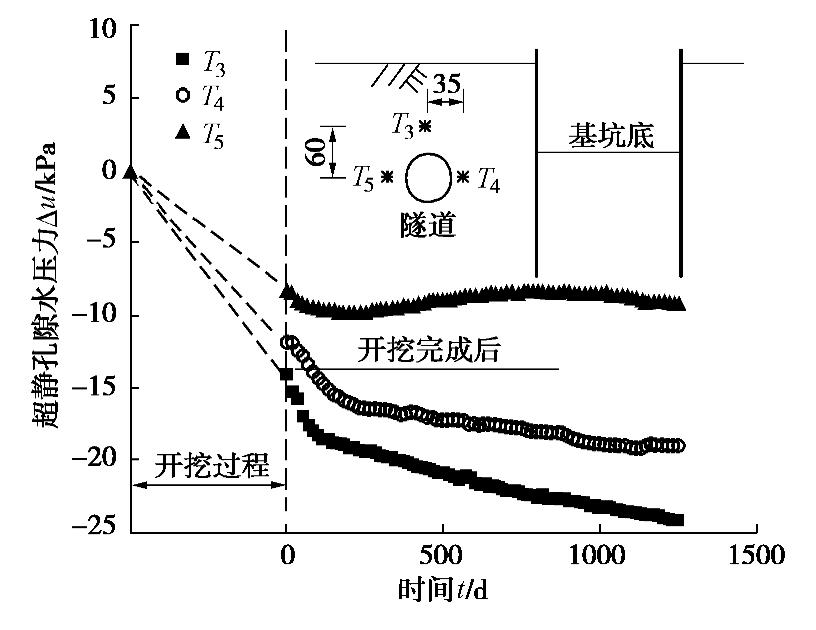
2.3 隧道周围土体孔隙水压力
为获得基坑开挖引起的隧道周围土体孔隙水压力变化,试验在隧道拱顶上方和拱腰两侧分别布置了微型孔隙水压力传感器T3,T4和T5。基于基坑开挖前的各传感器初始读数,本文获得了以上3个测点的超孔压。如图6所示,T3,T4和T5处的土体在基坑开挖阶段均产生了一定程度的负超孔压,大小分别为-14.0,-11.9,-8.2 kPa。
开挖完成后约100 d时间内,这3个测点的土体负超孔压均以较快的速度继续增大,随后除T5测点外均以较低速度增长。其中,拱顶上方的T3测点超孔压下降程度较大可能与隧道沉降持续发展对上方地层的牵扯作用有关,而隧道拱腰右侧的T4位置土体超孔压的持续增大则可能与围护墙和地层变形的持续发展有关。相比而言,T5测点的超孔压在开挖完成100 d后呈现先缓慢减小再逐渐增大的趋势,这可能与隧道整体位移和变形模式有关。另外,因隧道的阻隔作用,T5测点的超孔压总体变化程度较小。
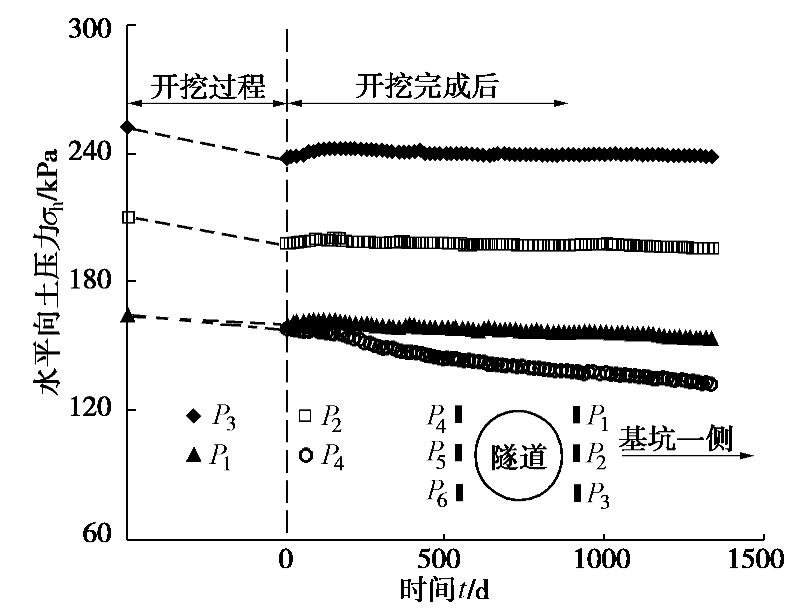
2.4 隧道周围地层水平向土压力
基坑开挖卸荷会改变隧道周围土体压力分布形式,从而引起隧道结构产生附加内力和变形。为此,本试验获得了基坑开挖引起的隧道周围地层水平向土压力演变规律。如图7所示,隧道周围地层水平向土压力在基坑开挖过程中均发生了衰减,其中P1,P2和P3分别下降了5.0,12.0,13.8 kPa。总体上看,这3个位置的水平向土压力变化程度随土体埋深增加而增大。上述3个位置的水平向土压力值在开挖完成后一段时间内均呈现微弱程度的恢复,且随着深度增加恢复程度逐渐增大。随后,水平向土压力随时间的推移逐渐缓慢下降,这是基坑底持续暴露导致的开挖卸载效应不断发展的结果。这一点可以从图5,6所示的土体孔隙水压力变化趋势得到验证。
![]()
图 7 隧道周围地层水平向土压力变化曲线Figure 7. Evolution of horizontal earth pressure of soils around tunnel另外,远离基坑一侧与隧道拱顶高度齐平的P4测点水平向土压力在开挖过程中下降了约6.4 kPa。其在排液完成后呈持续下降趋势且下降值远大于靠近基坑一侧的P1测点。隧道在基坑开挖完成后会朝向基坑方向运动,隧道位移由靠近围护墙一侧的土体位移决定。因此,在不考虑隧道与土体相互作用的情况下,隧道水平位移大于其左侧土体。上述现象是导致P4测点土压力在基坑开挖完成后的衰减程度明显大于P1测点的主要原因。
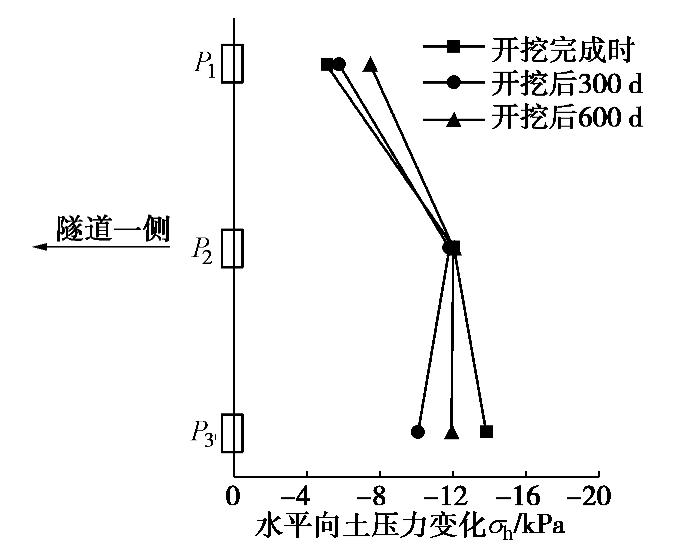
同时,图8描绘了基坑开挖完成不同时刻的隧道周围地层水平向土压力的分布规律。可以发现,开挖完成时,隧道周围土体水平向压力沿竖向衰减量呈现“上小下大”的趋势。其中隧道拱腰高度处的P2的水平向土压力随时间基本不变。开挖后300 d时,水平向土压力衰减程度呈现两头小中间大。开挖后600 d时,水平向土压力衰减程度在隧道拱底高度处和拱腰高度处基本持平,而拱顶高度处则明显偏小。以上隧道周围地层水平向土压力大小和分布形状的改变将影响隧道横断面的受力状况,从而导致隧道产生附加环向变形。
![]()
图 8 隧道右侧地层水平向土压力变化量沿深度分布Figure 8. Distribution of increments of horizontal earth pressure of soils at right side of existing tunnel2.5 地表沉降
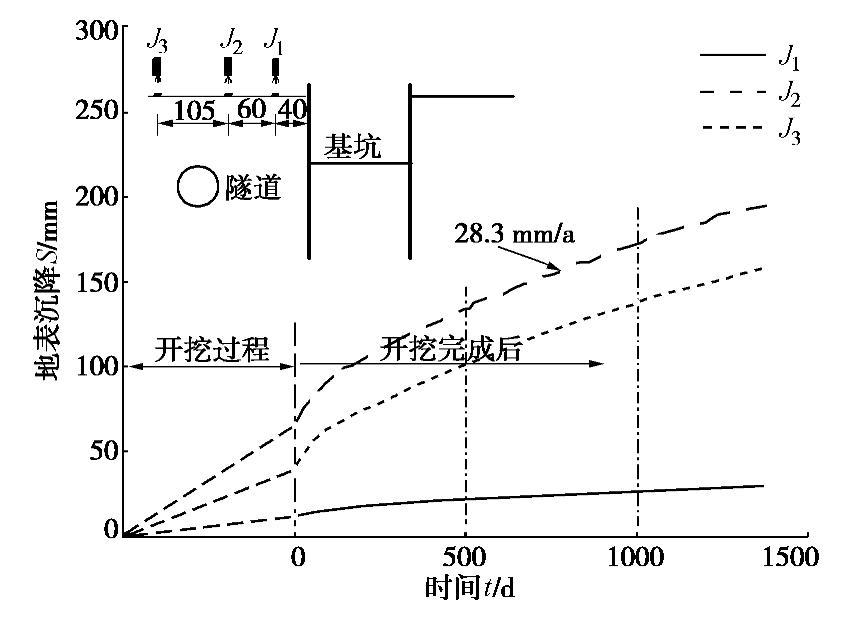
图9描绘了基坑开挖过程及开挖完成后地表沉降发展曲线。开挖完成后J1,J2和J3三个测点的地表沉降分别为11.8,64.5,39.9 mm。J1,J2和J3测点的地表沉降量在开挖完成后约1000 d时分别增加至27.0,172.6,137.7 mm。对比孔隙水压力监测结果,超孔压变化趋势逐渐减缓后地表沉降仍以较大增速持续发展（开挖后500～1000 d,J2测点约为28.3 mm/a）,这可能是地基产生蠕变导致的。例如,Harahap等[17]通过考虑时间效应的基坑开挖数值分析发现蠕变引起的沉降占总沉降的57.1%。以上结果说明在超孔压消散固结和土体蠕变的共同影响下,基坑底暴露会引起地表沉降持续发展,实际施工应减少基坑暴露时间。
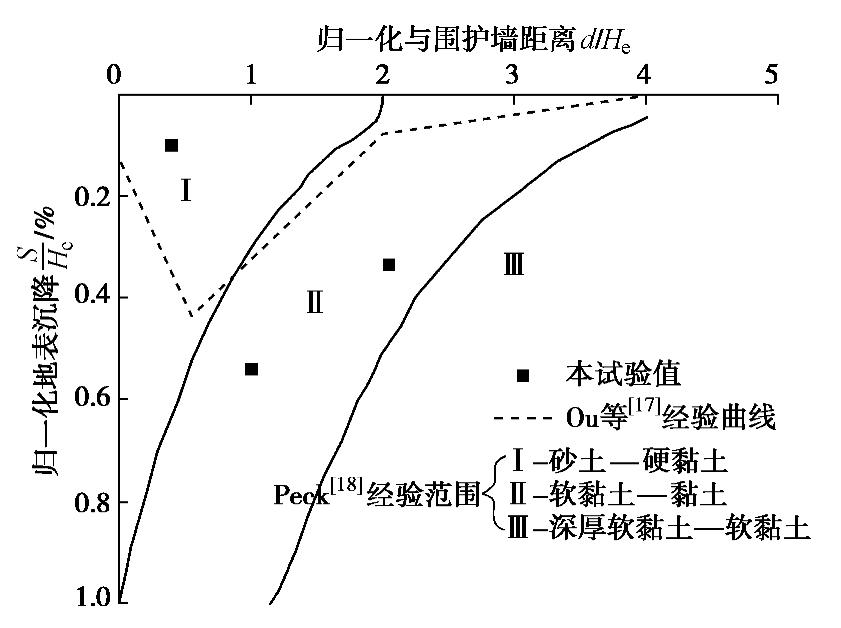
如图10,隧道上方的地表沉降为凹槽形,即随与围护墙板距离增加呈先增大后减小趋势。与Ou等[18]等基于粉质黏土地层的实测经验曲线相比,本次试验主要影响范围区大于2倍基坑开挖深度,这可能是因为本试验土层更加软弱。结合Peck[19]经验值,本试验主要分布在Ⅱ区,对应的地层为软黏土至黏土地层。实际上,本试验地基为单一软黏土地层,不考虑其他因素的情况下地表沉降应位于Ⅲ区。出现这种情况的原因是既有隧道对地表沉降有一定的抑制作用[4]。
![]()
图 10 围护墙外侧地表沉降分布Figure 10. Distribution of ground surface settlement behind diaphragm wall2.6 隧道沉降与弯矩
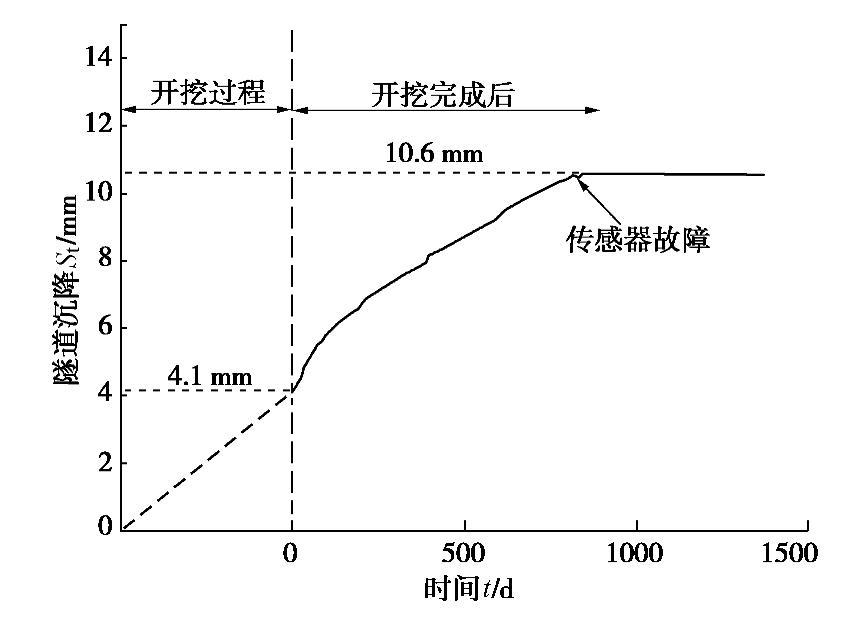
如图11所示,基坑开挖完成后,距离隧道中心点5D处的隧道沉降为4.1 mm（制模过程中2D处测点出现损坏,转机过程中8D处测点传感器损坏）。基坑开挖完成后的初期隧道沉降随时间增长速率较快,随后逐渐变缓。该点沉降在基坑开挖完成约815 d（即约2.2 a）后达到10.6 mm,增长速率为2.9 mm/a,此后激光位移计失效。此时,隧道总沉降量是基坑开挖期间沉降的1.6倍,说明基坑长时间暴露会引起旁侧隧道沉降发生可观的增长。
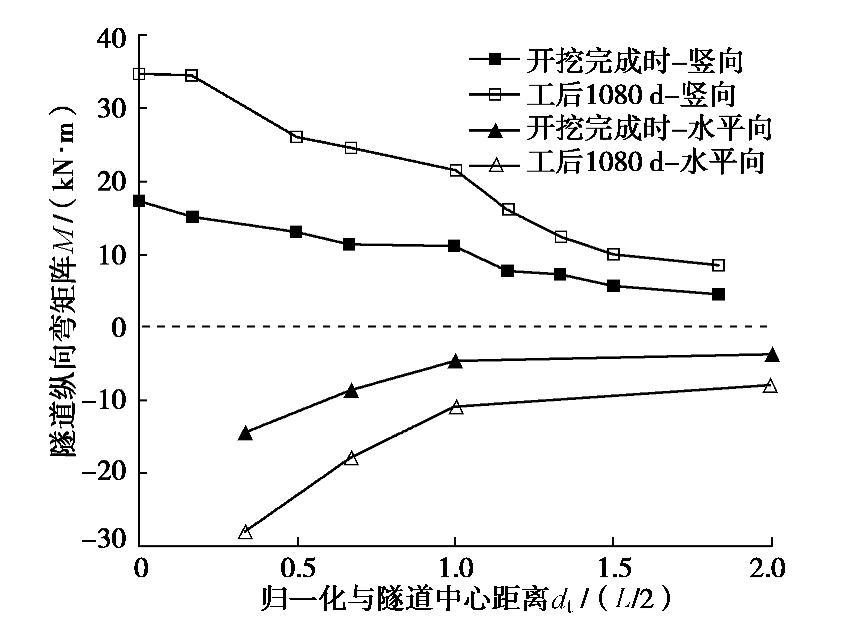
图12为隧道竖向和水平向弯矩沿纵向分布。开挖完成后,坑内土体的卸荷作用,隧道竖向上产生拱底受拉的弯矩,最大值出现在隧道纵向中心位置,为17.3 kN·m。竖向弯矩随与隧道中心距离增大而减小。隧道中心位置竖向弯矩在基坑开挖完成后1080 d时增大至34.8 kN·m,曲线整体上较开挖完成时变得更为陡峭。与开挖完成时相比,开挖完成后1080 d各测点弯矩值增加了约一倍。可见基坑底暴露会导致隧道弯矩持续增大。另外,隧道水平向弯矩规定以靠近基坑一侧拱腰受拉为负。其中隧道中心位置应变片损坏,距离隧道中心L/6位置的弯矩值为14.5 kN·m/m。总体上,隧道水平向弯矩随与隧道中心距离缩小而逐渐增大且增长梯度也越来越大。
![]()
图 12 隧道纵向弯矩分布Figure 12. Distribution of tunnel bending moment in longitudinal direction3. 结论与建议
本文开展了软黏土地层邻近既有隧道的基坑开挖离心模型试验,获取了既有隧道和地层在旁侧基坑开挖影响下的短期和长期响应规律。
（1）因基坑开挖卸载作用,隧道埋深范围内的土体不排水抗剪强度有所减小。开挖卸荷还会引起坑底土体产生负超孔压,随后经过较长时间逐渐消散为零。另外,基于Xu等[16]的土体扰动度计算公式,发现坑底下方土体扰动度随埋深增大而减小。
（2）坑底暴露导致隧道拱顶上方和靠近基坑一侧的拱腰附近土体负超孔压持续增大,而远离基坑的另一侧拱腰附近土体变化程度较小。靠近基坑一侧的隧道周围地层水平向土压力大小和分布模式逐渐变化,从而间接影响隧道结构受力状态并产生附加环向变形。
（3）土体蠕变和超孔隙水压力消散引起的固结变形是造成基坑开挖完成后地表沉降持续发展的主要因素,实际施工时应尽量减少基坑底暴露时间,从而有效抑制旁侧隧道变形和内力发展。
-
![]()
图 5 基坑底T1和T2测点超孔压演变过程
Figure 5. Development of excess pore water pressure at T1 and T2
![]()
图 7 隧道周围地层水平向土压力变化曲线
Figure 7. Evolution of horizontal earth pressure of soils around tunnel
![]()
图 8 隧道右侧地层水平向土压力变化量沿深度分布
Figure 8. Distribution of increments of horizontal earth pressure of soils at right side of existing tunnel
![]()
图 10 围护墙外侧地表沉降分布
Figure 10. Distribution of ground surface settlement behind diaphragm wall
![]()
图 12 隧道纵向弯矩分布
Figure 12. Distribution of tunnel bending moment in longitudinal direction
表 1 离心模型试验参数相似关系（模型/原型）
Table 1 Relevant scaling laws in centrifuge models (model/prototype)
物理量 相似比 物理量 相似比 重力加速度/(m·s-2) 120 质量密度/(kg·m-3) 1 几何尺寸/m 1×120-1 弹性模量 1 面积/m2 1×120-2 弯矩/(N·m-1) 1×120-3 应变 1 抗弯刚度/(N·m-2) 1×120-4 应力/kPa 1 时间/s 1×120-2 
下载: 导出CSV
表 2 试验模型和对应原型尺寸
Table 2 Dimensions of test model and corresponding prototype
模型 变量名 模型尺寸/mm 原型尺寸/m 围护墙 长×宽 300×150 36×18 围护墙板厚度 5 0.6 开挖深度 100 12.0 插入深度 160 19.2 隧道 与基坑距离 110 13.2 隧道外径 50 6 隧道长度 1100 132 隧道厚度 1 0.12 隧道拱顶埋深 100 12
下载: 导出CSV
-
[1] 陈仁朋, 王诚杰, 鲁立, 等. 开挖对地铁盾构隧道影响及控制措施[J]. 工程力学, 2017(12): 1-13. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201712002.htm CHEN Ren-peng, WANG Cheng-jie, LU Li, et al. Influence of excavation on exist metro shield tunnel and control measures[J]. Engineering Mechanics, 2017(12): 1-13. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201712002.htm
[2] 康志军, 谭勇, 李想, 等. 基坑围护结构最大侧移深度对周边环境的影响[J]. 岩土力学, 2016, 37(10): 2909-2914. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201610023.htm KANG Zhi-jun, TAN Yong, LI Xiang, et al. Influences of depth of maximum lateral deflection of excavation support on adjacent environment[J]. Rock and Soil Mechanics, 2016, 37(10): 2909-2914. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201610023.htm
[3] MENG F Y, CHEN R P, KANG X. Effects of tunneling-induced soil disturbance on post-construction settlement in structured soft soils[J]. Tunnelling and Underground Space Technology, 2018, 80: 53-63. doi: 10.1016/j.tust.2018.06.007
[4] CHEN R P, MENG F Y, LI Z C, et al. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils[J]. Tunnelling and Underground Space Technology, 2016, 58: 224-235. doi: 10.1016/j.tust.2016.06.002
[5] 郑刚, 杜一鸣, 刁钰, 等. 基坑开挖引起邻近既有隧道变形的影响区研究[J]. 岩土工程学报, 2016, 38(4): 599-612. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604004.htm ZHENG Gang, DU Yi-ming, DIAO Yu, et al. Influenced zones for deformation of existing tunnels adjacent to excavations[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 599-612. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604004.htm
[6] DOLEZALOVA M. Tunnel complex unloaded by a deep excavation[J]. Computers and Geotechnics, 2001, 28(6): 469-493.
[7] SHI J W, NG C W W, CHEN Y. Three-dimensional numerical parametric study of the influence of basement excavation on existing tunnel[J]. Computers and Geotechnics, 2015, 63: 146-158. doi: 10.1016/j.compgeo.2014.09.002
[8] NG C W W, SHI J W, HONG Y. Three-dimensional centrifuge modelling of basement excavation effects on an existing tunnel in dry sand[J]. Canadian Geotechnical Journal, 2013, 50(8): 874-888. doi: 10.1139/cgj-2012-0423
[9] ZHENG G, WEI S W, PENG S Y, et al. Centrifuge modeling of the influence of basement excavation on existing tunnels[C]//Physical Modelling in Geotechnics - Proceedings of the 7th International Conference on Physical Modelling in Geotechnics, 2010, Zurich: 523-527.
[10] 陈仁朋, ALMADHAGIASHRAF , 孟凡衍. 基坑开挖对旁侧隧道影响及隔断墙作用离心模型试验研究[J]. 岩土工程学报, 2018, 40(增刊2): 6-11. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S2004.htm CHEN Ren-peng, ALMADHAGIASHRAF , MENG Fan-yan. Three- dimensional centrifuge modeling of influence of nearby excavations on existing tunnels and effects of cut-off walls[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 6-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S2004.htm
[11] XIE Y, LEUNG C F, CHOW Y K. Centrifuge modelling of spudcan-pile interaction in soft clay[J]. Géotechnique, 2012, 62(9): 799-810. doi: 10.1680/geot.12.OG.003
[12] TAYLOR R N. Geotechnical Centrifuge Technology[M]. London: Blackie Academic and Professional, 1995.
[13] LAM S S Y. Ground Movements Due to Excavation in Clay: Physical and Analytical Models[D]. Cambridge: University of Cambridge, 2010.
[14] 魏少伟. 基坑开挖对坑底已建隧道影响的数值与离心试验研究[D]. 天津: 天津大学, 2010. WEI Shao-wei. Centrifuge and Numerical Studies of the Influence of Basement Excavation on the Underlying Tunnel[D]. Tianjin: Tianjin University, 2010. (in Chinese)
[15] 梁发云, 褚峰, 宋著, 等. 紧邻地铁枢纽深基坑变形特性离心模型试验研究[J]. 岩土力学, 2012, 33(3): 657-664. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201203004.htm LIANG Fa-yun, CHU Feng, SONG Zhu, et al. Centrifugal model test research on deformation behaviors of deep foundation pit adjacent to metro stations[J]. Rock and Soil Mechanics. 2012, 33(3): 657-664. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201203004.htm
[16] XU Y F, SUN D A, SUN J, et al. Soil disturbance of shanghai silty clay during EPB tunnelling[J]. Tunnelling and Underground Space Technology, 2003, 18(5): 537-545.
[17] HARAHAP S E, OU C Y. Finite element analysis of time- dependent behavior in deep excavations[J]. Computers and Geotechnics, 2019, 103300.
[18] OU C Y, LIAO J T, CHENG W L. Building response and ground movements induced by a deep excavation[J]. Géotechnique, 2000, 50(3): 209-220.
[19] PECK R B. Deep excavation and tunneling in soft ground. State-of-the-art-report[C]//Proc 7th Int Conf of Soil Mechanics and Foundation Engineering, International Society of Soil Mechanics and Geotechnical Engineering (ISSMGE), 1969, Mexico City: 225-281.
计量
- 文章访问数:
- HTML全文浏览量: 0
- PDF下载量:
