本文全文图片
-
![]() τ-σnet平面内临界状态线示意图
τ-σnet平面内临界状态线示意图
-
![]() e-ln(σnet)平面内临界状态线及状态变量的定义
e-ln(σnet)平面内临界状态线及状态变量的定义
-
![]() 弹性参数A和α的确定
弹性参数A和α的确定
-
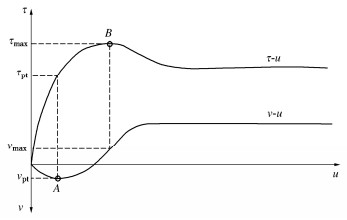
![]() 密砂-结构接触面τ-u和v-u曲线示意图
密砂-结构接触面τ-u和v-u曲线示意图
-
![]() 状态参数的确定
状态参数的确定
-
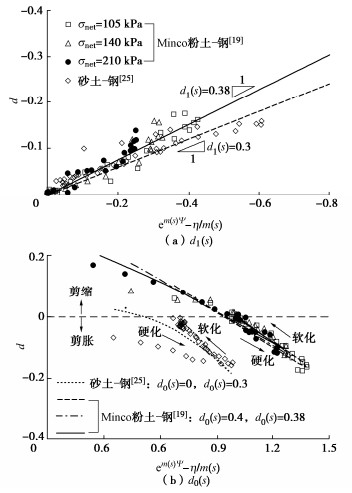
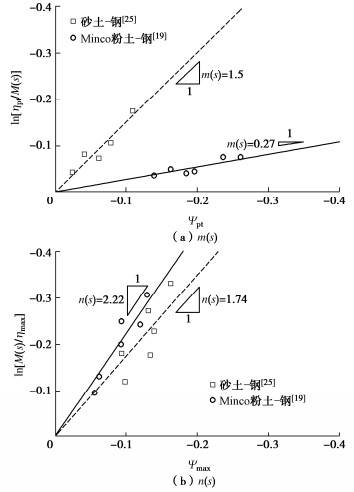
![]() 砂土-钢[25]和Minco粉土-钢[19](s=100 kPa)接触面剪胀参数的确定
砂土-钢[25]和Minco粉土-钢[19](s=100 kPa)接触面剪胀参数的确定
-
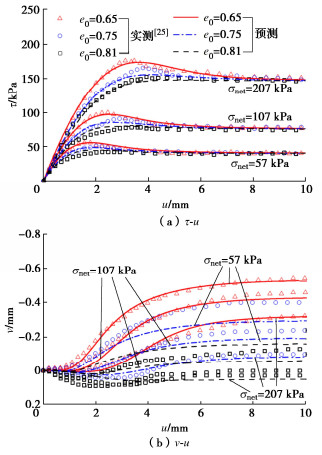
![]() 砂土-钢接触面模型预测结果与实测结果[25]的比较
砂土-钢接触面模型预测结果与实测结果[25]的比较
-
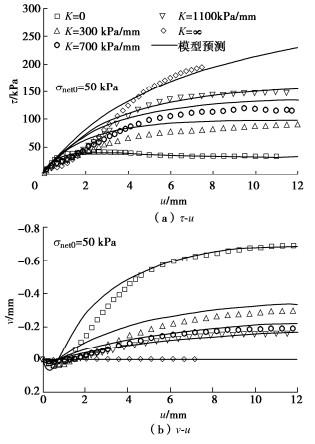
![]() 砂土-土工织物接触面在不同法向刚度下模型预测结果与实测结果[27]的比较
砂土-土工织物接触面在不同法向刚度下模型预测结果与实测结果[27]的比较
-
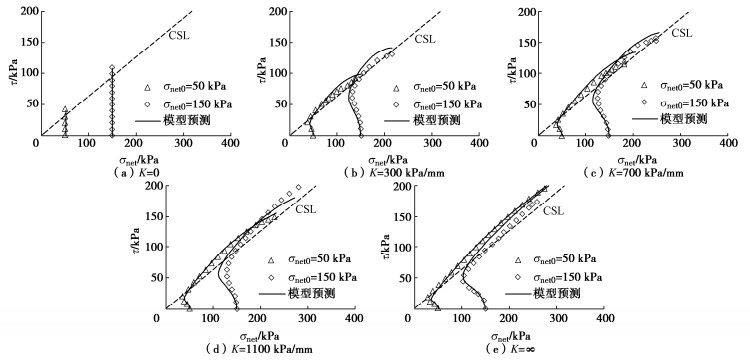
![]() 砂土-土工织物接触面在不同法向刚度下模型预测应力路径和实测结果[27]的比较
砂土-土工织物接触面在不同法向刚度下模型预测应力路径和实测结果[27]的比较
-
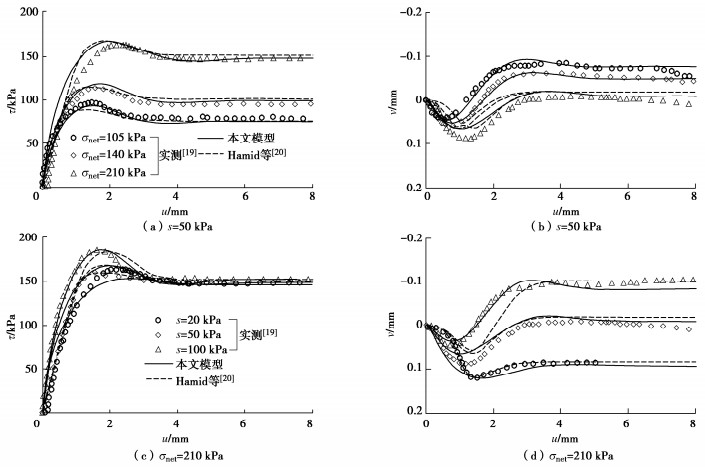
![]() 非饱和Minco粉土-钢接触面在不同净法向应力和吸力下模型预测结果与实测结果[19]的比较
非饱和Minco粉土-钢接触面在不同净法向应力和吸力下模型预测结果与实测结果[19]的比较
-
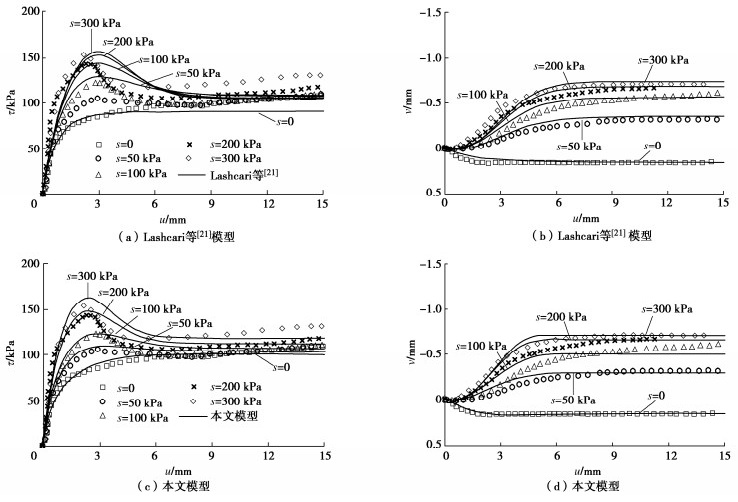
![]() 净法向应力σnet=100 kPa时非饱和CDG-混凝土接触面在不同吸力下模型预测结果与实测结果[22]的比较
净法向应力σnet=100 kPa时非饱和CDG-混凝土接触面在不同吸力下模型预测结果与实测结果[22]的比较
-
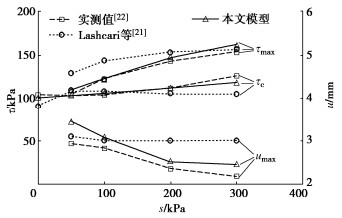
![]() τmax,τc和umax预测值与实测结果[22]的比较
τmax,τc和umax预测值与实测结果[22]的比较
本文全文表格
-
砂土-结构接触面的模型参数
参数类型 参数 砂土-钢[25] 砂土-土工织物[27] 临界状态参数 Γ(s) 0.842 0.985 ω(s) 0.075 0.173 M(s) 0.71 0.63 μ(s) (kPa) 0 0 弹性参数 A (kPa) 98 264.9 α 0.276 0.282 R 1.2 1.2 状态参数 m(s) 1.5 0.9 n(s) 1.74 1.05 剪胀参数 d0(s) 0 1.6 d1(s) 0.3 0.32 硬化参数 h(s) 3 0.3 接触面厚度 t/mm 4 3.5 -
非饱和土-结构接触面的模型参数
Minco粉土-钢[19] CDG-混凝土[22] Hamid等[20] 本文模型 Lashcari等[21] 本文模型 ξD1*=0.0318 mm Γ(s)=0.339e−0.035(s−20)+0.731[1−e−0.035(s−20)] Kt0e=0.25 MPa Γ(s)=0.447e−0.012s+1.244[1−e−0.012s] ξD2*=0.0951 mm ω(s)= 0.152[1−e−0.015(s−20)] Kn0e=0.32 MPa ω(s)=0.214e−0.016s+0.385[1−e−0.016s] n=8(4) M(s)=0.69 M=0.905 M(s)=0.996 μp1=0.2796 μ(s)=0.45+0.065(s−20) kPa e0=0.447 μ(s)=0.059s kPa μp2=0.0635 A=64.7 kPa λ=0.041 A=90.4 kPa μ01=0.3479 α=0.51 nb=0.92 α=0.517 μ02=0.049 R =1.2 nd=1.5 R =1.2 κ1=−2.9927(0.4728) m(s)=0.27 A0=0.2 m(s)=4.2 κ2=0.4001(−0.0316) n(s)=2.22 A1=0.2 n(s)=0.75 a=17.4 d0(s)=0.56−0.002(s−20) h0=1.0 d0(s)=0.1 b=2.85 d1(s)=0.38 a=0.07 d1(s)=0.2 λ(s)=0.399 h(s)=0.46+0.003(s−20) b=50 h(s)=0.3+0.005s λ1=−5.2285 t=1 mm Sr0=0.60 t=2 mm λ2=29.4865 aw=0.25 Kn=1000 kPa nv=2.20 Ks=150 kPa Ω=0.0 t=2 mm 注:s=20 kPa时n=8,s=50和100 kPa时n=4;s≤50 kPa时κ1=−2.9927和κ2=0.4001,s > 50 kPa时,分别为0.4728和-0.0316[20]。


 下载:
下载: