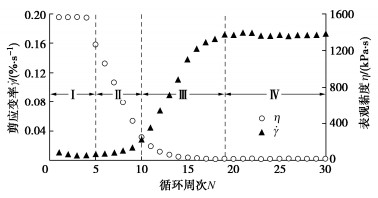
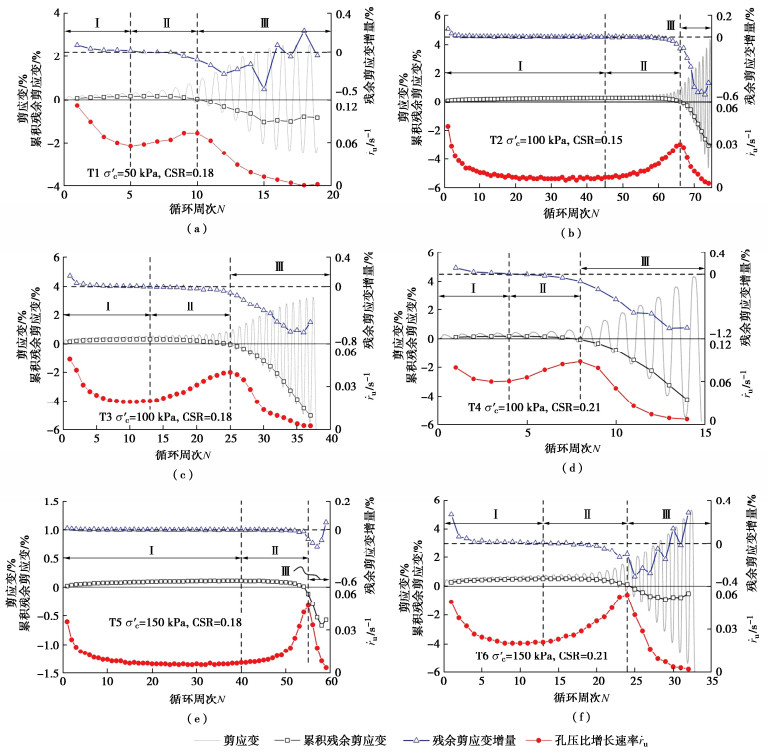
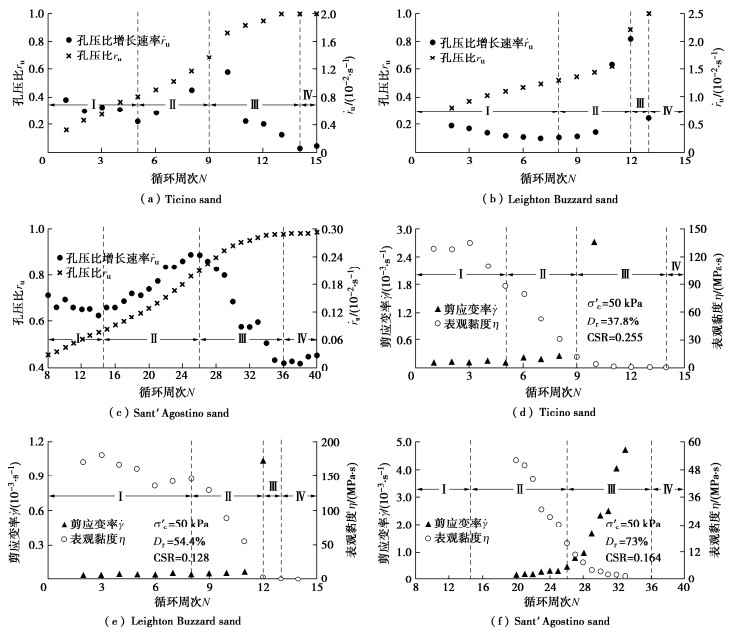
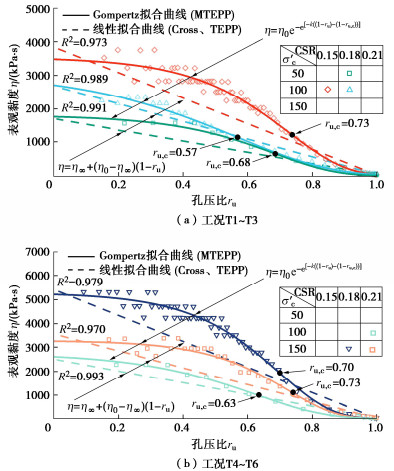
本文全文图片
本文全文表格
-
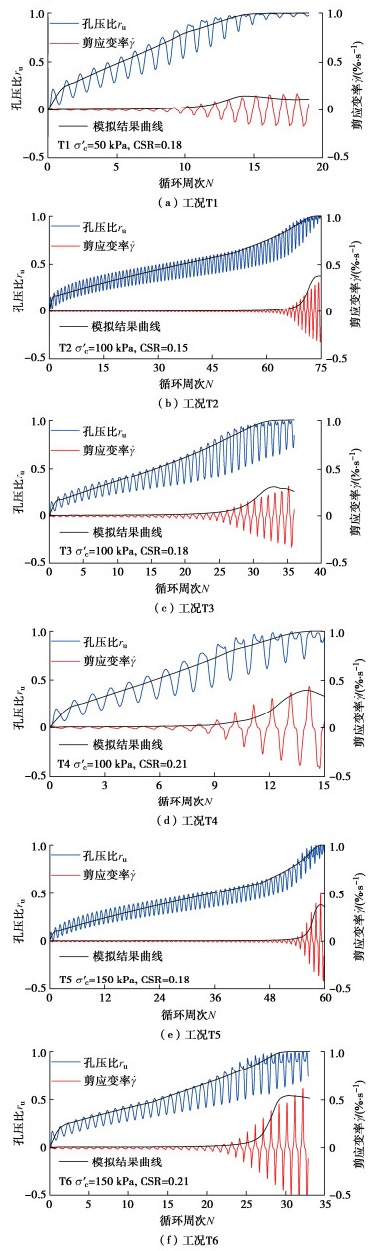
南京细砂循环三轴试验方案
工况 加载频率f/Hz 初始有效围压σ'c/kPa 循环应力比CSR T1 1 50 0.18 T2 1 100 0.15 T3 1 100 0.18 T4 1 100 0.21 T5 1 150 0.18 T6 1 150 0.21 -
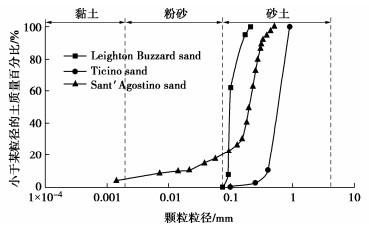
3种类型砂土的试验条件
试验编号 砂土名称 f/Hz Dr% CSR CTX_T2 Ticino sand 0.010 37.8 0.255 CTX_LB3 Leighton Buzzard sand 0.010 54.4 0.128 S_SA10 Sant' Agostino sand 0.008 73.0 0.164 -
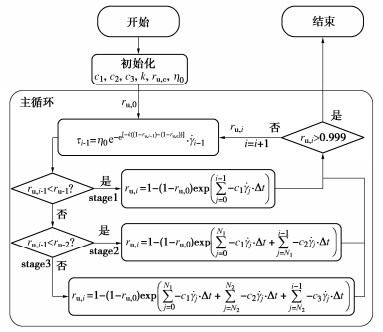
触变性流体本构模型
方程 Cross触变性流体模型[15] TEPP模型[16] MTEPP模型(本文提出) 状态方程 $ \tau = ({\eta _\infty } + a\lambda ) \cdot \dot \gamma $ $ \tau = [{\eta _\infty } + ({\eta _0} - {\eta _\infty }) \cdot (1 - {r_{\text{u}}})]\dot \gamma $ $ \tau = {\eta _0}{\text{e}^{ - {\text{e}^{\left[ { - k\left( {\left( {1 - {r_{\text{u}}}} \right) - \left( {1 - {r_{{\text{u,c}}}}} \right)} \right)} \right]}}}} \cdot \dot \gamma $ 速率方程 $ {\text{d}}\lambda /{\text{d}}t = b(1 - \lambda ) - c\lambda {\dot \gamma ^n} $ $ {\text{d}}(1 - {r_{\text{u}}})/{\text{d}}t = - c(1 - {r_{\text{u}}})\dot \gamma $ $ \text{d}(1-{r}_{\text{u}})/\text{d}t=-c(1-{r}_{\text{u}})\dot{\gamma }\text{ }\left(c=\left\{\begin{array}{c}{c}_{1}(\text{stage1})\text{ }\\ {c}_{2}(\text{stage2})\text{ }\\ {c}_{3}(\text{stage3})\text{ }\end{array}\right.\right) $ 表观黏度 $ \eta {\text{ = }}{\eta _\infty } + a\lambda $ $ \eta {\text{ = }}{\eta _\infty } + ({\eta _0} - {\eta _\infty })(1 - {r_{\text{u}}}) $ $ \eta {\text{ = }}{\eta _0}{\text{e}^{ - {\text{e}^{\left[ { - k\left( {\left( {1 - {r_{\text{u}}}} \right) - \left( {1 - {r_{{\text{u,c}}}}} \right)} \right)} \right]}}}} $ -
MTEPP模型参数拟合
工况 ${\sigma '_{\text{c}}}$/kPa CSR 拟合参数 c1 c2 c3 k ru, c η0/(kPa·s) T1 50 0.18 17 18.3 9.2 5.29 0.68 1812.68 T2 100 0.15 3.1 5.3 4.9 5.58 0.73 3543.70 T3 100 0.18 3.9 4.2 3.8 3.45 0.57 3117.99 T4 100 0.21 10.0 11.0 5.5 4.61 0.63 2767.69 T5 150 0.18 2.9 6.3 5.9 6.11 0.70 5287.53 T6 150 0.21 3.2 5.1 4.2 6.60 0.73 3295.47


 下载:
下载: