One-dimensional analytical model for contaminant transport through CCL under thermal diffusion and its application
-
摘要: 建立了污染物在对流、分子扩散和热扩散作用下压实黏土衬垫(CCL)的一维运移解析模型,并获得解析解。无量纲设计曲线表明对流作用对污染物在CCL中运移的影响至关重要;然而随着热扩散作用的增强,对流作用的影响会有所减弱。参数敏感性分析结果表明,当渗滤液水头达到3 m时,10 a的底部浓度和通量分别是无对流情况下的3.5~4.9倍和5.9~15.1倍;当热扩散作用较强(M=-5)时,10 a底部浓度和通量是无热扩散作用下的2.6倍和3.5倍;温度升高会增大土的渗透系数,从而影响污染物在CCL中的运移,在衬垫系统设计过程中应予以考虑。提出了衬垫厚度设计简化计算方法,并以西安江村沟填埋场为例,对CCL进行了简化设计;结果表明:若要保证渗滤液中的Cl-和As击穿CCL的时间大于50 a,则CCL的厚度分别需要不小于11.16 m和1.75 m。Abstract: A one-dimensional analytical model as well as the analytical solution for the contaminant transport in compacted clay liner (CCL) is proposed. The dimensionless design curves show that the advection has significant effects on the contaminant transport in CCL. However, with the increases of thermal diffusion, the effects of the advection will decrease. The results of parameter sensitive analysis show when the leachate head reaches 3 m, the 10-year bottom concentration and flux increase by the factors of 3.5~4.9 and 5.9~15.1, respectively, compared with those without the advection. When the thermal diffusion is great enough (M=-5), the bottom concentration and flux increase by the factors of 2.6 and 3.5, respectively, compared with those without the thermal diffusion. The effects of the temperature on the permeability coefficient of CCL should be considered in the design of landfill clay liners. A simplified method for determination of the thickness of the landfill liner is proposed. The simplified method is used to design the liner system at the Jiangcungou Landfill site in Xi 'an. When considering the chloride (Cl-) and arsenic (As) as the index contaminants, the breakthrough time will be longer than 50 years in the case with the thickness of CCL larger than 11.16 m and 1.75 m, respectively.
-
Keywords:
- analytical model /
- temperature /
- thermal diffusion /
- leachate /
- simplified design
-
0. 引言
近二十年来,随着中国城市化快速发展产生了大量的城市生活垃圾,垃圾处理技术的发展面临着巨大的挑战[1-3]。填埋法仍然是中国处理生活垃圾的其中一个主要方法,而且填埋场起到城市固废处置的兜底保障作用[1]。对于现代卫生垃圾填埋场,政府监管机构要求在填埋场底部建造衬垫系统,以容纳城市固体废物,并控制产生的渗滤液,以防止或尽量减少向周围环境释放有害污染物[4]。由于其低渗透性和与渗滤液污染物的相对良好兼容性,由天然黏土沉积或压实黏土衬垫(CCL)组成的黏土屏障在中国和世界范围内作为垃圾填埋场的底部衬垫使用最广泛[5-6]。
现代垃圾填埋场的优化设计需要深入了解污染物在黏土衬垫中迁移的基本机理,建立能够定量预测衬垫性能的数学模型[7]。目前,对污染物在填埋场衬垫系统中运移的研究主要包括数值法和解析解法。数值模型虽然能够模拟具有不同类型反应的污染物在衬垫系统中的运移,然而确需要大量的输入参数[8]。相比之下,具有高计算效率的解析解可以方便地分析涉及广泛的控制参数的众多情况[9]。对各种污染物在CCL中的分子扩散、降解、吸附、对流和固结等作用,已有大量学者建立了相关的耦合运移模型,并利用拉普拉斯变换等方法得到了相应的解析解[10-12]。然而,在垃圾填埋场内部,伴随着所填埋的废弃物的降解过程会产生大量的热,填埋场内部温度较高(可高达150℃),而含水层的温度通常为5~25℃,因此在填埋场底部衬垫层中会存在一个温度梯度[13]。温度梯度会对污染物在衬垫层中的运移产生驱动力,称之为热扩散作用。而目前对污染物在CCL中运移的解析模型大都忽略了热扩散作用的影响。相关研究表面,若忽略热扩散作用的影响,污染物击穿2 m厚CCL衬垫的时间将增加20%~76%,这表明衬垫系统性能被大大高估[14]。而对0.6 m厚的CCL衬垫,当其上表面温度达到30℃时,其底部通量是仅考虑分子扩散作用时的2~11倍,因此在进行填埋场黏土衬垫设计时需要考虑热扩散作用的影响[15]。此外,解析解虽然可以模拟污染物在垃圾填埋场衬垫系统中的运移,但在考虑对流、扩散和吸附等作用后污染物在衬垫系统中运移的解析解形式仍较为复杂较难被用于填埋场衬垫系统的设计中。
本文建立了考虑分子扩散、热扩散和对流等作用下污染物在CCL中的一维运移解析模型,并利用拉普拉斯变换法推导得到了相应的解析解。得到的解析解与数值法进行了比较。基于得到的解析解,对渗滤液水头和温度等参数进行了敏感性分析。以得到的解析解为基础,结合参数敏感性分析结果,通过数据拟合的方法得到了垃圾填埋场CCL衬垫厚度的简化计算公式。以西安江村沟填埋场为例,利用本文得到的简化计算公式及其设计曲线对填埋场衬垫系统的CCL厚度进行了设计。
1. 温度作用下污染物在CCL中的一维运移模型
1.1 数学模型
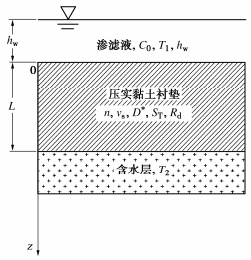
污染物在CCL中的运移解析模型主要考虑了热传导、分子扩散和对流等作用,主要假设有:①污染物通过CCL的运移是一维的;②CCL为均质且饱和介质;③热传导过程为一个稳态过程[16]。基于以上假设条件,建立了污染物在CCL中的一维运移模型,如图 1所示。
图 1中z轴的正方向为竖直向下,原点位于压实黏土衬垫的上表面处。其中C0为废弃物填埋场产生的渗滤液浓度,T1和T2分别为CCL的上、下表面温度,hw为渗滤液水头大小,L为CCL厚度,n为CCL的孔隙度,vs为水流在CCL中的渗流速度,D*为CCL的有效扩散系数,ST为索雷特系数,Rd为阻滞因子。
Sedighi等[17]针对污染物在多组分化系统中的运移进行了研究,推导了其在电化学和热扩散两种作用下的控制方程。Thomas等[18]则推导了污染物在化学扩散作用下的控制方程。本文以这两种控制方程为基础,将温度作用下的污染物在CCL中的一维运移控制方程简化如下:
∂C∂t=D∗Rd∂2C∂z2+1Rd∂∂z(DT∂T∂z)−vsRd∂C∂z, (1) 式中:C为污染物浓度,t为时间,z为污染物与CCL表面的竖直距离,DT为介质的热扩散系数,T为CCL的温度。
水流在CCL的渗流速度vs表示为
vs=k(L+hw)nL, (2) 式中:n为黏土层的孔隙度,k为黏土衬垫层的渗透系数。
介质的热扩散系数DT计算式如下:
DT=CSTD∗, (3) 将式(3)代入式(1)中得
∂C∂t=D∗Rd∂2C∂z2+STD∗Rd∂∂z(C∂T∂z)−vsRd∂C∂z。 (4) 基于先前的假设,热扩散为一稳态过程,并将热扩散简化为一维变化过程,得热扩散控制方程如下:
T=Aiz+Bi, (5) 式中:系数Ai和系数Bi为常数,根据实际黏土衬垫层的边界温度确定。
将式(5)代入式(4)中得
∂C∂t=D∗Rd∂2C∂z2+AiSTD∗−vsRd∂C∂z。 (6) 黏土衬垫层的初始条件为
C(z,0)=0。 (7) 基于先前假设,黏土衬垫的上部边界条件为
C(0,t)=C0。 (8) 底部边界条件采用Foose[19]在对衬垫系统研究中提出的半无限边界条件。
1.2 模型求解
由于黏土衬垫层的下部边界条件为半无限边界,因此:
∂C(∞,t)∂z=0。 (9) 将上下部边界条件式(8),(9),代入控制方程(6)中,并结合初始条件式(8)即可进行求解,首先引入拉普拉斯变换式,如下:
¯C(z,p)=∫∞0e−ptC(z,t)dt, (10) 式中:p为拉普拉斯变换参数,¯C(z,p)为拉普拉斯变换后的函数。
分别对控制方程式(6)、边界条件式(8)和式(9)进行拉普拉斯变换,得变换式如下:
p¯C(z,p)=D∗Rd∂2¯C(z,p)∂z2+AiSTD∗−vsRd∂¯C(z,p)∂z, (11) ¯C(0,p)=C0p, (12) ∂¯C(∞,p)∂z=0。 (13) 根据常微分方程的求解公式,式(11)的通解形式为
¯C(z,p)=A1eλ1z+A2eλ2z, (14) 式中:参数A1和参数A2为常数,需要通过边界条件来确定,对式(12),(13)进行分析,得到特征根的表达式如下:
λ1=−AiSTD∗−vs2D∗+√14(AiST−vsD∗)2+pRdD∗ ,λ2=−AiSTD∗−vs2D∗−√14(AiST−vsD∗)2+pRdD∗ 。} (15) 由下边界式(13)可得
A1=0。 (16) 因此式(14)即可变换为
¯C(z,p)=A2eλ2z。 (17) 再将式(17)代入式(12)可得
A2=C0p。 (18) 结合上式,可计算¯C(z,p)的解为
¯C(z,p)=C0peλ2z。 (19) 将式(15)中的λ2代入式(19)可得
¯C(z,p)=C0pexp[(−AiSTD∗−vs2D∗−(√14(AiST−vsD∗)2+pRdD∗)z] 。 (20) 依据Carslaw等[20]附录Ⅴ中的拉普拉斯反演公式(19),再结合拉普拉斯变换法的相关性质,对式(20)进行反演计算,得到污染物浓度在半无限域边界条件下的时域解,其表达式如下:
C(z,t)C0=12exp[−(AiSTD∗−vs)zD∗]⋅erfc[Rdz−(AiSTD∗−vs)t2√D∗Rdt]+12erfc[Rdz+(AiSTD∗−vs)t2√D∗Rdt]。 (21) 由式(5)可知,温度梯度可表示为下式:
Ai=ΔTL, (22) 式中:ΔT为CCL下表面与上表面温差(即ΔT= T2-T1)。
污染物的底部通量可以通过下列公式求得
J(z,t)=−nD∗∂C(z,t)∂z−nDTdTdz+nvsC(z,t), (23) 式中:J(z, t)为污染物的底部通量值。
将式(3)和式(21)代入式(23)中,得污染物在CCL中的底部通量表达式为
J(z,t)=C0nD∗Rd2√π D∗Rdtexp[−[Rdz+(AiSTD∗−vs)t]24D∗Rdt]+C0nD∗Rd2√π D∗Rdtexp[−(AiSTD∗−vs)zD∗]⋅exp[−[Rdz−t(AiSTD∗−vs)]24D∗Rdt]+C02(nvs−nAiSTD∗)⋅erfc[Rdz+(AiSTD∗−vs)t2√D∗Rdt]。 (24) 由式(21)可得到的无量纲浓度的解析解如下:
CN=C(z,t)C0=12exp[−(M−VR)]erfc[√TR(TR−1−M+VR)2]+12erfc[√TR(TR−1+M−VR)2], (25) 式中:
M=AiSTz, (26) TR=D∗tRdz2, (27) VR=vszD∗。 (28) 可以引入以下公式来表示污染物在CCL的底部通量的无量纲形式:
FN=J(L,t)LnD∗C0。 (29) 将式(24)和式(26)~(28)代入式(29)得到的无量纲通量的解析解如下:
FN=exp[−TR(TR−1+M−VR)24]2√π TR+exp[−(M−VR)−[TR(TR−1−M+VR)24]]2√π TR+ 12(VR−M)erfc[√TR(TR−1+M−VR)2]。 (30) 2. 与数值法的对比
为了验证本文得到的解析解的有效性与合理性,针对2 m厚的CCL,将得到的解析解与数值软件Comsol Multiphysics4.1计算结果进行了对比。以Cl-作为渗滤液中的代表性污染物,其在CCL中的运移参数取值如表 1所示[21-22]。
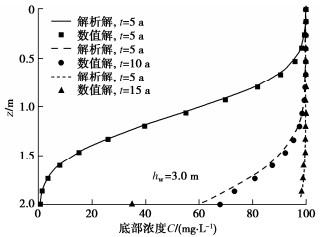
表 1 污染物在CCL中运移的参数取值表Table 1. Parameters of contaminant transport in CCL参数 符号 取值 渗滤液中污染物浓度 C0/(mg·L-1) 100 渗滤液水头 hw/m 0.3/3.0 有效扩散系数 D*/(m2·s-1) 4×10-10 黏土厚度 L /m 2.0 索雷特系数 ST /K-1 3×10-2 黏土层孔隙度 n 0.4 黏土层渗透系数 k /(m·s-1) 1×10-9 阻滞因子 Rd 1.0 黏土层两端温差 ΔT /K -50 图 2给出了解析解与数值软件Comsol Multiphysics 5.1计算得到的剖面浓度曲线。对3.0 m的渗滤液水头下,时间分别为5,10和15 a时的污染物剖面浓度分布进行了比较。结果表明,两种方法计算得到的结果吻合的较好。这也证明了本文解析解的合理性和有效性。
3. 无量纲设计曲线
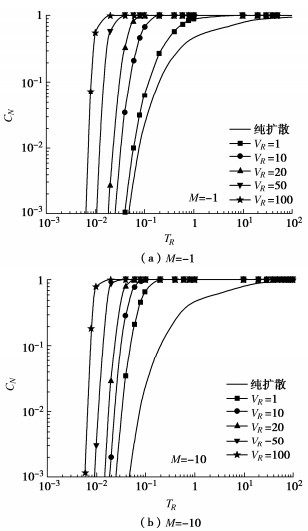
由式(25)得到无量纲浓度CN与热扩散因子M、对流因子VR和时间因子TR之间的关系曲线,分别如图 3所示。以TR=0.1,M=-1为例,VR=10的无量纲浓度是纯扩散的26.4倍,这说明对流作用对污染物在CCL中运移的影响至关重要。此外,当TR=0.1时、在M=-1和M=-10的情况下,VR=10的无量纲浓度分别是VR=1的10.5和1.5倍。这表明随着热扩散作用的增强,对流作用的影响会有所减弱。
4. 参数敏感性分析
为了研究不同参数对污染物在CCL中运移的影响规律,以Cl-为代表污染物,针对渗滤液水头hw和温度等参数进行了敏感性分析。
4.1 渗滤液水头hw对CCL防污性能影响
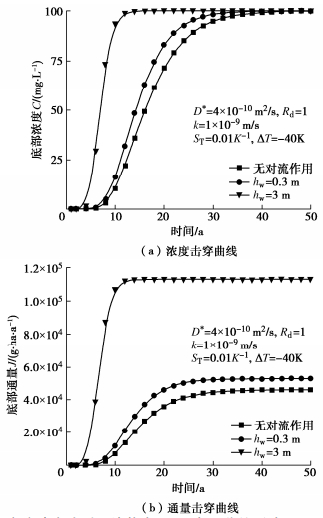
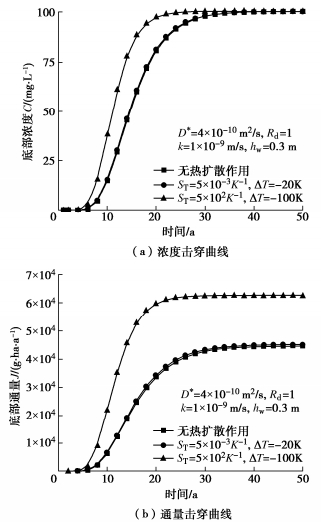
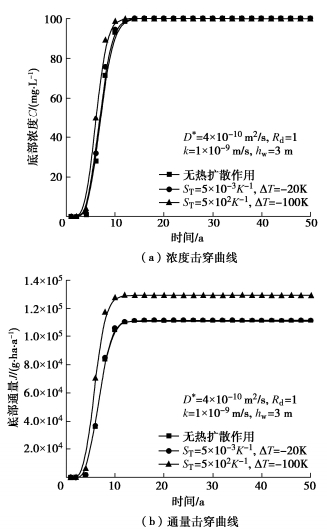
对渗滤液水头进行参数敏感性分析时,分别考虑渗滤液水头hw为0.3 m和3 m的情况,并与无对流作用时的情况进行了对比。索雷特系数和CCL顶底两端温差分别取1×10-2 K-1和-40 K和5×10-2 K-1和-100 K,其他参数与表 1相同[23]。结果如图 4,5所示。
由图 4可知,随着渗滤液水头的增大,污染物的底部浓度和通量增大。以10 a的污染物底部浓度和通量为例,当索雷特系数与黏土层两端温差分别取1×10-2 K-1与ΔT=-40 K(即M=-0.4)时,渗滤液水头为0.3和3 m时对应的底部浓度分别为16.4和93.6 mg/L,是无对流情况下的1.6和8.9倍;底部通量分别为11743.1和107384 g/ha/a,是无对流情况下的1.7和15.1倍。
由图 5可以得到,当温差较大,热扩散作用较强(M=-5),渗滤液水头为0.3和3 m时,10 a底部浓度是无对流情况下的1.4和3.5倍,底部通量是无对流情况下的1.4和5.9倍。可以看出,虽然热扩散作用会较弱渗滤液水头对污染物在CCL中运移的影响,但即使热扩散作用很强时,渗滤液水头对污染物在CCL中运移的影响仍然非常大。因此,提高圾填埋场的导排和收集系统的性能以降低渗滤液水头,是改善衬垫系统防污性能和保护周边地下水土资源的关键。
4.2 热扩散作用对CCL防污性能影响
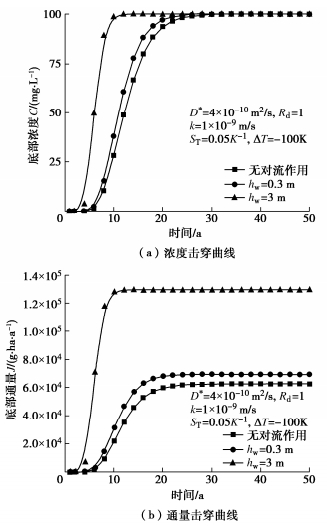
对于热扩散作用的影响,研究了不同的索雷特系数和CCL顶底两端温差作用下污染物的浓度和通量击穿曲线。分别考虑了无热扩散作用,ST=5×10-3 K-1,ΔT=-20 K以及ST=5×10-2 K-1,ΔT=-100 K 3种情况。渗滤液水头分别取0.3和3 m,其他参数与表 1相同。结果如图 6,7所示。
由图 6可以看出随着热扩散作用的增强,污染物在CCL中的移动速度在不断的加快,污染物在CCL底部的浓度和通量也在不断增大。以10 a的污染物底部浓度和通量为例,当渗滤液水头hw=0.3 m,索雷特系数与黏土层两端温差分别取5×10-3 K-1与ΔT=-20 K(M=-0.1)和5×10-2 K-1与ΔT=-100 K(M=-5)时,污染物底部浓度分别为15.4和38.3 mg/L,底部通量分别为6510.7和21866.1 g/ha/a;而无热扩散作用时的底部浓度和通量分别为15.0 mg/L和6323.4 g/ha/a。可以看出,温差较大,热扩散作用较强(M=-5)时,污染物底部浓度和通量是无热扩散作用情况的2.6倍和3.5倍;而当温差较小,热扩散作用较弱(M=-0.1)时,与无热扩散作用条件下相比,其底部浓度和通量变化较小(< 4%)。
而当hw=3 m,由图 7可以看出,温差较大、热扩散作用较强(M=-5)时,10 a污染物底部浓度和通量较无热扩散作用时分别增加了6%和22%;而温差较小、热扩散作用较弱(M=-0.1)时,其底部浓度和通量基本不变(< 2%)。可以看出,当索雷特的和黏土层两端温差较大时,热扩散作用对污染物在CCL中的运移会造成较大的影响,在进行填埋场衬垫系统设计时应该考虑填埋场内部的高温情况。然而,随着渗滤液水头的增加,热扩散作用的影响会被大大减弱。因此,相比于热扩散作用,渗滤液水头对污染物在CCL中的运移更为重要,在填埋场衬垫系统的设计以及周边水土污染控制中需要被着重考虑。
4.3 渗透系数的温度依赖性对污染物运移的影响
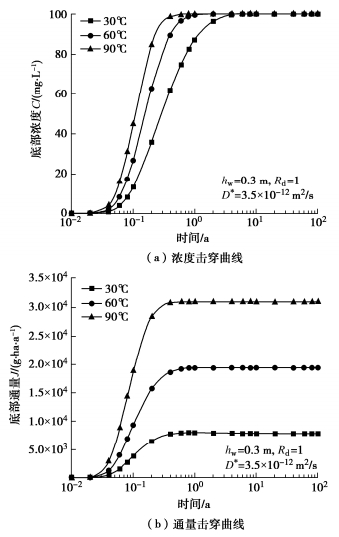
Park等[24]发现不同干密度的膨润土在加热过程中,温度从30℃增加到90℃,渗透系数增加了0.2~2倍,这是由于在加热过程中膨润土发生了不可逆的微观结构变化。渗透系数的改变对污染物的运移有很大的影响,将本文解析解与Park等[24]在膨润土平均温度为30℃,60℃,90℃下得到的渗透系数进行计算,研究了温度对污染物在膨润土中运移的影响。相关参数如表 2所示[25]。其他参数取值与表 1相同。
表 2 不同温度污染物在膨润土中运移的参数取值Table 2. Transport parameters for contaminant in bentonite liner under different temperatures膨润土平均温度
T0/℃膨润土渗透系数
k/(m·s-1)渗滤液水头
hw/m有效扩散系数
D*/(m2·s-1)膨润土厚度
L/m30 2.12×10-13 0.3 3.5×10-12 0.1 60 4.29×10-13 90 6.48×10-13 图 8给出了膨润土平均温度为30℃,60℃,90℃下得到的渗透系数对污染物浓度和通量的击穿曲线图。从图 8可以得到,由于膨润土的渗透系数会随着温度的增加而增大,污染物底部浓度和通量也有明显的增加。以0.1 a为例,膨润土平均温度为90℃下污染物底部浓度是30℃的3.4倍,底部通量是其5.0倍。由此可以得出,由于温度的升高对膨润土的渗透系数产生了不可逆的影响,从而导致了污染物底部浓度和通量的大幅度增加,因此在填埋场底部衬垫设计的过程中,需要视填埋场内部温度去选取合适的渗透系数,以有效评估衬垫层的服役性能。
5. 填埋场CCL厚度简化设计方法
5.1 CCL厚度简化计算过程
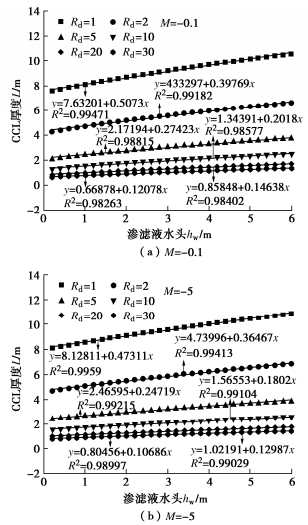
利用得到的温度作用下污染物在CCL中的一维运移解析解式(21),进行CCL厚度的简化设计。为了反应不同的热扩散条件,选取了不同的CCL两端温差ΔT和索雷特系数ST。为了体现不同污染物的影响,阻滞因子分别取Rd=1,2,5,10,20和30等情况。根据国内外垃圾填埋场中的渗滤液各组分的常见浓度范围以及张春华等提出的填埋场典型击穿标准,本次设计采用的击穿标准值为0.1[21]。考虑衬垫系统的服役寿命为50 a。其他参数取值与表 1相同。计算结果如图 9所示。
由图 9可知,CCL厚度L与渗滤液水头hw之间近似呈线性关系。因此,选用线性拟合方式对计算结果进行拟合,根据拟合结果,推导获得CCL厚度和水头的建议关系式:
L=E+Fhw, (31) 式中:参数E,F均为待定系数。
利用式(31)对图 9中的计算结果进行线性拟合,得到了拟合结果如图 9所示。
根据图 9中各曲线的拟合方程,可以得到不同热扩散条件下系数E和F与阻滞因子在的关系曲线。通过对系数E和F的数值拟合发现,当热扩散条件较弱时(即M=-0.1),系数E和F的表达式分别为
E=7.57046R−0.76406d, (32) F=0.51488Rd−0.40781。 (33) 将式(32),(33)分别代入式(31)中,可得到热扩散条件较弱时(即M=-0.1)的CCL厚度设计简化公式如下:
L=7.57046Rd−0.76406+0.51488Rd−0.40781hw。 (34) 当热扩散条件较强时(即M=-5),系数E和系数F的表达式分别为
E=8.05552Rd−0.72282, (35) F=0.47905Rd−0.42482。 (36) 将式(35)和(36)分别代入式(31)中,可得到热扩散条件较强时(即M=-5)的CCL厚度设计简化公式:
L=8.05552Rd−0.72282+0.47905Rd−0.42482hw。 (37) 5.2 实例分析
为了进一步验证该简化计算方法的实用性,本文对国内典型垃圾填埋场西安江村沟填埋场进行实例分析。基于其固有的稳定性及渗滤液中浓度较高等特点,Cl-被作为代表性污染物之一[26]。此外,根据西安江村沟填埋场渗滤液污染物组分分析结果,主要超标污染物As也被作为代表性污染物进行了分析 [27]。西安江村沟渗滤液水头约为6.8 m,CCL两端的温度差∆T=-60 K,索雷特系数ST=0.03 K-1,两种典型污染物Cl-和As在CCL衬垫系统中的阻滞因子R−0.42482d分别为1和18.9[28-30]。其他参数与表 1相同。基于以上西安江村沟填埋场参数取值,利用本文提出的CCL厚度设计简化计算方法,对西安江村沟填埋场所需的CCL的厚度进行了简化计算。
西安江村沟填埋场的热扩散条件为M=-1.8,通过线性插值得到惰性离子Cl-和As的系数E分别为7.75082和0.73885,系数F分别为0.5012和0.1491。由于西安江村沟填埋场的渗滤液水头为6.8 m,将相关参数代入式(31)中,得到填埋场所需的CCL的厚度分别为11.16 m和1.75 m。这表明,若要保证渗滤液中的Cl-和As击穿CCL时间大于50 a,则西安江村沟填埋场所需的CCL的厚度分别不小于11.16 m和1.75 m。可以看出,以Cl-为目标污染物时填埋场所需的CCL厚度远高于以As为目标污染物的情况。这表明,在进行填埋场衬垫系统的厚度设计时,应该尽可能以惰性污染物(如氯离子)为目标污染物进行设计,这样得到的结果才更为可靠。
6. 结论
本文建立了考虑分子扩散作用、热扩散作用和对流作用下污染物在CCL中的一维运移解析模型,利用拉普拉斯变换法得到了解析解,与数值计算结果对比发现,两种方法计算得到的结果吻合的较好,证明了本文解析解的合理性和有效性。得到以下5点结论。
(1)通过无量纲浓度设计曲线可知,对流作用对污染物在CCL中运移的影响至关重要。当TR=0.1时、在M=-1和-10的情况下,VR=10的无量纲浓度分别是VR=1的10.5和1.5倍。表明随着热扩散作用的增强,对流作用的影响会有所减弱。
(2)当渗滤液水头分别为0.3和3 m时,填埋场CCL衬垫系统的20 a底部浓度较无对流情况下分别增加了16%和41%,底部通量则分别增加了1.3和3.2倍。因此,尽可能降低渗滤液水头,对改善填埋场衬垫系统的服役寿命及保护周边水土环境具有重要意义。
(3)当CCL两端温差较大、热扩散作用较强(M= -5)时,10 a底部浓度和通量分别是无热扩散作用下的2.6倍和3.5倍。然而,随着渗滤液水头的增加,热扩散作用的影响会被大幅减弱。因此,相比于热扩散作用,渗滤液水头对污染物在CCL中的运移更为重要,其对衬垫系统服役性能的影响需要被着重考虑。
(4)温度会通过影响膨润土的渗透系数来改变其防污性能。以0.1 a为例,平均温度为90℃下污染物底部浓度是30℃的3.4倍,底部通量是其5.0倍。在填埋场底部衬垫设计的过程中,需要考虑温度引起的渗透系数变化的影响。
(5)得到了垃圾填埋场的CCL衬垫厚度的简化设计公式。以西安江村沟垃圾填埋场为例,若要保证渗滤液中的Cl-和As击穿CCL衬垫的时间大于50 a,则土工膜下覆的CCL的厚度分别不小于11.16 m和1.75 m。
-
表 1 污染物在CCL中运移的参数取值表
Table 1 Parameters of contaminant transport in CCL
参数 符号 取值 渗滤液中污染物浓度 C0/(mg·L-1) 100 渗滤液水头 hw/m 0.3/3.0 有效扩散系数 D*/(m2·s-1) 4×10-10 黏土厚度 L /m 2.0 索雷特系数 ST /K-1 3×10-2 黏土层孔隙度 n 0.4 黏土层渗透系数 k /(m·s-1) 1×10-9 阻滞因子 Rd 1.0 黏土层两端温差 ΔT /K -50 表 2 不同温度污染物在膨润土中运移的参数取值
Table 2 Transport parameters for contaminant in bentonite liner under different temperatures
膨润土平均温度
T0/℃膨润土渗透系数
k/(m·s-1)渗滤液水头
hw/m有效扩散系数
D*/(m2·s-1)膨润土厚度
L/m30 2.12×10-13 0.3 3.5×10-12 0.1 60 4.29×10-13 90 6.48×10-13 -
[1] 陈云敏. 环境土工基本理论及工程应用[J]. 岩土工程学报, 2014, 36(1): 1-46. doi: 10.11779/CJGE201401001 CHEN Yunmin. A fundamental theory of environmental geotechnics and its application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 1-46. (in Chinese) doi: 10.11779/CJGE201401001
[2] LEI M F, LIN D Y, LIU J W, et al. Modified chloride diffusion model for concrete under the coupling effect of mechanical load and chloride salt environment[J]. AIP Advances, 2018, 8(3): 035029. doi: 10.1063/1.5027540
[3] YU C, LIU J F, MA J J, et al. Study on transport and transformation of contaminant through layered soil with large deformation[J]. Environmental Science and Pollution Research, 2018, 25(13): 12764-12779. doi: 10.1007/s11356-018-1325-7
[4] PU H F, FOX P J, SHACKELFORD C D. Assessment of consolidation-induced contaminant transport for compacted clay liner systems[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(3): 04015091. doi: 10.1061/(ASCE)GT.1943-5606.0001426
[5] 田改垒, 张志红. 考虑热效应的污染物在土中扩散、渗透和固结耦合模型[J]. 岩土工程学报, 2022, 44(2): 278-287. doi: 10.11779/CJGE202202009 TIAN Gailei, ZHANG Zhihong. The coupled model of contaminant diffusion, osmosis and consolidation in soil considering thermal effect[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(2): 278-287. (in Chinese) doi: 10.11779/CJGE202202009
[6] YAN H X, XIE H J, WU J W, et al. Analytical model for transient coupled consolidation and contaminant transport in landfill liner system[J]. Computers and Geotechnics, 2021, 138: 104345. doi: 10.1016/j.compgeo.2021.104345
[7] YU C, WANG H, FANG D F, et al. Semi-analytical solution to one-dimensional advective-dispersive-reactive transport equation using homotopy analysis method[J]. Journal of Hydrology, 2018, 565: 422-428. doi: 10.1016/j.jhydrol.2018.08.041
[8] STOPPIELLO M G, LOFRANO G, CAROTENUTO M, et al. A comparative assessment of analytical fate and transport models of organic contaminants in unsaturated soils[J]. Sustainability, 2020, 12(7): 2949. doi: 10.3390/su12072949
[9] DING X H, FENG S J, ZHENG Q T, et al. A two-dimensional analytical model for organic contaminants transport in a transition layer-cutoff wall-aquifer system[J]. Computers and Geotechnics, 2020, 128: 103816. doi: 10.1016/j.compgeo.2020.103816
[10] 谢海建. 成层介质污染物的运移机理及衬垫系统防污性能研究[D]. 杭州: 浙江大学, 2008. XIE Haijian. A Study on Contaminant Transport in Layered Media and the Performance of Landfill Liner Systems[D]. Hangzhou: Zhejiang University, 2008. (in Chinese)
[11] 陈云敏, 谢海建, 柯瀚, 等. 层状土中污染物的一维扩散解析解[J]. 岩土工程学报, 2006, 28(4): 521-524. doi: 10.3321/j.issn:1000-4548.2006.04.018 CHEN Yunmin, XIE Haijian, KE Han, et al. Analytical solution of contaminant diffusion through multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(4): 521-524. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.04.018
[12] 张文杰, 赵培, 贾文强. 一维对流-扩散试验各种边界条件及其统一形式解析解[J]. 岩土力学, 2015, 36(10): 2759-2764. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510003.htm ZHANG Wenjie, ZHAO Pei, JIA Wenqiang. Boundary conditions of one-dimensional convection- diffusion column tests and unified analytical solution[J]. Rock and Soil Mechanics, 2015, 36(10): 2759-2764. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510003.htm
[13] HARRIS A P F, MCDERMOTT C I, KOLDITZ O, et al. Modelling groundwater flow changes due to thermal effects of radioactive waste disposal at a hypothetical repository site near Sellafield, UK[J]. Environmental Earth Sciences, 2015, 74(2): 1589-1602. doi: 10.1007/s12665-015-4156-6
[14] PENG M Q, FENG S J, CHEN H X, et al. Analytical model for organic contaminant transport through GMB/CCL composite liner with finite thickness considering adsorption, diffusion and thermodiffusion[J]. Waste Management, 2021, 120: 448-458. doi: 10.1016/j.wasman.2020.10.004
[15] XIE H J, ZHANG C H, SEDIGHI M, et al. An analytical model for diffusion of chemicals under thermal effects in semi-infinite porous media[J]. Computers and Geotechnics, 2015, 69: 329-337. doi: 10.1016/j.compgeo.2015.06.012
[16] THOMAS H R, SEDIGHI M, VARDON P J. Diffusive reactive transport of multicomponent chemicals under coupled thermal, hydraulic, chemical and mechanical conditions[J]. Geotechnical and Geological Engineering, 2012, 30(4): 841-857. doi: 10.1007/s10706-012-9502-9
[17] SEDIGHI M, THOMAS H, VARDON P. Modelling thermal impacts on reactive transport processes related to multicomponent chemicals in compacted clays[C]//2nd International Symposium on Computational Geomechanics(ComGeo Ⅱ). Dubrovnik, 2011: 538-546.
[18] THOMAS H R, SEDIGHI M. Thermal Effects on Chemical Diffusion in Multicomponent Ionic Systems[M]//Engineering Geology for Society and Territory-Volume 6. Cham: Springer International Publishing, 2014: 525-528.
[19] FOOSE G J. Transit-time design for diffusion through composite liners[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(7): 590-601. doi: 10.1061/(ASCE)1090-0241(2002)128:7(590)
[20] CARSLAW H S, JAEGER J C. Conduction of Heat in Solids[M]. 2d ed. Oxford: Clarendon Press, 1959.
[21] 张春华, 吴家葳, 陈赟, 等. 基于污染物击穿时间的填埋场复合衬垫厚度简化设计方法[J]. 岩土工程学报, 2020, 42(10): 1841-1848. doi: 10.11779/CJGE202010009 ZHANG Chunhua, WU Jiawei, CHEN Yun, et al. Simplified method for determination of thickness of composite liners based on contaminant breakthrough time[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(10): 1841-1848. (in Chinese) doi: 10.11779/CJGE202010009
[22] XIE H J, JIANG Y S, ZHANG C H, et al. An analytical model for volatile organic compound transport through a composite liner consisting of a geomembrane, a GCL, and a soil liner[J]. Environmental Science and Pollution Research, 2015, 22(4): 2824-2836. doi: 10.1007/s11356-014-3565-5
[23] HAO Z S, BARLAZ M A, DUCOSTE J J. Finite-element modeling of landfills to estimate heat generation, transport, and accumulation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(12): 04020134.
[24] PARK S, YOON S, KWON S, et al. Temperature effect on the thermal and hydraulic conductivity of Korean bentonite buffer material[J]. Progress in Nuclear Energy, 2021, 137: 103759.
[25] FOX P M, TINNACHER R M, CHESHIRE M C, et al. Effects of bentonite heating on U(VI)adsorption[J]. Applied Geochemistry, 2019, 109: 104392.
[26] ZHAN T L T, GUAN C, XIE H J, et al. Vertical migration of leachate pollutants in clayey soils beneath an uncontrolled landfill at Huainan, China: a field and theoretical investigation[J]. Science of the Total Environment, 2014, 470/471: 290-298.
[27] 何晓晓. 江村沟垃圾渗滤液尾水的深度处理研究[D]. 西安: 长安大学, 2013. HE Xiaoxiao. Deep Research on the Tail Water of Leachate from Jiang Cungou MSW Landfill[D]. Xi'an: Changan University, 2013. (in Chinese)
[28] 陈云敏, 刘晓成, 徐文杰, 等. 填埋生活垃圾稳定化特征与可开采性分析: 以中国第一代卫生填埋场为例[J]. 中国科学: 技术科学, 2019, 49(2): 199-211. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201902010.htm CHEN Yunmin, LIU Xiaocheng, XU Wenjie, et al. Analysis on stabilization characteristics and exploitability of landfilled municipal solid waste: case of a typical landfill in China[J]. Scientia Sinica(Technologica), 2019, 49(2): 199-211. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201902010.htm
[29] 张春华. 填埋场复合衬垫污染物热扩散运移规律及其优化设计方法[D]. 杭州: 浙江大学, 2018. ZHANG Chunhua. Mechanisms for Contaminant Transport in Landfill Composite Liners under Thermal Effect and Its Optimization Design Method[D]. Hangzhou: Zhejiang University, 2018. (in Chinese)
[30] ROWE R. Short-and long-term leakage through composite liners: The 7th Arthur Casagrande Lecture 1[J]. Canadian Geotechnical Journal, 2012, 49(2): 141-169.
-
期刊类型引用(1)
1. 张春华,黄江东,邓正定,谢海建,邓通发. 热渗透作用下有机污染物在双人工复合衬层中的一维运移模型. 岩土工程学报. 2024(06): 1254-1262 .  本站查看
本站查看
其他类型引用(1)



 下载:
下载: