0.   引言

平板载荷试验在工程实践中被广泛应用于测定地基承载力和推算土体抗剪强度参数,为地基设计和处理提供依据。由于地表浅层土和实际工程中的压实土层常位于地下水位以上,处于非饱和状态^[1-2],平板载荷现场试验大多是在非饱和土上开展的。

近年来,学者们通过模型试验开展了非饱和土地基承载力特性的研究,其中大多只针对黏土或砂土^[3-4]。然而,天然地基土一般并非纯黏土或纯砂土。含黏粒砂土广泛分布于中国东南、华南和中东部地区,实际工程建设中的吹填土地基、高速公路路基、土石坝坝基等都常为非饱和含黏粒砂土^[5],其非饱和力学和水力学特性与黏土和砂土都存在显著差异^[6]。

自然状态下的地基土会经历地下水位升降、降雨或蒸发等干湿变化,由于含黏粒砂土的土水特征曲线存在明显的滞回效应^[7-8],非饱和含黏粒砂土的基质吸力与饱和度的对应关系取决于经历的干湿变化过程。研究表明,滞回效应对非饱和土的力学特性影响显著^[7-8],但其对非饱和含黏粒砂土地基承载力的影响规律和机理尚不十分明确,使得在非饱和含黏粒砂土上开展平板载荷试验时,无法对试验数据进行准确分析,影响试验结果对地基设计的参考价值。

本文在经历不同干湿变化过程后的非饱和含黏粒砂土试样上开展了平板载荷模型试验,结合不同深度处的基质吸力和饱和度值,系统分析了干湿循环过程和基质吸力分布对承载力的影响,并提出了考虑干湿变化的平板载荷试验结果分析方法。

1.   非饱和含黏粒砂土平板载荷试验

1.1   试验土样

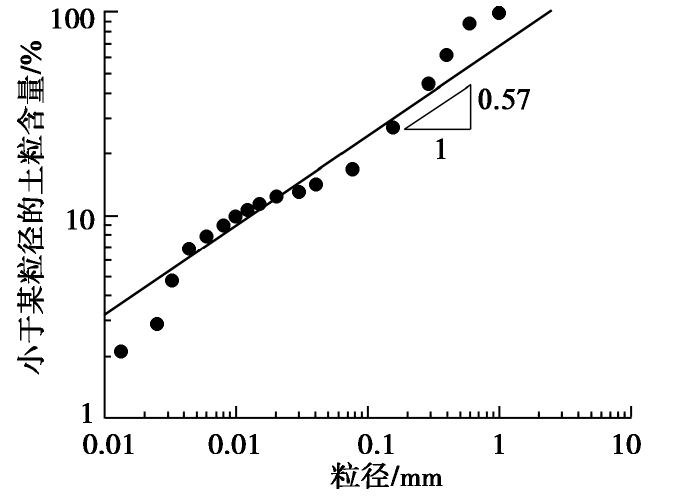
本文开展的平板载荷模型试验的土样为黏粒含量为15%的含黏粒砂土,由标准石英砂和高岭土均匀混合制成。土样相对质量密度G_s=2.64,最大干密度ρ_max=1.92 g/cm³,对应的孔隙比e_min=0.38；最小干密度ρ_min=1.56 g/cm³,对应的孔隙比e_max=0.69。临界状态黏聚力和内摩擦角分别为4.3 kPa和35.2°。采用双对数坐标系绘制粒径分布曲线（图1）,可以发现近似于一条直线,表明试验土样的粒径分布具有分形特征,分形维数D_s=2.43。

图  1  试验土样粒径分布曲线

Figure  1.  Grain-size distribution curves of test soils

下载: 全尺寸图片 幻灯片

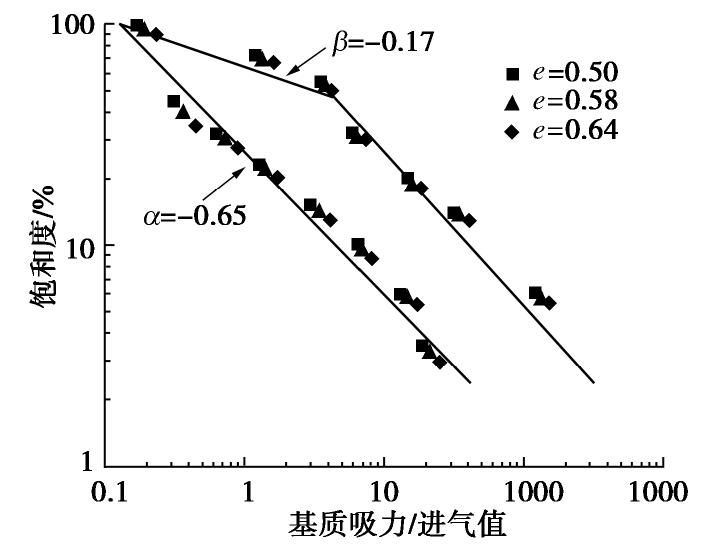
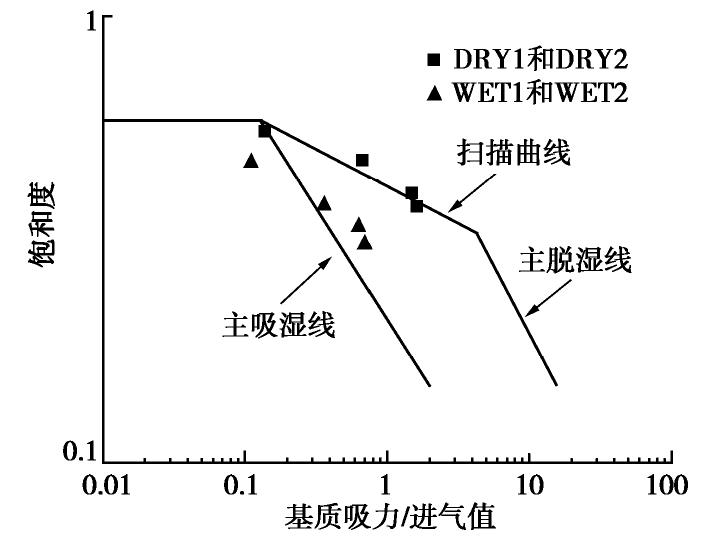
针对不同孔隙比的土样,采用压力板试验仪开展了脱湿和吸湿下土水特征曲线测定试验,将试验结果绘制于双对数坐标系中（图2）。可以看出,试验土样的土水特征曲线带有较为明显的滞回环。采用Russell模型^[7]对试验数据进行拟合,其表达式为

图  2  试验土样土水特征曲线

Figure  2.  Soil-water characteristic curves (SWCC) of test soils

下载: 全尺寸图片 幻灯片

式中,S_r,s分别为饱和度和基质吸力,s_e为进气值（在主脱湿线）或出气值（在主吸湿线）,s_rd为主脱湿线与扫描曲线的交点,s_rw为主吸湿线与扫描曲线的交点,α=-0.65和β=-0.17分别主吸/脱湿线和扫描曲线的斜率。

基于分形维数考虑孔隙比对土水特征曲线的影响^[7],进气值s_ae和出气值s_ex与孔隙比e的关系可表示为

非饱和土有效应力原理表达式为

式中,${\sigma }^{\prime }$,$\sigma$为有效应力和总应力,${\sigma }_{\text{net}}$为净应力,p_a,p_w为孔隙气压和水压,χ为有效应力系数^[8]：

1.2   试验仪器

平板载荷模型试验系统主要包括试验模型箱、自动加载系统和数据采集系统。

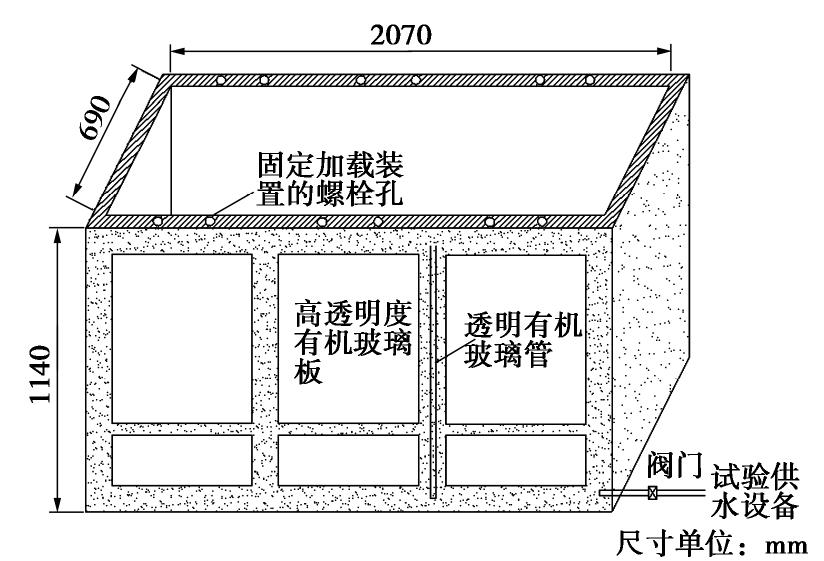
平板载荷试验模型箱（图3）的内部有效尺寸为2.07 m×0.69 m×1.14 m（长×宽×高）。模型箱的前侧面采用钢条加固的高透明度有机玻璃板,以便于在土样制备时观测土层厚度及土样中的水位。模型箱底部与试验室供水系统相连通,可通过底部阀门控制注/排水,调节土样中的水位。模型箱侧面接有一根透明有机玻璃管,用于观测和确认土样中的水位。

图  3  平板载荷试验专用模型箱示意图

Figure  3.  Schematic graph of testing rig of plate lost tests

下载: 全尺寸图片 幻灯片

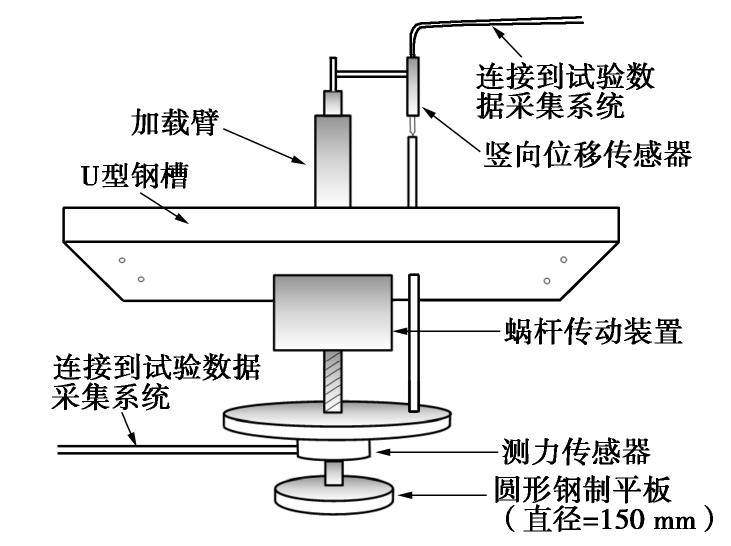
自动加载系统（图4）主要由圆形钢制平板、测力传感器、竖向位移传感器和蜗杆传动装置组成。圆形平板的直径为150 mm。加载系统可通过U型钢槽固定在模型箱顶部3个不同位置,试验进行加载时蜗杆传动装置对圆形平板以恒定速率施加竖向位移,对试验过程中竖向位移和荷载进行实时量测。

图  4  平板载荷试验自动加载系统示意图

Figure  4.  Schematic graph of modelling with different particle sizes

下载: 全尺寸图片 幻灯片

1.3   制样方法和基质吸力量测

试验采用砂雨法和振动法相结合的方法制备均质密实试样。首先运用砂雨法以30 cm的恒定淋砂高度制备干燥试样,然后采用振动仪以80 Hz的频率将模型箱整体振动5 min。本次试验共制备2个试样,相对密实度分别为0.84,0.81。

在干燥试样制备完成后,通过控制模型箱内水位,制备2个经历不同干湿循环变化的非饱和含黏粒砂土试样。制备吸水试样时,将水位控制在试样底部,水依靠毛细管效应向上移动；制备脱水试样时,先将水位提升到试样表面以上2 cm,使试样完全饱和,然后将水通过模型箱底部阀门排走,使水位降低并保持在试样底部。在试样的不同深度埋设振弦式孔压计量测基质吸力值,布置方式为深度700 mm处2个,220 mm处1个,370 mm处1个,520 mm处1个。当测得的基质吸力值在24 h内变化小于0.1 kPa时,可认为试样达到平衡状态,试样制备完成。

1.4   试验过程

试验过程中以0.02 mm/s的恒定速率对平板施加竖向位移,当到达破坏荷载时继续施加5～10 mm的竖向位移后终止试验,试验时间约为30 min,试验过程中记录竖向位移和荷载。

在每个试样上的不同位置进行3组试验,包括饱和状态下的1组试验和非饱和状态下的2组试验,试验顺序及编号如表1所示。试验采用直径为150 mm的圆形平板,模型箱宽度（0.69 m）和相邻两组试验位置间距（0.69 m）均为平板直径的4.6倍,可避免边界效应和单个土样上的多组试验间的相互影响。

表  1  试验编号及极限承载力的量测值和估算值

Table  1.  Test number and measured and calculated bearing capacities

试验编号	试样状态	承载力量测值/kPa	承载力估算值/kPa
SATD	饱和	966	996
DRY1	脱湿	3011	2254
DRY2	脱湿	2889	2254
SATW	饱和	1038	997
WET1	吸湿	1682	1385
WET2	吸湿	1549	1385

下载: 导出CSV 

| 显示表格

试验结束后,使用环刀在距离试验位置100 mm处的不同深度取样,测定含水率和孔隙比等参数。

2.   试验结果及分析

2.1   试验结果

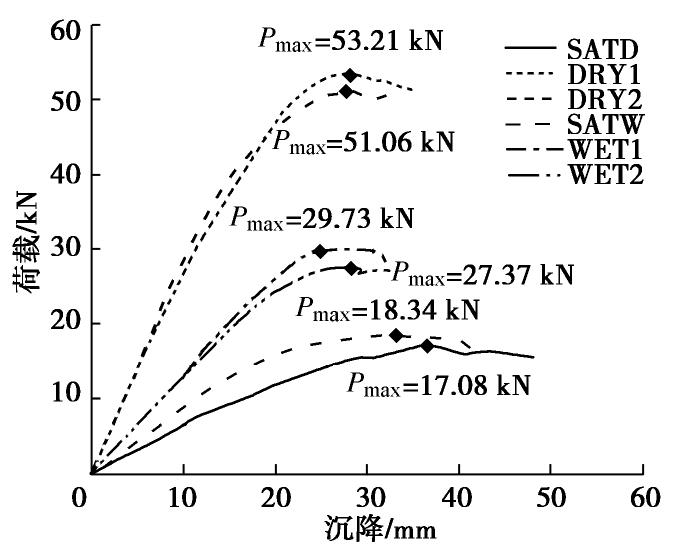
图5为平板载荷试验得到的荷载-沉降关系曲线,通过最大荷载计算得到极限承载力,并列于表1中。

图  5  平板载荷试验结果

Figure  5.  Results of plate load tests

下载: 全尺寸图片 幻灯片

从荷载-沉降关系曲线可以看出,荷载随着施加的竖向位移的增加而不断增大,直至达到最大荷载,随着进一步的竖向位移,荷载发生一定的减小或波动。对于在同一试样上进行的两组非饱和状态下的试验,得到的荷载-沉降关系曲线和最大荷载值几乎相同；同时,同一试样在非饱和状态下的最大荷载值明显大于饱和状态,证明了基质吸力对于极限承载力的影响。

2.2   干湿变化的影响

对于经历不同干湿变化过程的密实度接近的两个试样,进行平板载荷试验时水位高度一致,测得的极限承载力却有很大差距。结合不同深度处基质吸力和饱和度的量测值,分析试样制备过程中不同干湿过程在土水特征曲线上对应的移动过程,计算有效应力系数,从而考虑基质吸力对承载力的影响。

量测得到的不同深度处的基质吸力和饱和度列于表2,同时将量测值与土水特征曲线进行对照（图6）。可以发现,在经历脱湿过程后,土样状态位于扫描曲线上；在经历吸湿过程后,土样状态位于主吸湿线上。

表  2  不同深度处饱和度和基质吸力量测值及对应的χs值

Table  2.  Measured degrees of saturation and suctions at different depths and corresponding values of χs

试验编号	深度/m	饱和度	基质吸力/kPa	$\chi s$/kPa
DRY1,DRY2	0.07	0.56	13.7,14.2	9.78
	0.22	0.61	12.7	9.02
	0.37	0.76	5.7	4.53
	0.52	0.93	1.2	1.19
WET1,WET2	0.07	0.44	6.4,6.2	2.50
	0.22	0.49	5.7	2.37
	0.37	0.57	3.2	1.84
	0.52	0.76	1	1.09

下载: 导出CSV 

| 显示表格

图  6  干湿变化后试样状态在土水特征曲线上的对应位置

Figure  6.  Locations of hydraulic states on SWCC

下载: 全尺寸图片 幻灯片

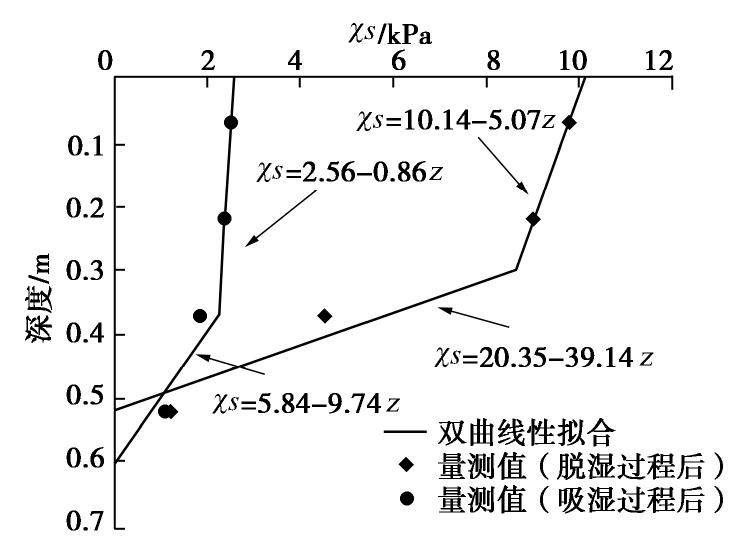
通过干湿变化过程后土样状态在土水特征曲线上对应的位置,可通过式（6）,（7）计算得到有效应力系数χ。基质吸力对有效应力和地基承载力的贡献可通过$\chi s$进行考虑,表2列出了不同深度处基于基质吸力量测值计算得到的$\chi s$值,可以发现在较浅深度处,$\chi s$随深度减小较小；在较深深度处,$\chi s$随深度减小较大。因此,采用两段直线对不同深度$\chi s$的分布进行了拟合（图7）。

图  7  基于量测值拟合的χs随深度分布

Figure  7.  Variation of χs with depth

下载: 全尺寸图片 幻灯片

2.3   试验结果分析

太沙基饱和土地基承载力$q_{\text{u}}$计算公式为

式中,c'为有效黏聚力,q'为上覆盖层压力,${\gamma }^{\prime }$为土的有效重度,N_c,N_q和N_γ为地基承载力系数。

非饱和土的抗剪强度τ可表示为

式中,c',${\phi }^{\prime }$为有效黏聚力和有效内摩擦角,$\chi s$tan${\phi }^{\prime }$即为基质吸力对非饱和土抗剪强度的贡献。

基于滑移线理论的研究表明有效黏聚力和$\chi s$$\tan {\phi }^{\prime }$对抗剪强度和地基承载力有相似且独立的贡献^[9],因此可将$\chi s$$\tan {\phi }^{\prime }$加入式（8）的第一项中,考虑基质吸力对地基承载力的影响。由于基质吸力与黏聚力对地基承载力的贡献相类似,因此可参考饱和土考虑非均布黏聚力的方法,结合$\chi s$随深度分布方程,将$\chi s$随深度变化系数加入式（8）的第三项中,使之能考虑基质吸力非均布情况。

假定$\chi s$随深度（z）分布方程为

式中,${\text{(}\chi s\text{)}}_0$为土体表面处的$\chi s$值,$K_{\chi s}$=∂($\chi s$)/∂z为一个常数。

由此可得到基质吸力非均匀分布时的非饱和土地基承载力计算公式：

式中,${\gamma }_t$为总重度。本次试验在土体表面进行,无上覆荷载,式（11）可简化为

土的有效内摩擦角${\phi }^{\prime }$与密实度相关^[10],本次平板载荷试验相对密实度较高,假定${\phi }^{\prime }$=38°,该值可通过饱和试样上的平板载荷试验结果进行反推验证。

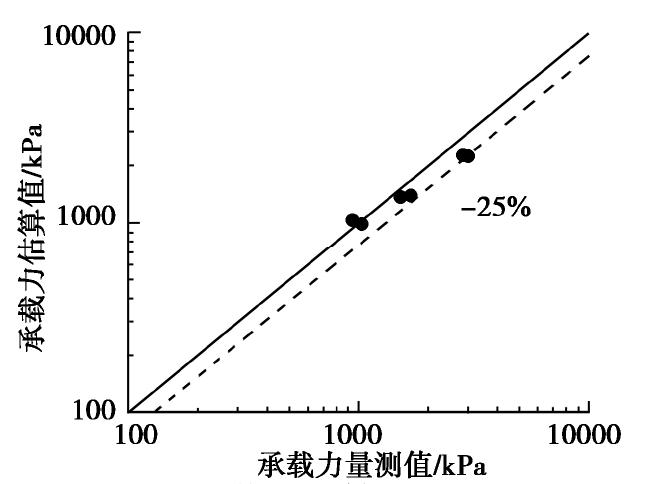
施加于浅基础的荷载对下方土体内应力的影响主要集中于小于1.5倍浅基础直径的深度范围内^[11],因此,计算地基承载力时仅需考虑较浅层土体中的$\chi s$分布,计算中地基承载力系数采用Martin^[12]针对圆形粗糙底面基础的取值,分别为N_c=195.89,N_γ=98.03。

运用式（12）对饱和及非饱和状态下的极限承载力进行计算,并列于表1中。图8对比了承载力估算值和量测值,所有结果的误差均在25%以内,说明采用式（12）估算非饱和土地基承载力的准确度较高。估算值存在误差的原因可部分归结于地基承载力系数的取值方法,地基承载力系数N_c和N_γ都是在一定假定基础上单独取值,在计算叠加使用时忽略了它们之间的相互影响,使计算结果略微偏低,在应用式（12）进行计算时需适当考虑。

图  8  极限承载力估算值与量测值对比

Figure  8.  Comparison between calculated and measure bearing capacities

下载: 全尺寸图片 幻灯片

3.   结论

本文开展了不同干湿变化下非饱和含黏粒砂土平板载荷模型试验,分析了干湿变化过程对地基承载力的影响机理,提出了非均布基质吸力条件下的非饱和土地基承载力计算公式。主要得到3点结论。

（1）含黏粒砂土地基在非饱和状态下承载力显著大于饱和状态,应考虑基质吸力对地基承载力的影响。

（2）当试样中水位相同,经历的干湿变化过程不同时,非饱和含黏粒砂土地基承载力存在显著差异。这是由于含黏粒砂土的土水特征曲线存在明显的滞回效应,地基土中基质吸力和饱和度的分布与经历的干湿变化过程相关。

（3）提出的地基承载力计算公式可考虑基质吸力随深度的非均匀分布,计算结果与量测值误差小于25%。