0.   引言

压实膨润土是核废料地质处置库最理想的缓冲回填材料^[1-2]。处置库散热效率很大程度上取决于压实膨润土的导热系数；同时,压实膨润土导热系数也是计算处置库温度场分布的基础参数之一。因此在处置库工程背景下,压实膨润土导热系数一直受到国内外学者的广泛关注^[3-4]。

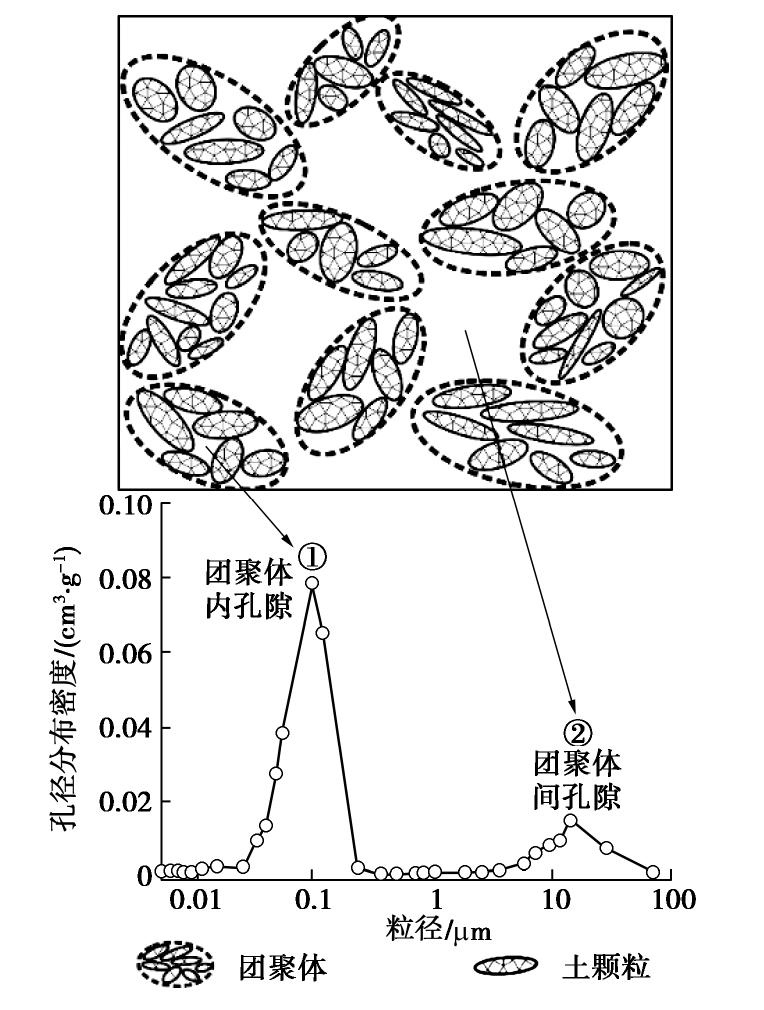
预测模型是膨润土导热研究中的重要内容之一,Kahr等^[5]最早归纳了膨润土导热系数与其密度、含水率的关系,并提出了对应的经验导热模型。随后,受Johansen归一化导热模型启发,Kuntsson^[6]提出了基于K_e数的膨润土导热系数预测模型。Sakashita等^[7]最早将压实膨润土中团聚体内孔隙和团聚体间孔隙近似为不同大小的长方体,通过理论计算得到了压实膨润土导热预测模型。该模型的突出特点是能够考虑压实膨润土双孔隙结构特征^[8-9]：孔径分布曲线呈双峰形态,其中较小孔径峰对应团聚体内孔隙,而较大孔径峰对应团聚体间孔隙（图1）,一般以0.15 μm作为压实膨润土中团聚体间孔隙和团聚体内孔隙的孔径分界点^[10]。Tang等^[11]测试了Mx-80压实膨润土导热性能,发现其与孔隙气体积呈明显的线性负相关关系,并据此提出了压实膨润土导热系数的线性拟合模型。Chen等^[12]基于“夹杂理论”建立了考虑压实膨润土双孔隙结构的细观导热模型,并特别指出双孔隙结构的差异会引起压实膨润土导热系数的变化,双孔隙结构对压实膨润土导热性能的影响不可忽视。

图  1  压实膨润土双孔隙结构示意图

Figure  1.  Schematic view of compacted dual-porosity bentonite

下载: 全尺寸图片 幻灯片

尽管前人已经提出了多类压实膨润土的导热预测模型,但总体而言,多是基于实测导热数据的简单拟合,或者基于结构简化和复杂推导的理论导热模型。实际上,数值模拟在预测土体导热系数方面具有很大优势,近年来有学者陆续提出了基于细观模拟的土体导热模型^[13-14],大幅拓展了土体导热系数的预测途径。然而,压实膨润土具有复杂的双孔隙结构特征,难以对其细观结构开展精确建模和导热模拟,加大了建立压实膨润土细观导热模型的难度。对于双孔隙结构细观建模的难点,Jiang等^[15-16]基于嵌套策略构造了岩土体的双孔隙结构。受此启发,本文尝试通过嵌套策略开展压实膨润土双孔隙结构的细观精细化建模,并结合稳态导热模拟计算整体导热系数,据此建立双孔隙压实膨润土的细观导热模型。最后,将模型预测值与已有压实膨润土的导热实测值进行比较,以检验模型的可靠性。

1.   双孔隙压实膨润土的细观建模

细观建模是构建压实膨润土细观导热模型的前提,建模精度很大程度上决定着模型的预测效果。对于压实膨润土,除双孔隙系统外,还需考虑水分的空间分布问题。膨润土以蒙脱石矿物为主,蒙脱石水化能力极强,特别是蒙脱石晶层间孔隙可吸附大量水分。虽然压实膨润土双孔隙内水分的空间分布未知,但近来有研究表明压实膨润土团聚体内蒙脱石会继续水化^[17-18],受此驱动团聚体间孔隙水将继续向团聚体内孔隙迁移,使得团聚体内孔隙最后总是趋向于优先饱和,呈明显的有偏水分布特征。针对压实膨润土双孔隙结构和有偏水分布特征^[19],通过分步嵌套策略逐一开展精细化建模表征,具体分为如下3部分。

1.1   团聚体间大孔隙建模

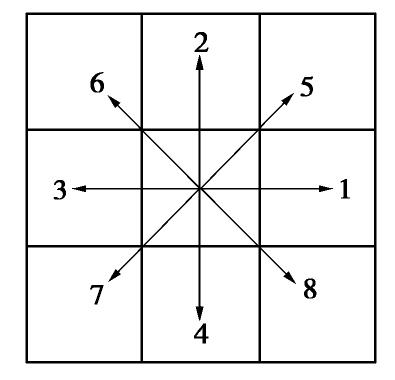
基于传统的四参数随机生长（QSGS）法^[20],团聚体间孔隙建模流程如下：①以气相（孔隙）为生长相,团聚体为背景相。根据C_dM（压实土中团聚体间孔隙的生长核概率分布值）在建模背景区域（网格空间）内随机分布团聚体间孔隙生长核。具体过程如下,给任意背景网格一个[0,1]之间的随机数,当该随机数值不大于C_dM时,则该团聚体网格变为气相（大孔隙）网格。②每个气相生长核逐步向四周背景区域扩张,二维条件下共有8个扩张方向（图2）。首先在8个方向上相邻网格内随机赋予一个[0,1]之间的随机数,只要该网格内随机数大小不超过该方向上的方向生长概率D_i,则该方向上相邻网格自动由背景相转为生长相。③重复步骤②直至气相（孔隙）的体积比例达到团聚体间孔隙的给定值（这里用团聚体间孔隙比e_M表示）为止,自此建立了团聚体间大孔隙,定为Ω_M；背景区域代表团聚体基质,定为Ω_A。

图  2  单元八方向生长示意图

Figure  2.  Schematic view of eight growing directions for each cell

下载: 全尺寸图片 幻灯片

1.2   团聚体内小孔隙建模

在团聚体基质区域（即Ω_A）,基于嵌套策略通过QSGS法再次构建团聚体内小孔隙系统,过程如下：①以固相（土颗粒）为生长相,根据土颗粒的概率分布密度值C_ds在Ω_A中随机分布土颗粒生长核。类似地,给各背景网格赋予一个[0, 1]间的随机数,当该数不大于土颗粒生长核概率密度C_ds时,则该背景网格转为土颗粒生长核。②每个土颗粒生长核沿周围8个方向扩张生长。给每个方向上相邻背景网格一个[0, 1]之间的随机数,当其值不大于该方向上的生长概率时,该网格自动变为土颗粒相网格。需要指出的是,当生长核处在Ω_A区域边界上时,扩张生长方向上相邻网格为团聚体间孔隙,则该方向上扩张生长无效。③重复步骤②直至土颗粒体积满足要求为止。Ω_A区域内固相区域即为压实膨润土颗粒骨架,定义为Ω_s；其他部分则构成团聚体内小孔隙系统,定义为Ω_m,对应孔隙比为e_m（即团聚体内孔隙比）,其与e_M（团聚体间孔隙比）之和为总孔隙比e。图3为不同孔隙比e下构建的压实膨润土双孔隙精细结构模型。

图  3  不同孔隙比下压实膨润土双孔隙建模（黑色：固相颗粒；白色：孔隙气）

Figure  3.  Modeling of dual-porosity for compacted bentonite with different void ratios (black: solid particle; white: pore air)

下载: 全尺寸图片 幻灯片

1.3   有偏水分布建模

在双孔隙空间内,基于区域选择性生长策略逐步开展有偏水分布的填充建模。步骤如下：①基于有偏水分布假设,首先指定Ω_m为孔隙水的优先生长域。分别设置如下两个方向生长概率I_i^sw和I_i^ww,其中I_i^sw为考虑固-液相互作用的孔隙水方向生长概率,而I_i^ww为考虑液-液相互作用的孔隙水方向生长概率,考虑膨润土固相颗粒（如蒙脱石等）的强烈水合作用,在此令I_i^sw =10 I_i^ww[21]。对于Ω_m中的每个网格,给一个[0, 1]之间的任意随机数,如果其i方向上相邻网格为固相网格,当该随机数不大于I_i^sw时,该背景网格变为水相网格（团聚体内水）。同样地,如果其i方向上相邻网格为水相网格,当该随机数不大于I_i^ww时,背景网格变为团聚体内水相网格。②在含水率较小时,水分不足以将团聚体内孔隙全部饱和,重复步骤①直至团聚体内水分含量与总含水率相等。此时所有孔隙水分布在Ω_m区域（团聚体内孔隙）中,呈典型有偏水分布特征。③当含水率较高时,除了率先将Ω_m（团聚体内孔隙）区域充满外,其余水分移置到Ω_M区域（团聚体间孔隙）内生长。在Ω_M区域,同样根据I_i^sw和I_i^ww,对Ω_M中每个网格赋予一个[0, 1]之间随机数,如果在该网格i方向上相邻网格为固相,或者是团聚体内孔隙水时,且随机数不大于I_i^sw,该网格变为孔隙水（团聚体间水）。如果i方向上相邻网格为团聚体间水网格,则当随机数不大于I_i^ww,则该网格也变为团聚体间水网格。④重复步骤③直至团聚体内水和团聚体间水的总量与总含水率相等为止。至此通过预先指定孔隙水生长区域,即可构建压实膨润土有偏水分布模型（图4）。

图  4  双孔隙中有偏水分布建模（黑色：固相颗粒；灰色：孔隙水；白色：孔隙气）

Figure  4.  Modeling of preferential water distribution within dual-porosity (black: solid particle; grey: pore water; white: pore air)

下载: 全尺寸图片 幻灯片

2.   稳态导热模拟

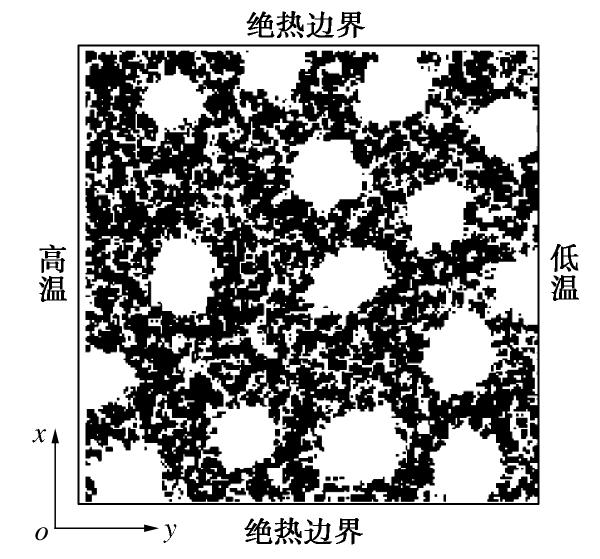
在精细建模基础上,为了进一步预测压实膨润土导热系数,必须开展相应的热传导模拟。对于二维热传导问题的模拟,相应边界条件如图5所示：左右为高低温边界,上下为绝热边界。本文采用稳态热传导模拟,稳态条件下格子i和格子j之间的热流密度为

图  5  稳态导热模拟的边界条件

Figure  5.  Boundary conditions of steady heat conduction

下载: 全尺寸图片 幻灯片

式中,$q_{ij}$为格子i和j之间的热流密度,L_ij为相邻两格子i和j之间的距离。T_i和T_j为格子i,j的中心温度,${\lambda }_{ij}$是相邻两格子之间的等效导热系数,通常采用调和平均模型^[14]进行计算。

当土体导热达到稳态时,温度维持不变,则流入和流出每个网格的热流密度之和为零：

根据式（2）,即可得到区域内各网格温度的离散方程组,采用高斯-塞德尔迭代法求出稳态温度场,并据此计算整体导热系数：

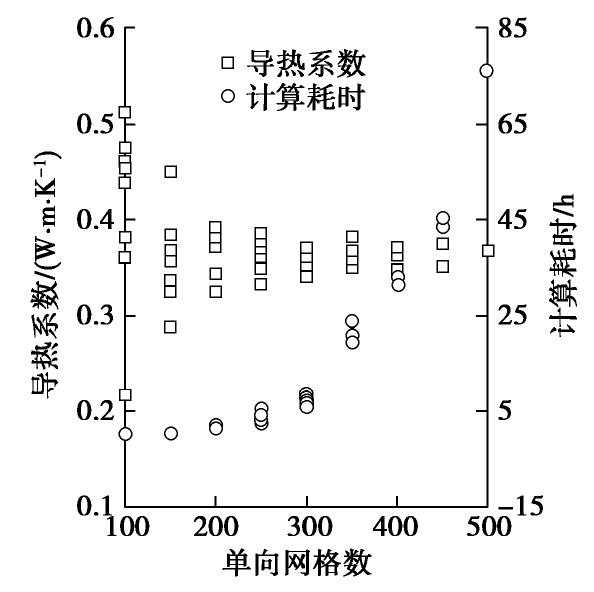
式中 $q_{ij}$为左右边界壁面上每个网格热流密度；n为竖直向网格数量；T_h为左侧高温边界温度；T_c为右侧低温边界温度；L为左右壁面之间距离。

文中采用方形网格,水平和竖直向上网格数量相等。在稳态导热模拟前,为节省计算代价并保持模拟稳定性,有必要对单向网格数量进行优化（图6）。

图  6  单向网格数优化分析

Figure  6.  Optimization analysis of grid number

下载: 全尺寸图片 幻灯片

由图6可知,导热系数计算值的波动幅度随单向网格数增加而迅速减小,而计算耗时快速上升。当单向网格数超过200后,导热系数波动较小,而模拟耗时即达2 h以上,计算代价较高。因此综合考虑本文选取单向最佳网格数为200。可见,在双孔隙结构和有偏水分布精细化建模的基础上,通过稳态导热模拟即可计算压实膨润土导热系数。至此基于数值模拟初步构建了双孔隙压实膨润土的细观导热模型。

3.   模型验证

与大多数导热预测模型一样,有必要验证导热模型的可靠性及精度,通常需要与压实膨润土实测导热数据进行比较分析。回顾既有压实膨润土导热研究^[11,22-24],本文选取Mx-80、Febex、Kyeongju、Kunnigel-V1和GMZ-07五种典型膨润土的实测导热数据与模拟数据进行比较。模拟中参数取值如下：水和空气的导热系数一般是不变的,因此孔隙水导热系数${\lambda }_{\text{w}}$取值为0.5974 W/m∙K,而孔隙气导热系数${\lambda }_{\text{g}}$为0.0243 W/m∙K。固相骨架的导热系数与土体矿物组成有关,通常石英含量$\zeta$越多,固相颗粒导热系数越大,可采用固相颗粒的导热系数${\lambda }_{\text{s}}$的表达式为

Mx-80、Febex、Kyeongju、Kunnigel-V1和GMZ- 07膨润土中石英含量分别为3%,2%,1%,0.6%,10%^[11,17,25]。固相颗粒导热系数分别为2.0825,2.0547,2.0271,2.0162和2.2886 W/m∙K。

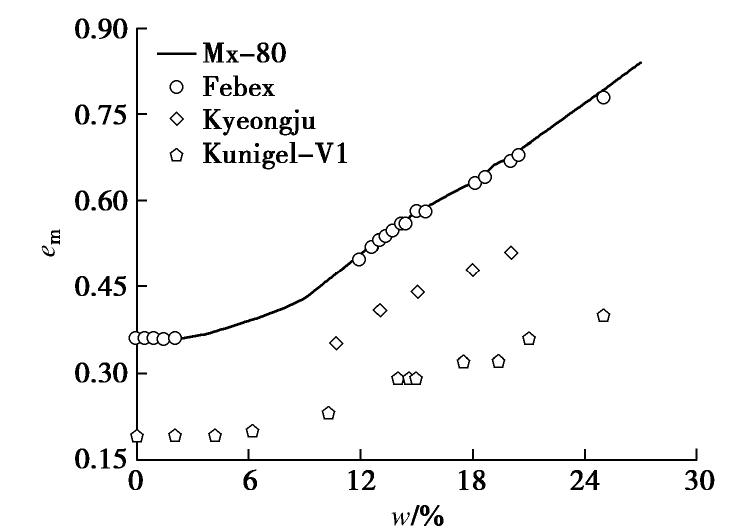
导热系数计算结果不仅与模拟中固、液、气三相的导热系数相关,土体结构和水分分布建模的精度更直接关系到导热系数的模拟结果。膨润土属膨胀性黏土,不同含水率下的e_m取值不同,建模过程中需特别注意。文献[17]给出了部分压实GMZ-07膨润土在不同含水率下的e_m,对于Mx-80膨润土,Tang等^[26]通过压汞试验获得了基质吸力与e_m之间的关系和土水特征曲线。通过基质吸力换算即可得到不同含水率下Mx-80压实膨润土的e_m值。Febex、Kyeongju以及Kunnigel-V1膨润土的e_m取值未知。根据3种膨润土中蒙脱石含量的相对大小,本文采用一种基于比较策略的e_m预估方法。即以92%蒙脱石含量的Mx-80膨润土e_m作为基准值,Febex、Kyeongju和Kunnigel-V1膨润土各自蒙脱石含量分别为92%,70%和47%。则相同含水率下3种膨润土e_m可根据其蒙脱石含量差异等比例换算求得（图7）。

图  7  基于Mx-80膨润土的其他三类膨润土e_m估计

Figure  7.  Estimation of e_m for other three compacted bentonites based on Mx-80 bentonite

下载: 全尺寸图片 幻灯片

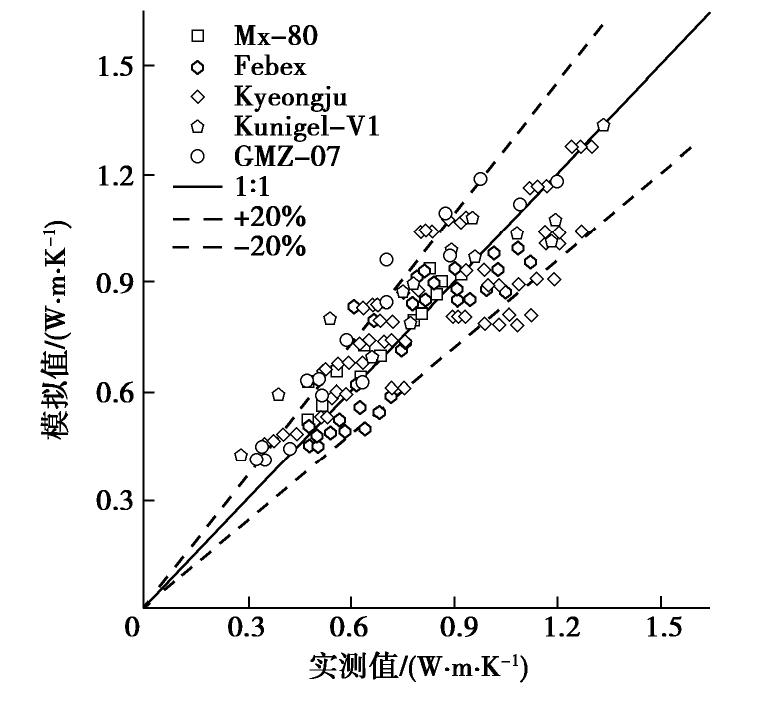
共统计了5种膨润土不同含水率和孔隙比下实测导热数据160个,根据其结构和矿物组成分别建模、模拟并计算相应的导热系数。最后将模型预测结果与实测导热值进行比较,结果如图8所示。可见,大部分模型预测值都在实测值±20%范围内,表明本文模型对压实膨润土导热性能具有较好的预测效果。

图  8  5种膨润土导热系数模拟值与实测值对比图

Figure  8.  Comparison between experimental and modeled thermal conductivities of five compacted bentonites

下载: 全尺寸图片 幻灯片

进一步地,为了更清楚地展示本文模型对压实膨润土导热系数的预测精度,定义模型相对误差D如下：

式中,${\lambda }_{\mathrm{mod}}$为模型预测值,${\lambda }_{\exp }$为实测导热值。

表1为本文模型对5种典型压实膨润土160个实测导热值与预测结果间相对误差的置信度分析。

表  1  不同相对误差下压实膨润土导热系数预测的置信度

Table  1.  Confidence degrees of predictive thermal conductivity of compacted bentonite under different relative errors

膨润土	Mx-80	Febex	Kyeongju	Kunigel-V1	GMZ-07
样本个数	22	37	71	14	16
D≤5%	41%	24%	21%	29%	25%
D≤15%	91%	81%	53%	71%	81%
D≤25%	95%	97%	86%	79%	88%

下载: 导出CSV 

| 显示表格

由表1可知,当相对误差D≤15%时,模型对于Mx-80和Febex和GMZ-07膨润土,有81%以上模型预测值满足此要求；而对于Kyeongju和Kunigel-V1膨润土,满足此要求的模型预测值不足总数71%。当D≤25%时,同样地,模型对Mx-80和Febex和GMZ-07膨润土的预测结果也要优于Kyeongju和Kunigel-V1膨润土。可见,本文所建模型对Mx-80、Febex和GMZ-07压实膨润土导热系数的预测精度较Kyeongju和Kunigel-V1膨润土更高。

对于本文模型在5种典型膨润土导热系数预测精度上的差异,这与建模过程中所采用的e_m取值方式及其估计误差密切相关。不同含水率下Mx-80和GMZ-07膨润土e_m数据是通过压汞试验直接计算得到的,故对Mx-80和GMZ-07压实膨润土结构建模最接近实际。而对于不同含水率下其他3种压实膨润土e_m,都是通过Mx-80膨润土间接求取的：以e_m为基准值,并默认e_m与蒙脱石含量成正比,然后通过比较其他膨润土与Mx-80膨润土之间的蒙脱石相对含量估计其e_m大小。显然,在Febex、Kyeongju和Kunnigel-V13种膨润土中,Febex膨润土的矿物组成与Mx-80最接近,因此Febex膨润土的建模效果是最好的,相应的模型预测精度也较好。而Kyeongju和Kunnigel-V1膨润土,其矿物组成与Mx-80膨润土差异更大,采用线性估计得到的e_m值可能与实际偏离较大,因而模型预测精度有所降低。

4.   讨论

预测模型是压实膨润土导热研究的重要议题之一。过去主要以经验模型为主^[5,8],难以考虑压实膨润土中双孔隙这一重要结构特征。实际上,基于土体结构的细观导热模型构建难度较大,该类导热模型数量明显少于经验模型。这方面当前最好的是Chen等^[19]基于“夹杂理论”构建的理论计算模型：通过将不同孔径孔隙等效为不同大小的椭球夹杂,以此反映双孔隙结构对土体导热的影响。作为联系微观结构和宏观性能的有效桥梁,基于细观建模的导热模拟也可计算土体导热系数。然而由于双孔隙结构的复杂性,压实膨润土细观结构的精细化建模较为困难,因而难以通过导热模拟构建双孔隙压实膨润土的细观导热模型。在本文中,通过对压实膨润土双孔隙结构和有偏水分布的精细化建模,进一步结合细观导热模拟,顺利构建了双孔隙压实膨润土导热系数的数值预测模型。在此基础上,通过与5种典型压实膨润土160个实测导热系数的比较,检验了模型的可靠性,为预测压实膨润土导热系数提供了新的途径与方法。

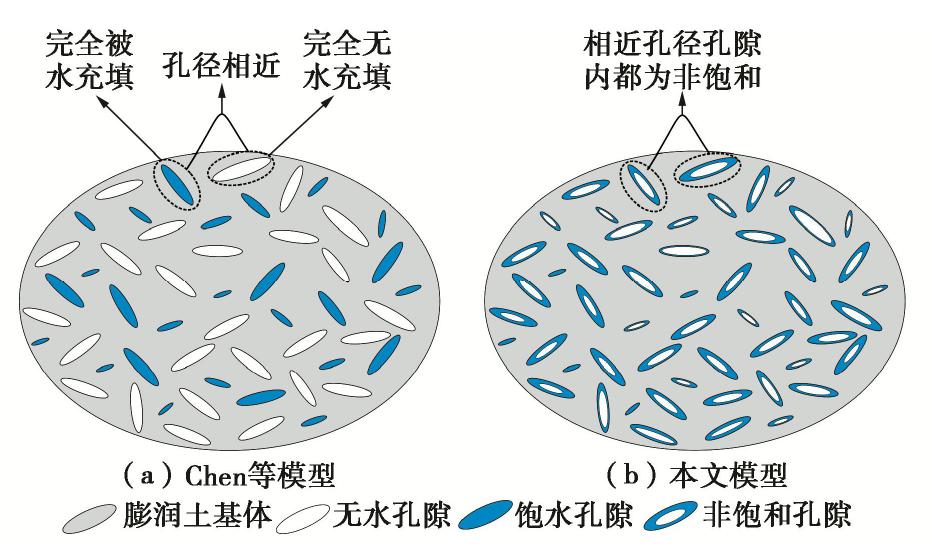
预测精度是土体导热模型研究的核心问题,而模型参数的选取是决定其精度的关键。对于经验模型,模型参数直接由实测导热数据拟合得到：通常拟合数据越多,参数取值越合理,预测精度也越高。但这些经验参数本身缺乏物理意义,难以与土体的本质特征相联系；同时,参数拟合前需要预先开展土体导热测试,耗时也较大。Chen等^[19]基于“夹杂理论”将团聚体内孔隙和团聚体间孔隙分别等效为不同大小、形状的随机椭球体,同时通过预先指定夹杂椭球的导热系数反映孔隙所含流体类型：若孔隙内为水,则椭球导热系数与水相同；若为空气,则椭球导热系数与空气相等。然后通过细观均匀化方法计算双孔隙压实膨润土导热系数。该理论模型物理概念清晰、预测精度较高,且能更清楚地揭示双孔隙结构的作用机理,相对于传统模型具有显著优势。

Chen等^[19]提出的模型中,代表孔隙的椭球体导热系数只有两个参考值,分别为水和空气的导热系数,分别反映孔隙干燥与饱和两种极端状态（图9（a））。遗憾的是,难以满足单一孔隙非饱和状态的表征问题。而本文中,压实膨润土孔隙内可以呈现非饱和状态（图4,9（b））,更接近压实膨润土孔隙内实际的水分分布。可见,本文模型不仅可反映压实膨润土双孔隙结构特征,继承了Chen等^[19]模型的优势；同时在孔隙水分布方面又有所改进,有助于提高模型的物理精度。

图  9  Chen等模型与本文模型水分布比较

Figure  9.  Comparison of water distribution between Chen et al. model and proposed model

下载: 全尺寸图片 幻灯片

此外,当前国际上核废料处置库中所用的膨润土规格都是一定的：其矿物组成已知,在模拟中可根据式（4）方便地计算固相颗粒导热系数；同时,关于膨润土双孔隙结构方面的研究成果日益增多,有利于开展压实膨润土的细观精细化建模。可见,由于在矿物和结构组成上的便利,本模型在预测压实膨润土导热系数方面具有很大的优势,通过模型计算可方便地求得不同状态下多类压实膨润土导热系数值。需要指出的是,除了压实膨润土外,对于其他复杂双孔隙结构土体（如红黏土^[27]）,本模型同样能反映双孔隙结构的影响,但有偏水分布的适用性值得商榷。实际上,在最优含水率干侧压实的黏性土都具有双孔隙特征,但并非所有黏性土压实后水分都偏向于优先饱和团聚体内孔隙。例如,在某些低塑性粉质黏土中,压实后团聚体内孔隙和团聚体间孔隙很可能都处于非饱和状态。而对于膨润土,在蒙脱石矿物强烈水化潜能驱动下,压实后团聚体间孔隙水还会继续向团聚体内孔隙迁移,使得团聚体内孔隙优先饱和。可见,相对于普通压实黏性土,压实膨润土内水分分布更加接近本文提出的有偏水分布模式。实际上,除了偏向于团聚体内孔隙这种极端有偏水分布外,还有另一种偏向于团聚体间孔隙的极端有偏水分布。而对于常规压实黏性土,双孔隙内水分布应在两种极端水分布之间,相应地,其导热系数也应在两种极端水分布模式下的模型预测值之间。可见,本文针对压实膨润土的细观导热模型也可为常规压实黏性土导热系数的预测提供一定参考。总体而言,本文模型可为复杂双孔隙土体（包含但不限于压实膨润土）导热系数的准确预测提供新的思路和方法。

最后,需要注意的是,任何模型都不是完美的,本文针对压实膨润土提出的细观导热模型还存在以下不足之处。首先是本文模型对蒙脱石晶层间孔隙考虑不足,难以反映晶层孔隙水化对膨润土固相密度、体积以及导热系数的影响。此外,本文模型考虑的都是常温条件,只能反映双孔隙结构对纯热传导的影响。实际上还需考虑孔隙水蒸发冷凝对膨润土导热系数的贡献,与实际处置库内的温度条件和传热过程有较大差异。因此,在今后工作中还应加强以上两方面工作。

5.   结论

压实膨润土导热系数是核废料处置库散热设计的关键指标,准确预测其导热系数对于处置库散热安全和温度场分布具有重要意义。基于精细化建模和细观导热模拟,本文提出了一种针对双孔隙压实膨润土的细观导热模型,并与多种压实膨润土160个实测导热系数进行比较,对模型的可靠性进行验证,得到以下4点结论。

（1）基于对双孔隙和有偏水分布的精细化建模,结合细观稳态热传导模拟,系统提出了压实膨润土导热系数的数值预测模型。并与160个典型压实膨润土实测导热结果进行比较,验证了该模型在压实膨润土导热系数预测方面的可靠性。

（2）本文模型是在Chen等^[19]模型上的进一步优化,不仅继承了该模型考虑双孔隙结构的优势,而且对Chen等模型中单一孔隙非饱和状态进行了细化表征,其水分分布更加接近实际。

（3）本文模型适用于复杂双孔隙土体导热系数的预测。然而由于压实膨润土内水分分布更加接近有偏水分布这种极限状态,相对于其他双孔隙压实黏性土,本模型在压实膨润土导热系数预测上的潜力更大。

（4）本文模型对膨润土内晶层孔隙考虑不足,难以反映晶层孔隙水化对膨润土颗粒固相密度、体积和导热系数的影响。此外,模型主要针对常温热传导过程,与实际处置库中膨润土温度条件和传热过程有一定差异,在今后工作中应着重补充这两方面的工作。