An automatic identification method for width of shear band of sand in PFC simulations
-
摘要: 从细观尺度研究颗粒材料的应变局部化有助于深刻理解其物理力学机制，而剪切带的出现和演化是应变局部化的典型特征。目前在离散元法（DEM）模拟中对砂土应变局部化特征（如剪切带宽度、倾角、分布类型等性质）的观测方法还主要依赖手动、目测和估计等方式。针对这一问题，采用PFC2D开展了大量密砂双轴压缩模拟试验，提出了一种基于“α-shape”和“Delaunay三角化”算法的剪切带及其宽度的自动识别方法。进而，基于多组砂土试样开展双轴压缩试验，验证了所提出的剪切带及其宽度自动识别方法的有效性。Abstract: Studying the strain localization of granular materials from the meso-scale is helpful for deeply understanding the physical and mechanical natures of strain localization, and the occurrence and evolution of shear bands are the typical characteristics of strain localization. In the numerical simulations of discrete element method (DEM), observing and measuring the evolution of strain localization of sand (such as the width, inclination angle and distribution type of shear bands, etc.) greatly rely on the manual, visual and estimation ways. Towards this problem, many numerical experiments on the dense sands in biaxial compression are carried out by using PFC2D. Based on the numerical experiments, an identification method based on "α-shape" and "Delaunay triangulation" algorithms is developed to automatically identify the shear bands and their widths. Furthermore, based on some groups of biaxial compression tests on the dense sands, the effectiveness of the proposed automatic identification method is validated.
-
0. 引言
岩土材料的破坏过程通常伴随着应变局部化现象, 例如土体达到和超过峰值强度的过程中，其变形会由均匀分布形式逐渐向某个狭窄的带状区域集中，这样的带状区域即为剪切带，剪切带的出现和演化则是应变局部化的典型特征。
众多学者对剪切带特性及其影响因素等问题进行了长期的探索，其中包括如何精确测量剪切带宽度和倾角的课题。通过砂土物理试验，Alshibl等[1]在试样中布置网格线，根据试验过程中网格线的变化来估测剪切带宽度。作为物理试验的重要补充，计算机数值模拟和仿真技术为开展颗粒土体应变局部化研究提供了更多的可能性。如王冬勇[2]在Cosserat有限元法中，通过等效塑性应变阴影图观测剪切带宽度。蒋明镜等[3]在DEM中，通过颗粒土试样局部变形网格图、颗粒等效转动图、孔隙比图对剪切带宽度进行估计，将剪切带宽度定义为几种方法获得宽度的平均。Tang等[4]在DEM中则是定义了有效应变，以观测剪切带宽度。Tian等[5]基于PFC2D软件开展颗粒土双轴压缩试验，人工勾勒出试验获得X型剪切带的轮廓，并将该轮廓细化为多个直线段，将这些直线段的宽度和倾角平均值定义为剪切带的宽度和倾角。
综上可知，当采用DEM开展颗粒土剪切带数值研究时，主要采用人工（染色）预处理、目测和估计等方法来获取剪切带宽度和倾角等特性，主观性影响较大。针对这一问题，本文基于PFC2D软件开展了密砂双轴压缩离散元数值试验，通过颗粒累计转角（rotation）图对剪切带进行观测，提出了一种基于“α-shape”和“Delaunay三角化”算法的剪切带及其宽度的自动识别方法，并对剪切带类型进行了定义。
1. 双轴加载模型试验
利用PFC2D离散元软件对砂土开展刚性墙体双轴压缩试验，模型参数取值如表 1所示。在模拟试验中设置5组不同粒径（见2.3节），逐层生成并压实试样。
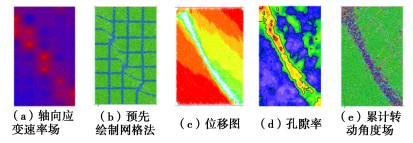
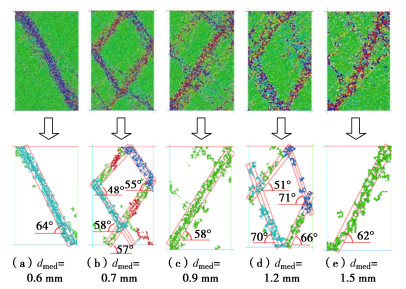
表 1 双轴压缩模型的参数取值Table 1. Parameters for the biaxial compression model物理意义 数值 物理意义 数值 试样大小 5 cm×10 cm 接触刚度kn/ks 2×107 N/m 颗粒密度 2.6×103 kg/m3 轴向应变速率 5%/min 孔隙率 0.15 目标轴向应变 10% 围压 100 kPa 阻尼系数 0.7 颗粒摩擦系数 0.5 墙壁摩擦系数 0 有多种方法可观察试样剪切带宽度，如图 1所示。其中，图 1（e）累计转动角度场图相对清晰易操作，因此选用累计转动角度场图进行剪切带宽度测量。
2. 一种可用于PFC中剪切带识别的方法
2.1 散点覆盖区域边界识别的α-shape算法原理
PFC2D模拟结果中，将累计转角介于–δ~δ范围的颗粒删除，并对剩余颗粒所在区域进行识别，所识别的区域被定义为剪切带区域。
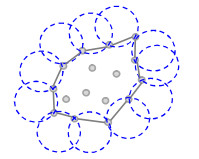
首先，采用“α-shape”算法对剩余颗粒所在区域的边界进行识别与绘制。图 2为“α-shape”算法基本原理，图中灰色散点为颗粒。“α-shape”算法可通过多种方法实现，其中滚球法可在给定颗粒区域中，测出颗粒群的特征间距h，通过预设的特征参数α，采用半径为α×h的圆形在区域边界上滚动，进而可检测出哪些颗粒在区域内部，哪些在区域边界上。
![]()
图 2 通过滚球法实现的“α-shape”算法Figure 2. α-shape algorithm accomplished by rolling ball method2.2 区域网格化的Delaunay三角化算法原理
进一步，对所识别剪切带区域内的颗粒应用Delaunay三角剖分，形成三角形网格。对三角形网格中所有三角形“单元”面积叠加，可获得剪切带区域的面积。
2.3 一种新的剪切带识别方法
首先，在PFC2D中，针对5 cm×10 cm大小的密砂试样，定义如下中值粒径dmed：
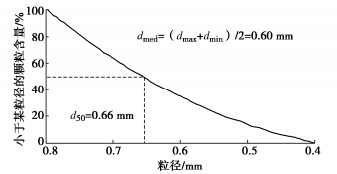
dmed=(dmax+dmin)/2， (1) 式中，dmax为粒组中颗粒最大粒径，dmin为最小粒径。为使方法适用于一定粒径范围内具有不同中值粒径的试样，设置了五组双轴压缩试验，试验中dmed分别取为0.6，0.7，0.9，1.2，1.5 mm，相应的颗粒数量分别为15400，10500，6400，3500，2300个。因此，经过上述数值试验确定的识别方法中的参数适用于中值粒径dmed∈[0.6 mm，1.5 mm]甚至更大的应用范围。现以第一组dmed=0.6 mm的试验为例，详细说明所提出的剪切带识别方法的实现过程。图 3为该组试验的颗粒级配曲线，粒径服从均匀级配。
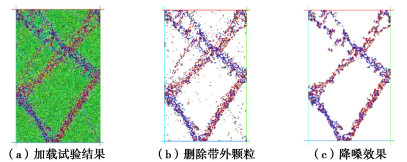
（1）第一步：应用PFC2D开展密砂双轴压缩试验，试样剪切破坏时颗粒累计转角图如图 4（a）所示。
![]()
图 4 删除转动角较小的颗粒后进行多次“降噪”Figure 4. Multiple times of "denoising" after deleting soil particles with relatively small rotation删除试样中累计转角较小（即–δ~δ范围，这里设δ=30°）的颗粒，如图 4（b）。进一步进行多次（这里设为3次）“降噪”，如图 4（c）。降噪思路为以某个颗粒为圆心，以ε为半径的圆域内，颗粒数量若小于nmin，则将该圆心颗粒视为“噪点”并删除。
（2）第二步：对于中值粒径dmed，获得剪切带宽度均值为Wave，则无量纲的平均带宽因子ηave为
ηave=Wave/dmed， (2) 式中，平均带宽因子ηave可由大量数值试验确定。
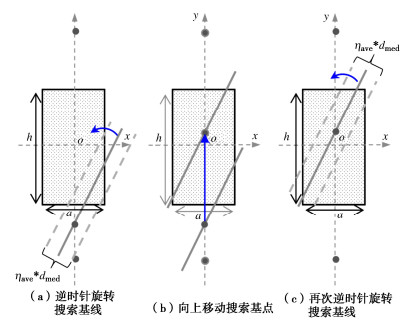
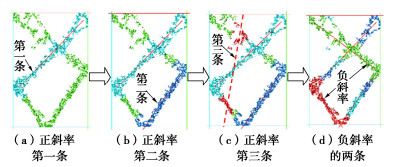
（3）第三步：剪切带主轴的搜索，如图 5所示，在试样垂直中轴线上，自下向上增量匀步确定多个“搜索基点”（此处为80个），如图 5（b）；首先搜索斜率为正值的前3条基线，对于每个“搜索基点”，过这点做多条斜率为正值的直线，作为“搜索基线”。“搜索基线”倾角从35°旋转到75°，每次转动1°。而后遍历试样中所有颗粒，找到距离“搜索基线”两侧ηave*dmed宽度范围内的颗粒数量，如图 5（a）。统计颗粒数量占总颗粒数的百分比。当计算出的百分比是所有“搜索基线”中最大的一条，且百分比大于一定值，则确定此条剪切带存在，如图 6（a）。搜索第二条基线时，需“删除”第一条基线两侧ηave*dmed宽度范围内的颗粒，避免第一条剪切带对后续剪切带识别的影响，搜索结果如图 6（b）。继续搜索正斜率基线，若第三条基线附近颗粒所占百分比较少，如图 6（c），可认为第三条剪切带不存在。
同理在105°~145°逆时针转动搜索基线来寻找负斜率基线，如图 6（d）所示。
（4）第四步：根据搜索获得的若干条基线的相对位置关系，判断剪切带的分布类型（具体见第3节），进而通过搜索到的剪切带基线，计算剪切带长度与倾角。
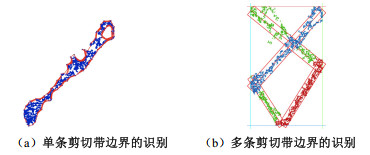
（5）第五步：输出每条剪切带基线两侧ηave* dmed宽度范围内颗粒的坐标，基于这些颗粒坐标，采用“α-shape”算法对剪切带边界识别，如图 7所示。
![]()
图 7 基于“α-shape”算法的剪切带边界的识别Figure 7. Identification of shear band boundary based on 'α-shape' algorithm（6）第六步：以剪切带颗粒为节点进行Delaunay三角化，累计计算三角形“单元”面积进而获得剪切带面积，即可算得宽度。
3. 剪切带样式的分类
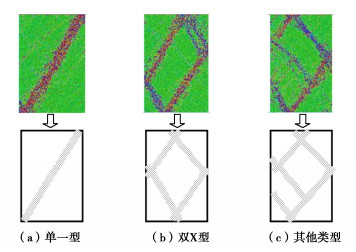
针对大量PFC2D双轴压缩试验后发现，在本研究给定的边界条件下，剪切带可以划分为以下3种主要类型，如图 8。
（1）单一型剪切带（Single shear band）：试样中仅形成一条剪切带，呈现出从左上到右下贯通或者从右上到左下贯通走势。
（2）双X型剪切带（Dual-X shear bands）：试样上下部分别形成X形剪切带，破坏区表现为菱形。
（3）其他分布类型（Other types）：剪切带分布呈现出不同于单一型剪切带和双X型剪切带的其他样式。图 8（c）只展示了其中的一种分布类型。
4. 自动识别方法的应用
采用所提出的剪切带自动识别方法，对dmed不同的五组试样开展PFC2D双轴压缩试验，图 9所示为5组试样加载剪切破坏后剪切带的识别结果。根据大量PFC2D试验结果，发现剪切带的分布类型具有较强的随机性，其具体分布类型与试样的初始缺陷的位置以及边界条件（如刚性/柔性墙）等因素有关。
![]()
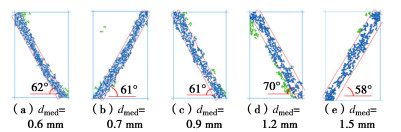
图 9 5组不同中值粒径试样的剪切带及识别结果Figure 9. Shear bands and identificated results from five groups of sand samples with different median diameters由于不同类型剪切带的宽度无法直接对比，因此仅将呈现单一型剪切带的试样（图 10）进行测量，并与预先绘制网格法（图 1（b））和孔隙率场（图 1（d））的宽度目测结果进行对比，计算相对误差。
![]()
图 10 5组不同中值粒径试样的单一型剪切带及识别结果Figure 10. Single shear bands and identificated results from five groups of sand samples with different median diameters由表 2可知，孔隙率场目测宽度最大，说明在剪切带附近较大范围内，存在孔隙率增大现象。而网格法目测宽度与程序识别宽度相似，说明编制的程序识别效果较为良好。
表 2 5组试样PFC2D双轴压缩试验及结果Table 2. Identificated results of five biaxial loading testsdmed
/mm识别宽度/mm 相对宽度 网格法宽度/mm 相对
误差/%孔隙率场宽度/mm 相对
误差/%6 8.0 13.3 7.2 -10 11.7 47 7 8.8 12.5 9.1 4 12.6 44 9 9.8 10.9 9.6 -2 13.3 36 12 11.7 9.8 12.6 7 16.2 38 15 13.5 9.0 15.0 11 17.8 32 5. 结论
本文采用PFC2D主要针对密砂开展了双轴压缩模拟试验，采用逐层生成并压实土样的技术，获得5组不同中值粒径的试样，观测剪切带在砂土中的发展状况。根据研究结果，获得3点结论。
（1）研究对比了PFC2D双轴压缩试验中剪切带的几种观察方式，认为基于累计转角场图来观测剪切带较为方便和可行。
（2）提出一种适用于PFC2D软件的基于“α-shape”和“Delaunay三角化”算法的快速、有效的剪切带宽度自动化识别方法，其中“α-shape”用于剪切带边界的识别，而“Delaunay三角化”算法用于剪切带面积的计算。进而，通过多组算例验证了所提出方法的有效性。
（3）采用所提出的剪切带宽度自动化识别方法对试验中观测到的剪切带分布类型进行了分类，结果表明密砂剪切带分布类型可大致划分为3大类，即单一剪切带、双X型剪切带和其他类型。
-
![]()
图 2 通过滚球法实现的“α-shape”算法
Figure 2. α-shape algorithm accomplished by rolling ball method
![]()
图 4 删除转动角较小的颗粒后进行多次“降噪”
Figure 4. Multiple times of "denoising" after deleting soil particles with relatively small rotation
![]()
图 7 基于“α-shape”算法的剪切带边界的识别
Figure 7. Identification of shear band boundary based on 'α-shape' algorithm
![]()
图 9 5组不同中值粒径试样的剪切带及识别结果
Figure 9. Shear bands and identificated results from five groups of sand samples with different median diameters
![]()
图 10 5组不同中值粒径试样的单一型剪切带及识别结果
Figure 10. Single shear bands and identificated results from five groups of sand samples with different median diameters
表 1 双轴压缩模型的参数取值
Table 1 Parameters for the biaxial compression model
物理意义 数值 物理意义 数值 试样大小 5 cm×10 cm 接触刚度kn/ks 2×107 N/m 颗粒密度 2.6×103 kg/m3 轴向应变速率 5%/min 孔隙率 0.15 目标轴向应变 10% 围压 100 kPa 阻尼系数 0.7 颗粒摩擦系数 0.5 墙壁摩擦系数 0 
下载: 导出CSV
表 2 5组试样PFC2D双轴压缩试验及结果
Table 2 Identificated results of five biaxial loading tests
dmed
/mm识别宽度/mm 相对宽度 网格法宽度/mm 相对
误差/%孔隙率场宽度/mm 相对
误差/%6 8.0 13.3 7.2 -10 11.7 47 7 8.8 12.5 9.1 4 12.6 44 9 9.8 10.9 9.6 -2 13.3 36 12 11.7 9.8 12.6 7 16.2 38 15 13.5 9.0 15.0 11 17.8 32
下载: 导出CSV
-
[1] ALSHIBLI K A, STURE S. Shear band formation in plane strain experiments of sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(6): 495–503. doi: 10.1061/(ASCE)1090-0241(2000)126:6(495)
[2] 王冬勇. 基于二阶锥规划有限元法的岩土体稳定性及应变局部化研究[D]. 北京: 北京交通大学, 2020. WANG Dong-yong. Stability and Strain Localization Analysis of Geotechnical Problems Based on Second-Order Cone Programming Optimized Finite Element Method[D]. Beijing: Beijing Jiaotong University, 2020. (in Chinese)
[3] 蒋明镜, 李秀梅. 双轴压缩试验中砂土剪切带形成的离散元模拟分析[J]. 山东大学学报(工学版), 2010, 40(2): 52–58. https://www.cnki.com.cn/Article/CJFDTOTAL-SDGY201002011.htm JIANG Ming-jing, LI Xiu-mei. DEM simulation of the shear band of sands in biaxial tests[J]. Journal of Shandong University (Engineering Science), 2010, 40(2): 52–58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SDGY201002011.htm
[4] TANG H X, DONG Y, WANG T, et al. Simulation of strain localization with discrete element-Cosserat continuum finite element two scale method for granular materials[J]. Journal of the Mechanics and Physics of Solids, 2019, 122: 450–471. doi: 10.1016/j.jmps.2018.09.029
[5] TIAN J Q, LIU E L, HE C. Shear band analysis of granular materials considering effects of particle shape[J]. Acta Mechanica, 2020, 231(11): 4445–4461. doi: 10.1007/s00707-020-02771-y
计量
- 文章访问数: 105
- HTML全文浏览量: 28
- PDF下载量: 27
