基于地震变形易损性的高土石坝抗震安全分析

靳聪聪; 迟世春; 聂章博

doi:10.11779/CJGE202002015

基于地震变形易损性的高土石坝抗震安全分析 English Version

大连理工大学建设工程学部工程抗震研究所,辽宁　大连116024

基金项目:

国家重点研发计划项目 2016YFB0201001

详细信息

作者简介:
靳聪聪（1987— ）,男,河南开封人,博士研究生,从事高土石坝地震易损性及抗震风险研究工作。E-mail：jincong3623@mail.dlut.edu.cn

通讯作者:
迟世春, E-mail：schchi@dlut.edu.cn

中图分类号: TV641
计量
- 文章访问数: 329
- HTML全文浏览量: 33
- PDF下载量: 107
出版历程
- 收稿日期: 2019-04-07
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-01-31

Seismic safety analysis of high earth-rockfill dams based on seismic deformational fragility

Institute of Earthquake Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China

摘要

摘要: 基于性能的地震易损性分析可有效估计地震作用下结构损害,是抗震安全评估的重要方法之一。以坝顶沉降最大值和坝顶横向水平位移最大值为性能参数,通过考虑坝址区域地震情况确定输入地震动数量,并提出采用性能参数突变点确定性能水平。首先,根据糯扎渡高土石坝坝址区域地震情况合理确定输入地震动数量,并采用改进PZC弹塑性模型和动力固结有限元程序SWANDYNE II进行高土石坝动力分析。以坝顶沉降最大值和坝顶横向水平位移最大值作为性能参数,通过对60条地震动的动力分析,确定性能水平。然后采用弹塑性模型-非线性方法进行动力分析,结合MSA方法得到各性能参数地震易损性曲线。通过分析性能参数平均值和标准差的变异系数与地震动数量的关系,确定地震动数量超过30条时,性能参数的平均值和标准差的变异系数基本不发生波动。最后,以地震易损性和地震危险性曲线确定糯扎渡高土石坝的抗震安全性,成果可为高土石坝抗震性能研究提供依据。
- 性能参数 /
- 地震易损性 /
- MSA法 /
- SWANDYNE II程序
Abstract: The performance-based seismic fragility analysis can effectively estimate structural damage under earthquake action and become one of the important methods for seismic safety assessment. The maximum settlement and the horizontal maximum displacement of the dam crest are taken as the performance parameters. It is proposed to consider the seismic situation of the dam site to determine the number of input ground motions. The performance levels are determined based on the catastrophe point of the performance parameters. Firstly, the ground motion of Nuozhadu earth-rockfill dam site is reasonably determined to be suitable for the ground motion of the high earth-rockfill dam, and the dynamic analysis is carried out by using the improved PZC elastoplastic constitutive model and the dynamic consolidation finite element program SWANDYNE II. By regarding the maximum settlement and the horizontal maximum displacement of the crest as the performance parameters, the performance level of the high earth-rockfill dam is determined through the dynamic analysis of 60 selected ground motions. The elastoplastic model-nonlinear method is used for dynamic analysis, and the MSA method is used to obtain the seismic fragility curve of the performance parameters. By analyzing the relationship between the variation coefficients of the average and standard deviations of performance parameters and the number of ground motions, it is determined that the variation coefficients of the average and standard deviations of performance parameters almost do not fluctuate when the number of ground motions exceeds 30. Finally, the seismic safety of Nuozhadu high earth-rockfill dam is determined by the results of seismic fragility and the seismic risk curve. The results may provide a basis for the researches on the seismic performance of high earth-rockfill dams.
- performance parameter /
- seismic fragility /
- MSA method /
- program SWANDYNE II

HTML全文

0. 引言

高坝大库是中国有序开发和合理配置水能资源重要举措,已建成的一系列高坝在国家防洪、减灾、抗旱等方面发挥了巨大作用。高土石坝兼具地形适应强、筑坝选材广、抗震能力强、现代化施工快速等诸多优势,在世界各国的水电建设中均得到广泛应用。中国水资源丰富的西部地区位于亚欧板块与印度洋板块之间,其特点是活断层多、地震频繁、强度高。在该地区已建、在建或拟建的糯扎渡、古水、两河口和如美等一批200～300 m级高土石坝,一旦遭受地震造成出险甚至溃决,后果将是灾难性的。因此,高土石坝抗震安全研究是十分重要且意义重大的。

鉴于地震灾害的突发性、不可预测性和强破坏性,大坝可能会遭受远超设计标准的破坏,如紫坪铺大坝在汶川地震时经受远远超过原设计标准的地震烈度^[1]。基于性能的抗震研究是现代结构抗震设计重点发展方向,在国内外建筑结构和桥梁等领域的抗震研究得到广泛应用^[2-5]。该理论在中国坝工领域也取得一系列研究成果^[6-8]。沈怀至等^[9]对重力坝坝体-地基系统地震易损性进行分析,并对混凝土重力坝进行抗震风险评价。孔宪京等^[7]采用增量动力法对250 m级高面板堆石坝进行抗震性能评价。庞锐等^[10]采用多条带分法对200 m级高心墙堆石坝进行地震沉降易损性分析。

如何合理选择性能指标、地震动记录选取以及性能水平划分是高土石坝地震易损性分析中的关键。王笃波等^[11]以坝顶震陷率为性能参数,结合震害资料采用三等级震害划分标准,通过3条地震动对100 m级高土石坝进行易损性分析。庞锐等^[10]以坝顶相对震陷率为性能参数,根据国内外震害资料和高土石坝极限抗震研究成果,确定各个性能指标的破坏等级划分标准,采用15条地震波对200 m级高土石坝进行易损性分析。现代高土石坝按照严格规范设计与现代化施工技术建设,抗震性能较之前建设的土石坝明显提高。因此,依靠以前土石坝震害统计资料指导高土石坝的性能水平划分是不太合理的。考虑到各个高土石坝地形地质和结构型式不尽相同。因此,通过坝址区域地震条件确定高土石坝输入地震动数量和采用高土石坝数值模拟确定性能参数的性能水平是有必要的。

本文根据糯扎渡高土石坝工程场地地震安全性评价资料确定输入地震动数量,以坝顶沉降最大值和坝顶横向水平位移最大值作为性能参数。然后采用弹塑性-非线性有限元方法进行动力分析,结合性能参数位移突变点确定性能水平。采用MSA方法计算性能参数的地震易损性曲线,分析大坝在不同强度地震作用下各性能水平概率。通过分析性能参数的平均值和标准差的变异系数与地震动数量的关系,得到地震动数量对性能参数的影响。最后,以地震易损性和地震危险性分析确定各性能参数的抗震安全概率。

1. 高土石坝性能参数选取

国内外学者^[12-14]对土石坝震害展开的调查研究发现,土石坝震损破坏形式主要分为裂缝、变形和滑坡等。朱晟^[13]通过对国内外土石坝震害调查研究发现,土石坝最普遍震害型式是变形和裂缝。刘君等^[14]通过搜集和整理123个土石坝震害实例,得出坝顶震陷是土石坝震害调查主要事项,也是坝体裂缝主要诱因。陈生水等^[15]指出坝体沉降一般大于水平位移,沉降和水平位移沿坝高逐渐增大,最大断面处坝顶沉降量最大,建议以坝顶震陷量作为大坝变形安全控制标准。楚金旺等^[16]分析国内外30余座土石坝地震永久变形,认为采用永久变形评价大坝抗震稳定与安全更为合理,并给出水平和竖直向变形的计算公式。Swaisgood^[12]调查69座土石坝,以坝顶相对沉陷率为指标,将震害情况分为4个破坏等级。Singh等^[17]分析122座土石坝地震情况和震害位移变形（水平和竖向）情况。因此,选取高土石坝的坝顶沉降最大值和坝顶横向水平位移最大值作为性能参数。

国内一些学者对高土石坝基于永久变形的极限抗震能力和地震易损性进行研究。陈生水等^[15]对高土石坝地震安全控制标准与极限抗震能力研究,建议将坝顶相对震陷量小于0.8%～1.0%作为地震变形控制标准,对坝高大于150 m取下限,即坝高的0.8%作为高心墙堆石坝地震变形控制标准。赵剑明等^[18]通过对两河口高心墙堆石坝极限抗震能力分析,指出最大震陷超过坝高的0.7%～0.8%时可产生明显震害。王笃波等^[11]取100 m的云鹏心墙堆石坝的坝顶相对震陷率的0.1%,0.4%,1.0%作为破坏等级标准。庞锐等^[10]提出200 m的规则高心墙堆石坝的坝顶相对震陷率的0.5%,0.8%,1.2%作为破坏等级标准。对于土石坝性能水平的划分,大多采用统计的震害资料和高土石坝的极限抗震能力得到。鉴于高土石坝遭受震害资料较少,直接结合震害资料作为性能水平划分依据难以合理反映高土石坝的抗震性能。因此,本文采用非线性分析响应结果与性能参数变化趋势定义性能水平。

2. 地震动记录选取

2.1 坝址区域地震情况

根据《工程场地地震安全性评价》（GB17741—2005）^[19],本文所指的研究区域为以糯扎渡高土石坝为中心,半径150 km范围内进行区域地震活动性分析。该坝位于青藏地震区的滇西南地震带,东北部有一角伸入鲜水河—滇东地震带。该区域范围内历史地震记载M≥4.7级地震125次,其中5.0级以上地震达89次,最大地震为7.6级地震,各震级地震次数见表1。

表 1 历史破坏性地震统计表

Table 1. Statistics of historical destructive earthquakes (次)

震级分档	4.7≤M<5	5≤M<6	6≤M<7	7≤M<8
地震数量	36	61	22	6

下载: 导出CSV

| 显示表格

2.2 地震动记录

地震动强度指标是影响地震易损性分析重要因素。进行Padgett^[20]等采用5种评判标准,对10种地震动强度指标研究,通过对地震动参数进行效率和适用性的比较发现：地震峰值加速度是较为适合的地震动强度指标。因此,选择PGA作为高土石坝地震易损性地震动强度指标。

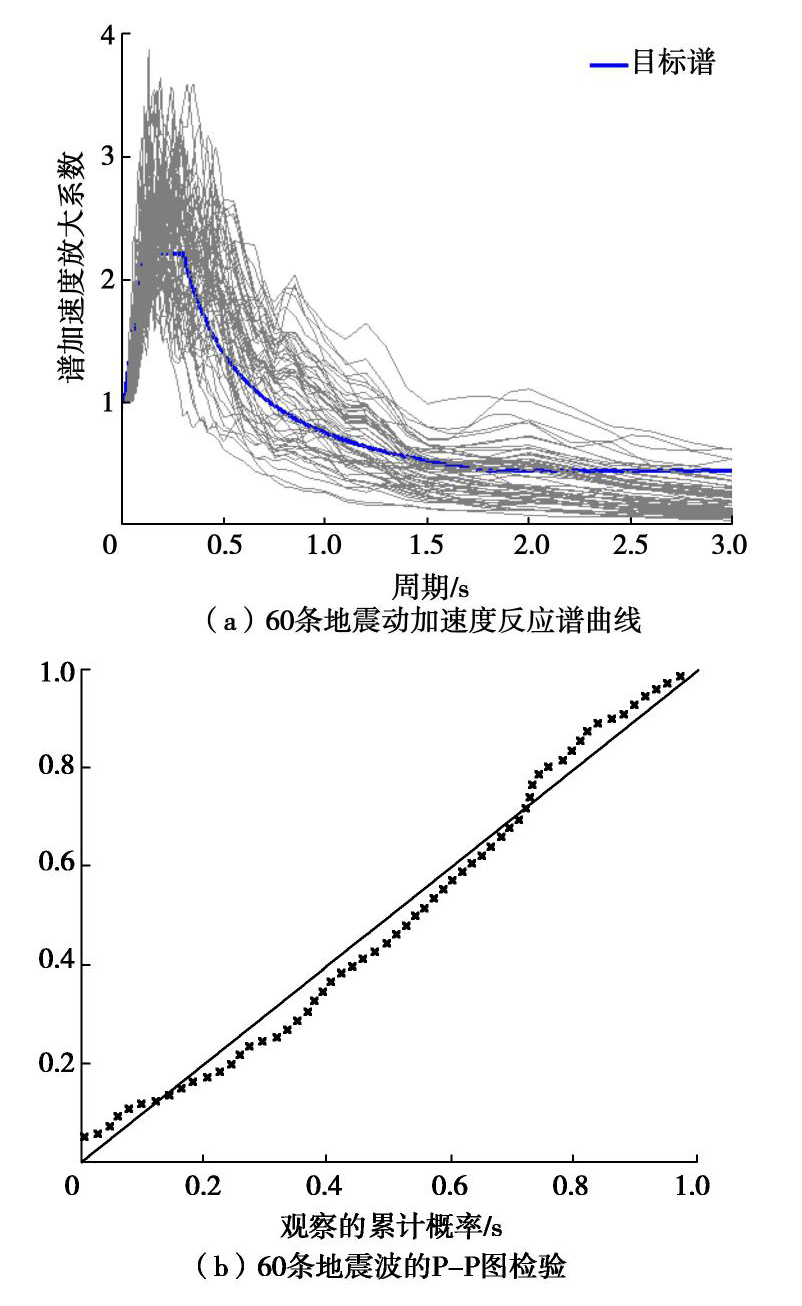
为确保高土石坝地震抗震性能合理性,选择合适输入地震动数量是关键因素之一。Shome^[21]指出使用对数正态假定模型,10～20条地震波可确保计算精度。考虑到高土石坝结构复杂,对于输入地震动数量确定进行研究是十分必要的。以糯扎渡高土石坝区域内历史上地震情况作为地震动数量选取基准,结合表1中各个震级分档,并综合考虑到高土石坝非线性计算工作量,从美国太平洋地震研究中心PEER数据库中选取60条实测地震记录。选取糯扎渡高土石坝设计地震动反应谱为目标反应谱,地震记录选取不考虑具有特殊性质的近断层地震动。选取的地震等级范围4.7～7.6,震中距10～60 km,场地为岩性地基,地震波震级数量分布具体如表2所示。

表 2 地震动选择数量

Table 2. Selected number of ground motion (次)

震级分档	4.7≤M<5	5≤M<6	6≤M<7	7≤M<8
地震数量	18	28	11	3

下载: 导出CSV

| 显示表格

60条地震动加速度反应谱和60条地震波P-P图检验分别如图1（a）,（b）所示。

图 1 60条地震波的分布图及加速度反应谱曲线

Figure 1. PGA distribution and acceleration spectrum curves of 60 earthquakes

下载: 全尺寸图片幻灯片

利用SPSS软件对60条地震波PGA及卓越周期统计分析发现,地震动峰值近似服从标准正态分布,验证本文所选取的60条地震波具有一定随机性。

3. 糯扎渡高土石坝地震易损性分析

3.1 计算模型及地震动输入

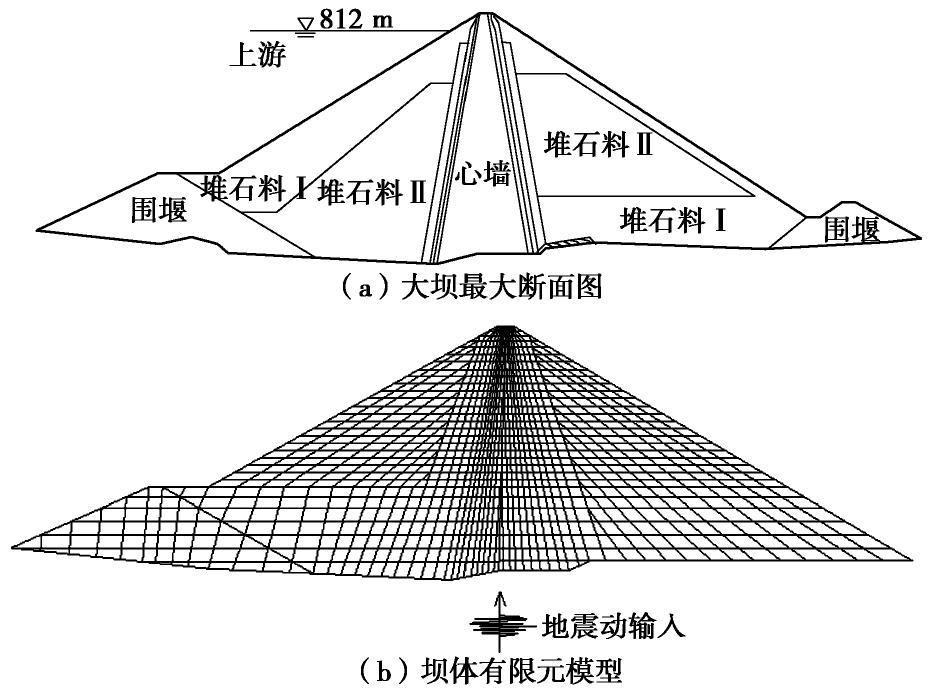
糯扎渡高土石坝位于云南省思茅区与澜沧县交界处,是澜沧江下游水电核心工程,为I等大（1）型工程。该坝坐落于基岩上,心墙基础最低建基面高程为560.0 m,最大坝高为261.5 m。坝体上游坝坡坡度为1∶1.9,下游坝坡坡度为1∶1∶8,水库正常蓄水位812 m,正常蓄水位以下库容为217.49×10⁸ m³,大坝最大断面图如图2（a）所示。有限元模型网格单元数为1197,节点数为1240个,具体如图2（b）所示。对糯扎渡高土石坝进行动力分析,输入的地震动采用从PEER数据库中选取与目标反应谱吻合良好的实测地震波。采用均匀一致的地震动输入方法从有限元模型底部输入地震加速度时程。地震波考虑同时从顺河向与竖向输入,其中,竖向地震加速度代表值取水平向加速度代表值的2/3。

图 2 大坝有限元模型

Figure 2. Finite element model for dam

下载: 全尺寸图片幻灯片

地震动输入采用的是输入地震动加速度时程,在进行动力计算前,需要对选取的地震波进行零线校正。对选取的60条地震动记录采用Seismosignal进行零线修正,避免结构的位移由地震波本身造成的可能。

3.2 本构模型和材料参数

采用弹塑性模型-非线性分析方法^[22]对高土石坝进行静动力分析能够更合理地反映坝体静动力特性。本文采用改进PZC弹塑性模型^[23]和动力固结理论对高土石坝进行动力分析。改进PZC模型是在PZC模型^[24]基础上引入临界状态理论和状态参数,因此能够统一描述筑坝料静动力特性。将该模型添加到有限元程序SWANDYNE II中^[25-26],然后对糯扎渡高土石坝进行动力分析。基于动力固结理论的u-p方程,

$σ_{i j, j} - ρ {\ddot{u}}_{i} + ρ b_{i} = 0$ ,

(1)

$α {\dot{ε}}_{i i} + {(k_{i j} (- p_{, j} - ρ_{f} {\ddot{u}}_{j} + ρ_{f} b_{j}))}_{, i} + \dot{p} / Q = 0$ 。

(2)

式中 $σ_{i j}$ 为应力；ρ为两相体密度；u_i为土体位移；b_i为单位质量上的力； $ε_{i i}$ 为体应变；k_ii为渗透系数；p为孔压； $ρ_{f}$ 为液相密度；Q为混合物压缩模型。

糯扎渡高土石坝筑坝料的改进PZC弹塑性模型参数^[23]如表3所示。

表 3 改进PZC模型参数

Table 3. Parameters of improved PZC model

堆石料	K_o	G_o	α_f	α_g	M_fc	M_gc	H₀	H_u0	γ	γ_u	m_g	m_b	γ_den	β_H	e_Γ	λ_c	ζ
堆石料	820	510	0.45	0.45	1.25	1.7	1400	1500	10	5	2	5	220	15	0.36	0.015	0.63
心墙料	K_o	G_o	α	M_c	H₀	μ	γ	m	m_b	γ_den	β_H	e_Γ	λ_c
心墙料	150	124	0.45	1.2	300	2	0	0	1	0	15	0.355	0.003

下载: 导出CSV

| 显示表格

3.3 性能水平定义

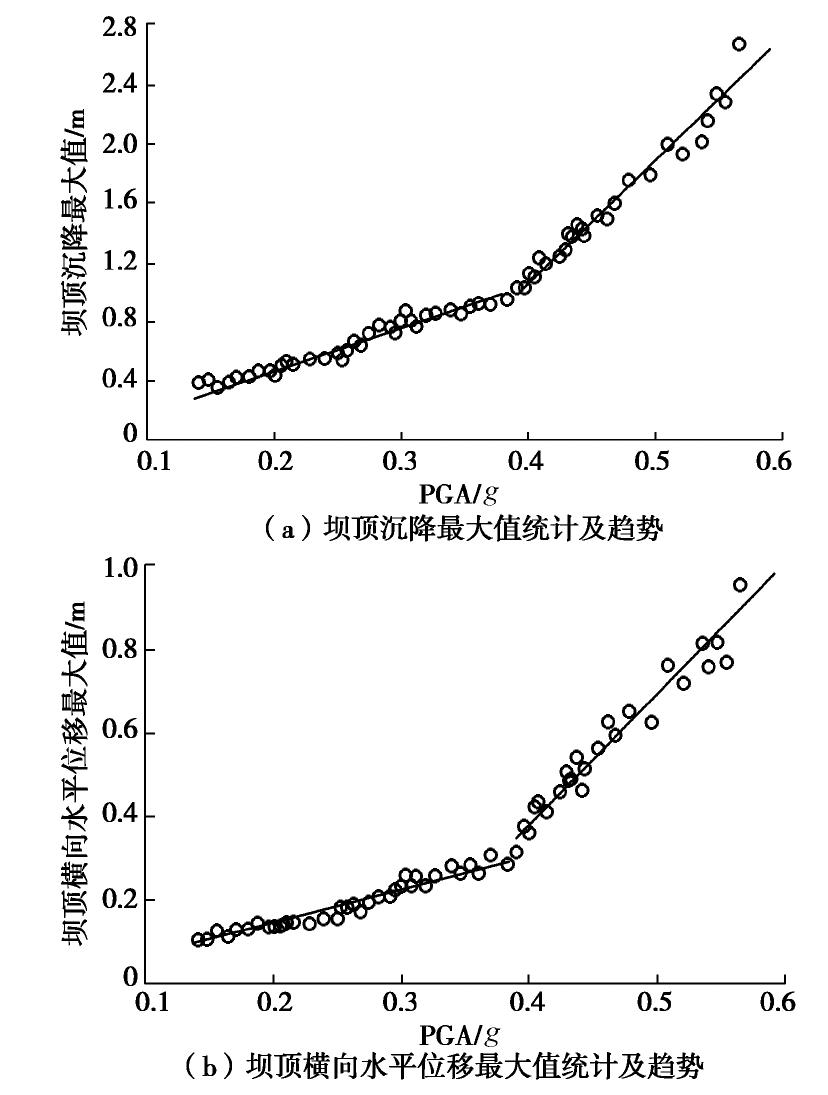
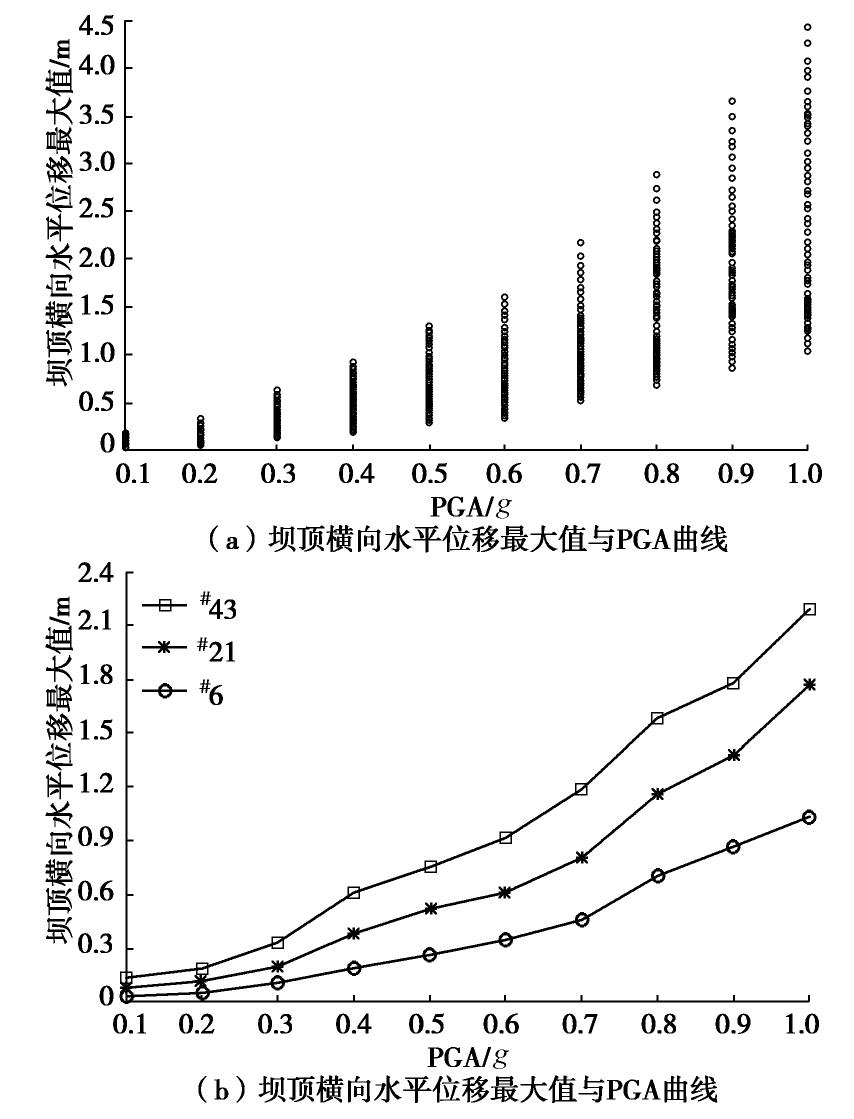
性能水平定义是地震易损性分析中重要组成部分,但对高土石坝的性能水平,因此目前尚未形成统一标准。本文通过对糯扎渡高土石坝动力分析结果定义性能水平。采用选取的60条地震波,不对这些地震波进行调幅等方式处理,以坝顶沉降最大值和坝顶横向水平位移作为性能参数,采用SWANDYNE II程序进行动力分析,具体如图3所示。

图 3 高土石坝性能参数统计及趋势

Figure 3. Statistics and trends of performance parameters of high earth-rock dam

下载: 全尺寸图片幻灯片

由图3可知,对于高土石坝在地震作用下坝顶沉降最大值和坝顶横向水平位移最大值随着PGA增大而增大。由图3（a）可知,坝顶沉降最大值起初在0.4 m处集中,当地震动强度超过0.4g,在1.0 m出现明显突变点,随着地震动强度增加而响应迅速增大,最大值达到2.7 m。图中直线为突变点前后数据的变化趋势线,可较好地反映坝顶沉降最大值随PGA变化趋势。由图3（b）可知,坝顶横向水平位移最大值变化趋势和坝顶沉降最大值变化趋势较为相似。当地震动较小时,位移集中在0.1 m处附近。然后随着PGA增加而增大,并且在0.3 m出现明显突变点。当地震动强度超过0.4g,坝顶横向水平位移增大幅度超过之前增幅,最后接近到1.0 m。图3说明随着地震强度增加,坝顶位移增大逐渐明显,坝体越容易发生破坏。因此,糯扎渡高土石坝坝顶沉降位移最大值0.4,1.0,2.7 m,坝顶横向水平位移最大值的各个性能水平为0.1,0.3,1.0 m。

3.4 MSA方法

多条带分析法（MSA）将极大似然估计法应用到条带分析法中,通过对地震动调幅计算结构响应参数,从而得到某一强度地震水平下条带,并考察不同强度水平下结构响应值,得到多个条带^[10]。Baker^[27]研究发现,MSA方法在一定结构分析数量下比IDA方法更有效估计易损性方程参数。地震易损性符合双参数对数正态分布模型,定义如下：

$P_{f} (LS | IM = X) = Φ (\frac{\ln (X / θ)}{β})$ 。

(3)

式中P_f为地震动强度IM=X作用下达到性能水平概率； $Φ$ 为标准正态分布函数； $ln θ$ 和 $β$ 为达到性能水平所需地震强度因子的对数平均值和对数标准差。

对于每一个地震动强度X_i,统计出地震波超过极限状态的地震波数量。对某一地震动强度,选取不同地震动记录对结构进行非线性分析,得到一条地震动强度IM与性能参数条带。每条地震波不超过或者超过结构破坏状态与其它地震波之间是相互独立的^[28-29],当IM=X_i时,在n_i地震波中有z_i条地震波导致结构破坏的概率由二项分布为

$P (z_{i}) = (\begin{matrix} n_{i} \\ z_{i} \end{matrix}) P_{i}^{z_{i}} {(1 - P_{i})}^{n_{i} - z_{i}}$ ,

(4)

式中,P_i为在IM=X_i时地震动下结构发生破坏的概率。

似然函数表示为

$L (\begin{matrix} θ \\ β \end{matrix}) = Π_{i = 1}^{m} (\begin{matrix} n_{i} \\ z_{i} \end{matrix}) Φ {(\frac{\ln (X_{i} / θ)}{β})}^{z_{i}} {[1 - Φ (\frac{\ln (X_{i} / θ)}{β})]}^{n_{i} - z_{i}} 。$

(5)

式中 $Π$ 为连乘符号,m为IM水平数量,n_i为超越极限状态的数量,z_i为IM=X_i时地震波的数量。

易损性方程参数θ和β的最大似然估计值为

$\begin{matrix} {\hat{θ}, \hat{β}} = \underset{θ, β}{\arg \max} \sum_{i = 1}^{m} {\ln (\begin{matrix} n_{i} \\ z_{i} \end{matrix}) + z_{i} \ln Φ (\frac{\ln (X_{i} / θ)}{β}) + \\ (n_{i} - z_{i}) \ln [1 - Φ (\frac{\ln (X_{i} / θ)}{β})]} 。 \end{matrix}$

(6)

3.5 地震易损性分析

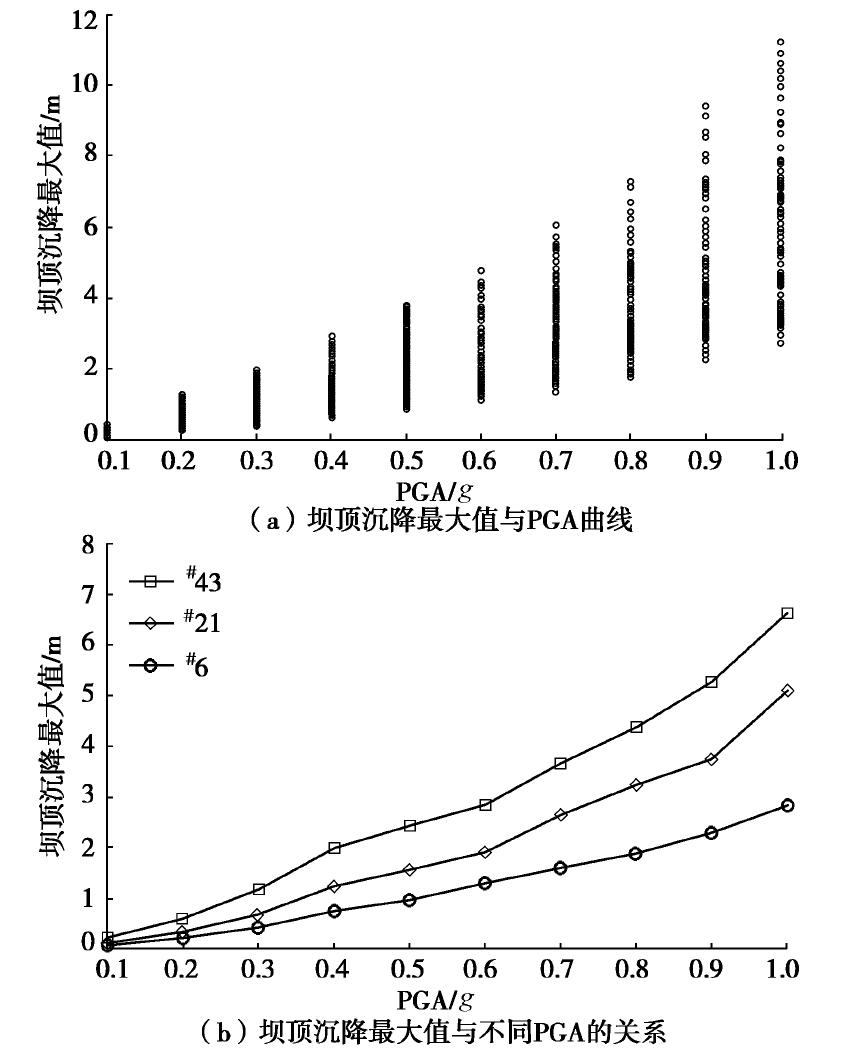
选取PGA作为地震强度参数,对60条地震动进行调幅,调幅范围为0.1g～1.0g,调幅步长为0.1g,即对每条地震波调幅9次。然后采用SWANDYNE II程序对高土石坝进行动力分析。PGA和坝顶沉陷最大值的MSA水平条带如图4（a）所示。因为对两个性能参数的动力计算工况上千组,条带分布密集难以显示变化规律,仅能体现变化趋势。因此,选取位于不同震级分档的3条地震波,分析计算高土石坝沉降最大值与PGA关系,具体如图4（b）所示。

图 4 坝顶沉降最大值与PGA关系的MSA水平条带

Figure 4. MSA level bands under relationship between maximum settlement of dam crest and PGA

下载: 全尺寸图片幻灯片

PGA和坝顶横向水平位移最大值的MSA水平条带如图5（a）所示。选取同样的3条地震波,通过分析计算得到高土石坝顶横向水平位移最大值与PGA的关系,具体如图5（b）所示。

图 5 坝顶横向水平位移最大值与PGA关系的MSA水平条带

Figure 5. MSA level bands under relationship between horizontal maximum displacement of dam crest and PGA

下载: 全尺寸图片幻灯片

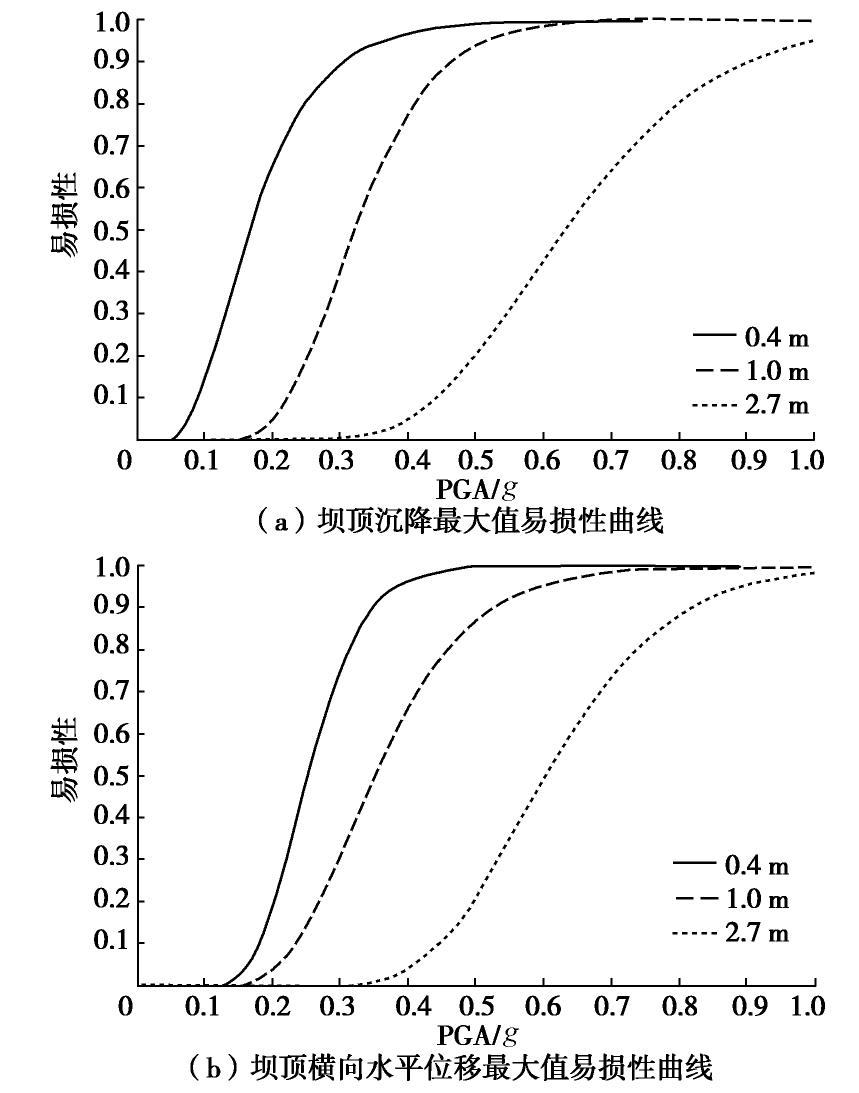
根据图4,5动力计算结果,采用MSA方法得到坝顶沉降最大值和坝顶横向水平位移的地震易损性曲线,具体如图6所示。

图 6 地震易损性曲线

Figure 6. Curves of earthquake fragility

下载: 全尺寸图片幻灯片

由图6（a）可知,坝顶沉降最大值对应的不同性能水平的地震易损性为50%时的PGA分别为0.168g,0.321g,0.63g。随着地震动强度不断增加,0.4 m性能水平易损性100%的PGA为0.532g,1.0 m性能水平在0.657g时的易损性为100%,2.7 m性能水平在1.0g时的易损性为95.2%。

同理,如图6（b）所示,性能参数坝顶横向水平位移最大值不同性能水平的地震易损性为50%对应的PGA分别为0.248g,0.352g,0.603g。随着地震动强度不断增加,0.1 m性能水平易损性100%时的PGA为0.486g,0.3 m性能水平在0.813g时的易损性为100%,1.0 m性能水平在0.984g时的易损性为98.4%。

3.6 地震动数量对性能参数的影响

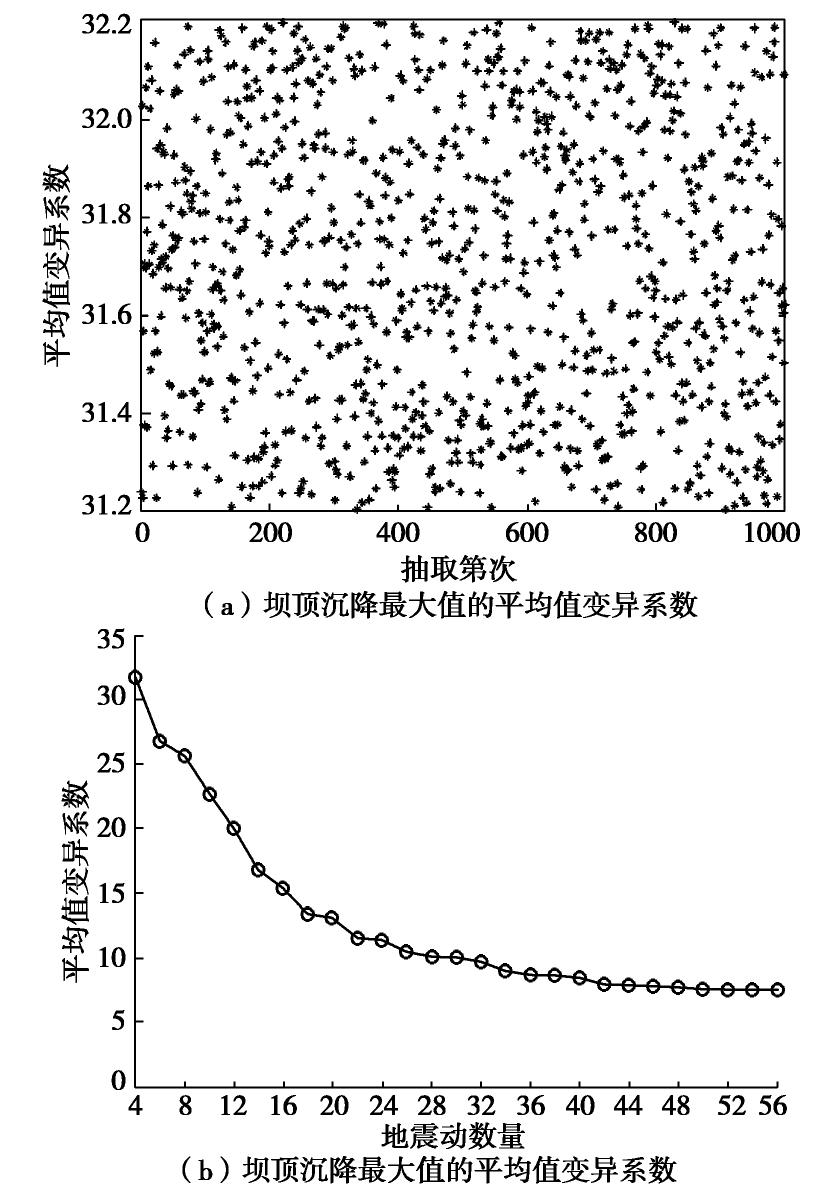
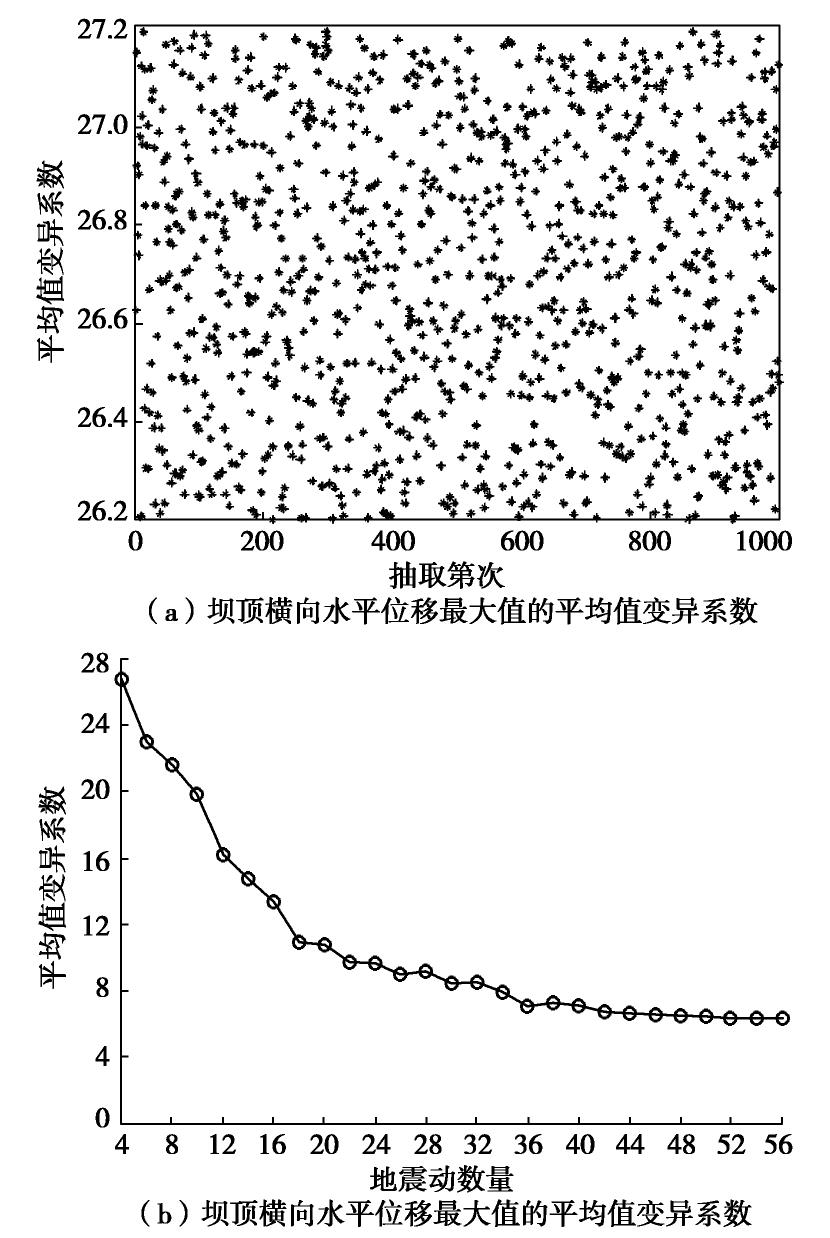
根据糯扎渡高土石坝两个性能参数与动力计算结果,进一步分析地震动数量对性能参数的影响。首先,从选取的60条地震波,随机抽取4个地震动,得到4个动力反应中坝顶沉降最大值,在这些最大值中得到一组平均值和标准差。依次采用此方法随机不重复抽取1000次,即可得到1000组平均值和标准差。然后对1000组数据计算得出平均值的变异系数和标准差的变异系数。以地震波数量间隔为2,逐步获取更多的地震动所对应的平均值变异系数和标准差变异系数。当输入地震动数量为4条时,坝顶沉降量最大值1000次计算得到的平均值的变异系数如图7（a）所示,坝顶沉降量最大值的平均值变异系数与地震动数量的关系如图7（b）所示。

图 7 不同地震波数量下坝顶沉降量最大值的平均值变异系数

Figure 7. Mean coefficients of variation of maximum settlement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

从图7（b）可知,坝顶沉降最大值的平均值变异系数整体上随着地震波数量的增加而减小。当地震动数量少于16条时,平均值变异系数下降速率较大,随着地震动数量不断增加,平均值变异系数变化减缓,当地震动数量达到26条后趋于稳定。

当输入地震动数量为4条时,坝顶沉降量最大值1000次计算得到的标准差变异系数如图8（a）所示,坝顶沉降量最大值的标准差变异系数与地震动数量关系如图8（b）所示。

图 8 不同地震波数量下坝顶沉降量最大值的标准值变异系数

Figure 8. Standard coefficients of variation of maximum settlement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

由图8（b）可知,坝顶沉降最大值的标准差变异系数随着地震波数量的增加而减小。当地震动数量超过30条时,地震波数量对平均值变异系数影响基本很小,随着地震动数量不断增加,平均值变异系数变化减缓,直至不再发生波动。

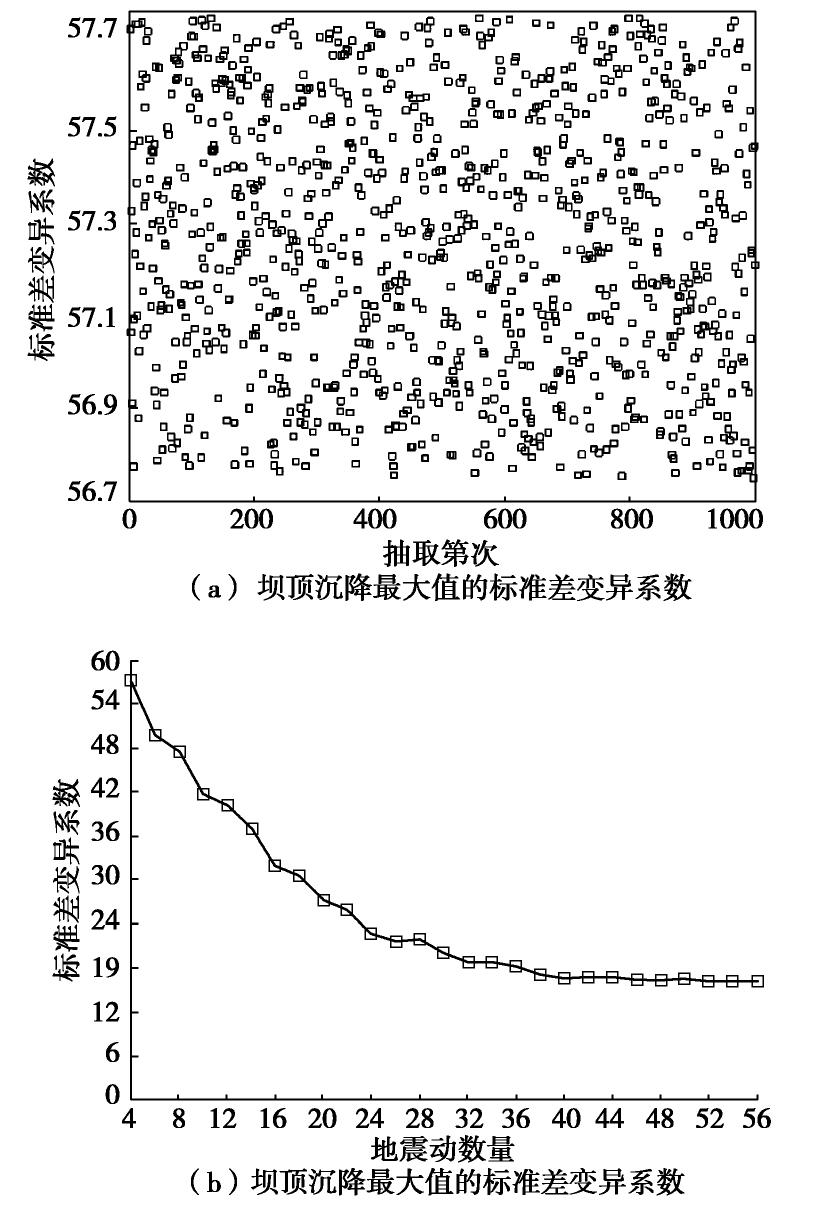
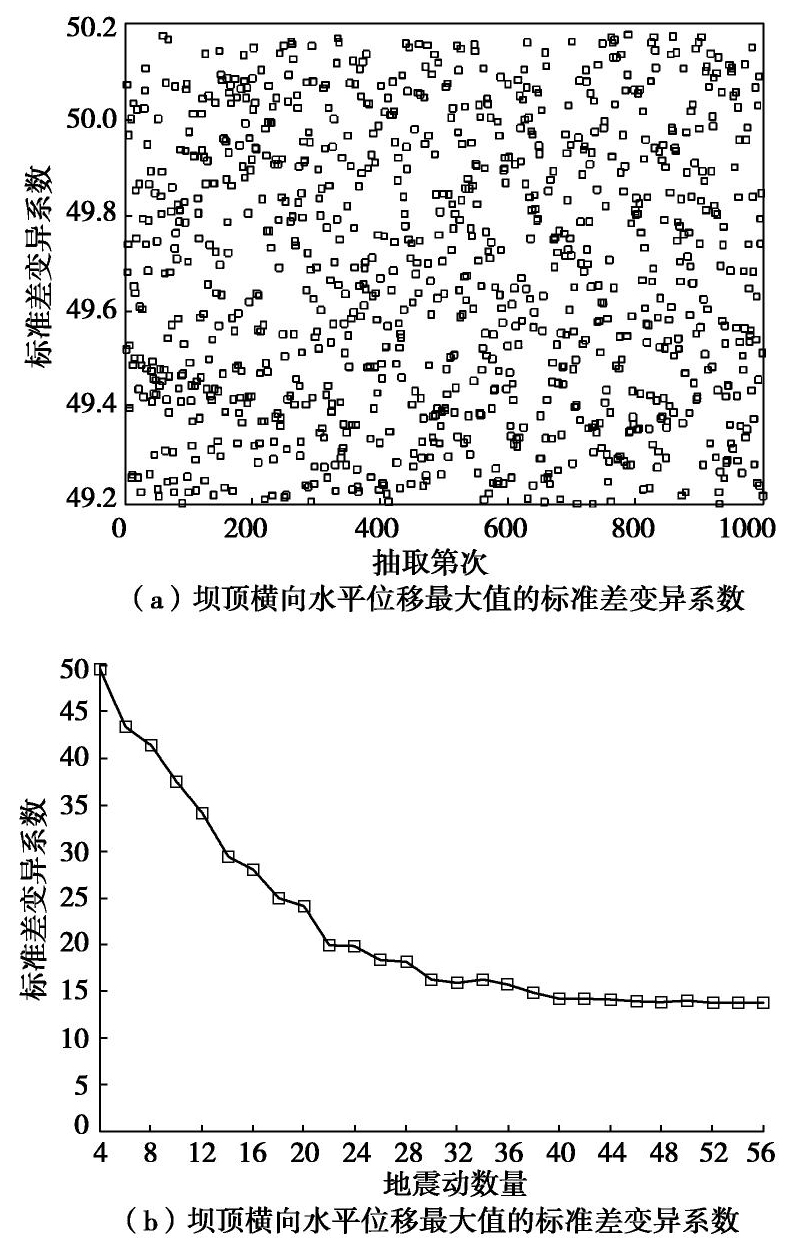
当输入地震动数量为4条时,坝顶横向水平位移最大值1000次计算得到的标准差变异系数如图9（a）所示,坝顶横向水平位移最大值的标准差变异系数与地震动数量的关系如图9（b）所示。

图 9 不同地震波数量下坝顶横向水平位移最大值的标准值变异系数

Figure 9. Mean coefficients of variation of horizontal maximum displacement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

从图9（b）中可以看出,坝顶横向水平位移最大值的标准差变异系数随着地震波数量增加而减小。当地震动数量超过26条时,地震波数量对平均值变异系数影响变化较小,随着地震动数量不断增加,平均值变异系数变化减缓,40条地震动之后基本不再变化。

地震动为4时,坝顶横向水平位移最大值1000次计算得到的标准差变异系数如图10（a）所示,坝顶横向水平位移最大值的标准差变异系数与地震动数量的关系如图10（b）所示。

图 10 不同地震波数量下坝顶横向水平位移最大值的标准差.变异系数

Figure 10. Standard coefficients of variation of horizontal maximum displacement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

由图10（b）可知,坝顶横向水平位移最大值的标准差变异系数随着地震波数量的增加而减小。当地震动数量大于30条时,地震波数量对平均值变异系数影响较小,随着地震动数量不断增加,平均值变异系数变化减缓,直至不再发生波动。

通过对地震动数量对高土石坝性能参数的影响分析可知,当地震动数量超过30条时,地震动数量对于性能参数基本无影响。

4. 高土石坝抗震安全分析

通过对坝址区地震危险性分析,确定坝址一定使用时间内PGA超过某一特定值概率。然后结合高土石坝地震易损性结果,评估未来发生不同强度地震时高坝发生不同等级破坏概率,确定高土石坝抗震安全。

4.1 地震危险性分析

Cornell^[30]提出地震危险性曲线 $λ$ 为地震动强度 $I M$ 的年平均超越概率,可以近似地用对数线性来表示如下：

$λ = k_{0} {(I M)}^{- k}$ ,

(7)

$ν = \frac{1}{λ} = \frac{I M^{k}}{k_{0}}$ ,

(8)

$I M = {(k_{0} ν)}^{\frac{1}{k}}$ 。

(9)

将式（9）代入式（3）,得到年超越概率曲线：

$P_{f} (LS | IM) = Φ (\frac{\frac{1}{k} \ln (k_{0} ν) - \ln θ}{β})$ ,

(10)

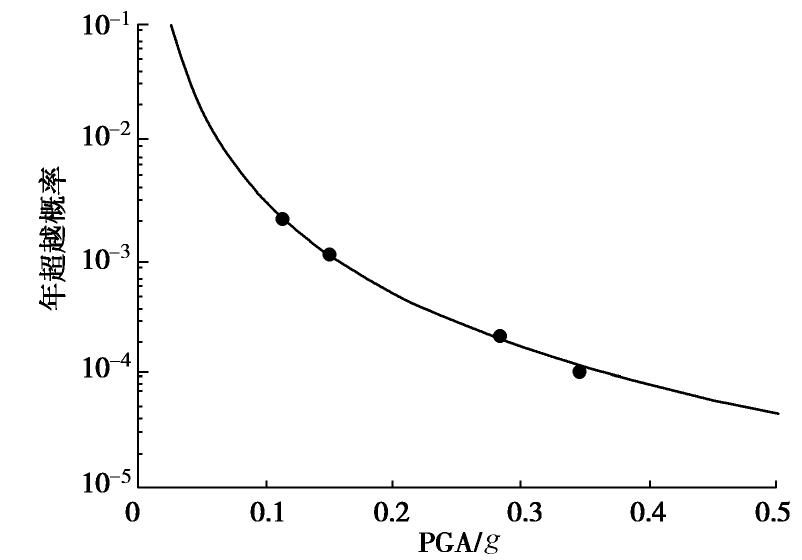
式中, $λ$ 为地震动参数IM年平均超越概率,k₀和k为经验常数, $ν$ 为重现期。

糯扎渡高土石坝坝址基岩场地相应超越概率的峰值加速度见表4。

表 4 坝址场地的地震动危险性参数

Table 4. Hazard parameters of ground motion of site

概率	50 a超越概率		100 a超越概率
概率	10%	5%	2%	1%
年超越概率	2.1×10^-3	1.03×10^-3	2.02×10^-4	1.005×10^-4
回归期/a	475	975	4950	9950
峰值加速度/g	0.113	0.15	0.283	0.345

下载: 导出CSV

| 显示表格

根据表4和式（10）对年均超越概率和峰值加速度进行拟合,得到工程场地地震危险性曲线,具体如图11所示。

图 11 坝址区地震危险性曲线

Figure 11. Seismic hazard curve of dam site

下载: 全尺寸图片幻灯片

4.2 高土石坝抗震安全分析

重大水工建筑物都需要进行专门的场址地震危险性分析工作,年超越概率 $P_{1}$ 与设计基准年 $T_{0}$ 年内超越概率 $P_{T_{0}}$ 间关系：

$P_{T_{0}} = 1 - {(1 - P_{1})}^{T_{0}}$ 。

(11)

高土石坝年超越概率曲线通过式（11）得到设计基准期内对应超越概率 $P_{T_{0}} (C_{1})$ ,并通过式（12）得到高土石坝性能参数第i个性能水平概率。

$P_{f} (1) = 1 - P_{T_{0}} (C_{1})$ ,

(12)

$P_{f} (i) = P_{T_{0}} (C_{i - 1}) - P_{T_{0}} (C_{i}) (i = 2, 3, 4)$ ,

(13)

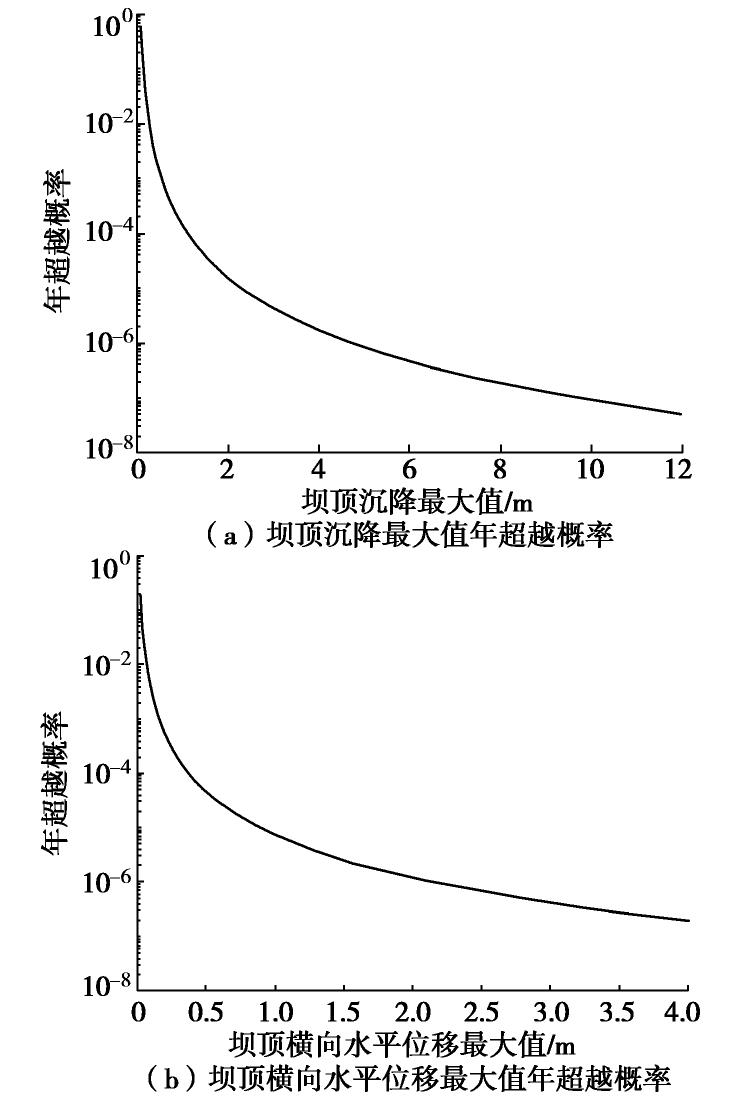
式中,C_i为坝体在地震作用下的性能水平, $P_{T_{0}}$ (C_i)为坝体在设计基准期内第i个性能水平下的超越概率, $P_{f}$ (i)为坝体在各个性能水平下的失效概率。

结合糯扎渡高土石坝坝址地震危险性结果和两个性能参数的易损性结果,得到性能参数年超越概率,具体如图12所示。

图 12 高土石坝性能参数的年超越概率

Figure 12. Annual excess probability of performance parameters of high earth-rockfill dam

下载: 全尺寸图片幻灯片

由上图中两个性能参数的性能水平对应的年超越概率,并结合式（10）,（11）得到糯扎渡大坝在100 a设计基准期内的安全概率,具体如表5和6所示。

表 5 100 a内坝顶沉降最大值安全概率

Table 5. Maximum safety probabilities of maximum settlement of dam crest in 100 years

最大沉降/m	0.4	1.0	2.7
概率/%	80.54	17.98	1.48

下载: 导出CSV

| 显示表格

表 6 100 a内坝顶横向水平位移最大值安全概率

Table 6. Maximum safety probabilities of horizontal maximum displacement of dam crest in 100 years

水平位移最大值/m	0.1	0.3	1.0
概率/%	74.93	23.49	1.58

下载: 导出CSV

| 显示表格

由表5可知,100 a设计基准期内发生0.4 m坝顶沉降的概率高达80.54%。但是在100 a设计基准期内发生2.7 m的概率仅为1.48%。

由表6可知,100 a设计基准期内发生0.1 m横向水平位移的概率高达74.93%。但是在100 a设计基准期内发生1.0 m的概率仅为1.58%。

5. 结论

（1）以糯扎渡高土石坝坝址区域内统计的历史上地震情况作为地震动记录选取依据,并通过PEER数据库选取符合条件的60条地震波,再结合SPSS软件分析地震动离散性。采用改进PZC弹塑性模型和SWANDYNE II有限元程序对选取的60条地震动进行动力分析。选取坝顶沉降最大值和坝顶横向水平位移作为高土石坝的性能参数,并以动力计算结果中的位移突变点作为高土石坝的性能水平。

（2）对选取的60条地震动进行调幅,采用弹塑性模型-非线性方法进行糯扎渡高土石坝的动力分析。基于MSA方法对动力计算结果进行地震易损性分析,得到两个性能参数与不同强度PGA的条带,最终得到地震作用下不同性能水平的地震易损性曲线。通过对不同地震波数量与高土石坝性能参数的分析可知,当地震波数量较少时,性能参数的平均值和标准差的变异系数变化较大；当地震动数量超过30条时,性能参数的平均值和标准差的变异系数基本不再发生波动。

（3）基于高土石坝两个性能参数的地震易损性曲线,并结合糯扎渡高土石坝地震危险性分析,获得坝顶沉降最大值和坝顶横向水平位移两个性能参数在100 a设计基准期内各个性能水平对应的破坏概率值和安全值。基于性能的高土石坝抗震安全评估在100 a设计基准期内发生较大变形的概率很小,但是坝顶发生较小沉降和横向水平位移的概率均超过74%。因此,基于地震变形易损性的高土石坝抗震安全分析可为高土石坝抗震性能设计和安全风险评估提供依据。

图 1 60条地震波的分布图及加速度反应谱曲线

Figure 1. PGA distribution and acceleration spectrum curves of 60 earthquakes

下载: 全尺寸图片幻灯片

图 2 大坝有限元模型

Figure 2. Finite element model for dam

下载: 全尺寸图片幻灯片

图 3 高土石坝性能参数统计及趋势

Figure 3. Statistics and trends of performance parameters of high earth-rock dam

下载: 全尺寸图片幻灯片

图 4 坝顶沉降最大值与PGA关系的MSA水平条带

Figure 4. MSA level bands under relationship between maximum settlement of dam crest and PGA

下载: 全尺寸图片幻灯片

图 5 坝顶横向水平位移最大值与PGA关系的MSA水平条带

Figure 5. MSA level bands under relationship between horizontal maximum displacement of dam crest and PGA

下载: 全尺寸图片幻灯片

图 6 地震易损性曲线

Figure 6. Curves of earthquake fragility

下载: 全尺寸图片幻灯片

图 7 不同地震波数量下坝顶沉降量最大值的平均值变异系数

Figure 7. Mean coefficients of variation of maximum settlement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

图 8 不同地震波数量下坝顶沉降量最大值的标准值变异系数

Figure 8. Standard coefficients of variation of maximum settlement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

图 9 不同地震波数量下坝顶横向水平位移最大值的标准值变异系数

Figure 9. Mean coefficients of variation of horizontal maximum displacement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

图 10 不同地震波数量下坝顶横向水平位移最大值的标准差.变异系数

Figure 10. Standard coefficients of variation of horizontal maximum displacement of dam crest under different earthquake records

下载: 全尺寸图片幻灯片

图 11 坝址区地震危险性曲线

Figure 11. Seismic hazard curve of dam site

下载: 全尺寸图片幻灯片

图 12 高土石坝性能参数的年超越概率

Figure 12. Annual excess probability of performance parameters of high earth-rockfill dam

下载: 全尺寸图片幻灯片

表 1 历史破坏性地震统计表

Table 1 Statistics of historical destructive earthquakes (次)

震级分档 4.7≤M<5 5≤M<6 6≤M<7 7≤M<8

地震数量 36 61 22 6

下载: 导出CSV

表 2 地震动选择数量

Table 2 Selected number of ground motion (次)

震级分档 4.7≤M<5 5≤M<6 6≤M<7 7≤M<8

地震数量 18 28 11 3

下载: 导出CSV

表 3 改进PZC模型参数

Table 3 Parameters of improved PZC model

堆石料 K_o G_o α_f α_g M_fc M_gc H₀ H_u0 γ γ_u m_g m_b γ_den β_H e_Γ λ_c ζ
820 510 0.45 0.45 1.25 1.7 1400 1500 10 5 2 5 220 15 0.36 0.015 0.63
心墙料 K_o G_o α M_c H₀ μ γ m m_b γ_den β_H e_Γ λ_c
150 124 0.45 1.2 300 2 0 0 1 0 15 0.355 0.003

下载: 导出CSV

表 4 坝址场地的地震动危险性参数

Table 4 Hazard parameters of ground motion of site

概率 50 a超越概率 100 a超越概率
10% 5% 2% 1%

年超越概率 2.1×10^-3 1.03×10^-3 2.02×10^-4 1.005×10^-4
回归期/a 475 975 4950 9950
峰值加速度/g 0.113 0.15 0.283 0.345

下载: 导出CSV

表 5 100 a内坝顶沉降最大值安全概率

Table 5 Maximum safety probabilities of maximum settlement of dam crest in 100 years

最大沉降/m 0.4 1.0 2.7

概率/% 80.54 17.98 1.48

下载: 导出CSV

表 6 100 a内坝顶横向水平位移最大值安全概率

Table 6 Maximum safety probabilities of horizontal maximum displacement of dam crest in 100 years

水平位移最大值/m 0.1 0.3 1.0

概率/% 74.93 23.49 1.58

下载: 导出CSV

参考文献(30)

[1]	赵剑明, 刘小生, 温彦锋, 等. 紫坪铺大坝汶川地震震害分析及高土石坝抗震减灾研究设想[J]. 水力发电, 2009, 35(5): 11-14. https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD200905004.htm ZHAO Jian-ming, LIU Xiao-sheng, WEN Yan-feng, et al. Analysis of earthquake damage of the Zipingpu Dam in Wenchuan Earthquake and the study proposal on the anti-earthquake and disaster reduction of high earth-rock dam[J]. Water Power, 2009, 35(5): 11-14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD200905004.htm
[2]	FRAGIADAKIS M, PAPADRAKAKIS M. Performance based optimum seismic design of reinforced concrete structures[J]. Earthquake Engineering & Structural Dynamics, 2008, 37(6): 825-844.
[3]	李建中, 管仲国. 基于性能桥梁抗震设计理论发展[J]. 工程力学, 2011, 28(增刊2): 24-30. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2011S2007.htm LI Jian-zhong, GUAN Zhong-guo. Performance-based seismic design for bridges[J]. Engineering mechanics, 2011, 28(S2): 24-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2011S2007.htm
[4]	ÖZUYGUR A R. Performance-based seismic design of an irregular tall building: a case study[J]. Structures, 2016, 5: 112-122. doi: 10.1016/j.istruc.2015.10.001
[5]	MACKIE K R, STOJADINOVIĆ B. Performance-based seismic bridge design for damage and loss limit states[J]. Earthquake Engineering & Structural Dynamics, 2010, 36(13): 1953-1971.
[6]	徐强, 徐舒桐, 陈健云, 等. 重力坝抗震性能的POA-ETA评价方法[J]. 水利学报, 2018, 49(8): 986-994. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201808010.htm XU Qiang, XU Shu-tong, CHEN Jian-yun, et al. POA-ETA method for seismic performance evaluation of concrete gravity dam[J]. Journal of Hydraulic Engineering, 2018, 49(8): 986-994. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201808010.htm
[7]	孔宪京, 庞锐, 邹德高, 等. 基于IDA的高面板堆石坝抗震性能评价[J]. 岩土工程学报, 2018, 40(6): 978-984. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201806003.htm KONG Xian-jing, PANG Rui, ZOU De-gao, et al. Seismic performance evaluation of high CFRDs based on incremental dynamic analysis[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 978-984. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201806003.htm
[8]	姚霄雯. 基于性能的高拱坝地震易损性分析与抗震安全评估[D]. 杭州: 浙江大学, 2013. YAO Xiao-wen. Performance- Based Seismic Fragility Analysis and Safety Assessment of High Arch Dams[D]. Hangzhou: Zhejiang University, 2013. (in Chinese)
[9]	沈怀至, 金峰, 张楚汉. 基于性能的重力坝-地基系统地震易损性分析[J]. 工程力学, 2008, 25(12): 86-91. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200812018.htm SHEN Huai-zhi, JIN Feng, ZHANG Chu-han. Performance-based seismic fragility analysis of concrete gravity-foundation system[J]. Engineering Mechanics, 2008, 25(12): 86-91. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200812018.htm
[10]	庞锐, 孔宪京, 邹德高, 等. 基于MSA法的高心墙堆石坝地震沉降易损性分析[J]. 水利学报, 2017, 48(7): 866-873. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201707014.htm PANG Rui, KONG Xian-jing, ZOU De-gao, et al. Seismic subsidence fragility analysis of high CRFDs based on MSA[J]. Journal of Hydraulic Engineering, 2017, 48(7): 866-873. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201707014.htm
[11]	王笃波, 刘汉龙, 于陶, 等. 基于变形的土石坝地震易损性分析[J]. 岩土工程学报, 2013, 35(5): 814-819. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201305002.htm WANG Du-bo, LIU Han-long, YU Tao, et al. Seismic fragility analysis for earth-rockfill dams based on deformation[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(5): 814-819. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201305002.htm
[12]	SWAISGOOD J R. Embankment dam deformations caused by earthquakes[C]//Pacific Conference on Earthquake Engineering. Christchurch, 2003.
[13]	朱晟. 土石坝震害与抗震安全[J]. 水力发电学报, 2011, 30(6): 40-51. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201106010.htm ZHU Sheng. Earthquake induced damage and aseismic safety of earth-rock dam[J]. Journal of Hydroelectric Engineering, 2011, 30(6): 40-51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201106010.htm
[14]	刘君, 刘博, 孔宪京. 地震作用下土石坝坝顶沉降估算[J]. 水力发电学报, 2012, 31(2): 183-191. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201202028.htm LIU Jun, LIU Bo, KONG Xian-jing. Estimation of earthquake-induced crest settlements of earth and rockfill dams[J]. Journal of Hydroelectric Engineering, 2012, 31(2): 183-191. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201202028.htm
[15]	陈生水, 李国英, 傅中志. 高土石坝地震安全控制标准与极限抗震能力研究[J]. 岩土工程学报, 2013, 35(1): 59-65. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201301002.htm CHEN Sheng-shui, LI Guo-ying, FU Zhong-zhi. Safety criteria and limit resistance capacity of high earth-rock dams subjected to earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 59-65. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201301002.htm
[16]	楚金旺, 朱晟, 黄亚梅. 基于实际震害的土石坝永久变形估算[J]. 中国水利水电科学研究院学报, 2017, 15(6): 409-417. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSX201706001.htm CHU Jin-wang, ZHU Sheng, HUANG Ya-mei. Estimation of earthquake-induced permanent deformation for earth dam based on seismic damage[J]. Journal of China Institute of Water Resources and Hydropower Research, 2017, 15(6): 409-417. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSX201706001.htm
[17]	SINGH R, ROY D, DAS D. A correlation for permanent earthquake-induced deformation of earth embankments[J]. Engineering Geology, 2007, 90(3/4): 174-185.
[18]	赵剑明, 刘小生, 陈宁, 等. 高心墙堆石坝的极限抗震能力研究[J]. 水力发电学报, 2009, 28(5): 97-102. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB200905019.htm ZHAO Jian-ming, LIU Xiao-sheng, CHEN Ning, et al. Research on the maximum anti-seismic capability of high earth core rock-fill dam[J]. Journal of Hydroelectric Engineering, 2009, 28(5): 97-102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB200905019.htm
[19]	工程场地地震安全性评价：GB17741—2005[S]. 2005. Evaluation of Seismic Safety for Engineering Sites: GB17741—2005[S]. 2005. (in Chinese)
[20]	PADGETT J E, NIELSON B G, DESROCHES R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J]. Earthquake Engineering and Structural Dynamics, 2008, 37(5): 711-726.
[21]	SHOME N. Probabilistic Seismic Demand Analysis of Nonlinear Structures[D]. Palo Alto: Stanford University, 1999.
[22]	吴永康, 王翔南, 董威信, 等. 考虑流固耦合作用的高土石坝动力分析[J]. 岩土工程学报, 2015, 37(11): 2007-2013. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201511013.htm WU Yong-kang, WANG Xiang-nan, DONG Wei-xin, et al. Dynamic analyses of a high earth-rockfill dam considering effects of solid-fluid coupling[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 2007-2013. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201511013.htm
[23]	董威信. 高心墙堆石坝流固耦合弹塑性地震动力响应分析[D]. 北京: 清华大学, 2015. DONG Wei-xin. Elasto Plastic Fluid-solid Coupling Analysis of Seismic Response of High Core-wall Rockfill Dam[D]. Beijing: Tsinghua University, 2015. (in Chinese)
[24]	靳聪聪, 迟世春, 聂章博. 土体PZC弹塑性本构模型参数的确定[J/OL]. 解放军理工大学学报(自然科学版): 1-6.[2020-01-10]. http://kns.cnki.net/kcms/detail/32.1430.N.20180109.1043.002.html.
[25]	CHAN A. User Manual for Diana Swandyne II[R]. Glasgow: Glasgow Department of Civil Engineering, Glasgow University, 1989.
[26]	ZIENKIEWICZ O C, CHAN A H C, PASTOR M, et al. Computational Geomechanics with Special Reference to Earthquake Engineering[M]. New York: John Wiley & Sons, 1998.
[27]	BAKER J W. Efficient analytical fragility function fitting using dynamic structural analysis[J]. Earthquake Spectra, 2015, 31(1): 579-599.
[28]	BAKER J, CORNELL C. Vector-valued Ground Motion Intensity Measures for Probabilistic Seismic Demand Analysis[M]. Palo Alto: Stanford University, 2006.
[29]	DANIEL S, ARMEN D K. Improved seismic fragility modeling from empirical data[J]. Structural Safety, 2008, 30(4): 320-336.
[30]	CORNELL C A. Calculating building seismic performance reliability:a basis for multi-level design norms[C]//Proceedings of the 11th World Conference on Earthquake Engineering. Acapulco, 1996: 5707-5712.

施引文献

资源附件(0)

图(12) / 表(6)

计量

文章访问数: 329
HTML全文浏览量: 33
PDF下载量: 107
被引次数: 0

0. 引言
1. 高土石坝性能参数选取
2. 地震动记录选取
2.1 坝址区域地震情况
2.2 地震动记录
3. 糯扎渡高土石坝地震易损性分析
3.1 计算模型及地震动输入
3.2 本构模型和材料参数
3.3 性能水平定义
3.4 MSA方法
3.5 地震易损性分析
3.6 地震动数量对性能参数的影响
4. 高土石坝抗震安全分析
4.1 地震危险性分析
4.2 高土石坝抗震安全分析
5. 结论

0. 引言
1. 高土石坝性能参数选取
2. 地震动记录选取
2.1 坝址区域地震情况
2.2 地震动记录
3. 糯扎渡高土石坝地震易损性分析
3.1 计算模型及地震动输入
3.2 本构模型和材料参数
3.3 性能水平定义
3.4 MSA方法
3.5 地震易损性分析
3.6 地震动数量对性能参数的影响
4. 高土石坝抗震安全分析
4.1 地震危险性分析
4.2 高土石坝抗震安全分析
5. 结论

参考文献(30)

施引文献

资源附件(0)

基于地震变形易损性的高土石坝抗震安全分析 English Version

作者简介: 靳聪聪（1987— ）,男,河南开封人,博士研究生,从事高土石坝地震易损性及抗震风险研究工作。E-mail：jincong3623@mail.dlut.edu.cn

通讯作者: 迟世春, E-mail：schchi@dlut.edu.cn

计量

出版历程