高铁路堑段地面环境振动特性现场实测与数值分析

毕俊伟; 张继严; 高广运; 汪益敏

doi:10.11779/CJGE2023S20043

高铁路堑段地面环境振动特性现场实测与数值分析 English Version

毕俊伟^1,,
张继严^{2, 3, ,},
高广运⁴,
汪益敏¹

1.
华南理工大学土木与交通学院, 广东广州 510641
2.
北方工业大学土木工程学院, 北京 100144
3.
北京工业大学城市建设学部, 北京 100124
4.
同济大学土木工程学院, 上海 200092

基金项目:

国家自然科学基金项目 42277130

广东省科技计划项目 2017A050501005

详细信息

作者简介:
毕俊伟(1990—)，男，博士，博士后，主要从事土动力学、环境振动与防治等研究。E-mail: bijw@alumni.tongji.edu.cn

通讯作者:
张继严，E-mail: jiyanzhxl@163.com

中图分类号: TU435
计量
- 文章访问数: 107
- HTML全文浏览量: 25
- PDF下载量: 19
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Field measurements and numerical analysis of ground vibrations generated by cutting

1.
School of Civil Engineering & Transportation, South China University of Technology, Guangzhou 510641, China
2.
School of Civil Engineering, North China University of Technology, Beijing 100144, China
3.
Faculty of Architecture, Civil and Transportation Engineering, Beijing University of Technology, Beijing 100124, China
4.
College of Civil Engineering, Tongji University, Shanghai 200092, China

摘要

摘要: 基于巴黎—布鲁塞尔高铁某路堑段地面环境振动现场实测，分析路堑段地面振动特性与传播衰减规律。基于2.5维有限元法基本原理，推导并建立高铁荷载下路堑段2.5维有限元动力计算模型，讨论了路堑设计参数对地面振动特性的影响。结果表明：近轨道处地面振动幅值主要受列车轴重影响，而距轨道较远处则由中间车相邻转向架轮对的叠加效应主导。路堑段地面环境振动随与轨道距离的增加而减小，中高频振动的衰减速率大于其他频段。地面振动1阶主频主要由列车荷载的基频f₁主导。路堑段地面环境振动随与轨道距离的衰减过程大致可分为3个阶段，且在堑顶处有较明显的振动局部放大现象。同时，随路堑深度增加，地面振动逐渐减小，当超过某一限值后，继续增加路堑深度难以有效减小地面振动。此外，在确保稳定性的前提下，较陡的路堑边坡更有利于减小高铁运行引起的地面振动。
- 高速铁路 /
- 地面环境振动 /
- 路堑 /
- 现场实测 /
- 2.5维有限元法
Abstract: A field measurement of ground vibration is performed on the Paris-Brussels high-speed railway, and the ground vibrations generated by cutting are analyzed. Based on the 2.5D finite element method (FEM), 2.5D FE models for the cutting are established to investigate the effects of the design parameters for cutting on ground vibration responses. The results show that, in the near track zone, the amplitudes of ground vibrations are dominated by the axle weight of train, but are mainly influenced by the superimposed effects far away from the track which is induced by the adjacent wheelsets and bogies of middle cars. With the increasing distance from track, the ground vibrations decrease gradually, and the decay rate for the medium- and high-frequency vibrations is higher than that for others. The primary frequency of ground vibrations is dominated by the basic frequency of train loading f₁. The process of ground vibration attenuation can be divided into three stages for the cutting track section. There are rebound phenomena of ground vibrations at the top of cutting slope. The ground vibration decreases with the increasing cutting depth. When the depth is beyond a critical value, such benefit of cutting on vibration reduction can hardly be increased further. In the precondition of the stability of cutting slopes, a larger inclined angle is beneficial to reducing vibrations.
- high-speed railway /
- ground vibration /
- cutting /
- field measurement /
- 2.5D FEM

HTML全文

0. 引言

高速铁路以其速度快、运输能力大、舒适方便等优点成为我国大力发展的交通基础设施。随着高铁网络迅速扩张以及运营速度的不断提高，列车运行引起的沿线地面环境振动问题也逐渐成为人们关注的焦点^[1-2]。近年来，许多学者针对轨道交通地面环境振动开展了大量的理论、数值和现场实测研究^[2]。

本文基于巴黎—布鲁塞尔高铁某路堑段地面环境振动现场实测，分析路堑段地面振动特性和传播衰减规律。在此基础上，推导并建立高铁荷载下路堑段2.5维有限元动力计算模型，对比分析路堑深度和路堑边坡坡度对地面环境振动特性的影响。

1. 高铁路堑段地面振动实测

1.1 测试概况

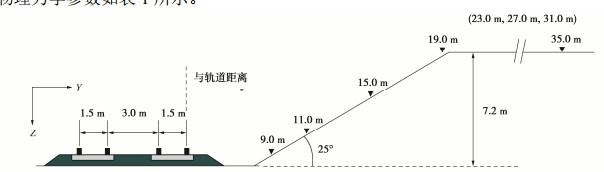
路堑测试段取自巴黎—布鲁塞尔高速铁路^[3-4]，位于比利时Braffe小镇西北侧，如图 1。线路为有砟轨道，采用UIC 60型钢轨和预应力轨枕，道床由0.3 m厚道砟层和0.2 m厚底砟层组成。测试采用SM-6型振动检波仪，灵敏度28.8 V/m/s，采样频率1000.0 Hz（图 2）。

图 1 路堑测试段

Figure 1. Test sections for field cutting

下载: 全尺寸图片幻灯片

图 2 SM-6型振动检波仪

Figure 2. SM-6 geophones for measurement

下载: 全尺寸图片幻灯片

如图 3所示，在路堑测试段距轨道9.0~35.0 m范围内依次布置8个测点，监测并记录高速列车通过路堑测试段时引起的地面环境振动。测试段路堑深度为7.2 m，路堑边坡坡度为25.0°。路堑测试段的地基土层分布与物理力学参数如表 1所示。

图 3 路堑测试段截面及测点布置示意图

Figure 3. Arrangement of measuring points for field tests on cutting section

下载: 全尺寸图片幻灯片

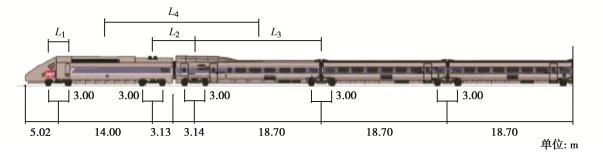
表 1 路堑测试段土层参数

Table 1. Mechanics parameters for cutting

土层	厚度/m	弹性模量E/MPa	泊松比μ	阻尼比ξ	密度ρ/(kg·m^-3)	剪切波速V_S/(m·s^-1)
道砟层	0.30	150.00	0.30	0.030	1700.0	184.21
底砟层	0.20	250.00	0.30	0.030	1900.0	224.96
①₁粉土	1.35	108.95	0.33	0.077	1600.0	160.00
①₂粉土	1.35	124.45	0.33	0.070	1600.0	171.00
②₁砂土	3.10	256.60	0.29	0.031	2000.0	223.00
②₂砂土	3.10	348.82	0.29	0.050	2000.0	260.00
注：表中土层厚度从道床底面算起，道床底面以上7.2 m厚的土层同①₁。

下载: 导出CSV

| 显示表格

列车荷载由TGV高速列车提供，列车由两端各一节动力车厢和中间6节客运车厢组成，其几何尺寸、物理参数分别如图 4和表 2所示。实测时，TGV列车以294.7 km/h的速度通过路堑测试段。

图 4 TGV高速列车示意图

Figure 4. Configuration for TGV high-speed train

下载: 全尺寸图片幻灯片

表 2 TGV高速列车参数

Table 2. Parameters of TGV high-speed train

项目	头（尾）车	中间车
车身质量/kg	55790.00	24000.00
转向架质量/kg	2380.00	3040.00
轮对质量/kg	2048.00	2003.00
一级悬挂刚度/(MN·m^-1)	2.45	1.40
一级悬挂阻尼/(kN·s·m^-1)	20.00	120.00
二级悬挂刚度/(MN·m^-1)	2.45	0.45
二级悬挂阻尼/(kN·s·m^-1)	40.00	40.00

下载: 导出CSV

| 显示表格

1.2 路堑测试段地面振动时频特性

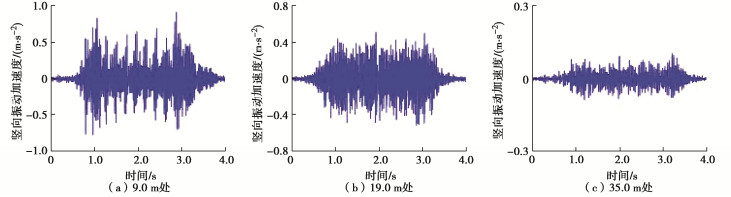
路堑测试段与轨道不同间距处的地面竖向振动加速度时程曲线如图 5所示。由图可知，距轨道较近处，可从时程曲线中清晰地分辨出由列车轮对引起的一系列周期性分布的振动加速度峰值。距路堑段轨道9.0 m处，头（尾）车引起的地面振动幅值略大于中间车，这主要是由于头（尾）车质量大于中间车所致（表 2）。随测点与轨道间距增加，列车运行引起的地面振动幅值逐渐减小，测点与轨道距离≥19.0 m后，列车轮对的周期性激励作用逐渐模糊。此外，距轨道较远处，中间车引起的地面振动幅值略大于头（尾）车，这主要是由中间车相邻转向架轮对引起的振动叠加效应所致。

图 5 路堑测试段测点与轨道不同距离处地面竖向振动加速度时程曲线

Figure 5. Time histories of vertical ground vibration accelerations of measuring points at various distances from cutting track

下载: 全尺寸图片幻灯片

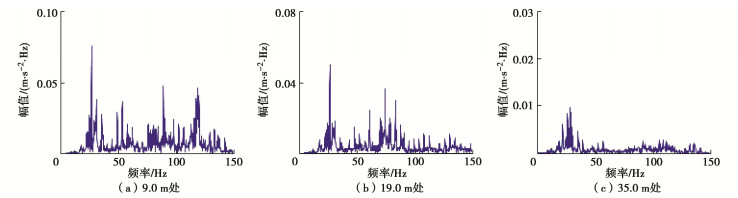
利用Fourier变换对地面振动时程进行处理，得到竖向振动加速度频谱图（图 6）。从图中可知，近轨道处的地面振动频率成分较为丰富，且以20.0~90.0 Hz频段为主。随测点与轨道距离增加，地面振动的中高频成分迅速衰减，而40.0 Hz以下频段的振动衰减速度较慢，测点与轨道距离≥35.0 m后路堑段地面振动主要集中在20.0~40.0 Hz之间。此外，高铁荷载下路堑段地面振动1阶主频随与轨道距离的增加基本维持在26.8 Hz左右，接近列车以294.7 km/h运行条件下的荷载基频（f₁=c/L₁=27.3 Hz，图 4，L₁=3.0 m）^[5]。

图 6 路堑测试段测点与轨道不同距离处地面竖向振动加速度频谱图

Figure 6. Frequency spectra of vertical ground vibration accelerations of measuring points at various distances from cutting track

下载: 全尺寸图片幻灯片

1.3 路堑测试段地面振动衰减特性

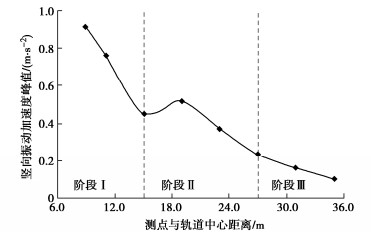
高铁荷载下路堑测试段地面竖向振动加速度峰值随测点与轨道距离增加的衰减曲线如图 7所示。从图 7分析可知，高铁荷载下路堑段地面环境振动随测点与轨道距离增加的衰减过程大致可分为3个阶段。阶段Ⅰ：距轨道9.0~15.0 m范围内，路堑段地面竖向振动加速度峰值迅速衰减，距轨道15.0 m处的地面振动峰值相较于距轨道9.0 m处减小了50.2%，称为“快速衰减”阶段。阶段Ⅱ：距轨道15.0~27.0 m范围内，路堑段地面竖向振动加速度峰值的衰减速度略小于距轨道15.0 m范围内，称为“较快衰减”阶段。阶段Ⅲ：地面竖向振动加速度峰值的衰减速率随测点与轨道距离增加进一步减缓，称为“缓慢衰减”阶段。此外，从图 7中可以看出，高铁荷载下路堑测试段地面振动峰值在堑顶处（距轨道19.0 m处）有较为明显的振动放大现象，这主要是由于瑞利波在堑顶处发生绕射所致^[6]。

图 7 路堑段地面竖向振动加速度峰值随测点与轨道距离的衰减曲线

Figure 7. Attenuation curves for peak ground accelerations with distance away from cutting track

下载: 全尺寸图片幻灯片

2. 2.5维有限元模型的建立与验证

2.5维有限元法通过在列车运行方向上进行波数展开，并对时间t进行Fourier变换，将3维动力问题转换为频域-波数域内的问题进行求解，再对结果进行Fourier逆变换得到时域-空间域内的解答。图 8为本文建立的路堑段2.5维有限元模型，记x方向为列车运行方向，z方向为竖直方向，y方向为水平面内垂直轨道方向，定义对时间t和坐标x的双重Fourier变换如式(1a)所示，对应的逆变换如式(1b)所示。

$\tilde {\bar{u}} ({\xi _x},y,z,\omega ) = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {u(x,y,z,t){{\text{e}}^{{\text{i}}{\xi _x}x}}{{\text{e}}^{ - {\text{i}}\omega t}}{\text{d}}x{\text{d}}t} } \text{，}$

(1a)

$u(x,y,z,t) = \frac{1}{{4{{\rm{\mathsf{π}}}^2}}}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\tilde {\bar{u}}({\xi _x},y,z,\omega ){{\text{e}}^{ - {\text{i}}{\xi _x}x}}{{\text{e}}^{{\text{i}}\omega t}}{\text{d}}{\xi _x}{\text{d}}\omega } } \text{，}$

(1b)

图 8 高铁路堑段2.5维有限元计算模型示意图

Figure 8. Schematic diagram for 2.5D finite element model

下载: 全尺寸图片幻灯片

式中：上标“-”和“~”分别用于表示频域和波数域内的量； $\omega$ 为圆频率； ${\xi _x}$ 为x方向上的波数。

2.1 轨道模型与列车荷载

既有研究表明^[7]，是否考虑钢轨下各部分耦合对列车荷载下地面振动计算结果的影响较小，故本文假定轨道结构在列车荷载下发生整体变形，并将其简化为铺设在路基上的Euler梁，轨道梁在频域-波数域内的动力方程如下：

$(EI\xi _x^4 - m{\omega ^2}){\tilde {\bar{u}}_{\text{r}}} = {\tilde {\bar{f}}_{\text{T}}}({\xi _x},\omega ) + \tilde {\bar{p}}({\xi _x},\omega ) \text{，}$

(2)

式中：EI为轨道结构弯曲刚度； ${u_{\text{r}}}$ 为振动位移；m为轨道结构的综合质量； ${\tilde {\bar{f}}_{\text{T}}}$ 为轨道与路基间的相互作用力； $\tilde {\bar{p}}$ 为列车荷载。

采用连续轴重荷载模拟列车荷载^[1]，其频域-波数域内的表达式为：

$\tilde {\bar{P}}({\xi _x},\omega ) = \sum\limits_{n = 1}^N {\frac{{2{\rm{\mathsf{π}}} }}{c}\delta \left( {{\xi _x} - \frac{{\omega - {\omega _0}}}{c}} \right)} {\chi _n}({\xi _x}) \text{，}$

(3)

式中： ${\chi _n}({\xi _x}) = {p_n}$ $\left[ {{{\text{e}}^{ - {\text{i}}{\xi _x}\sum\limits_{m = 0}^{n - 1} {{L_m}} }} + {{\text{e}}^{ - {\text{i}}{\xi _x}(\sum\limits_{m = 0}^{n - 1} {{L_m}} + a)}} + } \right.$ $\left. {{{\text{e}}^{ - {\text{i}}{\xi _x}(\sum\limits_{m = 0}^{n - 1} {{L_m}} + a + b)}} + {{\text{e}}^{ - {\text{i}}{\xi _x}(\sum\limits_{m = 0}^{n - 1} {{L_m}} + 2a + b)}}} \right]$ ；N为列车车厢数量； ${p_n}$ 为列车第n节车厢的单个轮对荷载； ${L_m}$ （m=1, 2, 3, …）为第m节车厢的长度， ${L_0}$ 为第1节车厢第1组轮对至坐标原点的距离；a为单个转向架下2个轮对间的距离；b为同一车厢下2个转向架的间距。

2.2 路堑段2.5维有限元模型

Xia等^[8]研究指出，轨道交通荷载引起的土体应变量一般为10^-5或更小量级，产生的振动波属于弹性波。因此，本文将地基土体视为黏弹性介质，其本构方程如下：

${\sigma _{ij}} = 2{\mu _d}{\varepsilon _{ij}} + {\lambda _d}{\delta _{ij}}e \text{，}$

(4)

式中： ${\sigma _{ij}}$ 为应力张量； ${\varepsilon _{ij}} = ({u_{i,j}} + {u_{j,i}})/2$ ，为应变张量； ${\delta _{ij}}$ 为Dirac函数； $e$ 为体应变；i，j代表空间坐标系x，y和z轴； ${\lambda _d}$ 和 ${\mu _{\text{d}}}$ 为考虑材料阻尼的Lamé常数，由式（5）算得。

${\lambda }_{\text{d}}=\lambda （1+2\beta \text{i}） \text{；} {\mu }_{\text{d}}=\mu （1+2\beta \text{i}）。$

(5)

式中： $\lambda = E\nu /[(1 + \nu )(1 - 2\nu )]$ ； $\mu = E/2(1 + \nu )$ ；E为弹性模量； $\nu$ 为泊松比；β为阻尼比；i为虚数单位。

将本构方程代入动力方程 ${\sigma _{ij,j}} + {F_i} = \rho {\ddot u_i}$ ，得到以位移表示的运动方程：

${\mu _{\text{d}}}{u_{i,jj}} + ({\lambda _{\text{d}}} + {\mu _{\text{d}}}){u_{j,ji}} = \rho {\ddot u_i} \text{，}$

(6)

式中，ρ为密度，上标“··”表示对时间的2阶导数。

利用式（1a）对上式进行双重Fourier变换，结合应力边界条件 ${\tilde \sigma _{ij}}{n_j} - {\tilde f_i} = 0$ ，基于Galerkin法，并采用8节点等参单元进行离散，整理得到频域-波数域内的有限元控制方程，其矩阵形式如下：

$\left(\tilde{\bar{\boldsymbol{K}}}-\omega^2 \boldsymbol{M}\right) \tilde{\bar{\boldsymbol{U}}}=\tilde{\bar{\boldsymbol{F}}}\text{，}$

(7)

式中： $\tilde{\bar{\boldsymbol{K}}}$ 为刚度矩阵； ${{\boldsymbol{M}}}$ 为质量矩阵； $\tilde{\bar{\boldsymbol{U}}}$ 为位移列阵； $\tilde{\bar{\boldsymbol{F}}}$ 为等效节点力列阵。

为消除模型截断边界处的反射波对计算结果造成影响，基于笔者先前的研究^[1]，采用无限元边界作为模型的边界条件。此外，高速铁路地面环境振动特性研究中通常仅考虑单次列车荷载作用，不同于列车循环荷载，单次列车荷载引起的土体固结沉降可忽略不计^[1]。因此，本文所建立路堑段2.5维有限元模型中各部分之间采用共节点的方式链接。

2.3 数值方法验证

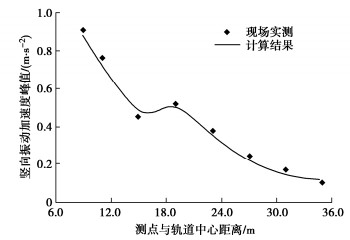
为验证本文2.5维有限元方法的正确性，基于前文TGV列车（表 2、图 4）和路堑测试段参数（图 3、表 1），建立高铁荷载下路堑段2.5维有限元模型。考虑车速294.7 km/h，路堑段地面竖向振动加速度峰值随测点与轨道距离衰减的实测与计算结果如图 9所示。由图可知，本文建立的2.5维有限元模型能较好地反映出高铁荷载下地面振动随测点与轨道距离的衰减趋势，与实测值相比，计算误差不超过13%，满足精度要求，验证了模型的正确性和可靠性。

图 9 地面振动峰值随与轨道距离变化的实测与计算结果

Figure 9. Measured and calculated results of variations of peak ground vibration acceleration

下载: 全尺寸图片幻灯片

3. 路堑参数对地面振动的影响

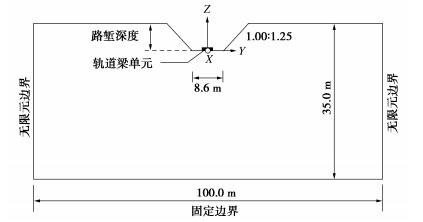
考虑单线轨道，建立如所示的路堑段2.5维有限元模型，模型宽100.0 m、深35.0 m，路堑底面宽度为8.6 m。选取CRTS II型板式无砟轨道^[5]，并模拟为铺设在路基上的Euler梁。地基土体的弹性模量E、泊松比 $\nu$ 、阻尼比ξ、密度ρ和瑞利波速v_R分别为64.0 MPa，0.38，0.05，1850.0 kg/m³，382.68 km/h。综合考虑计算效率与精度，选取6节编组的CRH380 AL型动车组作为列车荷载^[5]，分析路堑设计参数对地面环境振动特性的影响。

3.1 路堑深度的影响

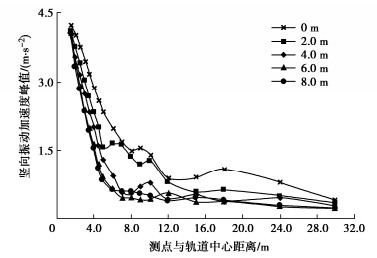
考虑车速为380.0 km/h，路堑边坡坡度为1.00∶1.25，不同路堑深度条件下（2.0，4.0，6.0，8.0 m）地面竖向振动加速度峰值随测点与轨道中心距离的变化曲线如图 10所示，并增设0.0 m的无路堑工况进行对比分析。由图 10可知，不同路堑深度条件下的地面振动均小于无路堑工况（0.0 m）。既有研究指出近轨道处的地面振动衰减由几何阻尼主导^[9]，路堑的存在增加了近轨道处的几何阻尼，从而减小了高铁运行引起的地面振动加速度峰值，且减振效果随路堑深度增加逐渐增强。当路堑深度≥6.0 m时，继续增加路堑深度将难以进一步有效减小地面环境振动。此外，由于堑顶处的瑞利波绕射^[6]，不同路堑深度条件下（2.0，4.0，6.0，8.0 m）其堑顶处附近（分别距轨道中心6.8，9.3，11.8，14.3 m）均可观察到地面振动的局部放大现象。

图 10 不同路堑深度下地面振动随测点与轨道中心距离的变化曲线

Figure 10. Variation of ground vibration with different cutting depths

下载: 全尺寸图片幻灯片

3.2 路堑边坡坡度的影响

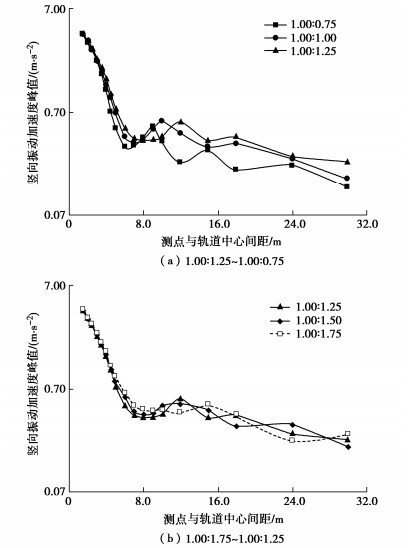
我国高速铁路路堑边坡的设计坡度通常介于1.00∶1.75~1.00∶0.75之间^[10]。考虑路堑深度为6.0 m，图 11为车速380.0 km/h时不同路堑边坡坡度条件下（1.00∶1.75~1.00∶0.75）地面竖向振动加速度峰值随测点与轨道中心距离的衰减曲线。由图 11（a）可知，当路堑边坡坡度在1.00∶1.25~1.00∶0.75（38.7°~53.1°）范围内时，地面环境振动随路堑边坡坡度的增大而减小。这主要与瑞利波在堑顶处的绕射程度有关，既有研究指出^[6]，当路堑边坡坡度在40.0°~60.0°范围内时，堑顶处瑞利波的绕射随坡度增大而减小，从而降低了高铁运行引起的路堑段地面振动。此外，随着路堑边坡坡度的进一步减小（图 11（b）），坡度变化对地面振动加速度峰值的影响较小。因此，实际工程中在保证路堑边坡安全稳定的前提下，较陡的路堑边坡更有利于减小高铁荷载下路堑段的地面环境振动。

图 11 不同路堑边坡坡度下地面振动随测点与轨道中心距离的变化曲线

Figure 11. Variation of ground vibration with different cutting slope angles

下载: 全尺寸图片幻灯片

4. 结论

（1）列车轴重对路堑段近轨道处的地面振动幅值有重要影响，随测点与轨道距离的增加，地面振动幅值逐渐衰减，中间车相邻转向架轮对引起的叠加效应对地面振动幅值的影响逐渐增强。

（2）路堑段地面振动随测点与轨道距离的衰减过程大致可分为3个阶段，且堑顶处有较明显的振动局部放大现象。中高频成分振动的衰减速率明显大于其他频段，且振动1阶主频由列车荷载的基频（f₁=c/L₁）主导。

（3）高铁荷载下地面振动随路堑深度增加而减小。当路堑深度超过某一限值（本文为6.0 m）时，继续增加路堑深度难以进一步有效降低地面环境振动。

（4）路堑段地面振动随路堑边坡坡度的增大而减小。在保证路堑边坡稳定性的前提下，较陡的路堑边坡更有利于减小高铁运行引起的地面环境振动。

致谢: 感谢D. P. Connolly教授在高速铁路地面振动实测研究方面对本文的帮助。

图 1 路堑测试段

Figure 1. Test sections for field cutting

下载: 全尺寸图片幻灯片

图 2 SM-6型振动检波仪

Figure 2. SM-6 geophones for measurement

下载: 全尺寸图片幻灯片

图 3 路堑测试段截面及测点布置示意图

Figure 3. Arrangement of measuring points for field tests on cutting section

下载: 全尺寸图片幻灯片

图 4 TGV高速列车示意图

Figure 4. Configuration for TGV high-speed train

下载: 全尺寸图片幻灯片

图 5 路堑测试段测点与轨道不同距离处地面竖向振动加速度时程曲线

Figure 5. Time histories of vertical ground vibration accelerations of measuring points at various distances from cutting track

下载: 全尺寸图片幻灯片

图 6 路堑测试段测点与轨道不同距离处地面竖向振动加速度频谱图

Figure 6. Frequency spectra of vertical ground vibration accelerations of measuring points at various distances from cutting track

下载: 全尺寸图片幻灯片

图 7 路堑段地面竖向振动加速度峰值随测点与轨道距离的衰减曲线

Figure 7. Attenuation curves for peak ground accelerations with distance away from cutting track

下载: 全尺寸图片幻灯片

图 8 高铁路堑段2.5维有限元计算模型示意图

Figure 8. Schematic diagram for 2.5D finite element model

下载: 全尺寸图片幻灯片

图 9 地面振动峰值随与轨道距离变化的实测与计算结果

Figure 9. Measured and calculated results of variations of peak ground vibration acceleration

下载: 全尺寸图片幻灯片

图 10 不同路堑深度下地面振动随测点与轨道中心距离的变化曲线

Figure 10. Variation of ground vibration with different cutting depths

下载: 全尺寸图片幻灯片

图 11 不同路堑边坡坡度下地面振动随测点与轨道中心距离的变化曲线

Figure 11. Variation of ground vibration with different cutting slope angles

下载: 全尺寸图片幻灯片

表 1 路堑测试段土层参数

Table 1 Mechanics parameters for cutting

土层	厚度/m	弹性模量E/MPa	泊松比μ	阻尼比ξ	密度ρ/(kg·m^-3)	剪切波速V_S/(m·s^-1)
道砟层	0.30	150.00	0.30	0.030	1700.0	184.21
底砟层	0.20	250.00	0.30	0.030	1900.0	224.96
①₁粉土	1.35	108.95	0.33	0.077	1600.0	160.00
①₂粉土	1.35	124.45	0.33	0.070	1600.0	171.00
②₁砂土	3.10	256.60	0.29	0.031	2000.0	223.00
②₂砂土	3.10	348.82	0.29	0.050	2000.0	260.00
注：表中土层厚度从道床底面算起，道床底面以上7.2 m厚的土层同①₁。

下载: 导出CSV

表 2 TGV高速列车参数

Table 2 Parameters of TGV high-speed train

项目	头（尾）车	中间车
车身质量/kg	55790.00	24000.00
转向架质量/kg	2380.00	3040.00
轮对质量/kg	2048.00	2003.00
一级悬挂刚度/(MN·m^-1)	2.45	1.40
一级悬挂阻尼/(kN·s·m^-1)	20.00	120.00
二级悬挂刚度/(MN·m^-1)	2.45	0.45
二级悬挂阻尼/(kN·s·m^-1)	40.00	40.00

下载: 导出CSV

参考文献(10)

[1]	毕俊伟, 高广运, 耿建龙. 高铁荷载下横观各向同性CFG桩桩土复合路基减振特性研究[J]. 振动与冲击, 2023, 42(4): 116-125. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202304014.htm BI Junwei, GAO Guangyun, GENG Jianlong. Vibration mitigation characteristics of CFG pile-supported transversely isotropic subgrade under high-speed train loading[J]. Journal of Vibration and Shock, 2023, 42(4): 116-125. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202304014.htm
[2]	THOMPSON D J, KOUROUSSIS G, NTOTSIOS E. Modelling, simulation and evaluation of ground vibration caused by rail vehicles[J]. Vehicle System Dynamics, 2019, 57(7): 936-983. doi: 10.1080/00423114.2019.1602274
[3]	CONNOLLY D P, KOUROUSSIS G, WOODWARD P K, et al. Field testing and analysis of high speed rail vibrations[J]. Soil Dynamics and Earthquake Engineering, 2014, 67: 102-118. doi: 10.1016/j.soildyn.2014.08.013
[4]	KOUROUSSIS G, CONNOLLY D P, OLIVIER B, et al. Railway cuttings and embankments: experimental and numerical studies of ground vibration[J]. The Science of the Total Environment, 2016, 557/558: 110-122. doi: 10.1016/j.scitotenv.2016.03.016
[5]	ZHAI W M, WEI K, SONG X L, et al. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track[J]. Soil Dynamics and Earthquake Engineering, 2015, 72: 24-36. doi: 10.1016/j.soildyn.2015.02.002
[6]	PILANT W L, KNOPOFF L, SCHWAB F. Transmission and reflection of surface waves at a corner: 3 Rayleigh waves (experimental)[J]. Journal of Geophysical Research, 1964, 69(2): 291-297. doi: 10.1029/JZ069i002p00291
[7]	KOUROUSSIS G, VERLINDEN O. Prediction of railway ground vibrations: accuracy of a coupled lumped mass model for representing the track/soil interaction[J]. Soil Dynamics and Earthquake Engineering, 2015, 69: 220-226. doi: 10.1016/j.soildyn.2014.11.007
[8]	XIA H, CAO Y M, DE ROECK G. Theoretical modeling and characteristic analysis of moving-train induced ground vibrations[J]. Journal of Sound and Vibration, 2010, 329: 819-832. doi: 10.1016/j.jsv.2009.10.007
[9]	GAO G Y, SONG J, YANG J. Identifying boundary between near field and far field in ground vibration caused by surface loading[J]. Journal of Central South University, 2014, 21(8): 3284-3294. doi: 10.1007/s11771-014-2301-0
[10]	国家铁路局. 铁路路基设计规范: TB 10001—2016[S]. 北京: 中国铁道出版社, 2017. National Railway Administration of the People's Republic of China. Code for Design of Earthworks and Track Bed for Railway: TB 10001—2016[S]. Beijing: China Railway Publishing House, 2017. (in Chinese)