重塑超固结饱和黏土蠕变试验与蠕变模型

胡敏云; 肖斌; 陆雨珂; 张雨惠; 张勇

doi:10.11779/CJGE2023S10040

重塑超固结饱和黏土蠕变试验与蠕变模型 English Version

胡敏云^{1, 2,},
肖斌^{1, 3},
陆雨珂⁴,
张雨惠¹,
张勇^1, ,

1.
浙江工业大学土木工程学院, 浙江杭州 310023
2.
中国水利水电科学研究院, 北京 100048
3.
浙江同济科技职业学院, 浙江杭州 311231
4.
浙江工业大学工程设计集团有限公司, 浙江杭州 310014

基金项目:

国家自然科学基金项目 51878616

浙江省基础公益研究计划项目 LHY19E090002

详细信息

作者简介:
胡敏云(1970—)，女，博士，教授，主要从事特殊土力学特性与模型方面的研究工作。E-mail: humy@iwhr.com

通讯作者:
张勇, E-mail: zhangyong@zjut.edu.cn

中图分类号: TU432
计量
- 文章访问数: 223
- HTML全文浏览量: 39
- PDF下载量: 72
出版历程
- 收稿日期: 2023-07-04
- 网络出版日期: 2023-11-23
- 刊出日期: 2023-10-31

Creep tests and creep model for reconstituted over-consolidated saturated clay

HU Minyun^{1, 2,},
XIAO Bin^{1, 3},
LU Yuke⁴,
ZHANG Yuhui¹,
ZHANG Yong^1, ,

1.
College of Civil Engineering, Zhejiang University of Technology, Hangzhou 310023, China
2.
China Institute of Water Resources and Hydropowver Research, Beijing 100048, China
3.
Zhejiang Tongji Vocational College of Science and Technology, Hangzhou 311231, China
4.
Zhejiang University of Technology Engineering Design Group., Ltd., Hangzhou 310014, China

摘要

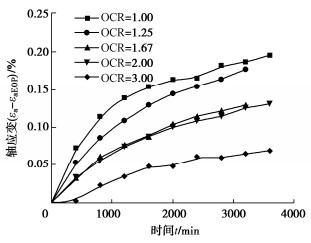
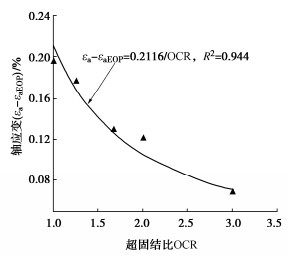
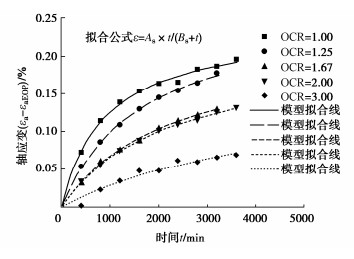
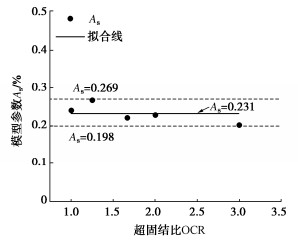
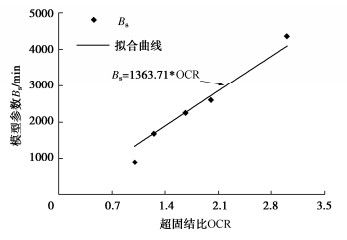
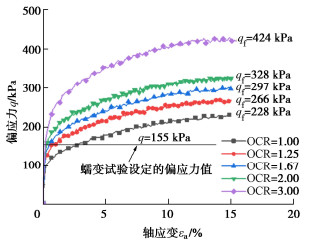
摘要: 采取杭州地区黏土制备重塑超固结土样（OCR=1.00，1.25，1.67，2.00，3.00）进行三轴剪切蠕变试验，研究超固结饱和黏土的时间变形特性和蠕变模型，对模型参数取值进行了分析。结果表明，重塑超固结饱和黏土的应力应变曲线具有应变硬化特征，在恒定偏应力下土样的时间变形曲线具有双曲线特征；超固结比越大，施加偏应力初始阶段试样中产生的超静孔压越小，试样变形进入蠕变阶段的时间越早，且在一定时间内试样的蠕变量发展越小。基于“孔压消散法”确定了超固结土的蠕变起始时间，采用双曲线蠕变模型可以高度拟合超固结饱和黏土剪切蠕变发展规律，曲线拟合分析表明：在相同的偏应力下，不同超固结比试样的最终蠕变量大致相等，但是超固结比越大时，土样蠕变发展越缓慢，表现为双曲线蠕变模型参数A_s在超固结比变化时几乎保持为常量，参数B_s则随超固结比的增大近似呈线性增长。
- 超固结饱和黏土 /
- 三轴蠕变试验 /
- 蠕变模型 /
- 模型参数
Abstract: The triaxial shear creep tests are carried out on the reconstituted over-consolidated clay samples (OCR=1.00, 1.25, 1.67, 2.00, 3.00) from Hangzhou, China. The time-dependent deformation characteristics and creep model for the over-consolidated saturated clay are studied, and the values of model parameters are analyzed. The results show that the stress-strain curve of the reconstituted over-consolidated saturated clay has strain-hardening characteristics. The time-deformation curves of the over-consolidated clays under constant deviator stress are of hyperbolic characteristics. The larger the over-consolidation ratio, the smaller the excess pore pressure generated at the initial stage of the deviator stress application, the earlier the creep stage starts, and the smaller the creep evolution of the sample within a certain time. Based on the "pore pressure dissipation method", the t_EOP of the over-consolidated clay is determined. The hyperbolic creep model can highly fit the shear creep curves of the over-consolidated saturated clay. The curve fitting analysis shows that under the same deviator stress, the final creep values of the samples with different over-consolidation ratios are roughly equal. However, the larger the over-consolidation ratio, the slower the creep development of clay. The hyperbolic creep model parameter A_s almost remains constant when the over-consolidation ratio changes, while the parameter B_s approximately linearly increases with the increase of the over-consolidation ratio.
- over-consolidated saturated clay /
- triaxial creep test /
- creep model /
- model parameter

HTML全文

图 1 不同超固结比试样的应力应变曲线

Figure 1. Stress-strain curves for over-consolidated clay in CU test

下载: 全尺寸图片幻灯片

图 2 偏应力加载过程响应曲线

Figure 2. Response curves during deviatoric stress loading process

下载: 全尺寸图片幻灯片

图 3 不同超固结比试样的蠕变曲线

Figure 3. Creep deformations of samples with different over-consolidation ratios

下载: 全尺寸图片幻灯片

图 4 蠕变量与超固结比的关系（t=4320 min）

Figure 4. Relationship between over-consolidation ratio and creep deformation of samples

下载: 全尺寸图片幻灯片

图 5 超固结土双曲线蠕变模型拟合曲线

Figure 5. Fitting of shear creep curves of samples with different over-consolidation ratios

下载: 全尺寸图片幻灯片

图 6 模型参数A_s与超固结比OCR关系

Figure 6. Relationship between model parameters A_s and OCR

下载: 全尺寸图片幻灯片

图 7 模型参数B_s与超固结比OCR关系

Figure 7. Relationship between model parameters B_s and OCR

下载: 全尺寸图片幻灯片

表 1 原状土的基本物理性质指标

Table 1 Index parameters of intact soil samples

取土深度/m	G_s	含水率w/kPa	天然密度 $\rho$ /(g·cm^-3)	液限w_L/%	塑限 w_P/%	塑性指数I_p	液性指数I_L
15~25	2.72	36.21	1.87	40.27	20.26	20.01	0.79

下载: 导出CSV

表 2 超固结土三轴试验方案

Table 2 Test schemes of over-consolidated ratio

试样编号	OCR	σ'_c/kPa	σ'₀/kPa	q/kPa	K
①	1.00	200	200	155	0.68
②	1.25	250	200	155	0.58
③	1.67	334	200	155	0.52
④	2.00	400	200	155	0.47
⑤	3.00	600	200	155	0.37
注：σ'_c为试样先期有效固结压力；σ '₀为初始有效围压；q为偏应力，q=σ₁-σ₃；K为蠕变偏应力和剪切强度q_f的比值。

下载: 导出CSV

表 3 剪切蠕变双曲线模型参数

Table 3 Fitting parameters of hyperbolic creep model

超固结比	偏应力/ kPa	A_s/%	B_s/min	相关系数R²/%
1.00	155	0.2397	904.33	99.64
1.25	155	0.2659	1685.06	99.89
1.67	155	0.2202	2248.02	99.78
2.00	155	0.2279	2602.10	99.74
3.00	155	0.2011	4352.29	95.64

下载: 导出CSV

参考文献(12)

[1]	王者超, 乔丽苹, 李术才. 荷载水平和孔隙比对土次压缩性质影响研究[J]. 土木工程学报, 2013, 46(1): 112-118. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301013.htm WANG Zhechao, QIAO Liping, LI Shucai. Influences of load level and void ratio on secondary compressibility of soil[J]. China Civil Engineering Journal, 2013, 46(1): 112-118. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301013.htm
[2]	曾玲玲, 洪振舜, 刘松玉, 等. 重塑黏土次固结性状的变化规律与定量评价[J]. 岩土工程学报, 2012, 34(8): 1496-1500. http://www.cgejournal.com/cn/article/id/14669 ZENG Lingling, HONG Zhenshun, LIU Songyu, et al. Variation law and quantitative evaluation of secondary consolidation behavior for remolded clays[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1496-1500. (in Chinese) http://www.cgejournal.com/cn/article/id/14669
[3]	YIN J H. Non-linear creep of soils in oedometer tests[J]. Géotechnique, 1999, 49(5): 699-707. doi: 10.1680/geot.1999.49.5.699
[4]	SINGH A, MITCHELL J K. General stress-strain-time function for soils[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(1): 21-46. doi: 10.1061/JSFEAQ.0001084
[5]	MESRI G, FEBRES-CORDERO E, SHIELDS D R, et al. Discussion: shear-stress-strain time behaviour of clays[J]. Géotechnique, 1982, 32(4): 407-411. doi: 10.1680/geot.1982.32.4.407
[6]	XIAO B, HU M Y, ZHOU P J, et al. Creep behavior of saturated clay in triaxial test and a hyperbolic model[J]. Geofluids, 2021: 1-12.
[7]	高彦斌. 超固结土一维次压缩特性实验研究[C]// 2004年度上海市土力学与岩土工程学术年会. 上海, 2004. Yanbin. Experimental study on one-dimensional compression characteristics of over-consolidated soil[C]// 2004 Annual Conference of Soil mechanics and Geotechnical Engineering in Shanghai. Shanghai, 2004. (in Chinese))
[8]	韩剑, 姚仰平, 尹振宇. 超固结度对超固结饱和黏土不排水蠕变特性的影响研究[J]. 岩土工程学报, 2018, 40(3): 426-430. doi: 10.11779/CJGE201803005 HAN Jian, YAO Yangping, YIN Zhenyu. Influences of overconsolidation ratio on undrained creep behavior of overconsolidated saturated clay[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 426-430. (in Chinese) doi: 10.11779/CJGE201803005
[9]	YIN J H, ZHU J G, GRAHAM J. A new elastic viscoplastic model for time-dependent behaviour of normally and overconsolidated clays: theory and verification[J]. Canadian Geotechnical Journal, 2002, 39(1): 157-173. doi: 10.1139/t01-074
[10]	胡亚元, 杨平, 余启致. 超固结土次固结系数的时间效应[J]. 中国公路学报, 2016, 29(9): 29-37. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201609003.htm HU Yayuan, YANG Ping, YU Qizhi. Time effect of secondary consolidation coefficient of over-consolidated soil[J]. China Journal of Highway and Transport, 2016, 29(9): 29-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201609003.htm
[11]	土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Soil Test Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[12]	肖斌. 重塑粉质黏土的蠕变特性及蠕变模型研究[D]. 杭州: 浙江工业大学, 2017. XIAO Bin. Study on Creep Characteristics and Creep Model of Reconstituted Silty Clay[D]. Hangzhou: Zhejiang University of Technology, 2017. (in Chinese)