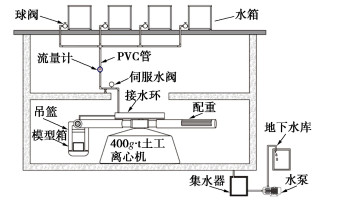
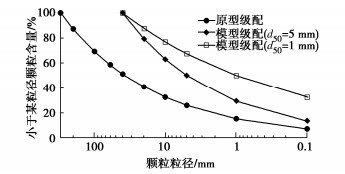
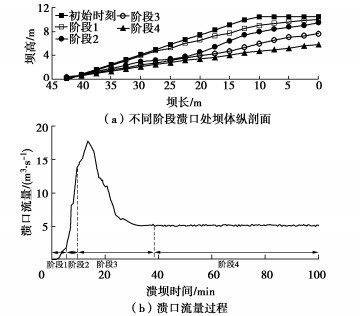
Centrifugal model tests on overtopping-induced breaching of landslide dams
-
摘要: 基于南京水利科学研究院400g·t溃坝离心模型试验系统,利用其高速旋转产生的超重力场的“时空放大”效应,开展离心模型试验研究了堰塞坝漫顶溃决时的溃口演化规律和溃决机理。首次通过离心模型试验研究了坝高、下游坡比、坝料级配对堰塞坝漫顶溃坝过程的影响。试验结果表明:堰塞坝漫顶溃坝过程可划分为表层冲刷、溯源冲蚀、沿程侵蚀和溃口稳定4个阶段;溃口峰值流量对坝高最为敏感,平均粒径次之;达峰时间主要受下游坡比影响,溃坝后相对残余坝高主要受平均粒径影响。Abstract: Based on the 400 g·t centrifugal model test system for dam breaching of Nanjing Hydraulic Research Institute, the centrifugal model tests are carried out to study the breach evolution law and breach mechanism of overtopping-induced breaching of landslide dams by using the "time-space amplification" effect of supergravity field generated by high-speed rotation. The effects of dam height, downstream slope ratio and dam material gradation on the overtopping failure process of landslide dams are investigated by the centrifugal model tests for the first time. The test results show that the breach process of a landslide dam can be divided into four stages, which are surface erosion, retrogressive erosion, erosion along the breach channel, and breach stabilization. Moreover, the peak breach flow is most sensitive to the dam height, followed by the mean particle size. The time to the peak is mainly affected by the downstream slope ratio, and the relative residual dam height after breaching is primarily susceptible to the mean particle size.
-
Keywords:
- landslide dam /
- overtopping /
- breach process /
- breach mechanism /
- centrifugal model test
-
0. 引言
管桩因其承载力高、施工便捷、运输方便等优势被广泛应用于各类构筑物基础的建设中[1]。开口管桩在沉桩过程中,桩端部分土体会被挤入桩内形成土塞。由于桩体尺寸、沉桩方式、土体性质等因素的影响,开口管桩会呈现完全闭塞,部分闭塞和完全非闭塞的状态[2]。土塞状态的改变会对管桩沉桩阻力和承载特性产生极大影响[3-4]。
目前,对开口管桩中土塞效应的研究主要包括理论、试验和数值模拟3个方面。在理论研究方面,Randolph等[5]基于土塞单元的静力平衡方程,求解了土塞中有效应力分布特征,建立了考虑土塞参数和加载速率的土塞承载力计算方程。郑俊杰等[6]基于圆孔扩张理论分析了管桩沉桩过程中土塞效应和挤土效应的相互作用特性。刘润等[7]考虑动力打桩过程中土塞所受的惯性力作用,提出了考虑惯性力影响的土塞拟静力平衡分析法。上述模型为土塞与管桩的相互作用分析提供了重要理论参考,但本质上仍是基于静力平衡方程,无法真实反映土塞与管桩的真实作用特征。试验是揭示桩土相互作用机理最可靠的手段[8-9]。然而由于管桩特殊的结构形式与施工扰动,无法通过应变片等手段对桩身各部分阻力进行区分,因此,多是在闭口管桩阻力计算公式的基础上引入经验系数来反映开口管桩的承载特性[9-10]。随着内外双壁管桩[9, 11]的出现,对土塞阻力的测量成为可能,这也进一步加深了土塞效应对管桩沉桩阻力与承载特性影响的认识;此外,粒子图像测速技术(particle image velocimetry)[12]、CT扫描技术[13]等新技术也被成功应用于土塞形成与演化机理的研究中。然而,上述技术手段成本高、尺寸受限,且难以模拟不同工况下,因此需要更为高效合理的手段对试验结果进行补充。近年来,考虑颗粒散体特性的离散元数值模拟方法被广泛应用于土塞效应的研究中[14-15]。周健等[14]基于半桩模型试验和离散元模拟,对砂土地基中静压管桩的沉桩过程进行了模拟,将土塞形成过程分为:初始阶段,主动拱形成阶段,被动拱形成阶段。Li等[15]基于离散元方法,分析了不同沉桩方式下土塞的演化过程,建立了桩侧土-管桩-土塞相互作用模型。上述数值模拟工作极大丰富了对管桩成塞机制的认识,但主要关注于土塞本身的形成与演化机理,土塞效应如何影响管桩的沉桩过程以及承载力发挥仍需深入研究。
本文拟采用离散元方法对砂土地基中静压开口管桩的沉桩与承载全过程进行研究。从宏细观角度出发,基于土体变形特性、土塞参数发展规律、贯入阻力等内容的分析,明确土塞对管桩沉桩阻力和承载特性发挥的影响,建立考虑土塞效应的管桩承载特性计算方法。
1. 数值模型建立
离散元方法的基本原理是将散体颗粒简化为圆盘(二维)或者球(三维),基于牛顿第二定律和接触力-相对位移关系,通过对颗粒间赋予接触参数对散体材料的宏观物理力学行为进行模拟[16-17]。
1.1 模型参数标定
西澳大学(UWA)硅质砂是一种颗粒形状接近亚圆形到压棱角形的商业用砂,其基本物理力学性质已经过系统标定,因此在岩土工程模型试验与数值模拟研究中得到了广泛应用[15, 18]。本文以UWA硅质砂为标定对象开展后续离散元模拟,其基本物理力学性质见表 1。为充分考虑计算效率与模拟准确性,依据实际砂样颗粒集配曲线放大15倍后生成等效的离散砂样模型。
表 1 UWA硅质砂及其等效离散砂样参数Table 1. Properties of UWA superfine sand and its DEM analogue参数 Gs 颗粒尺寸/mm Cu Cc φ′cs/(°) d10 d50 d60 试验值 2.67 0.12 0.18 0.20 1.67 1.020 33 模拟值 2.67 1.80 2.70 3.00 1.67 0.975 32 注:φ′cs为极限状态摩擦角,Cu,Cc分别为不均匀系数和曲率系数。 离散元模型中,土体颗粒通常采用标准的圆形(二维)或球体(三维),难以反映实际颗粒间的咬合与胶结作用,导致颗粒产生过量转动并低估土体强度[15]。为了反映不规则砂样间的接触特征,本文采用滚动阻力线性模型(rolling resistance linear model),通过在颗粒接触间施加扭矩来更好地模拟颗粒接触间的滚动摩擦特性[19-20]。确定颗粒尺寸与接触模型后,开展数值砂样的柔性膜双轴压缩试验,并基于UWA砂样应力-应变关系进行数值模型参数选取及有效性验证,见图 1。可以看出,数值模拟结果与试验结果在峰值强度和残余强度阶段能很好地吻合,基本能反映出中密到密实砂样的剪切特性。本次数值模拟中颗粒参数见表 2。
表 2 离散元模型参数Table 2. Parameters for discrete model地基土样 墙 桩 kn/(N·m-1) ks/(N·m-1) μ γ μr βn βs Md kn/(N·m-1) ks/(N·m-1) μw kn/(N·m-1) ks/(N·m-1) μp 1×108 2×107 0.5 0.1 0.45 0.1 0.1 3 1×1010 1×1010 0 1.5×109 1.5×109 0.5 注:kn,ks分别为法向刚度和剪切刚度;μ为摩擦系数;γ为阻尼比;μr为滚动摩擦系数;βn为法向极限阻尼比;βs为剪切极限阻尼比;Md为黏壶模式;μw为墙摩擦系数;μp为桩摩擦系数。 1.2 地基模型生成
高效地生成均质且应力沿深度均匀分布的地基模型是进行管桩沉桩过程模拟的前提。本文采用周期性单元复制法(periodic cell replication method)[15, 21]进行地基模型的生成。其基本原理是选择一定尺寸的表征单元体(REV)作为地基的基本单元,通过对REV在空间进行组合形成大尺寸的地基模型。由于REV已在相应围压下达到平衡,因此,地基模型在重力作用下能快速达到平衡。
为了提高计算效率并模拟现场情况,本次模拟在10倍重力加速度下开展,生成了如图 2所示的地基模型,其宽约15.6 m,高约13 m,颗粒总数为356976。进一步地,将达到平衡状态的地基土体颗粒接触力链分布情况进行提取并绘制于图 2左侧,可以看出,土体颗粒接触力链基本呈线性分布,且力链粗细随深度的增加而增加,这与实际土体中应力状态分布特征基本相符。为了进一步验证数值模型的有效性,在地基土内不同位置设置测量圆对达到平衡状态时土体参数进行提取,见图 3。可以看出,地基土体应力随深度基本呈线性分布,且孔隙率随深度波动较小,可以认为,生成的地基土体模型分布均匀,且应力状态稳定,能满足后续管桩贯入过程模拟的要求。
1.3 数值试验安排
本次模拟采用墙单元生成3组模型桩(P1,P2,P3),外径D分别为0.5,0.7,1.0 m,壁厚统一设置为10 cm。模型桩沿地基中轴线贯入,贯入深度为6 m。对于直径最大的P3,桩壁距地基模型边缘的距离约为7D,而对于直径最小的P1,其桩径约为35d50,结合数值模型结果可以得出,本次管桩贯入过程模拟的边界效应和尺寸效应可以忽略[20, 22]。
本次模拟中管桩的沉桩过程采用静压的方式实现,宏观贯入速度为2 m/s。沉桩过程中,离散元模型计算时步约为8×10-6 s,对应数值模型中的贯入速度约为1.6×10-4 mm每个dt,与Zhang等[20]和Ciantia等[21]离散元模型中管桩贯入速度接近。图 4展示了P2桩在不同贯入速度时沉桩阻力的发展特征。可以看出,在上述速度范围内,沉桩阻力差异不大。但本模型中,当以4 m/s速度贯入6 m深度时计算时间约为36 h,当以1 m/s速度贯入6 m深度时计算时间约为一周。因此,基于模拟效率与准确性的要求,模拟中管桩沉桩速度定为2 m/s。需要指出的是,由于孔隙水压力模拟的复杂性,模型中并未考虑地下水的影响。
贯入到预定深度后,对模型桩进行卸载并对离散元模型进行循环至稳定,随后开展管桩的承载过程模拟。考虑到管桩承载过程的准静态特性,同样采用位移加载的方式进行管桩承载过程的模拟[23],贯入速度为0.1 m/s,贯入深度50 cm。
2. 管桩沉桩过程模拟结果
2.1 桩周土体变形特征
为了直观分析沉桩过程对桩周土体变形特征的影响,模型桩贯入前对地基土体进行分层染色。图 5展示了模型桩沉桩结束时桩周土体的变形特征。可以看出,管桩沉桩过程对桩周土体产生了显著扰动,且不同尺寸模型桩中出现了不同程度的成塞现象。对于P1,桩周内外侧土体产生了显著剪切,且桩端土体产生了显著扰动,表明P1产生了成塞现象。对于P2,桩内侧土由于桩身的摩擦,形成了上凸的主动拱,而桩端处出现了清晰的下凹被动拱。随着桩径的增大,桩中土塞高度越高,土塞效应也越弱。
为了从细观角度对土塞的形成过程进行分析,选取桩端下部不同深度处(2,4,6 m)颗粒作为标记点,记录管桩沉桩过程中标记点颗粒相对于桩端的位置变化,如图 6。对于P1,随着管桩的贯入,初始时在桩端下2 m的颗粒被挤入桩中,且挤入后相对位置变化量显著减小。对于初始位置在桩端下4 m的颗粒,随着管桩的贯入,颗粒逐渐接近桩端,但并未被挤入桩中,而是在距桩端约1 m位置处出现靠近桩中的运动趋势,随后被挤出桩外,这样表明土塞效应逐渐显现。对于初始位置在桩端下4 m的颗粒,其初始时相对桩端无明显水平位移,随后呈现往桩外运移的趋势。对于P2,颗粒总体的运移特征与P1中相同,且对于初始时在桩端下4 m和6 m的颗粒,出现了更为明显的外-内-外运动轨迹。随着桩径的进一步增大,土塞效应逐渐减弱,颗粒的水平位移减小,更多的颗粒被挤入桩中。
2.2 土塞效应分析
土塞率(plug length ratio, PLR)和土塞增长率(increment filling ratio, IFR)是目前最为常用的描述土塞效应的参数[1, 2],其定义为
PLR=hH, (1) IFR=ΔhΔH。 (2) 式中:h为土塞高度;H为总贯入深度;Δh为单次贯入下土塞高度变化量,ΔH为单次贯入深度。当PLR=1或IFR=1时,管桩处于完全非闭塞状态;当0<IFR<1时,管桩处于部分闭塞状态;当IFR=0时,管桩处于完全闭塞状态。
图 7展示了管桩沉桩过程中PLR和IFR随贯入深度的变化趋势。随着管桩的贯入,PLR逐渐减小,且P1的PLR值要比P2和P3要小。相比于PLR,IFR对贯入深度的变化更为敏感。对于P1,初始贯入时IFR迅速减小,在贯入深度为3.5~5 m,IFR始终保持为0,表明这一阶段P1为完全闭塞状态,在5~6 m贯入深度内,IFR出现了一定波动,表明P1发生了开塞与再闭塞。P2的IFR值变化状态与P1相似,初始时IFR快速减小,在5~5.5 m贯入深度保持完全闭塞,随后开塞。对于P3,IFR始终保持波动减小的趋势,但始终未完全闭塞。
上述分析表明,IFR值相比于PLR值对土塞状态更为敏感,因此能更好地对土塞状态进行描述。然而实际工程中IFR值往往难以实时测量。因此,UWA-05方法[24-25]提出采用管桩贯入最后约3倍桩径时对应的IFR平均值来描述土塞状态。基于此,Liu等[26]与Paik等[27]基于数值模拟数据与现场试验数据,提出了PLR-IFR拟合公式:
IFR=2.355⋅PLR−1.44 , (3) IFR=1.613⋅PLR−0.61。 (4) 本文中IFR值与PLR值的拟合曲线绘制于图 8,可以看出,本文模拟结果与Paik等[27]基于现场试验数据得出的拟合关系较为接近,而与Liu等[26]基于离散元模拟得出的拟合关系差距较大,这可能是由于Liu等[26]模型中沉桩方式与桩基尺寸与本文模型的差异导致。总的来说,本文中IFR与PLR呈现较好的线性关系:
IFR=0.841⋅PLR+0.096。 (5) 这既反映出本次数值试验的合理性,也表明采用PLR进行IFR预测的可行性。
2.3 沉桩阻力分析
本节将开口管桩沉桩总阻力分为桩端阻力、外摩阻力和内摩阻力,不对管桩闭塞状态进行区分。由图 9可知,沉桩总阻力随着贯入深度的增加而增加。在初始约2 m贯入深度范围内,沉桩阻力主要由端阻力提供。随着继续贯入,端阻力增速减缓,内壁摩阻力逐渐增大并超过外壁摩阻力。可以看出,对于不同模型桩,其端阻力与外壁摩阻力的大小与变化趋势基本相同,主要差别在于内壁摩阻力,且内壁摩阻力的发挥趋势与IFR的变化趋势类似。当IFR为0时,即管桩处于完全闭塞状态,内壁摩阻力基本达到稳定,当IFR不为0时,内壁摩阻力随IFR变化趋势波动。然而,尽管P1中土塞效应最强,但P3中土塞阻力最大。为此,分别绘制管桩单位内壁摩阻力随贯入深度变化曲线与沉桩结束时内壁摩阻力沿桩身分布曲线。
由图 10可以看出,单位内摩阻力沿深度的变化趋势与IFR值基本相同。且当管桩完全闭塞时,单位内摩阻力达到最大值,约为3 MPa,并随着IFR值在最大值附近波动。结合图 11可以进一步得出,尽管P1中土塞效应最强,但P2和P3中土塞尺寸更大,能调动的阻力范围更大,因此总的摩阻力更大。可以得出,土塞阻力(或管桩内壁摩阻力)的发挥不仅与土塞效应的强弱有关,还与土塞尺寸有关。
3. 管桩静载过程模拟结果
3.1 土体变形特征
为了分析承载过程中桩周土体变形特征,静载模拟开始前对地基土体再次染色分层。由图 12可以看出,承载过程中土体的变形特征与沉桩过程中土体的变形特征显著不同。相对于沉桩过程,承载过程中管桩外侧土体的扰动程度显著减弱。而对于内部土塞,扰动相对较小,可以认为土塞随管桩产生整体移动,并对下部土体产生挤压。但随着桩径的增大,即沉桩结束时土塞效应的减弱,土塞对下部土体的挤压作用也逐渐减弱。大量研究表明,管桩沉桩过程中一般为部分闭塞状态,承载过程中一般为完全闭塞状态[2-3, 9]。因此,本次模拟结果与上述结论基本相符。
3.2 荷载位移曲线
图 13展示了承载过程中管桩贯入阻力变化特征。与沉桩阻力类似,不同模型桩的外摩阻力和端阻力的大小和发展规律基本不变,不同模型桩贯入阻力的主要区别在于内壁摩阻力。可以看出,内壁摩阻力随桩顶位移基本线性增大,且桩径越大,内摩阻力越大。上述管桩内摩阻力的线性发展规律与Han等[11]基于现场试验得出的规律相同。Fellenius[28]基于桩身荷载分布情况指出,开口管桩在静载作用下,内部土塞可以看做是“柔性桩”从桩端往上加载,土塞的荷载-位移响应呈近似弹塑性特征。可以看出,本次模拟中土塞的荷载-变形响应基本符合实际情况。
3.3 桩端阻力计算
考虑到静力触探试验(CPT)与管桩贯入过程的相似性,基于CPT锥尖阻力qc建立桩基承载力经验计算公式的方法得到了广泛应用[29-31]。为了考虑开口管桩土塞效应的影响,UWA-05方法[24-25]引入有效面积比Arb, eff来计算开口管桩的桩端承载力:
qb0.1/qc, avg=0.15+0.45Arb, eff。 (6) 式中,qb0.1为0.1D位移下的单位桩端阻力;qc, avg为桩端上下1.5D处qc平均值。
qb0.1=qb, annAr+qb, plug(1−Ar)。 (7) 式中:qb, ann为单位环壁端阻;qb, plug为单位土塞端阻,为管桩内摩阻力与土塞端面积之比;Ar为管桩面积比。
Ar=1−(Di/D)2, (8) Arb, eff=1−IFR(Di/D)2。 (9) 开展静力触探数值试验,将归一化的土塞端阻和环壁端阻数据点绘制于图 14。归一化的土塞端阻qb, plug/qc与IFR呈现较好的线性关系。当IFR为0时,即管桩呈完全闭塞状态,qb, plug/qc接近1,表明此时开口管桩可以按照闭口桩计算桩端承载力。这与Lehane等[32]基于现场试验得到的qb, plug/qc随IFR变化结果相近。对于归一化的单位环壁端阻,尽管qann/qc与IFR能通过线性近似拟合,但数据点较分散。这可能是由于数值模型中环壁面积仅为d50的4倍,导致环壁端阻波动较大。
进一步地,将基于式(7)计算得到的管桩端阻qb0.1对锥尖阻力qc进行归一化处理,并结合UWA-05方法中实测数据绘制于图 15。由图 15可以看出,基于离散元模型获得的qb/qc与Arb, eff呈现很好的线性相关性。这既表明了考虑土塞效应的管桩端阻力计算方法的合理性,也从侧面验证了本次数值模拟结果的有效性。然而,UWA-05方法中,qb/qc范围为0.15~0.6,而数值模型中qb/qc范围为0.27~1.13,约为UWA-05方法qb/qc的两倍。上述差异的原因可能是数值模型中将管桩贯入过程简化为平面问题,导致单位端阻力的计算是基于单位长度而不是面积。
4. 结论
本文基于离散元方法,对开口管桩沉桩与承载全过程进行了模拟,从宏细观角度分析了土塞效应的发挥机制及其对管桩承载特性的影响,得到以下4点结论。
(1)相较于土塞率(PLR),土塞增长率(IFR)对土塞状态的变化更为敏感。在现场难以测得IFR的情况下,可以通过PLR基于线形拟合关系对IFR值进行预测。
(2)土塞阻力的发挥趋势与IFR值变化趋势有较高的相似性,其大小同时受土塞效应和土塞尺寸的影响。
(3)开口管桩在静载作用下,内部土塞可以看作是“柔性桩”从桩端往上加载,土塞的荷载-位移响应呈近似弹塑性特征。
(4)基于离散元数值模拟结果,提出了考虑CPT锥尖阻力、土塞效应、管桩尺寸效应的静压开口管桩桩端阻力经验计算公式。
本文将开口管桩的三维贯入过程简化为平面应变问题。尽管本次二维离散元模型很好地揭示了土塞的形成过程与开口管桩的承载机制,仍需开展基于现场沉桩试验数据的三维离散元模拟分析,从而实现对开口管桩土塞效应的量化分析与承载力的准确设计。
-
表 1 常用物理量相似准则
Table 1 Similarity criteria of common physical quantities
物理量 加速度 长度 面积 体积 应力 相似比(模型/原型) N 1/N 1/N2 1/N3 1 物理量 孔隙比 密度 质量 流量 时间 相似比(模型/原型) 1 1 1/N3 1/N2 1/N 表 2 4种工况参数设定
Table 2 Parameter settings of four conditions
工况 坝高/mm 下游坡比 d50/mm 1 250 1∶3 5 2 350 1∶3 5 3 250 1∶5 5 4 250 1∶3 1 注:d50为级配平均粒径。 表 3 4种工况溃坝参数对比
Table 3 Comparison of dam breach parameters of four conditions
工况 影响因素 峰值流量/(m3·s−1) 变化幅度/% 达峰时间/min 变化幅度/% 相对残余坝高/% 变化幅度/% 1 — 11.4 18.9 66.4 2 坝高 18.6 +62.6 16.1 -14.8 55.4 -16.5 3 坡比 9.5 -16.6 24.5 +30.0 75.2 +13.3 4 级配 17.8 +56.0 13.4 -29.0 47.2 -28.9 注:变化幅度表示与工况1相比,各溃坝参数的增量。 -
[1] 钟启明, 陈生水, 王琳. 堰塞湖致灾风险评估技术及应用[M]. 北京: 科学出版社, 2021. ZHONG Qiming, CHEN Shengshui, WANG Lin. Risk Assessment Technology and Application of Dammed Lake Disaster[M]. Beijing: Science Press, 2021. (in Chinese)
[2] ZHONG Q M, WANG L, CHEN S S, et al. Breaches of embankment and landslide dams-State of the art review[J]. Earth-Science Reviews, 2021, 216: 103597. doi: 10.1016/j.earscirev.2021.103597
[3] MEI S Y, CHEN S S, ZHONG Q M, et al. Effects of grain size distribution on landslide dam breaching—insights from recent cases in China[J]. Frontiers in Earth Science, 2021, 9: 658578. doi: 10.3389/feart.2021.658578
[4] ZHENG H C, SHI Z M, SHEN D Y, et al. Recent advances in stability and failure mechanisms of landslide dams[J]. Frontiers in Earth Science, 2021, 9: 659935. doi: 10.3389/feart.2021.659935
[5] SHEN D Y, SHI Z M, PENG M, et al. Longevity analysis of landslide dams[J]. Landslides, 2020, 17(8): 1797-1821. doi: 10.1007/s10346-020-01386-7
[6] ZHOU G G D, LI S, LU X Q, et al. Large-scale landslide dam breach experiments: Overtopping and "overtopping and seepage" failures[J]. Engineering Geology, 2022, 304: 106680. doi: 10.1016/j.enggeo.2022.106680
[7] ZHU X H, LIU B X, PENG J B, et al. Experimental study on the longitudinal evolution of the overtopping breaching of noncohesive landslide dams[J]. Engineering Geology, 2021, 288: 106137. doi: 10.1016/j.enggeo.2021.106137
[8] PENG M, MA C Y, CHEN H X, et al. Experimental study on breaching mechanisms of landslide dams composed of different materials under surge waves[J]. Engineering Geology, 2021, 291: 106242. doi: 10.1016/j.enggeo.2021.106242
[9] 陈生水, 钟启明. 土石坝溃坝数学模型及应用[M]. 北京: 中国水利水电出版社, 2019. CHEN Shengshui, ZHONG Qiming. Numerical Models for Earth-Rock Dam Breaching and Their Applications[M]. Beijing: China Water & Power Press, 2019. (in Chinese)
[10] WAN C F, FELL R. Investigation of rate of erosion of soils in embankment dams[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(4): 373-380. doi: 10.1061/(ASCE)1090-0241(2004)130:4(373)
-
期刊类型引用(4)
1. 刘学增,房茂柳,吴德兴,李银萍,刘新根,李罡. 隧道结构病害快速检测技术的现状与发展. 隧道建设(中英文). 2025(04): 657-676 .  百度学术
百度学术
2. 李文博. 公路隧道无损检测技术与病害处理方法分析. 交通科技与管理. 2024(07): 79-81 .  百度学术
百度学术
3. 路德春,秦威,郭彩霞,李久林,杜修力. gprMax干扰消除方法优化隧道壁后空洞成像特征研究. 隧道建设(中英文). 2024(10): 1928-1940 .  百度学术
百度学术
4. 朱厚喜,曹伍富,李克飞,伊建峰,刘少华,李洪珏. 基于多模态特征融合的隧道渗水异常检测方法. 计算机应用. 2023(S2): 276-284 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: