A hybrid method to identify pulse-like ground motions and pulse periods based on ST-CNN
-
摘要: 如何快速准确地识别脉冲型地震动是困扰学术界和工程界的关键难题，定量识别方法虽然能够克服人工识别的经验性限制，但是传统定量识别方法存在识别结果不一致、适用范围不广泛、难以同时识别脉冲周期或识别的脉冲周期部分情况下差异明显等问题。为此建立了一种问题针对性融合学习规则并结合卷积神经网络（CNN），开发出了一种新的脉冲型地震动与脉冲周期同步识别方法。该学习规则通过对基于不同识别原理的多个传统典型识别方法进行融合学习并采用全球范围的30000条任意方向地震动数据进行训练和验证，摒弃了以往繁琐的人工标记过程并得到了3个问题针对性识别模型，分别命名为Strict识别模型、General识别模型以及TP识别模型。除此之外，为解决地震动时序输入信息不足从而导致模型泛化能力较弱的问题，对CNN的输入结构进行了优化增强，提出了ST-CNN模型。其引入了S变换层以将地震动时序变换至时频，从而增加了频域分布信息并进一步提高了识别精度。结果表明：Strict识别模型能严格区分脉冲型与非脉冲型地震动，识别结果得到已有方法的一致认可；General识别模型的识别能力更强，适用范围更加广泛；TP识别模型识别的脉冲周期更加准确，并可与前述识别模型并用以同步输出识别结果。提出的问题针对性融合学习规则还可推广至其他工程领域与其他机器学习模型，建立的识别方法可为脉冲型地震动研究提供科学指导。Abstract: The rapid and precise identification of the pulse-like ground motions is a key challenge that perplexes both the academic and engineering communities. The quantitative identification methods can overcome the empirical limitations of manual identification. However, the traditional quantitative identification methods suffer from inconsistencies in the identified results, limited applicability, and difficulties in simultaneously determining the accurate pulse periods. In response, a problem-targeted fusion learning rule is established, combined with a convolutional neural network (CNN) model, to develop a novel method to synchronously identify pulse-like ground motions and their pulse periods. This learning rule integrates multiple traditional typical identification methods based on different identification principles, thereby eliminating the cumbersome manual labeling process. It employs 30000 ground motion data from arbitrary directions worldwide for training and validation, resulting in three problem-targeted CNN models named the Strict, General, and TP identification models. To address the issue of insufficient temporal input information for ground motions leading to weak model generalization capability, the input structure of the CNN model is optimized, and the ST-CNN model is proposed, incorporating the S-transform layer to convert ground motion time series to time frequency, thereby enhancing frequency domain distribution information and further improving the identification accuracy. The results indicate that the Strict model can strictly differentiate between the pulse-like and non-pulse-like ground motions, with the results consistent with those of other methods. The General model can identify more pulse-like ground motions and has broader applicability. The TP model accurately identifies pulse periods and can be used in conjunction with the aforementioned models to synchronously output the identified results. The proposed problem-targeted fusion learning rule can also be extended to other engineering fields and other machine learning models, and the established identification method can provide scientific guidance for the study on the pulse-like ground motions.
-
0. 引言
脉冲型地震动一般是指在地震动速度时序中含有长周期、大振幅、短持时、高能量脉冲的地震动，其产生原因包括但不限于近断层方向性效应、滑冲效应、盆地效应、软土效应以及液化效应[1-2]。相较于非脉冲型地震动，脉冲型地震动对工程结构通常具有更强的破坏力，且脉冲周期与结构基本周期的比值会极大地影响结构的响应特征，因而受到地震学和地震工程学领域学者的广泛关注[3-4]。然而无论是考虑脉冲效应的概率地震危险性分析亦或是脉冲型地震动作用下结构的安全评估等研究[5-7]，其前提都需要一种快速、准确的脉冲型地震动与脉冲周期识别方法。
目前脉冲型地震动识别方法经历了从主观定性到半定性半定量再到完全定量的发展阶段。其中，主观识别方法由于受到个人经验限制，不具备通用性。半定性半定量识别方法虽采用简化的等效脉冲公式捕捉到地震动中的脉冲特征，但仍缺乏明确的判别准则[8]。自Shahi等[5-6]，Baker[9]提出以小波变换为基础的脉冲型地震动与脉冲周期定量识别方法后，其已作为一项独立研究并取得了显著的进展。然而即使多位学者指出Baker方法存在难以识别多脉冲型地震动从而导致识别能力不足等局限性，并提出了基于新的识别理论的脉冲型地震动与脉冲周期定量识别方法[10-12]，但这些方法仍以传统理论为主，其无论从时域还是频域的角度均会引入新的限制，如Chang等[10]使用对称的脉冲模型与实际情况经常不符，且识别能力依旧较弱；Zhai等[11]的方法虽可适用于多种类型的脉冲型地震动，但无法同时输出脉冲周期且易受到地震动高频震荡部分的影响。可以看到，传统识别方法存在不同的优势与限制，并且从这些研究的结果对比来看，基于不同识别理论的方法常常在识别结果上存在冲突。截至目前，尚缺乏一种能广泛适用于复杂多变的任意脉冲型地震动、识别结果得到其他方法一致认可并且能同时输出准确脉冲周期的高效识别方法。
为此，本文采用卷积神经网络（convolutional neural network，简称CNN）建立了一种新的脉冲型地震动与脉冲周期融合识别方法。与已有研究不同，本文提出了一种新的问题针对性融合学习规则，系统地建立了本文命名的识别结果得到广泛认可的Strict识别模型、识别能力更强的General识别模型以及能同时输出准确脉冲周期的TP识别模型，从而全面改善了传统识别方法存在的一系列问题。其次，针对脉冲型地震动低频能量分布较高的特性以及时序地震动输入信息不足的问题，本文提出了一种ST-CNN模型，其增加了频域分布信息从而在时频分布上对脉冲型地震动进行精准识别，并通过与普通CNN模型识别的结果对比验证了该模型的有效性。
1. 问题针对性融合学习
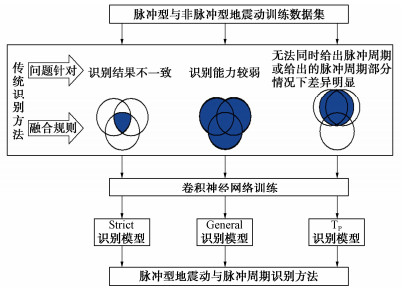
卷积神经网络[13]因其优异的识别能力，近年来在岩土和地震工程领域中应用广泛[14-15]。作为一种监督学习，卷积神经网络学习的数据标签来源于人工标记，学习的目标即为模拟人工标记的过程。面对海量的训练数据，人工标记费时费力，标记的结果还存在经验性限制。为此，本文提出了问题针对性融合学习的核心思想，其中融合学习被定义为一种深入挖掘并整合领域内现有知识的过程，通过这一过程，学习对象（标签）被转化为融合后的知识结构，从而避免人工标记的过程；而问题针对性则是指根据需解决的问题针对性地制定融合规则，这一过程也可有效解决已有方法中存在的诸多问题。本文将依据Strict、General、TP识别模型的建立过程，给出问题针对性融合学习规则的具体流程，见图 1所示。需要说明的是，该学习规则可无差别推广至其他机器学习模型与其他工程领域。
1.1 地震动数据
本文的地震动数据来源为美国太平洋地震研究中心中来自全球范围的地震动。选择了其中所有矩震级MW>5的地震事件中记录的三分量地震动速度时序原始记录，并对每组三分量地震动速度时序原始记录使用下式随机旋转至空间任意方向以扩充地震动速度时序数据量：
x(t,θ,∂)=(x1(t)cosθ+x2(t)sinθ)cos∂+x3(t)sin∂。 (1) 式中：x1(t)，x2(t)为水平方向相互垂直的两条地震动；x3(t)为竖向地震动；x(t,θ,∂)为旋转至空间任意角度θ和∂的地震动。
该过程每组共重复进行50次。同时，为消除由于地震动速度时序简单而类似脉冲的小振幅地震动[9-11]，进一步筛选了其中峰值速度PGV>30cm/s的地震动速度时序作为本研究的数据集。最终，共得到9660条空间任意方向的地震动速度时序数据，其分别来自于476组三分量地震动速度时序原始记录，各组三分量原始记录得到的数据样本详见本文数据和资源部分。除此之外，为平衡数据各标签类型数量，本文采用随机平移的方式将地震动速度时序在时间轴上向右随机平移5%时长范围内的任意长度（由于小幅度的平移并不改变地震动的波形，因而不会影响该地震动是否属于脉冲型地震动的标签），从而进一步得到新的同样标签的地震动速度时序数据，该过程重复进行直至共获取30000条标签数量平衡的地震动速度时序数据结束，并按照0.8，0.2的比例随机划分为训练数据集和验证数据集。需要说明的是，本研究拟对空间任意方向地震动进行识别并且建立的识别模型完全基于地震动速度时序，因而采用旋转地震动方向与随机平移的方式进一步扩充地震动速度时序的数量，从而提高卷积神经网络的泛化能力。
1.2 融合学习规则
本文针对传统识别方法中存在的3个主要问题，分别制定融合规则并建立对应的预测模型。
（1）针对传统识别方法彼此之间识别结果不一致的问题，本文将传统识别方法识别结果取交集作为卷积神经网络的预测标签，并将训练后的神经网络命名为Strict识别模型。即所有传统识别方法均识别为脉冲的标签为脉冲，而均识别为非脉冲的标签为非脉冲，剩余标签为模糊。该识别准则参照了Baker的方法，对识别的脉冲型地震动与非脉冲型地震动都具有较高的置信度，最终该融合标签获得所有传统识别方法的一致认可。
（2）针对传统识别方法识别能力较弱导致适用范围不广泛的问题，本文将传统方法识别结果取并集作为卷积神经网络的预测标签，并将训练后的神经网络命名为General识别模型。即所有传统识别方法中只要有一种识别为脉冲的标签为脉冲，剩余标签为非脉冲，这一识别准则与大部分识别准则相似，不设置模糊带，最后融合的标签包含所有传统识别方法能识别的脉冲型地震动。
（3）针对部分传统识别方法无法同时给出脉冲周期或给出的脉冲周期部分情况下差异明显的问题，本文融合规则取所有脉冲周期识别方法中结果最为接近的两种方法的均值作为卷积神经网络的预测标签，并将训练后的神经网络命名为TP识别模型。这是由于目前对于脉冲周期并不存在一个公认的定义，各识别方法得到的脉冲周期与其他方法在某些情景下相差巨大[9-10, 16]，而本文的融合学习规则能有效避免该不利情景的出现，并且可作为补充模型来同时输出脉冲周期。
还需要指出的是，本文提出的问题针对性融合学习规则不仅可以避免人工标记带来的经验性，解决传统识别方法存在的问题，还同时进一步消除了传统识别方法本身存在的经验性限制。这是由于传统识别方法的识别阈值或准则均只是在各学者自身识别标记后的脉冲型与非脉冲型地震动数据集下校正，这意味着其仍然存在一定的经验性限制。
1.3 传统识别方法样本
本文将用于卷积神经网络学习的传统识别方法作为训练的样本标签来源。目前对于脉冲型地震动Strict和General识别模型学习的方法为Baker[9]、Chang等[10]、Zhai等[11]，如前所述，选择这些方法的原因是由于这些方法应用较为广泛，且基于不同原理，具有不同的限制和适用性。而对于脉冲周期TP识别模型，由于Zhai等[11]不具备同时输出脉冲周期的能力，学习的方法在Baker[9]、Chang等[10]的基础上增加SvSd[17]识别方法，这是专门针对脉冲周期的识别方法，有助于改善常用的最大速度反应谱周期方法易受地震动高频部分影响的局限性。
最后，运用带有标签的数据集训练卷积神经网络模型从而完成输入到输出的识别过程与其他机器学习研究并无本质上的区别，在此不再赘述。
2. ST-CNN模型结构
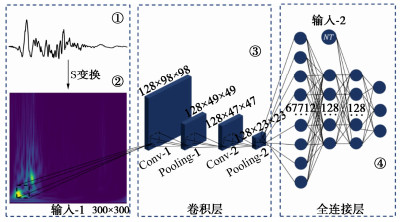
在完成标签数据集的准备后，如何建立高精度预测模型以完成脉冲型地震动与脉冲周期的同步识别是本研究的另一大难点。普通CNN模型的输入通常为地震动时序，这一方面会造成输入包含的信息量减少，从而导致模型的泛化能力降低，另一方面由于脉冲型地震动本质上是含低频高能量大脉冲的地震动，仅从时域上识别难以有效利用该特性从而容易引发误判。为此，本文在原有CNN的基础上，对模型的输入结构进行了优化增强，提出了ST-CNN模型，其通过增加S变换层将地震动时序变换至时频从而进一步提高了模型的性能。以ST-CNN-Strict为例的识别模型结构见图 2所示，以下将对本文提出的ST-CNN模型结构及有效性进行详细说明。
![]()
图 2 Strict神经网络识别模型结构图Figure 2. Structural diagram of Strict neural network identification model2.1 S变换有效性
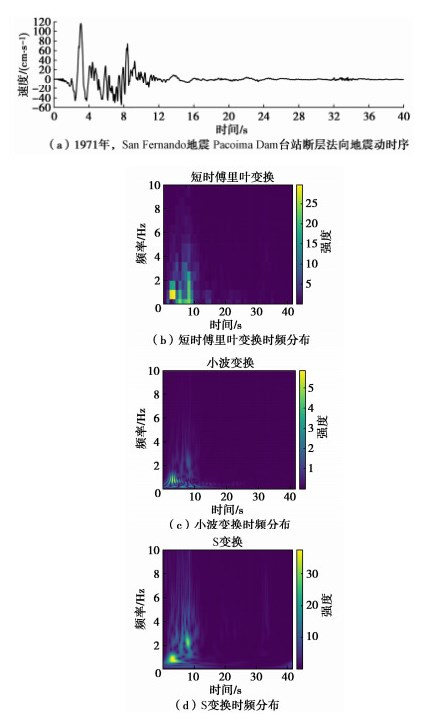
S变换是由Stockwell等[17]提出的一种可逆的时频分析技术，其可看作是时频窗口随频率可变的短时傅立叶变换或小波变换的相位校正形式。图 3显示了一条脉冲型地震动的3种时频分析结果的对比情况，图中强度体现了地震动在不同时间和频率范围内的能量分布。可以看出S变换时频分辨率高，地震动能量分布清晰，这是由于S变换能有效避免短时傅里叶变换精度对窗宽大小的依赖，以及小波变换精度对小波基函数类型的依赖，因而更加适用于非平稳地震信号的处理，其也说明了时频变换方法中选择S变换的有效性。
![]()
图 3 脉冲型地震动时序及其时频变换结果对比图Figure 3. Diagram of a pulse-like ground motion time series and comparison of its time-frequency transformation results其次，本文对比了同样数据量下CNN模型与本文提出的ST-CNN模型的性能表现，建立了两组4层卷积层、128个卷积核及全连接层神经元的各类型识别模型，其中一组输入为（100×100，1）的S变换时频（缩写为ST），另一组输入为（10000，1）的地震动时序（缩写为V，对于模型参数解释详见2.2节）。分析结果对比见图 4，其中对于分类模型Strict和General，选择的损失函数为分类交叉熵（categorical crossentropy，缩写为CC），评价指标为精度（accuray，缩写为Acc）；对于回归模型TP，选择的损失函数为均方误差（mean squared error，缩写为MSE），评价指标为平均绝对误差（mean absolute error，缩写为MAE）。由于MSE与MAE曲线类似，为避免混淆，图 4中只展示了MAE曲线。所有的损失函数和评价指标为
CC=−1NN∑i=1K∑j=1yijlnpij, (2) Acc=Ncorrect N, (3) MSE=1NN∑i=1(yi−ˆyi)2, (4) MAE =1NN∑i=1|yi−ˆyi|。 (5) ![]()
图 4 S变换时频输入与时序输入模型性能对比图Figure 4. Comparison of performance of S-transform time-frequency input models and time-series input models式中：N为样本数量；Ncorrect为预测正确的样本数量；在分类问题中，K为类别数量；yij为第i个样本的真实标签中类别j的值，如果样本属于类别j，则yij=1，否则为0；pij为模型对第i个样本在类别j上的预测概率；在回归问题中，yi为第i个样本的标签值，ˆyi为第i个样本的预测值。
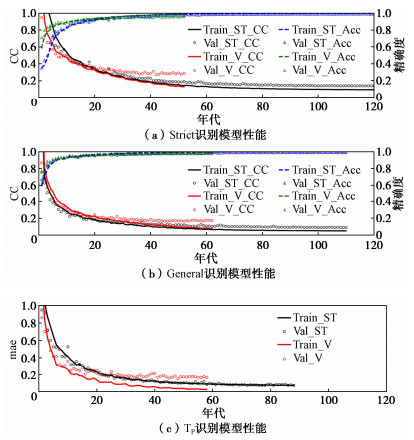
可以看出无论对于Strict识别模型、General识别模型还是TP识别模型，如果直接采用地震动时序作为输入，模型的泛化性能较差，表现为图中代表地震动时序输入训练损失的灰色点线与代表地震动时序输入验证损失的灰色方形点线偏离较大；而如果采用S变换时频作为输入，模型的泛化性能会显著提升，表现为图 4中代表S变换时频输入训练损失的黑色实线与代表S变换时频输入验证损失的黑色空心圆形点线偏离较小。这也进一步说明，本文提出的ST-CNN模型采用S变换增强输入的方法是有效的。
2.2 模型结构
模型的结构超参数见表 1所示，对于表格中具有多个数值的超参数，需要对每个数值各自建立神经网络模型，通过对比训练结果选择最优超参数以防止过拟合、欠拟合现象。其中，对于输入形式，括号前半部分为S变换的时频结果插值点数，后半部分为地震动速度时序的总时长NT（单位为s）。
表 1 ST-CNN模型结构超参数Table 1. Structural hyperparameters of ST-CNN models参数 值或函数 输入形式 （100×100，1），
（200×200，1），
（300×300，1）卷积层数量 2，3，4 卷积核数量 32，64，128 卷积核大小 （3×3） 池化层数量 2 池化函数 Maxpooling（2×2） 全连接层数量 4 全连接层神经元数量 32，64，128 激活函数 ReLU，Strict和General识别模型最后一层为Softmax，TP识别模型最后一层无激活函数 在训练过程中，优化器选择为Adam，学习率初始为0.001，每训练5个epoch学习率衰减至当前学习率的0.8倍。最大训练批次设置为200，batch size设置为32，当训练10次epoch模型的性能不再提升时，训练停止并自动恢复模型在表现最好时的权重。为进一步优化过拟合现象，在模型中增加随机失活层和L2正则化项。
3. 结果与分析
针对提出的问题针对性融合学习规则以及改进的ST-CNN模型结构，本节将进一步对脉冲型地震动与脉冲周期识别方法的整体可行性与有效性进行介绍。
3.1 最优模型训练结果
在2.2节中说明了本研究拟建立的卷积神经网络模型结构，然而对于输入大小、卷积层数、卷积核数量与全连接层神经元数量等超参数仅给了选择范围。这是由于这些超参数越复杂模型的性能越强，但是当过度复杂后会带来极大训练成本并导致过拟合问题，目前研究均通过采取多次试验取最优的方式来选择超参数。本研究对这些超参数范围进行组合，采取多次试验后最终选择的Strict识别模型最优超参数为(200×200,1)输入、2层卷积层、128个卷积核与全连接层神经元数量，General识别模型的最优超参数为(100×100,1)输入、4层卷积层、128个卷积核与全连接层神经元数量，TP识别模型的最优超参数为(300×300,1)输入、4层卷积层、128个卷积核与全连接层神经元数量，模型对应的性能表现见表 2。从表中可以看出，所有模型的CC、MSE、MAE接近于0，Acc接近于1，并且模型在训练和验证数据集上表现接近，说明了本文训练的识别模型性能优异，证明了方法的可行性。其中对于脉冲型地震动和脉冲周期的识别，3个最优识别模型的共同特点是卷积核数量最多，而卷积核数量越多的神经网络可以学习到时频输入中更高级和抽象的特征，这表明脉冲型地震动的识别和脉冲周期与地震动的时频高级特征具有重要关系，同时也说明目前运用时频变换再经过简单识别处理的方法可能是不精确的。
表 2 最优模型性能表现Table 2. Performance of optimal models模型 性能表现 值 Strict
最优识别模型Train CC 0.0657 Val CC 0.1072 Train Acc 0.9991 Val Acc 0.9915 General
最优识别模型Train CC 0.0499 Validation CC 0.0900 Train Acc 0.9995 Val Acc 0.9900 TP
最优识别模型Train MSE 0.0021 Val MSE 0.0252 Train MAE 0.0297 Val MAE 0.0598 3.2 Strict识别模型分析
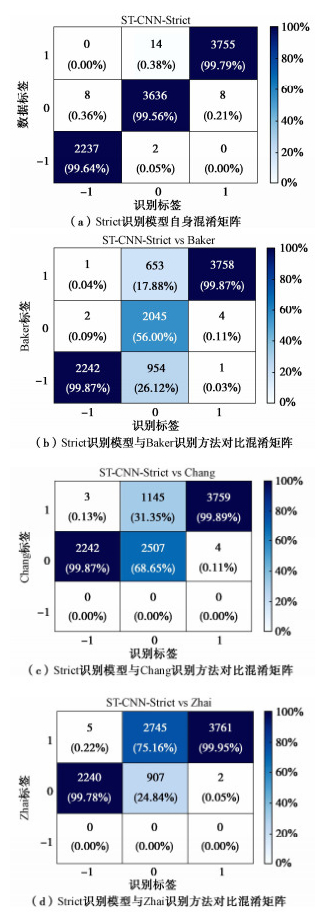
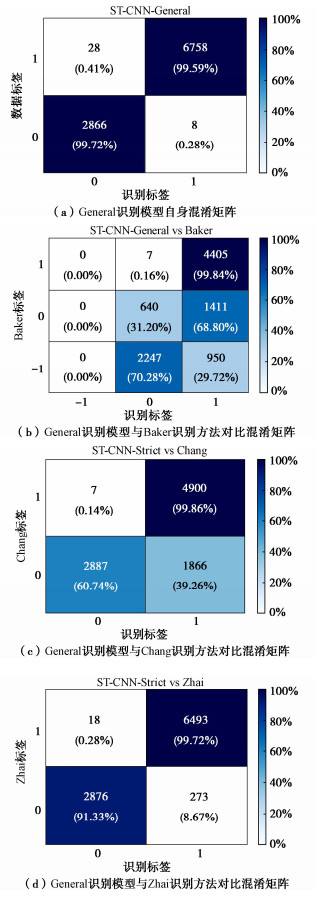
最优Strict识别模型及其与其他3种识别方法对比的混淆矩阵见图 5所示，图中横坐标为Strict识别模型识别的标签，纵坐标为数据标签或其他方法识别的标签，采用的对比验证数据集为原始未经过随机平移扩充的9660条地震动（下同）。其中数据标签、Strict识别模型识别标签、Baker识别标签中1为脉冲型地震动、0为模糊地震动、-1为非脉冲型地震动，Chang方法和Zhai方法由于只区分脉冲型与非脉冲型地震动，标签1为脉冲型地震动、0为非脉冲型地震动。图中百分比为数据占该列总数据量的比例，结果体现了其他方法与strict识别模型的一致性分析结果。
![]()
图 5 Strict识别模型自身及与其他方法对比混淆矩阵Figure 5. Confusion matrix of Strict identification model and comparison with other methods从图 5（a）中可以看出，Strict识别模型在各类型地震动识别上均取得了99.56%以上的准确率，不存在某一个类别识别较差的情况，这得益于本研究将各类型数据集平衡至相同数量。从图 5（b）~（d）中可以看出，两个方法同时标签为脉冲型地震动或非脉冲型地震动的数据占比均超过99.78%，因此Strict识别模型与其他3个方法的识别结果基本一致，表明该模型得到的识别结果被传统识别方法一致认可。这也说明了Strict识别模型具有极低的假阳性和假阴性率，能有效改进已有方法存在的识别结果不一致问题，因此可以作为需要严格区分脉冲型地震动和非脉冲型地震动研究的基础。
3.3 General识别模型分析
General识别模型自身及其与其他3种识别方法比较的混淆矩阵见图 6所示，图中百分比为数据占该行总数据量的比例，结果体现其他方法与General识别模型的识别能力对比。这里，数据标签、General识别模型识别标签中1为脉冲型地震动、0为非脉冲型地震动，其余解释与图 4相同。从图 6（a）中可以看出，General识别模型在各类型地震动识别上均取得了99.59%以上的准确率，同样不存在不同类别表现不均衡现象。从图 6（b）~（d）中还可以看出，当其他方法识别为脉冲型地震动时，基本均能被General识别模型同时识别为脉冲型地震动，表现为图中标签均为脉冲型地震动的数据占比均超过99.72%，并且General识别模型能识别其他3个方法无法识别的脉冲型地震动，表现为其他方法识别为非脉冲型地震动时但被General识别为脉冲型地震动的数据占比依旧较高。以上结果说明了General识别模型能够克服已有传统方法尤其是Baker方法和Chang方法识别能力较弱的问题，更加适用于任意类型脉冲型地震动如多脉冲型地震动的识别，即识别范围更广泛。
![]()
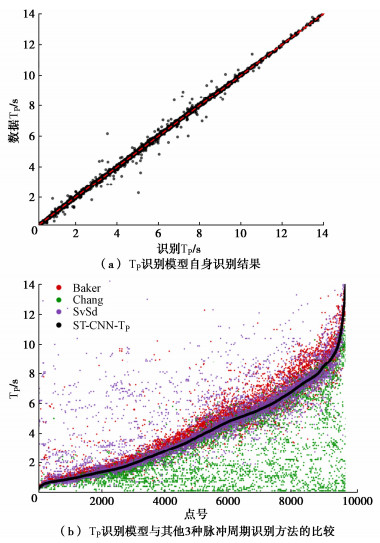
图 6 General识别模型自身及与其他方法对比混淆矩阵Figure 6. Confusion matrix of General identification model and comparison with other methods3.4 TP识别模型分析
脉冲周期TP识别模型自身及与其他3种脉冲周期识别方法的比较见图 7所示，图 7（a）中的横坐标表示TP识别模型识别的脉冲周期，纵坐标表示数据的脉冲周期。可以看出在整个数据集上脉冲周期识别结果较好，大部分点均在红色等值线上或附近，只有少数点存在偏差。图 7（b）中的横坐标表示点号（按照TP识别模型识别结果从小到大排序），纵坐标表示各方法识别的脉冲周期，从结果来看Baker方法识别的脉冲周期略有偏大，Chang方法识别的脉冲周期总体偏小，SvSd方法性能最优，但在某些地震动情况下会取得与其他方法相比偏大较多的结果。这一结果同样可以从对应的论文[16, 18]中得到直观展示，其是由于Chang方法使用的对称脉冲模型在实际情况下难以做到对地震动脉冲部分的完全包络，通常与实际相比更加细小；而SvSd方法使用了速度反应谱与位移反应谱乘积的最大值作为脉冲周期，虽然克服了仅使用速度反应谱最大值作为脉冲周期易受地震动高频震荡部分影响的缺陷，但是位移反应谱的引入也使得此时最大值对应的可能为大面积（周期更长）但是小幅度的速度脉冲，该速度脉冲并非为主要脉冲。
![]()
图 7 TP模型的识别结果及与其他3种脉冲周期识别方法的比较图Figure 7. Identification of TP identification model and comparison with other identification methods for pulse periods而TP识别模型识别的脉冲周期均处在其他3种识别方法识别的脉冲周期汇聚的地方，能有效避免识别的结果与其他方法偏离较大的不利情况。从TP识别模型的训练原理来看，这是由于使用了本文提出的问题针对性融合学习训练规则，其采用了脉冲周期识别结果最为接近的两种方法的均值作为卷积神经网络的预测标签，当且仅当只有一种方法识别准确、其余方法均识别错误时，该规则失效，因而更加具有鲁棒性。并且这一模型还有效解决了部分已有方法[11]存在的无法同时输出脉冲周期的问题。
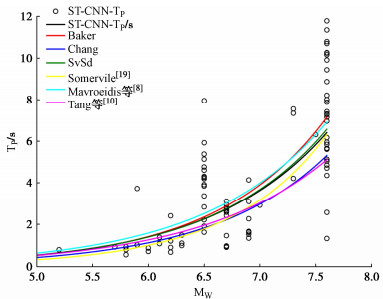
为进一步说明TP识别模型的性能，本文采用广泛用于对比的Baker[9]中91条断层法向脉冲型地震动数据库作为对比基准，识别相应的脉冲周期，并拟合其与震级大小的关系曲线，将该关系曲线与Somervile[19]，Mavroeidis[8]，Tang等[20]得到的典型关系曲线对比，结果见图 8和表 3。由于脉冲周期暂时还没有一个公认的定义，各方法得到脉冲周期的方式存在不同，但本研究得到的脉冲周期趋势与目前研究基本一致，拟合出的关系曲线较为折中，不存在偏离较大的情况，得到的回归函数可为工程提供更准确的指导。
![]()
图 8 本研究识别的脉冲周期与地震震级的关系及拟合曲线结果对比Figure 8. Relationship between pulse periods identified in this study and earthquake magnitude and comparison of fitting curves表 3 脉冲周期与地震震级的拟合曲线对比Table 3. Comparison of fitting curves between pulse periods and earthquake magnitude3.5 模型计算效率分析
另一个方法有效性的指标为方法的计算效率，其在大量地震动分析中尤为重要。以图 3中的地震动为例，本文提出的方法在芯片为M1 pro，代码语言为Python3.10的平台上，各计算模块多次试验平均耗时见表 4，总计算用时0.342 s，因此计算效率较高。并且后期随着学习数据和方法数量的增加也不会增加程序的运行时间，具备良好的可升级能力。
表 4 本文方法运行耗时Table 4. Time taken to run proposed method项目 S变换 Strict General TP 耗时/s 0.094 0.071 0.091 0.086 4. 结论
本文创建了一种问题针对性融合学习规则，提出了使用S变换优化增强输入的ST-CNN模型，建立了识别结果得到广泛认可的Strict识别模型、识别能力更强的General识别模型、能同时输出准确脉冲周期的TP识别模型，3个模型并行以作为本文开发的一种新的脉冲型地震动与脉冲周期同步识别方法。得到3点结论。
（1）问题针对性融合学习规则除了可以避免繁琐和经验性的人工标记数据过程，还可以充分利用领域内已有的知识，通过针对问题制定对应的融合规则，从而训练出一系列改进模型。虽然本文将其应用于卷积神经网络模型以及脉冲型地震动识别，但该学习规则可无差别推广至其他机器学习方法和其他工程领域。
（2）ST-CNN模型有效提升了卷积神经网络在脉冲识别中的泛化能力。最优模型结构超参数说明了脉冲识别与地震动的高级时频特征具有重要关系，也说明了目前采用时频变换再经过简单识别处理的方法可能是不精确的。
（3）经过结果分析与方法对比，证实了本文开发的脉冲型地震动与脉冲周期识别方法的可行性与有效性。此外，本文方法具有较高的计算效率并具备升级能力，可为脉冲型地震动研究提供科学指导。
需要说明的是，本文所得模型暂未对脉冲型地震动的产生原因进行分类识别，因此当需要特别考虑由近断层方向性效应引起的脉冲型地震动的影响时，还需要对识别的脉冲型地震动进行进一步划分。后续将开发模型的升级版本用于直接区分脉冲型地震动的产生因素。
-
![]()
图 2 Strict神经网络识别模型结构图
Figure 2. Structural diagram of Strict neural network identification model
![]()
图 3 脉冲型地震动时序及其时频变换结果对比图
Figure 3. Diagram of a pulse-like ground motion time series and comparison of its time-frequency transformation results
![]()
图 4 S变换时频输入与时序输入模型性能对比图
Figure 4. Comparison of performance of S-transform time-frequency input models and time-series input models
![]()
图 5 Strict识别模型自身及与其他方法对比混淆矩阵
Figure 5. Confusion matrix of Strict identification model and comparison with other methods
![]()
图 6 General识别模型自身及与其他方法对比混淆矩阵
Figure 6. Confusion matrix of General identification model and comparison with other methods
![]()
图 7 TP模型的识别结果及与其他3种脉冲周期识别方法的比较图
Figure 7. Identification of TP identification model and comparison with other identification methods for pulse periods
![]()
图 8 本研究识别的脉冲周期与地震震级的关系及拟合曲线结果对比
Figure 8. Relationship between pulse periods identified in this study and earthquake magnitude and comparison of fitting curves
表 1 ST-CNN模型结构超参数
Table 1 Structural hyperparameters of ST-CNN models
参数 值或函数 输入形式 （100×100，1），
（200×200，1），
（300×300，1）卷积层数量 2，3，4 卷积核数量 32，64，128 卷积核大小 （3×3） 池化层数量 2 池化函数 Maxpooling（2×2） 全连接层数量 4 全连接层神经元数量 32，64，128 激活函数 ReLU，Strict和General识别模型最后一层为Softmax，TP识别模型最后一层无激活函数 
下载: 导出CSV
表 2 最优模型性能表现
Table 2 Performance of optimal models
模型 性能表现 值 Strict
最优识别模型Train CC 0.0657 Val CC 0.1072 Train Acc 0.9991 Val Acc 0.9915 General
最优识别模型Train CC 0.0499 Validation CC 0.0900 Train Acc 0.9995 Val Acc 0.9900 TP
最优识别模型Train MSE 0.0021 Val MSE 0.0252 Train MAE 0.0297 Val MAE 0.0598
下载: 导出CSV
表 3 脉冲周期与地震震级的拟合曲线对比
Table 3 Comparison of fitting curves between pulse periods and earthquake magnitude
下载: 导出CSV
表 4 本文方法运行耗时
Table 4 Time taken to run proposed method
项目 S变换 Strict General TP 耗时/s 0.094 0.071 0.091 0.086
下载: 导出CSV
-
[1] SOMERVILLE P G, SMITH N F, GRAVES R W, et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J]. Seismological Research Letters, 1997, 68(1): 199-222. doi: 10.1785/gssrl.68.1.199
[2] SCHIAPPAPIETRA E, LANZANO G, SGOBBA S. Empirical predictive models for fling step and displacement response spectra based on the NESS database[J]. Soil Dynamics and Earthquake Engineering, 2022, 158: 107294. doi: 10.1016/j.soildyn.2022.107294
[3] 谢俊举, 温增平, 李小军, 等. 基于小波方法分析汶川地震近断层地震动的速度脉冲特性[J]. 地球物理学报, 2012, 55(6): 1963-1972. XIE Junju, WEN Zengping, LI Xiaojun, et al. Analysis of velocity pulses for near-fault strong motions from the Wenchuan earthquake based on wavelet method[J]. Chinese Journal of Geophysics, 2012, 55(6): 1963-1972. (in Chinese)
[4] 谢俊举, 李小军, 温增平. 近断层速度大脉冲对反应谱的放大作用[J]. 工程力学, 2017, 34(8): 194-211. XIE Junju, LI Xiaojun, WEN Zengping. The amplification effects of near-fault distinct velocity pulses on response spectra[J]. Engineering Mechanics, 2017, 34(8): 194-211. (in Chinese)
[5] SHAHI S K, BAKER J W. An empirically calibrated framework for including the effects of near-fault directivity in probabilistic seismic hazard analysis[J]. The Bulletin of the Seismological Society of America, 2011, 101(2): 742-755. doi: 10.1785/0120100090
[6] SHAHI S K, BAKER J W. An efficient algorithm to identify strong-velocity pulses in multicomponent ground motions[J]. The Bulletin of the Seismological Society of America, 2014, 104(5): 2456-2466. doi: 10.1785/0120130191
[7] 梅贤丞, 崔臻, 盛谦. 近断层/远场地震动作用下隧道结构易损性研究[J]. 岩石力学与工程学报, 2021, 40(2): 344-354. MEI Xiancheng, CUI Zhen, SHENG Qian. Research on vulnerability of tunnel structures subjected to near-fault and far-field ground motions[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(2): 344-354. (in Chinese)
[8] MAVROEIDIS G P. A mathematical representation of near-fault ground motions[J]. The Bulletin of the Seismological Society of America, 2003, 93(3): 1099-1131. doi: 10.1785/0120020100
[9] BAKER J W. Quantitative classification of near-fault ground motions using wavelet analysis[J]. The Bulletin of the Seismological Society of America, 2007, 97(5): 1486-1501. doi: 10.1785/0120060255
[10] CHANG Z W, SUN X D, ZHAI C H, et al. An improved energy-based approach for selecting pulse-like ground motions[J]. Earthquake Engineering & Structural Dynamics, 2016, 45(14): 2405-2411.
[11] ZHAI C H, LI C H, KUNNATH S, et al. An efficient algorithm for identifying pulse-like ground motions based on significant velocity half-cycles[J]. Earthquake Engineering & Structural Dynamics, 2018, 47(3): 757-771.
[12] 王东升, 陈笑宇, 张锐, 等. 基于希尔伯特-黄变换的近断层地震动脉冲特性研究[J]. 地震学报, 2022, 44(5): 824-844. WANG Dongsheng, CHEN Xiaoyu, ZHANG Rui, et al. Characteristics of pulses in near-fault ground motion based on Hilbert-Huang transform[J]. Acta Seismologica Sinica, 2022, 44(5): 824-844. (in Chinese)
[13] FUKUSHIMA K. Neocognitron: a self organizing neural network model for a mechanism of pattern recognition unaffected by shift in position[J]. Biological Cybernetics, 1980, 36(4): 193-202. doi: 10.1007/BF00344251
[14] XU Y, WEI S Y, BAO Y Q, et al. Automatic seismic damage identification of reinforced concrete columns from images by a region-based deep convolutional neural network[J]. Structural Control and Health Monitoring, 2019, 26(3): e2313. doi: 10.1002/stc.2313
[15] 姬建, 姜振, 殷鑫, 等. 边坡随机场数字图像特征CNN深度学习及可靠度分析[J]. 岩土工程学报, 2022, 44(8): 1463-1473. doi: 10.11779/CJGE202208011 JI Jian, JIANG Zhen, YIN Xin, et al. Slope reliability analysis based on deep learning of digital images of random fields using CNN[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(8): 1463-1473. (in Chinese) doi: 10.11779/CJGE202208011
[16] MIMOGLOU P, PSYCHARIS I N, TAFLAMPAS I M. Explicit determination of the pulse inherent in pulse-like ground motions[J]. Earthquake Engineering & Structural Dynamics, 2014, 43(15): 2261-2281.
[17] STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.
[18] ZHAI C, CHANG Z, LI S, et al. Quantitative identification of near-fault pulse-like ground motions based on energy[J]. The Bulletin of the Seismological Society of America, 2013, 103(5): 2591-2603.
[19] SOMERVILLE P G. Magnitude scaling of the near fault rupture directivity pulse[J]. Physics of the Earth and Planetary Interiors, 2003, 137(1/2/3/4): 201-212.
[20] TANG Y C, ZHANG J. Response spectrum-oriented pulse identification and magnitude scaling of forward directivity pulses in near-fault ground motions[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(1): 59-76.
-
其他相关附件
计量
- 文章访问数: 301
- HTML全文浏览量: 39
- PDF下载量: 76
