考虑级配影响的盾构泡沫改良粗粒土一维压缩理论计算模型

占永杰; 王树英; 杨秀竹; 王海波

doi:10.11779/CJGE20220657

考虑级配影响的盾构泡沫改良粗粒土一维压缩理论计算模型 English Version

占永杰^{1, 2,},
王树英^{1, 2, ,},
杨秀竹¹,
王海波³

1.
中南大学土木工程学院, 湖南长沙 410075
2.
中南大学隧地工程研究中心, 湖南长沙 410075
3.
中山大学土木工程学院, 广东广州 510275

基金项目:

国家自然科学基金项目 52022112

详细信息

作者简介:
占永杰(1995—)，男，硕士研究生，主要从事盾构渣土改良方面的研究工作。E-mail：yjzhan@csu.edu.cn

通讯作者:
王树英, E-mail: sywang@csu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 338
- HTML全文浏览量: 64
- PDF下载量: 91
出版历程
- 收稿日期: 2022-05-19
- 网络出版日期: 2023-02-23

One-dimensional compression theoretical model for shield foam-conditioned coarse-grained soil considering influences of gradation

ZHAN Yongjie^{1, 2,},
WANG Shuying^{1, 2, ,},
YANG Xiuzhu¹,
WANG Haibo³

1.
School of Civil Engineering, Central South University, Changsha 410075, China
2.
Tunnel and Underground Engineering Research Center, Central South University, Changsha 410075, China
3.
School of Civil Engineering, Sun Yat-Sen University, Guangzhou 510275, China

摘要

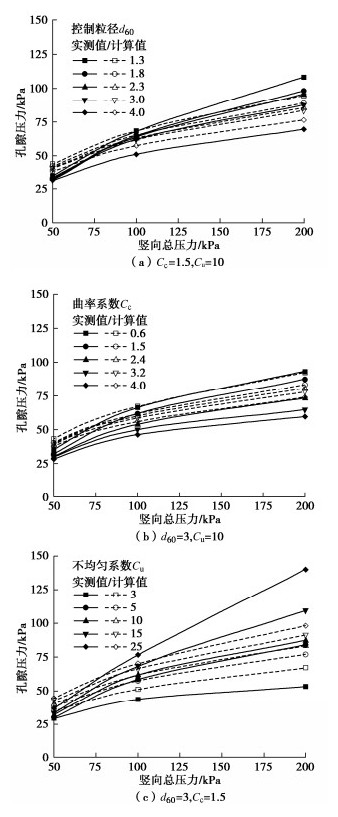
摘要: 盾构渣土在带压情况下会产生孔隙压力，能一定程度上平衡开挖面前方水压力，降低地下水入渗水平，因此盾构渣土一维压缩计算对指导盾构安全掘进具有重要意义。为此，基于波义耳定律和不连续颗粒堆积理论，建立考虑级配参数和渣土改良参数影响的泡沫改良粗粒土一维不排水压缩作用下孔隙压力计算模型。根据泡沫改良土的变形特征，提出初始压缩模量E_s的计算方法，建立泡沫改良土压缩计算模型。进一步地，将泡沫改良土压缩计算模型引入孔压计算模型，提出孔压简便计算模型。为验证一维不排水压缩作用下孔压与压缩计算模型的可靠性，采用自主设计的大型压缩仪对不同级配的泡沫改良粗粒土进行不排水一维压缩试验，获取孔压与压缩实测值。实测值与计算值的对比结果表明，建立的孔压模型和压缩模型能较好的描述不同级配下泡沫改良土的孔压和压缩变化规律，泡沫注入比和土体级配参数均会对泡沫改良土的孔隙压力产生明显影响。
- 土压平衡盾构 /
- 级配 /
- 泡沫改良粗粒土 /
- 孔隙压力 /
- 压缩计算模型
Abstract: Under the state of chamber pressure, the pore pressure of conditioned soil will be generated, and it can balance the water pressure in front of the excavation to reduce the level of groundwater infiltration. Therefore, one-dimensional compression calculation of conditioned soil is of great significance for guiding the safe excavation of shield. Therefore, based on the Boyer' s law and the discontinuous particle accumulation theory, the model for calculating the undrained pore pressure considering gradation parameters and soil-conditioning parameters is established. According to the deformation characteristics of foam-conditioned soil, the method for the initial compression modulus E_s is proposed, and the compression model for the foam-conditioned soil is established. Furthermore, the compression model is introduced into the pore pressure model, and a simple model for the pore pressure is proposed. In order to verify the reliability of the proposed model for the pore pressure and compression, the undrained one-dimensional compression tests on the foam-conditioned coarse-grained soil with different gradations are carried out by using the self-designed large-scale compression devices, and the measured values of pore pressure and compression are obtained. The comparison between the measured and calculated values shows that the pore pressure model and compression model can describe the variation of the pore pressure and compression of foam-conditioned soil under different gradations. The foam injection ratio and gradation have a significant impact on the pore pressure of the foam-conditioned soil.
- earth pressure balance shield /
- gradation /
- foam-conditioned coarse-grained soil /
- pore pressure /
- compression calculation model

HTML全文

0. 引言

顶管法施工是一种暗挖法工法,能够避免对地下构建筑物的破坏,不影响上方道路交通的正常通行,被广泛应用于压力管道,通信和电力等市政管线的铺设安装,以及微型隧道、地下通道和管幕支护结构的施工当中^[1-4]。合理地确定作用于顶管结构的土压力,对注浆压力及顶推力的控制有着重要作用,是顶管工程结构设计以及施工控制中的基本要求。由于开挖造成的地层运动,会使得结构上方土体间发生相对运动,进而使得作用在结构上的垂直土压力要比上覆土体的自重要小^[5-6]。

松动土压力的相关问题一直以来都是岩土工程中的热点问题,在隧道掘进、埋地管道、路堤加固等诸多工程中都有所涉及。Janssen^[7]分析了侧压力系数与摩擦力的关系,通过连续介质力学理论定量分析了筒仓效应。Marston等^[8]针对沟埋式和上埋式管道的特点,考虑了相对滑动造成土体的摩擦作用,对管道上方的土体进行了散体平衡分析,得到了Marston土压力计算公式,之后学者在此基础之上进行了相关探究^[9-10]。Terzaghi^[11]通过活动门试验,验证了土拱效应的存在,采用极限平衡理论推导出了活动门上方的松动土压力计算公式,并得到了广泛应用和深入研究^[12-14]。目前,基于Terzaghi活动门模型的土压力计算方法在顶管工程实践中得到了广泛应用^[15-16],但基于水平微分土条受力平衡分析还存在着不足,其中对土拱滑移面渐进发展过程的研究相对较少,活动门位置深度关系以及土体特性对土拱滑移面形态的影响也有待进一步深入研究。

本文在Terzaghi松动土压力模型的基础之上,结合顶管施工特点,考虑了主应力轴旋转,通过对水平微分土条的受力分析,通过对应力轴偏转角的合理分析,建立了平衡微分方程。分析了土拱的渐进发展中滑移面的偏转过程,并引入等沉面高度对最终稳定状态下的松动土压力进行了分析计算。通过对比分析,验证了计算模型的合理性,并在此基础之上进行了相关的参数分析。

1. 顶管施工中的模型转化

顶管施工过程中造成的地层损失会使得顶管结构上方土体与两侧土体之间发生相对错动,进而形成滑移破坏面,产生土拱效应^[6]。此时两侧滑移面间的土体应力状态也会发生改变,主应力轴在此过程中发生旋转,可将顶管施工中出现的土拱效应转化为经典的Terzaghi活动门模型来进行分析^[11]。

土拱现象的伴随着土体的滑移错动,从开始滑移到最终到达极限平衡状态,是一个渐进发展的过程。Iglesia等^[17-18]通过离心模型试验对活动门下移过程中的应力屈服状态与应力比和滑移面形状的发展过程进行了相对应的分析。图1给出了浅埋条件下滑移面随活动门位移 $δ$ 的偏转变化情况示意图,在起始阶段土体受到轻微扰动尚处于弹性阶段,土体只发生弹性变形并未产生剪切破坏,故无滑移面生成。随着活动门持续下移,部分土体开始出现屈服现象,此时从活动门两边边缘向中心形成抛物线、三角形或者塔型的滑移面。不少学者对活动门边缘滑移面与竖直方向的角度 $α$ 进行了分析,Evans^[19]、Stone等^[20]取 $α = ψ$ （ $ψ$ 为土体剪胀角）；Iglesia等^[18]认为 $α = φ$ （ $φ$ 为土体摩擦角）；Rui等^[21-23]则取 $α = π/ 4 - φ / 2$ 。夹角 $α$ 的大小受到土体膨胀性、应力状态以及密实度等因素的影响^[24],假设初始滑移面为与活动门边缘夹角取 $α = ψ$ 的斜线。随着活动门的下移,松动土体的范围也随着增大,而滑移面逐渐向竖直方向转动,最终滑移面发展为竖直面,即 $α =0$ ,此时土拱发展成为稳定状态,活动门上所受的竖向应力也不再变化。

图 1 浅埋条件下滑移破坏面发展示意图

Figure 1. Development of failure surface with shallow burial depth

下载: 全尺寸图片幻灯片

利用活动门模型来进行顶管施工过程中的上覆土压力计算,另一个需要明确的参数就是滑移面的宽度范围,如图2所示,许多学者针对极限滑移面的起始位置和发展方向进行了研究,随着管节埋置深度的增加,拱效应也会随之增强,滑移面的宽度范围也会随之增长^[25-26]。汪大海等^[27]通过数值模拟分析了埋深比对滑移面宽度范围的影响,认为滑移面的宽度范围应满足

$\begin{array}{l} 2 B = D (H \leq D), \\ 2 B = D + \frac{2 (H - D)}{3} \tan (π / 4 - φ / 2) (D < H \leq 4 D), \\ 2 B = D [1 + 2 \tan (π / 4 - φ / 2)] (H > 4 D) 。 \end{array}}$

(1)

图 2 滑移面的宽度范围（改自文献[28]）

Figure 2. Widths of failure surface in different theories

下载: 全尺寸图片幻灯片

式中 H为管节埋置深度；B为单侧滑移面距管节对称轴的距离；D为开挖面直径。当 $H / D \leq 1$ 时,滑移面范围符合Korner假设；当 $H / D > 4$ 时,滑移面范围符合Terzaghi假设；当 $1 < H / D \leq 4$ 时,滑移面范围在Korner假设与Terzaghi假设之间,且随上覆土厚度增加而增加。

2. 顶管施工中松动土压力计算

2.1 基本假设

分析模型以Terzaghi活动门模型为基础进行分析计算,模型的基本假设为：①滑移面为直线,滑移面形成时,其与竖直方向夹角为ψ,并最终可发展为竖直面的稳定状态；②滑移面处土体的内摩擦角充分发挥,并达到Mohr-Coulomb极限平衡状态；③水平微分土条上应力状态处于同一个莫尔应力圆；④土体均匀且各向同性。

2.2 水平微分土条受力状态

水平微分土条的受力分析是松动土压力计算的基础,如图3所示,由基本假设③,水平微分土条上任意处的应力可由主应力和主应力旋转角表示：

$τ = (σ_{h} - σ_{3}) \tan θ_{i}$ ,

(2)

$σ_{h} = σ_{1} \cos^{2} θ_{i} + σ_{3} \sin^{2} θ_{i}$ ,

(3)

$σ_{v} = σ_{1} \sin^{2} θ_{i} + σ_{3} \cos^{2} θ_{i}$ ,

(4)

$\bar{σ_{v}} = \int_{0}^{B} σ_{v} d x / B = \frac{σ_{1}}{B} \int_{0}^{B} [1 + (K_{a} - 1) \cos^{2} θ_{i}] d x$ 。

(5)

图 3 水平微分土条应力分布图

Figure 3. Distribution of stresses on horizontal soil element

下载: 全尺寸图片幻灯片

式中 $σ_{1}$ 为大主应力； $σ_{3}$ 为小主应力； $σ_{v}$ 为竖向应力； $σ_{h}$ 为侧向应力； $\bar{σ_{v}}$ 为水平微分土条所受竖向平均应力； $τ$ 为剪应力； $θ_{i}$ 为大主应力与水平方向夹角。则任意位置的侧向土压力系数可表示为

$K = \frac{σ_{h}}{σ_{v}} = \frac{\cos^{2} θ_{i} + K_{a} \sin^{2} θ_{i}}{\sin^{2} θ_{i} + K_{a} \cos^{2} θ_{i}}$ ,

(6)

式中, $K_{a} = σ_{3} / σ_{1} = (1 - \sin φ) / (1 + \sin φ)$ , $φ$ 为内摩擦角。

为了表示出水平微分土条的应力状态关系,Handy^[29]将小应力迹线假设为悬链线,由此将土条内不同位置的应力由主应力和主应力旋转角来表示。徐长节等^[30]则将大主应力迹线分别假设为圆弧形、悬链线形、抛物线形,以对水平土条内的土体应力状态进行分析,并得到上凸形的大主应力迹线计算结果更符合实际情况。汪大海等^[31]通过上凸形的大主应力迹线方法,并将 $θ_{i}$ 假设为线性分布,得到水平土条内的土体应力关系。

以对称轴与活动门表面的交点为原点,水平方向为x轴,竖直方向为z轴,将 $θ_{i}$ 假设为双曲正弦曲线,结合剪切面处（x=B时, $θ_{i} = θ_{s}$ ）和对称轴处（x=0时, $θ_{i} = 0$ ）的边界值,则有

$\cos 2 θ_{i} = \frac{2 e \cdot cos 2 θ_{s}}{e^{2} - 1} \sinh \frac{x}{B}$ ,

(7)

式中, $e$ 为自然常数, $θ_{s}$ 为剪切面处大主应力与水平方向夹角。则竖向平均应力可表示为

$\begin{matrix} \bar{σ_{v}} = \frac{σ_{1}}{2 B} \int_{0}^{B} [K_{a} + 1 + (K_{a} - 1) \cos 2 θ_{i}] d x \\ = \frac{σ_{1}}{2} [K_{a} + 1 + \frac{(e - 1) (K_{a} - 1) \cos 2 θ_{s}}{e + 1}] \end{matrix}$ 。

(8)

图4给出了水平微分土条在滑移面的应力状态以及主应力轴偏转状态示意图,根据单元体在水平方向和竖直方向的受力平衡条件可得

$\begin{matrix} τ_{s} S \cos α - σ_{ns} S \sin α \\ = σ_{1} S \cos (θ_{s} + α) \sin θ_{s} - σ_{3} S \sin (θ_{s} + α) \cos θ \end{matrix}$ ,

(9)

$\begin{matrix} σ_{ns} S \cos α + τ_{s} S \sin α \\ = σ_{1} S \cos (θ_{s} + α) \cos θ_{s} + σ_{3} S \sin (θ_{s} + α) \sin θ_{s} \end{matrix}$ 。

(10)

图 4 水平微分土条滑移面应力状态

Figure 4. Stresses on failure surface of horizontal soil element

下载: 全尺寸图片幻灯片

式中 $τ_{s}$ 为滑移面的剪应力； $σ_{ns}$ 为滑移面的法应力；S为滑移面面积。经整理,滑移面上的剪应力 $τ_{s}$ 和法应力 $σ_{ns}$ 可分别表示为

$σ_{ns} = σ_{1} \cos^{2} (θ_{s} + α) + σ_{3} \sin^{2} (θ_{s} + α)$ ,

(11)

$τ_{s} = (σ_{1} - σ_{3}) \cos (θ_{s} + α) \sin (θ_{s} + α)$ 。

(12)

2.3 水平微分土条的平衡微分方程

由于水平微分土条的受力状态具有对称性,由图5可知,以对称轴与活动门表面的交点为原点,水平方向为x轴,竖直方向为z轴,微分土条的受力具有以下平衡关系：

$P_{z} + F_{s} \cdot \cos α = P_{z} + d P_{z} + F_{ns} \cdot \sin α + W$ 。

(13)

图 5 水平微分土条受力分析图

Figure 5. Forces applied to horizontal soil element

下载: 全尺寸图片幻灯片

式中 $P_{z}$ 为z处微分土条的竖向力； $F_{s}$ 和 $F_{ns}$ 分别为微分土条侧向剪切力和法向力；W为微分土条的重力。

$\begin{array}{l} F_{s} = τ_{s} \cdot s = τ_{s} \cdot \sec α \cdot d z, \\ F_{ns} = σ_{ns} \cdot s = σ_{ns} \cdot \sec α \cdot d z, \\ P_{z} = \bar{σ_{v z}} \cdot B_{z} = (B - z \tan α) \bar{σ_{v z}}, \\ \begin{array}{l} d P_{z} = (B - z \tan α) d \bar{σ_{vz}} - \bar{σ_{v z}} \cdot \tan α \cdot d z, \\ W = γ (B - z \tan α - \frac{dz}{2} \tan α) d z 。 \end{array} \end{array}}$

(14)

式中 $\bar{σ_{vz}}$ 为z位置处微分土条的平均竖向应力。由式（8）,（11）,（12）的关系可做如下代换：

$σ_{1} = \frac{2 (e + 1)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ ,

(15)

$σ_{3} = \frac{2 K_{a} (e + 1)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ ,

(16)

$σ_{ns} = \frac{2 (e + 1) [\cos^{2} (θ_{s} + α) + K_{a} \sin^{2} (θ_{s} + α)]}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ ,

(17)

$τ_{s} = \frac{2 (1 - K_{a}) (e + 1) \cos (θ_{s} + α) \sin (θ_{s} + α)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \bar{σ_{v z}}$ 。

(18)

将式（17）,（18）代入式（13）,（14）中,忽略高阶项后整理可得

$\frac{t \bar{σ_{v z}} - γ (B - z \tan α)}{(B - z \tan α)} = \frac{d \bar{σ_{v z}}}{d z}$ ,

(19)

其中,

$\begin{matrix} t = \frac{τ_{s} + \bar{σ_{v z}} \tan α - σ_{ns} \tan α}{\bar{σ_{v z}}} \\ = \frac{2 (1 - K_{a}) (e + 1) \cos (θ_{s} + α) \sin (θ_{s} + α)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} + \tan α - \\ \frac{2 (e + 1) \tan α [K_{a} \cos^{2} (θ_{s} + α) + \sin^{2} (θ_{s} + α)]}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}} \end{matrix}$ 。

(20)

对式（19）进行求解,则其通解可表示为

$\bar{σ_{v z}} = C_{1} {(B - z \tan α)}^{- t \cdot \cot α} + \frac{γ (B - z \tan α)}{t + \tan α}$ 。

(21)

式（21）的解不包含 $α = 0$ （滑移面发展为竖直面）的情况,当 $α = 0$ 时,由式（13）所得的平衡方程可转化为

$\frac{m \bar{σ_{v z}} - γ B}{B} = \frac{d \bar{σ_{v z}}}{d z}$ ,

(22)

其中,

$m = \frac{τ_{s}}{\bar{σ_{v z}}} = \frac{2 (1 - K_{a}) (e + 1) \cos (θ_{s} + α) \sin (θ_{s} + α)}{(K_{a} + 1) (e + 1) + (e - 1) (K_{a} - 1) \cos 2 θ_{s}}$ ,

(23)

其通解为

$\bar{σ_{v z}} = C_{2} e^{\frac{m z}{B}} + \frac{γ B}{m}$

(24)

2.4 滑移面主应力轴偏转角的确定

土拱的形成和发展与地层的变形有着密切联系,一些学者建立了地层沉降量与滑移面主应力轴偏转角的关系^[32-34]：

$θ_{s} = arccot (\frac{4 λ}{1 - 4 λ^{2}})$ ,

(25)

式中, $λ = δ / 2 B$ 为顶部的相对变形量, $δ$ 为活动门位移,即顶管管节拱顶变形量。根据主应力轴偏转角与滑移破坏面的角度关系,可得滑移面与竖直方向的夹角为

$α = π/ 4 + φ / 2 - θ_{s}$ 。

(26)

结合Evans^[19]的试验数据和上文中 $α$ 值的假设条件,参照文献[31]的相关分析,假设滑移面夹角 $α$ 与相对变形量 $λ$ 的关系为

$α = {\begin{cases} ψ - \frac{\arctan (\frac{4 λ}{1 + 4 λ^{2}})}{π / 4} ψ (0 \leq λ < 0.5) \\ 0 (0.5 \leq λ) \end{cases}$ 。

(27)

滑动破坏面形成时,其与竖直方向的初始夹角为土体的剪胀角 $ψ$ ,随着活动门位移的继续增长,滑移破坏面也向竖直方向发生转动,逐渐发展成为竖直面。图6给出了式（27）的计算结果与实测数据对比,验证了该方法能够更好地反映土拱形态与地层变形之间的关系。

图 6 滑移破坏面与竖直方向夹角随变形发展关系

Figure 6. Normalized displacement versus angle between failure surface and vertical plane

下载: 全尺寸图片幻灯片

2.5 平衡方程的边界条件

如图7所示,在土拱的形成过程中,依据相对变形量 $λ$ 和土拱应力比 $η$ 的关系可分为4个阶段^[17-18],Han等^[35]将此过程简化为线性的3阶段模型,而在此简化模型中最小土拱应力比和稳定土拱应力比是模型的关键参数,并可由此表示出土拱的渐进发展过程。其土拱应力比 $η$ 可表示为

$η = {\bar{σ}}_{v z} / γ H$ 。

(28)

图 7 土拱应力比变化示意图(改自文献[35])

Figure 7. Soil-arching ratio versus normalized displacement

下载: 全尺寸图片幻灯片

在活动门发生位移的过程中,在较小的相对变形条件下,活动门上的应力发生显著下降,达到图7中的最小土拱比。此时,管节上方土体开始发生膨胀及相对错动,但并未达到稳定状态。此时滑移破坏面与竖直方向的夹角为 $ψ$ ,滑移面的高度具有以下可能的关系：

（1） $B \cot ψ \geq H$ ,此时破坏面延伸至地表,边界条件为 $z = H$ 时, ${\bar{σ}}_{vz} = 0$ ,则有

$C_{1} = - \frac{γ (B - H \tan α)}{t + \tan α} \cdot {(B - H \tan α)}^{t \cdot \cot α}$ 。

(29)

（2） $B \cot ψ < H$ ,此时破坏面在地表以下形成封闭三角形,由于滑移面处于初始形成状态,滑移面上方土体不能将上方土压力传递到滑移面以下土体,因此边界条件为 $z = B \cdot \cot ψ$ 时, ${\bar{σ}}_{v z} = 0$ ,则 $C_{1} = 0$ 。

随着相对变形量的增长,最终将会到达稳定状态。对于施工深度较浅的工况,通常可认为滑移破坏面延伸至地表。但随着施工深度的不断增加,上方土体的差异沉降逐渐减小,当上方土体高度增加到某一值时,差异沉降消失,这一平面被称之为等沉面,即等沉面上方土体不在发生相对滑动^[36]。此时如果还将滑移破坏面假设延伸至地表,其计算结果与竖向土压力测量值不一致,其计算结果往往不够准确^[5,10,37-38]。

假设施工过程中超挖及顶进偏差造成的地层损失全部由两侧滑移破坏面之间的土体所填补,如图8所示,滑移破坏面的高度则取决于土体的松动情况。可引入土体体积膨胀系数 $β$ 来反映土体的膨胀性^[6],滑移破坏面的高度可认为存在以下近似关系：

$\begin{array}{l} \frac{π}{4} [D^{2} - d^{2}] = \\ β \cdot [H_{e} (2 B - H_{e} \cdot \tan α) + \frac{{(2 B - D)}^{2} \cot ω}{4} + \frac{4 - π}{4} D^{2}] 。 \end{array}$

(30)

图 8 滑移破坏面高度关系示意图

Figure 8. Sketch of failure surface height

下载: 全尺寸图片幻灯片

式中 $β = Δ V / V_{0}$ ,通常砂土取值为0.1～0.18,黏土的取值为0.18～0.4； $H_{e}$ 为滑移破坏面的高度（等沉面高度）；D为开挖面直径；d为顶管结构物直径。

在土体达到稳定状态时,两侧滑移面交点的高度 $B \cot α$ 与等沉面高度 $H_{e}$ 以及上方土体高度H之间可能存在以下关系：

（1） $B \cot α > H$ 且 $H_{e} > H$ ,即破坏面延伸至地表,边界条件为 $z = H$ 时, ${\bar{σ}}_{v z} = 0$ ,此时C₁可按式（29）计算。若 $α$ =0,则有

$C_{2} = - \frac{γ B}{m} e^{- \frac{m H}{B}}$ 。

(31)

（2） $B \cot α > H_{e}$ 且 $H > H_{e}$ ,此时取等沉面高度为临界高度,边界条件为当 $z = H_{e}$ 时, ${\bar{σ}}_{v z} =$ $γ (H - H_{e})$ ,则有

$\begin{matrix} C_{1} = [γ (H - H_{e}) - \frac{γ (B - H_{e} \cdot \tan α)}{t + \tan α}] \cdot \\ (B - H_{e} \cdot \tan α) t \cdot \cot α, \end{matrix}$

(32)

$C_{2} = [γ (H - H_{e}) - \frac{γ B}{m}] \cdot e^{- \frac{m \cdot H_{e}}{B}}$ 。

(33)

3. 模型验证及参数分析

3.1 模型的对比验证

为验证解析解的合理性,本节内容从竖向土压力和侧向土压力两个方面进行对比验证,分别选用土拱应力比 $η$ 和平均侧向压力系数K_avg进行分析,其中侧向压力系数K_avg可表示为

$K_{avg} = \frac{σ_{h}}{{\bar{σ}}_{v z}} = \frac{2 (\cos^{2} θ_{s} + K_{a} \sin^{2} θ_{s})}{K_{a} + 1 + (e - 1) (K_{a} - 1) \cos 2 θ_{s} / (e + 1)}$ 。

(34)

对于最小土拱应力比的计算,此时的土体处于刚发生相对错动的状态,相对变形量很小,滑移破坏面之间土体的填补作用尚未发挥,因此不考虑等沉面高度的影响。在稳定土拱应力比的计算中,此时活动门的相对变形量较大,且滑移破坏面之间土体的填补作用已发挥,需要考虑等沉面的高度关系。Evans^[19]通过一系列的活动门模型试验,对干砂的松动土压力进行来研究,根据相对变形量的关系,计算出来初始倾斜滑移面状态下的最小土拱应力比和稳定状态下的土拱应力比,其中活动门的宽度D为38.1 mm,土体内摩擦角 $φ$ 为38°,从图9可以看出两种状态下的应力比范围与基本覆盖了模型试验的结果,特别是在深埋条件下,最终稳定状态的计算结果与试验结果具有更好的一致性,这也验证了考虑等沉面高度的必要性。

图 9 干砂试验结果与解析解计算结果对比

Figure 9. Comparison between trapdoor test and calculated results

下载: 全尺寸图片幻灯片

图10给出了采用不同理论计算的地基土侧向压力系数,Terzaghi理论认为侧向土压力系数为经验值,并建议取值为1.0。在考虑主应力轴偏转的基础上,侧向压力系数是随着土体摩擦角的变化而发生改变的。陈若曦等^[12]对侧向压力系数的修正中认为在剪切面上的水平向的应力大于竖直向应力,因此其大主应力轴与水平向的夹角小于竖直方向夹角,因此其侧向压力系数数值随摩擦角的增大而增大,区别于其他理论。本文的提出的平均侧向压力系数计算结果与已有的相关研究结果相近,主要区别在于主应力轴偏转角的设定以及偏转角与相对变形量关系的不同。

图 10 侧向土压力系数对比

Figure 10. Comparison of coefficients of lateral earth pressure under different internal friction angle

下载: 全尺寸图片幻灯片

3.2 松动土压力渐进发展过程

在顶管顶进施工过程中,地层损失主要是由超挖间隙和顶进偏差所造成的,因此正常施工条件下的相对变形量是较小的,其值通常不会超过0.1。图11给出了在相对变形量达到0.05,0.075和0.10时达到稳定状态条件下的土拱应力比发展情况,其中管道的外径为2 m,土体内摩擦角 $φ$ 为35°,随着相对变形量的增长,滑移面的偏转角会向竖直方向偏转,同时滑移面的最终长度也随之增加,因此土拱应力比呈下降趋势。而随着埋深比的增加,等效活动门模型中的活动门宽度也随之增加,进而等沉面高度H_e的增量随着埋深比的增长而减小,而土拱应力比的下降趋势也随之放缓。

图 11 土拱应力比随相对变形量发展

Figure 11. Soil-arching ratio versus normalized displacement

下载: 全尺寸图片幻灯片

本文所提出的计算模型考虑了土拱形成的渐进发展过程,从相对滑移形成的初始状态到最终的稳定状态,其中土体相对运动达到稳定状态后的等沉面高度对地层中的应力分布产生了重要影响,如图12所示。由图12可以看出,在等沉面上方土体的平均竖向应力与静止土压力的分布情况相同,在等沉面下方土体的平均竖向应力明显下降,与现有研究的整体趋势相近,计算结果偏高的主要原因正是由于等沉面的存在使得土体滑移破坏面的长度不同,使得平衡方程的边界条件发生变化。

图 12 顶管上方平均竖向应力沿深度方向分布

Figure 12. Distribution of mean vertical stress along depth

下载: 全尺寸图片幻灯片

3.3 剪胀角的影响

剪胀角的大小对土体滑移破坏面的初始形态具有重要影响,当剪胀角角度较大而且管节所处深度较浅的时候,两侧滑移破坏面在地层中有可能出现封闭的三角形。当剪胀角的角度越小,滑移破坏面则越接近竖直面。

如上所述剪胀角的增大会使得滑移破坏面更加倾向于水平方向,在相对变形量等其它条件不变的情况下,等沉面的高度也不会发生变化,因此倾斜角度更大的滑移破坏面,其发生相对摩擦的面积也会更大,土拱应力比也会越低；式（26）给出了滑移面夹角 $α$ 与应力偏转角 $θ_{s}$ 之间的关系,剪胀角越大则 $α$ 的值越大,相应的 $θ_{s}$ 值越小,则由式（34）计算所得的平均侧向土压力系数越大,如图13所示。

图 13 剪胀角与土拱应力比及平均侧向土压力系数的关系

Figure 13. Influences of dilatancy angle on soil-arching ratio and coefficient of lateral earth pressure

下载: 全尺寸图片幻灯片

3.4 内摩擦角的影响

土体的内摩擦角反映土的摩擦特性,土拱效应的本质正是由于土体之间相互错动产生的摩擦力平衡了部分的竖向应力,因此内摩擦角是影响土拱效应的重要因素。

图14给出了土体内摩擦角 $φ$ 与土拱应力比以及侧向土压力系数的关系。随着 $φ$ 值的增大,土体间的摩擦作用增强,土拱效应随之增强,土拱应力比呈现下降趋势；同时,内摩擦角的增大改变了土体的应力状态,其直接体现在 $K_{a}$ 值的减小,但应力偏转角 $θ_{s}$ 随着内摩擦角 $φ$ 的增大而减小,最终 $K_{a}$ 值对平均侧向土压力系数的影响更为显著,因此平均侧向土压力系数随着内摩擦角的增大而减小。

图 14 内摩擦角与土拱应力比及平均侧向土压力系数的关系

Figure 14. Influences of internal friction angle on soil-arching ratio and coefficient of lateral earth pressure

下载: 全尺寸图片幻灯片

4. 结论

本文对砂土地层中的顶管施工中的土拱形成及发展问题进行了探究,并得到以下4点结论。

（1）在Terzaghi松动土压力模型的基础之上,考虑了主应力轴的旋转,通过假设应力偏转角的方式,构造了水平微分土条的微分方程,并结合土拱的渐进发展状态进行求解,经与室内试验的对比分析,验证了解析解的合理性,可为顶管施工中的土压力计算提供参考依据。

（2）分析了土拱的渐进发展过程,建立了相对变形量与滑移面夹角的关系,随着相对变形量的增大,滑移面将逐步向竖直方向偏转,在相对变形充分的条件下最终偏转为竖直滑移面。结合顶管施工的实际,正常施工条件下的开挖地层损失所形成的相对变形量较小,故破坏面的最终形状为塔型。

（3）在土拱的渐进发展过程中,管节顶部的竖向应力在很小的相对变形量范围内发生了显著下降,达到最小土拱应力比。此时,管节上方土体开始发生膨胀及相对错动,破坏面的高度只取决于滑移面倾角和施工深度之间的关系。随着相对变形量的增大,土体达到稳定状态,此时滑移破坏面的高度则需要考虑上方土体的松动情况,其高度取决于等沉面高度、滑移面倾角和施工深度之间的关系。

（4）土体剪胀角的大小对土体滑移破坏面的初始形态具有重要影响,剪胀角的增大会使得滑移破坏面与水平面的夹角减小,增加了滑移摩擦接触面的长度和水平向的应力；土体的内摩擦角则反映了土体的摩擦特性是影响土拱效应的重要因素,内摩擦角的增大,会使得土体间的摩擦作用增强,减小竖向应力,但同时也改变了土体的应力状态,使得平均侧向土压力系数降低。

图 1 试验土样级配曲线

Figure 1. Grain-size distribution curves of various soil specimens

下载: 全尺寸图片幻灯片

图 2 大型压缩仪

Figure 2. Large-scale compression devices

下载: 全尺寸图片幻灯片

图 3 压缩曲线计算值与实测值对比图

Figure 3. Comparison between calculated and measured values of compression curves

下载: 全尺寸图片幻灯片

图 4 孔隙压力计算值与实测值对比图

Figure 4. Comparison between calculated and measured values of pore pressure

下载: 全尺寸图片幻灯片

图 5 孔隙压力计算值与实测值对比图

Figure 5. Comparison between calculated and measured values of pore pressure

下载: 全尺寸图片幻灯片

表 1 土样基本物理参数

Table 1 Basic physical parameters of various soil specimens

工况	d₆₀/ mm	C_c	C_u	干密度/ (g·cm^-3)	最大孔隙比	分类
1	1.3	1.5	10	1.632	0.809	SF
2	1.8	1.5	10	1.648	0.820	SW
3	2.3	1.5	10	1.621	0.877	SW
4	3.0	1.5	10	1.593	0.858	GW
5	4.0	1.5	10	1.623	0.854	GW
6	3.0	0.6	10	1.679	0.784	GP
7	3.0	2.4	10	1.489	0.908	GW
8	3.0	3.2	10	1.456	0.952	GP
9	3.0	4.0	10	1.402	0.990	GP
10	3.0	1.5	3	1.365	1.033	GP
11	3.0	1.5	5	1.493	0.917	GW
12	3.0	1.5	15	1.630	0.761	GW
13	3.0	1.5	25	1.695	0.737	SW

下载: 导出CSV

表 2 发泡及泡沫性能参数

Table 2 Foaming and performance parameters of foam

泡沫剂质量浓度/%	泡沫剂密度/(g·cm^-3)	发泡压力/ MPa	发泡倍率	半衰期/ min
3	1.08	0.3	11	16

下载: 导出CSV

表 3 不同级配泡沫改良土的初始孔隙比与饱和度

Table 3 Initial void ratios and saturations of foam-conditioned soils with different gradations

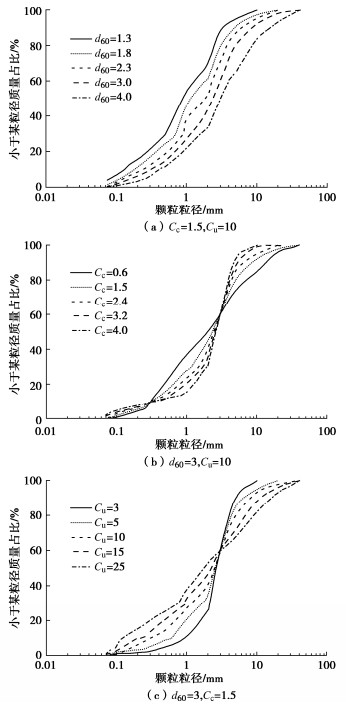
C_c=1.5, C_u=10			d₆₀=3 mm, C_u=10			d₆₀=3 mm, C_c=1.5
d₆₀/mm	${e_0}$	S_r	C_c	${e_0}$	S_r	C_u	${e_0}$	S_r
1.3	0.935	0.2853	0.6	0.985	0.2683	3	1.488	0.1785
1.8	1.027	0.2589	1.5	1.136	0.2340	5	1.251	0.2123
2.3	1.095	0.2429	2.4	1.219	0.2182	10	1.136	0.2340
3.0	1.136	0.2340	3.2	1.282	0.2074	15	1.006	0.2644
4.0	1.289	0.2061	4.0	1.383	0.1923	25	0.905	0.2938

下载: 导出CSV

表 4 不同级配试样粒度分布宽度

Table 4 Grain-size distribution widths of specimens with different gradations

C_c=1.5, C_u=10		d₆₀=3 mm, C_u=10		d₆₀=3 mm, C_c=1.5
d₆₀/mm	m	C_c	m	C_u	m
1.3	1.139	0.6	1.328	3	1.036
1.8	1.188	1.5	1.244	5	1.153
2.3	1.218	2.4	1.492	10	1.244
3.0	1.244	3.2	1.579	15	1.291
4.0	1.296	4.0	1.594	25	1.297

下载: 导出CSV

表 5 不同竖向压力作用下泡沫改良土体积变形量∆V

Table 5 Volume deformations of foam-conditioned soils under different vertical pressures

轴压/ kPa	C_c=1.5, C_u=10					d₆₀=3 mm, C_u=10					d₆₀=3 mm, C_c=1.5
	d₆₀/mm					C_c					C_u
	1.3	1.8	2.3	3	4	0.6	1.5	2.4	3.2	4	3	5	10	15	25
50	32.6	30.7	28.4	25.6	32.6	25.2	25.6	29.1	28.1	29.1	31.6	31.9	25.6	25.5	24.6
100	47.9	44.5	40.5	36.2	47.9	34.2	36.2	41.1	40.0	41.0	45.4	46.0	36.2	35.5	34.8
200	58.2	54.5	49.3	43.4	58.2	41.0	43.4	49.7	48.2	49.6	54.4	57.7	43.4	42.4	41.5

下载: 导出CSV

参考文献(32)

[1]	方勇, 王凯, 陶力铭, 等. 黏性地层面板式土压平衡盾构刀盘泥饼堵塞试验研究[J]. 岩土工程学报, 2020, 42(9): 1651-1658. doi: 10.11779/CJGE202009009 FANG Yong, WANG Kai, TAO Liming, et al. Experimental study on clogging of cutterhead for panel earth-pressure-balance shield tunneling in cohesive strata[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1651-1658. (in Chinese) doi: 10.11779/CJGE202009009
[2]	徐征杰, 郭晓阳. 基于响应面法的盾构施工膨润土改良参数优化[J]. 岩土工程学报, 2021, 43(1): 194-200. doi: 10.11779/CJGE202101023 XU Zhengjie, GUO Xiaoyang. Optimization of bentonite parameters for shield tunneling based on response surface method[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 194-200. (in Chinese) doi: 10.11779/CJGE202101023
[3]	黄硕. 盾构泡沫改良粗颗粒渣土渗流时变性及其理论预测方法研究[D]. 长沙: 中南大学, 2020: 34-36. HUANG Shuo. Research on Time Variation and Theoretical Prediction Method of Permeation Characteristics for Foam-conditioned Coarse-grained Soil in EPB Shield Tunneling[D]. Changsha: Central South University, 2020: 34-36. (in Chinese)
[4]	王树英, 刘朋飞, 胡钦鑫, 等. 盾构隧道渣土改良理论与技术研究综述[J]. 中国公路学报, 2020, 33(5): 8-34. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202005002.htm WANG Shuying, LIU Pengfei, HU Qinxin, et al. State-of-the-art on theories and technologies of soil conditioning for shield tunneling[J]. China Journal of Highway and Transport, 2020, 33(5): 8-34. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202005002.htm
[5]	贺少辉, 张淑朝, 李承辉, 等. 砂卵石地层高水压条件下盾构掘进喷涌控制研究[J]. 岩土工程学报, 2017, 39(9): 1583-1590. doi: 10.11779/CJGE201709005 HE Shaohui, ZHANG Shuchao, LI Chenghui, et al. Blowout control during EPB shield tunnelling in sandy pebble stratum with high groundwater pressure[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(9): 1583-1590. (in Chinese) doi: 10.11779/CJGE201709005
[6]	HUANG S, WANG S Y, XU C J, et al. Effect of grain gradation on the permeability characteristics of coarse-grained soil conditioned with foam for EPB shield tunneling[J]. KSCE Journal of Civil Engineering, 2019, 23(11): 4662-4674. doi: 10.1007/s12205-019-0717-7
[7]	WANG H B, WANG S Y, ZHONG J Z, et al, 2021. Undrained compressibility characteristics and pore pressure calculation model of foam-conditioned sand[J]. Tunnelling and Underground Space Technology, 118: 104161.
[8]	SILLS G C, WHEELER S J, THOMAS S D, et al. Behaviour of offshore soils containing gas bubbles[J]. Géotechnique, 1991, 41(2): 227-241. doi: 10.1680/geot.1991.41.2.227
[9]	HUARES B, RICO R. Mecanica de Suelos[M]. 3rded. Mexico: LIMUSA, 1980: 456-466. HUARES B, RICO R. Soil Mechanics[M]. 3rded. Mexico: LIMUSA, 1980: 456-466. (in Spanish)
[10]	林成功, 吴德伦. 非饱和黏土孔隙压力计算与实验研究[J]. 岩土工程学报, 2002, 24(5): 605-607. http://www.cgejournal.com/cn/article/id/11045 LIN Chenggong, WU Delun. Pore-pressure theory and experimental research for non-saturated clay[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 605-607. (in Chinese) http://www.cgejournal.com/cn/article/id/11045
[11]	HU Q X, WANG S Y, QU T M, et al. Effect of hydraulic gradient on the permeability characteristics of foam-conditioned sand for mechanized tunnelling[J]. Tunnelling and Underground Space Technology, 2020, 99: 103377.
[12]	LING F L, WANG S Y, HU Q X, et al. Effect of bentonite slurry on the function of foam for changing the permeability characteristics of sand under high hydraulic gradients[J]. Canadian Geotechnical Journal, 2022, 59(7): 1061-1070.
[13]	DANG T S, MESCHKE G. Influence of muck properties and chamber design on pressure distribution in EPB pressure chambers–Insights from computational flow simulations[J]. Tunnelling and Underground Space Technology, 2020, 99: 103333.
[14]	李一凡, 王俊刚, 徐仁宇, 等. 砂土孔隙压力影响因素的试验研究[J]. 山东理工大学学报(自然科学版), 2021, 35(4): 50-55. LI Yifan, WANG Jungang, XU Renyu, et al. Experimental study on factors affecting pore pressure of sand[J]. Journal of Shandong University of Technology (Natural Science Edition), 2021, 35(4): 50-55. (in Chinese)
[15]	陈正汉, 郭楠. 非饱和土与特殊土力学及工程应用研究的新进展[J]. 岩土力学, 2019, 40(1): 1-54. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201901002.htm CHEN Zhenghan, GUO Nan. New developments of mechanics and application for unsaturated soils and special soils[J]. Rock and Soil Mechanics, 2019, 40(1): 1-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201901002.htm
[16]	刘兴荣, 崔鹏, 王飞, 等. 不同粒径级配条件下工程弃渣泥石流启动机理研究[J]. 工程地质学报, 2018, 26(6): 1593-1599. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201806021.htm LIU Xingrong, CUI Peng, WANG Fei, et al. Study on the threshold motion mechanism of engineering slag debris flow with different particle size grading conditions[J]. Journal of Engineering Geology, 2018, 26(6): 1593-1599. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201806021.htm
[17]	FURNAS C C. Stock distribution and gas-solid contact in the blast furnace[J]. Bureau of Mines Reports of Investigation, 1928: 8-18.
[18]	CUBRINOVSKI M, ISHIHARA K. Maximum and minimum void ratio characteristics of sands[J]. Soils and Foundations, 2002, 42(6): 65-78.
[19]	张世文, 张立平, 袁君, 等. 基于分形理论和地质统计学的表层土壤颗粒大小分布变化特征[J]. 中国农业科学, 2014, 47(13): 2591-2601. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNYK201413011.htm ZHANG Shiwen, ZHANG Liping, YUAN Jun, et al. Characterizing variation of topsoil particle size distribution based on fractal theory and geostatistics[J]. Scientia Agricultura Sinica, 2014, 47(13): 2591-2601. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNYK201413011.htm
[20]	张程林. 级配颗粒堆积体密度估算方法研究[D]. 广州: 华南理工大学, 2013. ZHANG Chenglin. Study on the Calculation Method of Graded Granular Particle Packing Density[D]. Guangzhou: South China University of Technology, 2013. (in Chinese)
[21]	白雪梅, 赵松山. 浅谈算术平均数的作用[J]. 浙江统计, 2000(11): 12-13. https://www.cnki.com.cn/Article/CJFDTOTAL-ZJTJ200011005.htm BAI Xuemei, ZHAO Songshan. On the function of arithmetic average[J]. Zhe Jiang Statistics, 2000(11): 12-13. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZJTJ200011005.htm
[22]	杨光华. 现代地基设计理论的创新与发展[J]. 岩土工程学报, 2021, 43(1): 1-18. doi: 10.11779/CJGE202101001 YANG Guanghua. Innovation and development of modern theories for foundation design[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 1-18. (in Chinese) doi: 10.11779/CJGE202101001
[23]	彭长学, 杨光华. 软土e-p曲线确定的简化方法及在非线性沉降计算中的应用[J]. 岩土力学, 2008, 29(6): 1706-1710. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200806059.htm PENG Changxue, YANG Guanghua. A simplified method for determining e-p curve of soft soil and its application to analyzing nonlinear settlement of foundation[J]. Rock and Soil Mechanics, 2008, 29(6): 1706-1710. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200806059.htm
[24]	曹文贵, 李鹏, 张超, 等. 土的初始和再压缩曲线分析模型[J]. 岩石力学与工程学报, 2015, 34(1): 166-173. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501018.htm CAO Wengui, LI Peng, ZHANG Chao, et al. Analysis models of initial compression and recompression curves of soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 166-173. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501018.htm
[25]	BEZUIJEN A, SCHAMINEE P, KLEINJAN J A. Additive testing for earth pressure balance shields[C]// Geotechnical Engineering for Transportation Infrastructure: Theory and Practice, Planning and Design, Construction and Maintenance Vol. 3. Delft Geotechnics, Delft, Netherlands, 1999: 1-12.
[26]	MORI L S, MOONEY M, CHA M S. Characterizing the influence of stress on foam conditioned sand for EPB tunneling[J]. Tunnelling and Underground Space Technology, 2018, 71: 454-465.
[27]	土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Geotechnical Testing Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[28]	PSOMAS S. Properties of Foam/Sand Mixtures for Tunnelling Applications[D]. Oxford: University of Oxford, 2001.
[29]	PEÑA D M Á. Foam as a Soil Conditioner in Tunnelling: Physical and Mechanical Properties of Conditioned Sands[D]. Oxford: University of Oxford, 2007.
[30]	岩土工程仪器基本参数及通用技术条件: GB/T 15406—2007[S]. 北京: 中国标准出版社, 2007. Primary Parameter and General Specification for Geotechnical Engineering Instrument: GB/T 15406—2007[S]. Beijing: Standards Press of China, 2007. (in Chinese)
[31]	WU Y L, NAZEM A, MENG F Y, et al. Experimental study on the stability of foam-conditioned sand under pressure in the EPBM chamber[J]. Tunnelling and Underground Space Technology, 2020, 106: 103590.
[32]	宗睿, 徐飞鹏, 贾瑞卿, 等. 一种土壤水分传感器性能测试的方法及应用[J]. 灌溉排水学报, 2013, 32(1): 74-76. https://www.cnki.com.cn/Article/CJFDTOTAL-GGPS201301017.htm ZONG Rui, XU Feipeng, JIA Ruiqing, et al. A test method of soil moisture sensor[J]. Journal of Irrigation and Drainage, 2013, 32(1): 74-76. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GGPS201301017.htm

施引文献

资源附件(1)

其他相关附件
- PDF格式
  11-202308-G22-0657一文审稿意见与作者答复点击下载(690KB)

图(5) / 表(5)

计量

文章访问数: 338
HTML全文浏览量: 64
PDF下载量: 91
被引次数: 0

0. 引言
1. 顶管施工中的模型转化
2. 顶管施工中松动土压力计算
2.1 基本假设
2.2 水平微分土条受力状态
2.3 水平微分土条的平衡微分方程
2.4 滑移面主应力轴偏转角的确定
2.5 平衡方程的边界条件
3. 模型验证及参数分析
3.1 模型的对比验证
3.2 松动土压力渐进发展过程
3.3 剪胀角的影响
3.4 内摩擦角的影响
4. 结论

0. 引言
1. 顶管施工中的模型转化
2. 顶管施工中松动土压力计算
2.1 基本假设
2.2 水平微分土条受力状态
2.3 水平微分土条的平衡微分方程
2.4 滑移面主应力轴偏转角的确定
2.5 平衡方程的边界条件
3. 模型验证及参数分析
3.1 模型的对比验证
3.2 松动土压力渐进发展过程
3.3 剪胀角的影响
3.4 内摩擦角的影响
4. 结论

参考文献(32)

施引文献

资源附件(1)

考虑级配影响的盾构泡沫改良粗粒土一维压缩理论计算模型 English Version

作者简介: 占永杰(1995—)，男，硕士研究生，主要从事盾构渣土改良方面的研究工作。E-mail：yjzhan@csu.edu.cn

通讯作者: 王树英, E-mail: sywang@csu.edu.cn

计量

出版历程

One-dimensional compression theoretical model for shield foam-conditioned coarse-grained soil considering influences of gradation

0. 引言

1. 顶管施工中的模型转化

2. 顶管施工中松动土压力计算

2.1 基本假设

2.2 水平微分土条受力状态

2.3 水平微分土条的平衡微分方程

2.4 滑移面主应力轴偏转角的确定

2.5 平衡方程的边界条件

3. 模型验证及参数分析

3.1 模型的对比验证

3.2 松动土压力渐进发展过程

3.3 剪胀角的影响

3.4 内摩擦角的影响

4. 结论

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 顶管施工中的模型转化

2. 顶管施工中松动土压力计算

2.1 基本假设

2.2 水平微分土条受力状态

2.3 水平微分土条的平衡微分方程

2.4 滑移面主应力轴偏转角的确定

2.5 平衡方程的边界条件

3. 模型验证及参数分析

3.1 模型的对比验证

3.2 松动土压力渐进发展过程

3.3 剪胀角的影响

3.4 内摩擦角的影响

4. 结论

作者简介:
占永杰(1995—)，男，硕士研究生，主要从事盾构渣土改良方面的研究工作。E-mail：yjzhan@csu.edu.cn

通讯作者:
王树英, E-mail: sywang@csu.edu.cn