基于状态空间法的阶梯型变截面水平受荷桩分析方法

张晓笛; 王金昌; 杨仲轩; 龚晓南; 徐荣桥

doi:10.11779/CJGE20220384

基于状态空间法的阶梯型变截面水平受荷桩分析方法 English Version

张晓笛^{1, 2,},
王金昌^{1, 2, ,},
杨仲轩^{1, 3},
龚晓南^{1, 2},
徐荣桥^{1, 3}

1.
浙江大学建筑工程学院, 浙江杭州 310058
2.
浙江大学平衡建筑研究中心, 浙江杭州 310058
3.
公路数智养护浙江省工程研究中心, 浙江杭州 310051

基金项目:

浙江省“尖兵”“领雁”研发攻关计划项目 2022C03180

浙江省交通运输厅项目 ZJXL-JTT-202201A，202303

国家自然科学基金项目 52078457

浙江大学浙江交工协同创新联合研究中心研发项目 2021001

详细信息

作者简介:
张晓笛(1997—)，女，硕士研究生，主要从事土与结构相互作用的研究。E-mail：zxd6814@zju.edu.cn

通讯作者:
王金昌, E-mail: wjc501@zju.edu.cn

中图分类号: TU473
计量
- 文章访问数: 370
- HTML全文浏览量: 64
- PDF下载量: 124
出版历程
- 收稿日期: 1952-04-01
- 网络出版日期: 2023-09-06
- 刊出日期: 2023-08-31

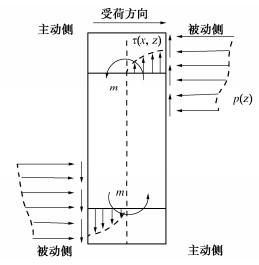
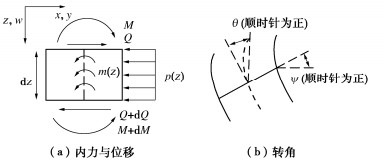
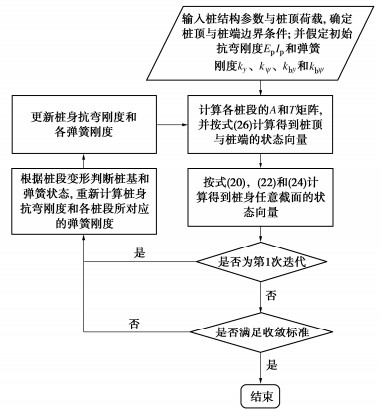
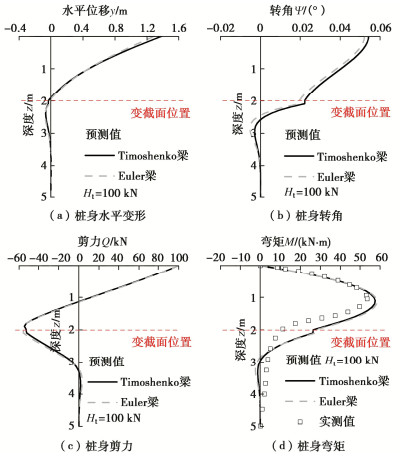
Analytical solutions for laterally loaded step-tapered piles by state space method

ZHANG Xiaodi^{1, 2,},
WANG Jinchang^{1, 2, ,},
YANG Zhongxuan^{1, 3},
GONG Xiaonan^{1, 2},
XU Rongqiao^{1, 3}

1.
College of Civil Engineering, Zhejiang University, Hangzhou 310058, China
2.
Center for Balance Architecture, Zhejiang University, Hangzhou 310058, China
3.
Zhejiang Provincial Engineering Research Center for Digital & Smart Maintenance of Highway, Hangzhou 310051, China

摘要

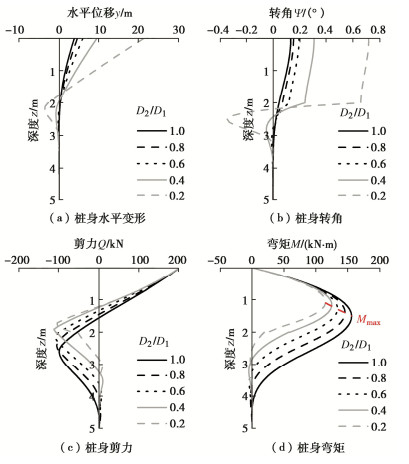
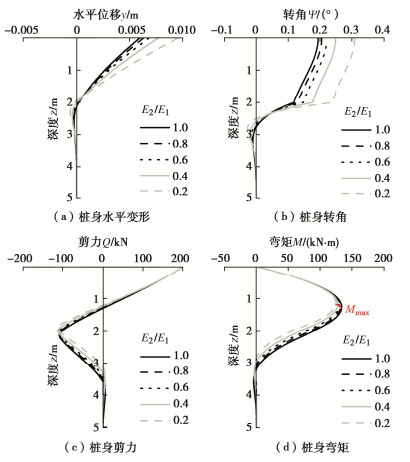
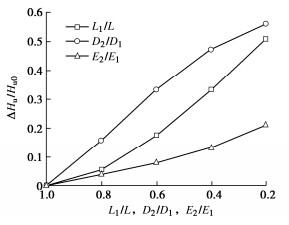
摘要: 为研究阶梯型变截面桩的水平承载特性，基于Timoshenko梁理论，建立了综合考虑桩基尺寸效应、剪切变形和桩基材料非线性效应的四弹簧模型及其状态方程，获得了非线性桩土相互作用下任意长细比的桩截面内力与变形解析解。通过与已有文献中现场试验结果对比分析，验证该方法的适用性和有效性，并讨论了变径位置、桩径比和弹性模量比对桩基受荷特性的影响。研究结果表明：①桩基水平承载力对三者的敏感性为：桩径比 > 变径位置 > 弹性模量比；②综合考虑桩承载能力和经济性，建议变径位置、桩径比和弹性模量比取0.6。
- 阶梯型变截面桩 /
- 水平受荷 /
- 桩土相互作用 /
- Timoshenko梁 /
- 四弹簧模型 /
- 状态空间法
Abstract: To analyze the response of laterally loaded step-tapered piles, a four-spring model is proposed based on the Timoshenko beam theory considering the effects of pile diameter, shear deformation and nonlinear pile material behavior. The analytical solutions for the internal forces and deformations with arbitrary slenderness ratio can be derived by the state space method considering the nonlinear pile–soil interaction. The solutions are validated through the available field test results in the literatures. Furthermore, the influences of pile parameters, such as the variation position of the diameter, diameter ratio and Young's modulus ratio, on the pile loading responses are proposed. The results show that: (1) The sensitivity of these parameters follows the descending order: pile diameter ratio > variation position of pile diameter > Young's modulus ratio. (2) After trade-off between the pile lateral bearing capacity and the cost, it is suggested that the optimal variation position of the diameter, the pile diameter ratio and Young's modulus ratio should be set as 0.6.
- step-tapered pile /
- lateral load /
- pile-soil interaction /
- Timoshenko beam /
- four-spring model /
- state space method

HTML全文

0. 引言

不排水不排气条件下的非饱和土力学特性与公路、铁路、机场、水利、建筑等行业实际工程问题紧密相关，伴随中国基建高速发展的步伐，非饱和土不排水不排气剪切条件下的变形、强度、回弹模量变化特性研究显得较为重要。近年来非饱和土理论、试验、工程方面得到了高速发展。如陈正汉等^[1]以压实黄土为对象，系统研究了非饱和黄土渗气性、渗水性、孔隙水压和孔隙气压在三轴不排水不排气剪切过程中的演化特性，苗强强等^[2]对广佛高速非饱和含黏砂土的水气运移规律和力学特性进行了系统研究，杨松等^[3]对云南非饱和红黏土的不排气、不排水三轴剪切特性进行了试验研究，刘文化等^[4]借助于数值模拟研究了不排水条件下非饱和土水力-力学耦合特性对非饱和土的不排水、不排气三轴剪切特性进行预测，詹良通等^[5]对深圳花岗岩风化料弃土快速堆填过程中不排水抗剪强度进行了评估。与此同时，回弹模量的测定和取值研究也是国内外众多道路科研机构和施工单位长期关切的问题。2002年，由美国材料试验协会（ASTM）举办路面材料回弹模量研讨出版了论文集^[6]。在AASHTO2002路面设计指南中^[7]，考虑了湿度对路基回弹模量的影响。WAI用干湿循环模拟路基土湿度变化^[8-9]，湿度增大，路基回弹模量减小；干湿循环对路基回弹模量也有影响。杨树荣等^[10]利用MTS动力三轴试验系统，探讨了非饱和黏性路基土之回弹模量特性及基质吸力对回弹模量之影响。李丹枫等^[11]提出了基于便携式落锤弯沉仪模量控制的路基承载力动态力学指标评价方法。刘君等^[12]对3类计算模型的可靠性及适用性进行对比评价。

综合国内外研究现状，对非饱和土不排水不排气三轴剪切试验孔压、体变、回弹模量等特性演化过程和机理研究还相对滞后并缺少相关配套仪器设备支撑研究试验。故本文使用自行改进的循环加卸载非饱和土三轴仪系统，探讨高速公路车辆运行过程中含黏砂土在不同含水率和压实度不排水不排气条件下，强度、变形和回弹模量变化特性。

1. 试验设备

试验设备系在后勤工程学院非饱和土三轴仪^[1]的基础上改进而成的循环加卸载非饱和土三轴仪系统（图 1）。该仪器主要组成部分有非饱和土三轴双层压力室、加卸载系统、围压控制系统、反压控制系统及数据采集系统等，主要部件的特色简介如下。

图 1 不排水不排气非饱和土三轴试验系统

Figure 1. Triaxial test system for undrained and unvented unsaturated soil

下载: 全尺寸图片幻灯片

（1）双层压力室，分为内压力室和外压力室，通过量测内压力室的水量变化计算试样的体积变化。内压力室试样底座上安装有高进气值陶土板，陶土板下面有螺旋槽，用以冲洗陶土板下面的气泡。

（2）轴向加载装置，采用活塞式加荷器，由空气压缩机提供压力源，用高精度气压调压阀和精密气压表控制施加的气压力。试验前用量力环对加荷器的输出压力进行了标定。加荷器可提供0~30 kN的轴向压力，相应的偏应力为0~2500 kPa。

（3）微型压力传感器（气压和水压）（图 2）。探头直径都是3 mm，用黏结剂胶接在外直径8 mm的空心螺母中。螺母下端约2 mm长的一段，用以保护传感器探头。气压传感器的引线从三轴仪底座原来安装排水管出口的地方引出。把量测气压的微型传感器装在试样帽上，从而提高了量测气压的精度，并实现了试样的小型化，这是该设备的一个重要特色。

图 2 微型压力传感器

Figure 2. Micro-sensors

下载: 全尺寸图片幻灯片

（4）数字应变仪（图 1），分别与孔隙水压力传感器和孔隙气压力传感器连接（图 2），采集孔压数据。试验前对微型传压力感器进行了标定，传感器与应变仪在工作中性能稳定，外界干扰对其几乎无影响，压力和输出数值之间有良好的线性关系，传感器的标定曲线如图 3所示。

图 3 传感器标定

Figure 3. Calibration of sensors

下载: 全尺寸图片幻灯片

2. 试验研究方案

本文以广州—佛山高速公路路基含黏砂土为研究对象，其物性指标如表 1所示。该土的最优含水率为13.63%，最大干密度为1.89 g/cm³。

表 1 试验所用含黏砂土的颗粒组成^[13]

Table 1. Grain sizes of clayey sand used in tests^[13]

G_s	颗粒组成/%
G_s	> 2 mm	0.5~2 mm	0.2~0.5 mm	0.2~0.075 mm	< 0.075 mm
2.68	10.39	19.58	32.46	22.75	14.82

下载: 导出CSV

| 显示表格

研究试样为重塑土样。采用后勤工程学院的重塑土制样设备和模具，把预先配制成一定含水率的土料分5层压实。试样的直径为39.1 mm，高80 mm。共做了2类21个试验：①12个不排水不排气三轴剪切试验，控制1.85 g/cm³，含水率分别为10.47%，13.63%，14.5%和16.02 %，控制分别围压为50，100，200 kPa；②9个循环加卸载条件下回弹模量试验，干密度控制为1.70，1.80，1.85 g/cm³分别对应压实度90%，95%和98%；对每一干密度配制3个含水率：10.47%，13.63%和16.02%；，试验控制围压100 kPa，最大偏应力200 kPa，采用应力控制式分6级进行加卸载。

第1类试验是为了探讨压实度和含水率在最优含水率附近变动对该土变形强度的影响，试样初始吸力为50 kPa。考虑到施加围压后试样体积压缩，饱和度提高，吸力有所降低，故可用传感器直接量测。若对含水率更低试样进行不排水剪切试验，量测吸力就需采用轴平移技术，施加适当的气压力使水压力变为正值或大于-70 kPa进行测定。为了与控制吸力的三轴试验相区别，将不排水不排气试验的围压称为总围压，用 ${\sigma _3}$ 表示；相应的，将该试验的平均应力称为总平均应力，用p表示。剪切速率为0.015 mm/min，剪切至轴向应变达15%需要13.5 h。

3. 试验结果及分析

3.1 不排水不排气三轴剪切试验

是干密度为1.85 g/cm³的砂土在不同含水率、不排水不排气条件下，在 ${p_{\text{f}}}$ – ${q_{\text{f}}}$ 平面内的强度包络线关系曲线，含水率相同、不同净围压的一组实验几乎在同一直线上，可由式（1），（2）和（3）描述。

$p = \frac{{{\sigma _1} + {\sigma _2} + {\sigma _3}}}{3} {, }$

(1)

$q = {\sigma _1} - {\sigma _3} {, }$

(2)

${q_{\text{f}}} = \xi + {p_{\text{f}}}\tan \varpi 。$

(3)

图 4

${p_{\text{f}}}$ –

${q_{\text{f}}}$ 平面内的强度包络线

Figure 4. Curves of strength on

${p_{\text{f}}}$ –

${q_{\text{f}}}$ plane

下载: 全尺寸图片幻灯片

式中p，q分别为总平均应力和偏应力； ${\sigma _1}$ ， ${\sigma _2}$ 和 ${\sigma _3}$ 是3个总主应力。 ${p_{\text{f}}}$ 破坏时总平均应力， ${q_{\text{f}}}$ 破坏时偏应力， $\xi$ 和 $\tan \varpi$ 分别为 ${p_{\text{f}}}$ – ${q_{\text{f}}}$ 平面上直线的截距和斜率。

土的不排水不排气内摩擦角、黏聚力分别由下式得出

$\sin {\varphi _{{\text{uu}}}} = \frac{{3\tan \varpi }}{{6 + \tan \varpi }} {, }$

(4)

${c_{{\text{uu}}}} = \frac{{3 - \sin {\varphi _{{\text{uu}}}}}}{{6\cos {\varphi _{{\text{uu}}}}}} 。$

(5)

为含黏砂土的 ${c_{{\text{uu}}}}$ –w关系曲线，由可知，在最优含水率范围，随含水率的增加，黏聚力增加，超过最优含水率后，随含水率的提高，黏聚力逐渐减小；为含黏砂土的 ${\varphi _{{\text{uu}}}}$ –w关系曲线，由图 6可知，在小于最优含水率时，随含水率的增加内摩擦角增大，但变化较小。超过最优含水率后，随含水率的提高，内摩擦角急剧减小。图 5，6共同反应了最优含水率是黏聚力和内摩擦角发生变化的临界值。

图 5 c_uu–w关系曲线

Figure 5. Relationship between c_uu and w

下载: 全尺寸图片幻灯片

图 6

${\varphi _{{\text{uu}}}}$ –w关系曲线

Figure 6. Relationship between

${\varphi _{{\text{uu}}}}$ and w

下载: 全尺寸图片幻灯片

图 7为不同含水率时孔隙水压力和孔隙气压力随轴向应变的变化曲线，其中，图中实心符号为气压力，空心符号为水压力。图 7可知，孔隙气压力和孔隙水压力与试样的体变密切相关，试样的体变峰值点基本上对应于孔隙气压力峰值点；剪缩时孔隙气压力升高，剪胀时孔隙气压降低。含水率越大，孔隙中水分就越多，气体占据量就较少，在相同围压作用下，含水率越大试样的初始孔隙压力也就越大。随试样剪切的进行，孔隙水压力和孔隙气压力都先增大再减小；伴随剪胀的发生，孔隙气压力与孔隙水压力曲线逐渐分开，这是由于发生剪胀，含水率不变，体积增大，相应基质吸力也增大；在相同含水率时，净围压越大，孔隙气压力和孔隙水压力也越大。

图 7 孔隙压力–轴向应变关系曲线^[2]

Figure 7. Relationship between pore pressure and axial strain ^[2]

下载: 全尺寸图片幻灯片

由图 7（a）可以看出，3组数据气压力出现峰值早于孔隙水压力，图 7（b）几乎相同，图 7（c）孔隙水压力略早于孔隙气压力，图 7（d）明显的是孔隙水压力出现的峰值早于孔隙气压力，而本文的试样最优含水率是13.63%，出现这种现象的原因可能是在最优含水率之前土样内部流体形式是气相占优，主要决定因素是气相，而水相可能不连续，当气相气压力稳定之后挤压水相，最终水相也达到峰值点；处于最优含水率时水气两相均连续分布较好，当外力作用时，两者同时达到峰值点；当水相占优势时和气相占优势同理孔隙水压力到达峰值点先于孔隙气压力。

3.2 循环加卸载条件下回弹模量试验

在不排水不排气剪切过程中，每个试样进行两次加卸载循环，采用加卸载应力–应变滞回圈上下两端点的连线AC的斜率表示回弹模量，如图 8（a）所示。回弹模量用式（6）计算。

${E_{\text{t}}} = \frac{{\Delta \sigma }}{{\Delta \varepsilon }} {, }$

(6)

图 8 含水率10.47 %时2次循环加卸载剪应力与轴向应变关系^[2]

Figure 8. Relationship between shear stress and axial strain under 2 loading-unloading cycles and of 10.47% water content^[2]

下载: 全尺寸图片幻灯片

式中， ${E_{\text{t}}}$ 回弹模量， $\Delta \sigma$ 循环加卸载中应力变化， $\Delta \varepsilon$ 循环加卸载中应变变化。

图 8为含水率10.47%时，初始压实度分别为98%，95%和90%的3个土样，经过2次循环加卸载时应力应变曲线。由图 8可以得出，相同含水率不同压实度的试样，压实度越大，试样首次加载到200 kPa时曲线越陡；滞回圈长轴连线（第一次卸载和第二次加载交点连线）斜率数值越大；随着压实度的减小，滞回圈轴向的斜率越来越小。

图 9，10分别为含水率13.63%和16.02%时，初始压实度分别为98%，95%和90%的3个试样经过2次循环加卸载时应力–应变曲线图。由该图可清晰看出，相同含水率不同压实度的试样反映的规律和图 8规律基本一致。这说明含水率一定时，压实度越大试样的回弹模量数值越大；在试验加卸载范围内，压实度小的试样所对应的滞回圈长轴连线的斜率越小；在试验含水率范围，含水率相同时，不同压实度试样回弹模量最大相差不超过2倍。从图 8~10和表 2可看出相同压实度，不同含水率的试样回弹模量相差较大，含水率10.47%和含水率16.02 %的两种土样回弹模量最大可相差接近5倍，这说明含水率对回弹模量的影响较为显著。

图 9 含水率13.63 %时2次循环加卸载剪应力与轴向应变关系^[2]

Figure 9. Relationship between shear stress and axial strain under 2 loading-unloading cycles and water content of 13.63%^[2]

下载: 全尺寸图片幻灯片

图 10 含水率16.02%时2次循环加卸载剪应力与轴向应变关系^[2]

Figure 10. Relationship between shear stress and axial strain under 2 loading-unloading cycles and water content of 16.02%^[2]

下载: 全尺寸图片幻灯片

表 2 回弹模量汇总

Table 2. Values of resilience modulus (MPa)

压实度/%	含水率/%
压实度/%	10.47	13.63	16.02
98	40.48	24.48	8.55
95	31.76	16.33	7.78
90	24.69	12.56	5.68

下载: 导出CSV

| 显示表格

为了更深入分析三者之间的关系，将压实度与回弹模量之间采用线性关系，将含水率与回弹模量之间的关系假定为指数函数关系，其关系表达为

$\frac{{{E_{\text{t}}}}}{{10{p_{\text{a}}}}} = A + B\lambda + C\exp \left( {\frac{{(w - D)}}{F}} \right) {, }$

(7)

式中， ${E_{\text{t}}}$ 回弹模量，单位为MPa， ${p_{\text{a}}}$ 为标准大气压约等于0.1 MPa， $\lambda$ 为压实度用百分数表示，w为含水率用百分数表示，A，B，C，D，F分别为与含水率、压实度相关的拟合系数。

将含水率、压实度和回弹模量试验数据，采用origin2016自定义函数非线性多元方式（即式（7））进行拟合，得到含水率、压实度与回弹模量之间的函数关系的具体表达式如式（8）所示。其中A= -139.295，B=1.395，C=114.742，D=3.569，F=6.896，R² =0.9121。

$\frac{{E}_{\text{t}}}{10{p}_{\text{a}}}=-139.295+1.395\lambda +114.72\mathrm{exp}\left(-\frac{(w-3.569)}{6.896}\right)。$

(8)

式（8）拟合的曲面与试验数值之间的关系如图 11所示，拟合曲面与试验数值较为接近，拟合效果较好，说明本文所提含水率、压实度、回弹模量的函数表达式是可行的，有一定的实际推广价值和工程应用前景。

图 11 含水率、压实度与回弹模量拟合与试验数据关系图

Figure 11. Relationship between fitting and test data of moisture content, compaction degree and resilience modulus

下载: 全尺寸图片幻灯片

4. 结论

（1）改进的非饱和土应力控制式三轴仪系统能够满足研究非饱和土在不排水不排气条件下的强度、变形、孔压演化和循环加卸载的回弹模量试验的要求。

（2）最优含水率是土样内摩擦角、黏聚力、破坏形态发生变化的临界值；剪胀强弱与围压和含水率有密切关系，围压越大、含水率越高，剪胀性越小；随剪切的进行，孔隙水压力和孔隙气压力都先增大再减小；伴随剪胀的发生，孔隙气压力与孔隙水压力曲线逐渐分开，吸力增大。

（3）通过对试验数据分析，构建了含水率、压实度、回弹模量之间的多元非线性函数表达式，拟合结果和试验数据较为接近。

（4）非饱和含黏砂土含水率和压实度均对回弹模量有显著影响，且含水率的影响远大于干密度的影响。故在公路建设施工中，在确保压实度满足工程要求的前提下，选择合适的含水率甚为重要。

图 1 阶梯型变截面桩分析模型

Figure 1. Analytical model for step-tapered pile

下载: 全尺寸图片幻灯片

图 2 侧摩阻力分布示意图

Figure 2. Sketch of distribution of vertical shaft shear stress

下载: 全尺寸图片幻灯片

图 3 梁单元内力与变形示意图

Figure 3. Internal forces and deformations of a beam element

下载: 全尺寸图片幻灯片

图 4 桩身响应计算流程图

Figure 4. Flow chart for calculation of pile response

下载: 全尺寸图片幻灯片

图 5 本文方法与试验数据的对比

Figure 5. Comparison between proposed analytical method and field test data

下载: 全尺寸图片幻灯片

图 6 本文方法与试验的荷载-位移响应对比

Figure 6. Comparison of load-displacement responses between proposed analytical method and field test data

下载: 全尺寸图片幻灯片

图 7 桩截面弯矩-曲率关系

Figure 7. Relationship between moment and curvature of pile section

下载: 全尺寸图片幻灯片

图 8 本文方法与试验的荷载-位移响应对比

Figure 8. Comparison of load-displacement responses between proposed analytical method and field test data

下载: 全尺寸图片幻灯片

图 9 H_t=200 kN时不同变径位置下桩身受荷响应

Figure 9. Pile responses under different L₁/L (H_t=200 kN)

下载: 全尺寸图片幻灯片

图 10 H_t=200 kN时不同桩径比下桩身受荷响应

Figure 10. Pile responses under different D₂/D₁ (H_t= 200 kN)

下载: 全尺寸图片幻灯片

图 11 H_t=200 kN时不同弹性模量比下桩身受荷响应

Figure 11. Pile responses under different E₂/E₁ (H_t= 200kN)

下载: 全尺寸图片幻灯片

图 12 L₁/L, D₂/D₁和E₂/E₁与∆H_u/H_u0的关系

Figure 12. Relationship among L₁/L, D₂/D₁, E₂/E₁ and ∆H_u/H_u0

下载: 全尺寸图片幻灯片

表 1 桩顶与桩端的约束边界条件

Table 1 Boundary conditions of pile head and end

桩顶/端	约束形式	边界条件
桩顶	自由	${M_{1,0}}{\text{ = }}{M_{\text{t}}},{\text{ }}{Q_{1,0}}{\text{ = }}{H_{\text{t}}}$
桩顶	固支	${\psi _{1,0}}{\text{ = }}0,{\text{ }}{Q_{1,0}}{\text{ = }}{H_t}$
桩端	自由	${M_{n,1}}{\text{ = }}{M_{\text{b}}},{\text{ }}{Q_{n,1}}{\text{ = }}{H_{\text{b}}}$
	铰接	${y_{n,1}}{\text{ = }}0,{\text{ }}{M_{n,1}}{\text{ = }}0$
	固支	${\psi _{n,1}}{\text{ = }}0,{\text{ }}{y_{n,1}}{\text{ = }}0$

下载: 导出CSV

参考文献(27)

[1]	ISMAEL N F. Behavior of step tapered bored piles in sand under static lateral loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(5): 669-676. doi: 10.1061/(ASCE)GT.1943-5606.0000265
[2]	常林越, 王金昌, 朱向荣, 等. 双层弹塑性地基水平受荷桩解析计算[J]. 岩土工程学报, 2011, 33(3): 433-440. http://www.cgejournal.com/cn/article/id/13959 CHANG Linyue, WANG Jinchang, ZHU Xiangrong, et al. Analytical calculation of laterally loaded piles in double-layered elastoplastic soils[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 433-440. (in Chinese) http://www.cgejournal.com/cn/article/id/13959
[3]	ZHU M X, ZHANG Y B, GONG W M, et al. Generalized solutions for axially and laterally loaded piles in multilayered soil deposits with transfer matrix method[J]. International Journal of Geomechanics, 2017, 17(4): 4016104-4016122. doi: 10.1061/(ASCE)GM.1943-5622.0000800
[4]	胡文韬, 刘豆, 耿大新, 等. 水平受荷阶梯形变截面桩的内力及变形分析[J]. 浙江大学学报(工学版), 2020, 54(4): 739-747. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202004014.htm HU Wentao, LIU Dou, GENG Daxin, et al. Internal force and deformation of step-tapered pile under lateral loads[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(4): 739-747. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202004014.htm
[5]	李丹, 简迪, 吴卓尔, 等. 三级阶梯型变截面嵌岩桩的承载特性研究[J]. 岩土力学, 2020(增刊2): 1-8. LI Dan, JIAN Di, WU Zhuoer, et al. Research on bearing characteristics of three-stage stepped rock-socketed piles[J]. Rock and Soil Mechanics, 2020(S2): 1-8. (in Chinese)
[6]	HAN J, FROST J D. Load-Deflection response of transversely isotropic piles under lateral loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(5): 509-529. doi: 10.1002/(SICI)1096-9853(20000425)24:5<509::AID-NAG79>3.0.CO;2-9
[7]	竺明星, 龚维明, 卢红前, 等. 考虑侧阻与端阻影响的基桩水平承载力传递矩阵解[J]. 工程力学, 2018, 35(增刊1): 230-238. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2018S1040.htm ZHU Mingxing, GONG Weiming, LU Hongqian, et al. Transfer matrix solutions for lateral behavior of pile foundation considering the skin and end resistance effect[J]. Engineering Mechanics, 2018, 35(S1): 230-238. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2018S1040.htm
[8]	竺明星, 戴国亮, 龚维明, 等. 水平荷载下桩身侧阻抗力矩的作用机制与计算模型研究[J]. 岩土力学, 2019, 40(7): 2593-2607, 2662. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907013.htm ZHU Mingxing, DAI Guoliang, GONG Weiming, et al. Mechanism and calculation models of resisting moment caused by shaft resistance for laterally loaded pile[J]. Rock and Soil Mechanics, 2019, 40(7): 2593-2607, 2662. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907013.htm
[9]	BYRNE B W, HOULSBY G T, BURD H J, et al. PISA design model for monopiles for offshore wind turbines: application to a stiff glacial clay till[J]. Géotechnique, 2020, 70(11): 1030-1047.
[10]	LIANG F Y, LI Y C, LI L, et al. Analytical solution for laterally loaded long piles based on fourier–laplace integral[J]. Applied Mathematical Modelling, 2014, 38(21/22): 5198-5216.
[11]	WANG J C, HUANG W M, XU R Q, et al. Analytical solution for segmental tunnel lining incorporating interaction between adjacent rings[J]. Journal of Engineering Mechanics, 2020, 146(7): 04020075-04020091.
[12]	ZHANG X D, WANG J C, CHEN Q J, et al. Analytical method for segmental tunnel linings reinforced by secondary lining considering interfacial slippage and detachment[J]. International Journal of Geomechanics, 2021, 21(6): 4021084.
[13]	REESE L, VAN I W, HOLTZ R. Single piles and pile groups under lateral loading[J]. Applied Mechanics Reviews, 2002, 55(1): B9-B10.
[14]	API (American Petroleum Institute). Recommended Practice Planning, Designing, and Constructing Fixed Offshore Platforms-Working Stress Design[S]. Washington D C: API Recommended Practice 2A-WSD, 2014.
[15]	俞剑, 黄茂松, 李森, 等. 黏土中海上风电水平受荷大直径单桩设计方法的思考[J]. 海洋开发与管理, 2018, 35(增刊1): 34-39. https://www.cnki.com.cn/Article/CJFDTOTAL-HKGL2018S1007.htm YU Jian, HUANG Maosong, LI Sen, et al. Thinking on design method of laterally loaded large diameter monopile for offshore wind turbines in clay[J]. Ocean Development and Management, 2018, 35(S1): 34-39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKGL2018S1007.htm
[16]	ZHANG Y H, ANDERSEN K H. Soil reaction curves for monopiles in clay[J]. Marine Structures, 2019, 65: 94-113.
[17]	MAHESHWARI B K, and WATANABE H. Nonlinear dynamic behavior of pile foundations: effects of separation at the soil-pile interface[J]. Soils and Foundations, 2006, 46(4): 437-448.
[18]	ASHOUR M, HELAL A. Contribution of vertical skin friction to the lateral resistance of large-diameter shafts[J]. Journal of Bridge Engineering, 2014, 19(2): 289-302.
[19]	RONDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1978, 104(12): 1465-1488.
[20]	WANG L Z, LAI Y Q, HONG Y, et al. A unified lateral soil reaction model for monopiles in soft clay considering various length-to-diameter (L/D) ratios[J]. Ocean Engineering, 2020, 212: 107492-107506.
[21]	王伯惠, 上官兴. 中国钻孔灌注桩新发展[M]. 北京: 人民交通出版社, 1999: 89-90. WANG Bohui, SHANGGUAN Xing. New Development of Bored pile in China[M]. Beijing: China Communications Press, 1999: 89-90. (in Chinese)
[22]	公路桥涵地基与基础设计规范: JTG 3363—2019[S]. 北京: 人民交通出版社, 2019. Specifications for Design of Foundation of Highway Bridges and Culverts: JTG 3363—2019[S]. Beijing: China Communications Press, 2019. (in Chinese)
[23]	GEROLYMOS N, GAZETAS G. Static and dynamic response of massive caisson foundations with soil and interface nonlinearities—validation and results[J]. Soil Dynamics and Earthquake Engineering, 2006, 26(5): 377-394.
[24]	KO J, JEONG S. Plugging effect of open-ended piles in sandy soil[J]. Canadian Geotechnical Journal, 2015, 52(5): 535-547.
[25]	REESE L C, WANG S T. Analysis of piles under lateral loading with nonlinear flexural rigidity[C]// Proceedings of International Conference on Design and Construction of Deep Foundation, Orlando, 1994.
[26]	COWPER G R. The shear coefficient in Timoshenko's beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 335-340.
[27]	WANG L Z, HE B, HONG Y, et al. Field tests of the lateral monotonic and cyclic performance of jet grouting Reinforced cast-in-place piles[J]. Journal of Geotechnica and Geoenvironmental Engineering, 2015, 141(5): 06015001.

施引文献

资源附件(1)

其他相关附件
- PDF格式
  20-202309-G22-0384一文审稿意见与作者答复点击下载(500KB)

图(12) / 表(1)

计量

文章访问数: 370
HTML全文浏览量: 64
PDF下载量: 124
被引次数: 0

0. 引言
1. 试验设备
2. 试验研究方案
3. 试验结果及分析
3.1 不排水不排气三轴剪切试验
3.2 循环加卸载条件下回弹模量试验
4. 结论

基于状态空间法的阶梯型变截面水平受荷桩分析方法 English Version

作者简介: 张晓笛(1997—)，女，硕士研究生，主要从事土与结构相互作用的研究。E-mail：zxd6814@zju.edu.cn

通讯作者: 王金昌, E-mail: wjc501@zju.edu.cn

计量

出版历程